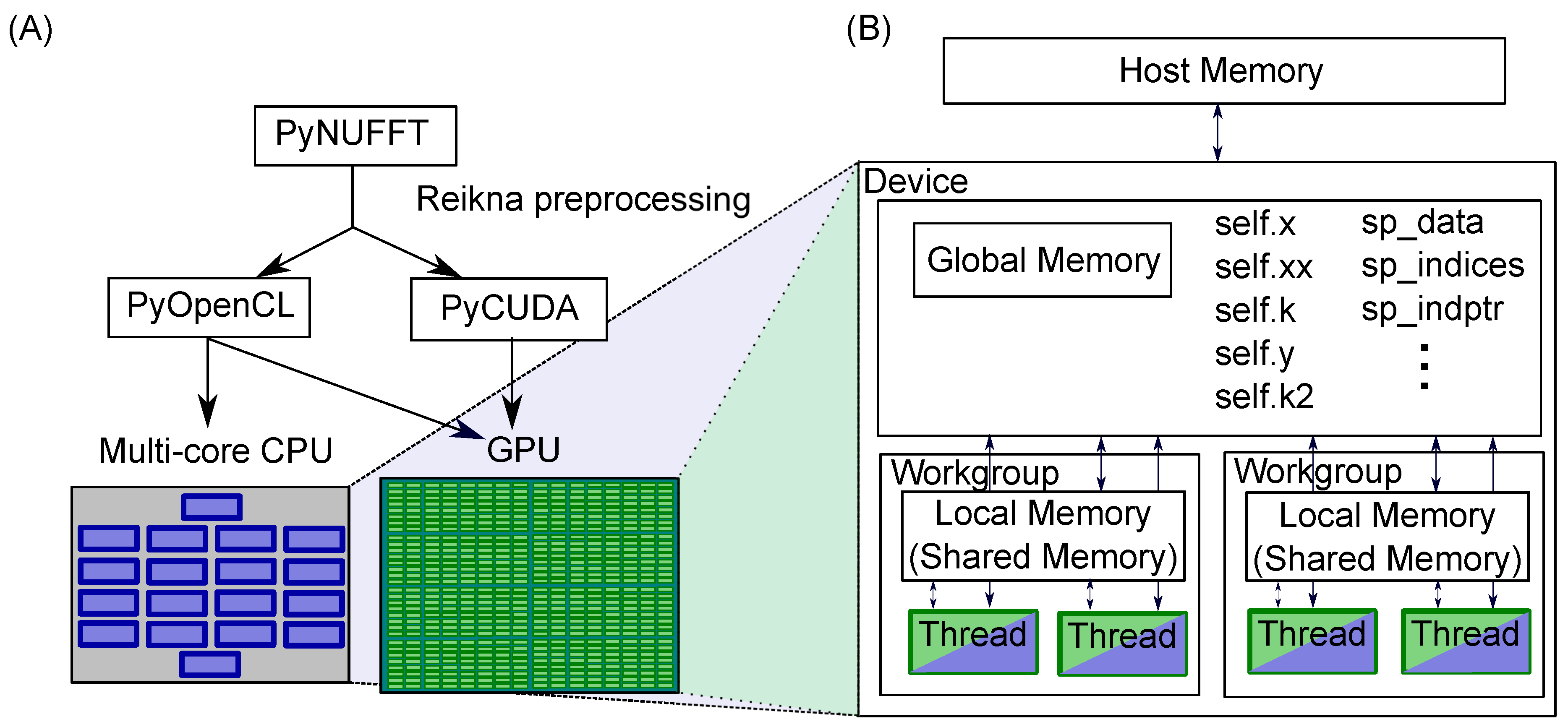
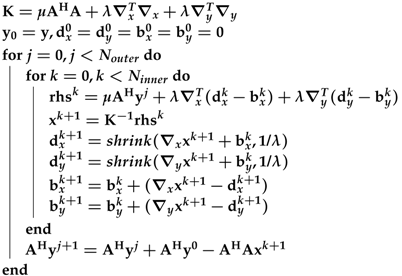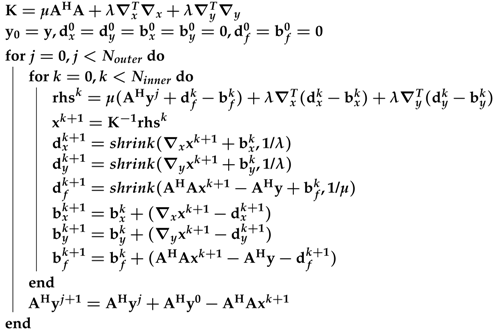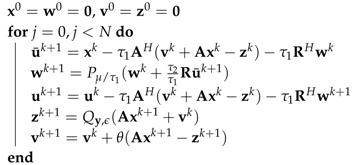Python Non-Uniform Fast Fourier Transform (PyNUFFT): An Accelerated Non-Cartesian MRI Package on a Heterogeneous Platform (CPU/GPU)
Abstract
1. Introduction
2. Materials and Methods
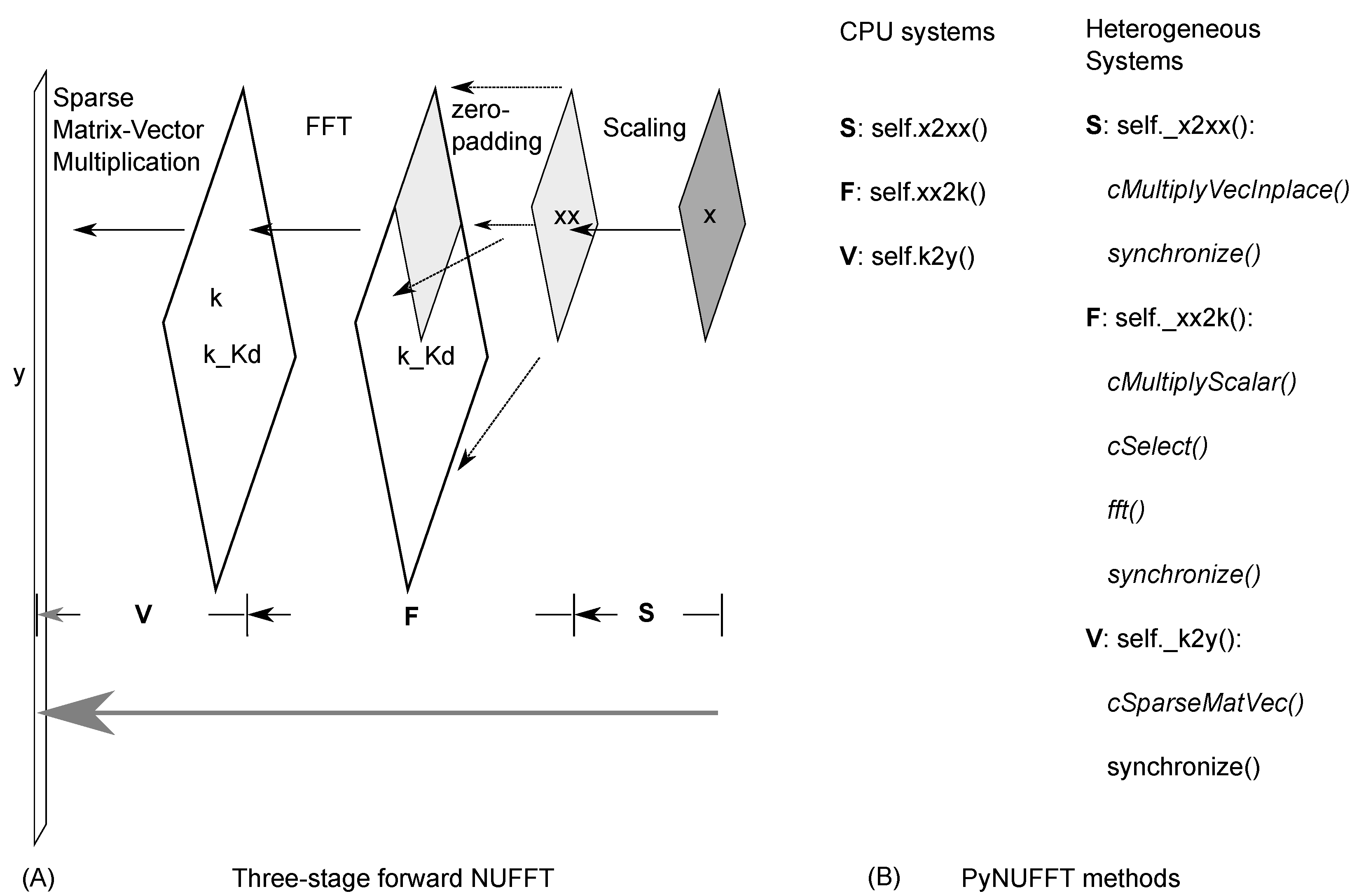
2.1. PyNUFFT: An NUFFT Implementation in Python
2.1.1. Scaling
2.1.2. Oversampled FFT
2.1.3. Interpolation
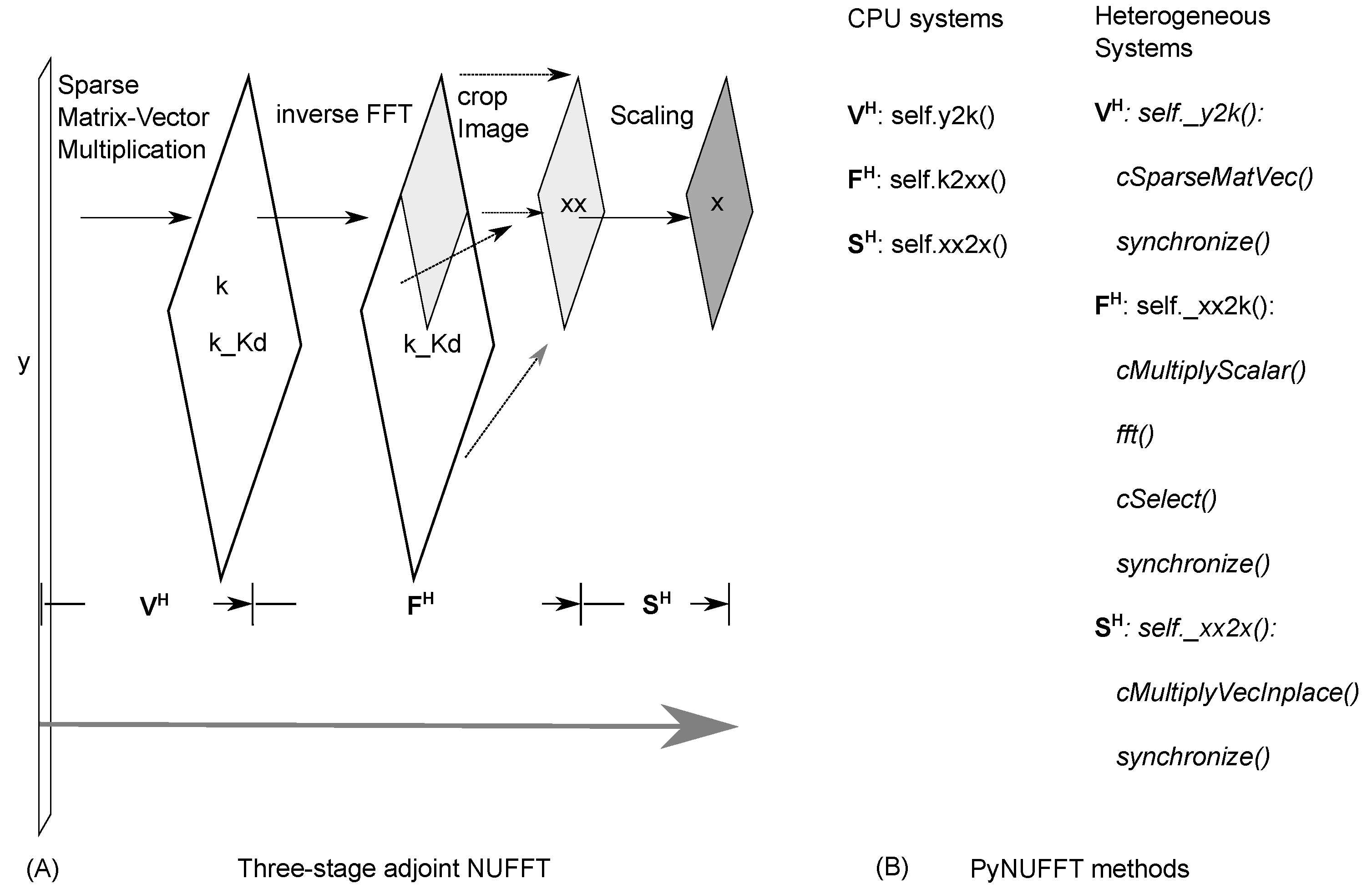
2.1.4. Adjoint PyNUFFT
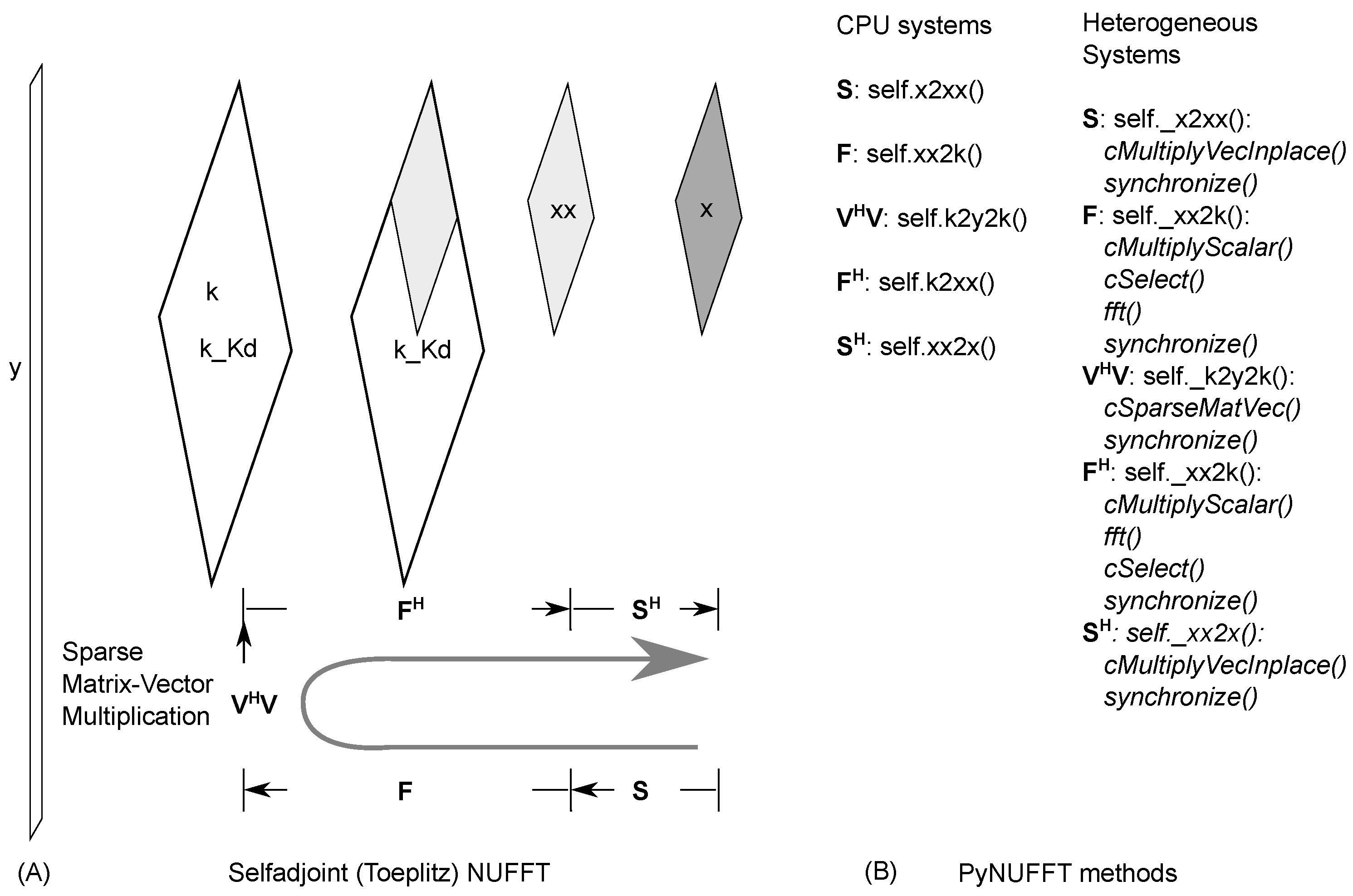
2.1.5. Self-Adjoint NUFFT (Toeplitz)
2.2. Solver
2.2.1. Density Compensation and Adjoint NUFFT
2.2.2. Least Square Regression
- Conjugate gradient method (cg): For Equation (7) there is the two-step solution:Once has been solved, the inverse of can be computed by the inverse FFT and then divided by the scaling factor:The most expensive step is to find in Equation (8). The conjugate gradient method is an iterative solution when the sparse matrix is a symmetric Hermitian matrix:Then each iteration generates the residue, which is used to compute the next value. The conjugate gradient method is also provided for heterogeneous systems.
- Other iterative methods for least-squares problems: Scipy [9] provides a variety of least square solvers, including Sparse Equations and Least Squares (lsmr and lsqr), biconjugate gradient method (bicg), biconjugate gradient stabilized method (bicgstab), generalized minimal residual method (gmres), and linear solver restarted generalized minimal residual method (lgmres). These solvers are integrated into the CPU version of PyNUFFT.
2.2.3. Iterative NUFFT Using Variable Splitting
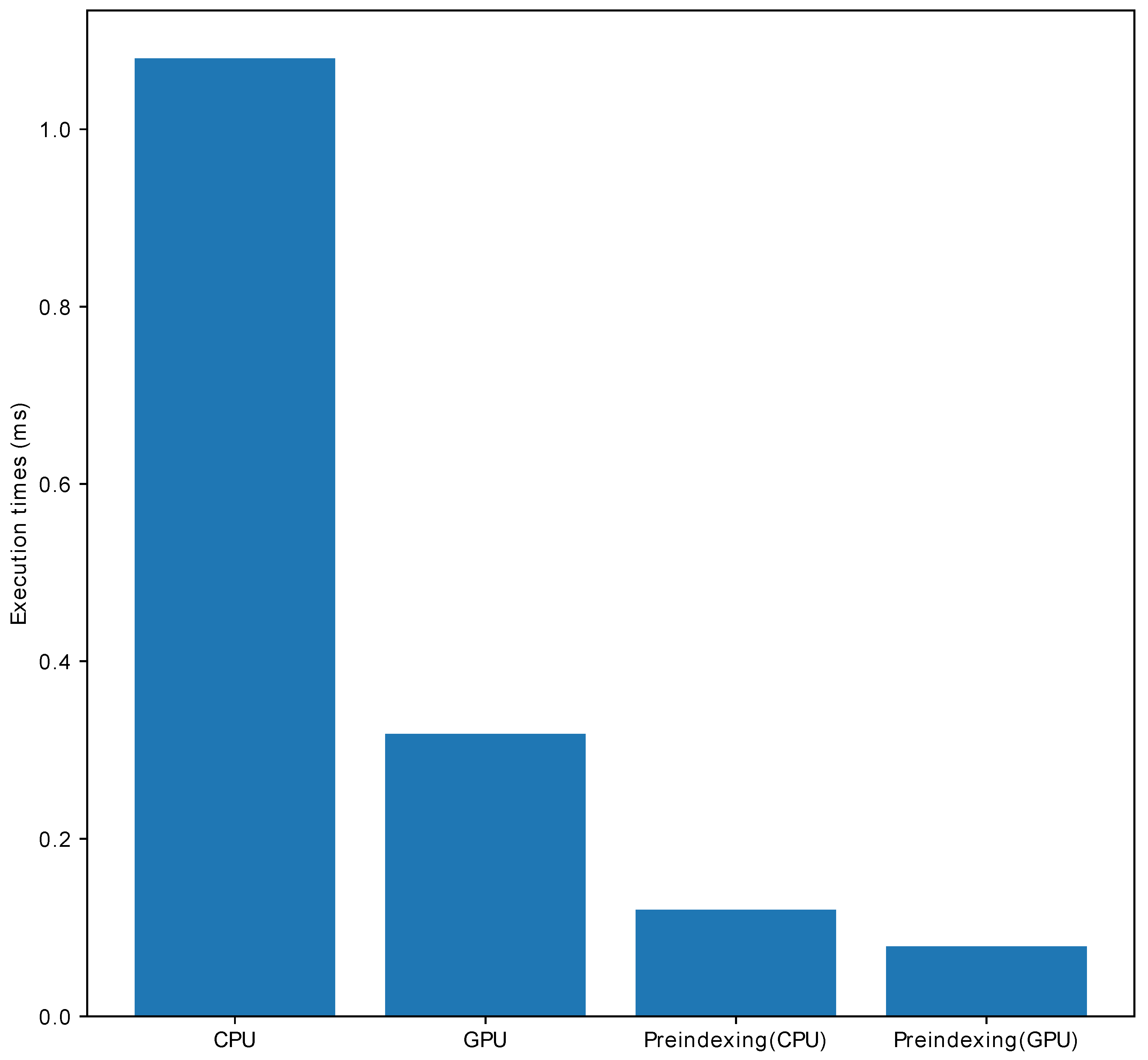
- Pre-indexing for fast image gradients: Total variation in basic image regularization has been extensively used in image denoising and image reconstruction. The image gradient is computed using the difference between adjacent pixels, which is represented as follows:where is the index of the i-th axis. Computing the image gradient requires image rolling, followed by a subtraction of the original image and the rolled image. However, multidimensional image rolling in heterogeneous systems is expensive and PyNUFFT adopts pre-indexing to save runtime. This pre-indexing procedure generates the indexes for the rolled image, and the indexes are offloaded to heterogeneous platforms before initiating the iterative algorithms. Thus, image rolling is not needed during the iterations. The acceleration of this pre-indexing method is demonstrated in Figure 3, in which pre-indexing makes the image gradient run faster on the CPU and GPU.
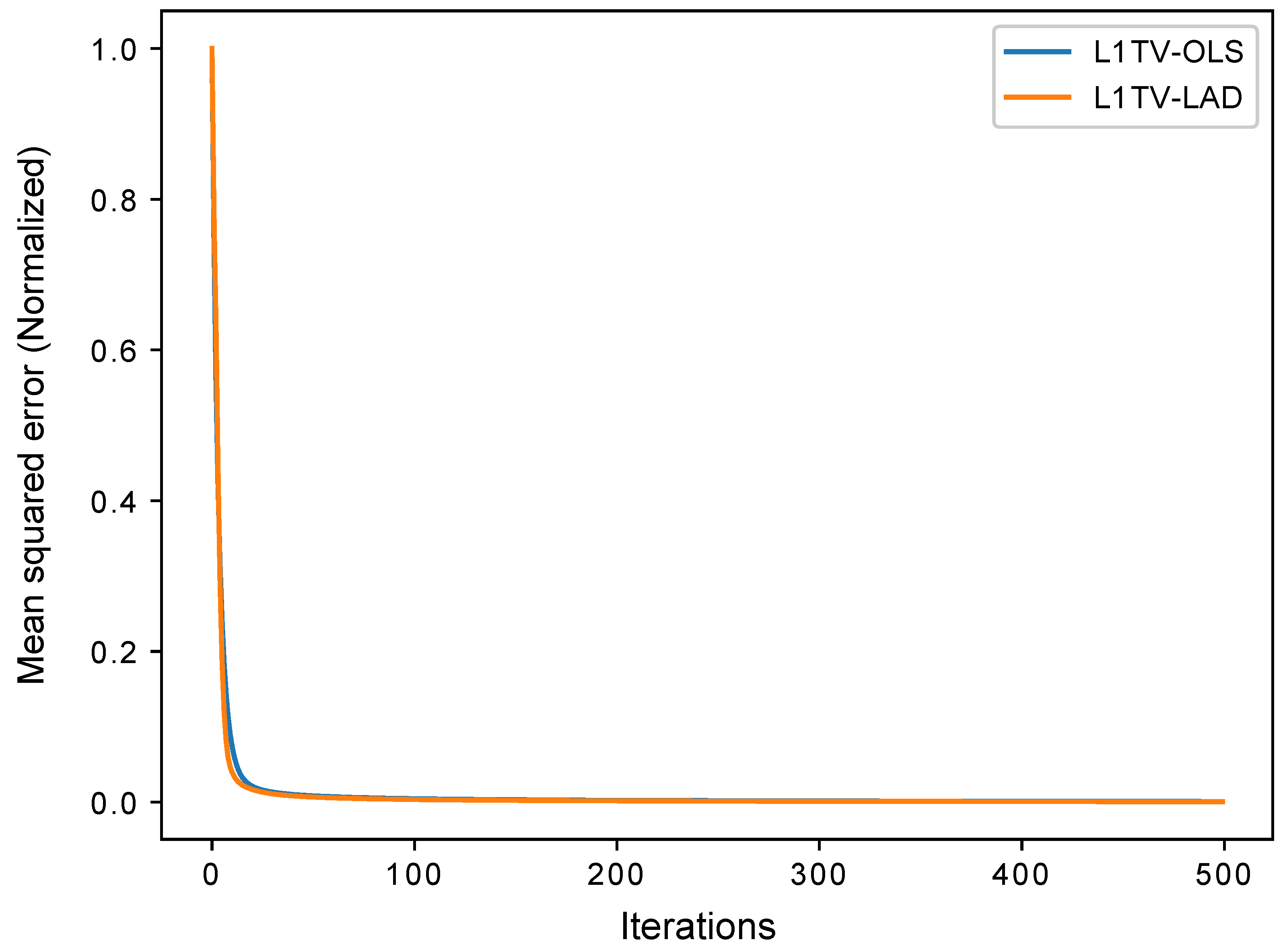
- ℓ1 total variation-regularized ordinary least square (L1TV-OLS): The ℓ1 total variation regularized reconstruction includes piece-wise smoothing into the reconstruction model.where is the total variation of the image:Here, the and are directional gradient operators applied to the image domain along the and axes. Equation (12) is solved by the variable-splitting method, which has already been developed [10,11,12].The iterations of L1TV-OLS are explicitly shown in Algorithm 1.
Algorithm 1: The pseudocode for the ℓ1 total variation-regularized ordinary least square (L1TV-OLS) algorithm - ℓ1 total variation-regularized least absolute deviation (L1TV-LAD): Least absolute deviation (LAD) is a statistical regression model which is robust to non-stationary noise distribution [13]. It is possible to solve the ℓ1 total variation-regularized problem with the LAD cost function [14]:where is the total variation of the image. Note that LAD is the ℓ1 norm of the data fidelity. The iterations of L1TV-LAD are as follows:Note that the shrinkage function (shrink) in Algorithm 2 can be quickly solved on the CPU as well as on heterogeneous systems.
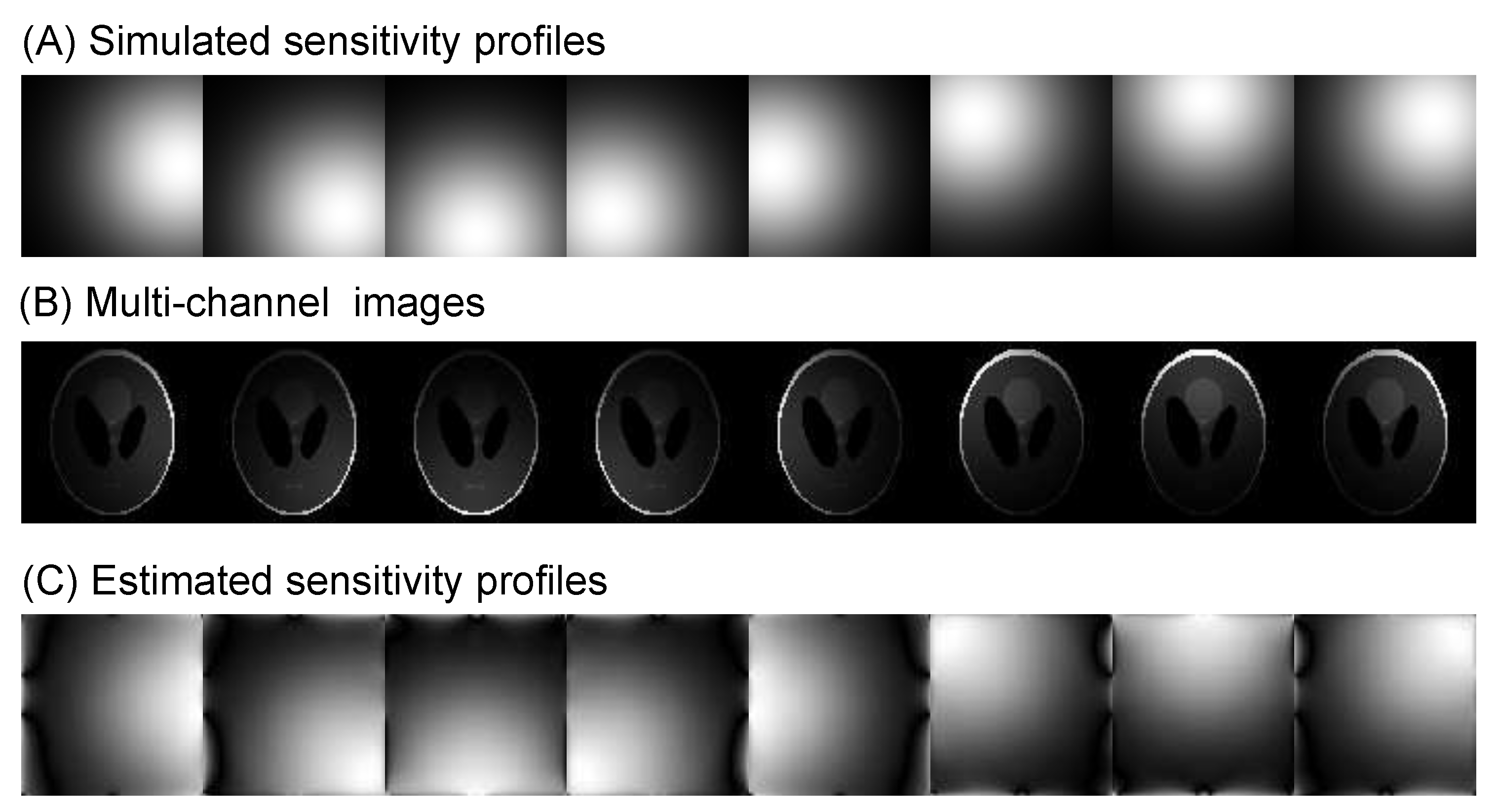
Algorithm 2: The pseudocode for the ℓ1 total variation-regularized least absolute deviation (L1TV-LAD) - Multi-coil image reconstruction: In multi-coil regularized image reconstruction, the self-adjoint NUFFT in Equation (4) is extended to multi-coil data:where the coil-sensitivities () of multiple channels multiply each channel before the NUFFT () and after the adjoint NUFFT (). Sensitivity profiles can be estimated either using the magnitude of smoothed images divided by the root-mean-squared image, or using the dedicated eigenvalue decomposition method [15]. See Figure 6 for a visual example of estimation of coil sensitivity profiles.
2.2.4. Iterative NUFFT Using the Primal-Dual Type Method
- Generalized basis pursuit denoising algorithm (GBPDNA)Here, the generalized basis pursuit denoising algorithm (GBPDNA) [19] is implemented, which reads as the following Algorithm 3.In Algorithm 3, the is the NUFFT in Equation (1). are intermediate variables initiated as zeros. is the step size: . The notation is the generic regularization term, which can be the image itself (as in the fast iterative shrinkage-thresholding algorithm (FISTA) [20]), or linearly transformed images. In the next section, the total variation-like regularization terms are explicitly formulated. satisfy and .
Algorithm 3: The pseudocode for the generic generalized basis pursuit denoising algorithm (GBPDNA) algorithm is the simple convex projection function applying to each component:is the constrained function, defined as follows: - Matrix form of total variation-like regularizationsThe piece-wise constant total variation regularization has been used in image denoising and image reconstruction. Total generalized variation [21] introduces the piece-wise smooth model and the additional variables and to mitigate the stair-casing artifacts. Such modification allows total generalized variation to include the divergence and the curl of the image.The total variation can be written as a compact block sparse matrix. The compact form of anisotropic total variation is as follows:which yields the explicit anisotropic TV using GBPDNA:
Algorithm 4: The pseudocode for the GBPDNA algorithm for anisotropic total variation Similarly, the explicit isotropic TV using GBPDNA is:Algorithm 5: The pseudocode for the GBPDNA algorithm for isotropic total variation Similar to total variation, the total generalized variation regularization can be expressed in a matrix form:where the above variables are modified to match the size of the regularization term.
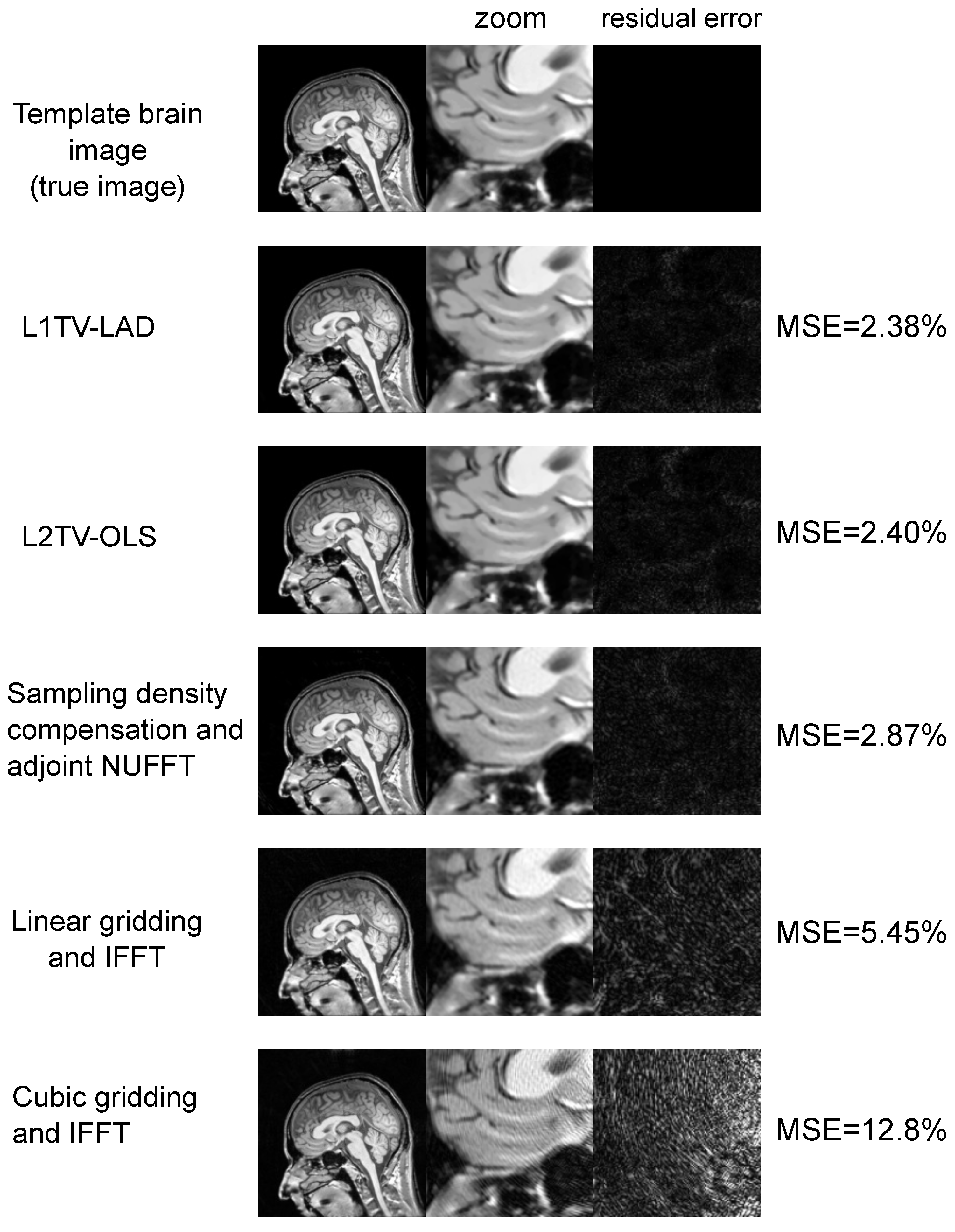
2.3. Applications to Brain MRI
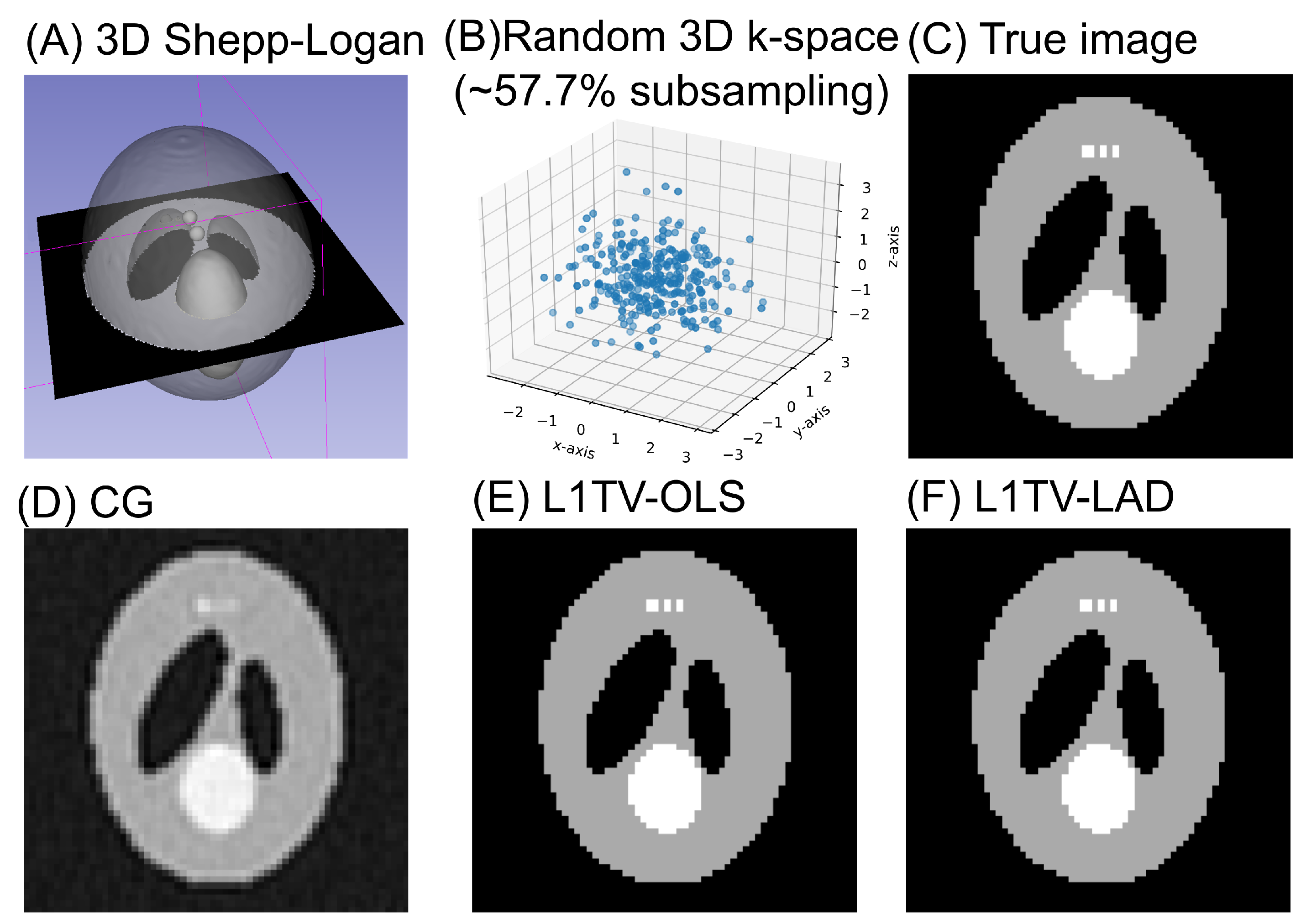
2.4. 3D Computational Phantom
2.5. Benchmark
- Multi-core CPU: The CPU instance (m4.16xlarge, Amazon Web Services) was equipped with 64 vCPUs (Intel E5 2686 v4) and 61 GB of memory. The number of vCPUs could be dynamically controlled by the CPU hotplug functionality of the Linux system, and computations were offloaded onto the Intel OpenCL CPU device with 1 to 64 threads. The single thread CPU computations were carried out with Numpy compiled with the FFTW library [25]. PyNUFFT was executed on the multi-core CPU instance with 1–64 threads. The PyNUFFT transforms were offloaded to the OpenCL CPU device and were executed 20 times. The runtimes required for the transforms were compared with the runtimes on the single-thread CPU.Iterative reconstructions were also tested on the multi-core CPU. The matrix size was 256 × 256, and kernel size was 6. The execution times of the conjugate gradient method, ℓ1 total variation regularized reconstruction and the ℓ1 total variation-regularized LAD were measured on the multi-core system.
- GPU: The GPU instance (p2.xlarge, Amazon Web Services) was equipped with 4 vCPUs (Intel E5 2686 v4) and one Tesla K80 (NVIDIA, Santa Clara, CA, USA) with two GK210 GPUs. Each GPU was composed of 2496 parallel processing cores and 12 GB of memory. Computations were preprocessed and offloaded onto one GPU by CUDA or OpenCL APIs. Computations were repeated 20 times to measure the average runtimes. The matrix size was 256 × 256, and kernel size was 6.Iterative reconstructions were also tested on the K80 GPU, and the execution times of the conjugate gradient method, ℓ1 total variation regularized reconstruction and ℓ1 total variation regularized LAD on the multi-core system were compared with the iterative solvers on the CPU with one thread.
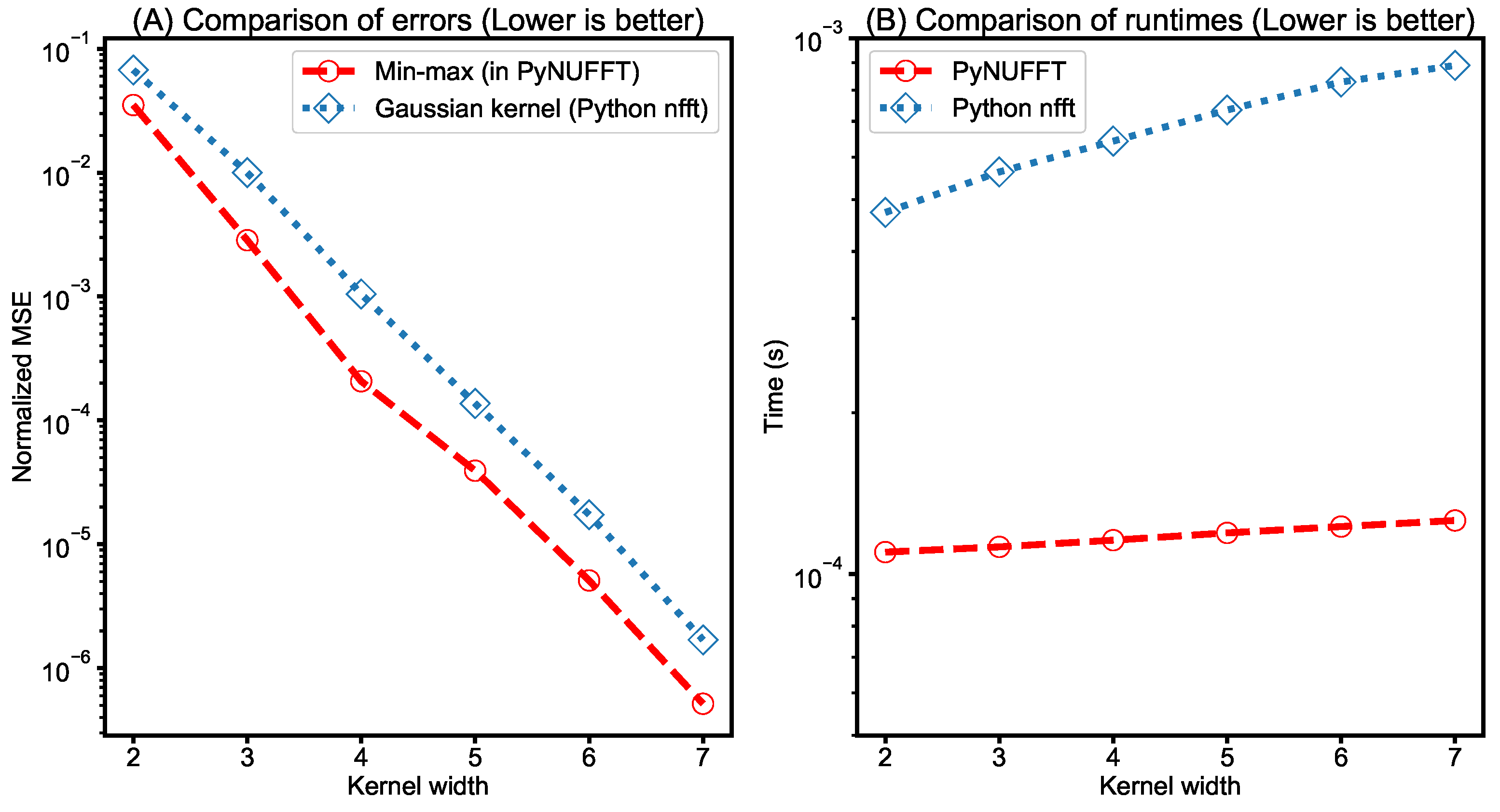
- Comparison between PyNUFFT and Python nfft: It was previously shown that the min–max interpolator yields a better estimation of DFT than the Gaussian kernel does for a kernel size of less than 8 [4]. Thus, a similar testing was carried out and the amplitudes of 1000 randomly scattered non-uniform locations of PyNUFFT and nfft were compared to the amplitudes of the DFT. The input 1D array length was 256, and the kernel size was 2–7.The computation times of PyNUFFT and Python nfft were also measured on a single CPU core. This testing used a Linux system equipped with an Intel Core i7-6700HQ running at 2.6–3.1 GHz (Intel, Santa Clara, CA, USA) with a system memory of 16 GB.
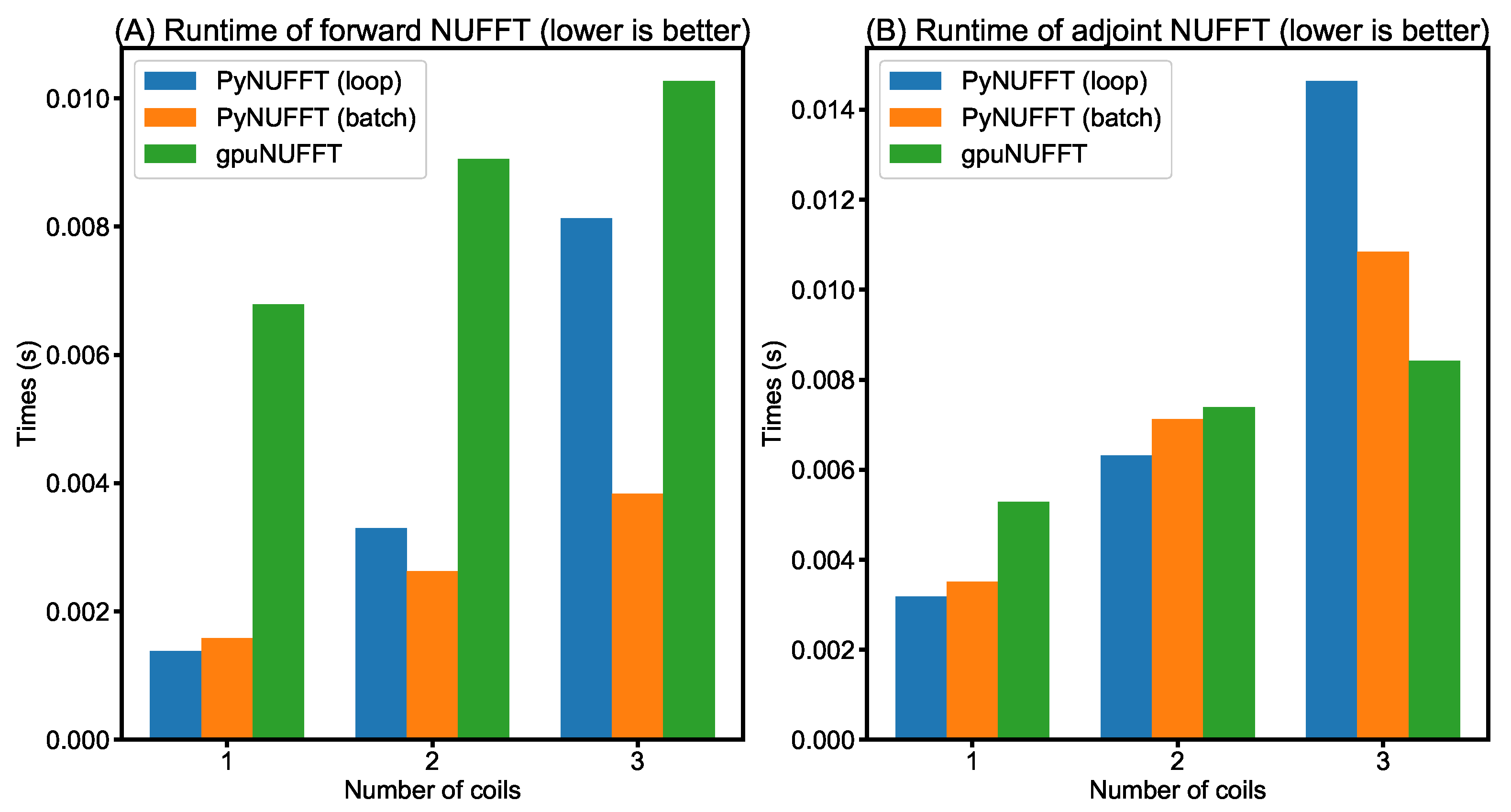
- Comparison between PyNUFFT and gpuNUFFT : This testing used a Linux system equipped with an Intel Core i7-6700HQ running at 2.6–3.1 GHz (Intel, Santa Clara, CA, USA), 16 GB of system memory, and an NVIDIA GeForce GTX 965M (945 MHz) (NVIDIA, Santa Clara, CA, USA) with 2 GB of video memory (driver version 387.22), using the CUDA toolkit version 9.0.176. The gpuNUFFT was compiled with FP16. The parameters of the testing were: image size = 256 × 256, oversampling ratio = 2, kernel size = 6. The GPU version of PyNUFFT was executed using the identical parameters to gpuNUFFT. A radial k-space with 64 spokes [26] was used for gpuNUFFT and PyNUFFT.
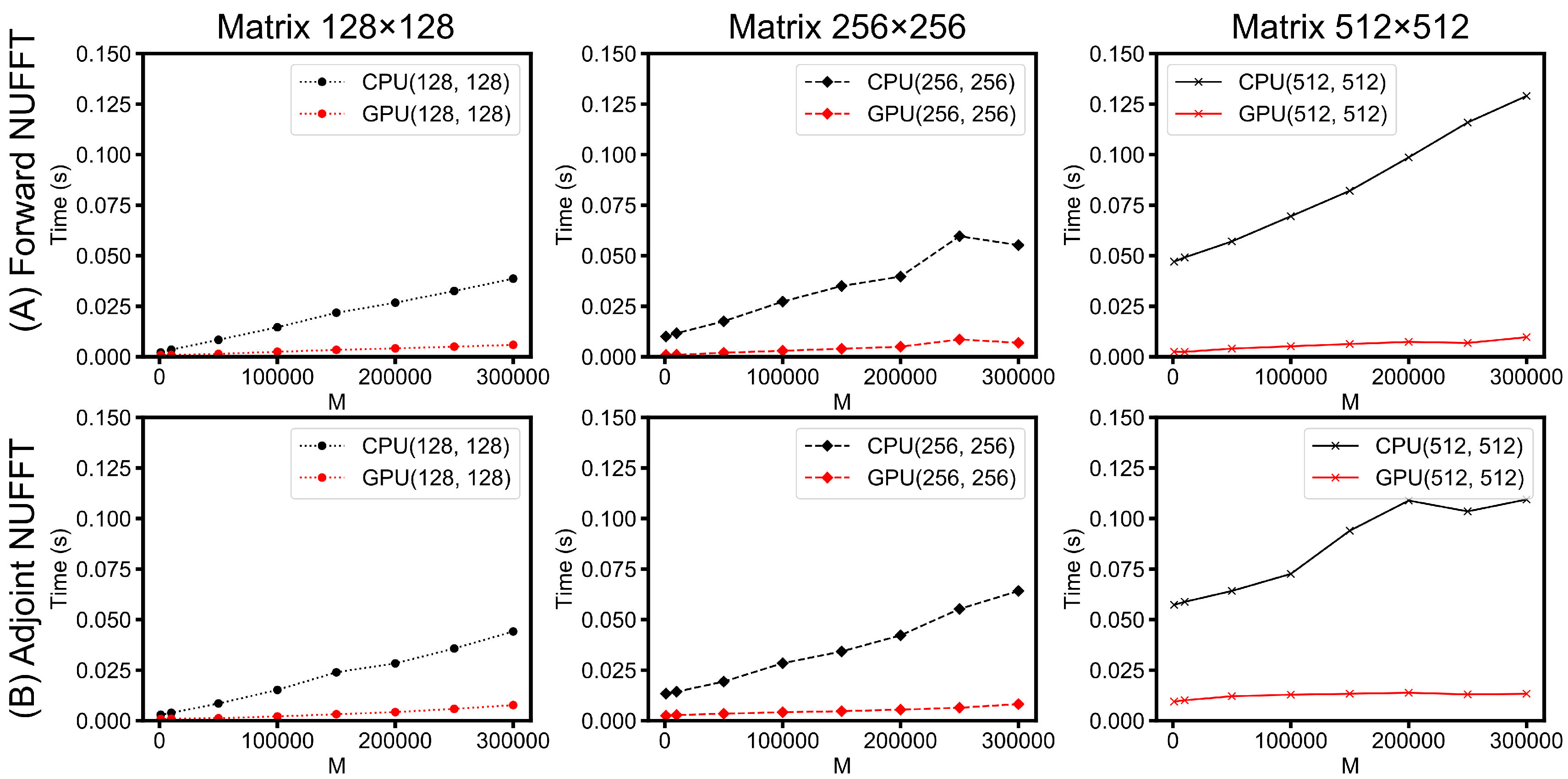
- Scalability of PyNUFFT: A study of the scalability of PyNUFFT was carried out to compare the runtimes of different matrix sizes and the number of non-uniform locations. The system was equipped with a CPU (Intel Core i7 6700HQ at 3500 MHz, 16 GB system memory) and a GPU (NVIDIA GeForce GTX 965m at 945 MHz, 2 GB device memory).
3. Results
3.1. Applications to Brain MRI
3.2. 3D Computational Phantom
3.3. Benchmarks
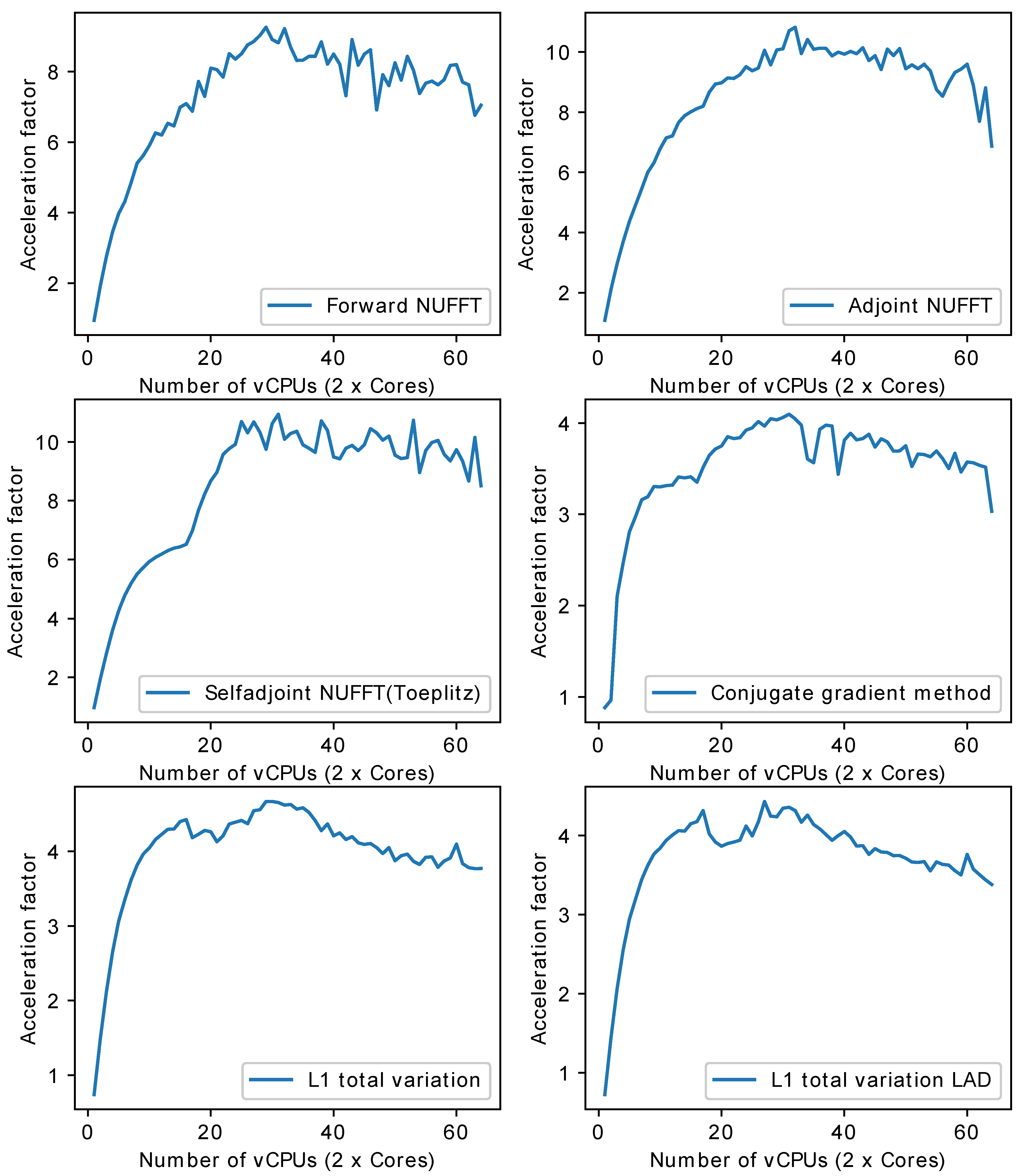
- Multi-core CPU: Table 1 lists the profile for each stage of forward NUFFT, adjoint NUFFT, and self-adjoint NUFFT (Toeplitz). The overall execution speed of PyNUFFT was faster on the multi-core CPU platform than the single-thread CPU, yet the acceleration factors of each stage varied from 0.95 (no acceleration) to 15.6. Compared with computations on a single thread, 32 threads accelerated interpolation and gridding by a factor of 12, and the FFT and IFFT were accelerated by a factor of 6.2–15.6.The benefits of 32 threads are limited for certain computations, including scaling, rescaling, and interpolation gridding (). In these computations, the acceleration factors of 32 threads range from 0.95 to 1.85. This limited performance gain is due to the high efficiency of single-thread CPUs, which leaves limited room for improvement. In particular, the integrated interpolation gridding () is already 10 times faster than the separate interpolation and regridding sequence. On a single-thread CPU, requires only 4.79 ms, whereas the separate interpolation () and gridding () require 49 ms. In this case, 32 threads only deliver an extra 83% of performance to .Figure 10 illustrates the acceleration on the multi-core CPU against the single thread CPU. The performance of PyNUFFT improved by a factor of 5–10 when the number of threads increased from 1 to 20, and the software achieved peak performance with 30–32 threads (equivalent to 15–16 physical CPU cores). More than 32 threads seem to bring no substantial improvement to the performance.Forward NUFFT, adjoint NUFFT and self-adjoint NUFFT (Toeplitz) were accelerated on 32 threads with an acceleration factor of 7.8–9.5. The acceleration factors of iterative solvers (conjugate gradient method, L1TV-OLS and L1TV-LAD) were from 4.2–5.
- GPU: Table 1 shows that GPU delivers a generally faster PyNUFFT transform, with the acceleration factors ranging from 2 to 31.Scaling and rescaling have led to a moderate degree of acceleration. The most significant acceleration took place in the interpolation-gridding () in which GPU was 26–31 times faster than single-thread CPU. This significant acceleration was faster than the acceleration factors for separate interpolation (, with 6× acceleration) and gridding ( with 4–4.6× acceleration).Forward NUFFT, adjoint NUFFT and self-adjoint NUFFT (Toeplitz) were accelerated on K80 GPU by 5.4–13. Iterative solvers on GPU were 6.3–8.9 faster than single-thread, and about twice as fast as with 32 threads.
- Comparison between PyNUFFT and Python nfft: A comparison between PyNUFFT and nfft (Figure 11) evaluated (1) the accuracy of the min–max interpolator and the Gaussian kernel; and (2) the runtimes of a single-core CPU. The min–max interpolator in PyNUFFT attains a lower error than Gaussian kernel. PyNUFFT also requires less CPU times than nfft, due to the fact that nfft recalculates the interpolation matrix with each nfft or nfft_adjoint call.
- Comparison between PyNUFFT and gpuNUFFT: Figure 12 compares the runtimes of different GPU implementations. In forward NUFFT, the fastest is the PyNUFFT (batch), followed by PyNUFFT (loop) and gpuNUFFT.In single-coil adjoint NUFFT, the performance of PyNUFFT (loop), PyNUFFT (batch) and gpuNUFFT is similar. Multi-coil NUFFT increases the runtimes, and the PyNUFFT (loop) is the slowest in the adjoint transform in the case of three coils.
- Scalability of PyNUFFT: Figure 13 evaluates the performance of forward NUFFT and adjoint NUFFT vs. the number of non-uniform locations (M) for different matrix sizes. The condition of M = 300,000 is close to a fully sampled 512 × 512 k-space (with 262,144 samples). The values at M = 0 (y-intercept ) indicate the runtimes for scaling () and FFT (), which change with the matrix size. The slope can be attributed to the runtimes versus M, which is due to interpolation () or gridding ().For a large problem size (matrix size = 512 × 512, M = 300,000), GPU PyNUFFT requires less than 10 ms in the forward transform, and less than 15 ms in the adjoint transform. For a small problem size (matrix size = 128 × 128, M = 1000), GPU PyNUFFT requires 830 ns in the forward transform, and 850 ns in the adjoint transform.
4. Discussion
4.1. Related Work
4.2. Discussions of PyNUFFT
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CG | conjugate gradient |
| CPU | central processing unit |
| CPU | central processing unit |
| DFT | discrete Fourier transform |
| GBPDNA | generalized basis pursuit denoising algorithm |
| GPU | graphic processing unit |
| IFFT | inverse fast Fourier transform |
| MRI | magnetic resonance imaging |
| MSE | mean squared error |
| NUFFT | non-uniform fast Fourier transform |
| TV | total variation |
References
- Klöckner, A.; Pinto, N.; Lee, Y.; Catanzaro, B.; Ivanov, P.; Fasih, A. PyCUDA and PyOpenCL: A scripting-based approach to GPU run-time code generation. Parallel Comput. 2012, 38, 157–174. [Google Scholar] [CrossRef]
- Opanchuk, B. Reikna, A Pure Python GPGPU Library. Available online: http://reikna.publicfields.net/ (accessed on 9 October 2017).
- Free Software Foundation. GNU General Public License. 29 June 2007. Available online: http://www.gnu.org/licenses/gpl.html (accessed on 7 March 2018).
- Fessler, J.; Sutton, B.P. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans. Signal Proc. 2003, 51, 560–574. [Google Scholar] [CrossRef]
- Danalis, A.; Marin, G.; McCurdy, C.; Meredith, J.; Roth, P.; Spafford, K.; Tipparaju, V.; Vetter, J. The Scalable HeterOgeneous Computing (SHOC) Benchmark Suite. In Proceedings of the 3rd Workshop on General-Purpose Computation on Graphics Processors (GPGPU 2010), Pittsburgh, PA, USA, 14 March 2010. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming, Volume 1 (3rd ed.): Fundamental Algorithms; Addison Wesley Longman Publishing Co., Inc.: Redwood City, CA, USA, 1997. [Google Scholar]
- Fessler, J.; Lee, S.; Olafsson, V.T.; Shi, H.R.; Noll, D.C. Toeplitz-based iterative image reconstruction for MRI with correction for magnetic field inhomogeneity. IEEE Trans. Signal Proc. 2005, 53, 3393–3402. [Google Scholar] [CrossRef]
- Pipe, J.G.; Menon, P. Sampling density compensation in MRI: Rationale and an iterative numerical solution. Magn. Reson. Med. 1999, 41, 179–186. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open source scientific tools for Python. 2001. Available online: http://www.scipy.org (accessed on 9 October 2017).
- Lin, J.M.; Patterson, A.J.; Chang, H.C.; Chuang, T.C.; Chung, H.W.; Graves, M.J. Whitening of Colored Noise in PROPELLER Using Iterative Regularized PICO Reconstruction. In Proceedings of the 23rd Annual Meeting of International Society for Magnetic Resonance in Medicine, Toronto, ON, Canada, 30 May–5 June 2015; p. 3738. [Google Scholar]
- Lin, J.M.; Patterson, A.J.; Lee, C.W.; Chen, Y.F.; Das, T.; Scoffings, D.; Chung, H.W.; Gillard, J.; Graves, M. Improved Identification and Clinical Utility of Pseudo-Inverse with Constraints (PICO) Reconstruction for PROPELLER MRI. In Proceedings of the 24th Annual Meeting of International Society for Magnetic Resonance in Medicine, Singapore, 7–13 May 2016; p. 1773. [Google Scholar]
- Lin, J.M.; Tsai, S.Y.; Chang, H.C.; Chung, H.W.; Chen, H.C.; Lin, Y.H.; Lee, C.W.; Chen, Y.F.; Scoffings, D.; Das, T.; et al. Pseudo-Inverse Constrained (PICO) Reconstruction Reduces Colored Noise of PROPELLER and Improves the Gray-White Matter Differentiation. In Proceedings of the 25th Annual Meeting of International Society for Magnetic Resonance in Medicine, Honolulu, HI, USA, 22–28 April 2017; p. 1524. [Google Scholar]
- Wang, L. The penalized LAD estimator for high dimensional linear regression. J. Multivar. Anal. 2013, 120, 135–151. [Google Scholar] [CrossRef]
- Lin, J.M.; Chang, H.C.; Chao, T.C.; Tsai, S.Y.; Patterson, A.; Chung, H.W.; Gillard, J.; Graves, M. L1-LAD: Iterative MRI reconstruction using L1 constrained least absolute deviation. In Proceedings of the 34th Annual Scientific Meeting of ESMRMB, Barcelona, Spain, 19–21 October 2017. [Google Scholar]
- Uecker, M.; Lai, P.; Murphy, M.J.; Virtue, P.; Elad, M.; Pauly, J.M.; Vasanawala, S.S.; Lustig, M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014, 71, 990–1001. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, T.; Osher, S. The split Bregman method for ℓ1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Chambolle, A.; Pock, T. A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 2011, 40, 120–145. [Google Scholar] [CrossRef]
- Boyer, C.; Ciuciu, P.; Weiss, P.; Mériaux, S. HYR2PICS: Hybrid Regularized Reconstruction for Combined Parallel Imaging and Compressive Sensing in MRI. In Proceedings of the 9th IEEE International Symposium on Biomedical Imaging (ISBI), Barcelona, Spain, 2–5 May 2012; pp. 66–69. [Google Scholar]
- Loris, I.; Verhoeven, C. Iterative algorithms for total variation-like reconstructions in seismic tomography. GEM Int. J. Geomath. 2012, 3, 179–208. [Google Scholar] [CrossRef][Green Version]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Knoll, F.; Bredies, K.; Pock, T.; Stollberger, R. Second order total generalized variation (TGV) for MRI. Magn. Reson. Med. 2011, 65, 480–491. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.M.; Patterson, A.J.; Chang, H.C.; Gillard, J.H.; Graves, M.J. An iterative reduced field-of-view reconstruction for periodically rotated overlapping parallel lines with enhanced reconstruction PROPELLER MRI. Med. Phys. 2015, 42, 5757–5767. [Google Scholar] [CrossRef] [PubMed]
- Lalys, F.; Haegelen, C.; Ferre, J.C.; El-Ganaoui, O.; Jannin, P. Construction and assessment of a 3-T MRI brain template. Neuroimage 2010, 49, 345–354. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Schabel, M. MathWorks File Exchange: 3D Shepp-Logan Phantom. Available online: https://uk.mathworks.com/matlabcentral/fileexchange/9416-3d-shepp-logan-phantom (accessed on 9 October 2017).
- Frigo, M.; Johnson, S. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
- Knoll, F.; Schwarzl, A.; Diwoky, C.S.D. gpuNUFFT—An open-source GPU library for 3D gridding with direct Matlab Interface. In Proceedings of the 22nd Annual Meeting of ISMRM, Milan, Italy, 20–21 April 2013; p. 4297. [Google Scholar]
- Potts, D.; Steidl, G. Fast summation at nonequispaced knots by NFFTs. SIAM J. Sci. Comput. 2004, 24, 2013–2037. [Google Scholar] [CrossRef]
- Keiner, J.; Kunis, S.; Potts, D. Using NFFT 3—A software library for various nonequispaced fast Fourier transforms. ACM Trans. Math. Softw. 2009, 36, 19. [Google Scholar] [CrossRef]
- Song, J.; Liu, Y.; Gewalt, S.L.; Cofer, G.; Johnson, G.A.; Liu, Q.H. Least-square NUFFT methods applied to 2-D and 3-D radially encoded MR image reconstruction. IEEE Trans. Biom. Eng. 2009, 56, 1134–1142. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Jacob, M. Mean square optimal NUFFT approximation for efficient non-Cartesian MRI reconstruction. J. Magn. Reson. 2014, 242, 126–135. [Google Scholar] [CrossRef] [PubMed]
- Greengard, L.; Lee, J.Y. Accelerating the nonuniform fast Fourier transform. SIAM Rev. 2004, 46, 443–454. [Google Scholar] [CrossRef]
- Liu, C.; Moseley, M.; Bammer, R. Fast SENSE Reconstruction Using Linear System Transfer Function. In Proceedings of the International Society of Magnetic Resonance in Medicine, Miami Beach, FL, USA, 7–13 May 2005; p. 689. [Google Scholar]
- Uecker, M.; Zhang, S.; Frahm, J. Nonlinear inverse reconstruction for real-time MRI of the human heart using undersampled radial FLASH. Magn. Reson. Med. 2010, 63, 1456–1462. [Google Scholar] [CrossRef] [PubMed]
- Ferrara, M. Implements 1D-3D NUFFTs Via Fast Gaussian Gridding. 2009. Matlab Central. Available online: http://www.mathworks.com/matlabcentral/fileexchange/25135-nufft-nfft-usfft (accessed on 2 March 2018).
- Bredies, K.; Knoll, F.; Freiberger, M.; Scharfetter, H.; Stollberger, R. The Agile Library for Biomedical Image Reconstruction Using GPU Acceleration. Comput. Sci. Eng. 2013, 15, 34–44. [Google Scholar]
- Cerjanic, A.; Holtrop, J.L.; Ngo, G.C.; Leback, B.; Arnold, G.; Moer, M.V.; LaBelle, G.; Fessler, J.A.; Sutton, B.P. PowerGrid: A open source library for accelerated iterative magnetic resonance image reconstruction. Proc. Intl. Soc. Mag. Reson. Med. 2016, 24, 525. [Google Scholar]
- Schaetz, S.; Voit, D.; Frahm, J.; Uecker, M. Accelerated computing in magnetic resonance imaging: Real-time imaging Using non-linear inverse reconstruction. Comput. Math. Methods Med. 2017. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.; Alley, M.; Demmel, J.; Keutzer, K.; Vasanawala, S.; Lustig, M. Fast-SPIRiT compressed sensing parallel imaging MRI: Scalable parallel implementation and clinically feasible runtime. IEEE Trans. Med. Imaging 2012, 31, 1250–1262. [Google Scholar] [CrossRef] [PubMed]
- Nadar, M.S.; Martin, S.; Lefebvre, A.; Liu, J. Multi-GPU FISTA Implementation for MR Reconstruction with Non-Uniform k-space Sampling. U.S. Patent 14/031,374, 27 March 2014. [Google Scholar]
- Stone, S.S.; Haldar, J.P.; Tsao, S.C.; Hwu, W.M.W.; Liang, Z.P.; Sutton, B.P. Accelerating Advanced MRI Reconstructions on GPUs. J. Parallel Distrib. Comput. 2008, 68, 1307–1318. [Google Scholar] [CrossRef] [PubMed]
- Gai, J.; Obeid, N.; Holtrop, J.L.; Wu, X.L.; Lam, F.; Fu, M.; Haldar, J.P.; Wen-Mei, W.H.; Liang, Z.P.; Sutton, B.P. More IMPATIENT: A gridding-accelerated Toeplitz-based strategy for non-Cartesian high-resolution 3D MRI on GPUs. J. Parallel Distrib. Comput. 2013, 73, 686–697. [Google Scholar] [CrossRef] [PubMed]
| Operations | 1 vCPU * | 32 vCPUs | PyOpenCL K80 | PyCUDA K80 |
|---|---|---|---|---|
| Scaling(S) | 709 µs | 557 µs (1.3×) | 133 µs (5.3×) | 300 µs (2.4×) |
| FFT(F) | 12.6 ms | 2.03 ms (6.2×) | 0.78 ms (16.2×) | 1.12 ms (11.3×) |
| Interpolation(V) | 25 ms | 2 ms (12×) | 4 ms(6×) | 4 ms (6×) |
| Gridding(VH) | 24 ms | 2 ms (12×) | 5 ms (4.8×) | 4.5 ms (5.4×) |
| IFFT(FH) | 16 ms | 3.1 ms (5.16×) | 4.0 ms (4×) | 3.5 (4.6×) |
| Rescaling (SH) | 566 µs | 595 µs (0.95×) | 122 µs (4.64×) | 283 µs (2×) |
| VHV | 4.79 ms | 2.62 ms (1.83×) | 0.18 ms (26×) | 0.15 ms (31×) |
| Forward (A) | 39 ms | 5 ms (7.8×) | 6 ms (6.5×) | 6 ms (6.5×) |
| Adjoint (AH) | 38 ms | 6 ms (6.3×) | 7 ms (5.4×) | 6 ms (6.3×) |
| Self-adjoint (AHA) | 34.7 ms | 11 ms (3.15×) | 9 ms (3.86×) | 8 ms (4.34×) |
| Solvers | 1 vCPU | 32 vCPUs | PyOpenCL K80 | PyCUDA K80 |
| Conjugate gradient | 11.8 s | 2.97 s (4×) | 1.32 s (8.9×) | 1.89 s (6.3×) |
| L1TV-OLS | 14.7 s | 3.26 s (4.5×) | 1.79 s (8.2×) | 1.68 s (8.7×) |
| L1TV-LAD | 15.1 s | 3.62 s (4.2×) | 1.93 s (7.8×) | 1.78 s (8.5×) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.-M. Python Non-Uniform Fast Fourier Transform (PyNUFFT): An Accelerated Non-Cartesian MRI Package on a Heterogeneous Platform (CPU/GPU). J. Imaging 2018, 4, 51. https://doi.org/10.3390/jimaging4030051
Lin J-M. Python Non-Uniform Fast Fourier Transform (PyNUFFT): An Accelerated Non-Cartesian MRI Package on a Heterogeneous Platform (CPU/GPU). Journal of Imaging. 2018; 4(3):51. https://doi.org/10.3390/jimaging4030051
Chicago/Turabian StyleLin, Jyh-Miin. 2018. "Python Non-Uniform Fast Fourier Transform (PyNUFFT): An Accelerated Non-Cartesian MRI Package on a Heterogeneous Platform (CPU/GPU)" Journal of Imaging 4, no. 3: 51. https://doi.org/10.3390/jimaging4030051
APA StyleLin, J.-M. (2018). Python Non-Uniform Fast Fourier Transform (PyNUFFT): An Accelerated Non-Cartesian MRI Package on a Heterogeneous Platform (CPU/GPU). Journal of Imaging, 4(3), 51. https://doi.org/10.3390/jimaging4030051