Confidence Estimation for Machine Learning-Based Quantitative Photoacoustics
Abstract
1. Introduction
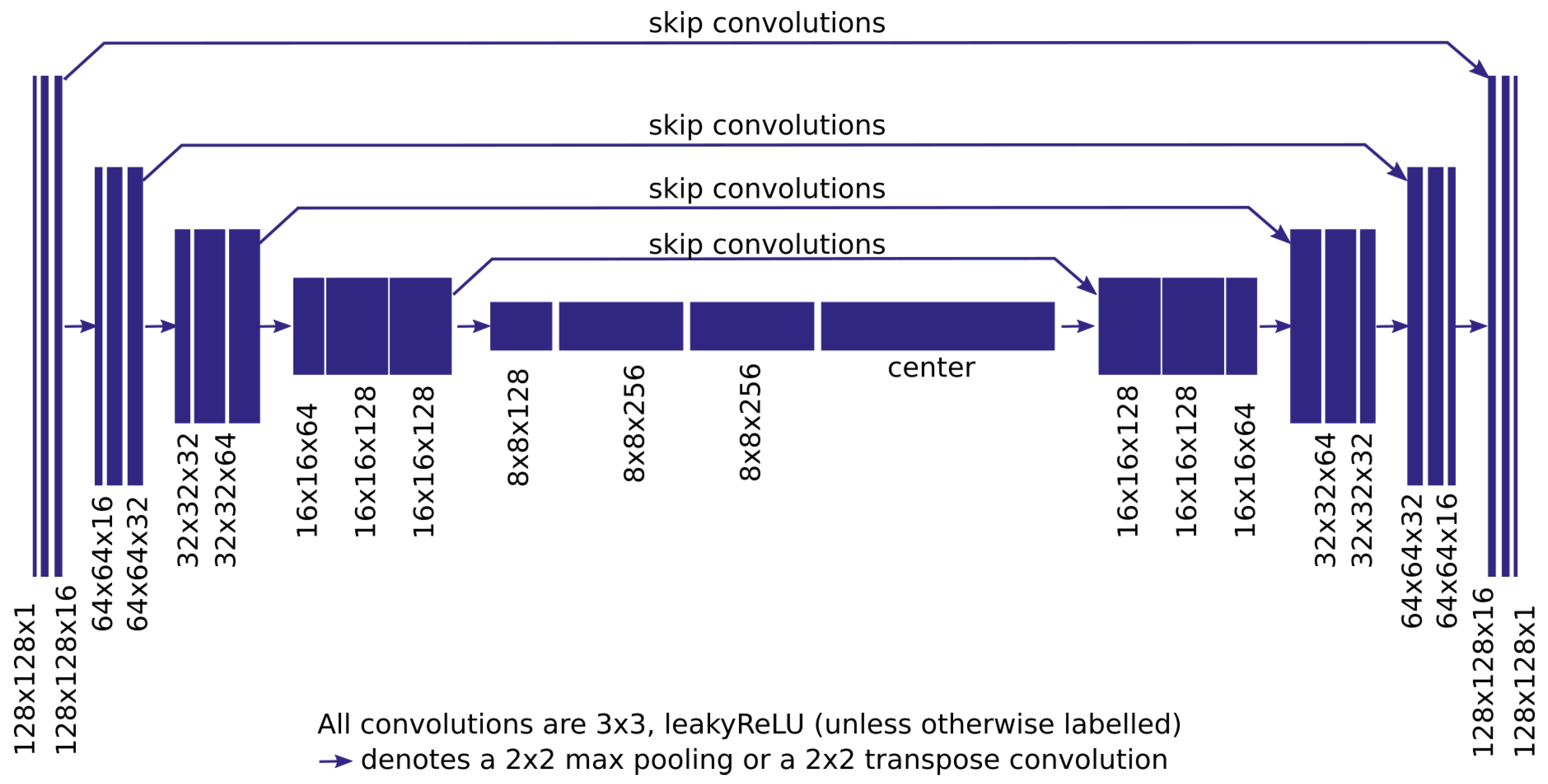
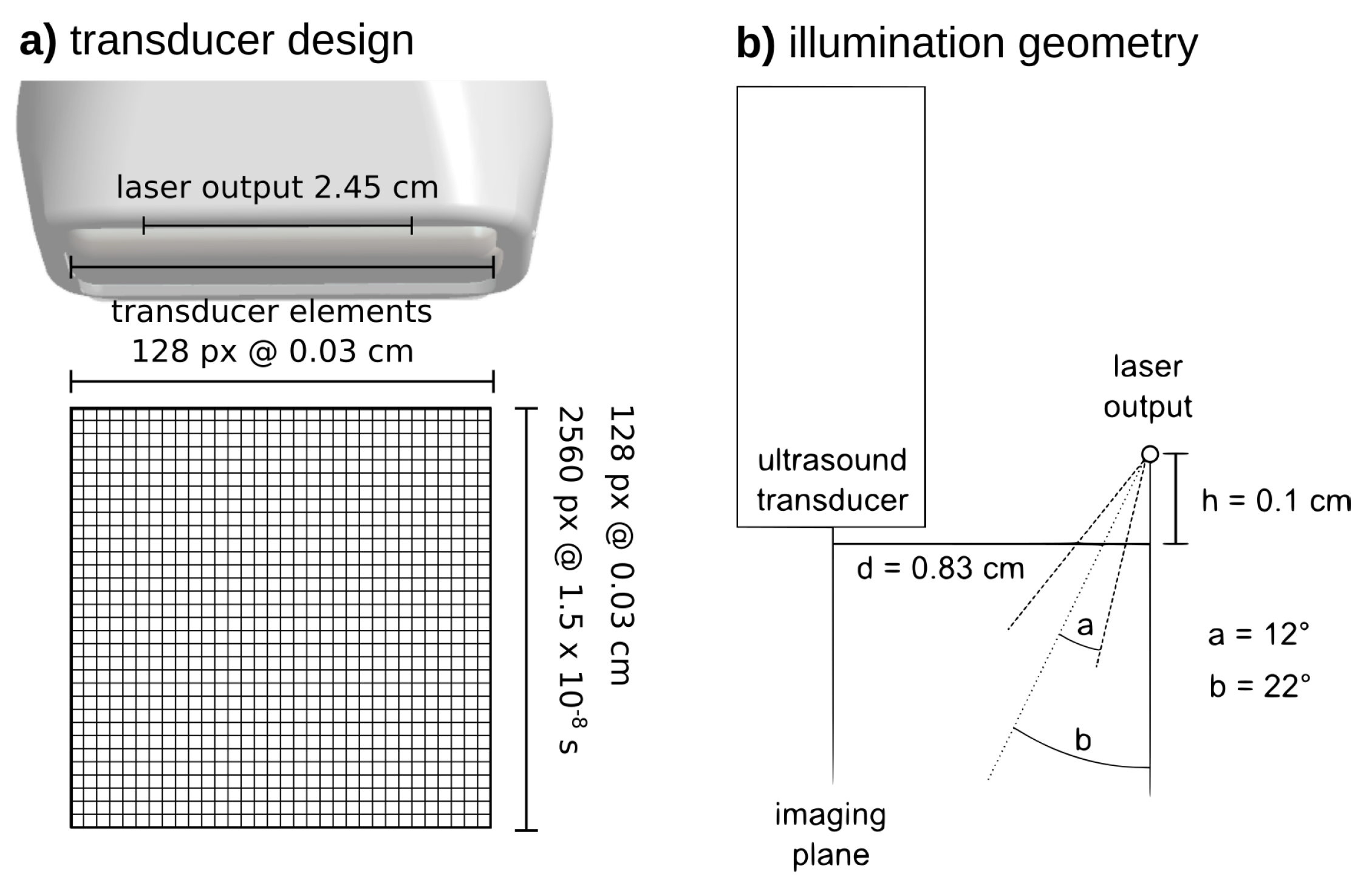
2. Materials and Methods
- (1)
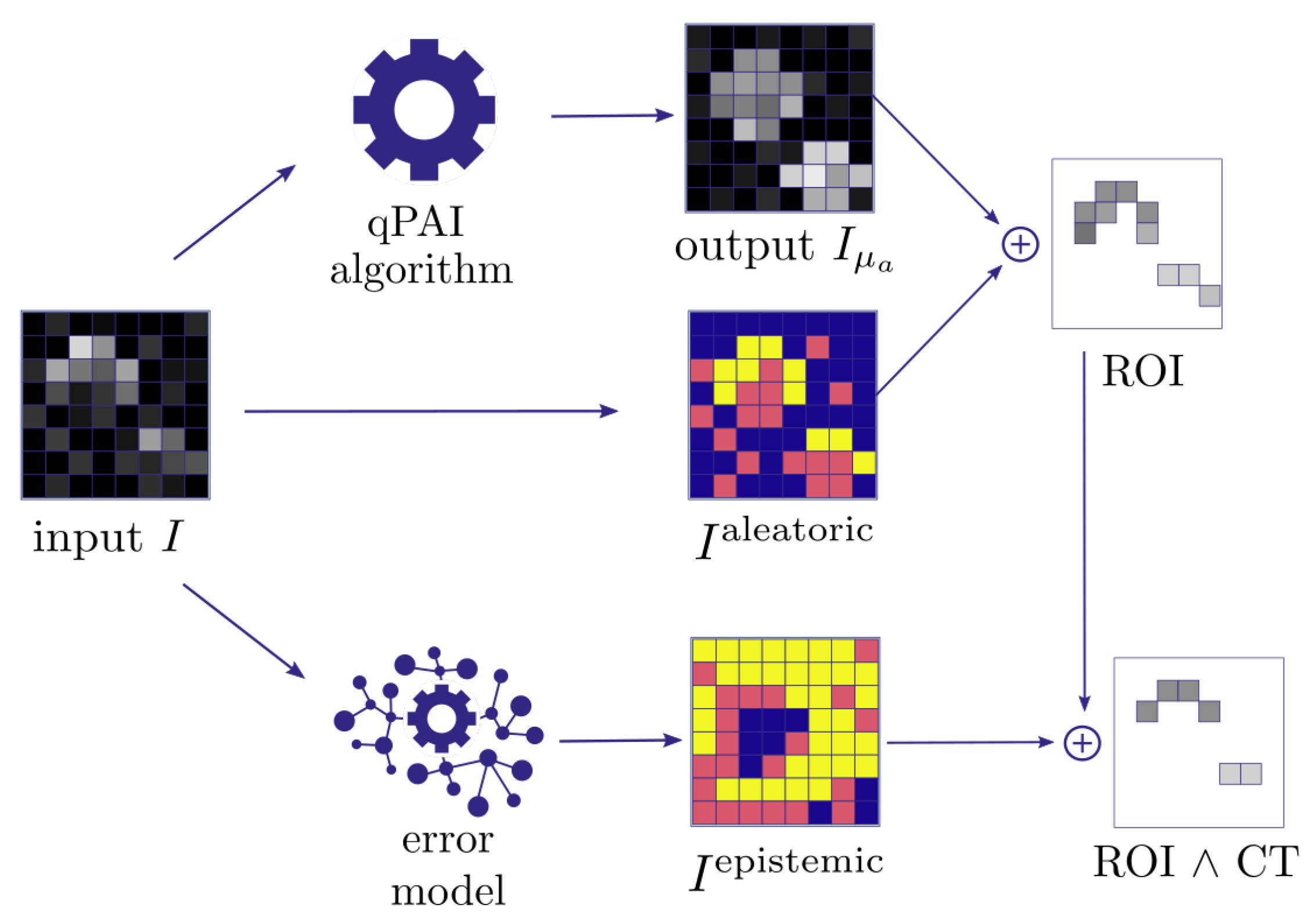
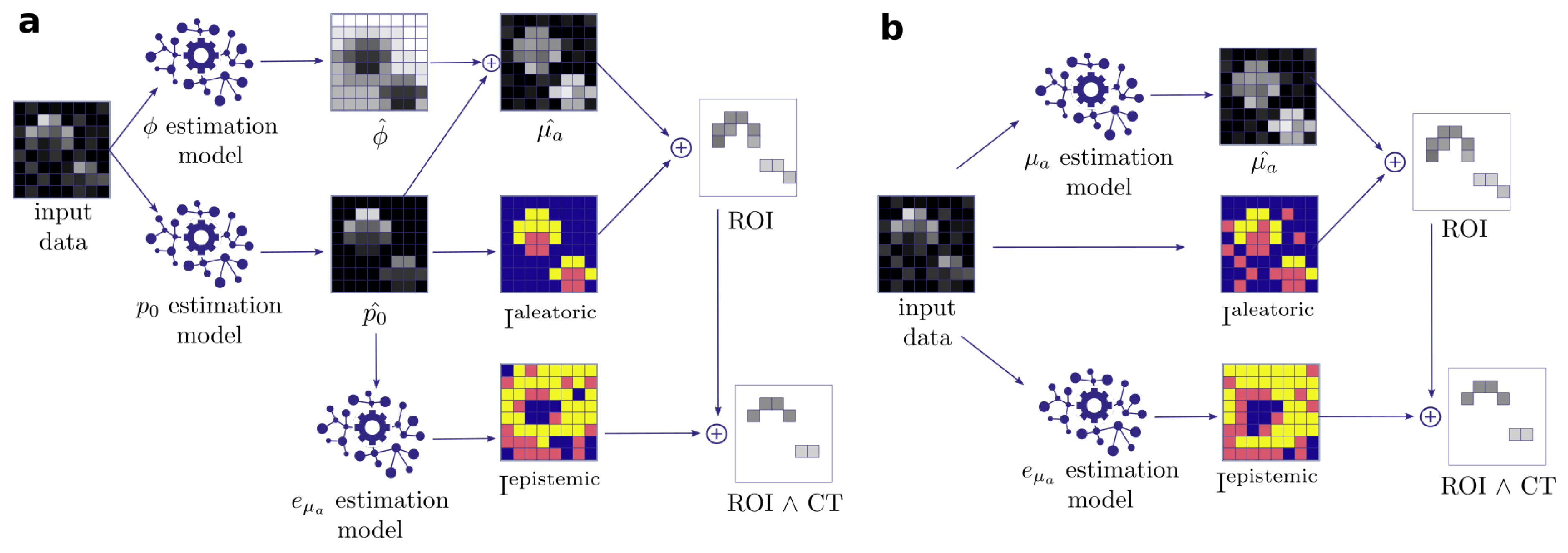
- Quantification of aleatoric uncertainty: I is converted into an image reflecting the aleatoric uncertainty. For this purpose, we use the contrast-to-noise-ratio (CNR), as defined by Welvaert and Rosseel [45], as , with S being the pixel signal intensity, and and being the mean and standard deviation of all background pixels in the dataset. Using this metric, we predefine our ROI to comprise all pixels with CNR > 5.
- (2)
- Quantification of epistemic confidence: I is converted into an image reflecting the epistemic confidence. For this purpose, we use the external model to estimate the quantification error of the qPAI algorithm.
- (3)
- Output generation: A threshold over yields a binary image with an ROI representing confident pixels in according to the input signal intensity. We then proceed to narrow down the ROI by applying a confidence threshold () which removes the n% least confident pixels according to .
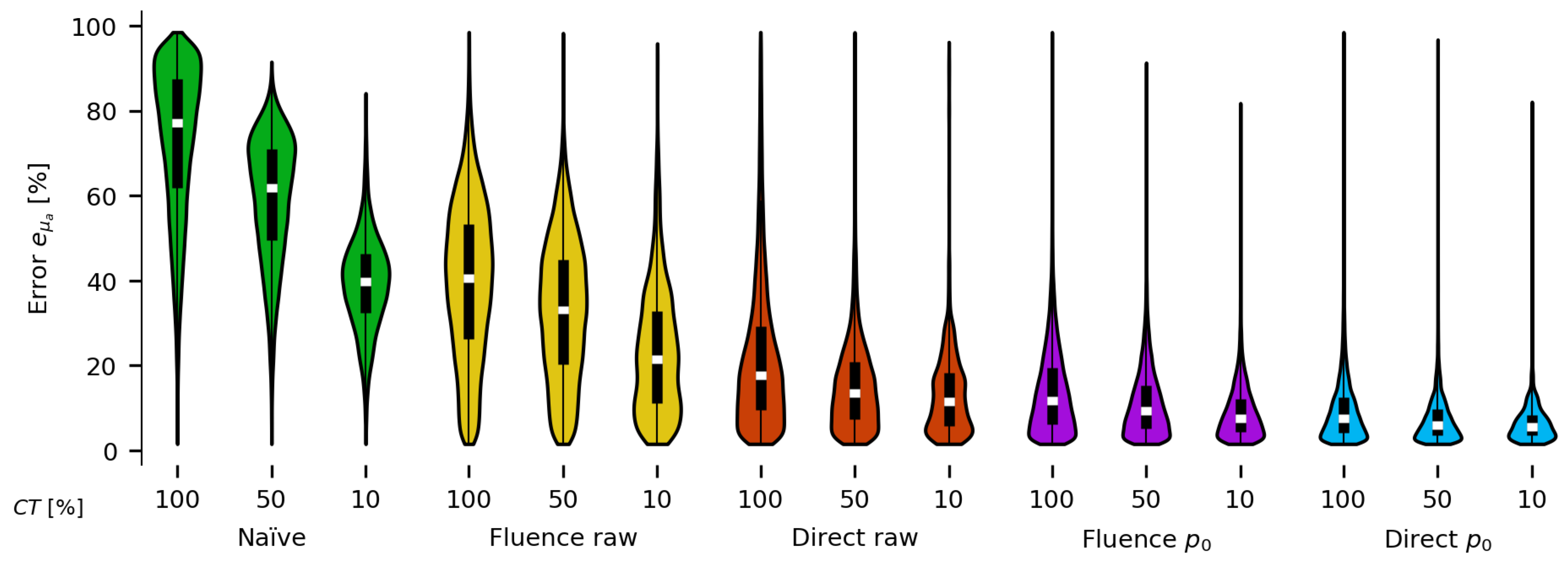
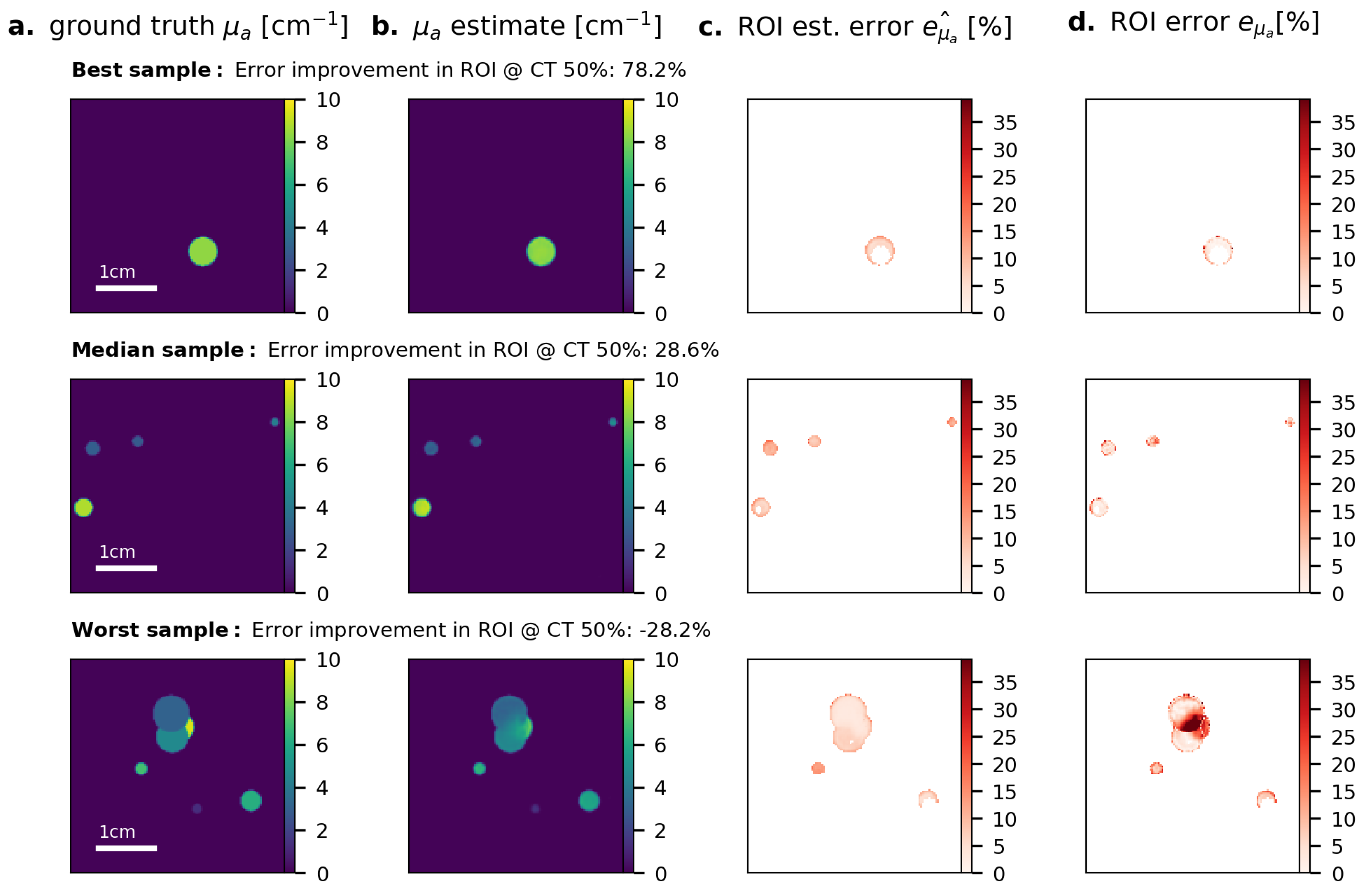
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CNR | Contrast-To-Noise-Ratio |
| PA | Photoacoustic |
| PAI | Photoacoustic Imaging |
| qPAI | quantitative PAI |
| ROI | Region of Interest |
| CT | Confidence Threshold |
Appendix A. Results for the Naïve Fluence Compensation Method

Appendix B. Results for Fluence Correction on Data
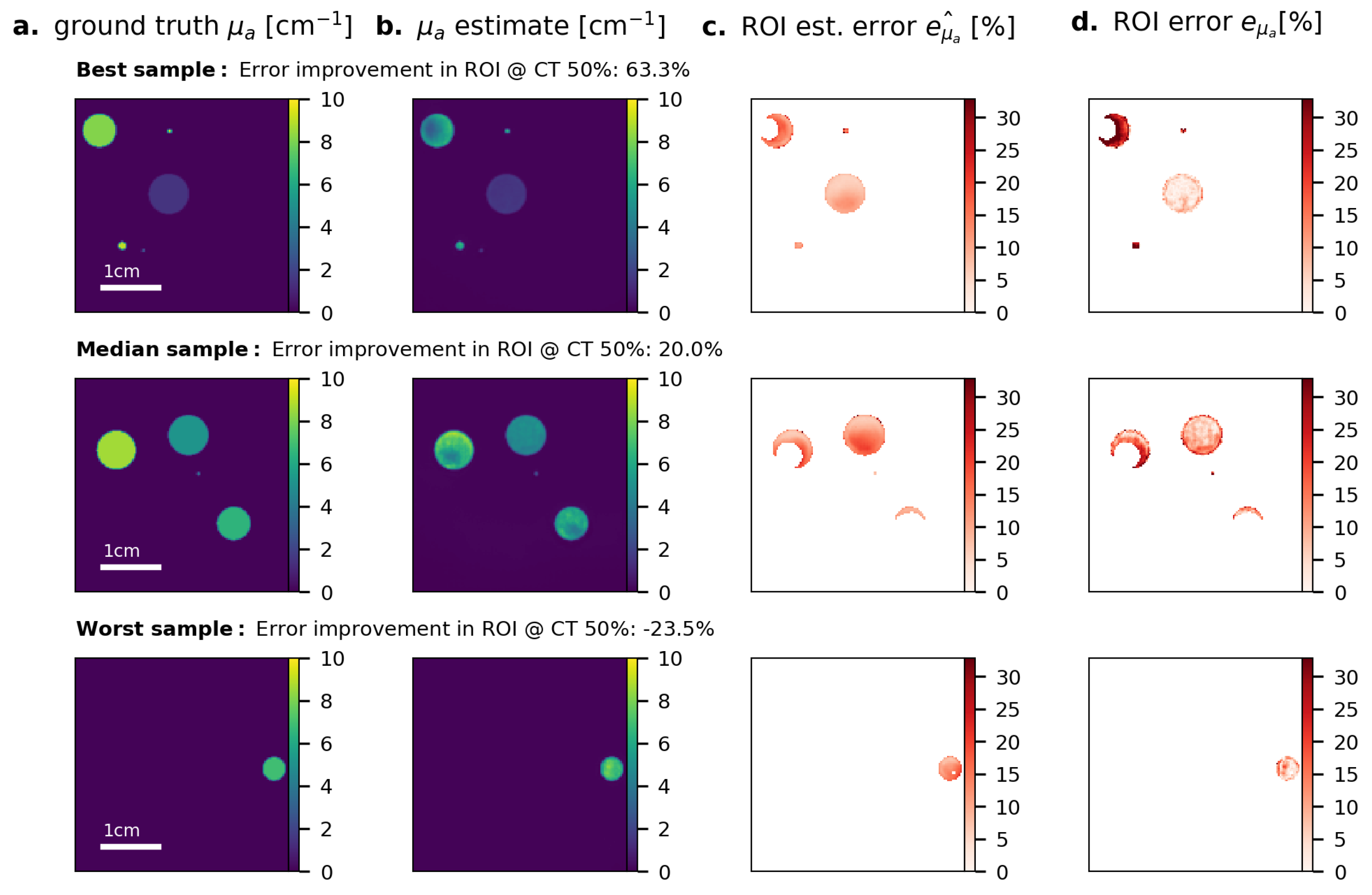
Appendix C. Results for Fluence Correction on Raw PA Time Series Data
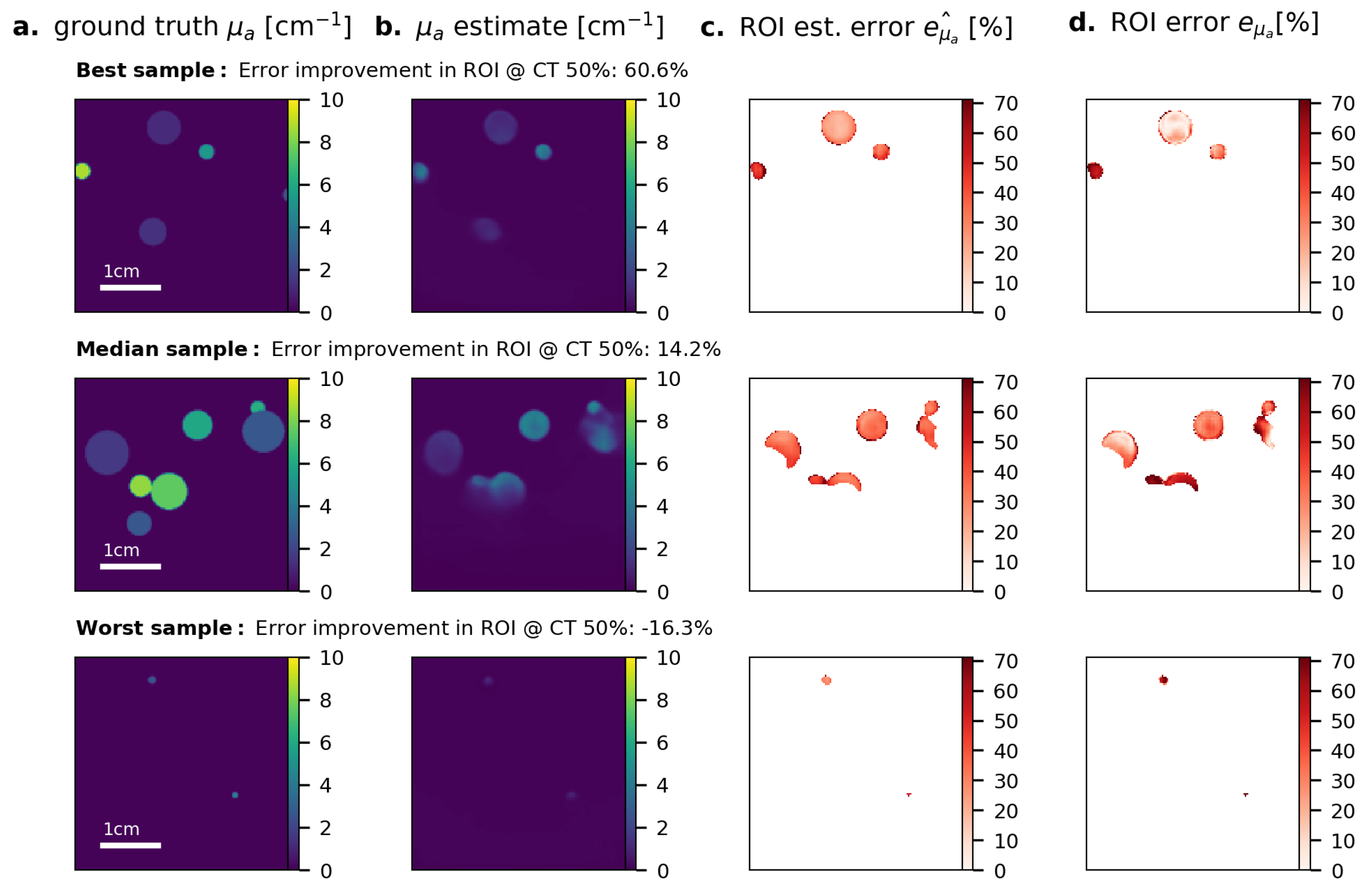
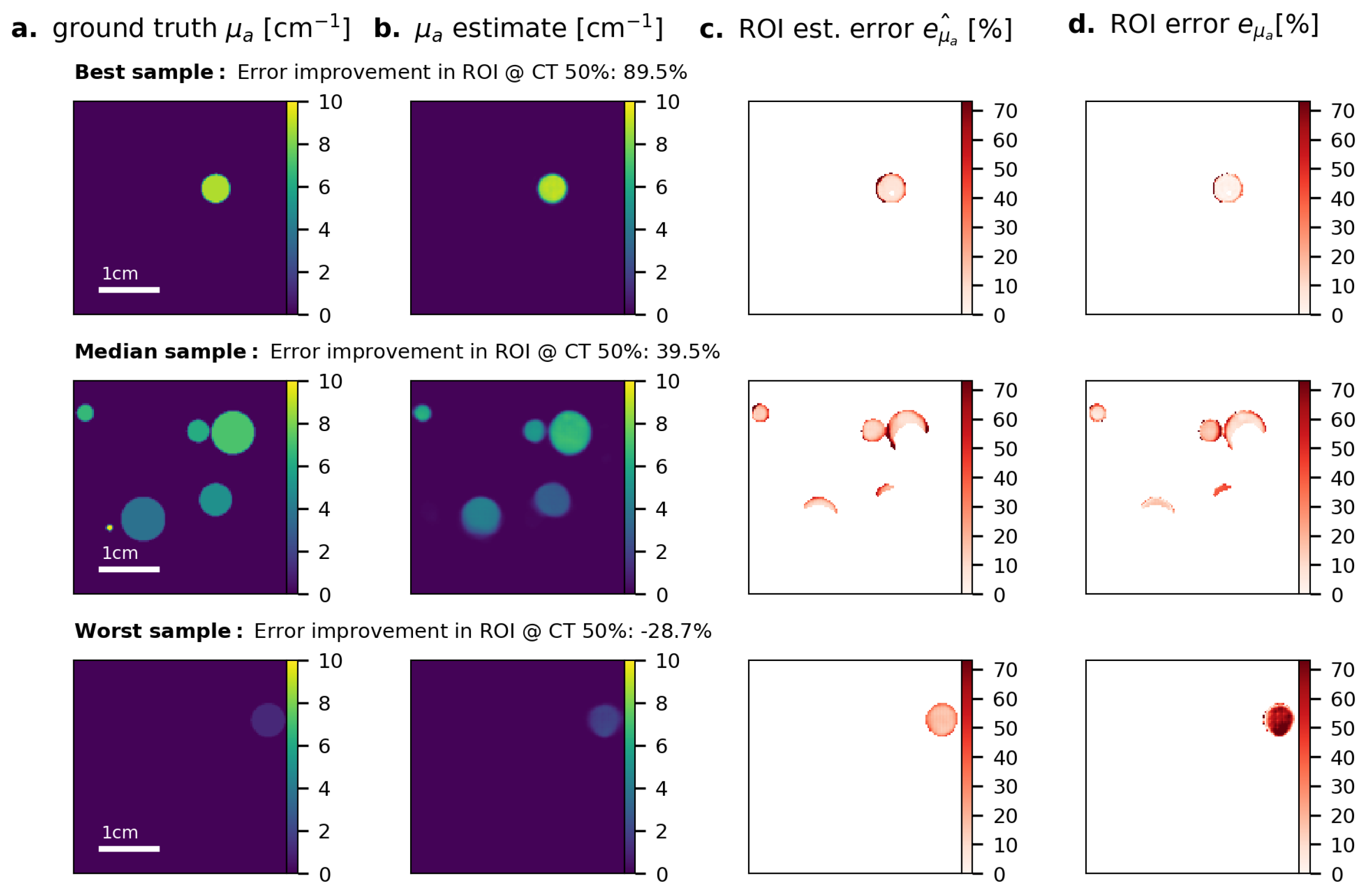
Appendix D. Results for Direct Estimation on Raw PA Time Series Data
References
- Valluru, K.S.; Willmann, J.K. Clinical photoacoustic imaging of cancer. Ultrason 2016, 35, 267–280. [Google Scholar] [CrossRef] [PubMed]
- Knieling, F.; Neufert, C.; Hartmann, A.; Claussen, J.; Urich, A.; Egger, C.; Vetter, M.; Fischer, S.; Pfeifer, L.; Hagel, A.; et al. Multispectral Optoacoustic Tomography for Assessment of Crohn’s Disease Activity. N. Engl. J. Med. 2017, 376, 1292–1294. [Google Scholar] [CrossRef] [PubMed]
- Laufer, J. Photoacoustic Imaging: Principles and Applications. In Quantification of Biophysical Parameters in Medical Imaging; Springer: Cham, The Netherlands, 2018; pp. 303–324. [Google Scholar] [CrossRef]
- Mitcham, T.; Taghavi, H.; Long, J.; Wood, C.; Fuentes, D.; Stefan, W.; Ward, J.; Bouchard, R. Photoacoustic-based SO2 estimation through excised bovine prostate tissue with interstitial light delivery. Photoacoust 2017, 7, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Boil. 2013, 58, R37. [Google Scholar] [CrossRef] [PubMed]
- Tzoumas, S.; Nunes, A.; Olefir, I.; Stangl, S.; Symvoulidis, P.; Glasl, S.; Bayer, C.; Multhoff, G.; Ntziachristos, V. Eigenspectra optoacoustic tomography achieves quantitative blood oxygenation imaging deep in tissues. Nat. Commun. 2016, 7, 12121. [Google Scholar] [CrossRef] [PubMed]
- Cox, B.T.; Arridge, S.R.; Köstli, K.P.; Beard, P.C. Two-dimensional quantitative photoacoustic image reconstruction of absorption distributions in scattering media by use of a simple iterative method. Appl. Opt. 2006, 45, 1866–1875. [Google Scholar] [CrossRef] [PubMed]
- Cox, B.; Laufer, J.; Beard, P. The challenges for quantitative photoacoustic imaging. Photons Plus Ultrasound: Imaging and Sensing. Int. Soc. Opt. Photonics 2009, 7177, 717713. [Google Scholar]
- Cox, B.; Laufer, J.G.; Arridge, S.R.; Beard, P.C. Quantitative spectroscopic photoacoustic imaging: A review. J. Biomed. Opt. 2012, 17, 061202. [Google Scholar] [CrossRef]
- Yuan, Z.; Jiang, H. Quantitative photoacoustic tomography: Recovery of optical absorption coefficient maps of heterogeneous media. Appl. Phys. Lett. 2006, 88, 231101. [Google Scholar] [CrossRef]
- Yuan, Z.; Jiang, H. Quantitative photoacoustic tomography. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2009, 367, 3043–3054. [Google Scholar] [CrossRef]
- Wang, Y.; He, J.; Li, J.; Lu, T.; Li, Y.; Ma, W.; Zhang, L.; Zhou, Z.; Zhao, H.; Gao, F. Toward whole-body quantitative photoacoustic tomography of small-animals with multi-angle light-sheet illuminations. Biomed. Opt. Express 2017, 8, 3778–3795. [Google Scholar] [CrossRef] [PubMed]
- Saratoon, T.; Tarvainen, T.; Cox, B.; Arridge, S. A gradient-based method for quantitative photoacoustic tomography using the radiative transfer equation. Inverse Probl. 2013, 29, 075006. [Google Scholar] [CrossRef]
- Tarvainen, T.; Pulkkinen, A.; Cox, B.T.; Arridge, S.R. Utilising the radiative transfer equation in quantitative photoacoustic tomography. Photons Plus Ultrasound Imaging Sens. 2017, 10064. [Google Scholar] [CrossRef]
- Haltmeier, M.; Neumann, L.; Rabanser, S. Single-stage reconstruction algorithm for quantitative photoacoustic tomography. Inverse Probl. 2015, 31, 065005. [Google Scholar] [CrossRef]
- Kaplan, B.A.; Buchmann, J.; Prohaska, S.; Laufer, J. Monte-Carlo-based inversion scheme for 3D quantitative photoacoustic tomography. Photons Plus Ultrasound: Imaging and Sensing. Int. Soc. Opt. Photonics 2017, 10064, 100645J. [Google Scholar]
- Tzoumas, S.; Ntziachristos, V. Spectral unmixing techniques for optoacoustic imaging of tissue pathophysiology. Philos. Trans. R. Soc. A 2017, 375, 20170262. [Google Scholar] [CrossRef] [PubMed]
- Perekatova, V.; Subochev, P.; Kleshnin, M.; Turchin, I. Optimal wavelengths for optoacoustic measurements of blood oxygen saturation in biological tissues. Biomed. Opt. Express 2016, 7, 3979–3995. [Google Scholar] [CrossRef]
- Glatz, J.; Deliolanis, N.C.; Buehler, A.; Razansky, D.; Ntziachristos, V. Blind source unmixing in multi-spectral optoacoustic tomography. Opt. Express 2011, 19, 3175–3184. [Google Scholar] [CrossRef]
- Cai, C.; Deng, K.; Ma, C.; Luo, J. End-to-end deep neural network for optical inversion in quantitative photoacoustic imaging. Opt. Lett. 2018, 43, 2752–2755. [Google Scholar] [CrossRef]
- Kirchner, T.; Gröhl, J.; Maier-Hein, L. Context encoding enables machine learning-based quantitative photoacoustics. J. Biomed. Opt. 2018, 23, 056008. [Google Scholar] [CrossRef]
- Fonseca, M.; Saratoon, T.; Zeqiri, B.; Beard, P.; Cox, B. Sensitivity of quantitative photoacoustic tomography inversion schemes to experimental uncertainty. SPIE BiOS. Int. Soc. Opt. Photonics 2016, 9708, 97084X. [Google Scholar]
- Maier-Hein, L.; Franz, A.M.; Santos, T.R.D.; Schmidt, M.; Fangerau, M.; Meinzer, H.; Fitzpatrick, J.M. Convergent Iterative Closest-Point Algorithm to Accomodate Anisotropic and Inhomogenous Localization Error. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1520–1532. [Google Scholar] [CrossRef] [PubMed]
- Alterovitz, R.; Branicky, M.; Goldberg, K. Motion Planning Under Uncertainty for Image-guided Medical Needle Steering. Int. J. Robot. Res. 2008, 27, 1361–1374. [Google Scholar] [CrossRef] [PubMed]
- Sykes, J.R.; Brettle, D.S.; Magee, D.R.; Thwaites, D.I. Investigation of uncertainties in image registration of cone beam CT to CT on an image-guided radiotherapy system. Phys. Med. Boil. 2009, 54, 7263–7283. [Google Scholar] [CrossRef] [PubMed]
- Risholm, P.; Janoos, F.; Norton, I.; Golby, A.J.; Wells, W.M. Bayesian characterization of uncertainty in intra-subject non-rigid registration. Med. Image Anal. 2013, 17, 538–555. [Google Scholar] [CrossRef] [PubMed]
- Nair, T.; Precup, D.; Arnold, D.L.; Arbel, T. Exploring Uncertainty Measures in Deep Networks for Multiple Sclerosis Lesion Detection and Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018; Springer: Berlin, Germany, 2018; pp. 655–663. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Li, Y.; Gal, Y. Dropout Inference in Bayesian Neural Networks with Alpha-divergences. arXiv, 2017; arXiv:1703.02914. [Google Scholar]
- Leibig, C.; Allken, V.; Ayhan, M.S.; Berens, P.; Wahl, S. Leveraging uncertainty information from deep neural networks for disease detection. Sci. Rep. 2017, 7, 17816. [Google Scholar] [CrossRef]
- Feindt, M. A Neural Bayesian Estimator for Conditional Probability Densities. arXiv, 2004; arXiv:Phys./0402093. [Google Scholar]
- Zhu, Y.; Zabaras, N. Bayesian deep convolutional encoder-decoder networks for surrogate modeling and uncertainty quantification. J. Comput. Phys. 2018, 366, 415–447. [Google Scholar] [CrossRef]
- Kohl, S.A.; Romera-Paredes, B.; Meyer, C.; De Fauw, J.; Ledsam, J.R.; Maier-Hein, K.H.; Eslami, S.; Rezende, D.J.; Ronneberger, O. A Probabilistic U-Net for Segmentation of Ambiguous Images. arXiv, 2018; arXiv:1806.05034. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv, 2013; arXiv:1312.6114. [Google Scholar]
- Mescheder, L.; Nowozin, S.; Geiger, A. Adversarial variational bayes: Unifying variational autoencoders and generative adversarial networks. arXiv, 2017; arXiv:1701.04722. [Google Scholar]
- Ardizzone, L.; Kruse, J.; Wirkert, S.; Rahner, D.; Pellegrini, E.W.; Klessen, R.S.; Maier-Hein, L.; Rother, C.; Köthe, U. Analyzing Inverse Problems with Invertible Neural Networks. arXiv, 2018; arXiv:1808.04730. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 6402–6413. [Google Scholar]
- Smith, L.; Gal, Y. Understanding Measures of Uncertainty for Adversarial Example Detection. arXiv, 2018; arXiv:1803.08533. [Google Scholar]
- Pulkkinen, A.; Cox, B.T.; Arridge, S.R.; Goh, H.; Kaipio, J.P.; Tarvainen, T. Direct estimation of optical parameters from photoacoustic time series in quantitative photoacoustic tomography. IEEE Trans. Med. Imaging 2016, 35, 2497–2508. [Google Scholar] [CrossRef] [PubMed]
- Pulkkinen, A.; Cox, B.T.; Arridge, S.R.; Kaipio, J.P.; Tarvainen, T. Estimation and uncertainty quantification of optical properties directly from the photoacoustic time series. Photons Plus Ultrasound: Imaging and Sensing 2017. Int. Soc. Opt. Photonics 2017, 10064, 100643N. [Google Scholar]
- Tick, J.; Pulkkinen, A.; Tarvainen, T. Image reconstruction with uncertainty quantification in photoacoustic tomography. J. Acoust. Soc. Am. 2016, 139, 1951–1961. [Google Scholar] [CrossRef] [PubMed]
- Tick, J.; Pulkkinen, A.; Tarvainen, T. Photoacoustic image reconstruction with uncertainty quantification. In EMBEC & NBC 2017; Eskola, H., Väisänen, O., Viik, J., Hyttinen, J., Eds.; Springer: Singapore, 2018; pp. 113–116. [Google Scholar]
- Gröhl, J.; Kirchner, T.; Maier-Hein, L. Confidence estimation for quantitative photoacoustic imaging. Photons Plus Ultrasound: Imaging and Sensing 2018. Int. Soc. Opt. Photonics 2018, 10494, 104941C. [Google Scholar] [CrossRef]
- Welvaert, M.; Rosseel, Y. On the Definition of Signal-To-Noise Ratio and Contrast-To-Noise Ratio for fMRI Data. PLoS ONE 2013, 8, e77089. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention (MICCAI); Springer: Berlin, Germany, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in PyTorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Isensee, F.; Petersen, J.; Klein, A.; Zimmerer, D.; Jaeger, P.F.; Kohl, S.; Wasserthal, J.; Koehler, G.; Norajitra, T.; Wirkert, S.; et al. nnU-Net: Self-adapting Framework for U-Net-Based Medical Image Segmentation. arXiv, 2018; arXiv:1809.10486. [Google Scholar]
- Bauer, A.Q.; Nothdurft, R.E.; Erpelding, T.N.; Wang, L.V.; Culver, J.P. Quantitative photoacoustic imaging: Correcting for heterogeneous light fluence distributions using diffuse optical tomography. J. Biomed. Opt. 2011, 16, 096016–096016. [Google Scholar] [CrossRef]
- Daoudi, K.; Hussain, A.; Hondebrink, E.; Steenbergen, W. Correcting photoacoustic signals for fluence variations using acousto-optic modulation. Opt. Express 2012, 20, 14117–14129. [Google Scholar] [CrossRef] [PubMed]
- Jacques, S.L. Coupling 3D Monte Carlo light transport in optically heterogeneous tissues to photoacoustic signal generation. Photoacoust 2014, 2, 137–142. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Cox, B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010, 15, 021314. [Google Scholar] [CrossRef] [PubMed]
- Waibel, D.; Gröhl, J.; Isensee, F.; Kirchner, T.; Maier-Hein, K.; Maier-Hein, L. Reconstruction of initial pressure from limited view photoacoustic images using deep learning. Photons Plus Ultrasound: Imaging and Sensing 2018. Int. Soc. Opt. Photonics 2018, 10494, 104942S. [Google Scholar] [CrossRef]
- Kirchner, T.; Wild, E.; Maier-Hein, K.H.; Maier-Hein, L. Freehand photoacoustic tomography for 3D angiography using local gradient information. Photons Plus Ultrasound Imaging Sens. 2016, 9708, 97083G. [Google Scholar] [CrossRef]
- Gröhl, J.; Kirchner, T.; Adler, T.; Maier-Hein, L. Silico 2D Photoacoustic Imaging Data; Zenodo: Meyrin, Switzerland, 2018. [Google Scholar] [CrossRef]
- Zimmerer, D.; Petersen, J.; Koehler, G.; Wasserthal, J.; Adler, T.; Wirkert, A. MIC-DKFZ/Trixi: Pre-Release; Zenodo: Meyrin, Switzerland, 2018. [Google Scholar] [CrossRef]
- Hauptmann, A.; Lucka, F.; Betcke, M.; Huynh, N.; Adler, J.; Cox, B.; Beard, P.; Ourselin, S.; Arridge, S. Model-Based Learning for Accelerated, Limited-View 3-D Photoacoustic Tomography. IEEE Trans. Med. Imaging 2018, 37, 1382–1393. [Google Scholar] [CrossRef]
- Antholzer, S.; Haltmeier, M.; Schwab, J. Deep learning for photoacoustic tomography from sparse data. Inverse Probl. Sci. Eng. 2018. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gröhl, J.; Kirchner, T.; Adler, T.; Maier-Hein, L. Confidence Estimation for Machine Learning-Based Quantitative Photoacoustics. J. Imaging 2018, 4, 147. https://doi.org/10.3390/jimaging4120147
Gröhl J, Kirchner T, Adler T, Maier-Hein L. Confidence Estimation for Machine Learning-Based Quantitative Photoacoustics. Journal of Imaging. 2018; 4(12):147. https://doi.org/10.3390/jimaging4120147
Chicago/Turabian StyleGröhl, Janek, Thomas Kirchner, Tim Adler, and Lena Maier-Hein. 2018. "Confidence Estimation for Machine Learning-Based Quantitative Photoacoustics" Journal of Imaging 4, no. 12: 147. https://doi.org/10.3390/jimaging4120147
APA StyleGröhl, J., Kirchner, T., Adler, T., & Maier-Hein, L. (2018). Confidence Estimation for Machine Learning-Based Quantitative Photoacoustics. Journal of Imaging, 4(12), 147. https://doi.org/10.3390/jimaging4120147




