Two-Dimensional Orthonormal Tree-Structured Haar Transform for Fast Block Matching
Abstract
1. Introduction
2. Basis Images of Two-Dimensional Orthonormal Tree-Structured Haar Transform for Fast Block Matching
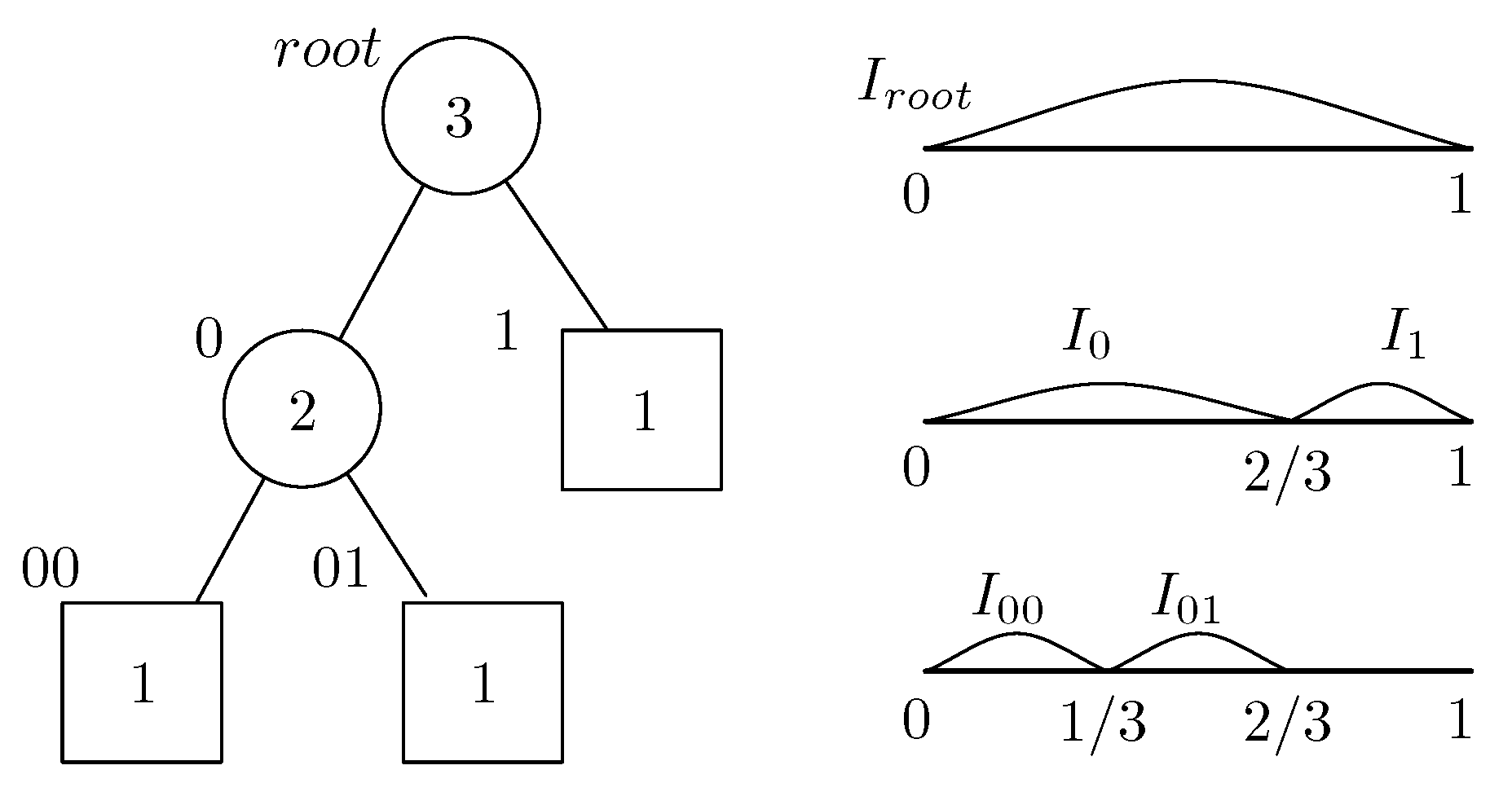
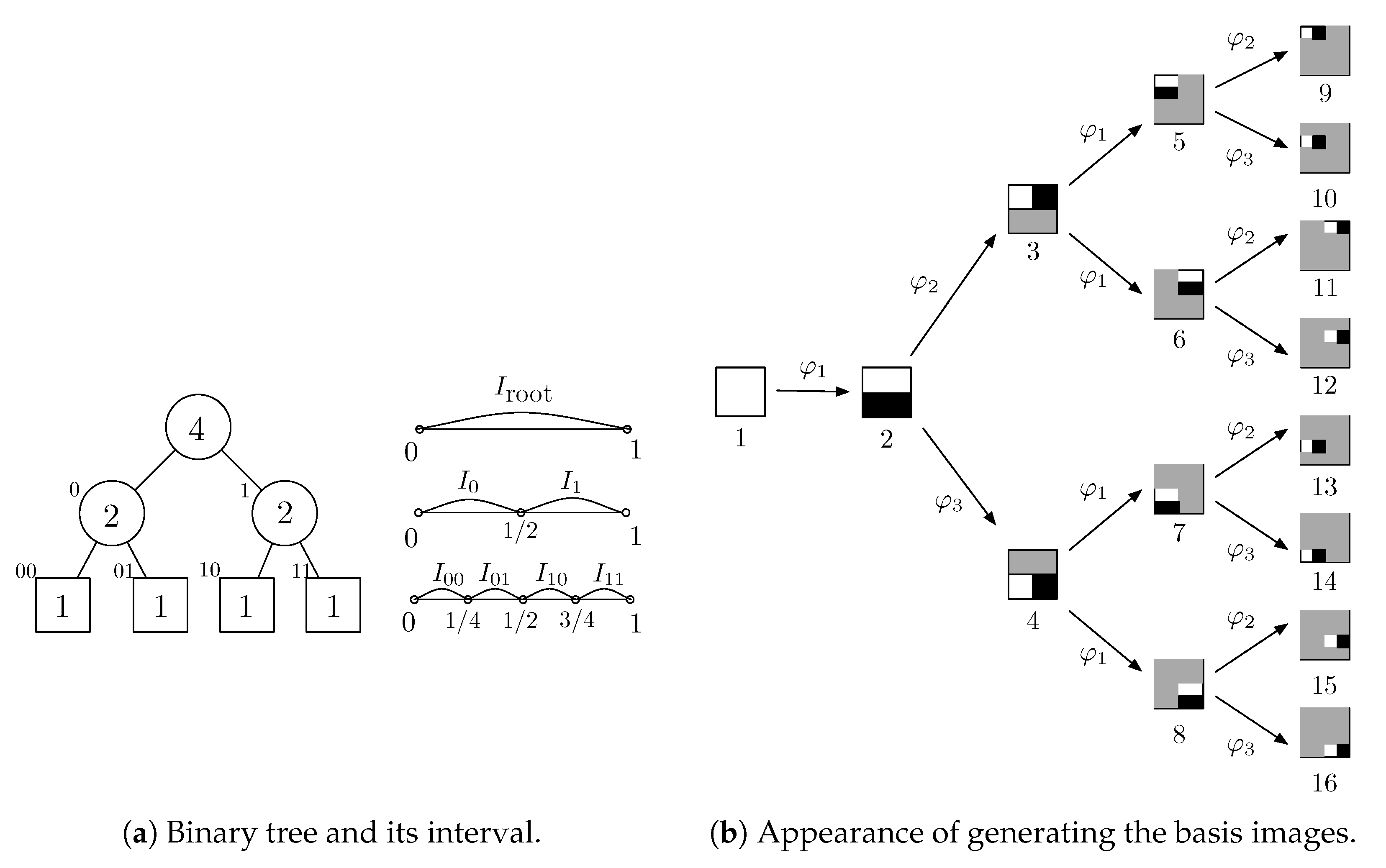
2.1. Binary Tree and Interval Subdivision
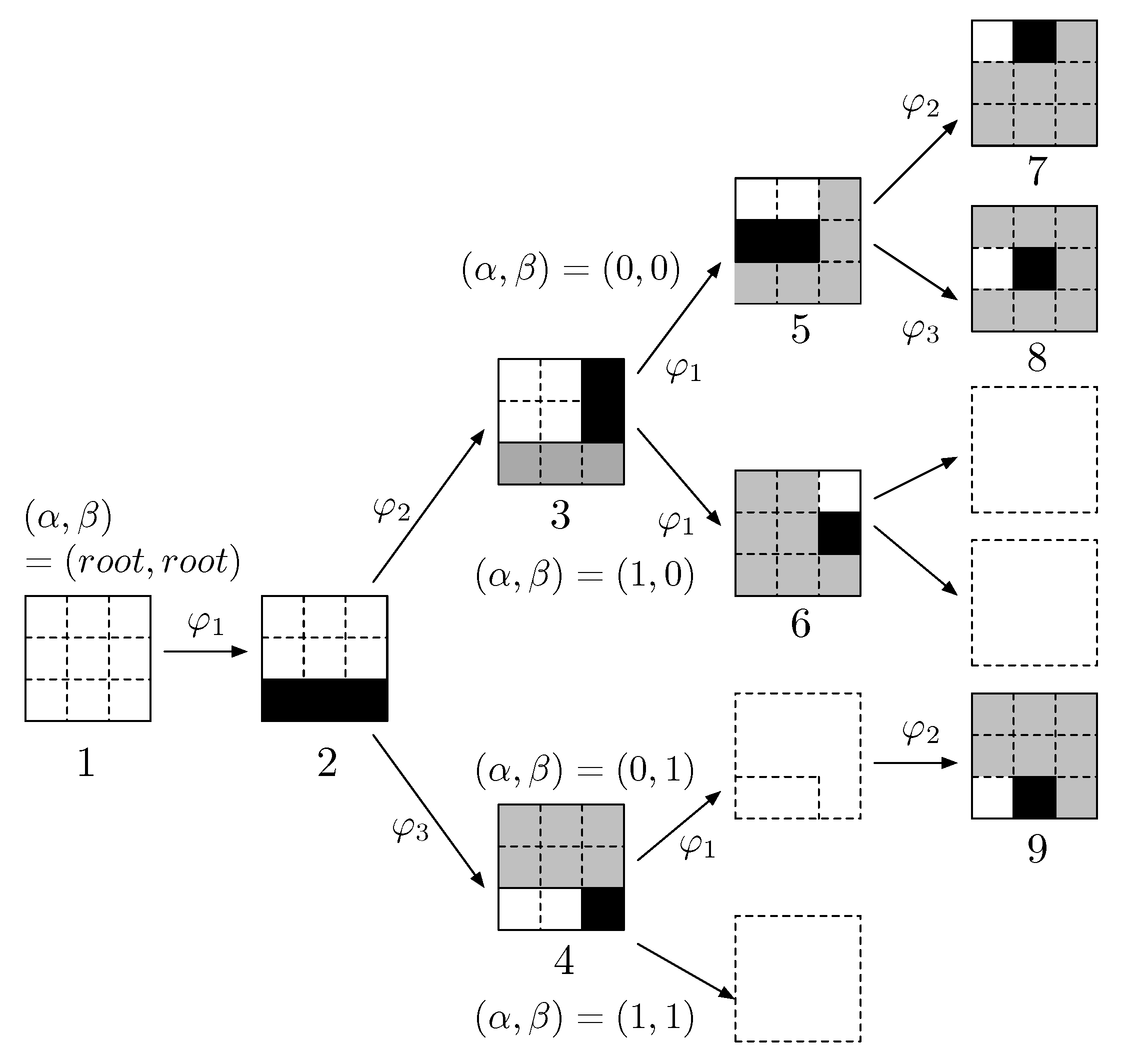
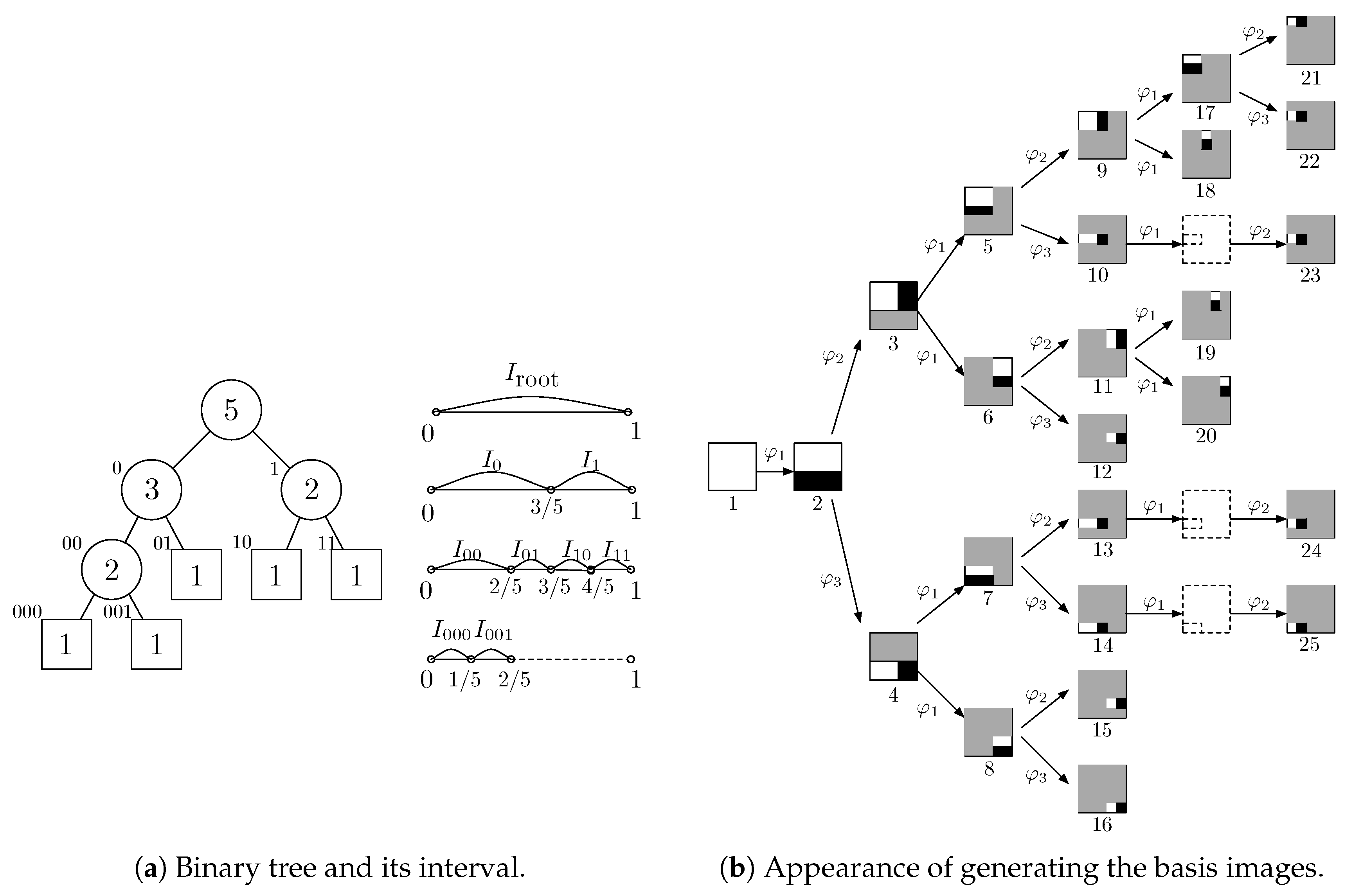
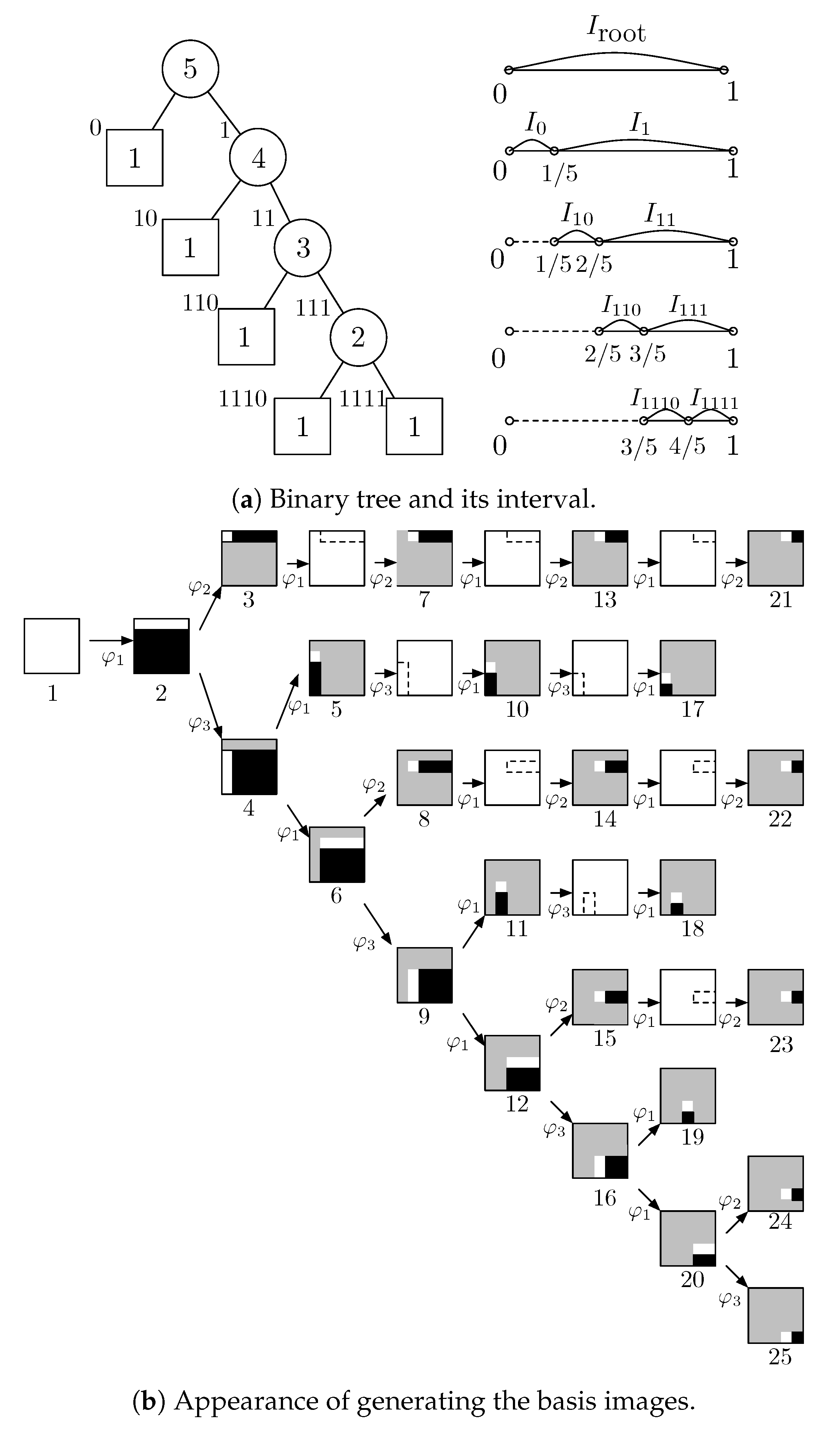
2.2. Orthonormal Tree-Structured Haar Transform Basis Images
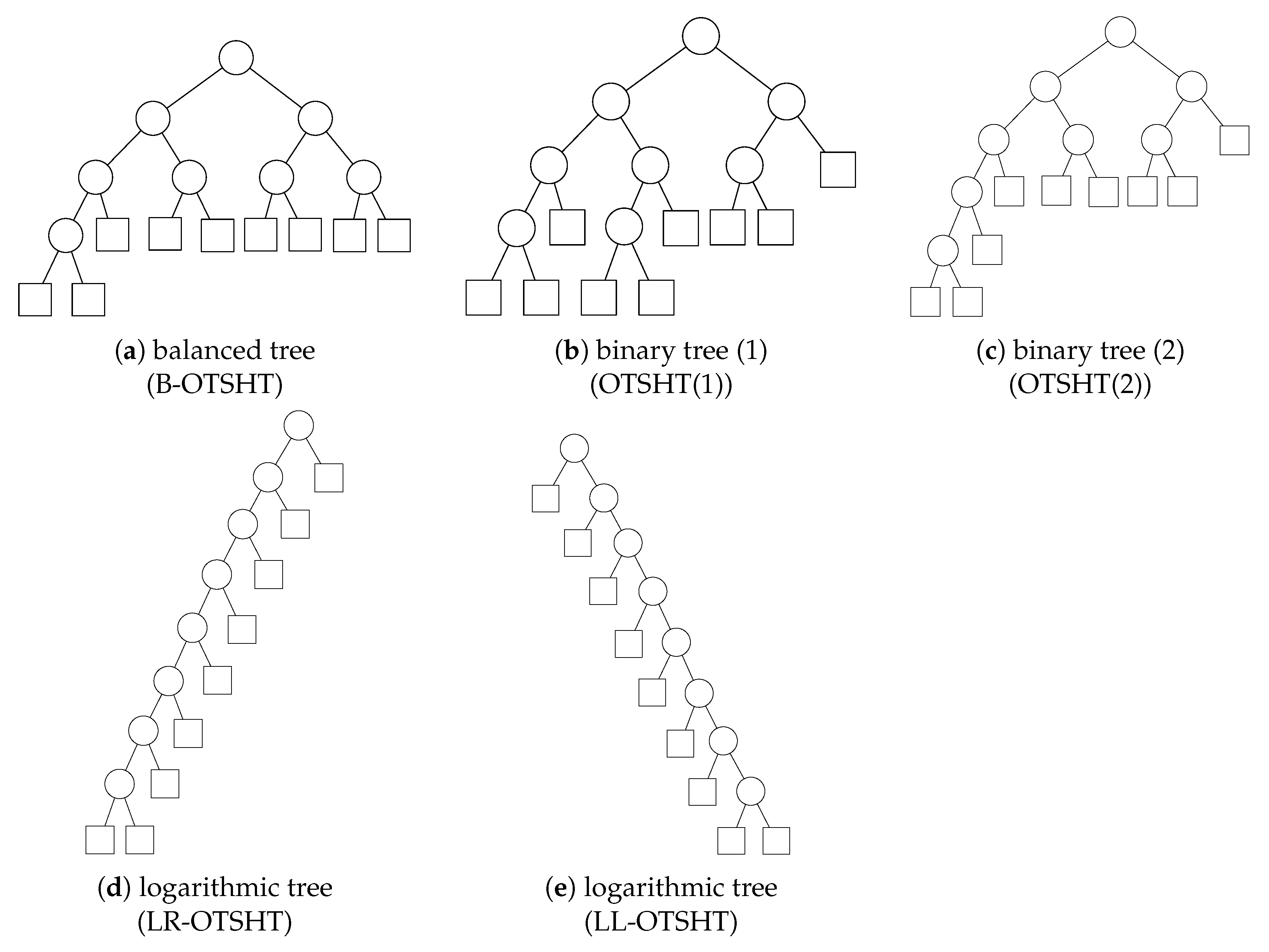
2.3. Balanced Binary Tree and Logarithmic Binary Tree
2.4. Relation between OHT and OTSHT
3. Fast Block Matching Algorithm Using Two-Dimensional Orthonormal Tree-Structured Haar Transform
3.1. FS-Equivalent Algorithm Using OTSHT
| Algorithm 1: FS-equivalent BM. |
Input: template of size and image
Output: estimated window |
3.2. Non FS-Equivalent Algorithm Using OTSHT
| Algorithm 2: non FS-equivalent BM. |
Input: template of size and image
Output: estimated window |
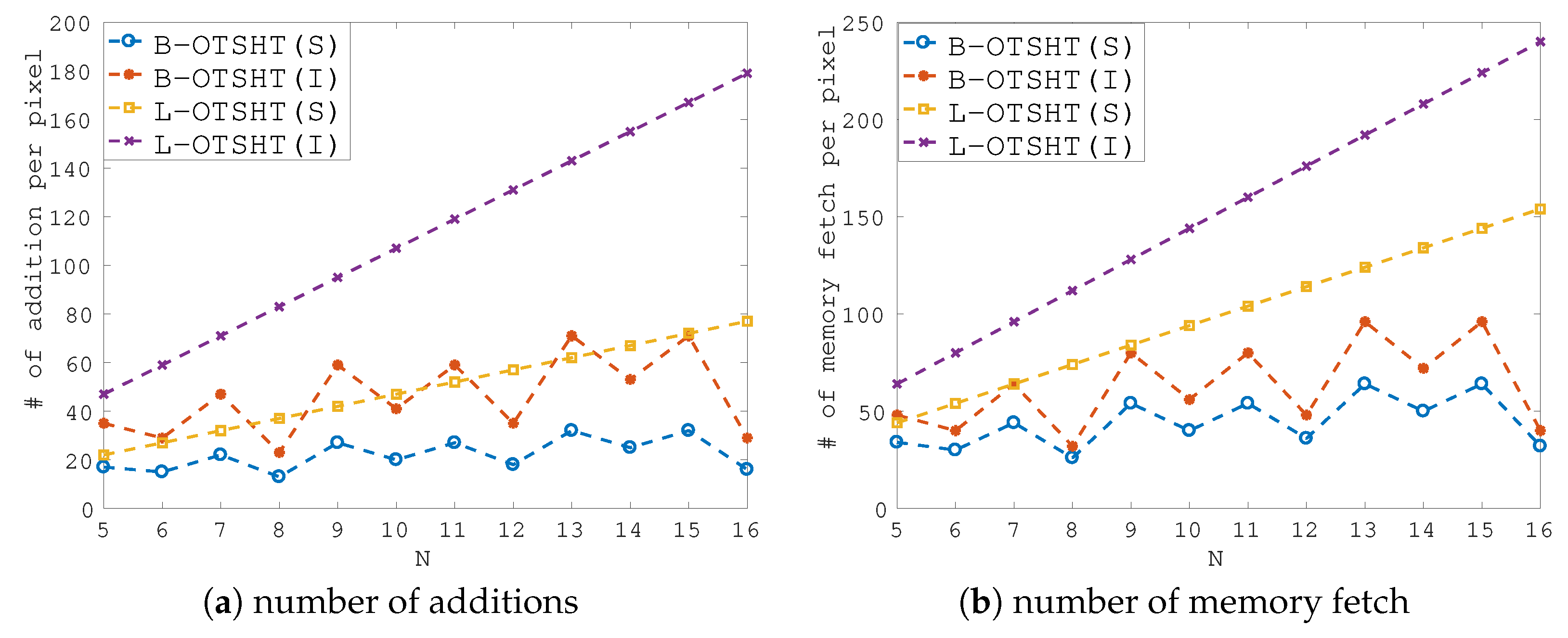
3.3. Computational Complexity
4. Experimental Section
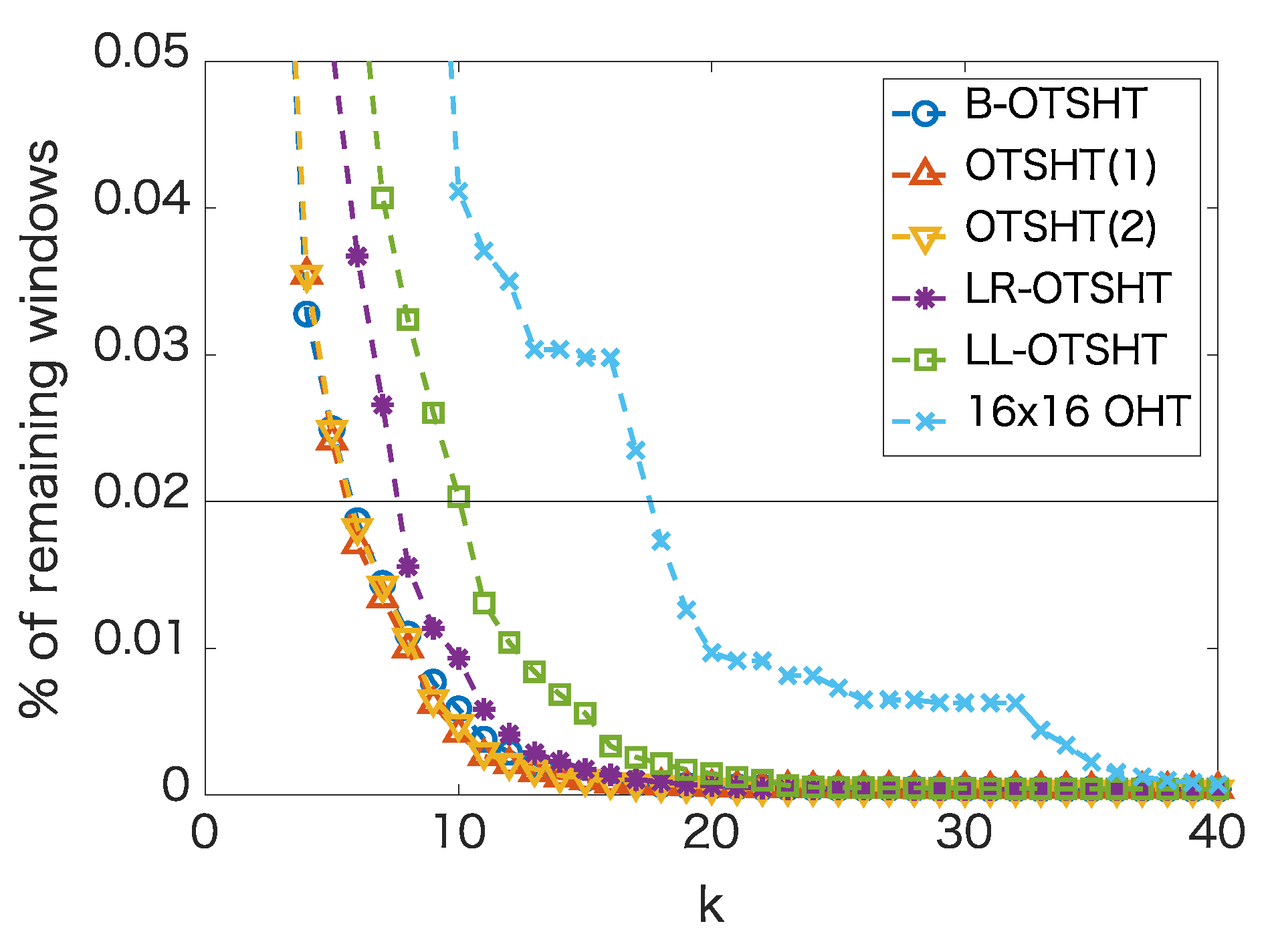
4.1. Pruning Performance of Different Tree Structures
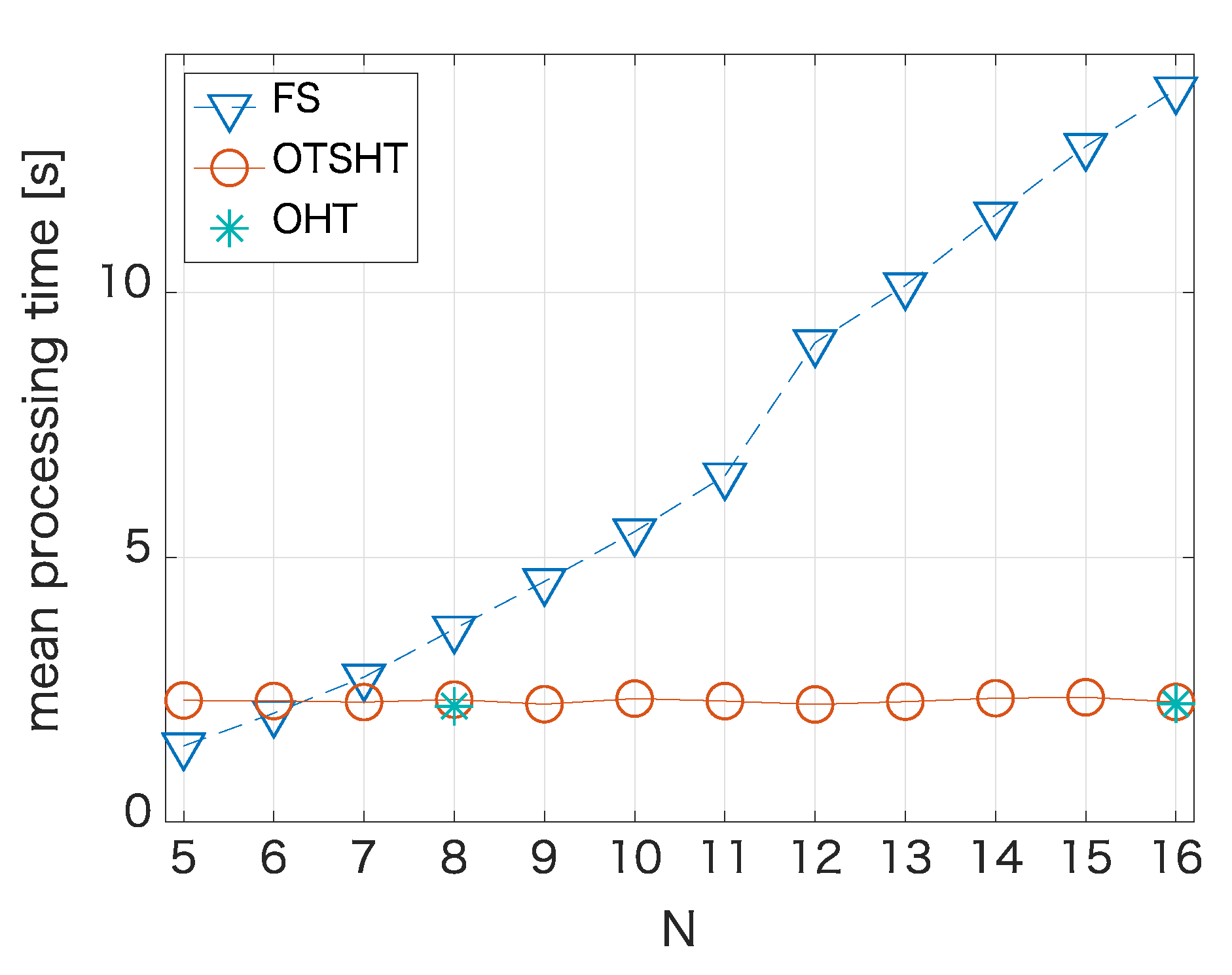
4.2. FS Equivalent Algorithm
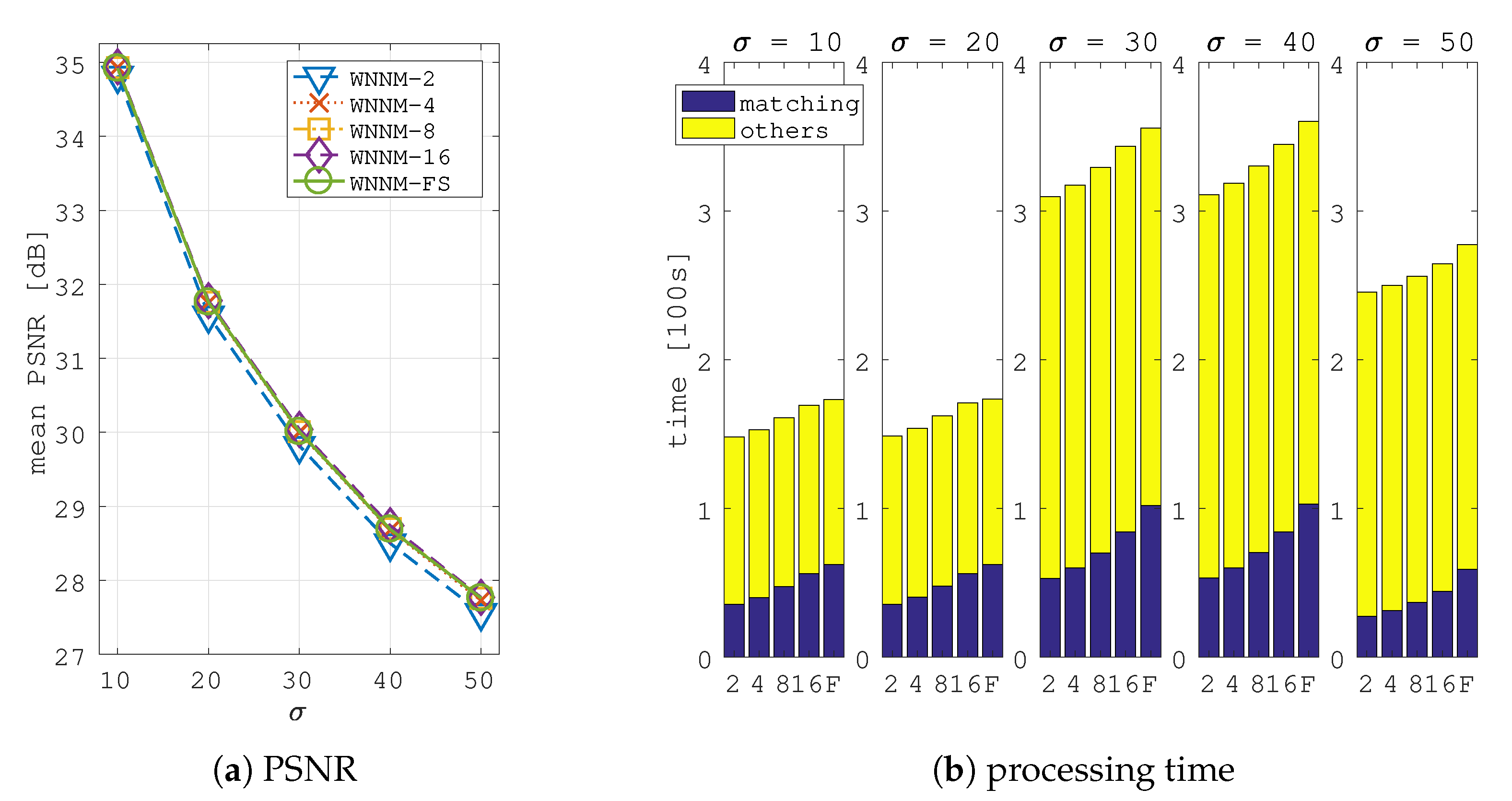
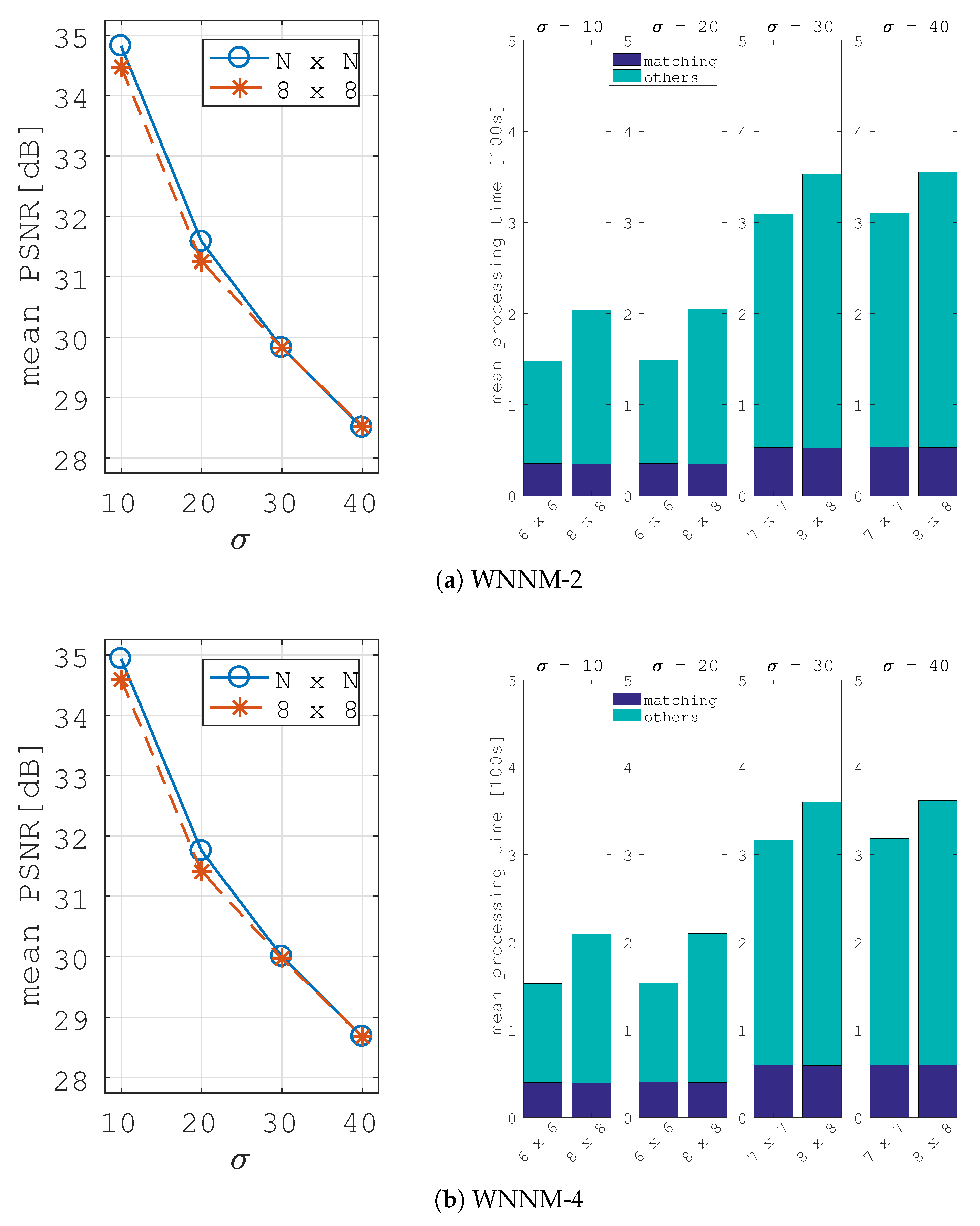
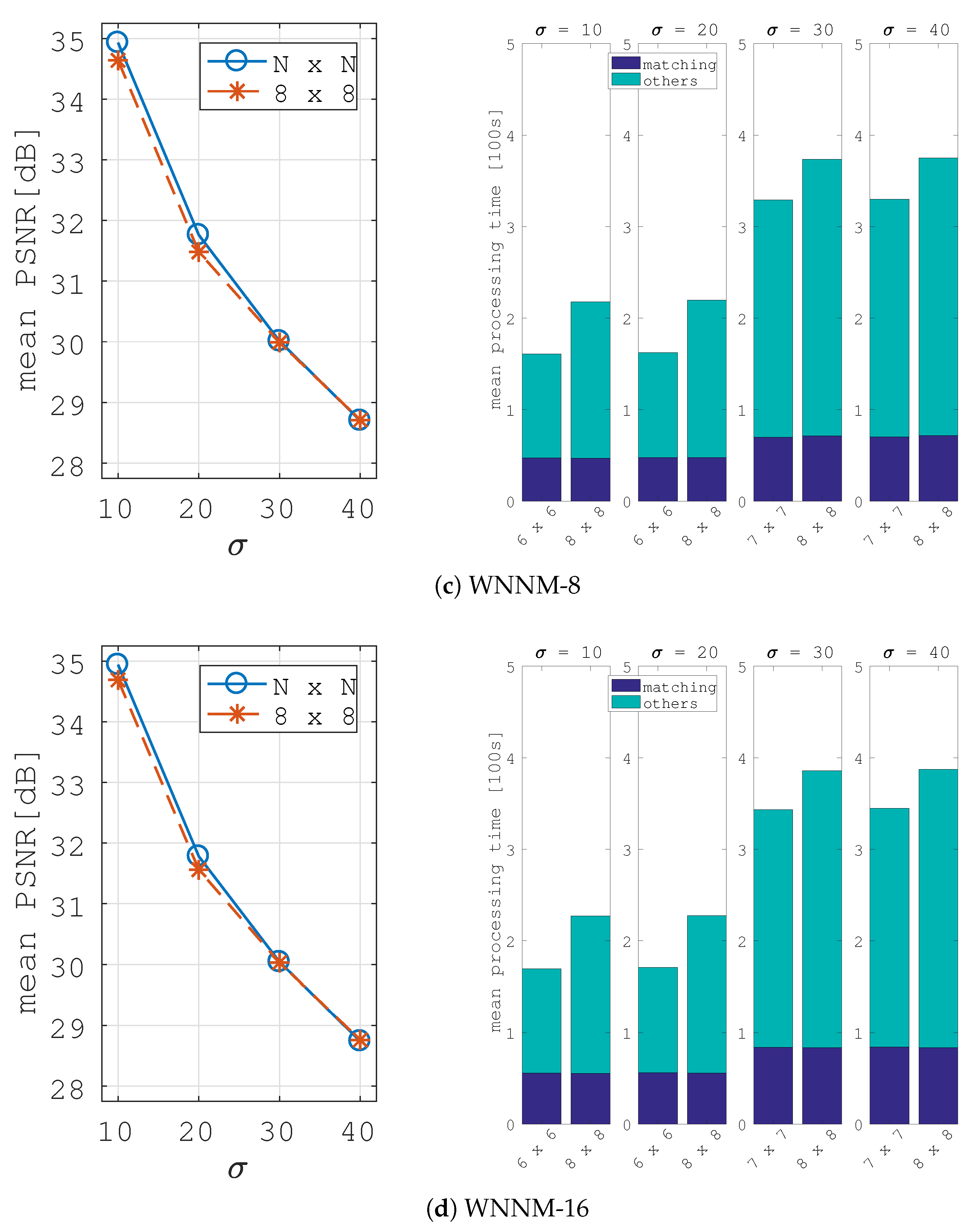
5. Image Denoising Application
| Algorithm 3: WNNM Image denoising. |
Input: Noisy image y
Output: clean image |
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dufour, R.; Miller, E.; Galatsanos, N. Template matching based object recognition with unknown geometric parameters. IEEE Trans. Image Process. 2002, 11, 1385–1396. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Xu, D.; Xiong, H.-C.; Li, Z.-Y. A novel object tracking algorithm based on enhanced perception hash and online template matching. In Proceedings of the 2016 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Changsha, China, 13–15 August 2016; pp. 494–499. [Google Scholar]
- Ding, L.; Goshtasby, A.; Satter, M. Volume image registration by template matching. Image Vis. Comput. 2001, 19, 821–832. [Google Scholar] [CrossRef]
- Sarraf, S.; Saverino, C.; Colestani, A.M. A robust and adaptive decision-making algorithm for detecting brain networks using functional mri within the spatial and frequency domain. In Proceedings of the 2016 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Las Vegas, NV, USA, 24–27 February 2016; pp. 53–56. [Google Scholar]
- Sarraf, S.; Anderson, J.; Tofighi, G. Deepad: Alzheimer disease classification via deep convolutional neural networks using MRI and fMRI. bioRxiv 2016, 070441. [Google Scholar] [CrossRef]
- Ouyang, W.; Tombari, F.; Mattocia, S.; Stefano, L.D.; Cham, W.-K. Performance Evaluation of Full Search Equivalent Pattern Matching Algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 127–143. [Google Scholar] [CrossRef] [PubMed]
- Tombari, F.; Mattoccia, S.; Stefano, L.D. Full search-equivalent pattern matching with incremental dissimilarity approximations. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 129–141. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, W.; Zhang, R.; Cham, W.-K. Fast pattern matching using orthogonal Haar transform. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3050–3057. [Google Scholar]
- Ouyang, W.; Cham, W.K. Fast algorithm for Walsh Hadamard transform on sliding windows. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 165–171. [Google Scholar] [CrossRef] [PubMed]
- Moshe, Y.; Hel-Or, H. Video block motion estimation based on Gray-code kernels. IEEE Trans. Image Process. 2009, 18, 2243–2254. [Google Scholar] [CrossRef] [PubMed]
- Crow, F. Summed-area tables for texture mapping. ACM SIGGRAPH Comput. Graph. 1984, 18, 207–212. [Google Scholar] [CrossRef]
- Viola, P.; Jones, M.J. Robust real-time object detection. Int. J. Comput. Vis. 2001, 57, 37–154. [Google Scholar]
- Li, Y.; Li, H.; Cai, Z. Fast orthogonal Haar transform pattern matching via image square sum. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1748–1760. [Google Scholar] [CrossRef] [PubMed]
- Alkhansari, M.G. A fast globally optimal algorithm for template matching using low-resolution pruning. IEEE Trans. Image Process. 2001, 10, 526–533. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by 3D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Criminisi, A.; Perez, P.; Toyama, K. Region Filling and Object Removal by Exemplar-Based Image Inpainting. IEEE Trans. Image Process. 2004, 13, 1200–1212. [Google Scholar] [CrossRef] [PubMed]
- Wexler, Y.; Shechtman, E.; Irani, M. Space-Time Completion of Video. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 463–476. [Google Scholar] [CrossRef] [PubMed]
- Egiazarian, K.; Astola, J. Tree-structured Haar Transform. J. Math. Imaging Vis. 2002, 16, 269–279. [Google Scholar] [CrossRef]
- Ito, I.; Egiazarian, K. Design of orthonormal Haar-like features for fast pattern matching. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 2452–2456. [Google Scholar]
- Ito, I.; Egiazarian, K. Full search equivalent fast block matching using orthonormal tree-structured Haar transform. In Proceedings of the 10th International Symposium on Image and Signal Processing and Analysis), Ljubljana, Slovenia, 18–20 September 2017. [Google Scholar] [CrossRef]
- Image Denoising with Block-Matching and 3D Filtering. Available online: http://www.cs.tut.fi/~foi/3D-DFT/ (accessed on 14 September 2018).

| N | B-OTSHT | L-OTSHT | ||||
|---|---|---|---|---|---|---|
| r | r | |||||
| 5 | 11 | 4 | 4 | 15 | 5 | 5 |
| 6 | 9 | 4 | 4 | 19 | 6 | 6 |
| 7 | 15 | 5 | 5 | 23 | 7 | 7 |
| 8 | 7 | 4 | 4 | 27 | 8 | 8 |
| 9 | 19 | 6 | 6 | 31 | 9 | 9 |
| 10 | 13 | 5 | 5 | 35 | 10 | 10 |
| 11 | 19 | 6 | 6 | 39 | 11 | 11 |
| 12 | 11 | 5 | 5 | 43 | 12 | 12 |
| 13 | 23 | 7 | 7 | 47 | 13 | 13 |
| 14 | 17 | 6 | 6 | 51 | 14 | 14 |
| 15 | 23 | 7 | 7 | 55 | 15 | 15 |
| 16 | 9 | 5 | 5 | 59 | 16 | 16 |
| Structure | r | Details | |
|---|---|---|---|
| B-OTSHT (Figure 8a) | 19 | 6 | , , , , , , , |
| , , , , , , , | |||
| , , , , | |||
| OTSHT (1) (Figure 8b) | 17 | 5 | , , , , , , , |
| , , , , , , , | |||
| , , , | |||
| OTSHT (2) (Figure 8c) | 25 | 6 | , , , , , , , |
| , , , , , , , | |||
| , , , , , , , | |||
| , , , | |||
| LR-OTSHT (Figure 8d) | 31 | 9 | , , , , , , , |
| , , , , , , , | |||
| , , , , , , , | |||
| , , , , , , , | |||
| , , | |||
| LL-OTSHT (Figure 8e) | 31 | 9 | , , , , , , , |
| , , , , , , , | |||
| , , , , , , , | |||
| , , , , , , , | |||
| , , |
| N | Iteration | Similar Patches | Search Window | |
|---|---|---|---|---|
| 10 | 6 | 8 | 70 | 60 × 60 |
| 20 | 6 | 8 | 70 | 60 × 60 |
| 30 | 7 | 12 | 90 | 60 × 60 |
| 40 | 7 | 12 | 90 | 60 × 60 |
| 50 | 8 | 14 | 120 | 60 × 60 |
| = 10 | WNNM-2 | WNNM-4 | WNNM-8 | WNNM-16 | WNNM-FS | ||||
| OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | ||
|---|---|---|---|---|---|---|---|---|---|
| Lena | 35.96 | 35.61 | 36.01 | 35.64 | 36.03 | 35.70 | 36.00 | 35.73 | 36.02 |
| Barbara | 35.13 | 34.80 | 35.31 | 34.95 | 35.35 | 35.03 | 35.47 | 35.12 | 35.49 |
| boat | 33.97 | 33.63 | 34.07 | 33.79 | 34.07 | 33.82 | 34.06 | 33.88 | 34.03 |
| house | 36.86 | 36.54 | 36.96 | 36.67 | 36.98 | 36.76 | 36.91 | 36.78 | 36.86 |
| peppers | 34.78 | 34.28 | 34.91 | 34.41 | 34.92 | 34.47 | 34.95 | 34.50 | 34.96 |
| man | 34.11 | 33.79 | 34.22 | 33.93 | 34.21 | 33.96 | 34.21 | 34.01 | 34.17 |
| couple | 33.98 | 33.66 | 34.11 | 33.79 | 34.10 | 33.83 | 34.12 | 33.88 | 34.11 |
| hill | 33.75 | 33.48 | 33.81 | 33.56 | 33.79 | 33.58 | 33.77 | 33.62 | 33.76 |
| average | 34.82 | 34.47 | 34.93 | 34.59 | 34.93 | 34.64 | 34.94 | 34.69 | 34.92 |
| = 20 | WNNM-2 | WNNM-4 | WNNM-8 | WNNM-16 | WNNM-FS | ||||
| OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | ||
| Lena | 32.98 | 32.65 | 33.13 | 32.74 | 33.12 | 32.82 | 33.13 | 32.91 | 33.11 |
| Barbara | 31.71 | 31.44 | 31.94 | 31.62 | 32.00 | 31.76 | 32.14 | 31.89 | 32.15 |
| boat | 30.81 | 30.46 | 30.98 | 30.68 | 30.94 | 30.70 | 30.95 | 30.80 | 30.95 |
| house | 33.85 | 33.41 | 33.97 | 33.61 | 34.13 | 33.76 | 34.09 | 33.77 | 34.05 |
| peppers | 31.32 | 30.84 | 31.52 | 30.97 | 31.54 | 31.05 | 31.58 | 31.13 | 31.55 |
| man | 30.65 | 30.38 | 30.79 | 30.52 | 30.76 | 30.57 | 30.74 | 30.62 | 30.71 |
| couple | 30.59 | 30.30 | 30.83 | 30.52 | 30.79 | 30.56 | 30.81 | 30.63 | 30.77 |
| hill | 30.75 | 30.48 | 30.87 | 30.60 | 30.82 | 30.64 | 30.81 | 30.70 | 30.77 |
| average | 31.58 | 31.25 | 31.75 | 31.41 | 31.76 | 31.48 | 31.78 | 31.56 | 31.76 |
| = 30 | WNNM-2 | WNNM-4 | WNNM-8 | WNNM-16 | WNNM-FS | ||||
| OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | ||
| Lena | 31.33 | 31.34 | 31.44 | 31.41 | 31.46 | 31.45 | 31.44 | 31.45 | 31.43 |
| Barbara | 29.90 | 29.96 | 30.11 | 30.14 | 30.17 | 30.22 | 30.27 | 30.32 | 30.28 |
| boat | 29.00 | 28.99 | 29.18 | 29.17 | 29.15 | 29.15 | 29.18 | 29.20 | 29.16 |
| house | 32.32 | 32.27 | 32.52 | 32.42 | 32.59 | 32.48 | 32.67 | 32.56 | 32.58 |
| peppers | 29.26 | 29.19 | 29.51 | 29.40 | 29.54 | 29.43 | 29.56 | 29.46 | 29.55 |
| man | 28.89 | 28.90 | 29.02 | 29.00 | 28.99 | 29.00 | 28.97 | 28.99 | 28.95 |
| couple | 28.72 | 28.73 | 28.94 | 28.94 | 28.96 | 28.96 | 28.97 | 28.99 | 28.94 |
| hill | 29.15 | 29.15 | 29.27 | 29.26 | 29.25 | 29.26 | 29.22 | 29.25 | 29.18 |
| average | 29.82 | 29.82 | 30.00 | 29.97 | 30.01 | 29.99 | 30.04 | 30.03 | 30.01 |
| = 40 | WNNM-2 | WNNM-4 | WNNM-8 | WNNM-16 | WNNM-FS | ||||
| OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | ||
| Lena | 29.99 | 30.03 | 30.12 | 30.13 | 30.12 | 30.15 | 30.14 | 30.18 | 30.07 |
| Barbara | 28.44 | 28.55 | 28.63 | 28.71 | 28.68 | 28.79 | 28.74 | 28.87 | 28.75 |
| boat | 27.67 | 27.68 | 27.88 | 27.88 | 27.88 | 28.89 | 27.88 | 27.91 | 27.86 |
| house | 30.95 | 30.93 | 31.21 | 31.15 | 31.31 | 31.24 | 31.49 | 31.42 | 31.34 |
| peppers | 27.84 | 27.82 | 28.05 | 27.95 | 28.11 | 28.03 | 28.15 | 28.07 | 28.13 |
| man | 27.70 | 27.72 | 27.85 | 27.84 | 27.82 | 27.82 | 27.79 | 27.80 | 27.76 |
| couple | 27.38 | 27.43 | 27.58 | 27.60 | 27.63 | 27.66 | 27.63 | 27.69 | 27.58 |
| hill | 28.01 | 28.03 | 28.12 | 28.15 | 28.09 | 28.13 | 28.07 | 28.12 | 28.02 |
| average | 28.50 | 28.52 | 28.68 | 28.68 | 28.70 | 28.71 | 28.74 | 28.76 | 28.69 |
| = 50 | WNNM-2 | WNNM-4 | WNNM-8 | WNNM-16 | WNNM-FS | ||||
| OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | OTSHT | OHT | ||
| Lena | 29.12 | 29.24 | 29.25 | 29.24 | 29.22 | ||||
| Barbara | 27.52 | 27.72 | 27.75 | 27.81 | 27.82 | ||||
| boat | 26.74 | 26.95 | 26.90 | 26.92 | 26.88 | ||||
| house | 29.96 | 30.18 | 30.39 | 30.41 | 30.38 | ||||
| peppers | 26.63 | 26.90 | 26.93 | 26.94 | 27.01 | ||||
| man | 26.85 | 26.95 | 26.95 | 26.93 | 26.91 | ||||
| couple | 26.47 | 26.62 | 26.62 | 26.64 | 26.63 | ||||
| hill | 27.19 | 27.32 | 27.28 | 27.27 | 27.24 | ||||
| average | 27.56 | 27.73 | 27.76 | 27.77 | 27.76 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ito, I.; Egiazarian, K. Two-Dimensional Orthonormal Tree-Structured Haar Transform for Fast Block Matching. J. Imaging 2018, 4, 131. https://doi.org/10.3390/jimaging4110131
Ito I, Egiazarian K. Two-Dimensional Orthonormal Tree-Structured Haar Transform for Fast Block Matching. Journal of Imaging. 2018; 4(11):131. https://doi.org/10.3390/jimaging4110131
Chicago/Turabian StyleIto, Izumi, and Karen Egiazarian. 2018. "Two-Dimensional Orthonormal Tree-Structured Haar Transform for Fast Block Matching" Journal of Imaging 4, no. 11: 131. https://doi.org/10.3390/jimaging4110131
APA StyleIto, I., & Egiazarian, K. (2018). Two-Dimensional Orthonormal Tree-Structured Haar Transform for Fast Block Matching. Journal of Imaging, 4(11), 131. https://doi.org/10.3390/jimaging4110131





