Green Stability Assumption: Unsupervised Learning for Statistics-Based Illumination Estimation
Abstract
:1. Introduction
2. Best-Known Statistics-Based Methods
2.1. Definition
2.2. Error Statistics
3. The Proposed Assumption
3.1. Practical Application
3.2. Motivation
3.3. Green Stability Assumption
4. Experimental Results
4.1. Experimental Setup
4.2. Accuracy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ebner, M. Color Constancy; The Wiley-IS&T Series in Imaging Science and Technology; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kim, S.J.; Lin, H.T.; Lu, Z.; Süsstrunk, S.; Lin, S.; Brown, M.S. A new in-camera imaging model for color computer vision and its application. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2289–2302. [Google Scholar] [PubMed]
- Gijsenij, A.; Gevers, T.; Van De Weijer, J. Computational color constancy: Survey and experiments. IEEE Trans. Image Process. 2011, 20, 2475–2489. [Google Scholar] [CrossRef] [PubMed]
- Barnard, K.; Cardei, V.; Funt, B. A comparison of computational color constancy algorithms. I: Methodology and experiments with synthesized data. IEEE Trans. Image Process. 2002, 11, 972–984. [Google Scholar] [CrossRef] [PubMed]
- Land, E.H. The Retinex Theory of Color Vision; Scientific America: New York, NY, USA, 1977. [Google Scholar]
- Funt, B.; Shi, L. The rehabilitation of MaxRGB. In Proceedings of the Color and Imaging Conference, San Antonio, TX, USA, 8–12 November 2010; Volume 2010, pp. 256–259. [Google Scholar]
- Banić, N.; Lončarić, S. Using the Random Sprays Retinex Algorithm for Global Illumination Estimation. In Proceedings of the Second Croatian Computer Vision Workshopn (CCVW 2013), Zagreb, Croatia, 19 September 2013; pp. 3–7. [Google Scholar]
- Banić, N.; Lončarić, S. Color Rabbit: Guiding the Distance of Local Maximums in Illumination Estimation. In Proceedings of the 2014 19th International Conference on Digital Signal Processing (DSP), Hong Kong, China, 20–23 August 2014; pp. 345–350. [Google Scholar]
- Banić, N.; Lončarić, S. Improving the White patch method by subsampling. In Proceedings of the 2014 21st IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 605–609. [Google Scholar]
- Buchsbaum, G. A spatial processor model for object colour perception. J. Frankl. Inst. 1980, 310, 1–26. [Google Scholar] [CrossRef]
- Finlayson, G.D.; Trezzi, E. Shades of gray and colour constancy. In Proceedings of the Color and Imaging Conference, Scottsdale, AZ, USA, 9–12 November 2004; Volume 2004, pp. 37–41. [Google Scholar]
- Van De Weijer, J.; Gevers, T.; Gijsenij, A. Edge-based color constancy. IEEE Trans. Image Process. 2007, 16, 2207–2214. [Google Scholar] [CrossRef] [PubMed]
- Gijsenij, A.; Gevers, T.; Van De Weijer, J. Improving color constancy by photometric edge weighting. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 918–929. [Google Scholar] [CrossRef] [PubMed]
- Joze, H.R.V.; Drew, M.S.; Finlayson, G.D.; Rey, P.A.T. The Role of Bright Pixels in Illumination Estimation. In Proceedings of the Color and Imaging Conference, Los Angeles, CA, USA, 12–16 November 2012; Volume 2012, pp. 41–46. [Google Scholar]
- Cheng, D.; Prasad, D.K.; Brown, M.S. Illuminant estimation for color constancy: Why spatial-domain methods work and the role of the color distribution. JOSA A 2014, 31, 1049–1058. [Google Scholar] [CrossRef] [PubMed]
- Finlayson, G.D.; Hordley, S.D.; Tastl, I. Gamut constrained illuminant estimation. Int. J. Comput. Vis. 2006, 67, 93–109. [Google Scholar] [CrossRef]
- Cardei, V.C.; Funt, B.; Barnard, K. Estimating the scene illumination chromaticity by using a neural network. JOSA A 2002, 19, 2374–2386. [Google Scholar] [CrossRef] [PubMed]
- Van De Weijer, J.; Schmid, C.; Verbeek, J. Using high-level visual information for color constancy. In Proceedings of the IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–20 October 2007; pp. 1–8. [Google Scholar]
- Gijsenij, A.; Gevers, T. Color Constancy using Natural Image Statistics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Gehler, P.V.; Rother, C.; Blake, A.; Minka, T.; Sharp, T. Bayesian color constancy revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Chakrabarti, A.; Hirakawa, K.; Zickler, T. Color constancy with spatio-spectral statistics. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1509–1519. [Google Scholar] [CrossRef] [PubMed]
- Banić, N.; Lončarić, S. Color Cat: Remembering Colors for Illumination Estimation. IEEE Signal Process. Lett. 2015, 22, 651–655. [Google Scholar] [CrossRef]
- Banić, N.; Lončarić, S. Using the red chromaticity for illumination estimation. In Proceedings of the 2015 9th International Symposium on Image and Signal Processing and Analysis (ISPA), Zagreb, Croatia, 7–9 September 2015; pp. 131–136. [Google Scholar]
- Banić, N.; Lončarić, S. Color Dog: Guiding the Global Illumination Estimation to Better Accuracy. In Proceedings of the VISAPP, Berlin, Germany, 11–14 March 2015; pp. 129–135. [Google Scholar]
- Banić, N.; Lončarić, S. Unsupervised Learning for Color Constancy. arXiv, 2017; arXiv:1712.00436. [Google Scholar]
- Finlayson, G.D. Corrected-moment illuminant estimation. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–3 December 2013; pp. 1904–1911. [Google Scholar]
- Chen, X.; Drew, M.S.; Li, Z.N.; Finlayson, G.D. Extended Corrected-Moments Illumination Estimation. Electron. Imaging 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Cheng, D.; Price, B.; Cohen, S.; Brown, M.S. Effective learning-based illuminant estimation using simple features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1000–1008. [Google Scholar]
- Barron, J.T. Convolutional Color Constancy. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 379–387. [Google Scholar]
- Barron, J.T.; Tsai, Y.T. Fast Fourier Color Constancy. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Bianco, S.; Cusano, C.; Schettini, R. Color Constancy Using CNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2015; pp. 81–89. [Google Scholar]
- Shi, W.; Loy, C.C.; Tang, X. Deep Specialized Network for Illuminant Estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 371–387. [Google Scholar]
- Hu, Y.; Wang, B.; Lin, S. Fully Convolutional Color Constancy with Confidence-weighted Pooling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4085–4094. [Google Scholar]
- Deng, Z.; Gijsenij, A.; Zhang, J. Source camera identification using Auto-White Balance approximation. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 57–64. [Google Scholar]
- Gijsenij, A.; Gevers, T.; Lucassen, M.P. Perceptual analysis of distance measures for color constancy algorithms. JOSA A 2009, 26, 2243–2256. [Google Scholar] [CrossRef] [PubMed]
- Finlayson, G.D.; Zakizadeh, R. Reproduction Angular Error: An Improved Performance Metric for Illuminant Estimation. Perception 2014, 310, 1–26. [Google Scholar]
- Banić, N.; Lončarić, S. A Perceptual Measure of Illumination Estimation Error. In Proceedings of the VISAPP, Berlin, Germany, 11–14 March 2015; pp. 136–143. [Google Scholar]
- Hordley, S.D.; Finlayson, G.D. Re-evaluating colour constancy algorithms. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; pp. 76–79. [Google Scholar]
- Finlayson, G.D.; Hordley, S.D.; Morovic, P. Colour constancy using the chromagenic constraint. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; pp. 1079–1086. [Google Scholar]
- Fredembach, C.; Finlayson, G. Bright chromagenic algorithm for illuminant estimation. J. Imaging Sci. Technol. 2008, 52, 40906-1. [Google Scholar] [CrossRef]
- Ciurea, F.; Funt, B. A large image database for color constancy research. In Proceedings of the Color and Imaging Conference, Scottsdale, AZ, USA, 3–7 November 2003; pp. 160–164. [Google Scholar]
- Joze, V.; Reza, H. Estimating the Colour of the Illuminant Using Specular Reflection and Exemplar-Based Method. Ph.D. Thesis, School of Computing Science, Simon Fraser University, Vancouver, BC, Canada, 2013. [Google Scholar]
- Rumsey, D.J. U Can: Statistics for Dummies; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Shi, L.; Funt, B. Re-Processed Version of the Gehler Color Constancy Dataset of 568 Images. Available online: http://www.cs.sfu.ca/~colour/data/ (accessed on 1 October 2018).
- Finlayson, G.D.; Hemrit, G.; Gijsenij, A.; Gehler, P. A Curious Problem with Using the Colour Checker Dataset for Illuminant Estimation. In Proceedings of the Color and Imaging Conference, Lillehammer, Norway, 11–15 September 2017; pp. 64–69. [Google Scholar]
- Lynch, S.E.; Drew, M.S.; Finlayson, K.G.D. Colour Constancy from Both Sides of the Shadow Edge. In Proceedings of the Color and Photometry in Computer Vision Workshop at the International Conference on Computer Vision, Melbourne, Australia, 15–18 September 2013. [Google Scholar]
- Banić, N.; Lončarić, S. Color Constancy—Image Processing Group. Available online: http://www.fer.unizg.hr/ipg/resources/color_constancy/ (accessed on 29 October 2018).
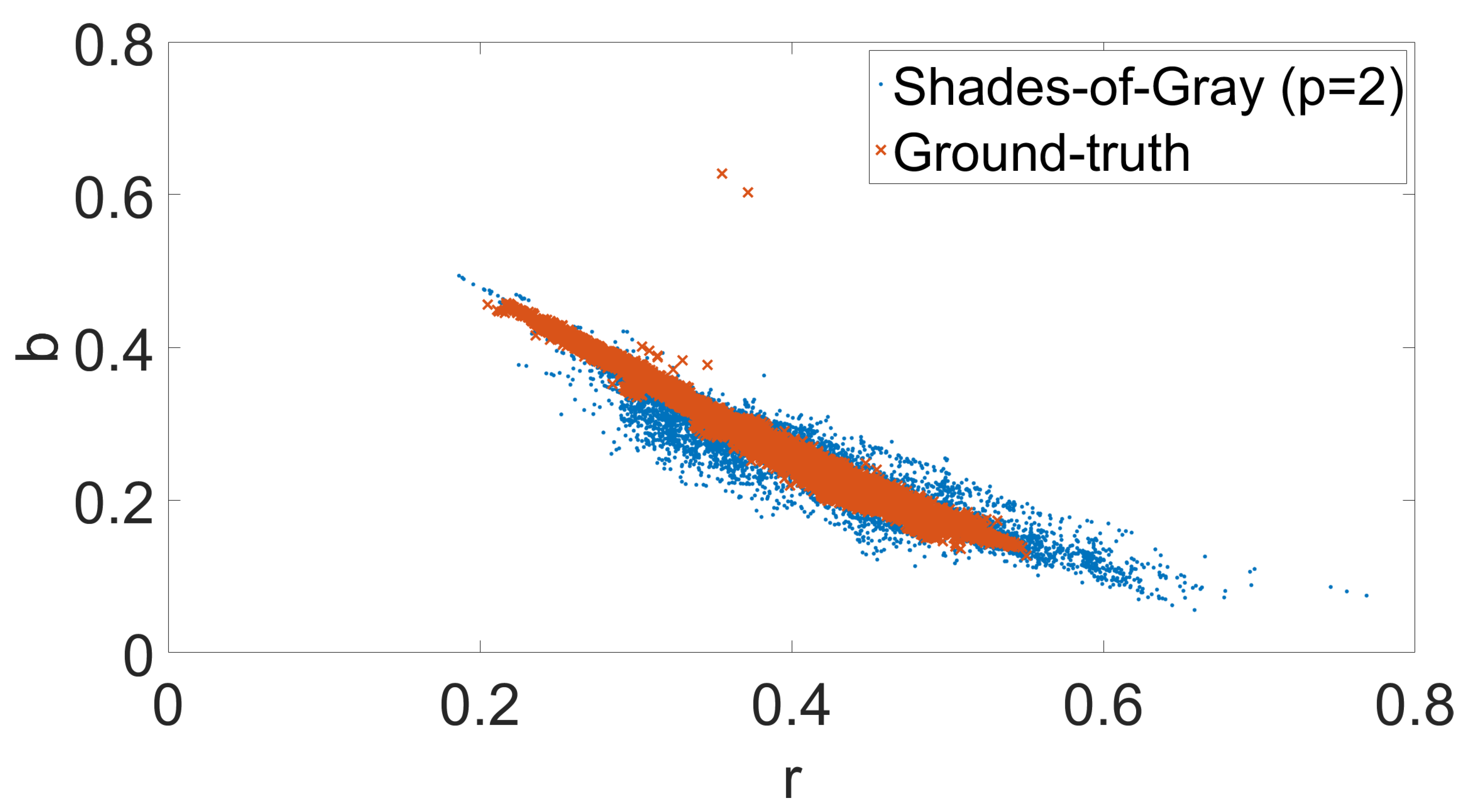
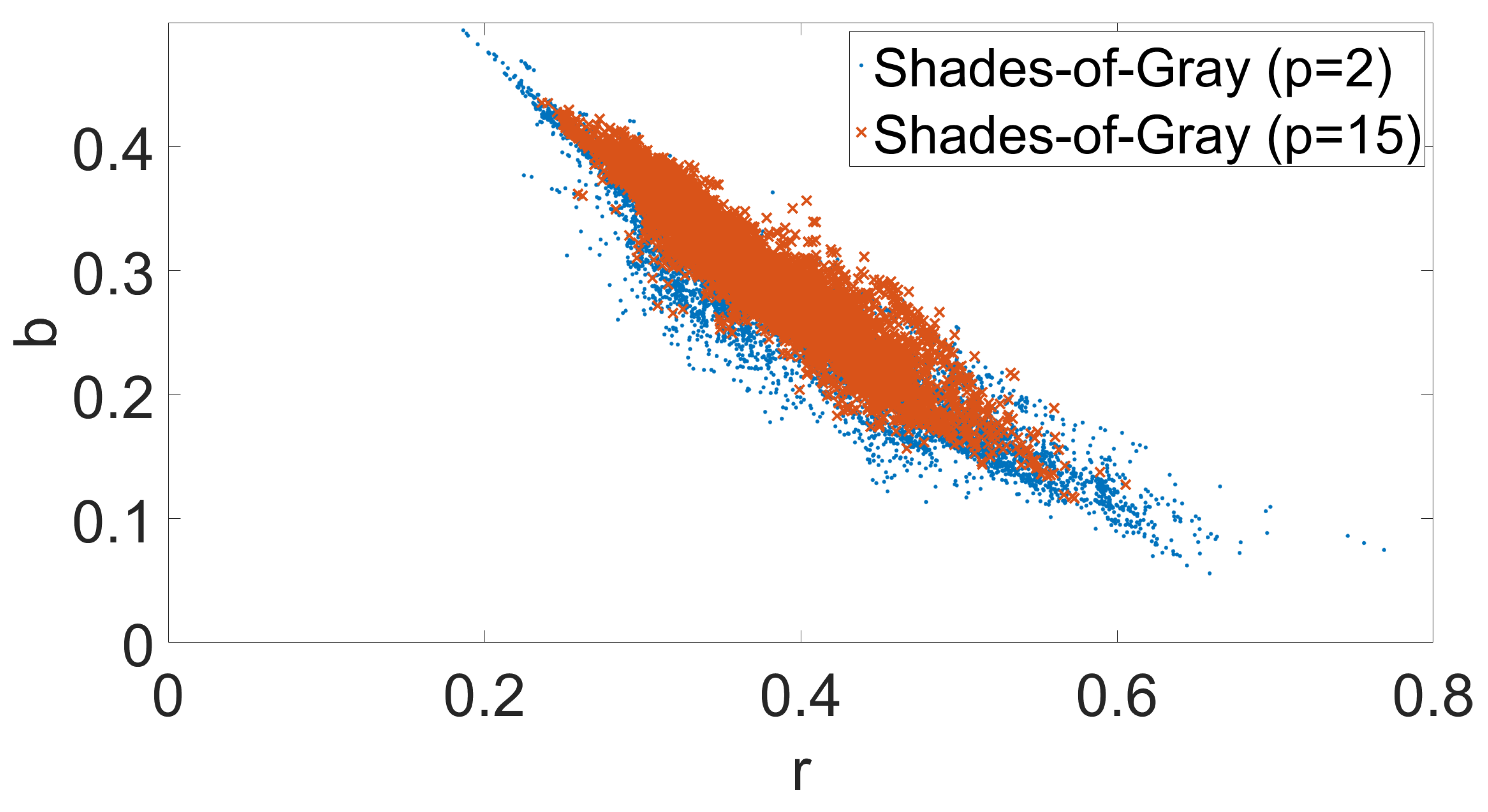
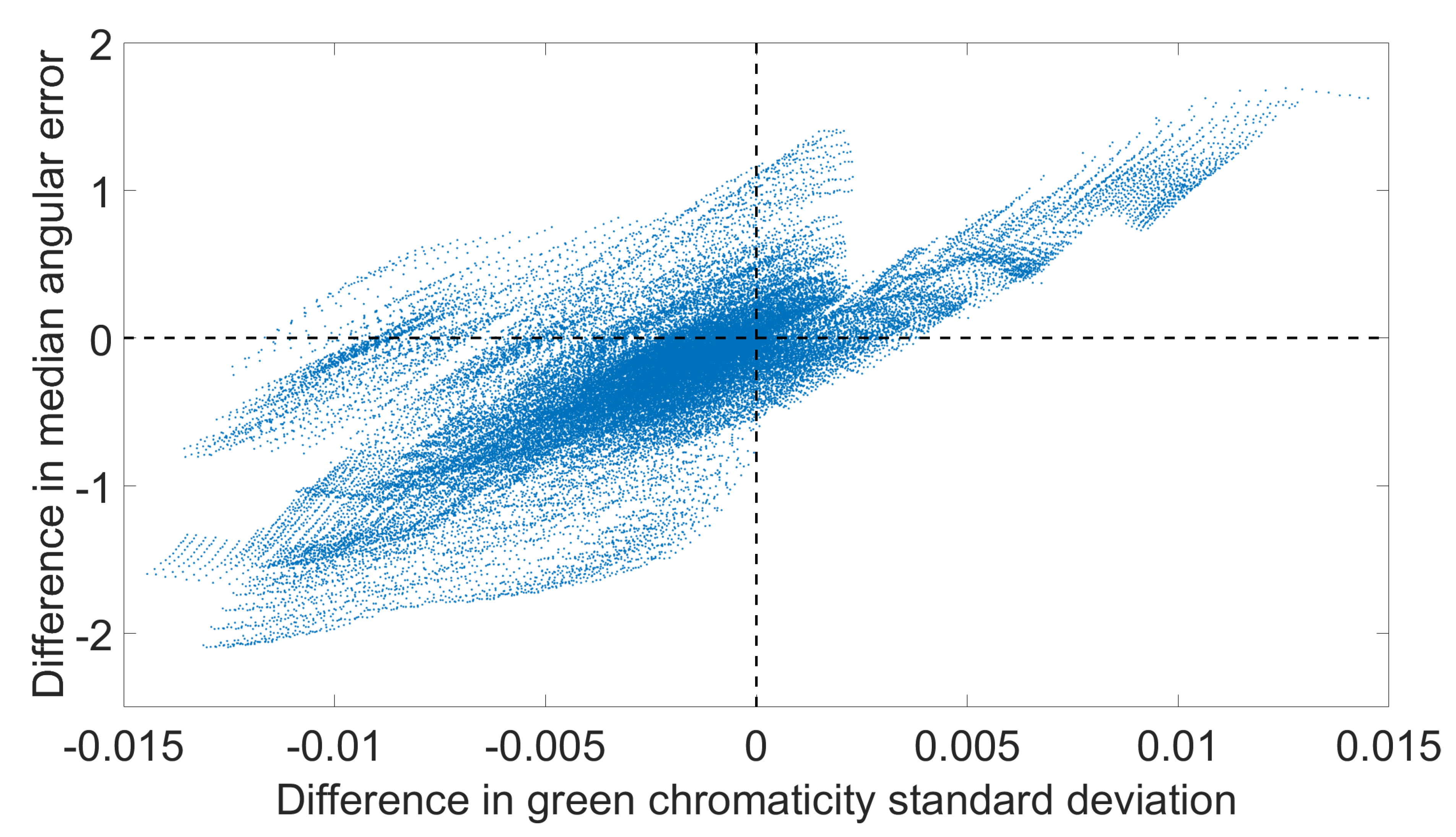
| Dataset | C1 | C2 | Fuji | N52 | Oly | Pan | Sam | Sony |
|---|---|---|---|---|---|---|---|---|
| Correlation | 0.9255 | 0.6381 | 0.8977 | 0.9443 | 0.8897 | 0.9644 | 0.8902 | 0.9095 |
| Algorithm | Mean | Med. | Tri. | Best 25% | Worst 25% | Avg. |
|---|---|---|---|---|---|---|
| Originally Reported Results | ||||||
| Shades-of-Gray [11] | 3.67 | 2.94 | 3.03 | 0.98 | 7.75 | 3.01 |
| General Gray-World [4] | 3.20 | 2.56 | 2.68 | 0.85 | 6.68 | 2.63 |
| 1st-order Gray-Edge [12] | 3.35 | 2.58 | 2.76 | 0.79 | 7.18 | 2.67 |
| 2nd-order Gray-Edge [12] | 3.36 | 2.70 | 2.80 | 0.89 | 7.14 | 2.76 |
| Revisited Results | ||||||
| Shades-of-Gray [11] | 3.48 | 2.63 | 2.81 | 0.81 | 7.62 | 2.76‘ |
| General Gray-World [4] | 3.37 | 2.49 | 2.61 | 0.73 | 7.58 | 2.61 |
| 1st-order Gray-Edge [12] | 3.12 | 2.19 | 2.39 | 0.71 | 7.11 | 2.42 |
| 2nd-order Gray-Edge [12] | 3.15 | 2.23 | 2.42 | 0.74 | 7.13 | 2.46 |
| Green Stability Assumption Results | ||||||
| Shades-of-Gray [11] | 3.44 | 2.65 | 2.81 | 0.83 | 7.41 | 2.75 |
| General Gray-World [4] | 3.40 | 2.63 | 2.76 | 0.77 | 7.42 | 2.69 |
| 1st-order Gray-Edge [12] | 3.29 | 2.36 | 2.55 | 0.79 | 7.36 | 2.58 |
| 2nd-order Gray-Edge [12] | 3.29 | 2.44 | 2.59 | 0.83 | 7.30 | 2.63 |
| Method | Mean | Median | Trimean |
|---|---|---|---|
| Originally Reported Results | |||
| Shades-of-Gray [11] | 6.14 | 5.33 | 5.51 |
| General Gray-World [4] | 6.14 | 5.33 | 5.51 |
| 1st-order Gray-Edge [12] | 5.88 | 4.65 | 5.11 |
| 2nd-order Gray-Edge [12] | 6.10 | 4.85 | 5.28 |
| Revisited Results | |||
| Shades-of-Gray [11] | 7.80 | 7.15 | 7.21 |
| General Gray-World [4] | 7.61 | 6.85 | 6.92 |
| 1st-order Gray-Edge [12] | 6.14 | 5.32 | 5.49 |
| 2nd-order Gray-Edge [12] | 6.89 | 5.84 | 6.06 |
| Green Stability Assumption Results | |||
| Shades-of-Gray [11] | 6.80 | 5.30 | 5.77 |
| General Gray-World [4] | 6.80 | 5.30 | 5.77 |
| 1st-order Gray-Edge [12] | 5.97 | 4.64 | 5.10 |
| 2nd-order Gray-Edge [12] | 6.69 | 5.17 | 5.72 |
| Method | Mean | Median | Trimean |
|---|---|---|---|
| Originally Reported Results | |||
| Shades-of-Gray [11] | 11.55 | 9.70 | 10.23 |
| General Gray-World [4] | 11.55 | 9.70 | 10.23 |
| 1st-order Gray-Edge [12] | 10.58 | 8.84 | 9.18 |
| 2nd-order Gray-Edge [12] | 10.68 | 9.02 | 9.40 |
| Revisited Results | |||
| Shades-of-Gray [11] | 13.32 | 11.57 | 12.10 |
| General Gray-World [4] | 13.69 | 12.11 | 12.55 |
| 1st-order Gray-Edge [12] | 11.06 | 9.54 | 9.81 |
| 2nd-order Gray-Edge [12] | 10.73 | 9.21 | 9.49 |
| Green Stability Assumption Results | |||
| Shades-of-Gray [11] | 12.68 | 10.50 | 11.25 |
| General Gray-World [4] | 12.68 | 10.50 | 11.25 |
| 1st-order Gray-Edge [12] | 13.41 | 11.04 | 11.87 |
| 2nd-order Gray-Edge [12] | 12.83 | 10.70 | 11.44 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banić, N.; Lončarić, S. Green Stability Assumption: Unsupervised Learning for Statistics-Based Illumination Estimation. J. Imaging 2018, 4, 127. https://doi.org/10.3390/jimaging4110127
Banić N, Lončarić S. Green Stability Assumption: Unsupervised Learning for Statistics-Based Illumination Estimation. Journal of Imaging. 2018; 4(11):127. https://doi.org/10.3390/jimaging4110127
Chicago/Turabian StyleBanić, Nikola, and Sven Lončarić. 2018. "Green Stability Assumption: Unsupervised Learning for Statistics-Based Illumination Estimation" Journal of Imaging 4, no. 11: 127. https://doi.org/10.3390/jimaging4110127
APA StyleBanić, N., & Lončarić, S. (2018). Green Stability Assumption: Unsupervised Learning for Statistics-Based Illumination Estimation. Journal of Imaging, 4(11), 127. https://doi.org/10.3390/jimaging4110127




