Fusing Multiple Multiband Images
Abstract
1. Introduction
2. Data Model
2.1. Forward Observation Model
2.2. Linear Mixture Model
2.3. Fusion Model
3. Problem
3.1. Maximum-Likelihood Estimation
3.2. Regularization
4. Algorithm
4.1. Iterations
4.2. Solutions of Subproblems
| Algorithm 1 The proposed algorithm |
| 1: initialize 2: % if is not known and has full spectral resolution 3: upscale and interpolate the output of 4: for 5: 6: 7: , 8: , 9: for % until a convergence criterion is met or a given maximum number of iterations is reached 10: 11: 12: for 13: 14: 15: for 16: 17: 18: for 19: 20: 21: 22: calculate the fused image 23: |
4.3. Convergence
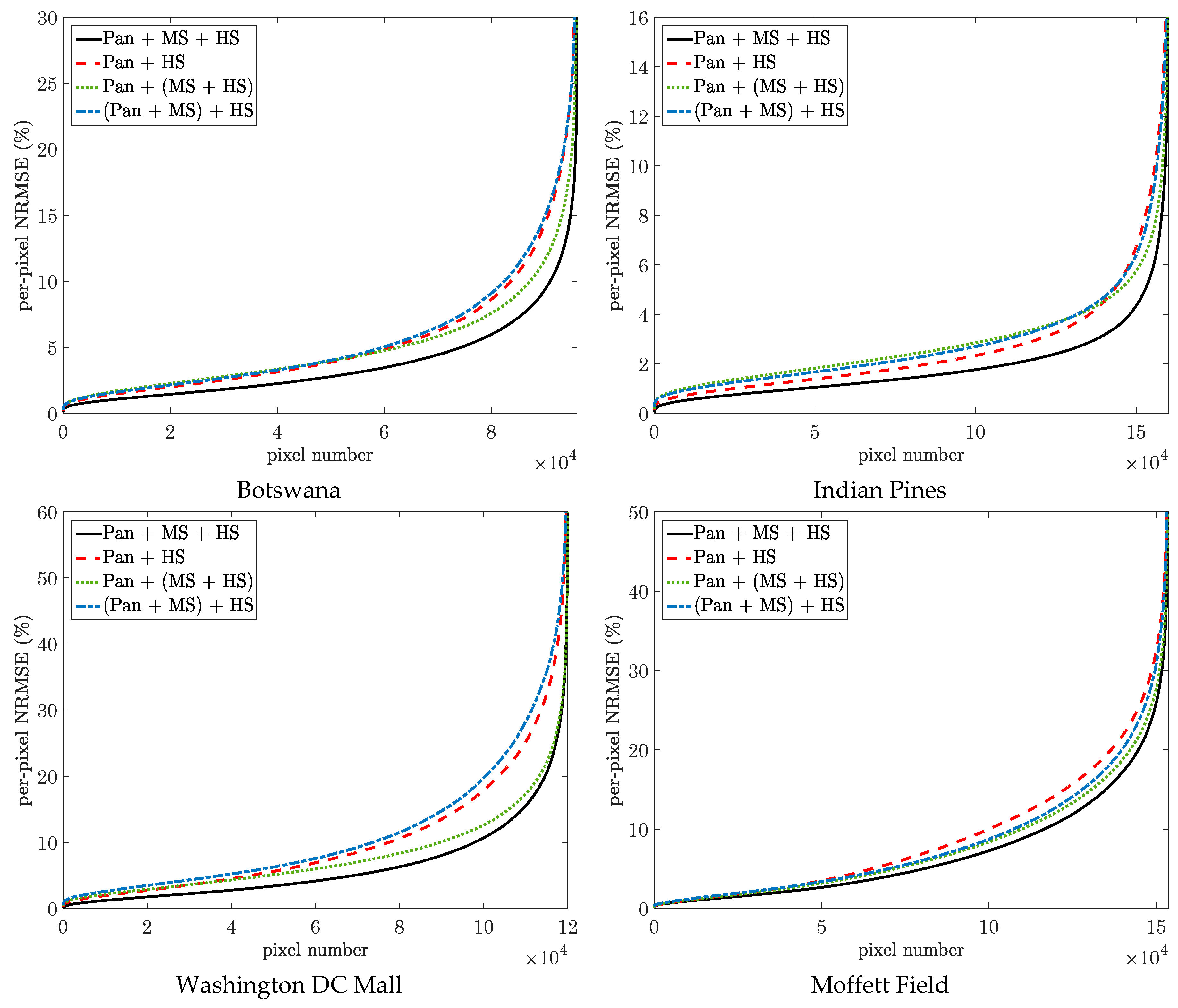
5. Simulations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arablouei, R. Fusion of multiple multiband images with complementary spatial and spectral resolutions. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Courbot, J.-B.; Mazet, V.; Monfrini, E.; Collet, C. Extended faint source detection in astronomical hyperspectral images. Signal Process. 2017, 135, 274–283. [Google Scholar] [CrossRef]
- Du, B.; Zhang, Y.; Zhang, L.; Zhang, L. A hypothesis independent subpixel target detector for hyperspectral Images. Signal Process. 2015, 110, 244–249. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Tavakoli, A.; Zoej, M.J.V. Road extraction based on fuzzy logic and mathematical morphology from pansharpened IKONOS images. Photogramm. Rec. 2006, 21, 44–60. [Google Scholar] [CrossRef]
- Souza, C., Jr.; Firestone, L.; Silva, L.M.; Roberts, D. Mapping forest degradation in the Eastern amazon from SPOT 4 through spectral mixture models. Remote Sens. Environ. 2003, 87, 494–506. [Google Scholar] [CrossRef]
- Du, B.; Zhao, R.; Zhang, L.; Zhang, L. A spectral-spatial based local summation anomaly detection method for hyperspectral images. Signal Process. 2016, 124, 115–131. [Google Scholar] [CrossRef]
- Licciardi, G.A.; Villa, A.; Khan, M.M.; Chanussot, J. Image fusion and spectral unmixing of hyperspectral images for spatial improvement of classification maps. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Caiafa, C.F.; Salerno, E.; Proto, A.N.; Fiumi, L. Blind spectral unmixing by local maximization of non-Gaussianity. Signal Process. 2008, 88, 50–68. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Shaw, G.A.; Burke, H.-H.K. Spectral imaging for remote sensing. Lincoln Lab. J. 2003, 14, 3–28. [Google Scholar]
- Greer, J. Sparse demixing of hyperspectral images. IEEE Trans. Image Process. 2012, 21, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Arablouei, R.; de Hoog, F. Hyperspectral image recovery via hybrid regularization. IEEE Trans. Image Process. 2016, 25, 5649–5663. [Google Scholar] [CrossRef] [PubMed]
- Arablouei, R. Spectral unmixing with perturbed endmembers. IEEE Trans. Geosci. Remote Sens 2018, in press. [Google Scholar] [CrossRef]
- Arablouei, R.; Goan, E.; Gensemer, S.; Kusy, B. Fast and robust push-broom hyperspectral imaging via DMD-based scanning. In Novel Optical Systems Design and Optimization XIX, Proceedings of the Optical Engineering + Applications 2016—Part of SPIE Optics + Photonics, San Diego, CA, USA, 6–10 August 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9948. [Google Scholar]
- Satellite Sensors. Available online: https://www.satimagingcorp.com/satellite-sensors/ (accessed on 10 October 2018).
- NASA’s airborne visible/infrared imaging spectrometer (AVIRIS). Available online: https://aviris.jpl.nasa.gov/data/free_data.html (accessed on 10 October 2018).
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. 25 years of pansharpening: A critical review and new developments. In Signal and Image Processing for Remote Sensing, 2nd ed.; Chen, C.H., Ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Loncan, L.; Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simões, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Yin, H. Sparse representation based pansharpening with details injection model. Signal Process. 2015, 113, 218–227. [Google Scholar] [CrossRef]
- Pajares, G.; de la Cruz, J.M. A wavelet-based image fusion tutorial. Pattern Recognit. 2004, 37, 1855–1872. [Google Scholar] [CrossRef]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-sharpening: A first approach on SIM-GA data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Eismann, M.T.; Hardie, R.C. Application of the stochastic mixing model to hyperspectral resolution enhancement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1924–1933. [Google Scholar] [CrossRef]
- Huang, B.; Song, H.; Cui, H.; Peng, J.; Xu, Z. Spatial and spectral image fusion using sparse matrix factorization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1693–1704. [Google Scholar] [CrossRef]
- Zhang, Y.; de Backer, S.; Scheunders, P. Noise-resistant wavelet-based Bayesian fusion of multispectral and hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3834–3843. [Google Scholar] [CrossRef]
- Kawakami, R.; Wright, J.; Tai, Y.-W.; Matsushita, Y.; Ben-Ezra, M.; Ikeuchi, K. High-resolution hyperspectral imaging via matrix factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition( CVPR 2011), Colorado Springs, CO, USA, 20–25 June 2011; pp. 2329–2336. [Google Scholar]
- Wycoff, E.; Chan, T.-H.; Jia, K.; Ma, W.-K.; Ma, Y. A non-negative sparse promoting algorithm for high resolution hyperspectral imaging. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 1409–1413. [Google Scholar]
- Cawse-Nicholson, K.; Damelin, S.; Robin, A.; Sears, M. Determining the intrinsic dimension of a hyperspectral image using random matrix theory. IEEE Trans. Image Process. 2013, 22, 1301–1310. [Google Scholar] [CrossRef] [PubMed]
- Bioucas-Dias, J.; Nascimento, J. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Yuan, Y.; Fu, M.; Lu, X. Low-rank representation for 3D hyperspectral images analysis from map perspective. Signal Process. 2015, 112, 27–33. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Clevers, J.G.P.W.; Schaepman, M.E. Unmixing-based landsat TM and MERIS FR data fusion. IEEE Geosci. Remote Sens. Lett. 2008, 5, 453–457. [Google Scholar] [CrossRef]
- Rudin, L.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [PubMed]
- Bresson, X.; Chan, T. Fast dual minimization of the vectorial total variation norm and applications to color image processing. Inverse Probl. Imaging 2008, 2, 455–484. [Google Scholar] [CrossRef]
- Simões, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
- He, X.; Condat, L.; Bioucas-Dias, J.; Chanussot, J.; Xia, J. A new pansharpening method based on spatial and spectral sparsity priors. IEEE Trans. Image Process. 2014, 23, 4160–4174. [Google Scholar] [CrossRef] [PubMed]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A new pansharpening algorithm based on total variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J. Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, X. Hyperspectral image super-resolution via non-negative structured sparse representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef] [PubMed]
- Grohnfeldt, C.; Zhu, X.X.; Bamler, R. Jointly sparse fusion of hyperspectral and multispectral imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 4090–4093. [Google Scholar]
- Akhtar, N.; Shafait, F.; Mian, A. Bayesian sparse representation for hyperspectral image super resolution. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3631–3640. [Google Scholar]
- Wei, Q.; Dobigeon, N.; Tourneret, J.-Y. Bayesian fusion of multiband images. IEEE J. Sel. Top. Signal Process. 2015, 9, 1117–1127. [Google Scholar] [CrossRef]
- Hardie, R.C.; Eismann, M.T.; Wilson, G.L. MAP estimation for hyperspectral image resolution enhancement using an auxiliary sensor. IEEE Trans. Image Process. 2004, 13, 1174–1184. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Duijster, A.; Scheunders, P. A Bayesian restoration approach for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3453–3462. [Google Scholar] [CrossRef]
- Veganzones, M.A.; Simões, M.; Licciardi, G.; Yokoya, N.; Bioucas-Dias, J.M.; Chanussot, J. Hyperspectral super-resolution of locally low rank images from complementary multisource data. IEEE Trans. Image Process. 2016, 25, 274–288. [Google Scholar] [CrossRef] [PubMed]
- Berne, O.; Helens, A.; Pilleri, P.; Joblin, C. Non-negative matrix factorization pansharpening of hyperspectral data: An application to mid-infrared astronomy. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral superresolution by coupled spectral unmixing. In Proceedings of the IEEE ICCV, Santiago, Chile, 7–13 December 2015; pp. 3586–3594. [Google Scholar]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.-Y.; Chen, M.; Godsill, S. Multiband image fusion based on spectral unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7236–7249. [Google Scholar] [CrossRef]
- Kwan, C.; Budavari, B.; Bovik, A.C.; Marchisio, G. Blind quality assessment of fused WorldView-3 images by using the combinations of pansharpening and hypersharpening paradigms. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1835–1839. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Hyperspectral, multispectral, and panchromatic data fusion based on coupled non-negative matrix factorization. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Afonso, M.; Bioucas-Dias, J.M.; Figueiredo, M. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process. 2011, 20, 681–695. [Google Scholar] [CrossRef] [PubMed]
- Eckstein, J.; Bertsekas, D.P. On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 1992, 55, 293–318. [Google Scholar] [CrossRef]
- Gabay, D.; Mercier, B. A dual algorithm for the solution of nonlinear variational problems via finite-element approximation. Comput. Math. Appl. 1976, 2, 17–40. [Google Scholar] [CrossRef]
- Glowinski, R.; Marroco, A. Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation-dualité d’une classe de problèmes de Dirichlet non linéaires, Revue française d’automatique, informatique, recherche opérationnelle. Analyse Numérique 1975, 9, 41–76. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Esser, E. Applications of Lagrangian-Based Alternating Direction Methods and Connections to Split-Bregman; CAM Reports 09-31; Center for Computational Applied Mathematics, University of California: Los Angeles, CA, USA, 2009. [Google Scholar]
- Gao, B.-C.; Montes, M.J.; Davis, C.O.; Goetz, A.F. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar] [CrossRef]
- Zare, A.; Ho, K.C. Endmember variability in hyperspectral analysis. IEEE Signal Process. Mag. 2014, 31, 95–104. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.-Y.; Richard, C.; Bermudez, J.C.M.; McLaughlin, S.; Hero, A.O. Nonlinear unmixing of hyperspectral images: Models and algorithms. IEEE Signal Process. Mag. 2014, 31, 89–94. [Google Scholar] [CrossRef]
- USGS Digital Spectral Library 06. Available online: https://speclab.cr.usgs.gov/spectral.lib06/ (accessed on 10 October 2018).
- Stockham, T.G., Jr. High-speed convolution and correlation. In Proceedings of the ACM Spring Joint Computer Conference, New York, NY, USA, 26–28 April 1966; pp. 229–233. [Google Scholar]
- Donoho, D.; Johnstone, I. Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Combettes, P.; Pesquet, J.-C. Proximal splitting methods in signal processing. In Fixed-Point Algorithms for Inverse Problems in Science and Engineering; Springer: New York, NY, USA, 2011; pp. 185–212. [Google Scholar]
- Condat, L. Fast projection onto the simplex and the l1 ball. Math. Program. 2016, 158, 575–585. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting image. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1391–1402. [Google Scholar]
- Hyperspectral Remote Sensing Scenes. Available online: www.ehu.eus/ccwintco/?title=Hyperspectral_Remote_Sensing_Scenes (accessed on 10 October 2018).
- Baumgardner, M.; Biehl, L.; Landgrebe, D. 220 band AVIRIS Hyperspectral Image Data set: June 12, 1992 Indian Pine Test Site 3; Purdue University Research Repository; Purdue University: West Lafayette, IN, USA, 2015. [Google Scholar]
- Fusing multiple multiband images. Available online: https://github.com/Reza219/Multiple-multiband-image-fusion (accessed on 10 October 2018).
- Landsat 8. Available online: https://landsat.gsfc.nasa.gov/landsat-8/ (accessed on 10 October 2018).
- Alparone, L.; Baronti, S.; Aiazzi, B.; Garzelli, A. Spatial methods for multispectral pansharpening: Multiresolution analysis demystified. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2563–2576. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 228–236. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Lee, J.; Lee, C. Fast and efficient panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2010, 48, 155–163. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. An MTF-based spectral distortion minimizing model for pan-sharpening of very high resolution multispectral images of urban areas. In Proceedings of the 2nd GRSS/ISPRS Joint Workshop Remote Sensing Data Fusion URBAN Areas, Berlin, Germany, 22–23 May 2003; pp. 90–94. [Google Scholar]
- Wei, Q.; Dobigeon, N.; Tourneret, J.-Y.; Bioucas-Dias, J.M.; Godsill, S. R-FUSE: Robust fast fusion of multiband images based on solving a Sylvester equation. IEEE Signal Process. Lett. 2016, 23, 1632–1636. [Google Scholar] [CrossRef]
- Wei, Q.; Dobigeon, N.; Tourneret, J.-Y. Fast fusion of multi-band images based on solving a Sylvester equation. IEEE Trans. Image Process. 2015, 24, 4109–4121. [Google Scholar] [CrossRef] [PubMed]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and multispectral data fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Proceedings of the Fusion of Earth data: Merging point measurements, raster maps and remotely sensed images, Nice, France, 26–28 January 2000; pp. 99–103. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS): Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F. Hypercomplex quality assessment of multi/hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. A global quality measurement of pan-sharpened multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 313–317. [Google Scholar] [CrossRef]
- Nascimento, J.; Bioucas-Dias, J. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.; Figueiredo, M. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Golub, G.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
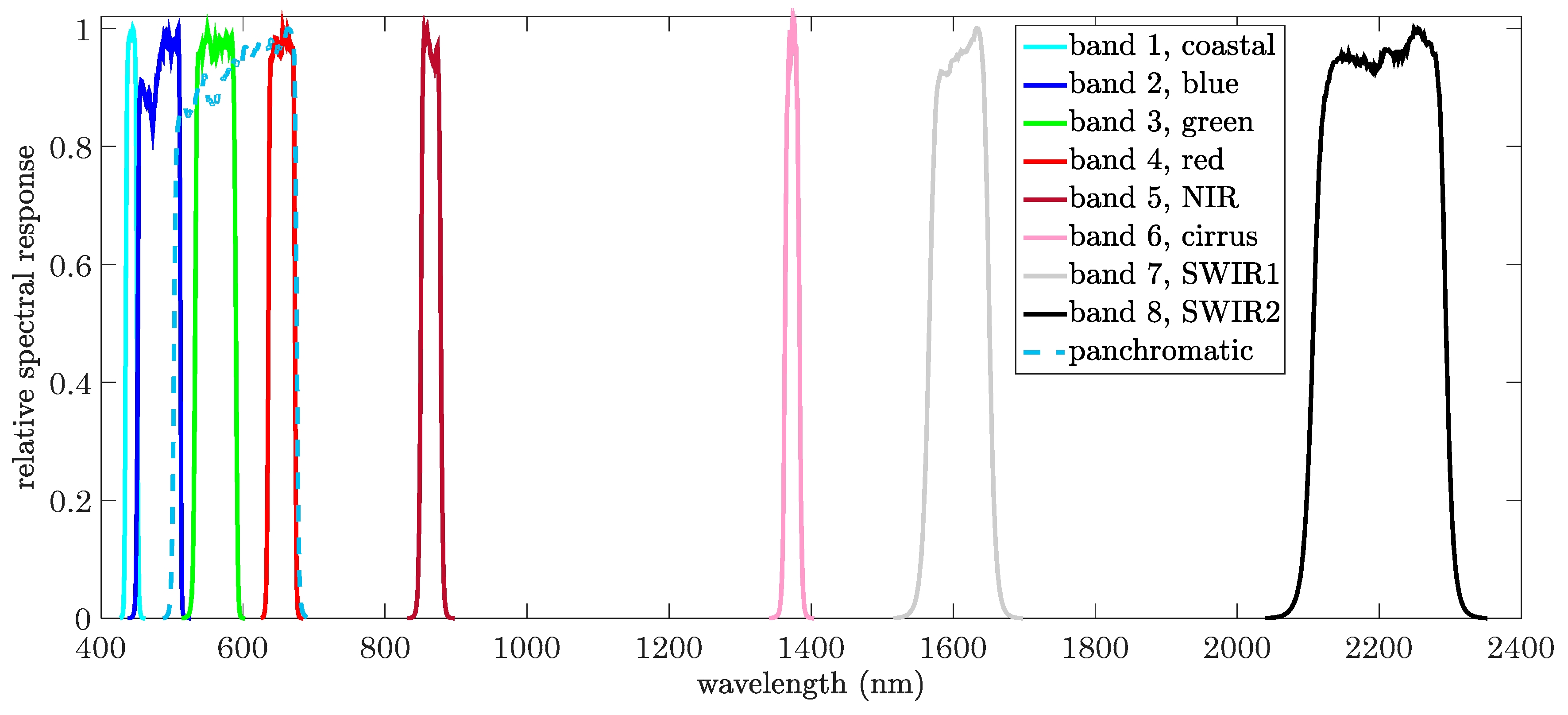
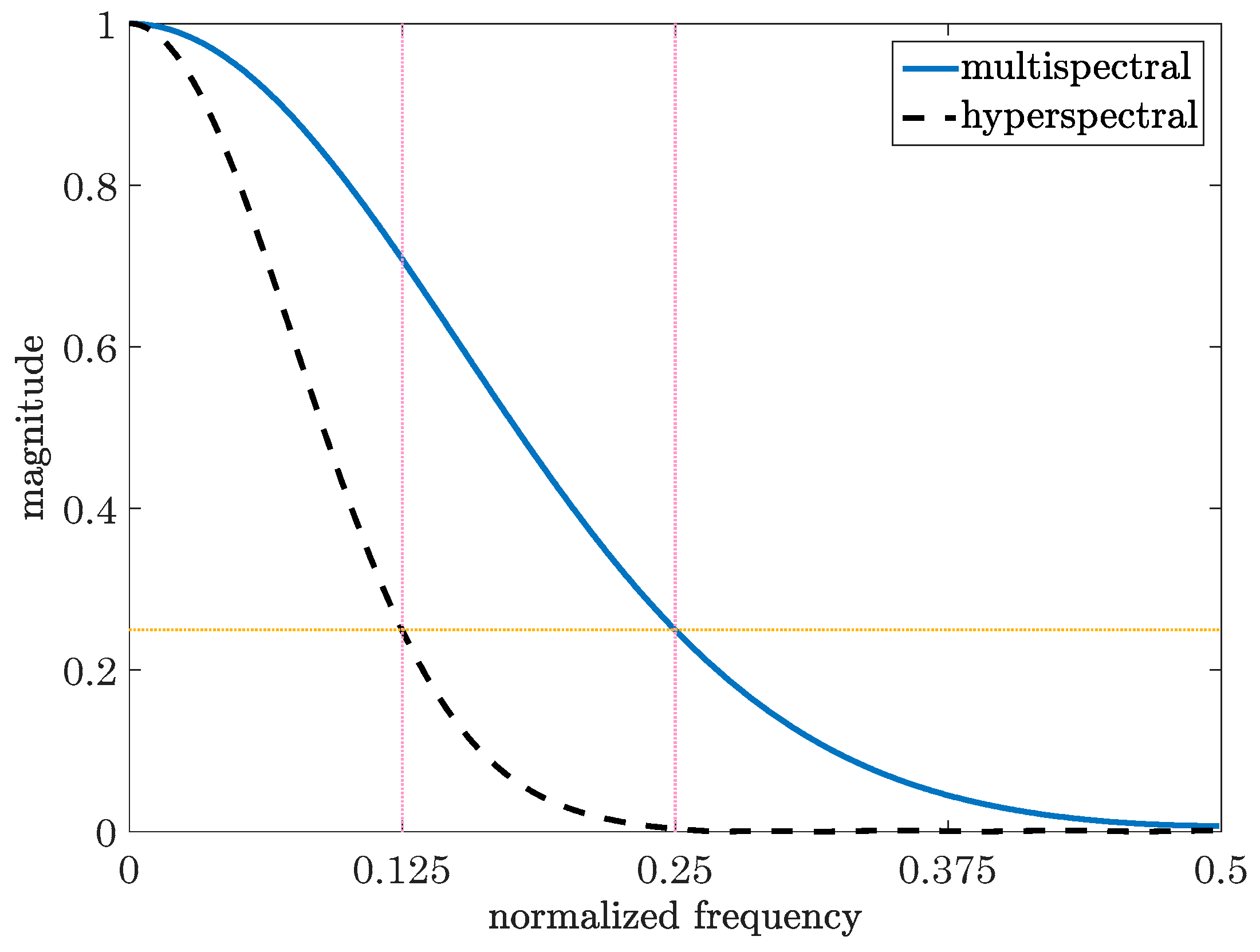

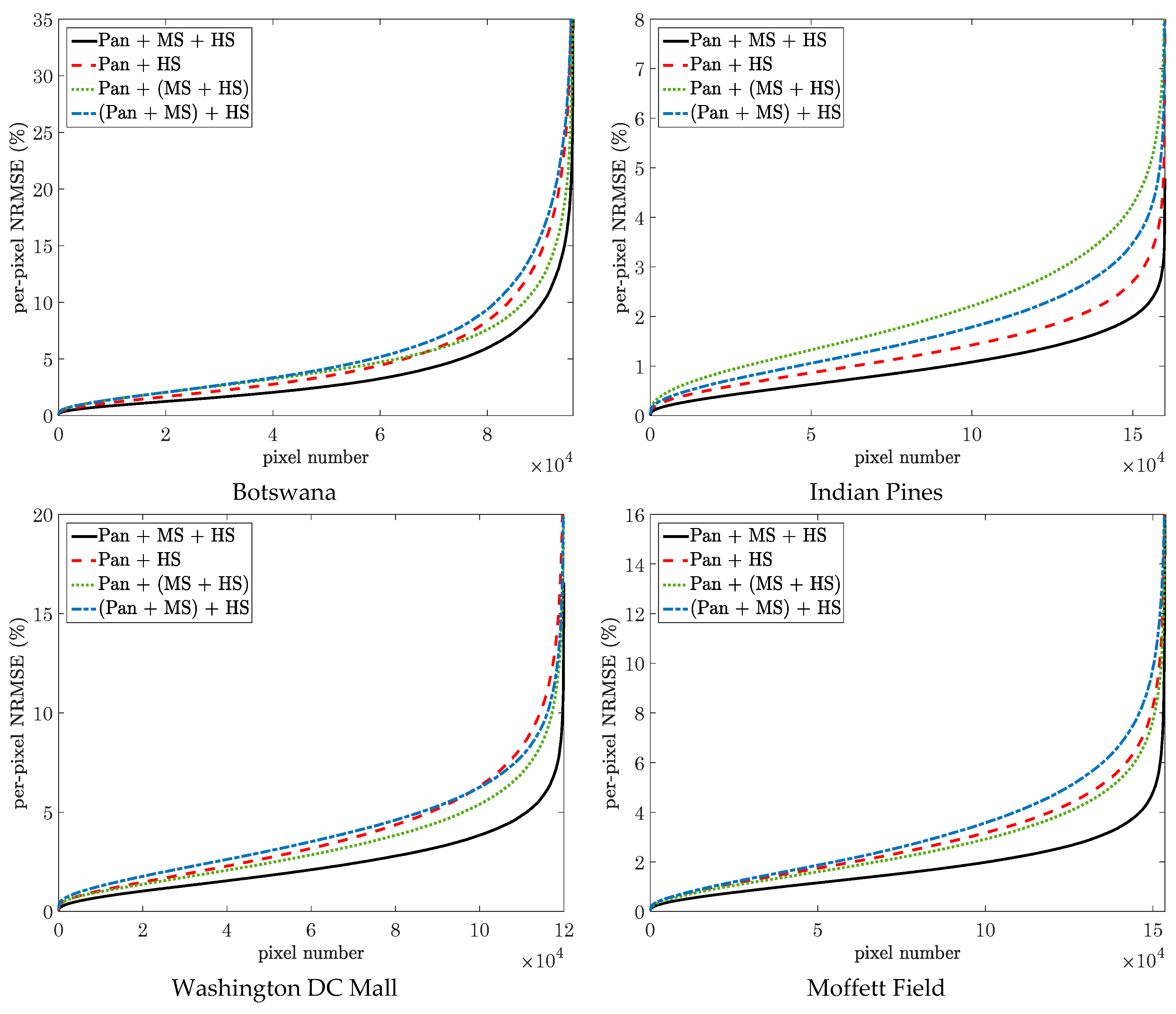
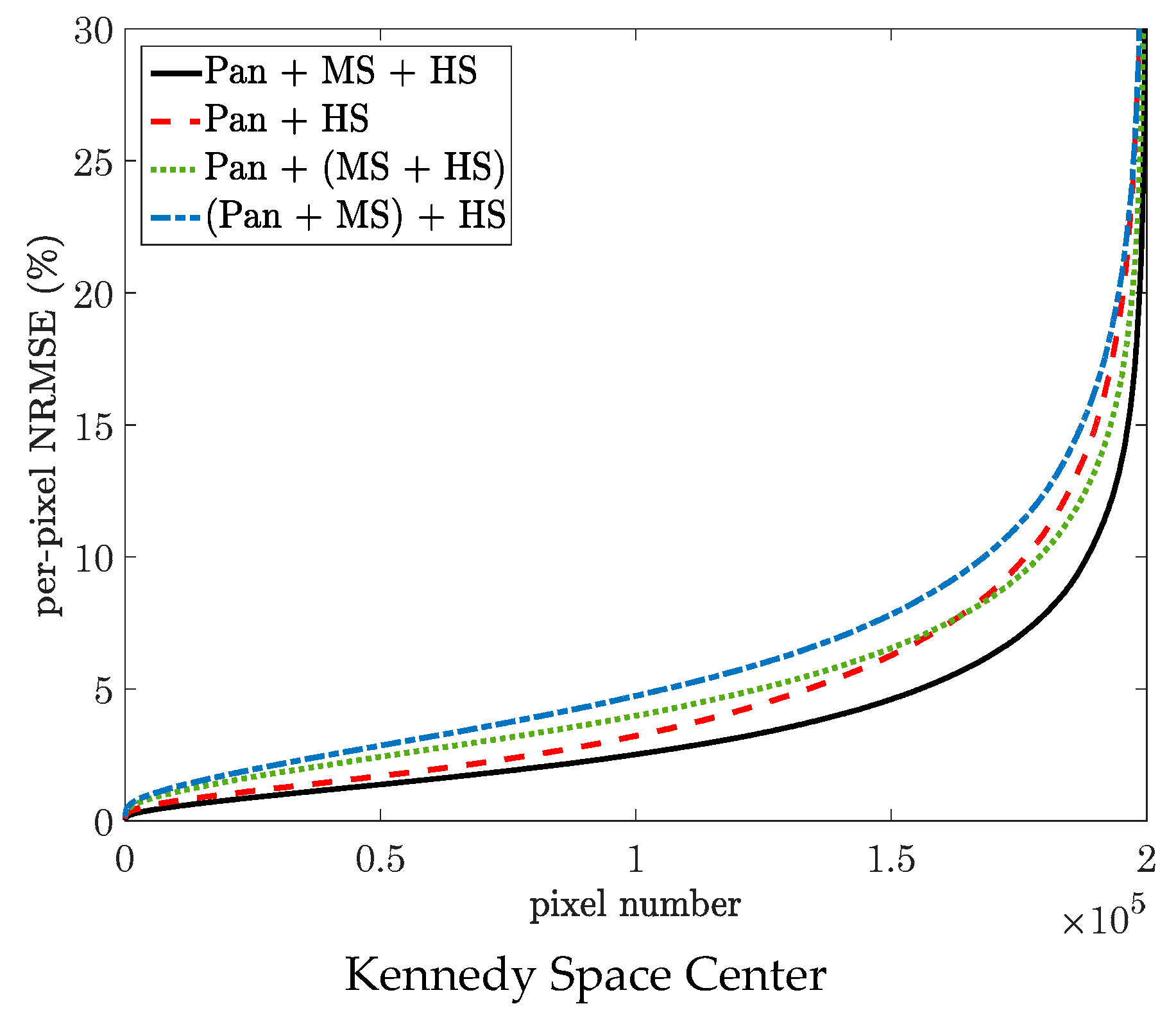



| Image | No. of Rows | No. of Columns | No. of Bands | |
|---|---|---|---|---|
| Botswana | ||||
| Indian Pines | ||||
| Washington DC Mall | ||||
| Moffett Field | ||||
| Kennedy Space Center |
| Fusion | Algorithm(s) | Spectrum of Pan | Entire Spectrum | Time (s) | ||||
|---|---|---|---|---|---|---|---|---|
| ERGAS | SAM (°) | ERGAS | SAM (°) | |||||
| Pan + MS + HS | proposed | 0.900 | 1.355 | 0.980 | 1.637 | 1.575 | 0.956 | 47.01 |
| Pan + HS | HySure | 1.273 | 1.975 | 0.967 | 1.839 | 2.435 | 0.946 | 61.20 |
| R-FUSE-TV | 1.272 | 1.974 | 0.967 | 1.840 | 2.436 | 0.946 | 61.17 | |
| Pan + (MS + HS) | HySure | 1.256 | 1.721 | 0.962 | 1.992 | 2.101 | 0.937 | 78.28 |
| R-FUSE-TV | 1.265 | 1.734 | 0.961 | 2.002 | 2.113 | 0.937 | 79.44 | |
| (Pan + MS) + HS | BDSD & HySure | 1.393 | 1.971 | 0.955 | 2.458 | 2.359 | 0.912 | 62.58 |
| BDSD & R-FUSE-TV | 1.392 | 1.977 | 0.956 | 2.461 | 2.365 | 0.912 | 62.10 | |
| MTF-GLP-HPM & HySure | 1.441 | 2.120 | 0.957 | 2.181 | 2.442 | 0.931 | 62.78 | |
| MTF-GLP-HPM & R-FUSE-TV | 1.440 | 2.124 | 0.957 | 2.185 | 2.446 | 0.931 | 62.20 | |
| Fusion | Algorithm(s) | Spectrum of Pan | Entire Spectrum | Time (s) | ||||
|---|---|---|---|---|---|---|---|---|
| ERGAS | SAM (°) | ERGAS | SAM (°) | |||||
| Pan + MS + HS | proposed | 0.304 | 0.293 | 0.990 | 0.500 | 0.761 | 0.969 | 80.21 |
| Pan + HS | HySure | 0.420 | 0.547 | 0.986 | 0.813 | 1.108 | 0.632 | 106.75 |
| R-FUSE-TV | 0.425 | 0.555 | 0.986 | 0.813 | 1.113 | 0.632 | 106.47 | |
| Pan + (MS + HS) | HySure | 0.656 | 0.641 | 0.961 | 0.834 | 1.117 | 0.594 | 134.79 |
| R-FUSE-TV | 0.695 | 0.642 | 0.953 | 0.875 | 1.120 | 0.573 | 134.32 | |
| (Pan + MS) + HS | BDSD & HySure | 0.538 | 0.517 | 0.972 | 0.803 | 1.183 | 0.670 | 108.33 |
| BDSD & R-FUSE-TV | 0.539 | 0.520 | 0.972 | 0.794 | 1.182 | 0.674 | 107.34 | |
| MTF-GLP-HPM & HySure | 0.566 | 0.563 | 0.972 | 0.959 | 1.268 | 0.626 | 108.48 | |
| MTF-GLP-HPM & R-FUSE-TV | 0.567 | 0.567 | 0.972 | 0.947 | 1.270 | 0.628 | 107.51 | |
| Fusion | Algorithm(s) | Spectrum of Pan | Entire Spectrum | Time (s) | ||||
|---|---|---|---|---|---|---|---|---|
| ERGAS | SAM (°) | ERGAS | SAM (°) | |||||
| Pan + MS + HS | proposed | 0.731 | 1.116 | 0.997 | 2.484 | 2.795 | 0.970 | 59.52 |
| Pan + HS | HySure | 1.171 | 2.047 | 0.992 | 3.822 | 4.539 | 0.930 | 79.02 |
| R-FUSE-TV | 1.171 | 2.042 | 0.992 | 3.832 | 4.537 | 0.930 | 78.38 | |
| Pan + (MS + HS) | HySure | 0.937 | 1.718 | 0.994 | 3.233 | 3.592 | 0.949 | 99.74 |
| R-FUSE-TV | 1.204 | 1.738 | 0.991 | 3.270 | 3.664 | 0.947 | 100.53 | |
| (Pan + MS) + HS | BDSD & HySure | 1.114 | 2.039 | 0.992 | 4.174 | 5.048 | 0.918 | 79.68 |
| BDSD & R-FUSE-TV | 1.104 | 2.060 | 0.992 | 4.251 | 5.033 | 0.916 | 78.41 | |
| MTF-GLP-HPM & HySure | 1.308 | 1.870 | 0.991 | 4.380 | 5.147 | 0.911 | 79.28 | |
| MTF-GLP-HPM & R-FUSE-TV | 1.298 | 1.884 | 0.991 | 4.440 | 5.114 | 0.910 | 78.13 | |
| Fusion | Algorithm(s) | Spectrum of Pan | Entire Spectrum | Time (s) | ||||
|---|---|---|---|---|---|---|---|---|
| ERGAS | SAM (°) | ERGAS | SAM (°) | |||||
| Pan + MS + HS | proposed | 0.572 | 0.786 | 0.992 | 4.232 | 3.148 | 0.885 | 77.37 |
| Pan + HS | HySure | 0.902 | 1.151 | 0.985 | 6.507 | 4.233 | 0.823 | 107.73 |
| R-FUSE-TV | 0.914 | 1.152 | 0.984 | 6.416 | 4.210 | 0.827 | 106.20 | |
| Pan + (MS + HS) | HySure | 0.826 | 1.004 | 0.986 | 5.078 | 3.603 | 0.868 | 134.78 |
| R-FUSE-TV | 0.964 | 1.014 | 0.977 | 5.100 | 3.670 | 0.845 | 135.20 | |
| (Pan + MS) + HS | BDSD & HySure | 1.061 | 1.135 | 0.980 | 5.325 | 4.065 | 0.829 | 108.91 |
| BDSD & R-FUSE-TV | 1.058 | 1.134 | 0.980 | 5.244 | 4.039 | 0.834 | 106.12 | |
| MTF-GLP-HPM & HySure | 1.396 | 1.122 | 0.968 | 5.924 | 4.384 | 0.824 | 108.98 | |
| MTF-GLP-HPM & R-FUSE-TV | 1.396 | 1.123 | 0.969 | 5.835 | 4.360 | 0.830 | 106.28 | |
| Fusion | Algorithm(s) | Spectrum of Pan | Entire Spectrum | Time (s) | ||||
|---|---|---|---|---|---|---|---|---|
| ERGAS | SAM (°) | ERGAS | SAM (°) | |||||
| Pan + MS + HS | proposed | 1.024 | 1.628 | 0.984 | 2.468 | 3.211 | 0.909 | 99.94 |
| Pan + HS | HySure | 1.451 | 2.426 | 0.979 | 3.544 | 3.995 | 0.890 | 138.16 |
| R-FUSE-TV | 1.518 | 2.496 | 0.974 | 3.680 | 3.795 | 0.886 | 134.97 | |
| Pan + (MS + HS) | HySure | 1.462 | 2.203 | 0.967 | 2.851 | 3.546 | 0.909 | 172.18 |
| R-FUSE-TV | 1.875 | 2.343 | 0.939 | 2.986 | 4.155 | 0.878 | 172.25 | |
| (Pan + MS) + HS | BDSD & HySure | 1.738 | 2.594 | 0.949 | 3.727 | 4.824 | 0.850 | 138.66 |
| BDSD & R-FUSE-TV | 1.691 | 2.547 | 0.953 | 3.534 | 4.584 | 0.865 | 135.74 | |
| MTF-GLP-HPM & HySure | 6.801 | 3.250 | 0.912 | 9.532 | 5.183 | 0.805 | 138.60 | |
| MTF-GLP-HPM & R-FUSE-TV | 8.143 | 3.264 | 0.914 | 11.130 | 5.197 | 0.816 | 135.58 | |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arablouei, R. Fusing Multiple Multiband Images. J. Imaging 2018, 4, 118. https://doi.org/10.3390/jimaging4100118
Arablouei R. Fusing Multiple Multiband Images. Journal of Imaging. 2018; 4(10):118. https://doi.org/10.3390/jimaging4100118
Chicago/Turabian StyleArablouei, Reza. 2018. "Fusing Multiple Multiband Images" Journal of Imaging 4, no. 10: 118. https://doi.org/10.3390/jimaging4100118
APA StyleArablouei, R. (2018). Fusing Multiple Multiband Images. Journal of Imaging, 4(10), 118. https://doi.org/10.3390/jimaging4100118





