Segmentation and Shape Analysis of Macrophages Using Anglegram Analysis †
Abstract
1. Introduction
2. Materials and Methods
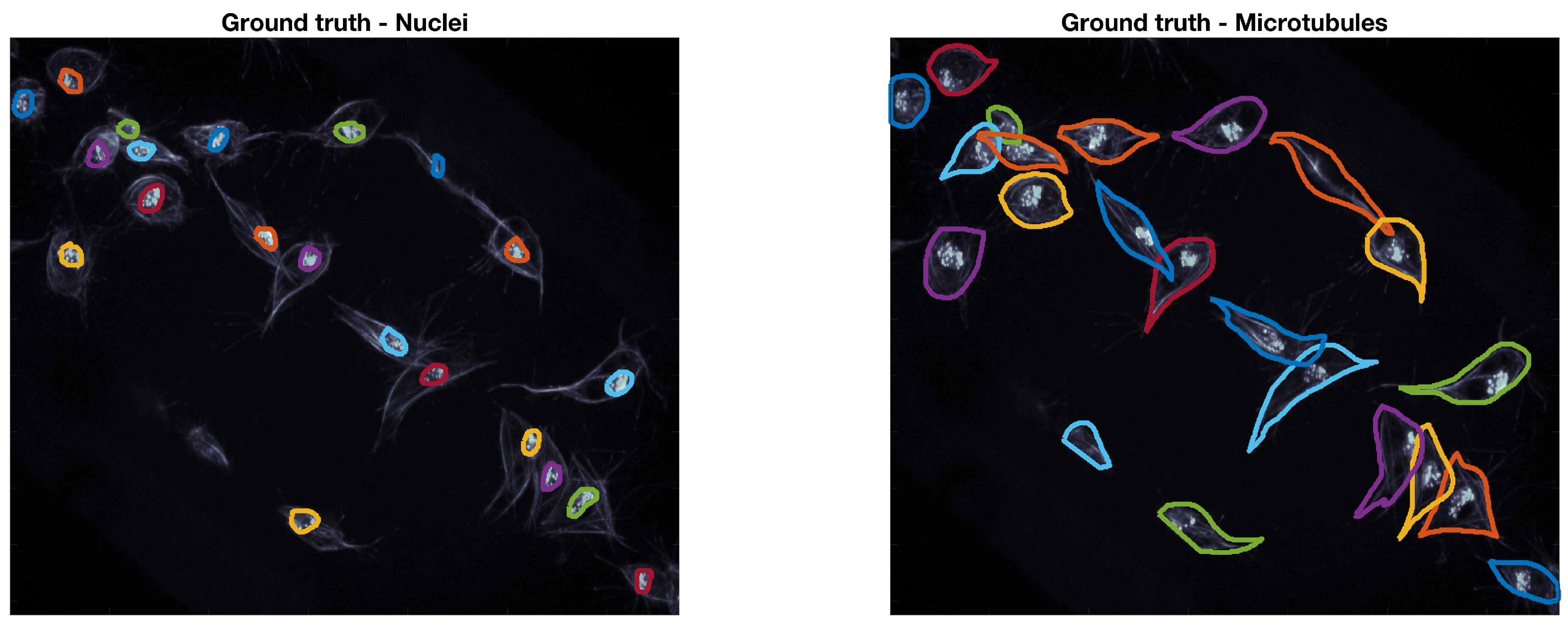
2.1. Macrophages Embryos
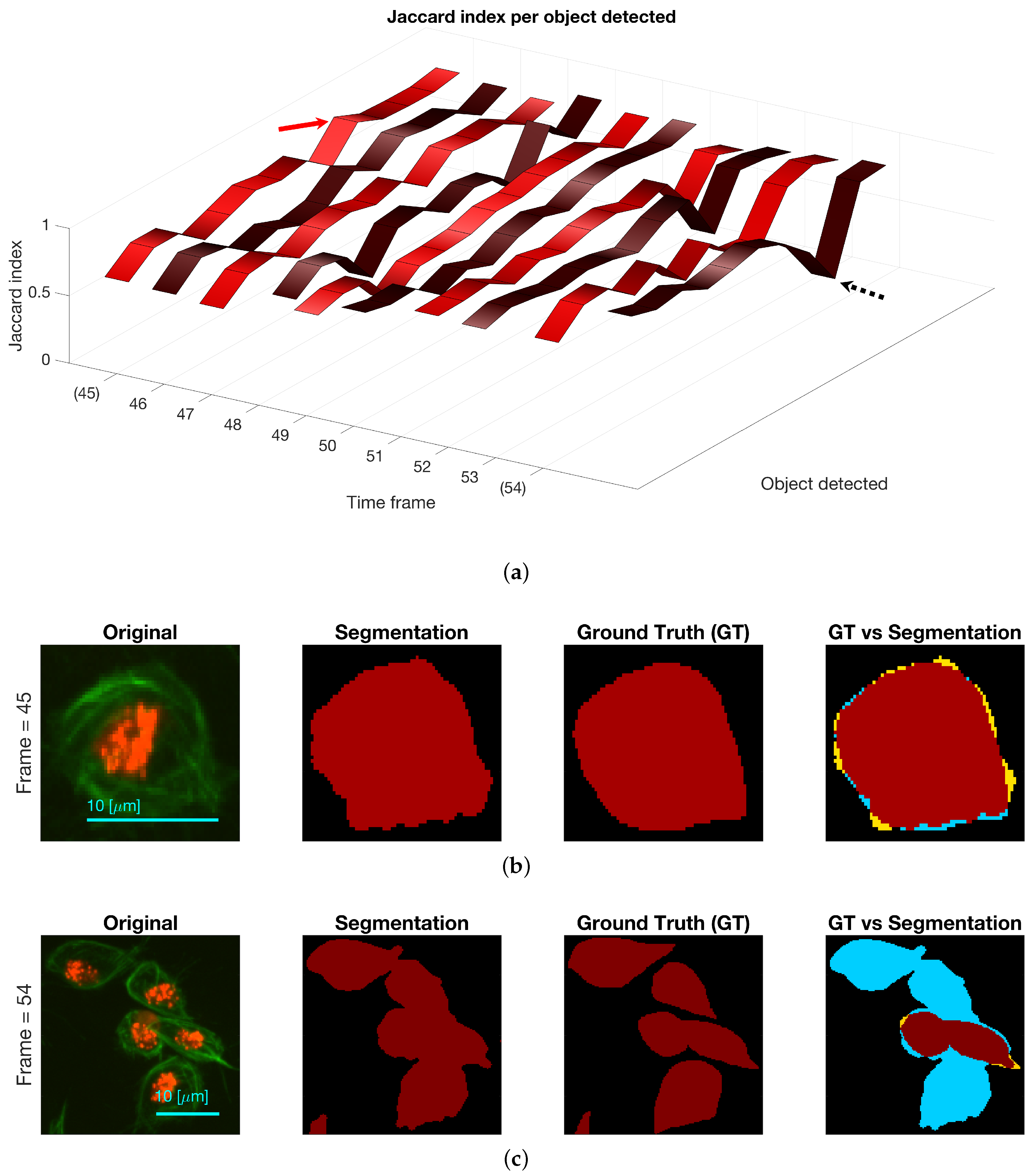
Ground Truth of Macrophages Data
2.2. Synthetic Data
2.2.1. Synthetic Data of Overlapping Ellipses
2.2.2. Object Detection: Single Objects and Clumps
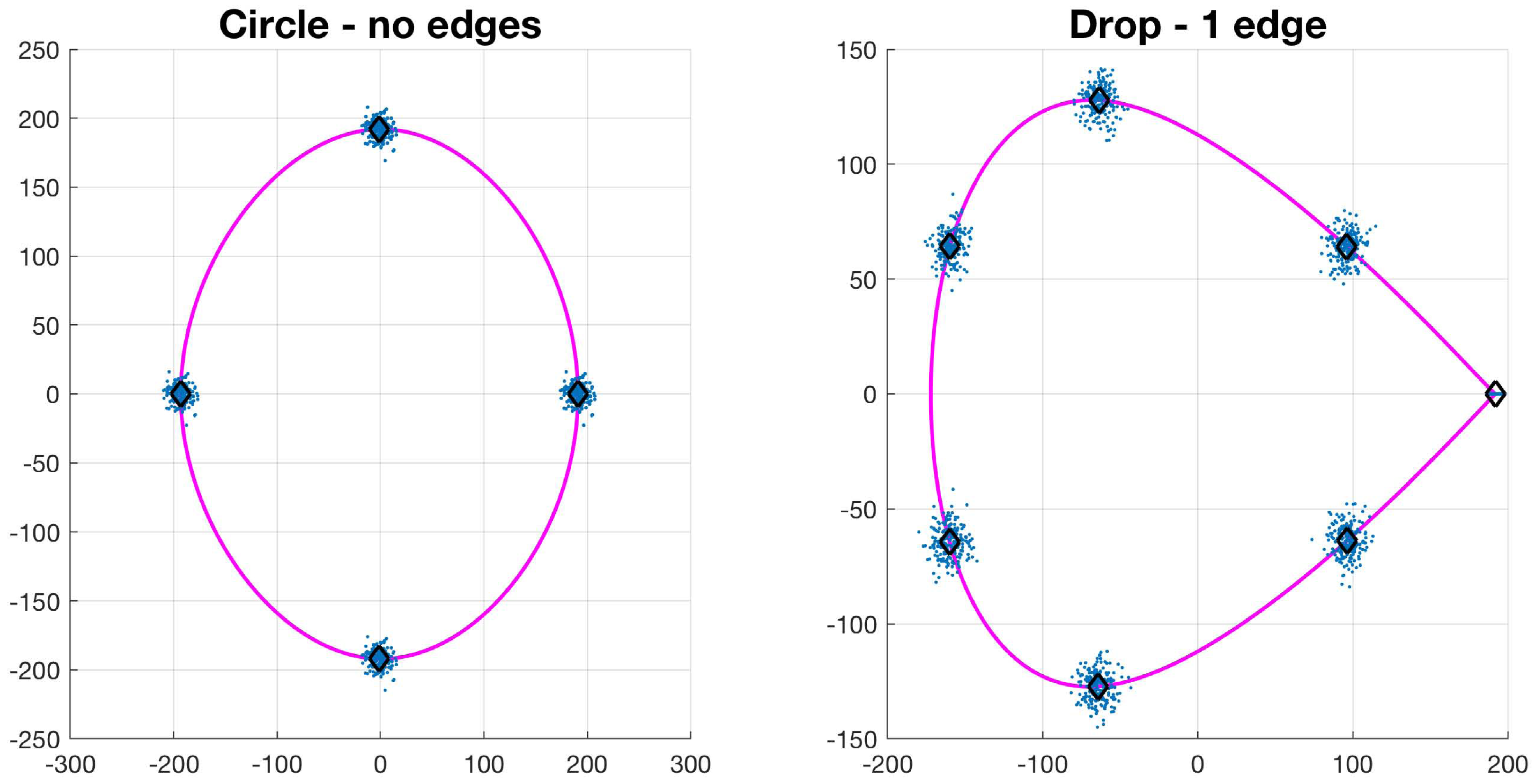
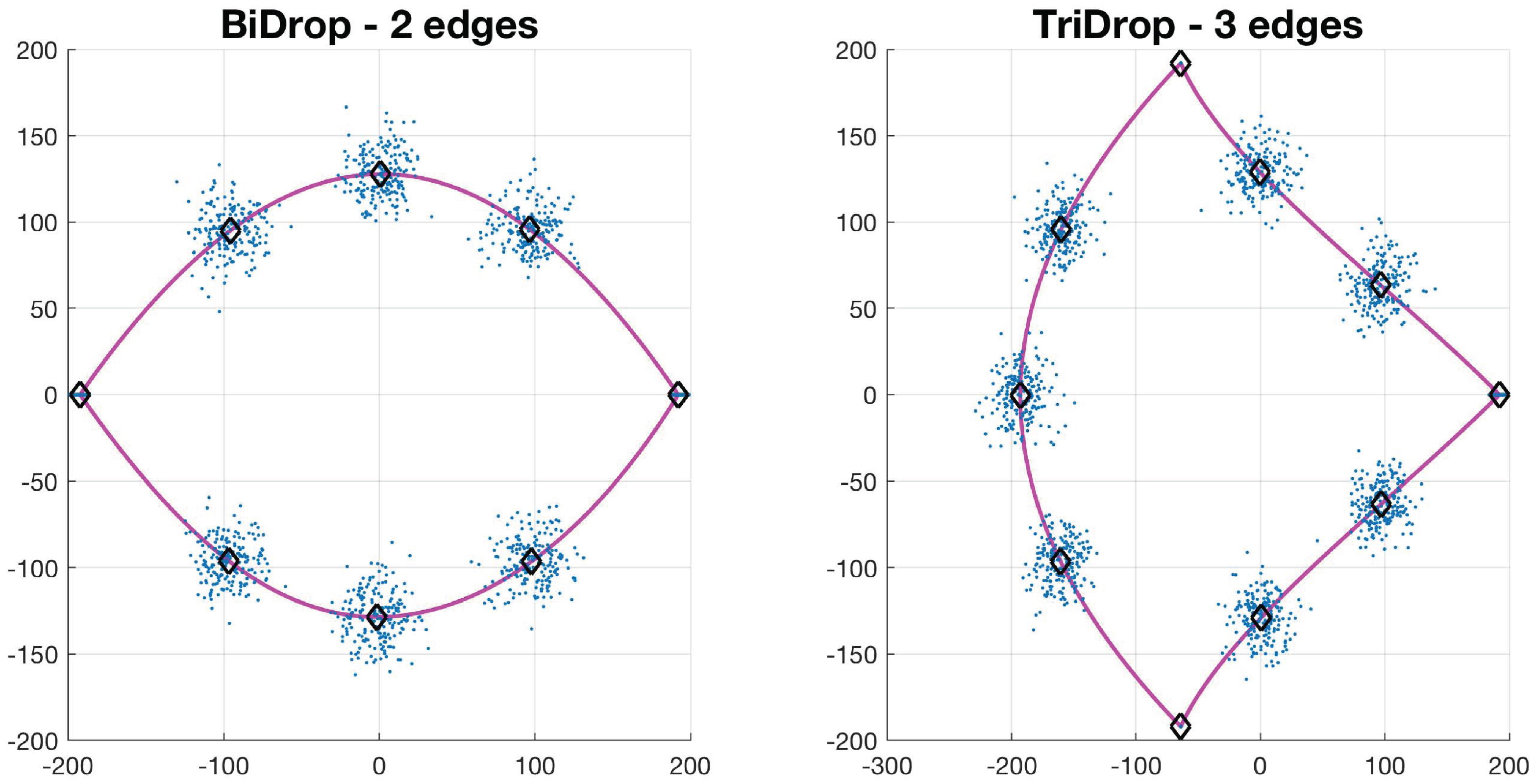
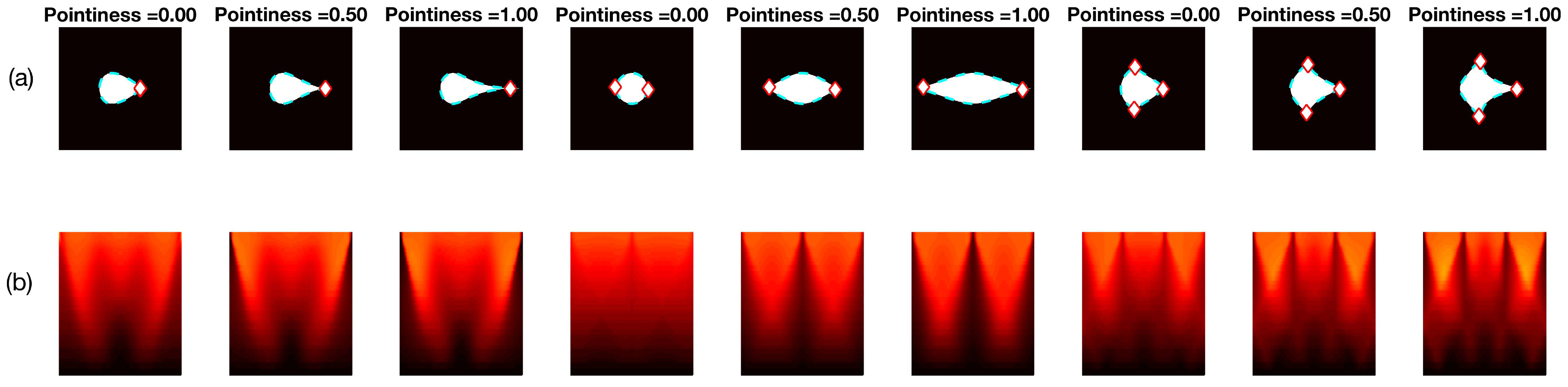
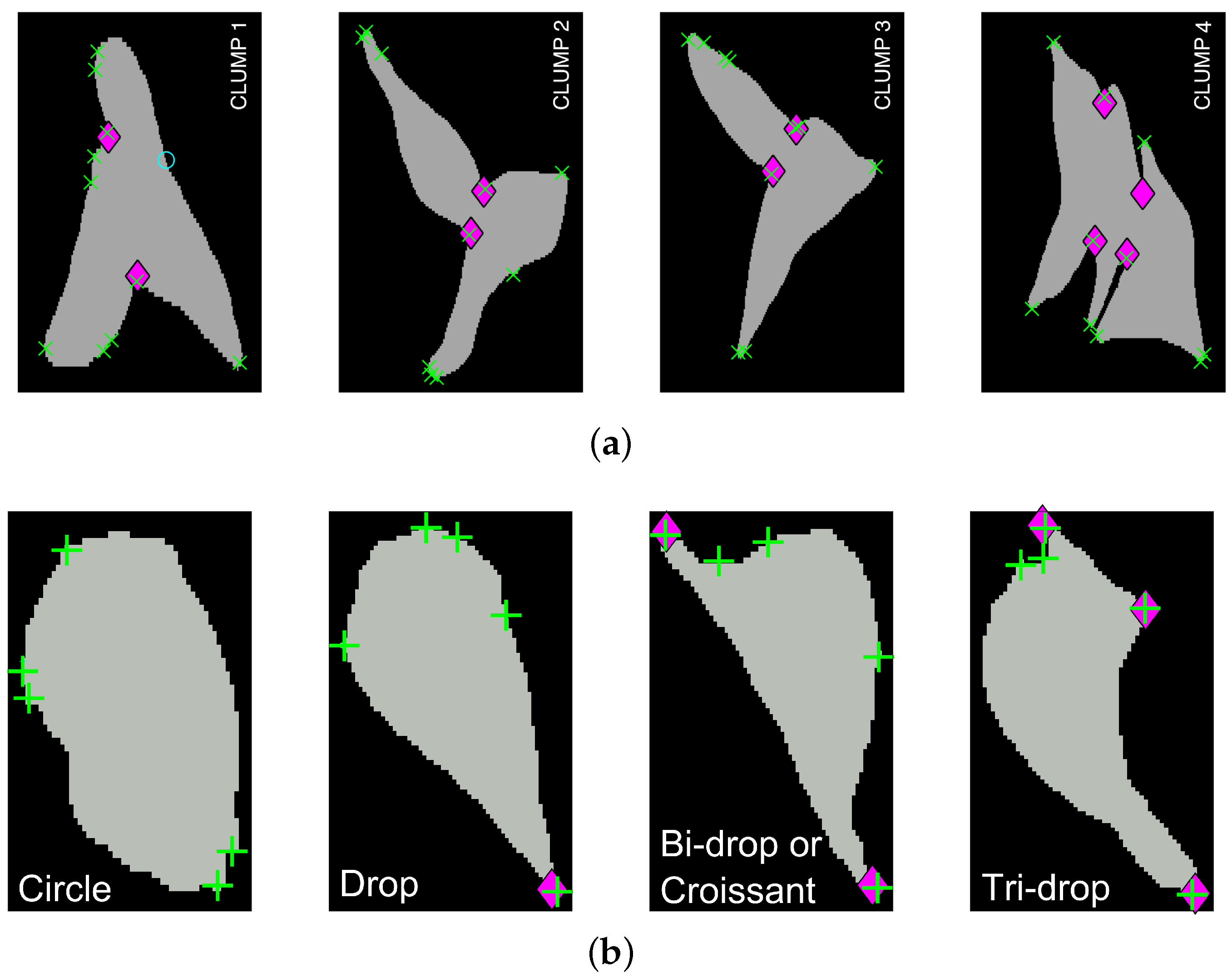
2.2.3. Basic Shapes Synthetic Data
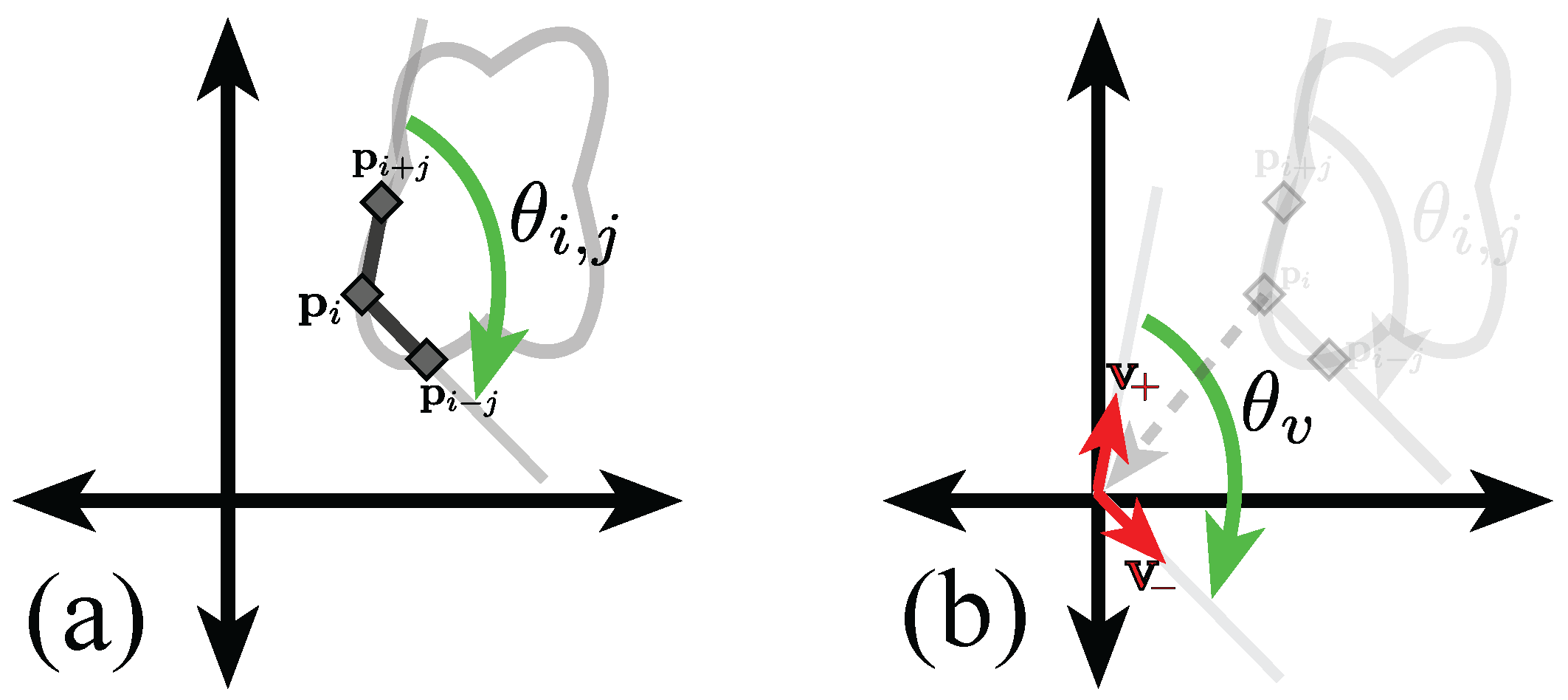
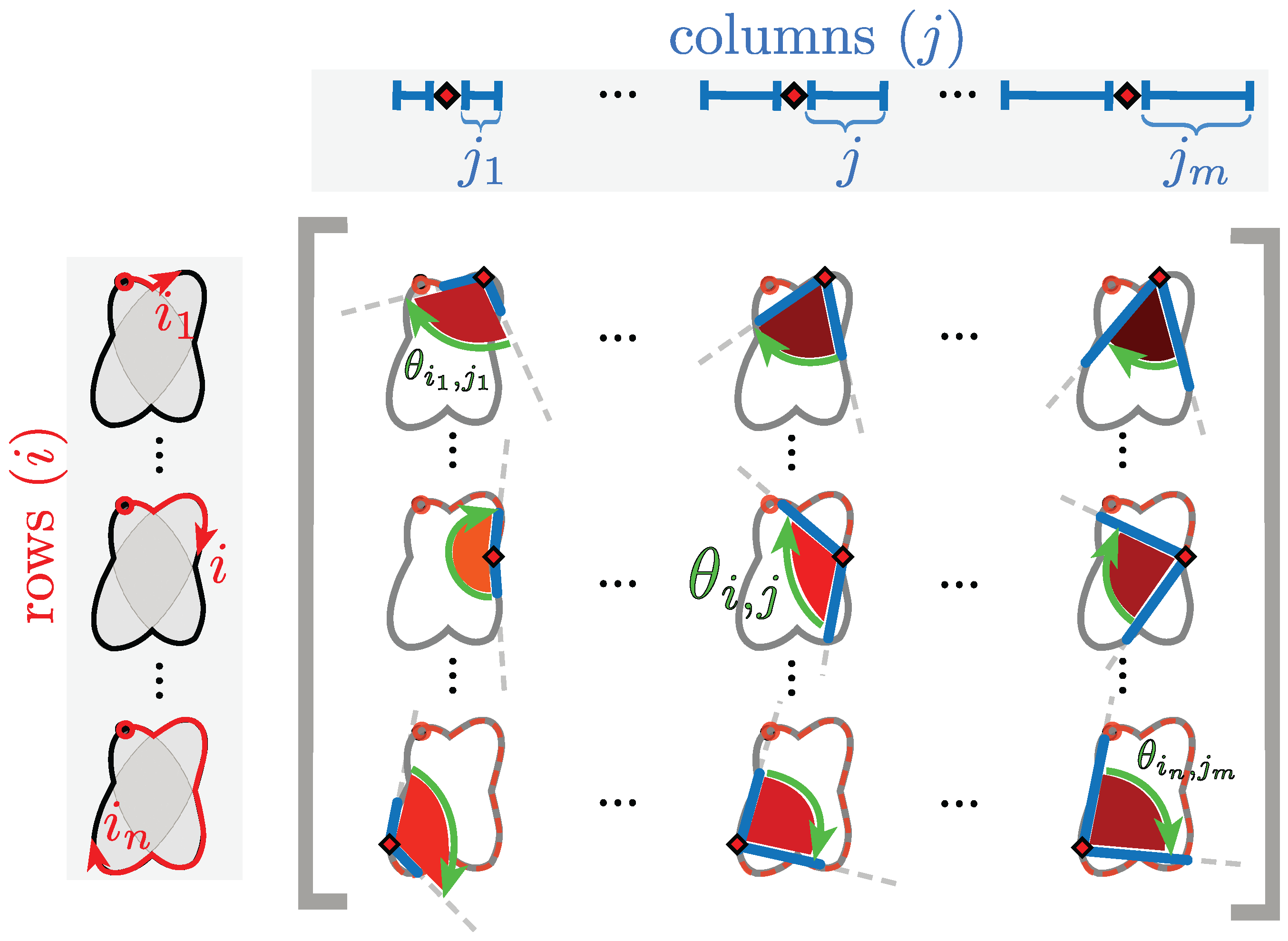
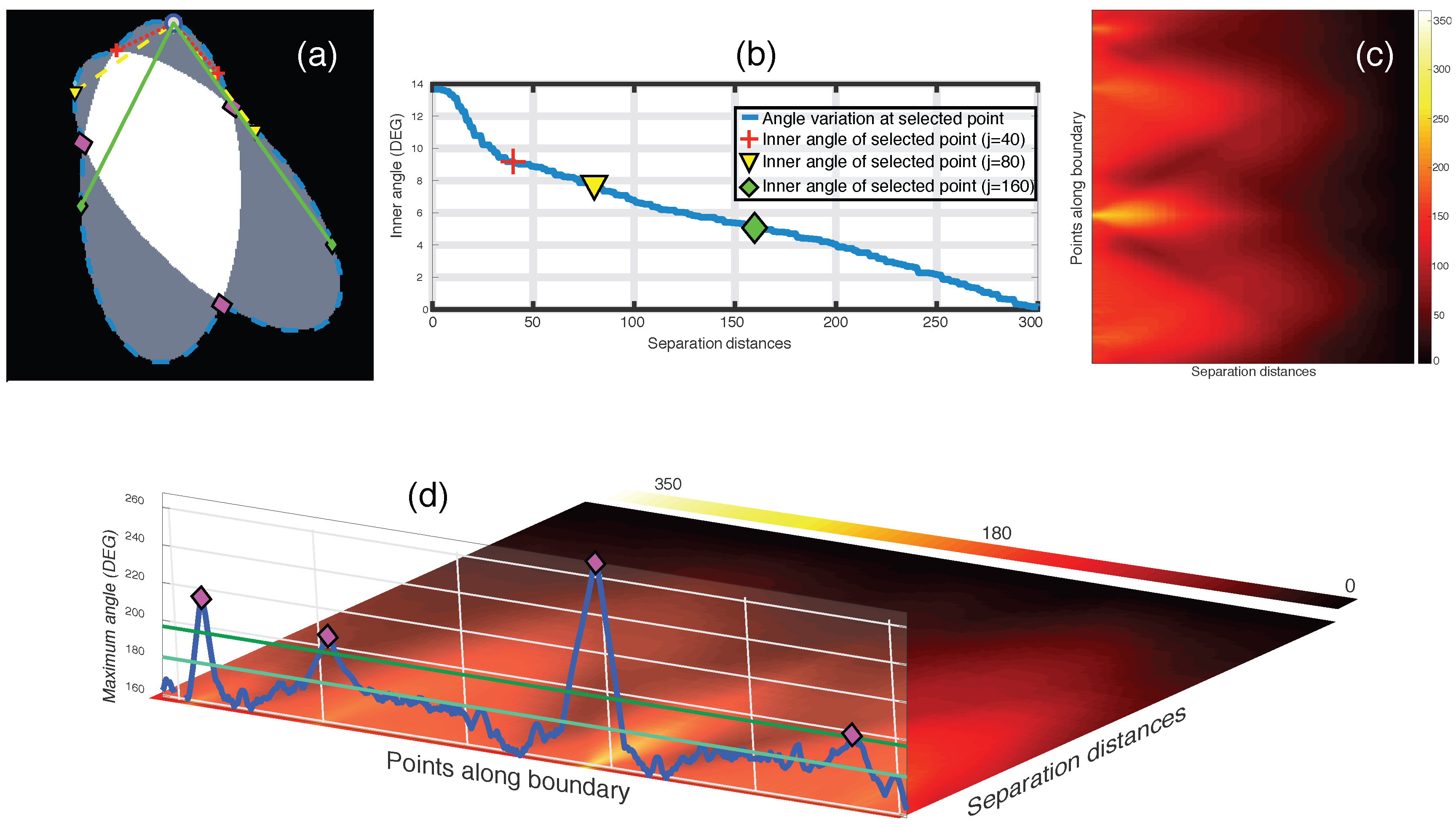
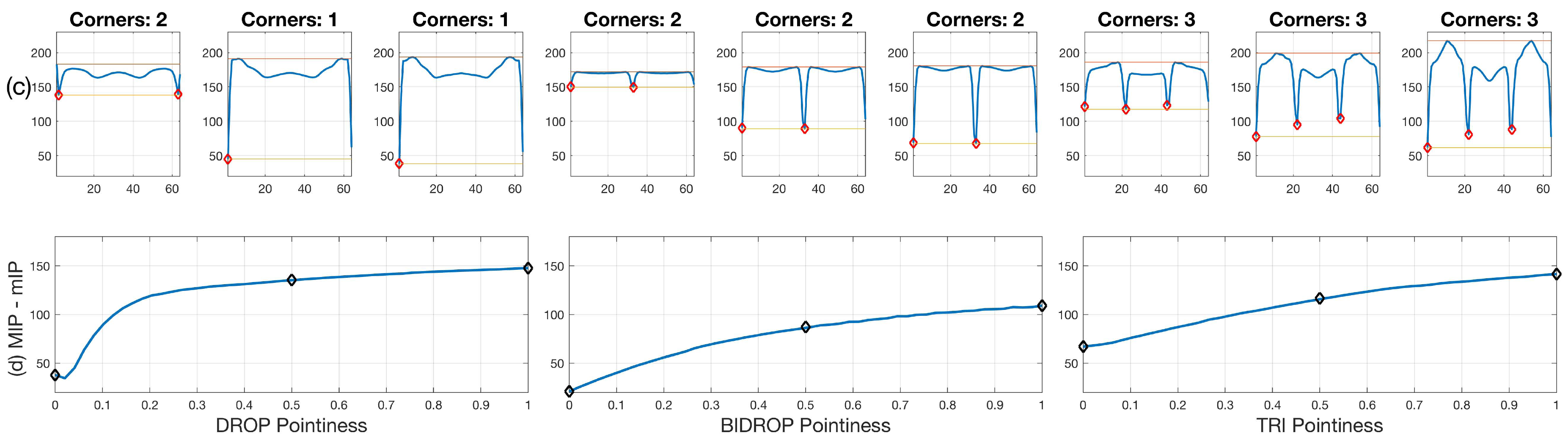
2.3. Junction Detection through Angle Variations
Criteria to Detect Junctions from the Anglegram
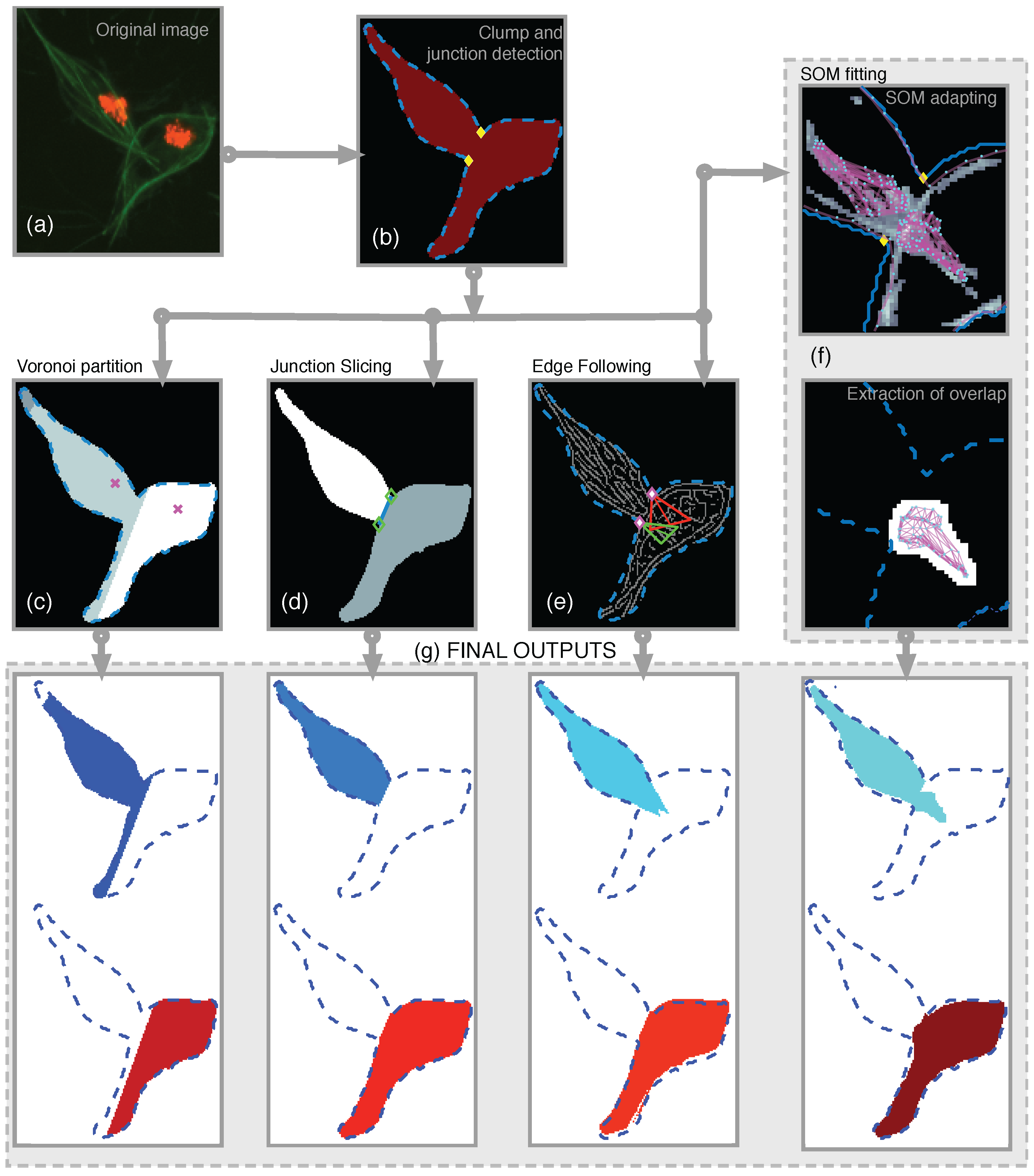
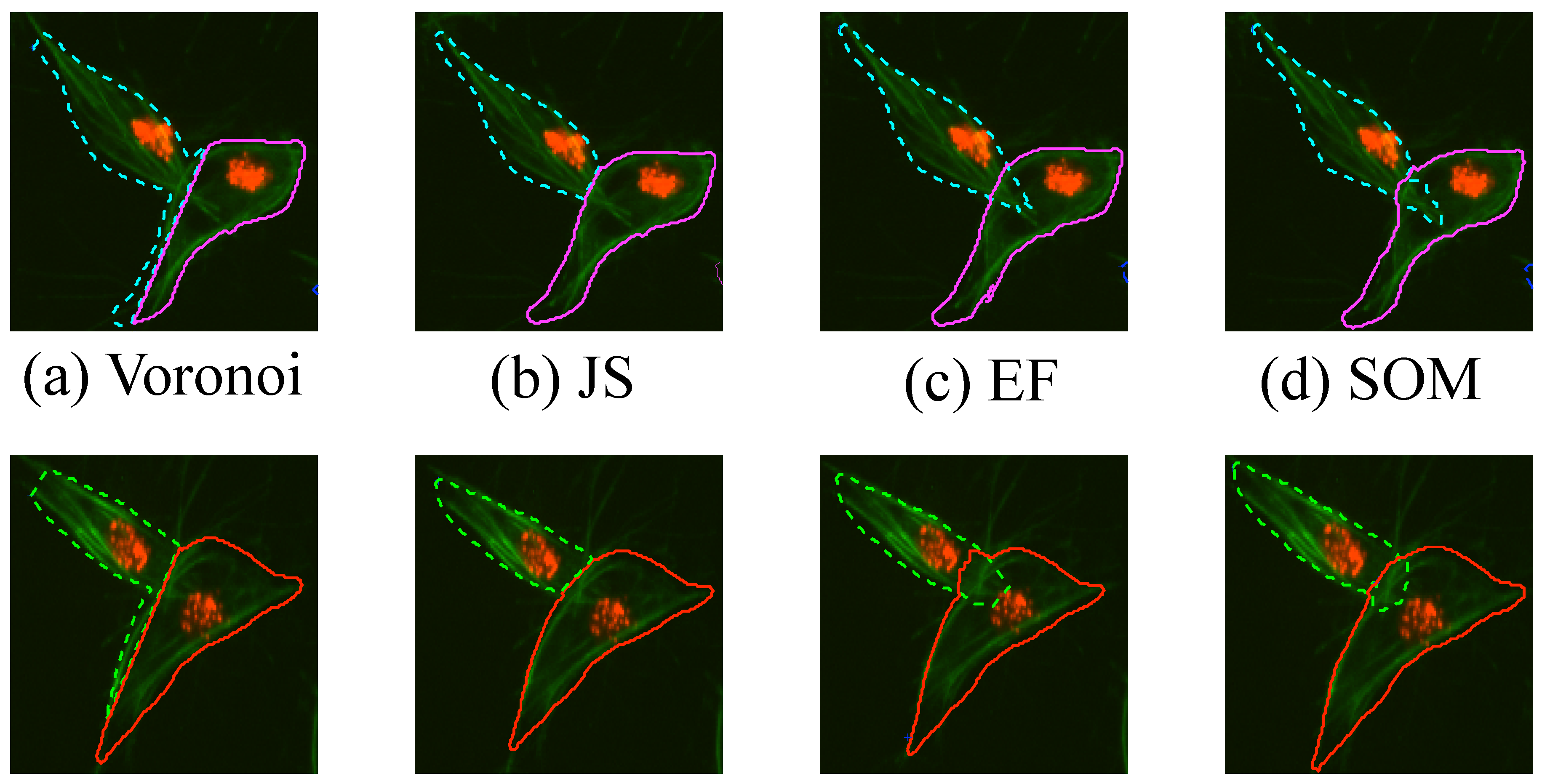
2.4. Segmentation of Overlapping Regions
2.4.1. Voronoi Partition
2.4.2. Junction Slicing (JS)
2.4.3. Edge Following (EF)
2.4.4. Self-organising Maps (SOM) Fitting
3. Results
3.1. Bend Detection in Overlapping Objects
3.2. Corner Detection in Single Objects
Detection of Objects and Segmentation of Clumps
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| EF | Edge Following |
| JS | Junction Slicing |
| MIP | Maximum Intensity Projection |
| mIP | Minimum Intensity Projection |
| ROI | Region of interest |
| SOM | Self-organising maps |
References
- Martinez, F.O.; Sica, A.; Mantovani, A.; Locati, M. Macrophage activation and polarization. Front. Biosci. J. Virtual Libr. 2008, 13, 453–461. [Google Scholar] [CrossRef]
- Wood, W.; Martin, P. Macrophage Functions in Tissue Patterning and Disease: New Insights from the Fly. Dev. Cell 2017, 40, 221–233. [Google Scholar] [CrossRef] [PubMed]
- Pocha, S.M.; Montell, D.J. Cellular and molecular mechanisms of single and collective cell migrations in Drosophila: Themes and variations. Ann. Rev. Genet. 2014, 48, 295–318. [Google Scholar] [CrossRef] [PubMed]
- Stramer, B.; Moreira, S.; Millard, T.; Evans, I.; Huang, C.Y.; Sabet, O.; Milner, M.; Dunn, G.; Martin, P.; Wood, W. Clasp-mediated microtubule bundling regulates persistent motility and contact repulsion in Drosophila macrophages in vivo. J. Cell Biol. 2010, 189, 681–689. [Google Scholar] [CrossRef] [PubMed]
- Maška, M.; Ulman, V.; Svoboda, D.; Matula, P.; Matula, P.; Ederra, C.; Urbiola, A.; España, T.; Venkatesan, S.; Balak, D.M.W.; et al. A benchmark for comparison of cell tracking algorithms. Bioinformatics (Oxford) 2014, 30, 1609–1617. [Google Scholar] [CrossRef] [PubMed]
- Ulman, V.; Maška, M.; Magnusson, K.E.G.; Ronneberger, O.; Haubold, C.; Harder, N.; Matula, P.; Matula, P.; Svoboda, D.; Radojevic, M.; et al. An objective comparison of cell-tracking algorithms. Nat. Methods 2017, 14, 1141–1152. [Google Scholar] [CrossRef] [PubMed]
- Henry, K.M.; Pase, L.; Ramos-Lopez, C.F.; Lieschke, G.J.; Renshaw, S.A.; Reyes-Aldasoro, C.C. PhagoSight: An Open-Source MATLAB® Package for the Analysis of Fluorescent Neutrophil and Macrophage Migration in a Zebrafish Model. PLoS ONE 2013, 8, e72636. [Google Scholar] [CrossRef] [PubMed]
- Dufour, A.; Shinin, V.; Tajbakhsh, S.; Guillén-Aghion, N.; Olivo-Marin, J.C.; Zimmer, C. Segmenting and tracking fluorescent cells in dynamic 3-D microscopy with coupled active surfaces. IEEE Trans. Image Process. 2005, 14, 1396–1410. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Transa. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Plissiti, M.E.; Nikou, C. Overlapping Cell Nuclei Segmentation Using a Spatially Adaptive Active Physical Model. IEEE Transa. Image Process. 2012, 21, 4568–4580. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Carneiro, G.; Bradley, A.P. An Improved Joint Optimization of Multiple Level Set Functions for the Segmentation of Overlapping Cervical Cells. IEEE Transa. Image Process. 2015, 24, 1261–1272. [Google Scholar]
- Reyes-Aldasoro, C.C.; Aldeco, A.L. Image segmentation and compression using neural networks. In Advances in Artificial Perception and Robotics; CIMAT: Guanajuato, Mexico, 2000; pp. 23–25. [Google Scholar]
- Hannah, I.; Patel, D.; Davies, R. The use of variance and entropic thresholding methods for image segmentation. Pattern Recognit. 1995, 28, 1135–1143. [Google Scholar] [CrossRef]
- Caselles, V.; Kimmel, R.; Sapiro, G. Geodesic Active Contours. Int. J. Comput. Vis. 1997, 22, 61–79. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector. In Proceedings of the 4th Alvey Vision Conference Alvety Vision Club, University of Manchester, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Lindeberg, T. Junction detection with automatic selection of detection scales and localization scales. In Proceedings of the 1st International Conference on Image Processing, Austin, TX, USA, 13–16 November 1994; Volume 1, pp. 924–928. [Google Scholar]
- Solís-Lemus, J.A.; Stramer, B.; Slabaugh, G.; Reyes-Aldasoro, C.C. Segmentation of Overlapping Macrophages Using Anglegram Analysis. In Communications in Computer and Information Science, Proceedings of the Medical Image Understanding and Analysis, Edinburgh, UK, 11–13 July 2017; Springer: Cham, Switzerland, 2017; pp. 792–803. [Google Scholar]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N.; Kendall, D.G. Algorithms for Computing Voronoi Diagrams. In Spatial Tessellations; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; pp. 229–290. [Google Scholar]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Jaccard, P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vaud. Sci. Nat. 1901, 37, 547–579. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. The One-Sample Location Problem. In Nonparametric Statistical Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 39–114. [Google Scholar]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Active Shape Models-Their Training and Application. Comput. Vis. Image Underst. 1995, 61, 38–59. [Google Scholar] [CrossRef]
- Gooya, A.; Lekadir, K.; Castro-Mateos, I.; Pozo, J.M.; Frangi, A.F. Mixture of Probabilistic Principal Component Analyzers for Shapes from Point Sets. IEEE Trans. Pattern Anal. Mach. Intell. 2017, PP. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the data and the code used to compute the anglegram algorithm are available at https://github.com/alonsoJASL/matlab.anglegram, or upon request to the corresponding author. Also, the code to generate ground truth is available in https://github.com/alonsoJASL/matlab.manualSegmentation. |




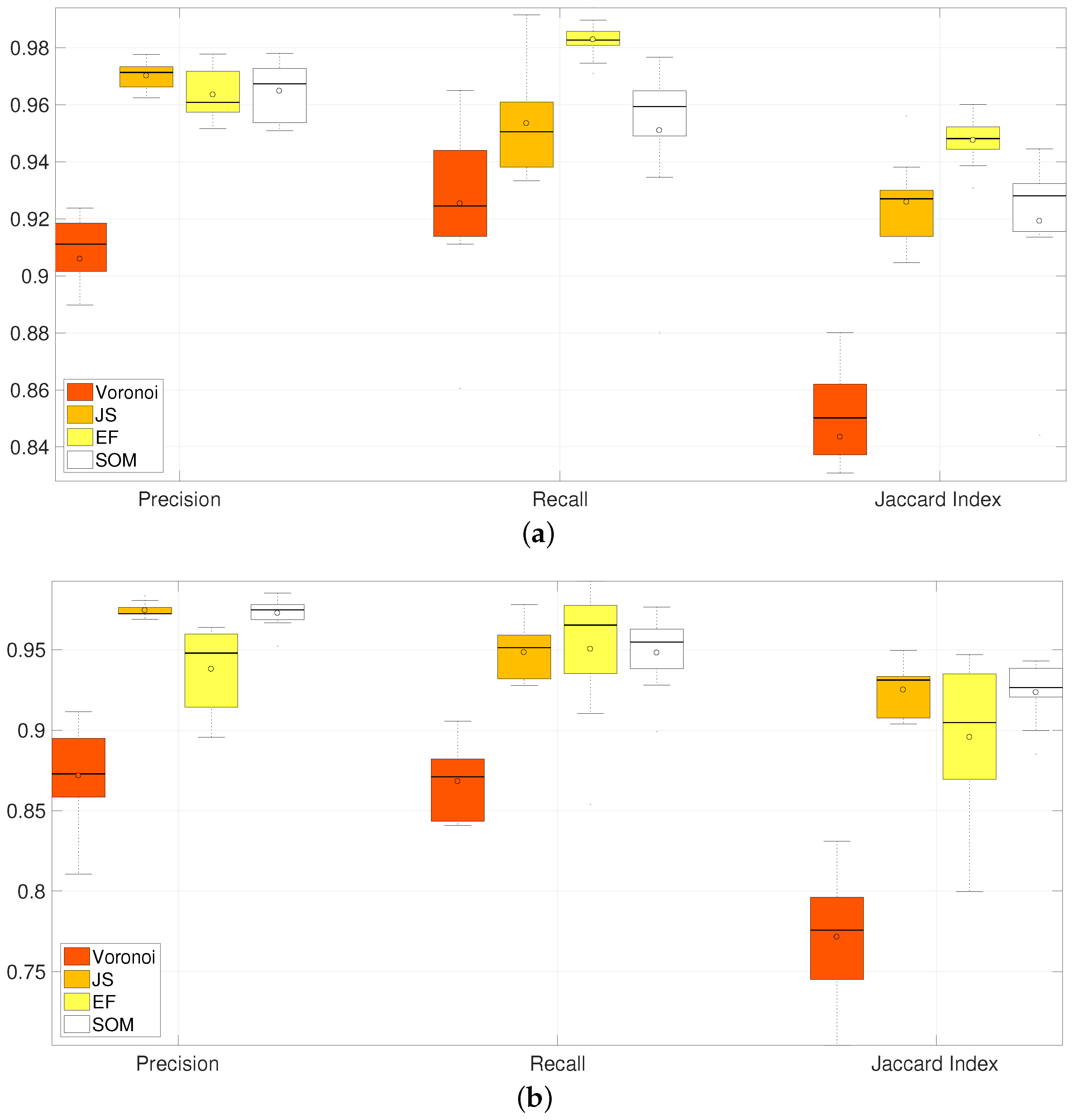
| CLUMP 2 | CLUMP 3 | |||||
|---|---|---|---|---|---|---|
| Precision | Recall | Jaccard Index | Precision | Recall | Jaccard Index | |
| Voronoi | 0.906 | 0.925 | 0.843 | 0.872 | 0.868 | 0.771 |
| JS | 0.970 | 0.953 | 0.926 | 0.974 | 0.948 | 0.925 |
| EF | 0.964 | 0.983 | 0.948 | 0.938 | 0.950 | 0.896 |
| SOM | 0.965 | 0.951 | 0.919 | 0.973 | 0.948 | 0.923 |
| CLUMP 2 | CLUMP 3 | ||||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | Jaccard Index | Precision | Recall | Jaccard Index | ||
| Voronoi vs. | JS | ||||||
| EF | |||||||
| SOM | |||||||
| JS vs. | EF | ||||||
| SOM | |||||||
| EF vs. | SOM | ||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solís-Lemus, J.A.; Stramer, B.; Slabaugh, G.; Reyes-Aldasoro, C.C. Segmentation and Shape Analysis of Macrophages Using Anglegram Analysis. J. Imaging 2018, 4, 2. https://doi.org/10.3390/jimaging4010002
Solís-Lemus JA, Stramer B, Slabaugh G, Reyes-Aldasoro CC. Segmentation and Shape Analysis of Macrophages Using Anglegram Analysis. Journal of Imaging. 2018; 4(1):2. https://doi.org/10.3390/jimaging4010002
Chicago/Turabian StyleSolís-Lemus, José Alonso, Brian Stramer, Greg Slabaugh, and Constantino Carlos Reyes-Aldasoro. 2018. "Segmentation and Shape Analysis of Macrophages Using Anglegram Analysis" Journal of Imaging 4, no. 1: 2. https://doi.org/10.3390/jimaging4010002
APA StyleSolís-Lemus, J. A., Stramer, B., Slabaugh, G., & Reyes-Aldasoro, C. C. (2018). Segmentation and Shape Analysis of Macrophages Using Anglegram Analysis. Journal of Imaging, 4(1), 2. https://doi.org/10.3390/jimaging4010002






