Placido Sub-Pixel Edge Detection Algorithm Based on Enhanced Mexican Hat Wavelet Transform and Improved Zernike Moments
Abstract
1. Introduction
2. Enhanced Mexican Hat Wavelet Transform Edge Detection Algorithm
2.1. Enhanced Mexican Hat Wavelet Transform
2.2. Multi-Scale Multi-Position Image Algorithm
3. Improved Zernike Moment Sub-Pixel Edge Detection Algorithm
3.1. Zernike Moment Edge Detection Principle
3.2. Double Adaptive Threshold Zernike Moment Sub-Pixel Edge Detection Algorithm
3.2.1. An Adaptive Thresholding Algorithm Based on Local Gradient and Variance
3.2.2. An Adaptive Thresholding Algorithm Based on the Hessian Matrix
4. Experimental Procedures and Result Analysis
4.1. Image Acquisition and Algorithm Enhancement Process
4.1.1. Image Acquisition Process
4.1.2. Algorithm Enhancement Process
- (1)
- First, the image is convolved with the multi-scale and multi-position Mexican Hat Wavelet function introduced in this paper. The cumulative response is weighted and fused to achieve preliminary localization of the “coarse” edge of the image.
- (2)
- A 9 × 9 Zernike moment template is applied to convolve the “coarse” edge, extracting four parameters for each pixel.
- (3)
- The optimal segmentation thresholds and are determined using the two adaptive threshold segmentation algorithms proposed herein. The values of and for the obtained pixels are jointly evaluated to further ascertain whether the pixel qualifies as an edge point and to calculate its sub-pixel coordinates.
- (4)
- Step 2 is repeated until all edge points have been assessed.
4.2. Experimental Result Analysis
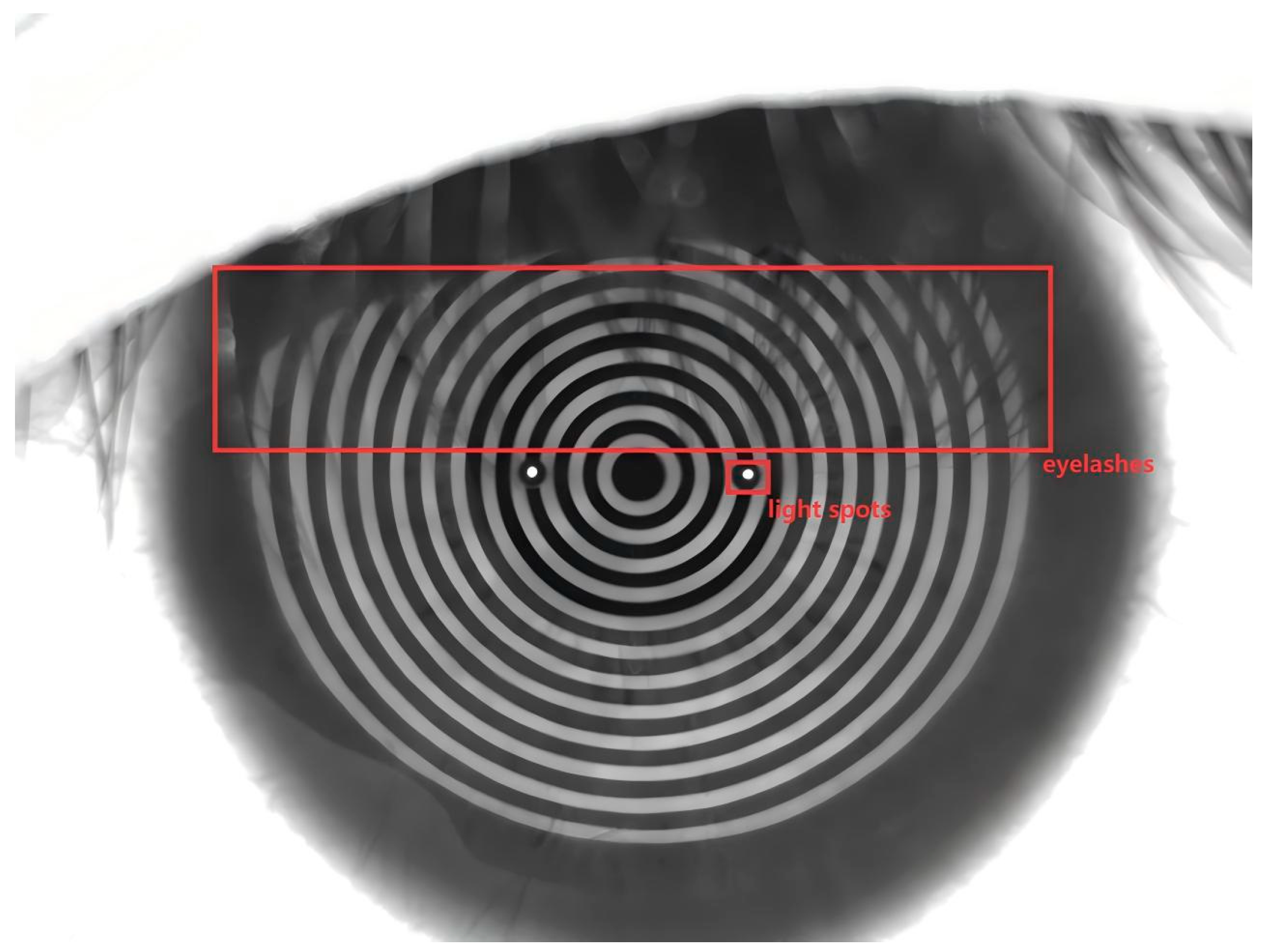
4.2.1. The Eyelash Interference Effect
4.2.2. Accuracy and Noise Immunity of Sub-Pixel Algorithms
4.2.3. Multi-Scale and Multi-Position Parameter Selection
4.2.4. Corneal Placido Image Processing Capability
4.2.5. The Performance of the Improved Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Campos-García, M.; Huerta-Carranza, O.; Moreno-Oliva, V.I.; Aguirre-Aguirre, D.; Pantoja-Arredondo, L.Á. Corneal topography using a smartphone-based corneal topographer considering a biconical model for the corneal surface. Opt. Contin. 2024, 3, 751–767. [Google Scholar] [CrossRef]
- Gomez-Tejada, D.; Hernández, D.M. A proposal to eliminate the skew ray error in corneal topography using Placido disks images. In Proceedings of the Applied Optical Metrology III, San Diego, CA, USA, 11–15 August 2019; SPIE: Bellingham, WA, USA, 2019; Volume 11102, pp. 26–31. [Google Scholar]
- Vaishnavi, L.L.; Bhavana, M.; Manideep, D.C.M.; Venugopal, V. A Fast and Accurate Object Counting using Sobel Edge Detection System for Real–Time Star Gazing. In Proceedings of the 2024 Asia Pacific Conference on Innovation in Technology (APCIT), Mysore, India, 26–27 July 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar]
- Mogos, G. Quantum Image Processing Using Edge Detection Based on Roberts Cross Operators. In Proceedings of the International Conference on Smart Computing and Communication, Zhengzhou, China, 18–20 October 2024; Springer: Singapore, 2024; pp. 149–157. [Google Scholar]
- Ma, P.; Yuan, H.; Chen, Y.; Chen, H.; Weng, G.; Liu, Y. A Laplace operator-based active contour model with improved image edge detection performance. Digit. Signal Process. 2024, 151, 104550. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, Y. Adaptive Canny edge detection based on fast median filtering. In Proceedings of the Fifth International Conference on Computer Vision and Data Mining (ICCVDM 2024), Changchun, China, 19–21 July 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13272, pp. 112–117. [Google Scholar]
- Umar, M.; Ahmad, Z.; Ullah, S.; Saleem, F.; Siddique, M.F.; Kim, J.-M. Advanced Fault Diagnosis in Milling Machines Using Acoustic Emission and Transfer Learning. IEEE Access 2025, 13, 100776–100790. [Google Scholar] [CrossRef]
- Zhu, S.; Zeng, C.; Xu, W.; Zhu, Q. Research on multidirectional wavelet transform in optical measurement. In Proceedings of the Third International Conference on Optics and Image Processing (ICOIP 2023), Hangzhou, China, 14–16 April 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12747, pp. 148–155. [Google Scholar]
- Du, Z.; Zhang, W.; Qin, J.; Lu, H.; Chen, Z.; Zheng, X. A Novel Subpixel Curved Edge Localization Method. In Proceedings of the Intelligent Computation in Big Data Era: International Conference of Young Computer Scientists. In Proceedings of the Engineers and Educators, ICYCSEE 2015, Harbin, China, 10–12 January 2015; Springer: Berlin/Heidelberg, Germany, 2015; Volume 2025, pp. 117–127. [Google Scholar]
- Qi, Y.; Wu, G.; Li, Y.; Dong, Y. Research on double cubic interpolation combined with Gaussian fitting sub-pixel edge detection method. In Proceedings of the 10th International Symposium on Test Automation & Instrumentation (ISTAI 2024), Shenzhen, China, 14–16 August 2024; IET: London, UK, 2024; Volume 2024, pp. 295–303. [Google Scholar]
- Du, G.; Tong, Q.; Hou, L.; Yang, D.; Liang, X. Sub-pixel edge detection method based on canny-franklin moments. Comput. Integr. Manuf. Syst. 2025, 31, 903. [Google Scholar]
- Hagara, M.; Šatka, A.; Kubinec, P.; Stojanović, R. Vibration monitoring using sub-pixel edge localization. In Proceedings of the 2024 13th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 11–14 June 2024; IEEE: New York, NY, USA, 2024; Volume 2024, pp. 1–4. [Google Scholar]
- Ghosal, S.; Mehrotra, R. Detection of composite edges. IEEE Trans. Image Process. 1994, 3, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.Y.; Qi, Y.J. Improved algorithm for sub-pixel edge detection based on Zernike moments. Adv. Mater. Res. 2012, 341, 763–767. [Google Scholar] [CrossRef]
- Bao, E. Improved Canny-Zernike moment-based subpixel edge detection algorithm. In Proceedings of the 6th International Conference on Mechatronics and Intelligent Robotics (ICMIR2022), Wuhan, China, 18–20 November 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12301, pp. 601–611. [Google Scholar]
- Kong, X.; Yi, J.; Wang, X.; Luo, K.; Hu, J. Full-field mode shape identification based on subpixel edge detection and tracking. Appl. Sci. 2023, 13, 747. [Google Scholar] [CrossRef]
- Xie, X.; Ge, S.; Xie, M.; Hu, F.; Jiang, N. An improved industrial sub-pixel edge detection algorithm based on coarse and precise location. J. Ambient Intell. Humaniz. Comput. 2020, 11, 2061–2070. [Google Scholar] [CrossRef]
- Singh, A.; Raghuthaman, N.; Rawat, A.; Singh, J. Representation theorems for the Mexican hat wavelet transform. Math. Methods Appl. Sci. 2020, 43, 3914–3924. [Google Scholar] [CrossRef]
- Xiang, F.; Wang, Z.; Yuan, X. Subpixel edge detection: An Improved Zernike orthogonal moments method. In Proceedings of the 2013 5th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2013; IEEE: New York, NY, USA, 2013; Volume 1, pp. 19–22. [Google Scholar]
- Huang, C.; Jin, W.; Xu, Q.; Liu, Z.; Xu, Z. Sub-pixel edge detection algorithm based on canny–zernike moment method. J. Circuits Syst. Comput. 2020, 29, 2050238. [Google Scholar] [CrossRef]












| Detection Method | Actual Coordinates | Sub-Pixel Coordinates | Coordinate Error |
|---|---|---|---|
| 7 × 7 Zernike algorithm | (251, 341) | (251.438, 341.576) | (0.438, 0.576) |
| (106, 83) | (106.370, 83.519) | (0.370, 0.519) | |
| (78, 287) | (78.562, 287.520) | (0.562, 0.520) | |
| (304, 92) | (304.462, 92.308) | (0.462, 0.308) | |
| (349, 182) | (349.565, 181.495) | (0.565, 0.505) | |
| Interpolation method | (251,341) | (251.327, 341.462) | (0.327, 0.462) |
| (106,83) | (106.271, 83.193) | (0.270, 0.193) | |
| (78,287) | (77.691, 287.499) | (0.309, 0.499) | |
| (304,92) | (304.179, 91.832) | (0.179, 0.168) | |
| (349,182) | (348.393, 181.633) | (0.607, 0.367) | |
| Algorithm in reference [16] | (251, 341) | (251.266, 341.284) | (0.266, 0.284) |
| (106, 83) | (106.101, 82.808) | (0.101, 0.192) | |
| (78, 287) | (77.872, 287.258) | (0.128, 0.258) | |
| (304, 92) | (304.194, 91.888) | (0.194, 0.112) | |
| (349, 182) | (349.307, 182.061) | (0.307, 0.061) | |
| Algorithm in reference [17] | (251, 341) | (251.156, 341.164) | (0.156, 0.164) |
| (106, 83) | (105.762, 83.166) | (0.238, 0.166) | |
| (78, 287) | (78.208, 287.173) | (0.208, 0.173) | |
| (304, 92) | (304.113, 91.733) | (0.113, 0.267) | |
| (349, 182) | (348.814, 182.251) | (0.186, 0.251) | |
| Algorithm in this paper | (251, 341) | (251.023, 341.063) | (0.023, 0.063) |
| (106, 83) | (106.046, 83.057) | (0.046, 0.057) | |
| (78, 287) | (77.878, 287.086) | (0.122, 0.086) | |
| (304, 92) | (304.051, 91.947) | (0.051, 0.053) | |
| (349, 182) | (348.919, 182.071) | (0.082, 0.071) |
| 7 × 7 Zernike Algorithm | Interpolation Method | Algorithm in Reference [16] | Algorithm in Reference [17] | Algorithm in This Paper | |
|---|---|---|---|---|---|
| Maximum Distance Error | 0.765 | 0.709 | 0.389 | 0.312 | 0.149 |
| Minimum Distance Error | 0.555 | 0.245 | 0.217 | 0.226 | 0.067 |
| Mean Distance Error | 0.688 | 0.487 | 0.286 | 0.278 | 0.094 |
| Standard Deviation | 0.3071 | 0.3628 | 0.1793 | 0.1900 | 0.0687 |
| p-value | 0.9940 | 0.9982 | 0.9984 | 0.9991 | 0.9998 |
| 7 × 7 Zernike Algorithm | Interpolation Method | Algorithm in Reference [16] | Algorithm in Reference [17] | Algorithm in This Paper | |
|---|---|---|---|---|---|
| Average Execution Times (ms) | 653 | 319 | 461 | 322 | 384 |
| Algorithm | Mean Distance Error | Standard Deviation | p-Value |
|---|---|---|---|
| MHWT + Zernike | 0.632 | 0.2739 | 0.9981 |
| Multi-scale and Position Enhanced MHWT + Zernike | 0.127 | 0.2183 | 0.9988 |
| MHWT + Improved Zernike | 0.281 | 0.0917 | 0.9992 |
| Proposed Algorithm | 0.094 | 0.0687 | 0.9998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liang, J.; Xiao, Y.; Liu, X.; Li, J.; Cui, G.; Zhang, Q. Placido Sub-Pixel Edge Detection Algorithm Based on Enhanced Mexican Hat Wavelet Transform and Improved Zernike Moments. J. Imaging 2025, 11, 267. https://doi.org/10.3390/jimaging11080267
Wang Y, Liang J, Xiao Y, Liu X, Li J, Cui G, Zhang Q. Placido Sub-Pixel Edge Detection Algorithm Based on Enhanced Mexican Hat Wavelet Transform and Improved Zernike Moments. Journal of Imaging. 2025; 11(8):267. https://doi.org/10.3390/jimaging11080267
Chicago/Turabian StyleWang, Yujie, Jinyu Liang, Yating Xiao, Xinfeng Liu, Jiale Li, Guangyu Cui, and Quan Zhang. 2025. "Placido Sub-Pixel Edge Detection Algorithm Based on Enhanced Mexican Hat Wavelet Transform and Improved Zernike Moments" Journal of Imaging 11, no. 8: 267. https://doi.org/10.3390/jimaging11080267
APA StyleWang, Y., Liang, J., Xiao, Y., Liu, X., Li, J., Cui, G., & Zhang, Q. (2025). Placido Sub-Pixel Edge Detection Algorithm Based on Enhanced Mexican Hat Wavelet Transform and Improved Zernike Moments. Journal of Imaging, 11(8), 267. https://doi.org/10.3390/jimaging11080267






