Recovery and Characterization of Tissue Properties from Magnetic Resonance Fingerprinting with Exchange
Abstract
1. Introduction
2. Background
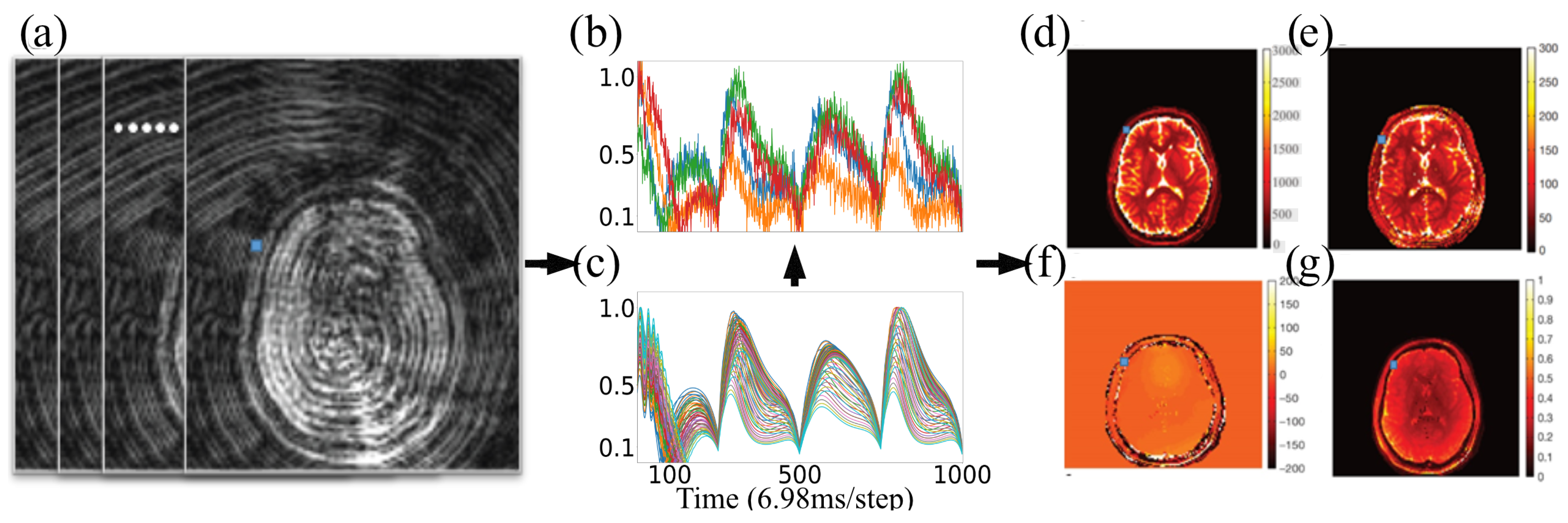
2.1. Magnetic Resonance Fingerprinting
2.2. Tissue Property Recovery from MRF Using Explicit Dictionary
2.3. Magnetic Resonance Fingerprinting with Exchange (MRF-X)
2.4. MRF-X Modeling Using Bloch–McConnell Equations
2.5. Deep Learning for High-Dimensional MRF
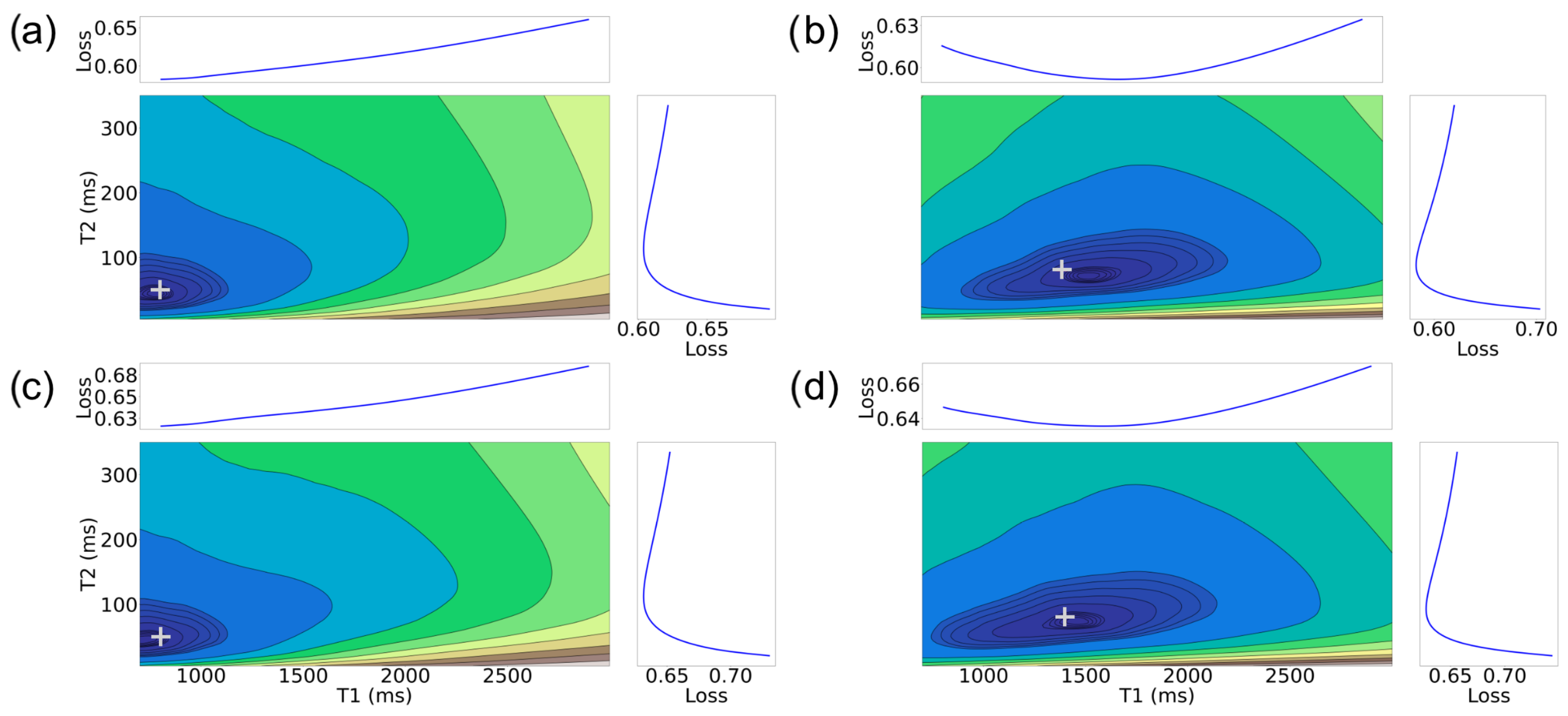
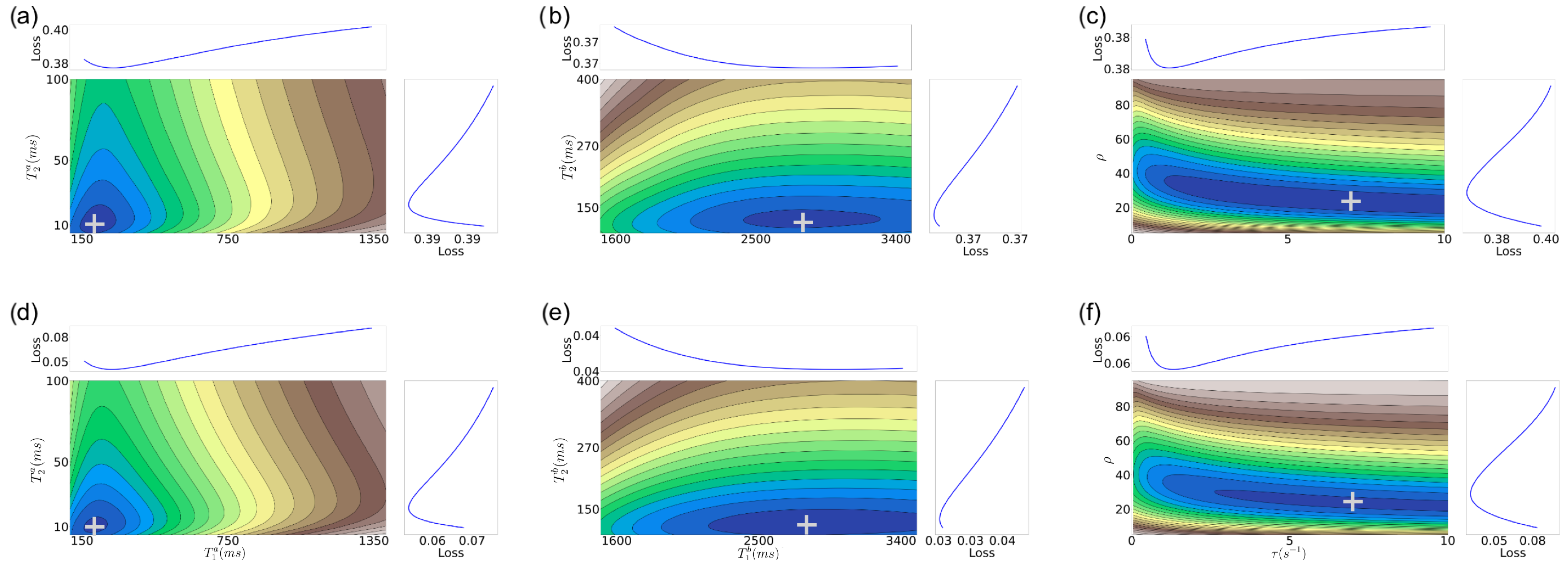
3. Nature of MRF Objective Function
- Similar to the 2D case, there are still well-defined, non-disjoint regions with minimum f in the space. So it is feasible (in theory) to achieve solutions close to the target values, as in the 2D case.
- The gradient structure is generally steeper in some regions than in the 2D case, as indicated by the larger number of narrower contours.
- For higher SNRs, there is still a relatively good alignment between some of the target tissue properties, such as for (, , ), with the actual target. This observation aligns with expectations, given that the MRF-X scan is sensitive to the tissue properties and [27]. Observing (, ) property pairs (sub-figures d,e), it is evident that the minimum of the error surface closely matches the actual target shown represented by + symbol.
- There are large “plateaus” of the error function around the minimum for some tissue properties even for high SNRs. Thus, even when the minimum aligns well with the true parameters, there may be algorithmic challenges finding it due to the error function structure, which has a combination of both steep gradients and large plateaus.
- As expected, the alignment between the minimum of the error surface and the actual target is notably more accurate for SNR 5 compared to SNR 1.
- Estimating the (, ) tissue properties is the most challenging aspect of tissue characterization. Assuming a two-compartment model, we hypothesize that the rate of exchange of protons () and the volume ratio of a compartment (without loss of generality we can assume it is the ratio of compartment b over the total volume) () to the voxel are intrinsically related. If we assume that protons do not “leak” between voxels and exchange only happens inside each measured region (conservation of protons), then at equilibrium there must be an inverse relation between the rate of exchange and the proportion of the compartment to the voxel volume. This implies that multiple different combinations of tissue properties could lead to the same equilibrium state.
4. Methods
4.1. Broyden–Fletcher–Goldfarb–Shanno
4.2. Limited Memory BFGS Algorithm with Bound Constraints
| Algorithm 1 L-BFGS-B (f, , , m, M) |
|
4.3. Simplicial Homology Global Optimization
| Algorithm 2 SHGO (f, , N, local minimizer L) |
|
5. Results and Discussion
5.1. MRF Results
5.2. MRF-X Results
6. Conclusions
- Estimating six tissue properties (especially and ) from MRF-X signals is a challenging optimization problem due to complex error surfaces with plateaus and misaligned minima at lower SNRs.
- Because of the lack of standard optimization approaches for this problem, we created a “Gold Standard” which, although impractical in clinical practice, provides a baseline for comparison of our results.
- Our proposed SHGO + L-BFGS-B algorithm comes within 10–20% of L-BFGS-B with “Gold Standard” initialization, demonstrating its effectiveness for practical applications.
- The 6D recovery problem (including both and ) presents fundamental challenges, with these two parameters being particularly difficult to estimate simultaneously.
- Visualization of the error surfaces reveals an exploitable structure that can guide the development of more effective optimization strategies for MRF-X tissue property recovery.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Larsson, H.B.W.; Frederiksen, J.; Petersen, J.; Nordenbo, A.; Zeeberg, I.; Henriksen, O.; Olesen, J. Assessment of demyelination, edema, and gliosis by in vivo determination of T1 and T2 in the brain of patients with acute attack of multiple sclerosis. Magn. Reson. Med. 1989, 11, 337–348. [Google Scholar] [CrossRef] [PubMed]
- Kim, R.J.; Wu, E.; Rafael, A.; Chen, E.L.; Parker, M.A.; Simonetti, O.; Klocke, F.J.; Bonow, R.O.; Judd, R.M. The use of contrast-enhanced magnetic resonance imaging to identify reversible myocardial dysfunction. N. Engl. J. Med. 2000, 343, 1445–1453. [Google Scholar] [CrossRef]
- Jack, C.R.; Bernstein, M.A.; Fox, N.C.; Thompson, P.; Alexander, G.; Harvey, D.; Borowski, B.; Britson, P.J.; Whitwell, J.L.; Ward, C.; et al. The Alzheimer’s Disease Neuroimaging Initiative (ADNI): MRI methods. J. Magn. Reson. Imaging 2008, 27, 685–691. [Google Scholar] [CrossRef] [PubMed]
- Stabile, A.; Giganti, F.; Rosenkrantz, A.B.; Taneja, S.S.; Villeirs, G.; Gill, I.S.; Allen, C.; Emberton, M.; Moore, C.M.; Kasivisvanathan, V. Multiparametric MRI for prostate cancer diagnosis: Current status and future directions. Nat. Rev. Urol. 2020, 17, 41–61. [Google Scholar] [CrossRef] [PubMed]
- Johnson, L.M.; Turkbey, B.; Figg, W.D.; Choyke, P.L. Multiparametric MRI in prostate cancer management. Nat. Rev. Clin. Oncol. 2014, 11, 346–353. [Google Scholar] [CrossRef]
- Shen, S.; Koonjoo, N.; Boele, T.; Lu, J.; Waddington, D.E.; Zhang, M.; Rosen, M.S. Enhancing organ and vascular contrast in preclinical ultra-low field MRI using superparamagnetic iron oxide nanoparticles. Commun. Biol. 2024, 7, 1197. [Google Scholar] [CrossRef]
- Brady, A.P. Error and discrepancy in radiology: Inevitable or avoidable? Insights Imaging 2017, 8, 171–182. [Google Scholar] [CrossRef]
- Gulani, V.; Seiberlich, N. Quantitative MRI: Rationale and challenges. In Advances in Magnetic Resonance Technology and Applications; Elsevier: Amsterdam, The Netherlands, 2020; Volume 1, pp. xxxvii–li. [Google Scholar]
- Ma, D.; Gulani, V.; Seiberlich, N.; Liu, K.; Sunshine, J.L.; Duerk, J.L.; Griswold, M.A. Magnetic resonance fingerprinting. Nature 2013, 495, 187–192. [Google Scholar] [CrossRef]
- Jiang, Y.; Ma, D.; Keenan, K.E.; Stupic, K.F.; Gulani, V.; Griswold, M.A. Repeatability of magnetic resonance fingerprinting T1 and T2 estimates assessed using the ISMRM/NIST MRI system phantom. Magn. Reson. Med. 2017, 78, 1452–1457. [Google Scholar] [CrossRef]
- Crawley, A.P.; Henkelman, R.M. A comparison of one-shot and recovery methods in T1 imaging. Magn. Reson. Med. 1988, 7, 23–34. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef]
- Deoni, S.C.L.; Rutt, B.K.; Peters, T.M. Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magn. Reson. Med. 2003, 49, 515–526. [Google Scholar] [CrossRef] [PubMed]
- Fram, E.K.; Herfkens, R.J.; Johnson, G.A.; Glover, G.H.; Karis, J.P.; Shimakawa, A.S.; Perkins, T.G.; Pelc, N.J. Rapid calculation of T1 using variable flip angle gradient refocused imaging. Magn. Reson. Imaging 1987, 5, 201–208. [Google Scholar] [CrossRef]
- Welsch, G.H.; Scheffler, K.; Mamisch, T.C.; Hughes, T.; Millington, S.; Deimling, M.; Trattnig, S. Rapid estimation of cartilage T2 based on double echo at steady state (DESS) with 3 Tesla. Magn. Reson. Med. Off. J. Int. Soc. Magn. Reson. Med. 2009, 62, 544–549. [Google Scholar] [CrossRef]
- Bieri, O.; Scheffler, K.; Welsch, G.H.; Trattnig, S.; Mamisch, T.C.; Ganter, C. Quantitative mapping of T2 using partial spoiling. Magn. Reson. Med. 2011, 66, 410–418. [Google Scholar] [CrossRef] [PubMed]
- McGivney, D.F.; Boyacıoğlu, R.; Jiang, Y.; Poorman, M.E.; Seiberlich, N.; Gulani, V.; Keenan, K.E.; Griswold, M.A.; Ma, D. Magnetic resonance fingerprinting review part 2: Technique and directions. J. Magn. Reson. Imaging 2020, 51, 993–1007. [Google Scholar] [CrossRef]
- Bernstein, M.A.; King, K.F.; Zhou, X.J. Handbook of MRI Pulse Sequences; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Nayak, K.S.; Lee, H.; Hargreaves, B.A.; Hu, B.S. Wideband SSFP: Alternating repetition time balanced steady state free precession with increased band spacing. Magn. Reson. Med. 2007, 58. [Google Scholar] [CrossRef]
- Bloch, F. Nuclear Induction. Phys. Rev. 1946, 70, 460–474. [Google Scholar] [CrossRef]
- Jiang, Y.; Ma, D.; Seiberlich, N.; Gulani, V.; Griswold, M.A. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn. Reson. Med. 2015, 74, 1621–1631. [Google Scholar] [CrossRef]
- Chen, Y.; Panda, A.; Pahwa, S.; Hamilton, J.I.; Dastmalchian, S.; McGivney, D.F.; Ma, D.; Batesole, J.; Seiberlich, N.; Griswold, M.A.; et al. Three-dimensional MR fingerprinting for quantitative breast imaging. Radiology 2019, 290, 33–40. [Google Scholar] [CrossRef]
- Hong, T.; Han, D.; Kim, D.H. Simultaneous estimation of PD, T1, T2, T2*, and ΔB0 using magnetic resonance fingerprinting with background gradient compensation. Magn. Reson. Med. 2018, 81, 2614–2623. [Google Scholar] [CrossRef] [PubMed]
- Cauley, S.F.; Setsompop, K.; Ma, D.; Jiang, Y.; Ye, H.; Adalsteinsson, E.; Griswold, M.A.; Wald, L.L. Fast group matching for MR fingerprinting reconstruction. Magn. Reson. Med. 2015, 74, 523–528. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Ma, D.; Jiang, Y.; Hamilton, J.; Seiberlich, N.; Griswold, M.A.; McGivney, D. Low rank approximation methods for MR fingerprinting with large scale dictionaries. Magn. Reson. Med. 2018, 79, 2392–2400. [Google Scholar] [CrossRef] [PubMed]
- McGivney, D.F.; Pierre, E.; Ma, D.; Jiang, Y.; Saybasili, H.; Gulani, V.; Griswold, M.A. SVD Compression for Magnetic Resonance Fingerprinting in the Time Domain. IEEE Trans. Med Imaging 2014, 33, 2311–2322. [Google Scholar] [CrossRef]
- Hamilton, J.I.; Griswold, M.A.; Seiberlich, N. MR Fingerprinting with chemical exchange (MRF-X) to quantify subvoxel T1 and extracellular volume fraction. J. Cardiovasc. Magn. Reson. 2015, 17, 1–3. [Google Scholar] [CrossRef]
- Deoni, S.C.; Matthews, L.; Kolind, S.H. One component? Two components? Three? The effect of including a nonexchanging “free” water component in multicomponent driven equilibrium single pulse observation of T1 and T2. Magn. Reson. Med. 2013, 70, 147–154. [Google Scholar] [CrossRef]
- McConnell, H.M. Reaction rates by nuclear magnetic resonance. J. Chem. Phys. 1958, 28, 430–431. [Google Scholar] [CrossRef]
- Donahue, K.M.; Weisskoff, R.M.; Burstein, D. Water diffusion and exchange as they influence contrast enhancement. J. Magn. Reson. Imaging 1997, 7, 102–110. [Google Scholar] [CrossRef]
- Lundervold, A.S.; Lundervold, A. An overview of deep learning in medical imaging focusing on MRI. Z. Für Med. Phys. 2019, 29, 102–127. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Ma, D.; Mehta, B.B.; Griswold, M.A. Game of learning Bloch equation simulations for MR fingerprinting. arXiv 2020, arXiv:2004.02270. [Google Scholar]
- Hamilton, J.I.; Seiberlich, N. Machine learning for rapid magnetic resonance fingerprinting tissue property quantification. Proc. IEEE 2019, 108, 69–85. [Google Scholar] [CrossRef] [PubMed]
- Cohen, O.; Zhu, B.; Rosen, M.S. MR fingerprinting deep reconstruction network (DRONE). Magn. Reson. Med. 2018, 80, 885–894. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Chen, Y.; Liu, M.; Xiang, L.; Zhang, Q.; Wang, Q.; Lin, W.; Shen, D. Deep learning for fast and spatially constrained tissue quantification from highly accelerated data in magnetic resonance fingerprinting. IEEE Trans. Med Imaging 2019, 38, 2364–2374. [Google Scholar] [CrossRef]
- Buonincontri, G.; Kurzawski, J.W.; Kaggie, J.D.; Matys, T.; Gallagher, F.A.; Cencini, M.; Donatelli, G.; Cecchi, P.; Cosottini, M.; Martini, N.; et al. Three dimensional MRF obtains highly repeatable and reproducible multi-parametric estimations in the healthy human brain at 1.5 T and 3T. Neuroimage 2021, 226, 117573. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, J.I.; Deshmane, A.; Griswold, M.; Seiberlich, N. MR fingerprinting with chemical exchange (MRF-X) for in vivo multi-compartment relaxation and exchange rate mapping. In Proceedings of the 24th Annual Meeting and Exhibition of the International Society for Magnetic Resonance in Medicine (ISMRM 2016), Singapore, 7–13 May 2016. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Lochschmidt, M.E.; Gassenhuber, M.; Riederer, I.; Hammel, J.; Birnbacher, L.; Busse, M.; Boeckh-Behrens, T.; Ikenberg, B.; Wunderlich, S.; Liesche-Starnecker, F.; et al. Five material tissue decomposition by dual energy computed tomography. Sci. Rep. 2022, 12, 17117. [Google Scholar] [CrossRef]
- Roshdy, A.; Al Kork, S.; Beyrouthy, T.; Nait-ali, A. Simplicial Homology Global Optimization of EEG Signal Extraction for Emotion Recognition. Robotics 2023, 12, 99. [Google Scholar] [CrossRef]
- Soritz, S.; Moser, D.; Gruber-Wölfler, H. Comparison of Derivative-Free Algorithms for their Applicability in Self-Optimization of Chemical Processes. Chem.-Methods 2022, 2, e202100091. [Google Scholar] [CrossRef]
- Endres, S.C.; Sandrock, C.; Focke, W.W. A simplicial homology algorithm for Lipschitz optimisation. J. Glob. Optim. 2018, 72, 181–217. [Google Scholar] [CrossRef]
- Törn, A.; Viitanen, S. Topographical global optimization. In Recent Advances in Global Optimization; Princeton University Press: Princeton, NJ, USA, 1992; pp. 384–398. [Google Scholar]
- Paulavičius, R.; Žilinskas, J. Advantages of simplicial partitioning for Lipschitz optimization problems with linear constraints. Optim. Lett. 2016, 10, 237–246. [Google Scholar] [CrossRef]
- Sobol’, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. Zhurnal Vychislitel’noi Mat. I Mat. Fiz. 1967, 7, 784–802. [Google Scholar] [CrossRef]
- Lee, D.T.; Schachter, B.J. Two algorithms for constructing a Delaunay triangulation. Int. J. Comput. Inf. Sci. 1980, 9, 219–242. [Google Scholar] [CrossRef]
- Cohen, D.I. On the Sperner lemma. J. Comb. Theory 1967, 2, 585–587. [Google Scholar] [CrossRef]
- Panda, A.; Mehta, B.B.; Coppo, S.; Jiang, Y.; Ma, D.; Seiberlich, N.; Griswold, M.A.; Gulani, V. Magnetic resonance fingerprinting–an overview. Curr. Opin. Biomed. Eng. 2017, 3, 56–66. [Google Scholar] [CrossRef]
- Guennebaud, G.; Jacob, B.; He, C.-P.; Ferro, D.G.; Steiner, B.; Luitz, D.J.; Margaritis, K.A.; Brun, G.; Zoppitelli, P.; Garg, R.; et al. Eigen v3; Eigen Library Developers: Lausanne, Switzerland, 2010; Available online: http://eigen.tuxfamily.org (accessed on 4 May 2025).


| Tissue Property | Min | Max | Step |
|---|---|---|---|
| Two-tissue property model | |||
| (ms) | 700 | 3000 | 0.23 |
| (ms) | 5 | 350 | 0.03 |
| Six-tissue property model | |||
| (ms) | 100 | 1400 | 13 |
| (ms) | 5 | 100 | 0.95 |
| (ms) | 1500 | 3500 | 20 |
| (ms) | 100 | 400 | 3 |
| () | 0.05 | 10 | 0.01 |
| (%) | 5 | 95 | 0.9 |
| Boundaries | Gold Std. | |||
|---|---|---|---|---|
| Property | Minimum | Maximum | Extent | Max Error. |
| (ms) | 800 | 1400 | 300 | 0.18 |
| (ms) | 20 | 150 | 20 | 0.50 |
| (ms) | 1500 | 2800 | 300 | 0.10 |
| (ms) | 200 | 350 | 20 | 0.05 |
| () | 0.1 | 5 | 0.3 | 1.5 |
| (%) | 5 | 95 | 6 | 0.6 |
| TP | Dictionary Match with Gold Std. * | L-BFGS-B with Gold Std. * | L-BFGS-B | SHGO + L-BFGS-B |
|---|---|---|---|---|
| TP | Dictionary Match with Gold Std. * | L-BFGS-B with Gold Std. * | L-BFGS-B | SHGO + L-BFGS-B |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nallapareddy, N.; Ray, S. Recovery and Characterization of Tissue Properties from Magnetic Resonance Fingerprinting with Exchange. J. Imaging 2025, 11, 169. https://doi.org/10.3390/jimaging11050169
Nallapareddy N, Ray S. Recovery and Characterization of Tissue Properties from Magnetic Resonance Fingerprinting with Exchange. Journal of Imaging. 2025; 11(5):169. https://doi.org/10.3390/jimaging11050169
Chicago/Turabian StyleNallapareddy, Naren, and Soumya Ray. 2025. "Recovery and Characterization of Tissue Properties from Magnetic Resonance Fingerprinting with Exchange" Journal of Imaging 11, no. 5: 169. https://doi.org/10.3390/jimaging11050169
APA StyleNallapareddy, N., & Ray, S. (2025). Recovery and Characterization of Tissue Properties from Magnetic Resonance Fingerprinting with Exchange. Journal of Imaging, 11(5), 169. https://doi.org/10.3390/jimaging11050169






