SwinTCS: A Swin Transformer Approach to Compressive Sensing with Non-Local Denoising
Abstract
1. Introduction
- We propose a novel deep compressive sensing framework named SwinTCS, which integrates the shifted window Transformer (Swin Transformer) and convolutional neural network (CNN) to enhance the quality and efficiency of image reconstruction. The Swin Transformer, with its shifted window attention mechanism, effectively eliminates boundary artifacts inherent in block-based compressive sensing models while significantly reducing computational complexity. Meanwhile, the CNN component strengthens local feature extraction, further optimizing the overall performance of the model.
- We design an advanced noise suppression module within the SwinTCS framework, utilizing the Non-Local Feature Means (NLM) algorithm to enhance model robustness. This module leverages the global similarity of image features to effectively mitigate the impact of complex noise, improving the reconstruction process’s adaptability and stability under diverse noise conditions.
- We introduced an Attention Fusion module in SwinTCS, which integrates global features captured by the Transformer with local features extracted by the CNN. This module further enhances the interaction and consistency between global and local information, significantly improving image reconstruction quality and detail recovery.
2. Related Works
2.1. Deep Compressive Sensing
2.1.1. Category I: Traditional Model-Driven Approaches
2.1.2. Category II: Data-Driven Deep Learning Approaches
2.2. Swin Transformer
2.3. Non-Local Means Denoising
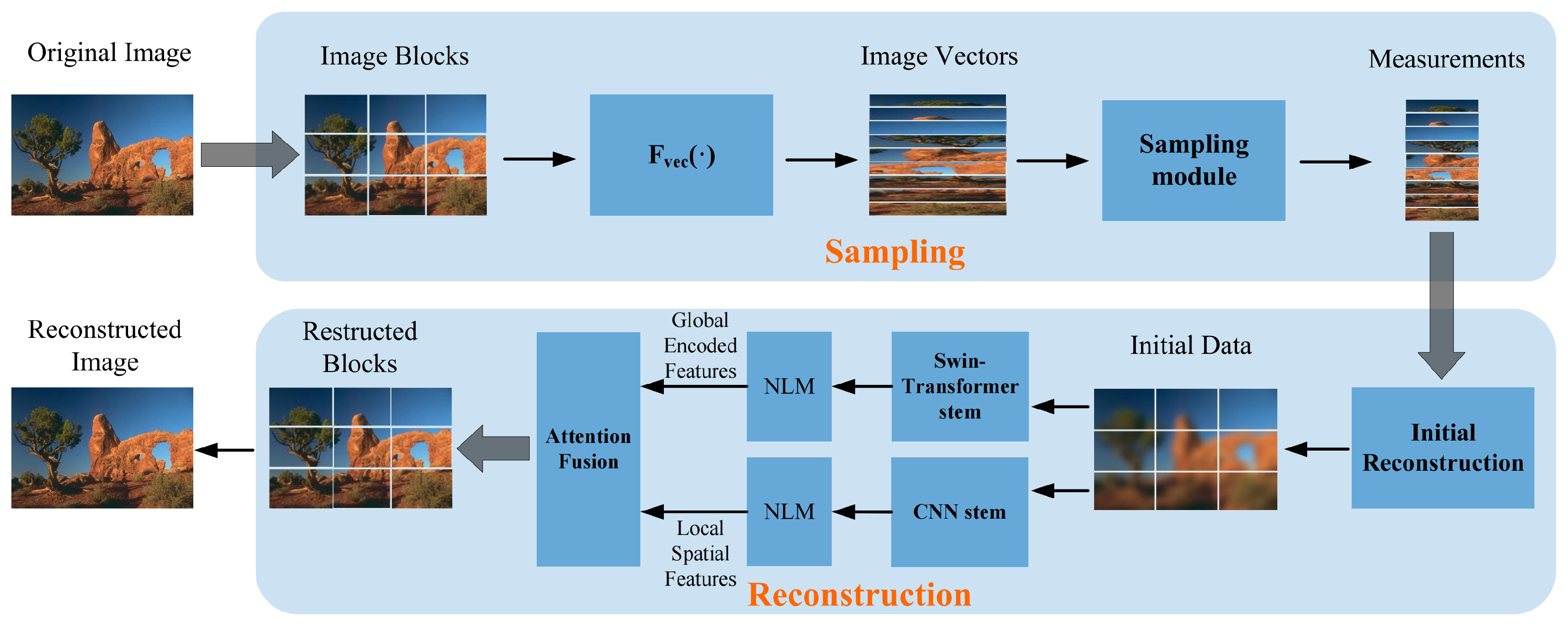
3. Proposed Method
3.1. Sampling Module
3.2. Reconstruction Module
3.2.1. Initial Reconstruction
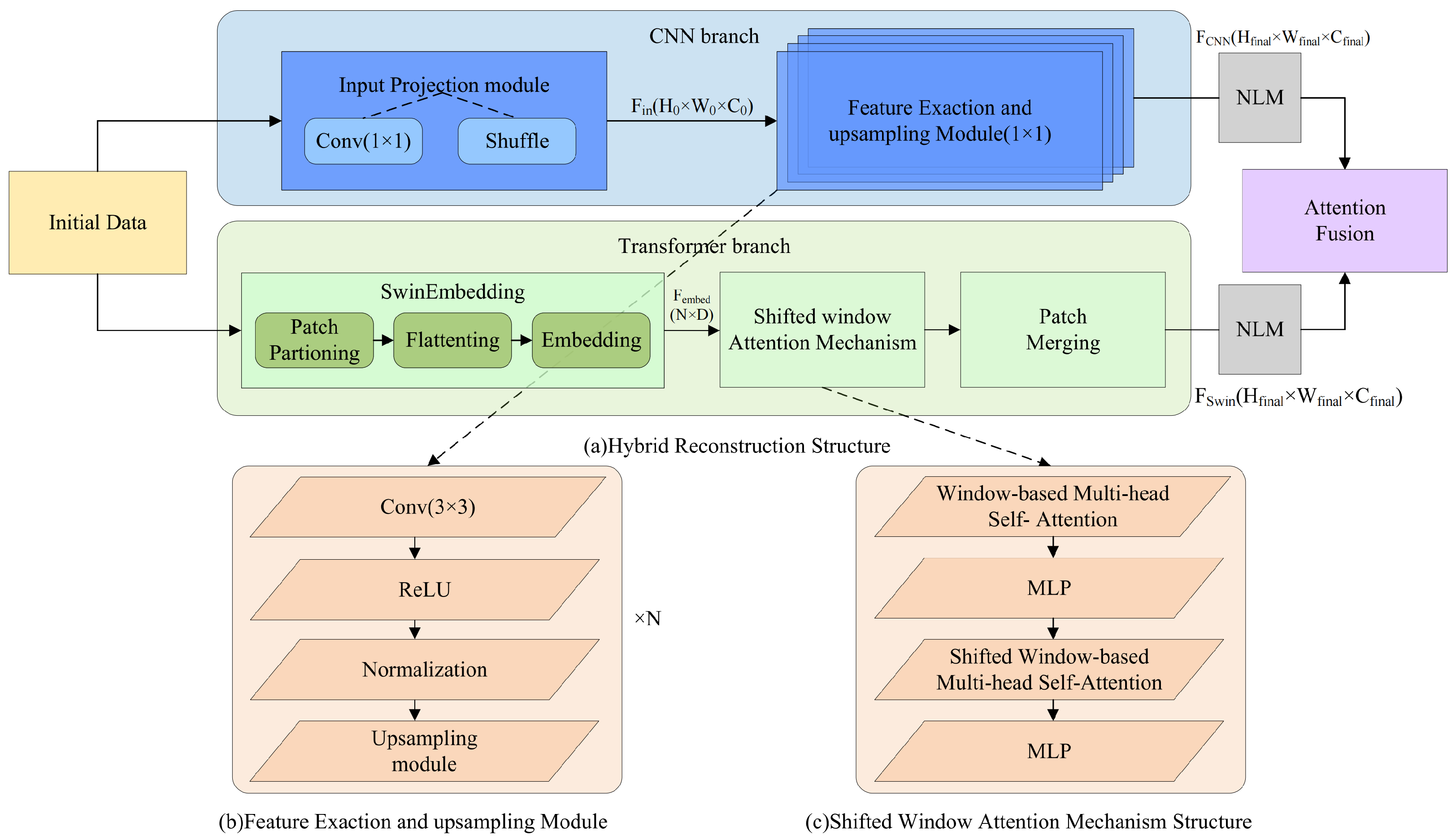
3.2.2. Hybrid Reconstruction
- a
- CNN branch
- b
- Swin Transformer branch
| Algorithm 1 Formulations in the Transformer Branch. |
| Operation Mathematical Expression |
| Input Image feature map |
| Output Processed feature map |
| 1: Patch Reshaping |
| 2: Patch Embedding |
| 3: N Calculation |
| 4: QKV Calculation |
| 5: Calculation |
| 6: Attention Calculation |
| 7: WMSA Output |
| 8: SWMSA Output |
| 9: Residual Connection |
| 10: Patch Merging |
| 11: Output |
Non-Local Denoising Layer
Feature Fusion Module
3.3. Loss Function
4. Experimental Results
4.1. Experimental Settings
4.1.1. Experimental Datasets
4.1.2. Training Details
4.2. Comparisons with State-of-the-Art Methods
4.2.1. Quantitative Comparisons
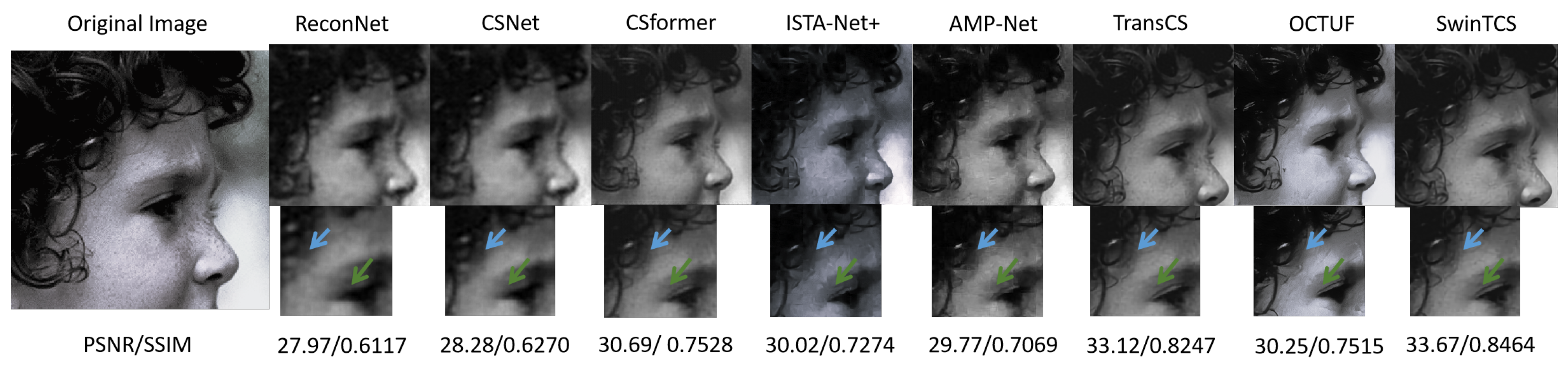
4.2.2. Visual Comparisons
4.3. Noise Robustness
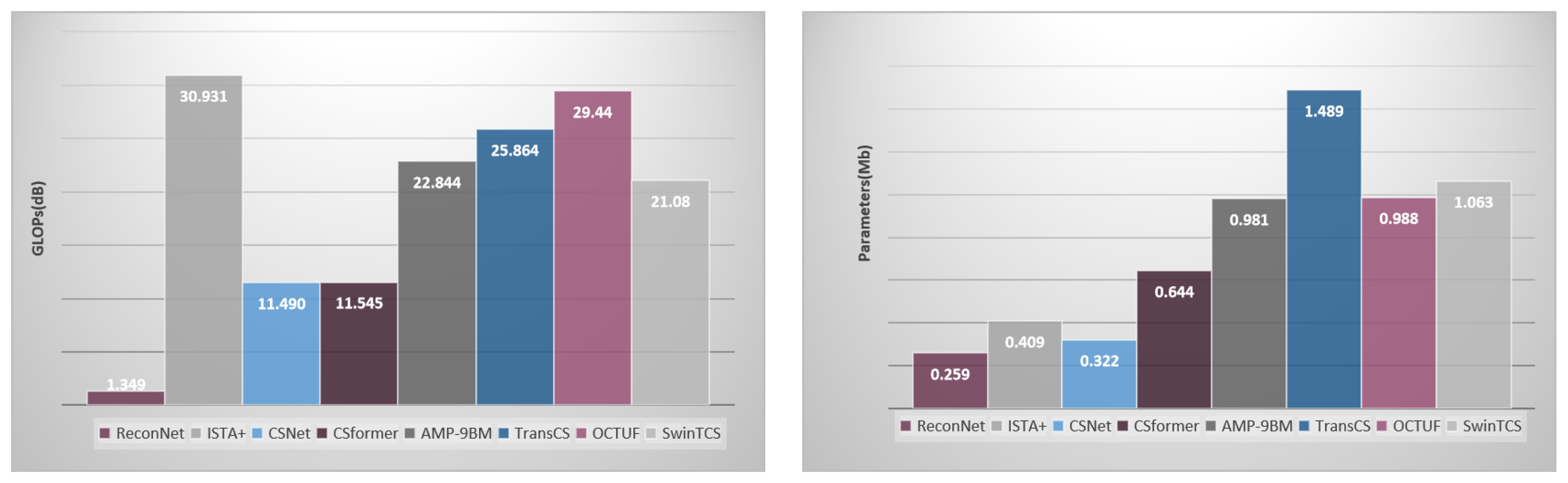
4.4. Complexity Analysis
4.5. Ablation Experiments
4.5.1. Non-Local Means Denoising
4.5.2. Attention Fusion
5. Conclusions and Future Work
- Optimize the shift strategy and network depth to enhance performance on complex visual scenes and better balance global–local information extraction.
- Dynamically adjust learning rates and optimization strategies to improve convergence stability and training efficiency.
- Further accelerate the model to meet the low-latency requirements of real-time IoT applications, considering deployment on edge devices with strict resource limitations.
- Investigate privacy-preserving mechanisms such as encryption or federated learning to protect sensitive visual data during reconstruction.
- Develop ethical guidelines for responsible deployment and evaluate the social impact of image reconstruction in practical applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6G Internet of Things: A comprehensive survey. IEEE Internet Things J. 2021, 9, 359–383. [Google Scholar] [CrossRef]
- Habibzadeh, H.; Dinesh, K.; Shishvan, O.R.; Boggio-Dandry, A.; Sharma, G.; Soyata, T. A survey of healthcare Internet of Things (HIoT): A clinical perspective. IEEE Internet Things J. 2019, 7, 53–71. [Google Scholar] [CrossRef]
- Suo, Z.; Xia, C.; Jiang, D.; Peng, H.; Tong, F.; Chen, X. Multi-tiered Reversible Data Privacy Protection Scheme for IoT Based on Compression Sensing and Digital Watermarking. IEEE Internet Things J. 2023, 11, 11524–11539. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, Y.; Wang, T.; Wen, W.; Xiang, Y.; Cao, X. Visual content privacy protection: A survey. arXiv 2023, arXiv:2303.16552. [Google Scholar] [CrossRef]
- Du, X.; Liang, K.; Lv, Y.; Qiu, S. Fast reconstruction of EEG signal compression sensing based on deep learning. Sci. Rep. 2024, 14, 5087. [Google Scholar] [CrossRef]
- Li, X.; Da Xu, L. A review of Internet of Things—Resource allocation. IEEE Internet Things J. 2020, 8, 8657–8666. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Jiang, D.; Tsafack, N.; Boulila, W.; Ahmad, J.; Barba-Franco, J. ASB-CS: Adaptive sparse basis compressive sensing model and its application to medical image encryption. Expert Syst. Appl. 2024, 236, 121378. [Google Scholar] [CrossRef]
- Damian, C.; Garoi, F.; Udrea, C.; Coltuc, D. The evaluation of single-pixel camera resolution. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 2517–2523. [Google Scholar] [CrossRef]
- Pauly, J.M. Compressed sensing MRI. Signal Process. Mag. IEEE 2008, 25, 72–82. [Google Scholar]
- Zhuang, L.; Shen, L.; Wang, Z.; Li, Y. Ucsnet: Priors guided adaptive compressive sensing framework for underwater images. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 5587–5604. [Google Scholar] [CrossRef]
- Gui, Y.; Lu, H.; Jiang, X.; Wu, F.; Chen, C.W. Compressed pseudo-analog transmission system for remote sensing images over bandwidth-constrained wireless channels. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 3181–3195. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Dinh, K.Q.; Jeon, B. Iterative weighted recovery for block-based compressive sensing of image/video at a low subrate. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 2294–2308. [Google Scholar] [CrossRef]
- Zhou, S.; He, Y.; Liu, Y.; Li, C.; Zhang, J. Multi-channel deep networks for block-based image compressive sensing. IEEE Trans. Multimed. 2020, 23, 2627–2640. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-CSNet: A deep learning approach for image compressive sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 521–538. [Google Scholar] [CrossRef]
- Gilton, D.; Ongie, G.; Willett, R. Neumann networks for linear inverse problems in imaging. IEEE Trans. Comput. Imaging 2019, 6, 328–343. [Google Scholar] [CrossRef]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1828–1837. [Google Scholar]
- Zhang, Z.; Liu, Y.; Liu, J.; Wen, F.; Zhu, C. AMP-Net: Denoising-based deep unfolding for compressive image sensing. IEEE Trans. Image Process. 2020, 30, 1487–1500. [Google Scholar] [CrossRef]
- Yao, H.; Dai, F.; Zhang, S.; Zhang, Y.; Tian, Q.; Xu, C. Dr2-net: Deep residual reconstruction network for image compressive sensing. Neurocomputing 2019, 359, 483–493. [Google Scholar] [CrossRef]
- Kulkarni, K.; Lohit, S.; Turaga, P.; Kerviche, R.; Ashok, A. Reconnet: Non-iterative reconstruction of images from compressively sensed measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 449–458. [Google Scholar]
- Shi, W.; Jiang, F.; Liu, S.; Zhao, D. Image compressed sensing using convolutional neural network. IEEE Trans. Image Process. 2019, 29, 375–388. [Google Scholar] [CrossRef]
- Song, J.; Mou, C.; Wang, S.; Ma, S.; Zhang, J. Optimization-inspired cross-attention transformer for compressive sensing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 6174–6184. [Google Scholar]
- Ye, D.; Ni, Z.; Wang, H.; Zhang, J.; Wang, S.; Kwong, S. CSformer: Bridging convolution and transformer for compressive sensing. IEEE Trans. Image Process. 2023, 32, 2827–2842. [Google Scholar] [CrossRef]
- Shen, M.; Gan, H.; Ning, C.; Hua, Y.; Zhang, T. TransCS: A transformer-based hybrid architecture for image compressed sensing. IEEE Trans. Image Process. 2022, 31, 6991–7005. [Google Scholar] [CrossRef]
- Tanchenko, A. Visual-PSNR measure of image quality. J. Vis. Commun. Image Represent. 2014, 25, 874–878. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: New York, NY, USA, 2010; pp. 2366–2369. [Google Scholar]
- Guo, Z.; Zhang, J. Lightweight Dilated Residual Convolution AMP Network for Image Compressed Sensing. In Proceedings of the 2023 4th International Conference on Computer Engineering and Application (ICCEA), Hangzhou, China, 7–9 April 2023; IEEE: New York, NY, USA, 2023; pp. 747–752. [Google Scholar]
- Gan, H.; Wang, X.; He, L.; Liu, J. Learned two-step iterative shrinkage thresholding algorithm for deep compressive sensing. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 3943–3956. [Google Scholar] [CrossRef]
- Yang, S.; Xiang, X.; Tong, F.; Zhao, D.; Li, X. Image Compressed Sensing Using Multi-Scale Characteristic Residual Learning. In Proceedings of the 2023 IEEE International Conference on Multimedia and Expo (ICME), Brisbane, Australia, 10–14 July 2023; IEEE: New York, NY, USA, 2023; pp. 1595–1600. [Google Scholar]
- Li, W.; Chen, B.; Liu, S.; Zhao, S.; Du, B.; Zhang, Y.; Zhang, J. D3C2-Net: Dual-Domain Deep Convolutional Coding Network for Compressive Sensing. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 9341–9355. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. Non-local means denoising. Image Process. Line 2011, 1, 208–212. [Google Scholar] [CrossRef]
- Manjón, J.V.; Carbonell-Caballero, J.; Lull, J.J.; García-Martí, G.; Martí-Bonmatí, L.; Robles, M. MRI denoising using non-local means. Med. Image Anal. 2008, 12, 514–523. [Google Scholar] [CrossRef]
- Li, L.; Si, Y.; Jia, Z. Remote sensing image enhancement based on non-local means filter in NSCT domain. Algorithms 2017, 10, 116. [Google Scholar] [CrossRef]
- Xie, C.; Wu, Y.; Maaten, L.v.d.; Yuille, A.L.; He, K. Feature denoising for improving adversarial robustness. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 501–509. [Google Scholar]
- Alnuaimy, A.N.; Jawad, A.M.; Abdulkareem, S.A.; Mustafa, F.M.; Ivanchenko, S.; Toliupa, S. BM3D Denoising Algorithms for Medical Image. In Proceedings of the 2024 35th Conference of Open Innovations Association (FRUCT), Tampere, Finland, 24–26 April 2024; IEEE: New York, NY, USA, 2024; pp. 135–141. [Google Scholar]
- Marmolin, H. Subjective MSE measures. IEEE Trans. Syst. Man Cybern. 1986, 16, 486–489. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi-Morel, M.L. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the 23rd British Machine Vision Conference (BMVC), Surrey, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the Curves and Surfaces: 7th International Conference, Avignon, France, 24–30 June 2010; Revised Selected Papers 7. Springer: Berlin/Heidelberg, Germany, 2012; pp. 711–730. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; IEEE: New York, NY, USA, 2001; Volume 2, pp. 416–423. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]






| Datasets | Method | GBsR | ReconNet | CSNet | Csformer | ISTA-Net+ | AMP-Net | TransCS | OCTUF | Average | SwinTCS | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (TIP2014) | (CVPR2016) | (TIP2019) | (TIP2023) | (CVPR2018) | (TIP2021) | (TIP2022) | (CVPR2023) | (Ours) | |||||||||||||
| Ratio | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| Set5 | 0.01 | 18.89 | 0.4919 | 22.34 | 0.5895 | 22.74 | 0.5864 | 23.90 | 0.6571 | 20.25 | 0.5608 | 20.43 | 0.5776 | 21.29 | 0.5787 | —— | —— | 21.41 | 0.5774 | 23.97(2.56↑) | 0.6311(0.0537↑) |
| 0.04 | 23.82 | 0.7032 | 24.89 | 0.7392 | 25.22 | 0.7307 | 27.70 | 0.7931 | 24.65 | 0.7219 | 24.06 | 0.7274 | 25.19 | 0.7378 | —— | —— | 25.08 | 0.7362 | 28.97(3.89↑) | 0.8395(0.1033↑) | |
| 0.1 | 27.12 | 0.8401 | 27.89 | 0.8418 | 27.92 | 0.8413 | 30.36 | 0.8676 | 29.16 | 0.8515 | 29.56 | 0.8682 | 29.77 | 0.8805 | 30.39 | 0.8751 | 29.02 | 0.8583 | 33.73(4.72↑) | 0.9328(0.0745↑) | |
| 0.25 | 31.72 | 0.8832 | 31.9 | 0.8993 | 33.07 | 0.9160 | 33.36 | 0.9230 | 34.17 | 0.9372 | 34.88 | 0.9486 | 35.15 | 0.9510 | 35.25 | 0.9300 | 33.69 | 0.9235 | 38.89(5.20↑) | 0.9697(0.0462↑) | |
| 0.5 | 37.56 | 0.9599 | 37.94 | 0.9611 | 38.28 | 0.9623 | 39.11 | 0.9639 | 39.49 | 0.9806 | 40.50 | 0.9868 | 41.31 | 0.9909 | 40.63 | 0.9744 | 39.35 | 0.9724 | 43.64(4.29↑) | 0.9895(0.0170↑) | |
| Set14 | 0.01 | 18.26 | 0.4884 | 21.73 | 0.5583 | 21.92 | 0.5485 | 22.73 | 0.5681 | 19.82 | 0.5414 | 20.02 | 0.5430 | 21.03 | 0.5454 | —— | —— | 20.79 | 0.5419 | 21.97(1.18↑) | 0.5481(0.0062↑) |
| 0.04 | 22.69 | 0.6534 | 24.25 | 0.6755 | 24.72 | 0.7062 | 25.54 | 0.6922 | 23.78 | 0.6808 | 23.53 | 0.6880 | 24.78 | 0.6958 | —— | —— | 24.18 | 0.6845 | 25.59(1.41↑) | 0.7119(0.0279↑) | |
| 0.1 | 26.04 | 0.7836 | 27.15 | 0.8002 | 27.45 | 0.8037 | 27.71 | 0.7886 | 28.26 | 0.8289 | 28.76 | 0.8354 | 28.97 | 0.8552 | 27.55 | 0.7827 | 27.74 | 0.8098 | 28.79(1.05↑) | 0.8381(0.0213↑) | |
| 0.25 | 30.82 | 0.8938 | 31.2 | 0.8357 | 31.98 | 0.8959 | 31.35 | 0.8956 | 32.92 | 0.9386 | 33.38 | 0.9412 | 33.75 | 0.9464 | 31.4 | 0.8937 | 32.10 | 0.9051 | 33.91(1.81↑) | 0.9342(0.0291↑) | |
| 0.5 | 35.47 | 0.9119 | 35.86 | 0.9210 | 36.39 | 0.9572 | 37.07 | 0.9569 | 38.28 | 0.9685 | 38.52 | 0.9722 | 39.42 | 0.9757 | 36.12 | 0.951 | 37.14 | 0.9518 | 39.57(2.43↑) | 0.9725(0.0207↑) | |
| BSD100 | 0.01 | 20.14 | 0.5030 | 22.96 | 0.5843 | 23.21 | 0.5884 | 23.61 | 0.5954 | 21.86 | 0.5674 | 21.97 | 0.5723 | 22.44 | 0.5856 | —— | —— | 22.31 | 0.5709 | 23.11(0.80↑) | 0.5791(0.0082↑) |
| 0.04 | 24.12 | 0.6919 | 25.58 | 0.7441 | 25.87 | 0.7432 | 26.58 | 0.7406 | 25.23 | 0.7223 | 25.12 | 0.7289 | 26.25 | 0.7393 | —— | —— | 25.54 | 0.7300 | 25.92(0.38↑) | 0.7305(0.0005↑) | |
| 0.1 | 27.88 | 0.8230 | 28.12 | 0.8315 | 28.31 | 0.8381 | 29.92 | 0.8314 | 30.04 | 0.8443 | 30.24 | 0.8666 | 30.79 | 0.8761 | 26.32 | 0.738 | 28.95 | 0.8311 | 30.52(1.57↑) | 0.8434(0.0123↑) | |
| 0.25 | 32.21 | 0.8688 | 32.26 | 0.8872 | 33.70 | 0.9093 | 34.75 | 0.9085 | 35.04 | 0.9295 | 35.45 | 0.9352 | 36.16 | 0.9498 | 29.83 | 0.8675 | 33.68 | 0.9070 | 35.46(1.78↑) | 0.9269(0.0199↑) | |
| 0.5 | 37.63 | 0.9487 | 38.04 | 0.9540 | 38.49 | 0.9579 | 38.85 | 0.9756 | 40.73 | 0.9773 | 41.34 | 0.9745 | 42.07 | 0.9888 | 34.58 | 0.9481 | 38.97 | 0.9656 | 40.06(1.09↑) | 0.9714(0.0058↑) | |
| Urban100 | 0.01 | 18.26 | 0.3786 | 18.02 | 0.3785 | 17.74 | 0.3724 | 20.85 | 0.4938 | 16.66 | 0.3731 | 17.00 | 0.3563 | 18.02 | 0.3711 | —— | —— | 18.08 | 0.3919 | 19.69(1.61↑) | 0.4943(0.1024↑) |
| 0.04 | 21.69 | 0.5258 | 21.72 | 0.6688 | 20.79 | 0.5781 | 22.97 | 0.6533 | 19.66 | 0.5369 | 19.93 | 0.5415 | 23.23 | 0.7107 | —— | —— | 21.43 | 0.6021 | 22.99(1.57↑) | 0.6959(0.0973↑) | |
| 0.1 | 25.04 | 0.7385 | 26.35 | 0.7937 | 25.54 | 0.7525 | 25.06 | 0.7558 | 23.51 | 0.7199 | 23.11 | 0.6946 | 26.72 | 0.841 | 26.45 | 0.8156 | 25.22 | 0.7639 | 26.49(1.27↑) | 0.8279(0.0639↑) | |
| 0.25 | 28.28 | 0.8218 | 30.08 | 0.8589 | 27.80 | 0.8039 | 27.51 | 0.8497 | 28.9 | 0.8831 | 28.37 | 0.8672 | 31.7 | 0.9329 | 31.16 | 0.9224 | 29.22 | 0.8674 | 31.85(2.63↑) | 0.9345(0.0670↑) | |
| 0.5 | 31.47 | 0.9011 | 33.79 | 0.9257 | 30.36 | 0.9394 | 30.06 | 0.9096 | 34.35 | 0.9569 | 34.27 | 0.9529 | 37.18 | 0.976 | 36.02 | 0.967 | 33.44 | 0.9411 | 38.24(4.80↑) | 0.9781(0.0370↑) | |
| SR () | ISTA-Net+ | CSformer | CSNet | OCTUF | SwinTCS | |
|---|---|---|---|---|---|---|
| PSNR / SSIM | ||||||
| 0.0005 | 0.01 | 18.96/0.3387 | 17.37/0.4654 | 20.77/0.4449 | — | 22.45/0.4581 |
| 0.04 | 21.43/0.4589 | 19.51/0.5534 | 22.78/0.5244 | — | 25.09/0.6997 | |
| 0.1 | 23.72/0.5912 | 22.67/0.6410 | 23.43/0.5622 | 25.60/0.7012 | 27.33/0.7909 | |
| 0.25 | 26.77/0.7559 | 25.69/0.7512 | 24.60/0.6343 | 28.10/0.8021 | 31.07/0.8828 | |
| 0.001 | 0.01 | 18.61/0.3020 | 17.37/0.4654 | 20.76/0.4444 | — | 22.01/0.3953 |
| 0.04 | 20.88/0.4155 | 19.51/0.5534 | 22.76/0.5228 | — | 24.15/0.5569 | |
| 0.1 | 22.92/0.5418 | 22.67/0.6409 | 23.40/0.5599 | 25.12/0.6783 | 26.12/0.6897 | |
| 0.25 | 25.55/0.7067 | 25.68/0.7508 | 24.55/0.6296 | 27.13/0.7531 | 28.80/0.7873 | |
| 0.002 | 0.01 | 18.14/0.2546 | 17.37/0.4654 | 20.74/0.4436 | — | 21.60/0.3104 |
| 0.04 | 20.12/0.3577 | 19.50/0.5534 | 22.70/0.5197 | — | 23.96/0.4715 | |
| 0.1 | 21.90/0.4779 | 22.67/0.5558 | 23.34/0.5599 | 24.40/0.6287 | 25.36/0.5836 | |
| 0.25 | 24.08/0.6456 | 25.67/0.7504 | 24.42/0.6206 | 25.83/0.6801 | 26.32/0.6706 | |
| 0.003 | 0.01 | 17.81/0.2223 | 17.37/0.4654 | 20.73/0.4429 | — | 21.12/0.2745 |
| 0.04 | 19.58/0.3189 | 19.50/0.5534 | 22.65/0.5168 | — | 22.67/0.4194 | |
| 0.1 | 21.19/0.4356 | 22.67/0.6408 | 23.27/0.5519 | 23.85/0.5921 | 24.06/0.6006 | |
| 0.25 | 23.09/0.6051 | 25.66/0.7500 | 24.30/0.6123 | 24.91/0.6265 | 25.75/0.7306 | |
| SR() | 0.01 | 0.04 | 0.1 | 0.25 | 0.5 | |
|---|---|---|---|---|---|---|
| SwinTCS (PSNR/SSIM) | −NLM | 22.12/0.4988 | 25.95/0.7551 | 31.92/0.8529 | 36.67/0.9138 | 42.19/0.9616 |
| +NLM | 23.97/0.6311 | 28.97/0.8695 | 33.73/0.9328 | 38.89/0.9697 | 43.64/0.9895 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, H.; Liao, H.; Suo, Z.; Chen, X.; Han, J. SwinTCS: A Swin Transformer Approach to Compressive Sensing with Non-Local Denoising. J. Imaging 2025, 11, 139. https://doi.org/10.3390/jimaging11050139
Li X, Li H, Liao H, Suo Z, Chen X, Han J. SwinTCS: A Swin Transformer Approach to Compressive Sensing with Non-Local Denoising. Journal of Imaging. 2025; 11(5):139. https://doi.org/10.3390/jimaging11050139
Chicago/Turabian StyleLi, Xiuying, Haoze Li, Hongwei Liao, Zhufeng Suo, Xuesong Chen, and Jiameng Han. 2025. "SwinTCS: A Swin Transformer Approach to Compressive Sensing with Non-Local Denoising" Journal of Imaging 11, no. 5: 139. https://doi.org/10.3390/jimaging11050139
APA StyleLi, X., Li, H., Liao, H., Suo, Z., Chen, X., & Han, J. (2025). SwinTCS: A Swin Transformer Approach to Compressive Sensing with Non-Local Denoising. Journal of Imaging, 11(5), 139. https://doi.org/10.3390/jimaging11050139







