Distributed Sparse Manifold-Constrained Optimization Algorithm in Linear Discriminant Analysis
Abstract
1. Introduction
- This paper proposes a novel distributed sparse manifold-constrained linear discriminant analysis (DSCLDA) method, which introduces sparse and manifold constraints to maintain the local and global structure.
- We designed an effective solution scheme that combines local and global variables using the manifold proximal gradient (ManPG) to obtain explicit solutions for each subproblem.
- We conducted a series of experiments on several public datasets to verify the effectiveness of the proposed method and discuss the convergence and feature distribution.
2. Notations and Preliminaries
2.1. Notations
2.2. Preliminaries
3. Methodology
3.1. Optimization Problem
3.2. Optimization Algorithm
3.2.1. Updating
3.2.2. Updating Y
3.3. Convergence Analysis
3.4. Complexity Analysis
| Algorithm 1 Optimization algorithm for (11) |
Input: Data X, parameters s,l,,. Initialize: Data , parameter . Output: Data Y. While not converged do
End while |
| Algorithm 2 Optimization algorithm for (12) |
Input: Data X, parameters , , . Initialize: , , when . Output: While not converged do
End while |
| Algorithm 3 Optimization algorithm for (20) |
Input: Parameters . Initialize: , . Output: . While not converged do
End while |
4. Simulation Studies
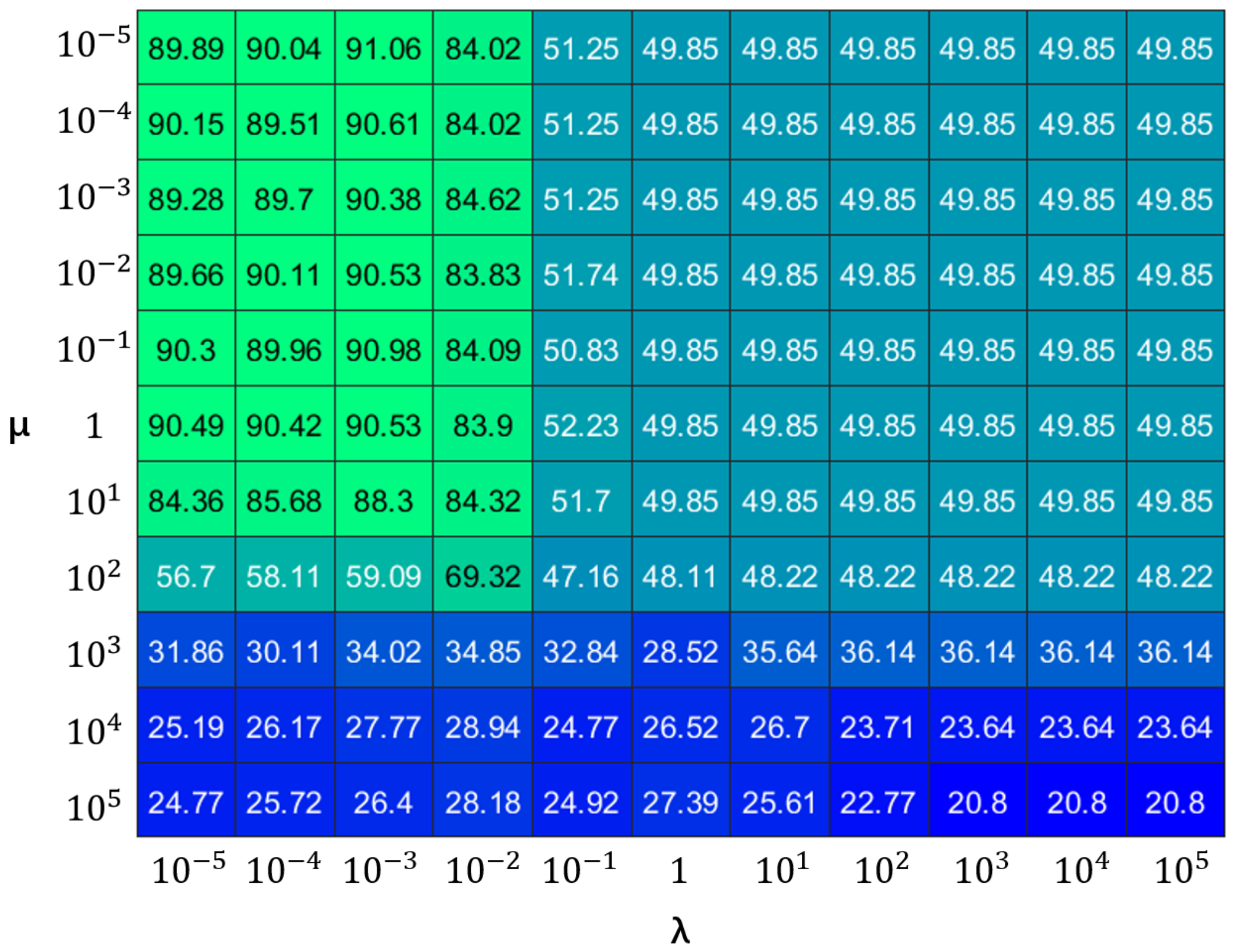
4.1. Experiment Settings
4.2. Experiment Based on Sample Size
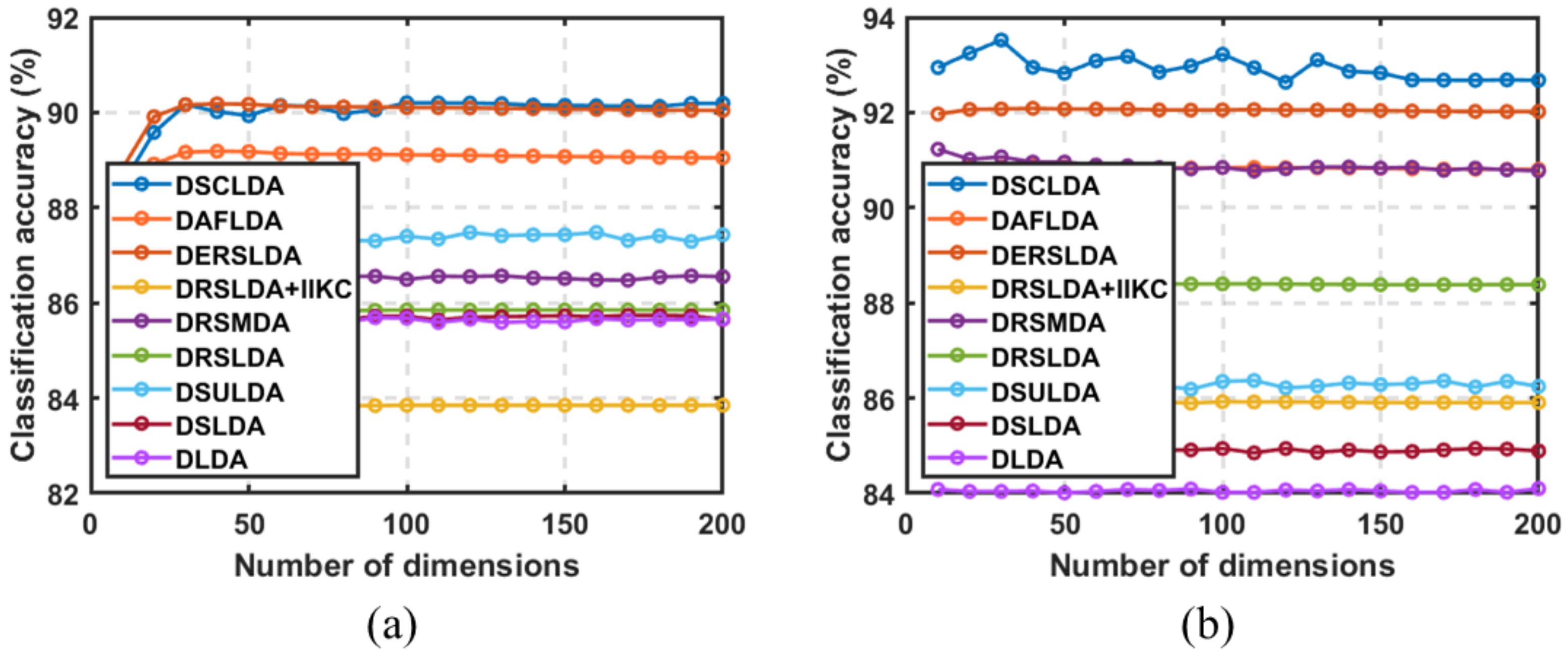
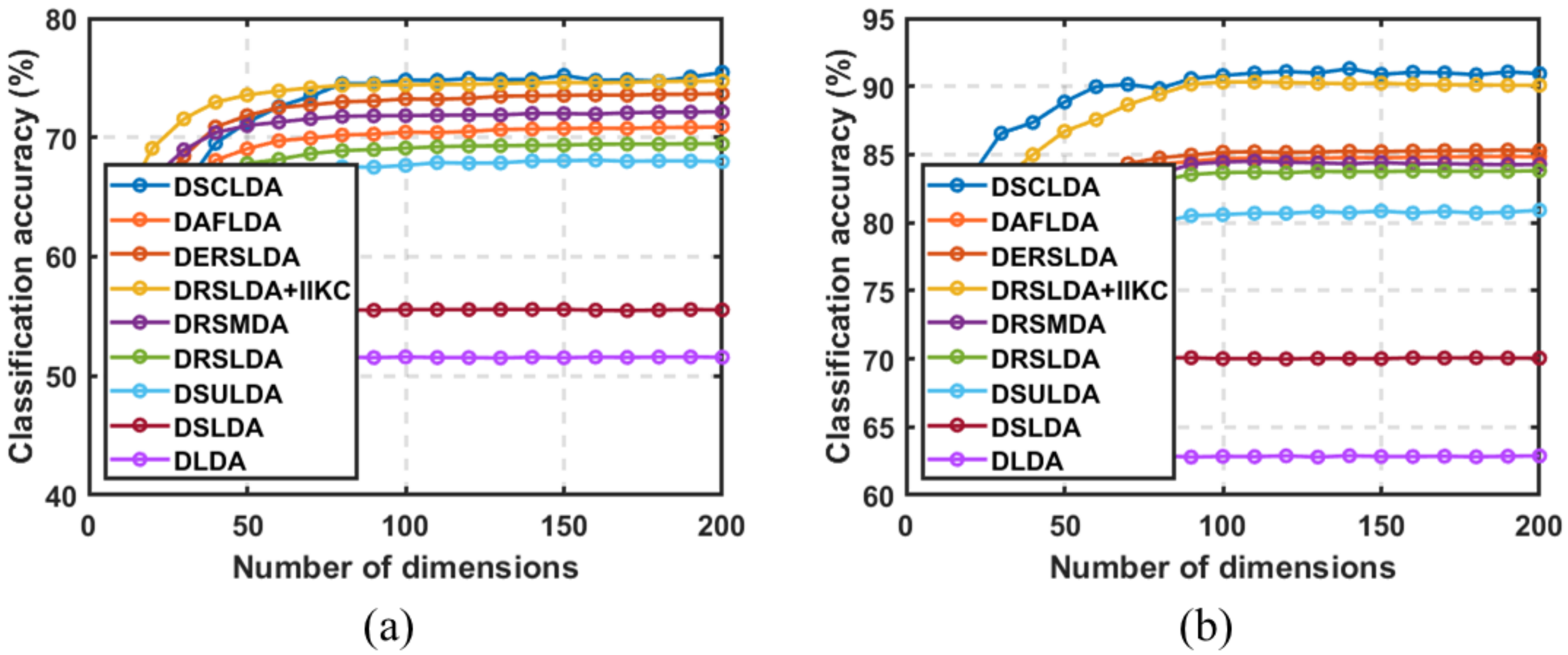
4.3. Experiment Based on the Number of Dimensions
4.4. Experiments with Deep Learning Methods
4.5. Convergence Analysis
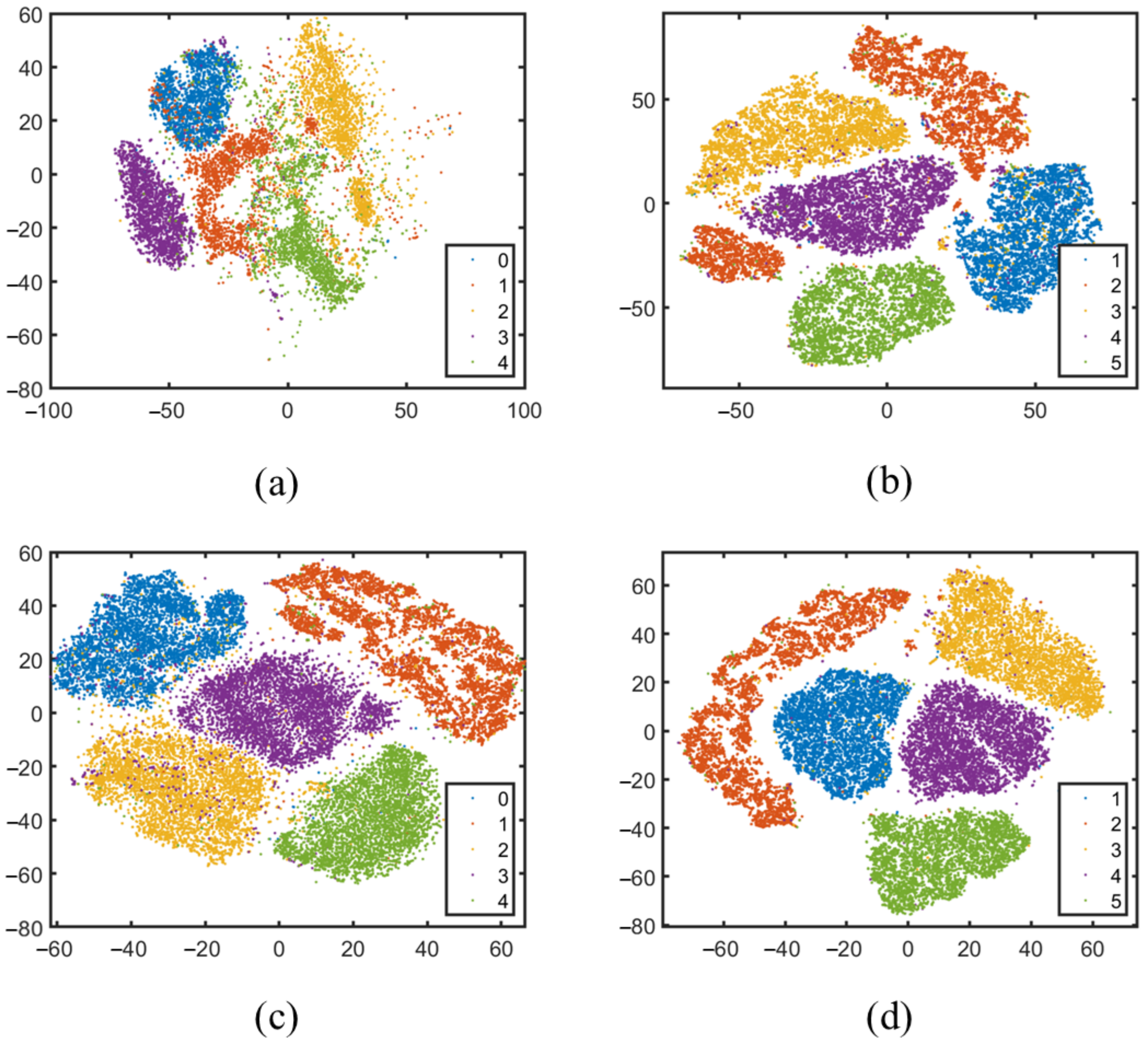
4.6. t-SNE Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, W.; Zhu, Q.; Zheng, N.; Huang, J.; Zhou, M.; Zhao, F. Learning non-uniform-sampling for ultra-high-definition image enhancement. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 1412–1421. [Google Scholar]
- Yu, X.; Dai, P.; Li, W.; Ma, L.; Shen, J.; Li, J.; Qi, X. Towards efficient and scale-robust ultra-high-definition image demoiréing. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 646–662. [Google Scholar]
- McLachlan, G.J. Discriminant Analysis and Statistical Pattern Recognition; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ullah, S.; Ahmad, Z.; Kim, J.M. Fault Diagnosis of a Multistage Centrifugal Pump Using Explanatory Ratio Linear Discriminant Analysis. Sensors 2024, 24, 1830. [Google Scholar] [CrossRef] [PubMed]
- Mai, Q.; Zou, H. A note on the connection and equivalence of three sparse linear discriminant analysis methods. Technometrics 2013, 55, 243–246. [Google Scholar] [CrossRef]
- Ye, J.; Xiong, T. Null space versus orthogonal linear discriminant analysis. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 1073–1080. [Google Scholar]
- Ye, J.; Janardan, R.; Li, Q.; Park, H. Feature reduction via generalized uncorrelated linear discriminant analysis. IEEE Trans. Knowl. Data Eng. 2006, 18, 1312–1322. [Google Scholar]
- Shi, Y.; Huang, W.; Ye, H.; Ruan, C.; Xing, N.; Geng, Y.; Dong, Y.; Peng, D. Partial least square discriminant analysis based on normalized two-stage vegetation indices for mapping damage from rice diseases using PlanetScope datasets. Sensors 2018, 18, 1901. [Google Scholar] [CrossRef]
- Bach, F. High-dimensional analysis of double descent for linear regression with random projections. SIAM J. Math. Data Sci. 2024, 6, 26–50. [Google Scholar] [CrossRef]
- Xu, H.L.; Chen, G.Y.; Cheng, S.Q.; Gan, M.; Chen, J. Variable projection algorithms with sparse constraint for separable nonlinear models. Control Theory Technol. 2024, 22, 135–146. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, Y.; Liu, J.; Wu, J.; An, D. A hyperspectral band selection method based on sparse band attention network for maize seed variety identification. Expert Syst. Appl. 2024, 238, 122273. [Google Scholar] [CrossRef]
- Clemmensen, L.; Hastie, T.; Witten, D.; Ersbøll, B. Sparse discriminant analysis. Technometrics 2011, 53, 406–413. [Google Scholar] [CrossRef]
- Zhang, X.; Chu, D.; Tan, R.C. Sparse uncorrelated linear discriminant analysis for undersampled problems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1469–1485. [Google Scholar] [CrossRef]
- Wen, J.; Fang, X.; Cui, J.; Fei, L.; Yan, K.; Chen, Y.; Xu, Y. Robust sparse linear discriminant analysis. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 390–403. [Google Scholar] [CrossRef]
- Li, S.; Zhang, H.; Ma, R.; Zhou, J.; Wen, J.; Zhang, B. Linear discriminant analysis with generalized kernel constraint for robust image classification. Pattern Recognit. 2023, 136, 109196. [Google Scholar] [CrossRef]
- Sheikhpour, R.; Berahmand, K.; Mohammadi, M.; Khosravi, H. Sparse feature selection using hypergraph Laplacian-based semi-supervised discriminant analysis. Pattern Recognit. 2025, 157, 110882. [Google Scholar] [CrossRef]
- Wang, J.; Yin, H.; Nie, F.; Li, X. Adaptive and fuzzy locality discriminant analysis for dimensionality reduction. Pattern Recognit. 2024, 151, 110382. [Google Scholar] [CrossRef]
- Vivekanand, V.; Mishra, D. Framework for Segmented threshold L0 gradient approximation based network for sparse signal recovery. Neural Netw. 2023, 162, 425–442. [Google Scholar]
- Chen, K.; Che, H.; Li, X.; Leung, M.F. Graph non-negative matrix factorization with alternative smoothed L0 regularizations. Neural Comput. Appl. 2023, 35, 9995–10009. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Nie, F.; Li, X. Sparse feature selection via fast embedding spectral analysis. Pattern Recognit. 2023, 139, 109472. [Google Scholar] [CrossRef]
- Chen, D.W.; Miao, R.; Yang, W.Q.; Liang, Y.; Chen, H.H.; Huang, L.; Deng, C.J.; Han, N. A feature extraction method based on differential entropy and linear discriminant analysis for emotion recognition. Sensors 2019, 19, 1631. [Google Scholar] [CrossRef]
- Zheng, W.; Lu, S.; Yang, Y.; Yin, Z.; Yin, L. Lightweight transformer image feature extraction network. PeerJ Comput. Sci. 2024, 10, e1755. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Q.; Zeng, S.; Zhang, B.; Fang, L. Latent linear discriminant analysis for feature extraction via isometric structural learning. Pattern Recognit. 2024, 149, 110218. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Zhang, K.; Wu, Q.; Zhang, M. Robust sparse manifold discriminant analysis. Multimed. Tools Appl. 2022, 81, 20781–20796. [Google Scholar] [CrossRef]
- Zhang, K.; Zheng, D.; Li, J.; Gao, X.; Lu, J. Coupled discriminative manifold alignment for low-resolution face recognition. Pattern Recognit. 2024, 147, 110049. [Google Scholar] [CrossRef]
- Chen, S.; Ma, S.; Man-Cho So, A.; Zhang, T. Proximal gradient method for nonsmooth optimization over the Stiefel manifold. SIAM J. Optim. 2020, 30, 210–239. [Google Scholar] [CrossRef]
- Xiao, N.; Liu, X.; Yuan, Y.x. Exact Penalty Function for L2,1 Norm Minimization over the Stiefel Manifold. SIAM J. Optim. 2021, 31, 3097–3126. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X. Decentralized optimization over the Stiefel manifold by an approximate augmented Lagrangian function. IEEE Trans. Signal Process. 2022, 70, 3029–3041. [Google Scholar] [CrossRef]
- Beck, A.; Eldar, Y.C. Sparsity constrained nonlinear optimization: Optimality conditions and algorithms. SIAM J. Optim. 2013, 23, 1480–1509. [Google Scholar] [CrossRef]
- Zhou, S.; Xiu, N.; Qi, H.D. Global and quadratic convergence of Newton hard-thresholding pursuit. J. Mach. Learn. Res. 2021, 22, 1–45. [Google Scholar]
- Li, G.; Qin, S.J.; Zhou, D. Geometric properties of partial least squares for process monitoring. Automatica 2010, 46, 204–210. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, J.; Xie, L.; Luo, S.; Su, H. Structured joint sparse principal component analysis for fault detection and isolation. IEEE Trans. Ind. Inform. 2018, 15, 2721–2731. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, S.X.; Peng, T.; Yang, C.; Gui, W. Fault detection for non-Gaussian processes using generalized canonical correlation analysis and randomized algorithms. IEEE Trans. Ind. Electron. 2017, 65, 1559–1567. [Google Scholar] [CrossRef]
- Li, H.; Liu, D.; Wang, D. Manifold regularized reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 932–943. [Google Scholar] [CrossRef]
- Li, J.; Ma, S. Federated learning on Riemannian manifolds. arXiv 2022, arXiv:2206.05668. [Google Scholar]
- Rockafellar, R.T.; Wets, R.J.B. Variational Analysis; Springer Science & Business Media: Berlin, Germany, 2009; Volume 317. [Google Scholar]
- Liu, J.; Feng, M.; Xiu, X.; Liu, W.; Zeng, X. Efficient and Robust Sparse Linear Discriminant Analysis for Data Classification. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 9, 617–629. [Google Scholar] [CrossRef]
- Deng, L. The mnist database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Mantecón, T.; del Blanco, C.R.; Jaureguizar, F.; García, N. Hand gesture recognition using infrared imagery provided by leap motion controller. In Proceedings of the Advanced Concepts for Intelligent Vision Systems: 17th International Conference, ACIVS 2016, Lecce, Italy, 24–27 October 2016; Proceedings 17. Springer: Berlin/Heidelberg, Germany, 2016; pp. 47–57. [Google Scholar]
- Nene, S.A.; Nayar, S.K.; Murase, H. Columbia Object Image Library (Coil-20); Department of Computer Science, Columbia University: New York, NY, USA, 1996. [Google Scholar]
- Bao, Y.; Song, K.; Liu, J.; Wang, Y.; Yan, Y.; Yu, H.; Li, X. Triplet-graph reasoning network for few-shot metal generic surface defect segmentation. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Kinnunen, T.; Kamarainen, J.K.; Lensu, L.; Lankinen, J.; Käviäinen, H. Making visual object categorization more challenging: Randomized caltech-101 data set. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 476–479. [Google Scholar]
- Molchanov, P.; Yang, X.; Gupta, S.; Kim, K.; Tyree, S.; Kautz, J. Online detection and classification of dynamic hand gestures with recurrent 3d convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4207–4215. [Google Scholar]
- Carreira, J.; Zisserman, A. Quo vadis, action recognition? A new model and the kinetics dataset. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6299–6308. [Google Scholar]
- D’Eusanio, A.; Simoni, A.; Pini, S.; Borghi, G.; Vezzani, R.; Cucchiara, R. A transformer-based network for dynamic hand gesture recognition. In Proceedings of the 2020 International Conference on 3D Vision (3DV), Fukuoka, Japan, 25–28 November 2020; pp. 623–632. [Google Scholar]
- Zhang, Z.; Sabuncu, M. Generalized cross entropy loss for training deep neural networks with noisy labels. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. [Google Scholar]






| Method | Optimization Problem | Constraint |
|---|---|---|
| LDA | ||
| SLDA | ||
| SULDA | ||
| RSLDA | ||
| RSMDA | ||
| RSLDA+IIKC | ||
| ERSLDA | ||
| DSCLDA |
| Dataset | Image Types | Images | Color Type | Original Resolution |
|---|---|---|---|---|
| Mnist [38] | 10 | 60,000 | Gray | |
| Hand Gesture Recognition [39] | 10 | 20,000 | Gray | |
| Coil20 [40] | 20 | 1440 | Gray | |
| NEU surface defects [41] | 6 | 1200 | Gray | |
| Car_image | 10 | 200 | RGB | to |
| Caltech-101 [42] | 101 | 9146 | RGB and gray | About |
| Methods | Mnist | Hand Gesture Recognition | COIL20 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 50 | 100 | 200 | 4 | 5 | 6 | 7 | 3 | 6 | 9 | 12 | |
| DLDA | 75.20 | 85.59 | 84.02 | 83.78 | 75.95 | 80.38 | 87.81 | 89.35 | 65.29 | 74.97 | 81.58 | 80.40 |
| DSLDA | 80.42 | 85.64 | 84.85 | 84.46 | 81.50 | 83.69 | 90.69 | 92.23 | 70.84 | 78.28 | 84.46 | 84.02 |
| DSULDA | 87.78 | 87.34 | 86.37 | 93.38 | 84.76 | 88.62 | 90.11 | 91.65 | 74.10 | 83.21 | 83.88 | 86.37 |
| DRSLDA | 84.03 | 85.85 | 88.40 | 96.58 | 87.40 | 89.73 | 88.98 | 90.52 | 76.74 | 84.32 | 82.75 | 86.75 |
| DRSMDA | 83.62 | 86.56 | 90.77 | 97.51 | 87.62 | 85.49 | 90.85 | 92.39 | 76.96 | 80.08 | 84.62 | 87.30 |
| DRSLDA+IIKC | 73.27 | 83.85 | 85.92 | 96.94 | 90.30 | 90.86 | 92.89 | 94.43 | 79.64 | 85.45 | 86.66 | 86.94 |
| DERSLDA | 86.77 | 90.10 | 92.06 | 97.62 | 88.12 | 90.26 | 89.81 | 91.35 | 77.46 | 84.85 | 83.58 | 88.73 |
| DAFLDA | 85.91 | 89.11 | 90.84 | 96.34 | 87.93 | 88.28 | 88.76 | 90.67 | 76.24 | 82.17 | 83.36 | 85.23 |
| DSCLDA | 86.92 | 90.20 | 92.94 | 97.82 | 90.37 | 91.39 | 93.48 | 95.02 | 79.71 | 85.98 | 87.25 | 90.95 |
| Methods | NEU Surface Defects | Car_IMAGE | Caltech-101 | |||||||||
| 25 | 50 | 75 | 100 | 10 | 15 | 20 | 25 | 10 | 15 | 20 | 25 | |
| DLDA | 41.27 | 38.87 | 43.26 | 48.08 | 20.64 | 25.00 | 34.50 | 44.77 | 51.54 | 58.16 | 62.82 | 65.21 |
| DSLDA | 43.03 | 44.93 | 48.15 | 50.53 | 37.03 | 39.93 | 42.15 | 42.08 | 55.56 | 67.60 | 70.02 | 74.32 |
| DSULDA | 42.18 | 48.73 | 52.45 | 54.82 | 37.18 | 42.73 | 47.45 | 48.82 | 67.89 | 77.09 | 80.69 | 86.11 |
| DRSLDA | 42.73 | 46.20 | 50.89 | 56.50 | 36.73 | 40.20 | 44.89 | 50.50 | 69.22 | 83.60 | 83.70 | 87.04 |
| DRSMDA | 52.18 | 53.33 | 57.85 | 60.83 | 47.18 | 47.33 | 51.85 | 54.83 | 71.86 | 83.33 | 84.51 | 86.25 |
| DRSLDA+IIKC | 52.30 | 57.80 | 61.70 | 64.92 | 46.30 | 51.80 | 55.70 | 59.92 | 74.45 | 87.52 | 90.32 | 91.02 |
| DERSLDA | 47.52 | 54.53 | 55.85 | 62.92 | 42.52 | 49.53 | 50.85 | 56.92 | 73.20 | 85.10 | 85.20 | 88.25 |
| DAFLDA | 45.64 | 50.91 | 52.68 | 56.12 | 40.58 | 46.37 | 48.25 | 53.76 | 70.45 | 83.68 | 84.71 | 85.99 |
| DSCLDA | 54.55 | 57.80 | 62.22 | 65.58 | 50.32 | 53.57 | 57.99 | 61.35 | 74.79 | 88.28 | 90.98 | 91.47 |
| HGR | CIFAR-100 | ||
|---|---|---|---|
| Method | Acc. (%) | Method | Acc. (%) |
| DSCLDA | 90.37 | DSCLDA | 63.45 |
| R3D-CNN | 83.80 | R3D-CNN | 90.62 |
| I3D | 85.70 | I3D | 94.82 |
| Transformer | 87.60 | Transformer | 95.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Chen, X.; Feng, M.; Liu, J. Distributed Sparse Manifold-Constrained Optimization Algorithm in Linear Discriminant Analysis. J. Imaging 2025, 11, 81. https://doi.org/10.3390/jimaging11030081
Zhang Y, Chen X, Feng M, Liu J. Distributed Sparse Manifold-Constrained Optimization Algorithm in Linear Discriminant Analysis. Journal of Imaging. 2025; 11(3):81. https://doi.org/10.3390/jimaging11030081
Chicago/Turabian StyleZhang, Yuhao, Xiaoxiang Chen, Manlong Feng, and Jingjing Liu. 2025. "Distributed Sparse Manifold-Constrained Optimization Algorithm in Linear Discriminant Analysis" Journal of Imaging 11, no. 3: 81. https://doi.org/10.3390/jimaging11030081
APA StyleZhang, Y., Chen, X., Feng, M., & Liu, J. (2025). Distributed Sparse Manifold-Constrained Optimization Algorithm in Linear Discriminant Analysis. Journal of Imaging, 11(3), 81. https://doi.org/10.3390/jimaging11030081







