Structure-Aware Progressive Multi-Modal Fusion Network for RGB-T Crack Segmentation
Abstract
1. Introduction
- An end-to-end edge-guided progressive multi-modal segmentation network is proposed in this work. The developed framework is designed to jointly leverage both RGB and thermal infrared information while incorporating structural priors. By embedding edge-aware supervision throughout the decoding process, the overall accuracy and robustness of crack segmentation are significantly enhanced, effectively addressing the boundary blurring issue commonly encountered in conventional approaches.
- A progressive multi-modal feature fusion strategy is designed to hierarchically integrate cross-modal features. For shallow-level features characterized by rich spatial details, a Gated Control Attention (GCA) module is introduced to dynamically recalibrate modal contributions through a gating mechanism, thereby enhancing texture perception in local crack regions. For deep-level features carrying high-level semantics, an Attention Feature Fusion (AFF) module is employed to align and complement cross-modal representations via joint local–global attention, effectively strengthening semantic consistency in structural prediction.
- A structure-prior-guided segmentation prediction strategy is proposed, which utilizes edge prediction consistency constraints to preserve the original structural characteristics in segmentation results. By formulating a joint optimization objective comprising edge-guided loss, multi-scale focal loss, and adaptive fusion loss, the structural integrity and boundary accuracy of the final predictions are significantly improved.
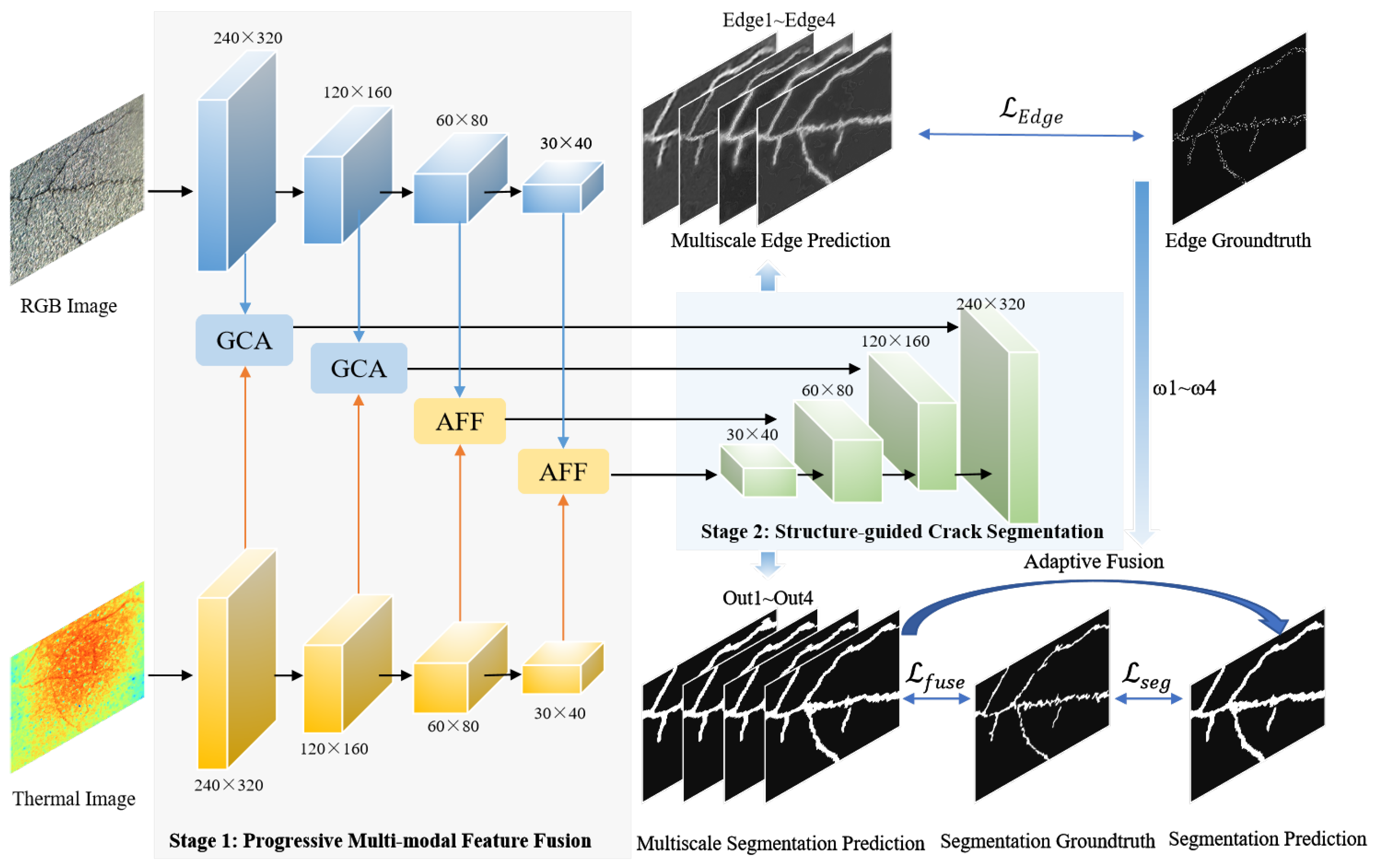
2. Proposed Method
2.1. Progressive Multi-Modal Feature Fusion
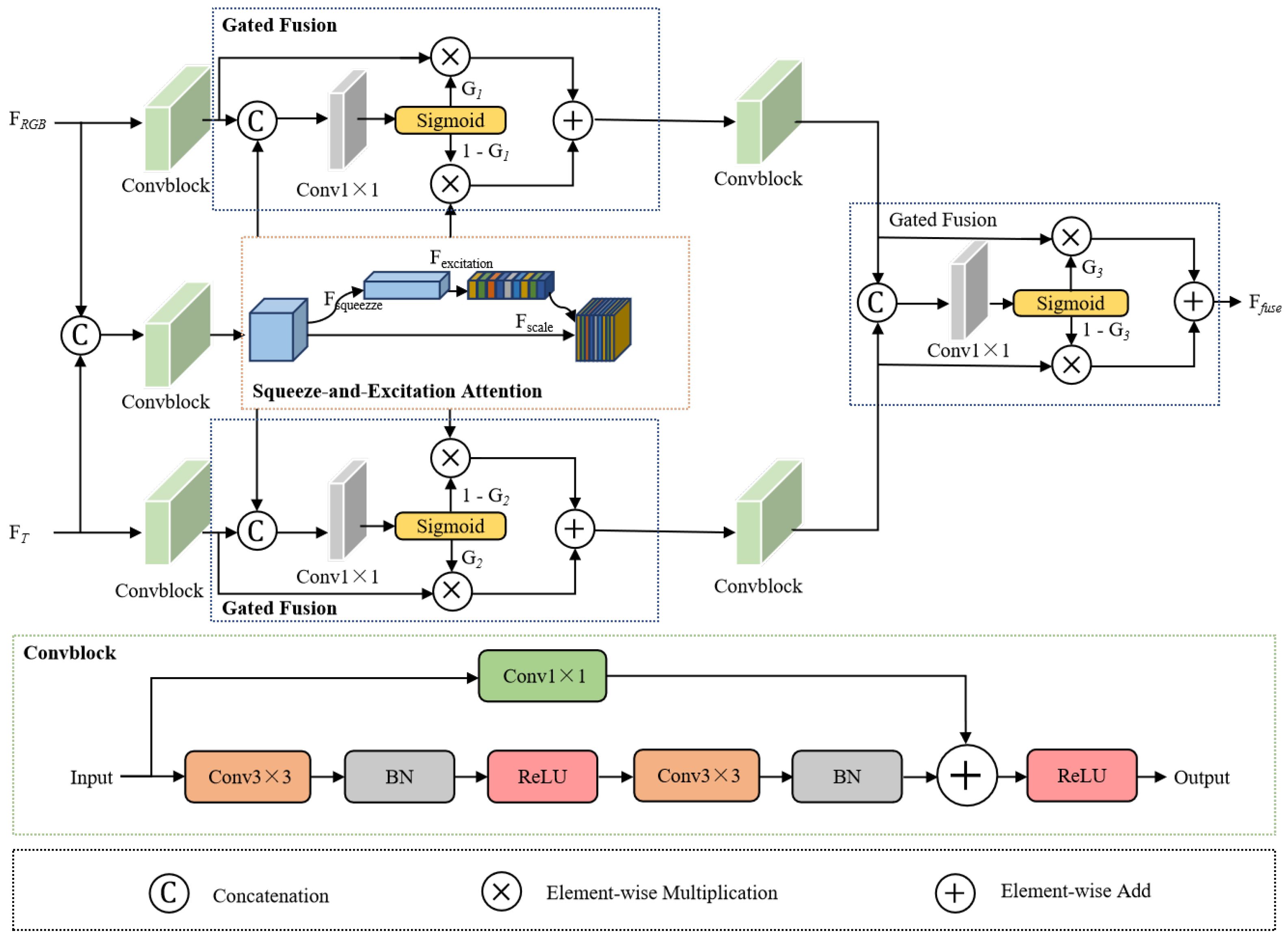
2.1.1. Gate Control Attention Module
2.1.2. Attention Feature Fusion
2.2. Structure-Guided Crack Segmentation
2.3. Loss Function
2.3.1. Edge-Guided Loss
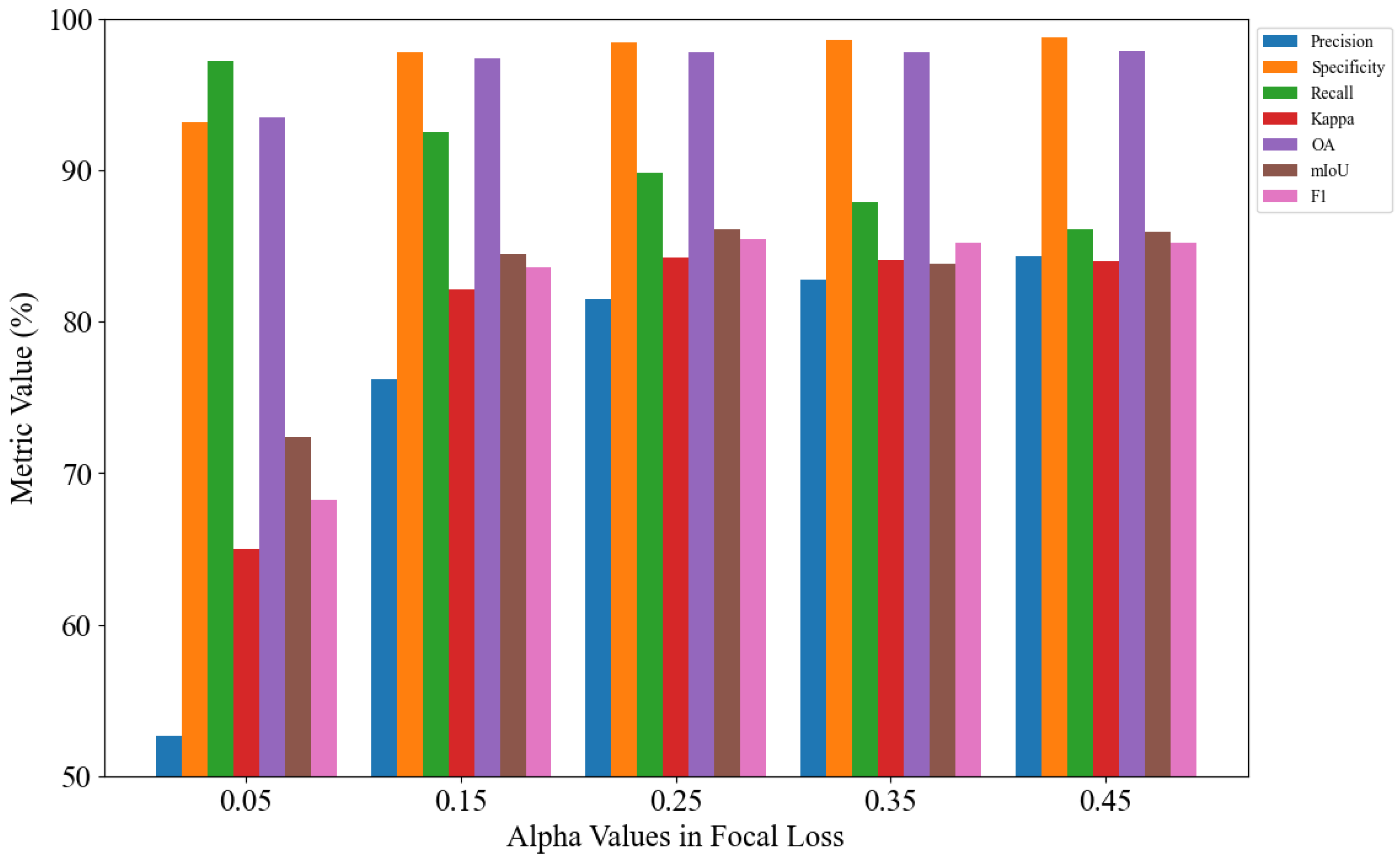
2.3.2. Multi-Scale Focal Loss
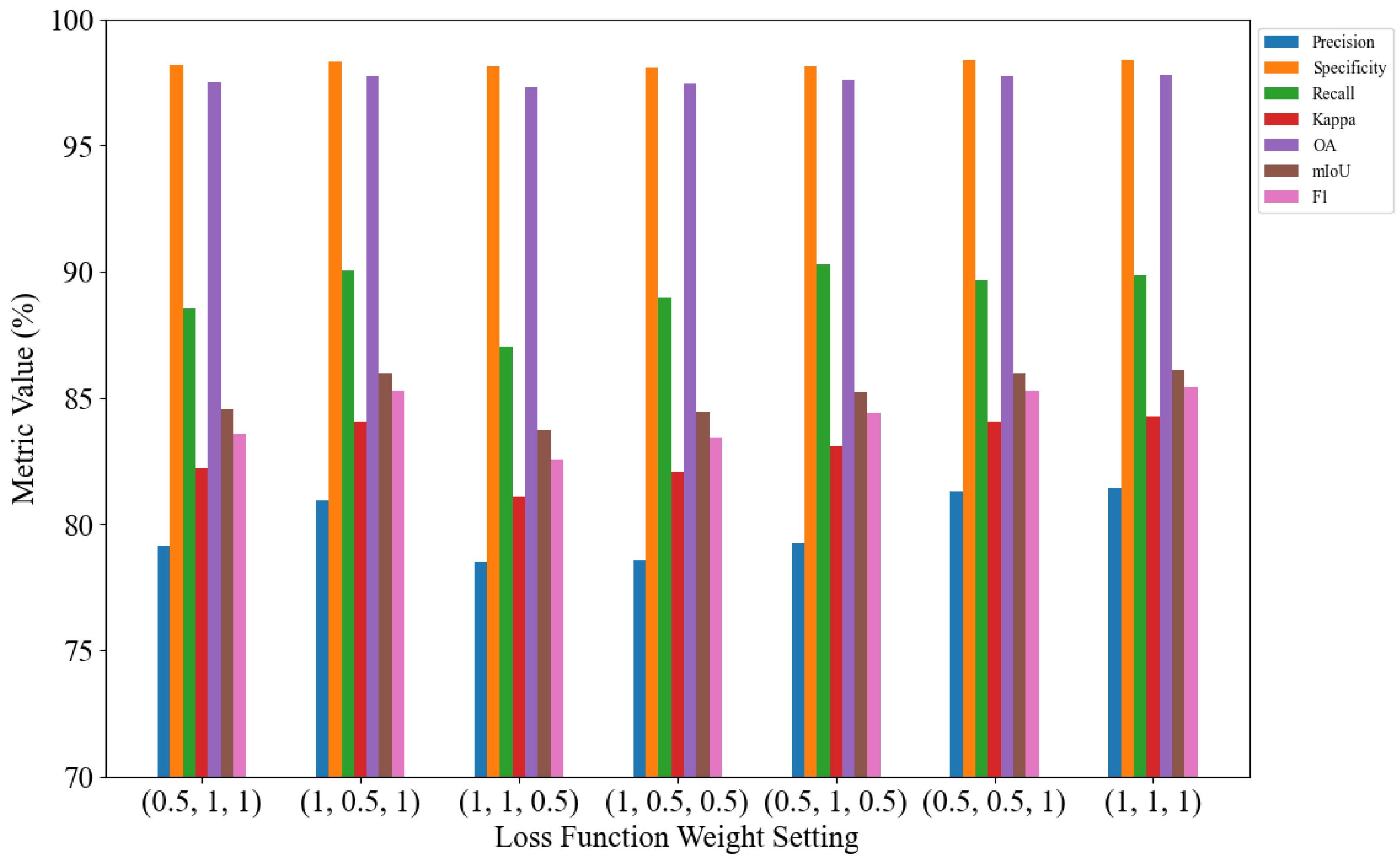
2.3.3. Adaptive Fusion Loss
2.3.4. Total Loss
3. Experiment
3.1. Dataset
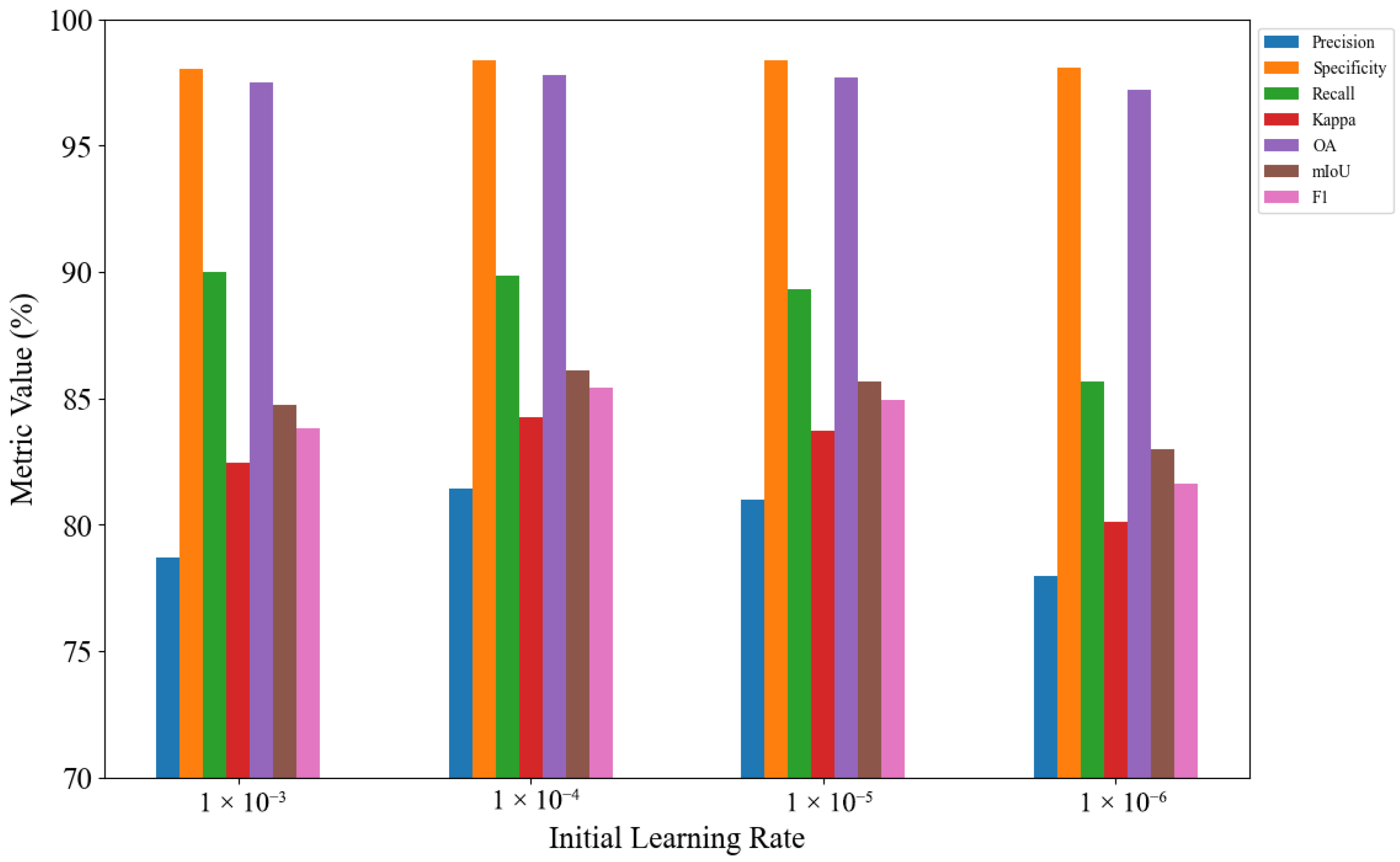
3.2. Implementation Details
3.3. Evaluation Metrics
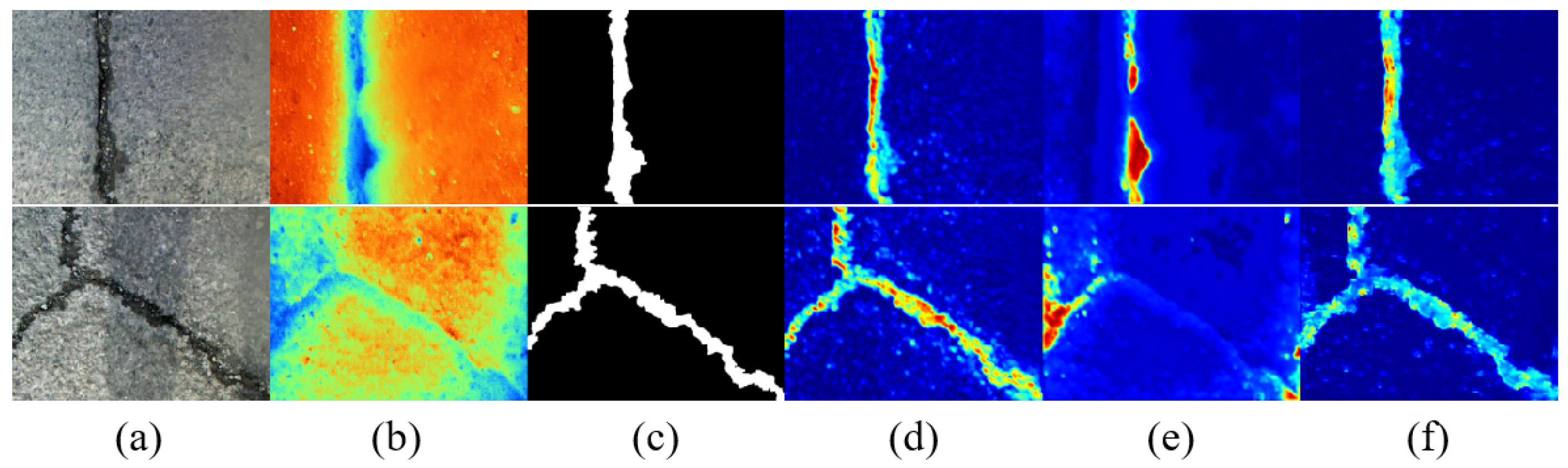
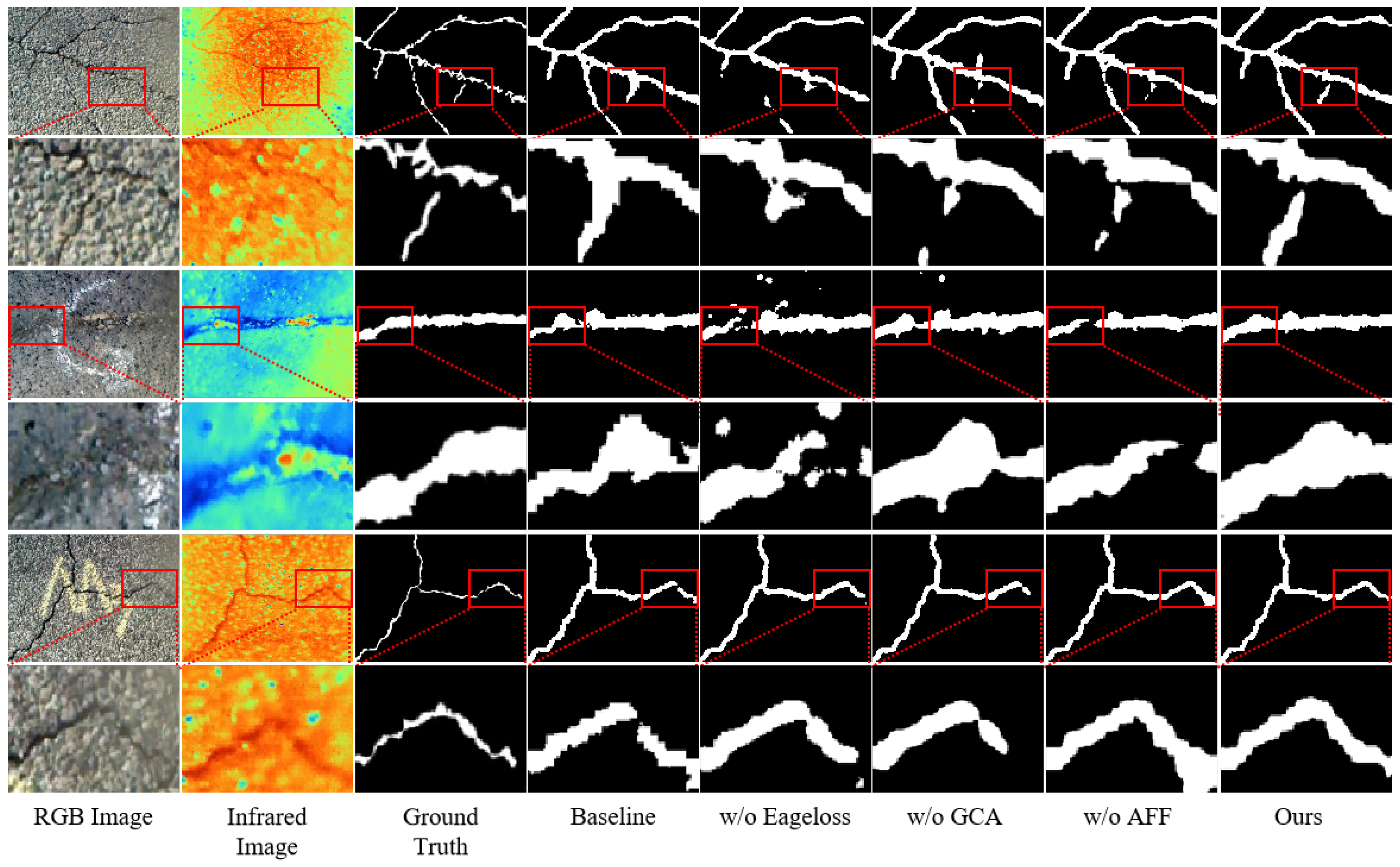
3.4. Ablation Study
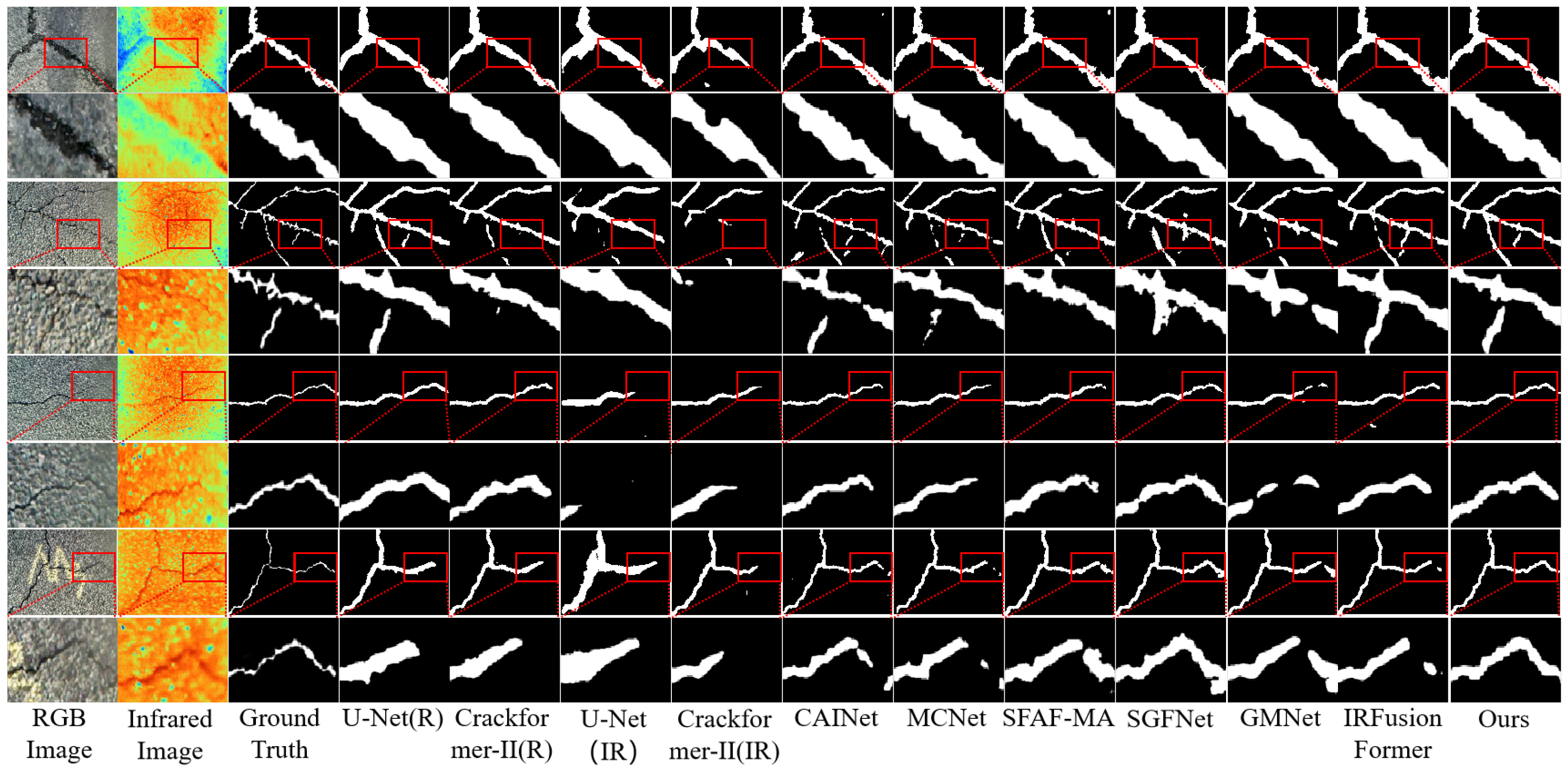
3.5. Comparison Experiments with Different Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Wu, G.; Liu, Y. Efficient generative-adversarial U-Net for multi-organ medical image segmentation. J. Imaging 2025, 11, 19. [Google Scholar] [CrossRef]
- Dais, D.; Bal, I.E.; Smyrou, E.; Sarhosis, V. Automatic crack classification and segmentation on masonry surfaces using convolutional neural networks and transfer learning. Autom. Constr. 2021, 125, 103606. [Google Scholar] [CrossRef]
- Tran, T.S.; Nguyen, S.D.; Lee, H.J.; Tran, V.P. Advanced crack detection and segmentation on bridge decks using deep learning. Constr. Build. Mater. 2023, 400, 132839. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Dang, L.M.; Lee, S.; Moon, H. Pixellevel tunnel crack segmentation using a weakly supervised annotation approach. Comput. Ind. 2021, 133, 103545. [Google Scholar] [CrossRef]
- Han, C.; Yang, H.; Ma, T.; Wang, S.; Zhao, C.; Yang, Y. Crackdiffusion: A two-stage semantic segmentation framework for pavement crack combining unsupervised and supervised processes. Autom. Constr. 2024, 160, 105332. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Springer: Munich, Germany, 2015; pp. 234–241. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Du, Y.; Zhang, X.; Li, F.; Sun, L. Detection of crack growth in asphalt pavement through use of infrared imaging. Transp. Res. Rec. 2017, 2645, 24–31. [Google Scholar] [CrossRef]
- Ma, M.; Lei, Y.; Liu, Y.; Yu, H. An attention-based progressive fusion network for pixelwise pavement crack detection. Measurement 2024, 226, 114159. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J.; Miao, X.; Mertz, C. CrackFormer network for pavement crack segmentation. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9240–9252. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, J.; Hong, Z.; Lu, W.; Yin, J.; Zou, L.; Shen, X. Image-based concrete crack detection in tunnels using deep fully convolutional networks. Constr. Build. Mater. 2020, 234, 117367. [Google Scholar] [CrossRef]
- Liu, Y. DeepLabV3+ Based Mask R-CNN for Crack Detection and Segmentation in Concrete Structures. Int. J. Adv. Comput. Sci. Appl. 2025, 16, 423. [Google Scholar] [CrossRef]
- Hou, W.; He, J.; Cui, C.; Zhong, F.; Jiang, X.; Lu, L.; Zhang, J.; Tu, C. Segmentation refinement of thin cracks with minimum strip cuts. Adv. Eng. Inf. 2025, 65, 103249. [Google Scholar] [CrossRef]
- Li, S.; Gou, S.; Yao, Y.; Chen, Y.; Wang, X. Physically informed prior and cross-correlation constraint for fine-grained road crack segmentation. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Urumqi, China, 18–20 October 2024; Springer Nature: Singapore, 2024. [Google Scholar]
- Yoon, H.; Kim, H.K.; Kim, S. PPDD: Egocentric crack segmentation in the port pavement with deep learning-based methods. Appl. Sci. 2025, 15, 5446. [Google Scholar] [CrossRef]
- Sun, W.; Liu, X.; Lei, Z. Research on tunnel crack identification localization and segmentation method based on improved YOLOX and UNETR++. Sensors 2025, 25, 3417. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhuang, Y.; Song, W.; Wu, J.; Ye, X.; Zhang, H.; Xu, Y.; Shi, G. ISTD-CrackNet: Hybrid CNN-transformer models focusing on fine-grained segmentation of multi-scale pavement cracks. Measurement 2025, 251, 117215. [Google Scholar] [CrossRef]
- Wang, L.; Wu, G.; Tossou, A.I.H.C.F.; Liang, Z.; Xu, J. Segmentation of crack disaster images based on feature extraction enhancement and multi-scale fusion. Earth Sci. Inform. 2025, 18, 55. [Google Scholar] [CrossRef]
- Si, J.; Lu, J.; Zhang, Y. An FCN-based segmentation network for fine linear crack detection and measurement in metals. Int. J. Struct. Integr. 2025, 16, 1117–1137. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Z.; Huang, F.; Sherratt, R.S.; Alfarraj, O.; Tolba, A.; Zhang, J. A U-Net-like full convolutional pavement crack segmentation network based on multi-layer feature fusion. Int. J. Pavement Eng. 2025, 26, 2508919. [Google Scholar] [CrossRef]
- Wang, C.; Liu, H.; An, X.; Gong, Z.; Deng, F. DCNCrack: Pavement crack segmentation based on large-scaled deformable convolutional network. J. Comput. Civ. Eng. 2025, 39, 04025009. [Google Scholar] [CrossRef]
- Guo, X.; Tang, W.; Wang, H.; Wang, J.; Wang, S.; Qu, X. MorFormer: Morphology-aware transformer for generalized pavement crack segmentation. IEEE Trans. Intell. Transp. Syst. 2025, 26, 8219–8232. [Google Scholar] [CrossRef]
- Zeng, L.; Zhang, C.; Cai, S.; Yan, X.; Wang, S. Deep crack segmentation: A semi-supervised approach with coordinate attention and adaptive loss. Meas. Sci. Technol. 2025, 36, 065011. [Google Scholar] [CrossRef]
- Liang, F.; Li, Q.; Yu, H.; Wang, W. CrackCLIP: Adapting vision-language models for weakly supervised crack segmentation. Entropy 2025, 27, 127. [Google Scholar] [CrossRef]
- Kütük, Z.; Algan, G. Semantic segmentation for thermal images: A comparative survey. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–23 June 2022; pp. 286–295. [Google Scholar]
- Wang, Z.; Zhang, H.; Qian, Z.; Chen, L. A complex scene pavement crack semantic segmentation method based on dual-stream framework. Int. J. Pavement Eng. 2023, 24, 2286461. [Google Scholar] [CrossRef]
- Ha, Q.; Watanabe, K.; Karasawa, T.; Ushiku, Y.; Harada, T. MFNet: Towards real-time semantic segmentation for autonomous vehicles with multi-spectral scenes. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 5108–5115. [Google Scholar]
- Zhang, Q.; Zhao, S.; Luo, Y.; Zhang, D.; Huang, N.; Han, J. ABMDRNet: Adaptive-weighted bi-dTectional modality difference reduction network for RGB-T semantic segmentation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 2633–2642. [Google Scholar]
- Zhou, W.; Liu, J.; Lei, J.; Yu, L.; Hwang, J. GMNet: Graded-feature multilabel-learning network for RGB-thermal urban scene semantic segmentation. IEEE Trans. Image Process. 2021, 30, 7790–7802. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Dong, S.; Xu, C.; Yaguan, Q. Edge-aware guidance fusion network for RGB-thermal scene parsing. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22–30 January 2022; pp. 3571–3579. [Google Scholar]
- Zhou, W.; Zhang, H.; Yan, W.; Lin, W. MMSMCNet: Modal memory sharing and morphological complementary networks for RGB-T urban scene semantic segmentation. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 7096–7108. [Google Scholar] [CrossRef]
- Yang, Y.; Shan, C.; Zhao, F.; Liang, W.; Han, J. On exploring shape and semantic enhancements for RGB-X semantic segmentation. IEEE Trans. Intell. Veh. 2024, 9, 2223–2235. [Google Scholar] [CrossRef]
- Wang, Q.; Yin, C.; Song, H.; Shen, T.; Gu, Y. UTFNet: Uncertainty-guided trustworthy fusion network for RGB-Thermal semantic segmentation. IEEE Geosci. Remote Sens. Lett. 2023, 20, 7001205. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Qin, H.; Mu, X. DHFNet: Decoupled hierarchical fusion network for RGB-T dense prediction tasks. Neurocomputing 2024, 583, 127594. [Google Scholar] [CrossRef]
- Zhao, G.; Huang, J.; Peng, T. Open-vocabulary RGB-Thermal semantic segmentation. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; pp. 304–320. [Google Scholar]
- Liu, C.; Liu, H.; Ma, H. Implicit alignment and query refinement for RGB-T semantic segmentation. Pattern Recognit. 2026, 169, 111951. [Google Scholar] [CrossRef]
- Liu, J.; Liu, H.; Xu, X. MiLNet: Multiplex interactive learning network for RGB-T semantic segmentation. IEEE Trans. Image Process. 2025, 34, 1686–1699. [Google Scholar] [CrossRef]
- Tang, L.; Yuan, J.; Ma, J. Image fusion in the loop of high-level vision tasks: A semantic-aware real-time infrared and RGB image fusion network. Inform. Fusion 2022, 82, 28–42. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 13–18 June 2018; pp. 7132–7141. [Google Scholar]
- Dai, Y.; Gieseke, F.; Oehmcke, S.; Wu, Y. Attentional feature fusion. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual, 5–9 January 2021. [Google Scholar]
- Liu, F.; Liu, J.; Wang, L. Asphalt pavement crack detection based on convolutional neural network and infrared thermography. IEEE Trans. Intell. Transport. Syst. 2022, 23, 22145–22155. [Google Scholar] [CrossRef]
- Huang, H.; Cai, Y.; Zhang, C. Crack detection of masonry structure based on thermal and visible image fusion and semantic segmentation. Autom. Constr. 2024, 158, 105213. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, Z.; Li, G. Context-aware interaction network for RGB-T semantic segmentation. IEEE Trans. Multimedia 2024, 26, 6348–6360. [Google Scholar] [CrossRef]
- Guo, X.; Liu, T.; Mou, Y.; Chai, S.; Ren, B.; Wang, Y. Transferring prior thermal knowledge for snowy urban scene semantic segmentation. IEEE Trans. Intell. Transp. Syst. 2025, 26, 12474–12487. [Google Scholar] [CrossRef]
- He, X.; Wang, M.; Liu, T.; Zhao, L.; Yue, Y. SFAF-MA: Spatial feature aggregation and fusion with modality adaptation for RGB-thermal semantic segmentation. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Liu, Z. SGFNet: Semantic-guided fusion network for RGB-thermal semantic segmentation. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 7737–7748. [Google Scholar] [CrossRef]
- Xiao, R.; Chen, X. IRFusionFormer: Enhancing Pavement Crack Segmentation with RGB-T Fusion and Topological-Based Loss. arXiv 2024, arXiv:2409.20474. [Google Scholar]





| Settings | SPMFNet |
|---|---|
| Optimizer | Adam |
| Learning Rate | |
| Epochs | 200 |
| Batch Size | 4 |
| Image Size | 480 × 640/288 × 384 |
| Variants | P | Spec | Rec | Kappa | OA | mIoU | F1 |
|---|---|---|---|---|---|---|---|
| w/o loss1 | 76.15 | 97.73 | 92.81 | 82.25 | 97.37 | 84.55 | 83.66 |
| w/o loss2 | 55.03 | 95.32 | 73.30 | 59.51 | 93.72 | 69.61 | 62.87 |
| w/o loss3 | 74.71 | 97.83 | 82.15 | 76.47 | 96.69 | 80.38 | 78.25 |
| SPMFNet | 81.45 | 98.40 | 89.84 | 84.23 | 97.78 | 86.10 | 85.44 |
| Variants | P | Spec | Rec | Kappa | OA | mIoU | F1 |
|---|---|---|---|---|---|---|---|
| baseline | 81.01 | 98.05 | 84.42 | 81.29 | 97.44 | 83.87 | 82.68 |
| w/o EageLoss | 80.71 | 98.39 | 86.42 | 82.13 | 97.52 | 84.49 | 83.47 |
| w/o GCA | 78.56 | 98.09 | 89.56 | 82.34 | 97.47 | 84.63 | 83.70 |
| w/o AFF | 80.07 | 98.29 | 88.07 | 82.56 | 97.55 | 84.81 | 83.88 |
| SPMFNet | 81.45 | 98.40 | 89.84 | 84.24 | 97.78 | 86.10 | 85.44 |
| Type | Model | P | Spec | Rec | Kappa | OA | mIoU | F1 |
|---|---|---|---|---|---|---|---|---|
| RGB | U-Net [6] | 78.24 | 98.06 | 89.07 | 81.91 | 97.42 | 84.31 | 83.30 |
| RGB | Crackformer-II [11] | 80.07 | 98.28 | 88.38 | 82.70 | 97.56 | 84.92 | 84.42 |
| T | U-Net [6] | 54.61 | 94.90 | 78.53 | 61.09 | 91.73 | 70.42 | 64.44 |
| T | Crackformer-II [11] | 67.82 | 97.83 | 84.50 | 70.98 | 94.98 | 70.24 | 62.76 |
| RGB-T | CAINet [44] | 81.06 | 98.51 | 81.85 | 81.00 | 97.30 | 82.82 | 81.46 |
| RGB-T | MCNet [45] | 78.95 | 98.24 | 84.63 | 81.06 | 97.25 | 83.13 | 82.08 |
| RGB-T | SFAF-MA [46] | 78.85 | 97.62 | 85.97 | 83.61 | 97.31 | 85.19 | 82.54 |
| RGB-T | SGFNet [47] | 77.62 | 98.01 | 88.48 | 82.96 | 97.26 | 84.65 | 83.52 |
| RGB-T | GMNet [30] | 78.28 | 98.09 | 82.39 | 81.44 | 97.17 | 82.44 | 82.98 |
| RGB-T | IRfusionFormer [48] | 79.57 | 98.27 | 86.23 | 81.36 | 97.40 | 83.91 | 82.77 |
| RGB-T | SPMFNet | 81.45 | 98.40 | 89.84 | 84.24 | 97.78 | 86.10 | 85.44 |
| Type | Model | P | Spec | Rec | Kappa | OA | mIoU | F1 |
|---|---|---|---|---|---|---|---|---|
| RGB | U-Net [6] | 56.60 | 99.77 | 57.62 | 56.88 | 99.55 | 69.76 | 57.10 |
| RGB | Crackformer-II [11] | 42.77 | 99.68 | 45.92 | 43.99 | 99.41 | 63.93 | 44.29 |
| T | U-Net [6] | 63.54 | 99.81 | 64.96 | 64.06 | 99.63 | 73.47 | 64.24 |
| T | Crackformer-II [11] | 59.16 | 99.77 | 64.37 | 61.45 | 99.59 | 72.07 | 61.65 |
| RGB-T | CAINet [44] | 58.98 | 99.81 | 52.31 | 55.23 | 99.57 | 68.96 | 55.45 |
| RGB-T | MCNet [45] | 64.13 | 99.83 | 59.41 | 61.49 | 99.62 | 72.11 | 61.68 |
| RGB-T | SFAF-MA [46] | 53.31 | 99.72 | 62.01 | 57.09 | 99.52 | 69.85 | 57.33 |
| RGB-T | SGFNet [47] | 47.06 | 99.64 | 62.64 | 53.47 | 99.45 | 68.09 | 53.74 |
| RGB-T | GMNet [30] | 59.02 | 99.78 | 59.92 | 59.26 | 99.58 | 70.95 | 59.47 |
| RGB-T | IRfusionFormer [48] | 42.11 | 99.56 | 61.94 | 49.83 | 99.37 | 66.41 | 50.14 |
| RGB-T | SPMFNet | 66.63 | 99.83 | 64.89 | 65.58 | 99.65 | 74.31 | 65.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Z.; Ding, X.; Xia, X.; He, Y.; Fang, H.; Yang, B.; Fu, W. Structure-Aware Progressive Multi-Modal Fusion Network for RGB-T Crack Segmentation. J. Imaging 2025, 11, 384. https://doi.org/10.3390/jimaging11110384
Yuan Z, Ding X, Xia X, He Y, Fang H, Yang B, Fu W. Structure-Aware Progressive Multi-Modal Fusion Network for RGB-T Crack Segmentation. Journal of Imaging. 2025; 11(11):384. https://doi.org/10.3390/jimaging11110384
Chicago/Turabian StyleYuan, Zhengrong, Xin Ding, Xinhong Xia, Yibin He, Hui Fang, Bo Yang, and Wei Fu. 2025. "Structure-Aware Progressive Multi-Modal Fusion Network for RGB-T Crack Segmentation" Journal of Imaging 11, no. 11: 384. https://doi.org/10.3390/jimaging11110384
APA StyleYuan, Z., Ding, X., Xia, X., He, Y., Fang, H., Yang, B., & Fu, W. (2025). Structure-Aware Progressive Multi-Modal Fusion Network for RGB-T Crack Segmentation. Journal of Imaging, 11(11), 384. https://doi.org/10.3390/jimaging11110384






