No Reproducibility, No Progress: Rethinking CT Benchmarking
Abstract
1. Introduction
1.1. Modern Challenges of Reproducibility and Benchmarking in CT Reconstruction
1.2. Contribution
- Critical analysis of current practices. We systematically reviewed the state of benchmarking in CT, identifying systemic shortcomings, including the scarcity of open datasets, inadequate or opaque documentation, reliance on non-transparent ground truth definitions, and inconsistent use of evaluation metrics. These issues collectively undermine reproducibility and hinder methodological progress.
- Formalization of benchmarking workflows. We introduced a data model and formally described the data preparation and quality assessment schemes commonly used in practice. This formalization provides a structured view of benchmarking pipelines, clarifying hidden assumptions and sources of variability that have previously limited reproducibility.
- Extension of existing dataset preparation schemes. Building on this formalization, we proposed extended schemes that support dataset preparation across a wider range of tasks and domains. The extended schemes explicitly incorporate reproducibility as a guiding principle, enabling more reliable comparisons of CT reconstruction methods under diverse experimental conditions.
- Checklist for reproducible benchmarking. We formulated a practical checklist for dataset curation, quality evaluation, and benchmarking procedures. This checklist emphasizes transparency, standardization, and reproducibility, drawing on established practices from ML and DL research. Importantly, we highlight the underutilized potential of virtual CT (vCT) with analytically computable phantoms as a robust source of realistic and fully controllable data.
- Path toward standardization. Taken together, these contributions lay the groundwork for the establishment of a standardized, reproducible benchmarking framework in CT. By aligning benchmarking practices in CT with those already well-developed in other scientific domains, this work advances the methodological rigor of CT research and supports the development of trustworthy, generalizable reconstruction methods for both clinical and industrial applications.
1.3. Paper Organization
2. Context and Terms
2.1. X-Ray CT Reconstruction
- Beam-hardening artifacts (BH artifacts): suppression algorithms, referred to as beam-hardening correction (BHC) methods, are employed to improve the quality of polychromatic data reconstruction within the monochromatic model [17];
- Scatter artifacts: resulting from the scattering of X-rays [20];
- Low-dose artifacts: occurring when the radiation dose is reduced [21];
- Denoising: denoising task in CT involves processing either raw projection data (sinograms) or reconstructed volumes to reduce noise [22];
- Sparse-angle (sparse-view, or few-view) artifacts: observed when reconstructing from a sparse array of projection data [23];
- Limited-angle artifacts: occurring with a restricted angular scanning range [24];
- Ring artifacts [28]: typically caused by miscalibrated detector cells;
- Motion artifacts: including specific cases such as sample vibration and jitter during measurement [31].
- Preprocessing (projection-domain, sinogram-domain): this involves additional processing of sinograms before reconstruction to reduce the presence and severity of artifacts in the final reconstruction;
- Postprocessing (reconstruction-domain, image-domain): processing the already reconstructed dataset to mitigate artifacts;
- Task-oriented reconstruction methods (dual-domain): combining sinogram preprocessing and volume postprocessing.
2.2. The Consumer Landscape of CT
2.3. Repeatability, Reproducibility and Replicability
3. Open Sources Review
3.1. Datasets
3.2. Modeling Through Sinogram Modification (Without Simulating Forward Projections)
3.3. vCT-Based Modeling of the Forward Projections
3.3.1. LoDoPaB-CT
3.3.2. SynDeepLesion
3.3.3. AAPM Truth-Based CT (TrueCT) Reconstruction Grand Challenge
3.3.4. AAPM CT Metal Artifact Reduction (CT-MAR) Grand Challenge
3.3.5. ICASP CBCT
3.4. CT Reconstruction Quality Assessment
- high-precision positioning systems for the object during scanning;
- specially manufactured physical reference objects with high geometric accuracy;
- comparison of reconstructed images with high-precision geometric descriptions of reference objects obtained using a coordinate measuring machine.
3.5. Benchmarks
3.6. Conclusions on Publicly Available vCT Datasets
4. Flaws in Current Datasets and Benchmarks
4.1. Limitations of Public Datasets and Benchmarking Protocols in CT Reconstruction
- There is no consensus on a representative dataset. Different studies use different datasets or subsets thereof. This issue is well illustrated for LDCT in [32], where the authors also propose a potential standardization strategy for reconstruction-domain LDCT methods. However, even this attempt does not resolve the issue of including projection- or dual-domain methods in comparative analyses.
- Different tasks rely on different base datasets, largely because there is no dataset with sufficient diversity in both imaging conditions and object types that could support cross-task evaluations (e.g., LDCT and MAR) or enable consistent benchmarking of various baseline CT reconstruction methods.
4.2. Constraints Imposed by Simplified vCT Models
4.3. Lack of Raw Data
4.4. Using the Best Reconstruction as the GT
4.5. Data Verification
4.6. Implicit Specification of the Region of Interest and/or Its Inaccuracy
4.7. Vague Descriptions Without Publication of the Corresponding Quality Assessment Code
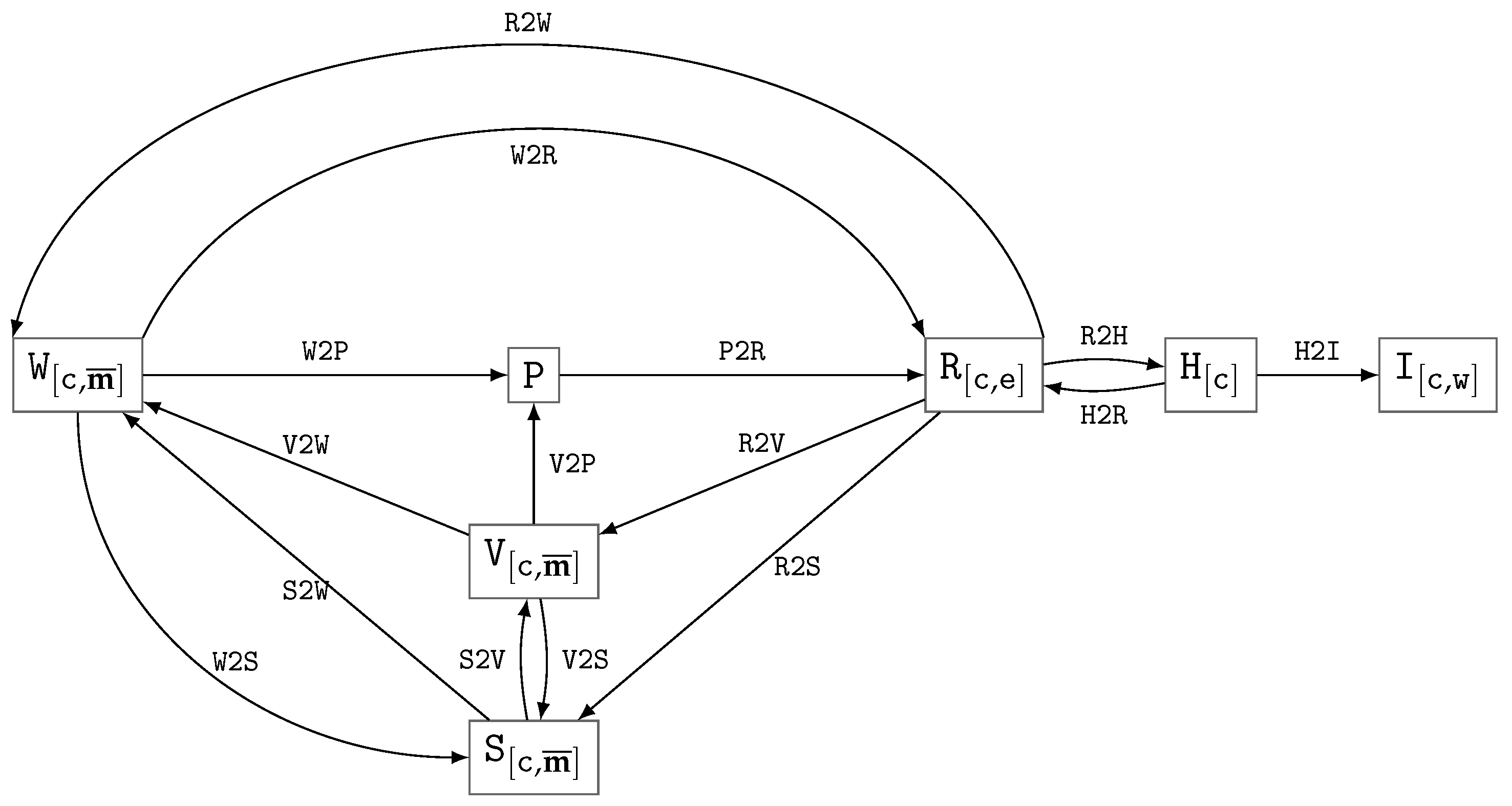
5. Model
5.1. Basic Notation
5.2. Digital (Object) Model
- —vector model in the coordinate system c;
- —material weight mask in the coordinate system c;
- —segmentation mask in the coordinate system c;
- —reconstruction (LAC values) in the coordinate system c at a given reference energy e;
- —reconstruction in HU units in the coordinate system c;
- —reconstruction in the coordinate system c with a given HU-window .
5.3. Data Transformations
- det—weakly variable (the transformation algorithm is unambiguous, and when fixed parameters are used, a high degree of reproducibility at level L2 is achieved);
- var—highly variable (the transformation may be performed in different ways, and algorithms of varying degrees of accuracy exist; to achieve reproducibility beyond level L1, a precise description is required);
- rnd—randomized (the algorithms are specifically designed to model stochastic processes, in particular physical phenomena such as absorption, scattering, etc.; reproducibility requires not only detailed descriptions/code but also the ability to control the random seed).
5.4. Specifics of Using HU Units and Windowing
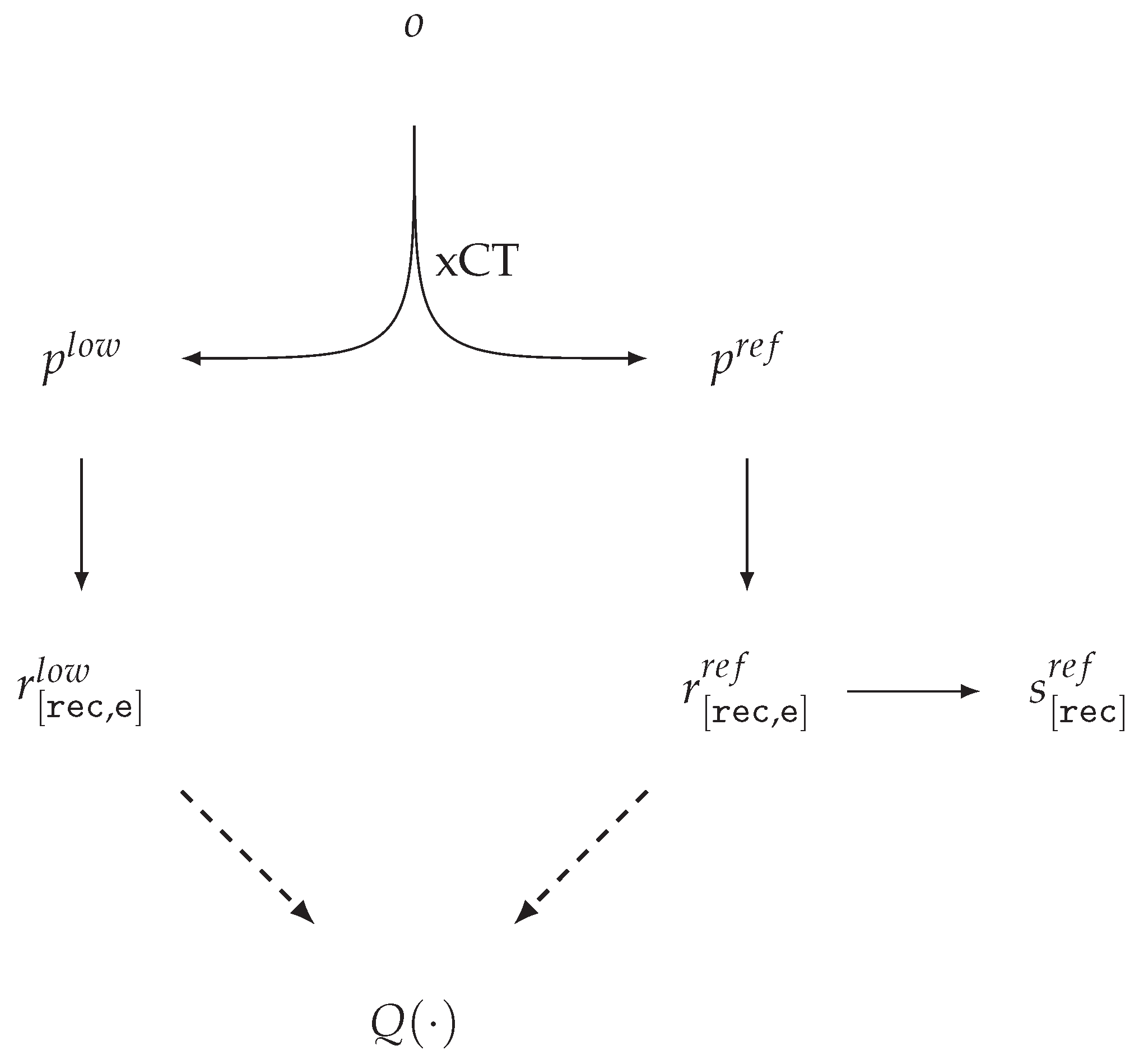
5.5. Types of Functions for Assessing Reconstruction Quality
5.6. Model for the Assessment of xCT Reconstruction Quality
5.7. A Model for Assessing CT Reconstruction When Sinogram Modification Is Used
5.8. A Model for Assessing CT Reconstruction in the MAR Task
5.9. A Model for Assessing CT Reconstruction Using Vector Models and vCT (TrueCT)
6. Extended Frameworks for Data Preparation and Benchmarking
- selection of optimal acquisition modes and parameters, including object orientation, projection angles, source spectrum, exposure, etc.;
- evaluation of the robustness of learning-based reconstruction methods to input variability, including robustness to adversarial attacks [99].
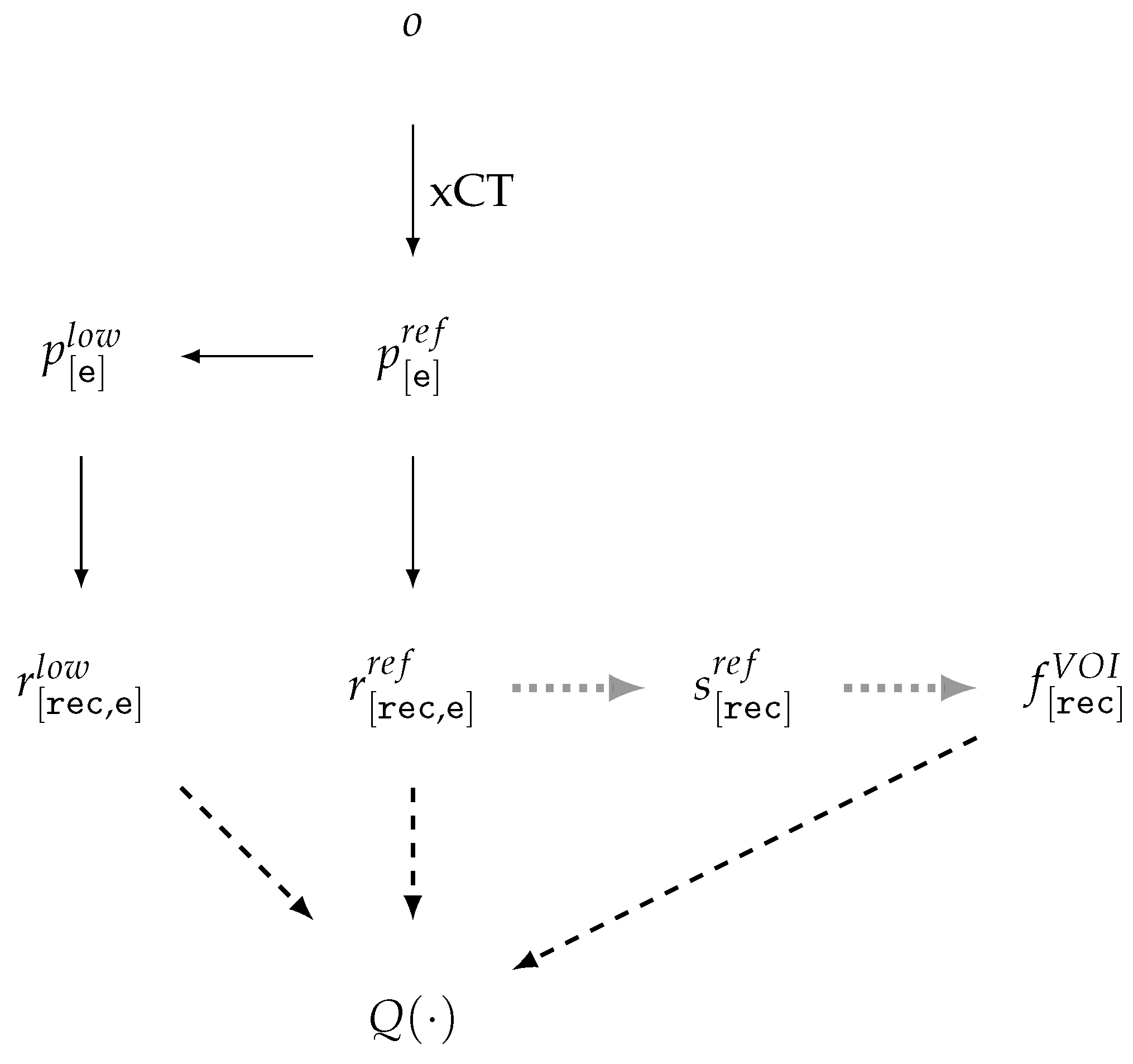
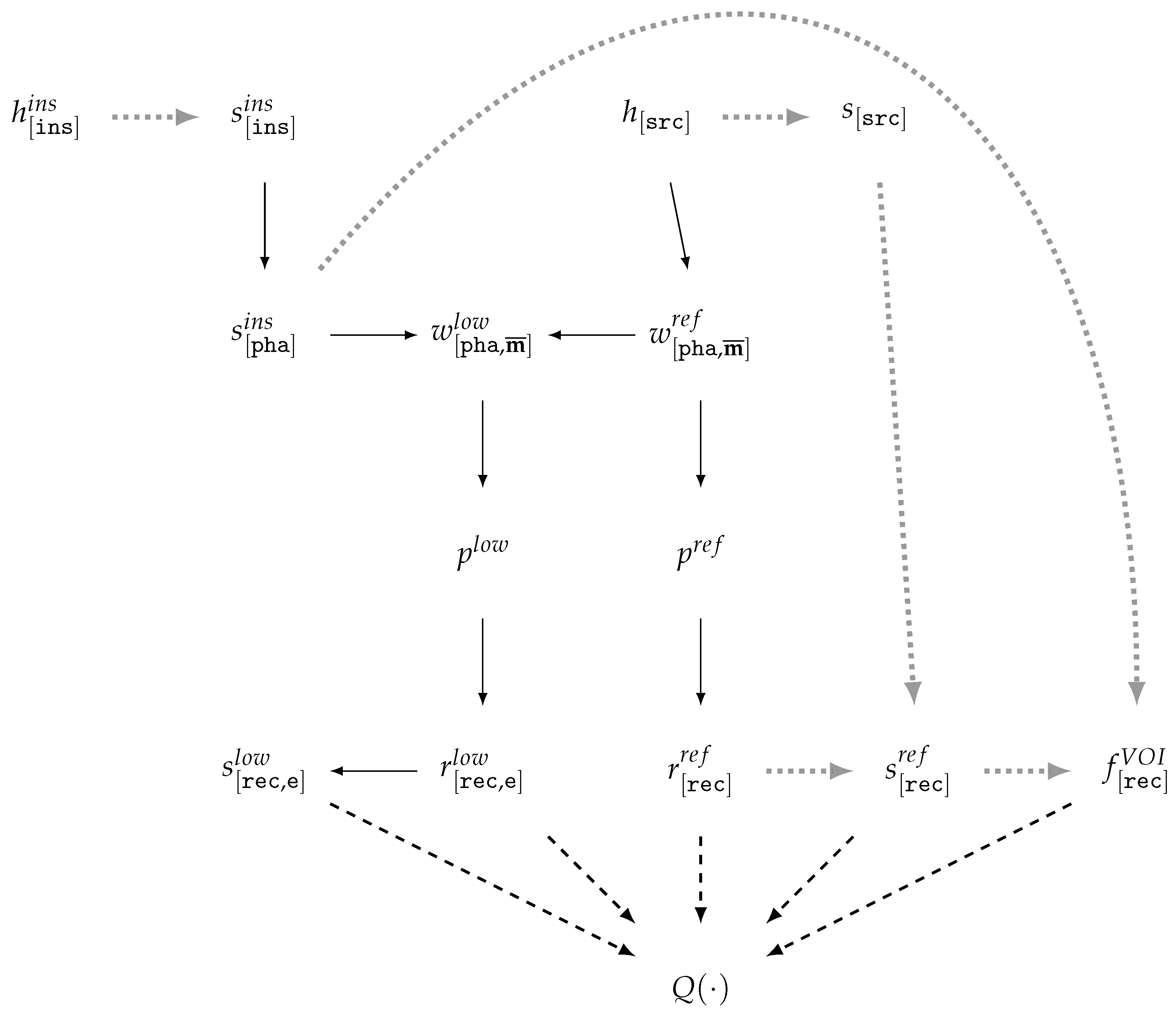
6.1. Extended Model for CT Data Evaluation in xCT Scanning
6.2. Extended Model for CT Data Evaluation in vCT Scanning
6.3. Proposals for Practices in CT Dataset and Benchmark Creation Conducive to Reproducibility
7. Future Works
7.1. Enhancing Reproducibility
7.2. Development of Evaluation Methods
7.3. Creating New Open Multitask and Multidomain CT Datasets
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BH | beam hardening |
| BHC | beam hardening correction |
| CAD | computer-aided design |
| CNN | convolutional neural network |
| CNR | contrast-to-noise ratio |
| conCT | conveyor computed tomography |
| CS | coordinate system |
| CT | computed tomography |
| DL | deep learning |
| ESF | edge spread function |
| FID | Fréchet inception distance |
| FOV | field of view |
| FR-IQA | full-reference image quality assessment |
| GCS | global coordinate system |
| HU | Hounsfield units |
| indCT | industrial computed tomography |
| IQM | image quality metric |
| labCT | laboratory computed tomography |
| LAC | linear attenuation coefficient |
| LDCT | low-dose computed tomography |
| LDR | low-dose reconstruction |
| LSF | line spread function |
| MAR | metal artifact reduction |
| medCT | medical computed tomography |
| ML | machine learning |
| MTF | modulation transfer function |
| MRI | magnetic resonance imaging |
| NPS | noise power spectrum |
| NR-IQA | no-reference image quality assessment |
| PET | positron emission tomography |
| OCS | object’s coordinate system |
| PSF | point spread function |
| PSNR | peak signal-to-noise ratio |
| RFS | radiomic feature similarity |
| RIC | ring artifact correction |
| RMSE | root mean square error |
| ROI | region(s) of interest |
| RQA | reference-based quality assessment |
| SAT | subjective assessment techniques |
| SSIM | structural similarity index measure |
| TSM | triangulated surface mesh |
| TTF | task transfer function |
| vCT | virtual computed tomography |
| VIF | visual information fidelity |
| VOI | volume(s) of interest |
| WMM | weighted material map |
| xCT | X-ray computed tomography |
References
- Weber, L.M.; Saelens, W.; Cannoodt, R.; Soneson, C.; Hapfelmeier, A.; Gardner, P.P.; Boulesteix, A.L.; Saeys, Y.; Robinson, M.D. Essential guidelines for computational method benchmarking. Genome Biol. 2019, 20, 125. [Google Scholar] [CrossRef]
- Ioannidis, J.P. Why most published research findings are false. PLoS Med. 2005, 2, e124. [Google Scholar] [CrossRef]
- Shimron, E.; Tamir, J.I.; Wang, K.; Lustig, M. Implicit data crimes: Machine learning bias arising from misuse of public data. Proc. Natl. Acad. Sci. USA 2022, 119, e2117203119. [Google Scholar] [CrossRef]
- Maier-Hein, L.; Reinke, A.; Godau, P.; Tizabi, M.D.; Buettner, F.; Christodoulou, E.; Glocker, B.; Isensee, F.; Kleesiek, J.; Kozubek, M.; et al. Metrics reloaded: Recommendations for image analysis validation. Nat. Methods 2024, 21, 195–212. [Google Scholar] [CrossRef] [PubMed]
- Polevoy, D.V.; Kazimirov, D.D.; Mehova, M.S.; Gilmanov, M.I. X-Ray Computed Tomography Traps and Challenges for Deep Learning Scientist. In Proceedings of the SPRA 2024, Istanbul, Turkey, 11–13 November 2024; Pang, X., Ed.; SPIE: Bellingham, WA, USA, 2025; Volume 13540, p. 135400F. [Google Scholar] [CrossRef]
- Gundersen, O.E. The fundamental principles of reproducibility. Philos. Trans. R. Soc. A 2021, 379, 20200210. [Google Scholar] [CrossRef] [PubMed]
- Semmelrock, H.; Ross-Hellauer, T.; Kopeinik, S.; Theiler, D.; Haberl, A.; Thalmann, S.; Kowald, D. Reproducibility in machine-learning-based research: Overview, barriers, and drivers. AI Mag. 2025, 46, e70002. [Google Scholar] [CrossRef]
- Desai, A.; Abdelhamid, M.; Padalkar, N.R. What is reproducibility in artificial intelligence and machine learning research? AI Mag. 2025, 46, e70004. [Google Scholar] [CrossRef]
- Chikin, P.S.; Soldatova, Z.V.; Ingacheva, A.S.; Polevoy, D.V. Virtual data generation pipeline for the analysis of computed tomography methods. Tr. ISA RAN (Proc. ISA RAS) 2024, 74, 46–55. [Google Scholar] [CrossRef]
- Arlazarov, V.L.; Nikolaev, D.P.; Arlazarov, V.V.; Chukalina, M.V. X-ray Tomography: The Way from Layer-by-layer Radiography to Computed Tomography. Comput. Opt. 2021, 45, 897–906. [Google Scholar] [CrossRef]
- Bellens, S.; Guerrero, P.; Vandewalle, P.; Dewulf, W. Machine learning in industrial X-ray computed tomography–a review. CIRP J. Manuf. Sci. Technol. 2024, 51, 324–341. [Google Scholar] [CrossRef]
- Renard, F.; Guedria, S.; Palma, N.D.; Vuillerme, N. Variability and reproducibility in deep learning for medical image segmentation. Sci. Rep. 2020, 10, 13724. [Google Scholar] [CrossRef]
- Polevoy, D.; Gilmanov, M.; Kazimirov, D.; Chukalina, M.; Ingacheva, A.; Kulagin, P.; Nikolaev, D. Tomographic reconstruction: General approach to fast back-projection algorithms. Mathematics 2023, 11, 4759. [Google Scholar] [CrossRef]
- Polevoy, D.V.; Kazimirov, D.D.; Chukalina, M.V.; Nikolaev, D.P. Complexity-Preserving Transposition of Summing Algorithms: A Data Flow Graph Approach. Probl. Inf. Transm. 2024, 60, 344–362. [Google Scholar] [CrossRef]
- Levine, Z.H.; Peskin, A.P.; Holmgren, A.D.; Garboczi, E.J. Preliminary X-ray CT investigation to link Hounsfield unit measurements with the International System of Units (SI). PLoS ONE 2018, 13, e0208820. [Google Scholar] [CrossRef] [PubMed]
- Buzug, T.M. Computed tomography. In Springer Handbook of Medical Technology; Springer: Berlin/Heidelberg, Germany, 2011; pp. 311–342. [Google Scholar]
- Ingacheva, A.S.; Chukalina, M.V. Polychromatic CT Data Improvement with One-Parameter Power Correction. Math. Probl. Eng. 2019, 2019, 1405365. [Google Scholar] [CrossRef]
- Gilmanov, M.; Kirkicha, A.; Ingacheva, A.; Chukalina, M.; Nikolaev, D. Stability of artificial intelligence methods in computed tomography metal artifacts reduction task. In Proceedings of the SPRA 2024, Istanbul, Turkey, 11–13 November 2024; Pang, X., Ed.; SPIE: Bellingham, WA, USA, 2025; Volume 13540, p. 135400D. [Google Scholar] [CrossRef]
- Shutov, M.; Gilmanov, M.; Polevoy, D.; Buzmakov, A.; Ingacheva, A.; Chukalina, M.; Nikolaev, D. CT metal artifacts simulation under x-ray total absorption. In Proceedings of the ICMV 2023, Yerevan, Armenia, 15–18 November 2023; Osten, W., Nikolaev, D., Debayle, J., Eds.; SPIE: Bellingham, WA, USA, 2024; Volume 13072, p. 130720Z. [Google Scholar] [CrossRef]
- Zhao, W.; Vernekohl, D.; Zhu, J.; Wang, L.; Xing, L. A model-based scatter artifacts correction for cone beam CT. Med. Phys. 2016, 43, 1736–1753. [Google Scholar] [CrossRef] [PubMed]
- Yamaev, A.V.; Chukalina, M.V.; Nikolaev, D.P.; Sheshkus, A.V.; Chulichkov, A.I. Neural Network for Data Preprocessing in Computed Tomography. Autom Remote Control 2021, 82, 1752–1762. [Google Scholar] [CrossRef]
- Yamaev, A.V.; Chukalina, M.V.; Nikolaev, D.P.; Sheshkus, A.V.; Chulichkov, A.I. Lightweight Denoising Filtering Neural Network For FBP Algorithm. In Proceedings of the ICMV 2020, Rome, Italy, 2–6 November 2020; SPIE: Bellingham, WA, USA, 2021; Volume 11605, p. 116050L. [Google Scholar] [CrossRef]
- Yamaev, A.V.; Chukalina, M.V.; Nikolaev, D.P.; Kochiev, L.G.; Chulichkov, A.I. Neural network regularization in the problem of few-view computed tomography. Comput. Opt. 2022, 46, 422–428. [Google Scholar] [CrossRef]
- Buzmakov, A.; Zolotov, D.; Chukalina, M.; Ingacheva, A.; Asadchikov, V.; Nikolaev, D.; Krivonosov, Y.; Dyachkova, I.; Bukreeva, I. Iterative Reconstruction of Incomplete Tomography Data: Application Cases. In Proceedings of the ICMV 2020, Rome, Italy, 2–6 November 2020; SPIE: Bellingham, WA, USA, 2021; Volume 11605, p. 1160523. [Google Scholar] [CrossRef]
- Gilmanov, M.I.; Bulatov, K.B.; Bugai, O.A.; Ingacheva, A.S.; Chukalina, M.V.; Nikolaev, D.P.; Arlazarov, V.V. Applicability and potential of monitored reconstruction in computed tomography. PLoS ONE 2024, 19, e0307231. [Google Scholar] [CrossRef]
- Bulatov, K.B.; Ingacheva, A.S.; Gilmanov, M.I.; Kutukova, K.; Soldatova, Z.V.; Buzmakov, A.V.; Chukalina, M.V.; Zschech, E.; Arlazarov, V.V. Towards monitored tomographic reconstruction: Algorithm-dependence and convergence. Comput. Opt. 2023, 47, 658–667. [Google Scholar] [CrossRef]
- Ingacheva, A.; Bulatov, K.; Soldatova, Z.; Kutukova, K.; Chukalina, M.; Nikolaev, D.; Arlazarov, V.; Zschech, E. Comparison convergence of the reconstruction algorithms for monitored tomography on synthetic dataset. In Synchrotron and Free Electron Laser Radiation: Generation and Application (SFR-2022); Institute of Nuclear Physics G.I. Budker SB RAS: Novosibirsk, Russia, 2022; pp. 37–39. [Google Scholar]
- Kazimirov, D.; Polevoy, D.; Ingacheva, A.; Chukalina, M.; Nikolaev, D. Adaptive automated sinogram normalization for ring artifacts suppression in CT. Opt. Express 2024, 32, 17606–17643. [Google Scholar] [CrossRef]
- Kazimirov, D.; Ingacheva, A.; Buzmakov, A.; Chukalina, M.; Nikolaev, D. Robust Automatic Rotation Axis Alignment Mean Projection Image Method in Cone-Beam and Parallel-Beam CT. In Proceedings of the ICMV 2023, Yerevan, Armenia, 15–18 November 2023; Osten, W., Nikolaev, D., Debayle, J., Eds.; SPIE: Bellingham, WA, USA, 2024; Volume 13072, p. 1307212. [Google Scholar] [CrossRef]
- Kazimirov, D.; Ingacheva, A.; Buzmakov, A.; Marina, C.; Dmitry, N. Mean projection image application to the automatic rotation axis alignment in cone-beam CT. In Proceedings of the ICMV 2022, Rome, Italy, 18–20 November 2022; Osten, W., Nikolaev, D., Zhou, J., Eds.; SPIE: Bellingham, WA, USA,, 2023; Volume 12701. [Google Scholar] [CrossRef]
- Kyme, A.Z.; Fulton, R.R. Motion estimation and correction in SPECT, PET and CT. Phys. Med. Biol. 2021, 66, 18TR02. [Google Scholar] [CrossRef]
- Eulig, E.; Ommer, B.; Kachelrieß, M. Benchmarking deep learning-based low-dose CT image denoising algorithms. Med. Phys. 2024, 51, 8776–8788. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, A.; Longabaugh, W.J.; Pot, D.; Clunie, D.A.; Pieper, S.D.; Gibbs, D.L.; Bridge, C.; Herrmann, M.D.; Homeyer, A.; Lewis, R.; et al. National cancer institute imaging data commons: Toward transparency, reproducibility, and scalability in imaging artificial intelligence. Radiographics 2023, 43, e230180. [Google Scholar] [CrossRef] [PubMed]
- Elfer, K.; Gardecki, E.; Garcia, V.; Ly, A.; Hytopoulos, E.; Wen, S.; Hanna, M.G.; Peeters, D.J.; Saltz, J.; Ehinger, A.; et al. Reproducible reporting of the collection and evaluation of annotations for artificial intelligence models. Mod. Pathol. 2024, 37, 100439. [Google Scholar] [CrossRef] [PubMed]
- Samala, R.K.; Gallas, B.D.; Zamzmi, G.; Juluru, K.; Khan, A.; Bahr, C.; Ochs, R.; Carranza, D.; Granstedt, J.; Margerrison, E.; et al. Medical Imaging Data Strategies for Catalyzing AI Medical Device Innovation. J. Imaging Inform. Med. 2025, 1–8. [Google Scholar] [CrossRef]
- Zwanenburg, A.; Vallières, M.; Abdalah, M.A.; Aerts, H.J.; Andrearczyk, V.; Apte, A.; Ashrafinia, S.; Bakas, S.; Beukinga, R.J.; Boellaard, R.; et al. The image biomarker standardization initiative: Standardized quantitative radiomics for high-throughput image-based phenotyping. Radiology 2020, 295, 328–338. [Google Scholar] [CrossRef]
- Kuhl, C.K.; Truhn, D. The long route to standardized radiomics: Unraveling the knot from the end. Radiology 2020, 295, 339–341. [Google Scholar] [CrossRef]
- Kocak, B.; Baessler, B.; Bakas, S.; Cuocolo, R.; Fedorov, A.; Maier-Hein, L.; Mercaldo, N.; Müller, H.; Orlhac, F.; Pinto dos Santos, D.; et al. CheckList for EvaluAtion of Radiomics research (CLEAR): A step-by-step reporting guideline for authors and reviewers endorsed by ESR and EuSoMII. Insights Imaging 2023, 14, 75. [Google Scholar] [CrossRef]
- McCollough, C.H.; Bartley, A.C.; Carter, R.E.; Chen, B.; Drees, T.A.; Edwards, P.; Holmes III, D.R.; Huang, A.E.; Khan, F.; Leng, S.; et al. Low-dose CT for the detection and classification of metastatic liver lesions: Results of the 2016 Low Dose CT Grand Challenge. Med. Phys. 2017, 44, e339–e352. [Google Scholar] [CrossRef]
- Moen, T.R.; Chen, B.; Holmes III, D.R.; Duan, X.; Yu, Z.; Yu, L.; Leng, S.; Fletcher, J.G.; McCollough, C.H. Low-dose CT image and projection dataset. Med. Phys. 2021, 48, 902–911. [Google Scholar] [CrossRef]
- Kiss, M.B.; Coban, S.B.; Batenburg, K.J.; van Leeuwen, T.; Lucka, F. 2DeteCT-A large 2D expandable, trainable, experimental Computed Tomography dataset for machine learning. Sci. Data 2023, 10, 576. [Google Scholar] [CrossRef]
- Kazantsev, D.; Beveridge, L.; Shanmugasundar, V.; Magdysyuk, O. Conditional generative adversarial networks for stripe artefact removal in high-resolution x-ray tomography. Tomogr. Mater. Struct. 2024, 4, 100019. [Google Scholar] [CrossRef]
- Vo, N.T.; Atwood, R.C.; Drakopoulos, M. Superior techniques for eliminating ring artifacts in X-ray micro-tomography. Opt. Express 2018, 26, 28396–28412. [Google Scholar] [CrossRef] [PubMed]
- Vo, N.T.; Atwood, R.C.; Drakopoulos, M. Tomographic data for testing, demonstrating, and developing methods of removing ring artifacts. Zenodo 2018. [Google Scholar] [CrossRef]
- Kudo, H.; Suzuki, T.; Rashed, E.A. Image reconstruction for sparse-view CT and interior CT—introduction to compressed sensing and differentiated backprojection. Quant. Imaging Med. Surg. 2013, 3, 147. [Google Scholar] [PubMed]
- Kiss, M.B.; Biguri, A.; Shumaylov, Z.; Sherry, F.; Batenburg, K.J.; Schönlieb, C.B.; Lucka, F. Benchmarking learned algorithms for computed tomography image reconstruction tasks. Appl. Math. Mod. Challenges 2025, 3, 1–43. [Google Scholar] [CrossRef]
- Guo, J.; Qi, H.; Xu, Y.; Chen, Z.; Li, S.; Zhou, L. Iterative Image Reconstruction for Limited-Angle CT Using Optimized Initial Image. Comput. Math. Methods Med. 2016, 2016, 5836410. [Google Scholar] [CrossRef]
- Leuschner, J.; Schmidt, M.; Ganguly, P.S.; Andriiashen, V.; Coban, S.B.; Denker, A.; Bauer, D.; Hadjifaradji, A.; Batenburg, K.J.; Maass, P.; et al. Quantitative comparison of deep learning-based image reconstruction methods for low-dose and sparse-angle CT applications. J. Imaging 2021, 7, 44. [Google Scholar] [CrossRef]
- Usui, K.; Kamiyama, S.; Arita, A.; Ogawa, K.; Sakamoto, H.; Sakano, Y.; Kyogoku, S.; Daida, H. Reducing image artifacts in sparse projection CT using conditional generative adversarial networks. Sci. Rep. 2024, 14, 3917. [Google Scholar] [CrossRef]
- Piccolomini, E.L.; Evangelista, D.; Morotti, E. Deep Guess acceleration for explainable image reconstruction in sparse-view CT. Comput. Med Imaging Graph. 2025, 123, 102530. [Google Scholar] [CrossRef] [PubMed]
- Bulatov, K.; Chukalina, M.; Buzmakov, A.; Nikolaev, D.; Arlazarov, V.V. Monitored Reconstruction: Computed Tomography as an Anytime Algorithm. IEEE Access 2020, 8, 110759–110774. [Google Scholar] [CrossRef]
- Yamaev, A.V. Monitored reconstruction improved by post-processing neural network. Comput. Opt. 2024, 48, 601–609. [Google Scholar] [CrossRef]
- Yu, L.; Shiung, M.; Jondal, D.; McCollough, C.H. Development and validation of a practical lower-dose-simulation tool for optimizing computed tomography scan protocols. J. Comput. Assist. Tomogr. 2012, 36, 477–487. [Google Scholar] [CrossRef]
- Žabić, S.; Wang, Q.; Morton, T.; Brown, K.M. A low dose simulation tool for CT systems with energy integrating detectors. Med. Phys. 2013, 40, 031102. [Google Scholar] [CrossRef]
- Zeng, D.; Huang, J.; Bian, Z.; Niu, S.; Zhang, H.; Feng, Q.; Liang, Z.; Ma, J. A simple low-dose X-ray CT simulation from high-dose scan. IEEE Trans. Nucl. Sci. 2015, 62, 2226–2233. [Google Scholar] [CrossRef]
- Gibson, N.M.; Lee, A.; Bencsik, M. A practical method to simulate realistic reduced-exposure CT images by the addition of computationally generated noise. Radiol. Phys. Technol. 2024, 17, 112–123. [Google Scholar] [CrossRef]
- Yadav, A.; Welland, S.H.; Hoffman, J.M.; Kim, H.; Brown, M.S.; Prosper, A.E.; Aberle, D.R.; McNitt-Gray, M.F.; Hsu, W. A comparative analysis of image harmonization techniques in mitigating differences in CT acquisition and reconstruction. Phys. Med. Biol. 2025, 70, 055015. [Google Scholar] [CrossRef]
- Kiss, M.B.; Biguri, A.; Schönlieb, C.B.; Batenburg, K.J.; Lucka, F. Learned denoising with simulated and experimental low-dose CT data. arXiv 2024, arXiv:2408.08115. [Google Scholar] [CrossRef]
- Leuschner, J.; Schmidt, M.; Baguer, D.O.; Maass, P. LoDoPaB-CT, a benchmark dataset for low-dose computed tomography reconstruction. Sci. Data 2021, 8, 109. [Google Scholar] [CrossRef]
- Leuschner, J.; Schmidt, M.; Otero Baguer, D. LoDoPaB-CT Dataset. 2019. Available online: https://zenodo.org/records/3384092 (accessed on 25 September 2025). [CrossRef]
- Zhang, Y.; Yu, H. Convolutional neural network based metal artifact reduction in X-ray computed tomography. IEEE Trans. Med Imaging 2018, 37, 1370–1381. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Z.; Li, X.; Xing, L. Deep sinogram completion with image prior for metal artifact reduction in CT images. IEEE Trans. Med Imaging 2020, 40, 228–238. [Google Scholar] [CrossRef]
- Wang, H. SynDeepLesion. 2023. Available online: https://github.com/hongwang01/SynDeepLesion (accessed on 27 September 2025).
- Sakamoto, M.; Hiasa, Y.; Otake, Y.; Takao, M.; Suzuki, Y.; Sugano, N.; Sato, Y. Automated segmentation of hip and thigh muscles in metal artifact contaminated CT using CNN. In Proceedings of the International Forum on Medical Imaging in Asia 2019, Singapore, 7–9 January 2019; SPIE: Bellingham, WA, USA, 2019; Volume 11050, pp. 124–129. [Google Scholar]
- Abadi, E.; Segars, W.P.; Felice, N.; Sotoudeh-Paima, S.; Hoffman, E.A.; Wang, X.; Wang, W.; Clark, D.; Ye, S.; Jadick, G.; et al. AAPM Truth-based CT (TrueCT) reconstruction grand challenge. Med. Phys. 2025, 52, 1978–1990. [Google Scholar] [CrossRef]
- American Association of Physicists in Medicine. AAPM CT-MAR Grand Challenge. 2021. Available online: https://www.aapm.org/GrandChallenge/CT-MAR/ (accessed on 23 April 2025).
- AAPM CT-MAR Challenge. 2025. Available online: https://github.com/xcist/example/tree/main/AAPM_datachallenge (accessed on 27 September 2025).
- Biguri, A.; Mukherjee, S.; Zhao, X.; Liu, X.; Wang, X.; Yang, R.; Du, Y.; Peng, Y.; Brudfors, M.; Graham, M.; et al. Advancing the Frontiers of Deep Learning for Low-Dose 3D Cone-Beam CT Reconstruction. TechRxiv 2024. [Google Scholar] [CrossRef]
- Biguri, A. Test dataset for the ICASSP-2024 3D-CBCT challenge (Part 1). Zenodo 2024. [Google Scholar] [CrossRef]
- Herman, G.T. Correction for beam hardening in computed tomography. Phys. Med. Biol. 1979, 24, 81. [Google Scholar] [CrossRef] [PubMed]
- Wirgin, A. The Inverse Crime. arXiv 2004, arXiv:math-ph/0401050. [Google Scholar] [CrossRef]
- Lewitt, R.M. Reconstruction algorithms: Transform methods. Proc. IEEE 2005, 71, 390–408. [Google Scholar] [CrossRef]
- Wu, M.; FitzGerald, P.; Zhang, J.; Segars, W.P.; Yu, H.; Xu, Y.; De Man, B. XCIST—an open access x-ray/CT simulation toolkit. Phys. Med. Biol. 2022, 67, 194002. [Google Scholar] [CrossRef]
- Samei, E.; Bakalyar, D.; Boedeker, K.L.; Brady, S.; Fan, J.; Leng, S.; Myers, K.J.; Popescu, L.M.; Ramirez Giraldo, J.C.; Ranallo, F.; et al. Performance evaluation of computed tomography systems: Summary of AAPM Task Group 233. Med. Phys. 2019, 46, e735–e756. [Google Scholar] [CrossRef]
- Xun, S.; Li, Q.; Liu, X.; Huang, P.; Zhai, G.; Sun, Y.; Wu, M.; Tan, T. Charting the path forward: CT image quality assessment-an in-depth review. J. King Saud Univ. Comput. Inf. Sci. 2025, 37, 92. [Google Scholar] [CrossRef]
- Kim, W.; Jeon, S.Y.; Byun, G.; Yoo, H.; Choi, J.H. A systematic review of deep learning-based denoising for low-dose computed tomography from a perceptual quality perspective. Biomed. Eng. Lett. 2024, 14, 1153–1173. [Google Scholar] [CrossRef]
- Herath, H.; Herath, H.; Madusanka, N.; Lee, B.I. A Systematic Review of Medical Image Quality Assessment. J. Imaging 2025, 11, 100. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef] [PubMed]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper/2017/hash/8a1d694707eb0fefe65871369074926d-Abstract.html (accessed on 25 September 2025).
- Karner, C.; Gröhl, J.; Selby, I.; Babar, J.; Beckford, J.; Else, T.R.; Sadler, T.J.; Shahipasand, S.; Thavakumar, A.; Roberts, M.; et al. Parameter choices in HaarPSI for IQA with medical images. In Proceedings of the 2025 IEEE International Symposium on Biomedical Imaging (ISBI), Houston, TX, USA, 14–17 April 2025. [Google Scholar]
- Verdun, F.; Racine, D.; Ott, J.; Tapiovaara, M.; Toroi, P.; Bochud, F.; Veldkamp, W.; Schegerer, A.; Bouwman, R.; Giron, I.H.; et al. Image quality in CT: From physical measurements to model observers. Phys. Medica 2015, 31, 823–843. [Google Scholar] [CrossRef]
- Ohashi, K.; Nagatani, Y.; Yoshigoe, M.; Iwai, K.; Tsuchiya, K.; Hino, A.; Kida, Y.; Yamazaki, A.; Ishida, T. Applicability Evaluation of Full-Reference Image Quality Assessment Methods for Computed Tomography Images. J. Digit. Imaging 2023, 36, 2623–2634. [Google Scholar] [CrossRef]
- Breger, A.; Karner, C.; Selby, I.; Gröhl, J.; Dittmer, S.; Lilley, E.; Babar, J.; Beckford, J.; Else, T.R.; Sadler, T.J.; et al. A study on the adequacy of common IQA measures for medical images. arXiv 2024, arXiv:2405.19224. [Google Scholar] [CrossRef]
- Lee, W.; Wagner, F.; Galdran, A.; Shi, Y.; Xia, W.; Wang, G.; Mou, X.; Ahamed, M.A.; Imran, A.A.Z.; Oh, J.E.; et al. Low-dose computed tomography perceptual image quality assessment. Med. Image Anal. 2025, 99, 103343. [Google Scholar] [CrossRef]
- Nikolaev, D.; Buzmakov, A.; Chukalina, M.; Yakimchuk, I.; Gladkov, A.; Ingacheva, A. CT Image Quality Assessment Based on Morphometric Analysis of Artifacts. In Proceedings of the ICRMV 2016, Moscow, Russia, 14–16 September 2016; Bernstein, A.V., Olaru, A., Zhou, J., Eds.; SPIE: Bellingham, WA, USA, 2017; Volume 10253, pp. 1–5. [Google Scholar] [CrossRef]
- Ingacheva, A.; Chukalina, M.; Buzmakov, A.; Nikolaev, D. Method for numeric estimation of Cupping effect on CT images. In Proceedings of the ICMV 2019, Amsterdam, The Netherlands, 16–18 November 2019; Osten, W., Nikolaev, D., Zhou, J., Eds.; SPIE: Bellingham, WA, USA, 2020; Volume 11433, p. 1143331. [Google Scholar] [CrossRef]
- Ingacheva, A.S.; Tropin, D.V.; Chukalina, M.V.; Nikolaev, D.P. Blind CT images quality assessment of cupping artifacts. In Proceedings of the ICMV 2020, Rome, Italy, 2–6 November 2020; SPIE: Bellingham, WA, USA, 2021; Volume 11605, p. 1160516. [Google Scholar] [CrossRef]
- Tunissen, S.A.M.; Oostveen, L.J.; Moriakov, N.; Teuwen, J.; Michielsen, K.; Smit, E.J.; Sechopoulos, I. Development, validation, and simplification of a scanner-specific CT simulator. Med. Phys. 2023, 51, 2081–2095. [Google Scholar] [CrossRef]
- Alsaihati, N.; Solomon, J.; McCrum, E.; Samei, E. Development, validation, and application of a generic image-based noise addition method for simulating reduced dose computed tomography images. Med. Phys. 2025, 52, 171–187. [Google Scholar] [CrossRef]
- Tan, Y.; Kiekens, K.; Welkenhuyzen, F.; Angel, J.; De Chiffre, L.; Kruth, J.P.; Dewulf, W. Simulation-aided investigation of beam hardening induced errors in CT dimensional metrology. Meas. Sci. Technol. 2014, 25, 064014. [Google Scholar] [CrossRef][Green Version]
- Kronfeld, A.; Rose, P.; Baumgart, J.; Brockmann, C.; Othman, A.E.; Schweizer, B.; Brockmann, M.A. Quantitative multi-energy micro-CT: A simulation and phantom study for simultaneous imaging of four different contrast materials using an energy integrating detector. Heliyon 2024, 10, e23013. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Pack, J.; De Man, B. A virtual imaging trial framework to study cardiac CT blooming artifacts. In Proceedings of the 7th International Conference on Image Formation in X-Ray Computed Tomography, Baltimore, MD, USA, 12–16 June 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12304, pp. 247–251. [Google Scholar]
- Paramonov, P.; Francken, N.; Renders, J.; Iuso, D.; Elberfeld, T.; Beenhouwer, J.D.; Sijbers, J. CAD-ASTRA: A versatile and efficient mesh projector for X-ray tomography with the ASTRA-toolbox. Opt. Express 2024, 32, 3425–3439. [Google Scholar] [CrossRef] [PubMed]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Ohashi, K.; Nagatani, Y.; Yamazaki, A.; Yoshigoe, M.; Iwai, K.; Uemura, R.; Shimomura, M.; Tanimura, K.; Ishida, T. Development of a No-Reference CT Image Quality Assessment Method Using RadImageNet Pre-trained Deep Learning Models. J. Imaging Inform. Med. 2025, 1–13. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Zhang, H.; Chen, J.; Ma, K.; Meng, D.; Zheng, Y. InDuDoNet: An Interpretable Dual Domain Network for CT Metal Artifact Reduction. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2021; pp. 107–118. [Google Scholar]
- Kyriakou, Y.; Meyer, E.; Prell, D.; Kachelrieß, M. Empirical beam hardening correction (EBHC) for CT. Med. Phys. 2010, 37, 5179–5187. [Google Scholar] [CrossRef]
- Madesta, F.; Sentker, T.; Rohling, C.; Gauer, T.; Schmitz, R.; Werner, R. Monte Carlo-based simulation of virtual 3 and 4-dimensional cone-beam computed tomography from computed tomography images: An end-to-end framework and a deep learning-based speedup strategy. Phys. Imaging Radiat. Oncol. 2024, 32, 100644. [Google Scholar] [CrossRef]
- Smolin, A.; Yamaev, A.; Ingacheva, A.; Shevtsova, T.; Polevoy, D.; Chukalina, M.; Nikolaev, D.; Arlazarov, V. Reprojection-based numerical measure of robustness for CT reconstruction neural networks algorithms. Mathematics 2022, 10, 4210. [Google Scholar] [CrossRef]
- Karius, A.; Bert, C. QAMaster: A new software framework for phantom-based computed tomography quality assurance. J. Appl. Clin. Med. Phys. 2022, 23, e13588. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, M.; FitzGerald, P.; Araujo, S.; De Man, B. Development and tuning of models for accurate simulation of CT spatial resolution using CatSim. Phys. Med. Biol. 2024, 69, 045014. [Google Scholar] [CrossRef]
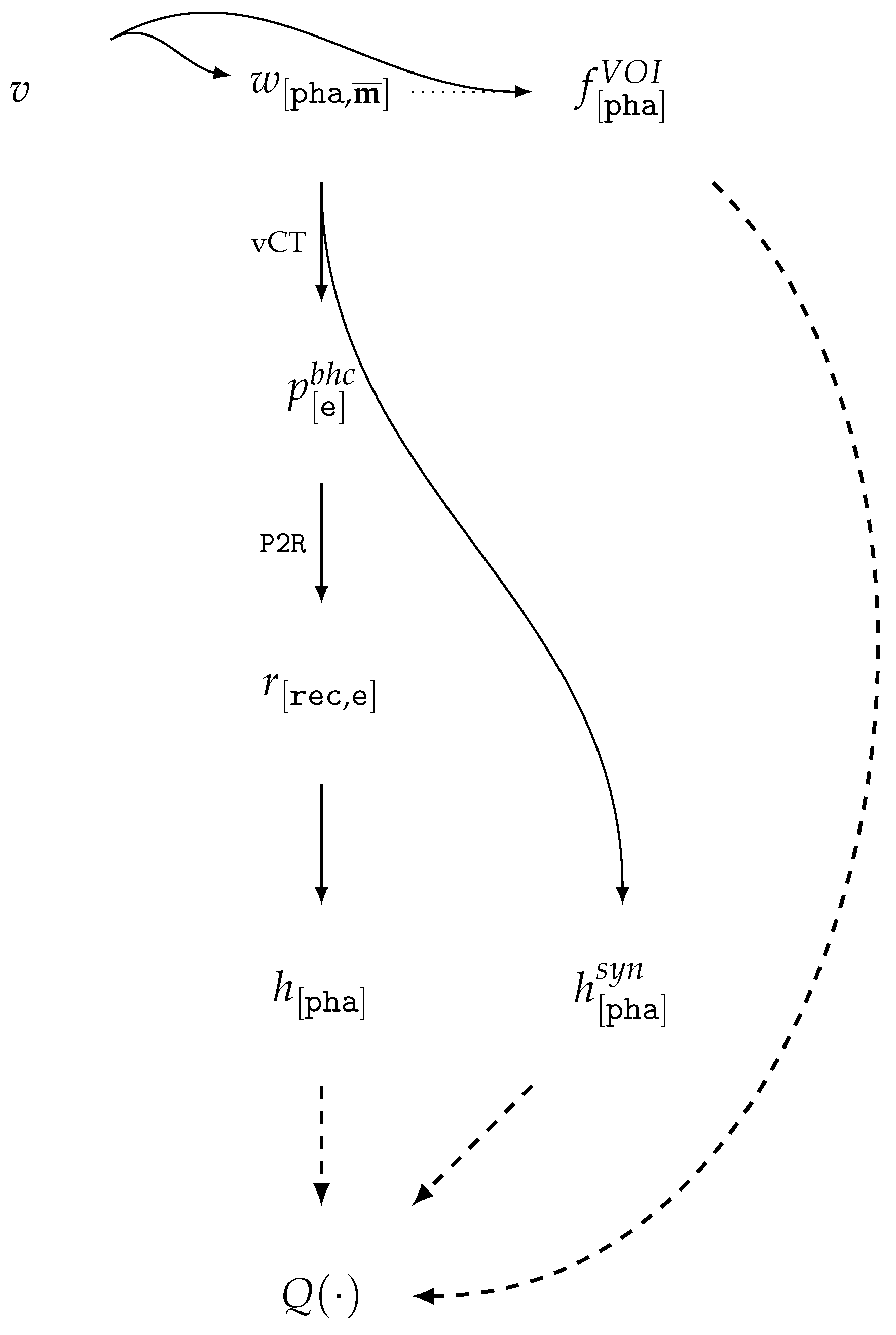
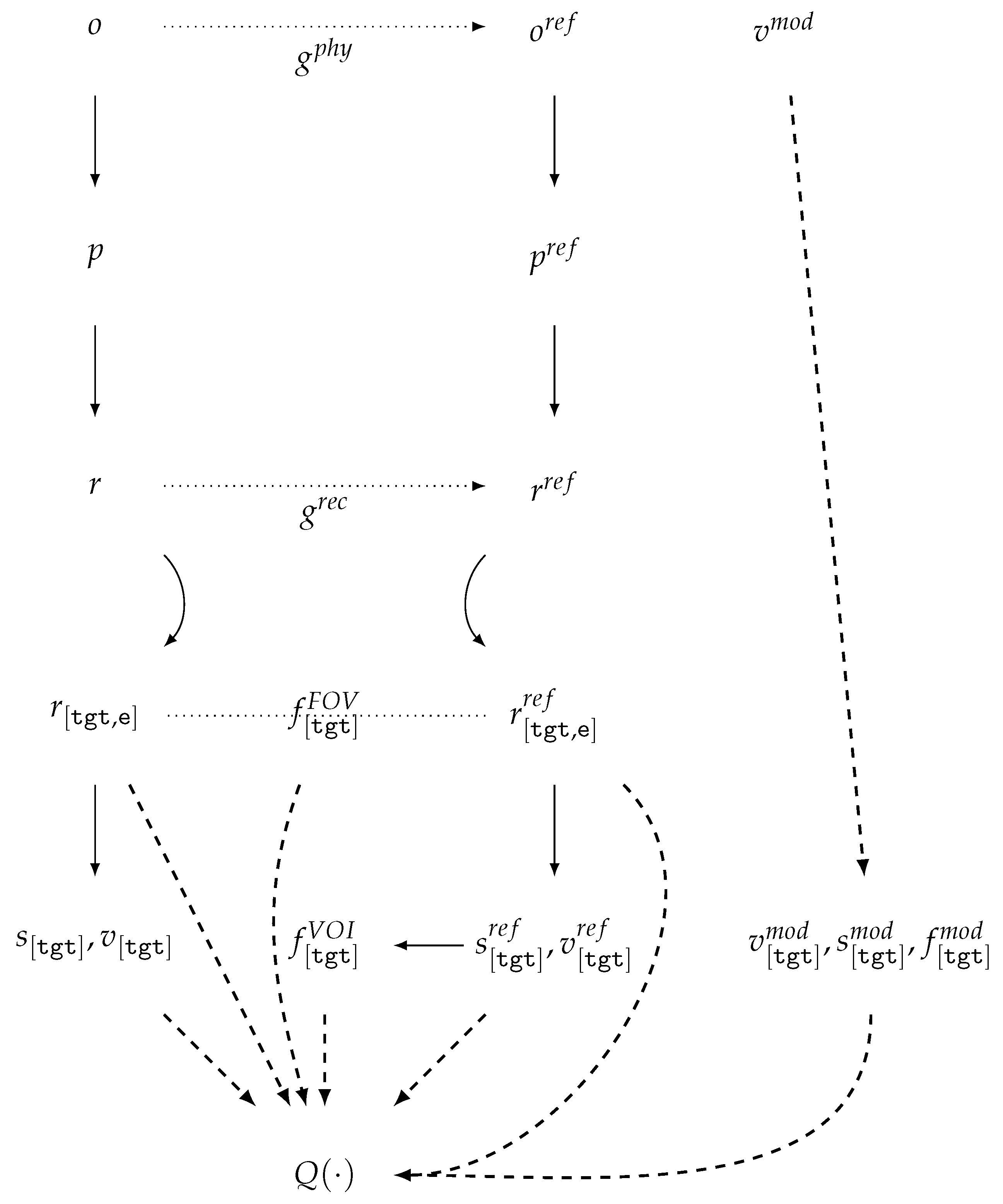
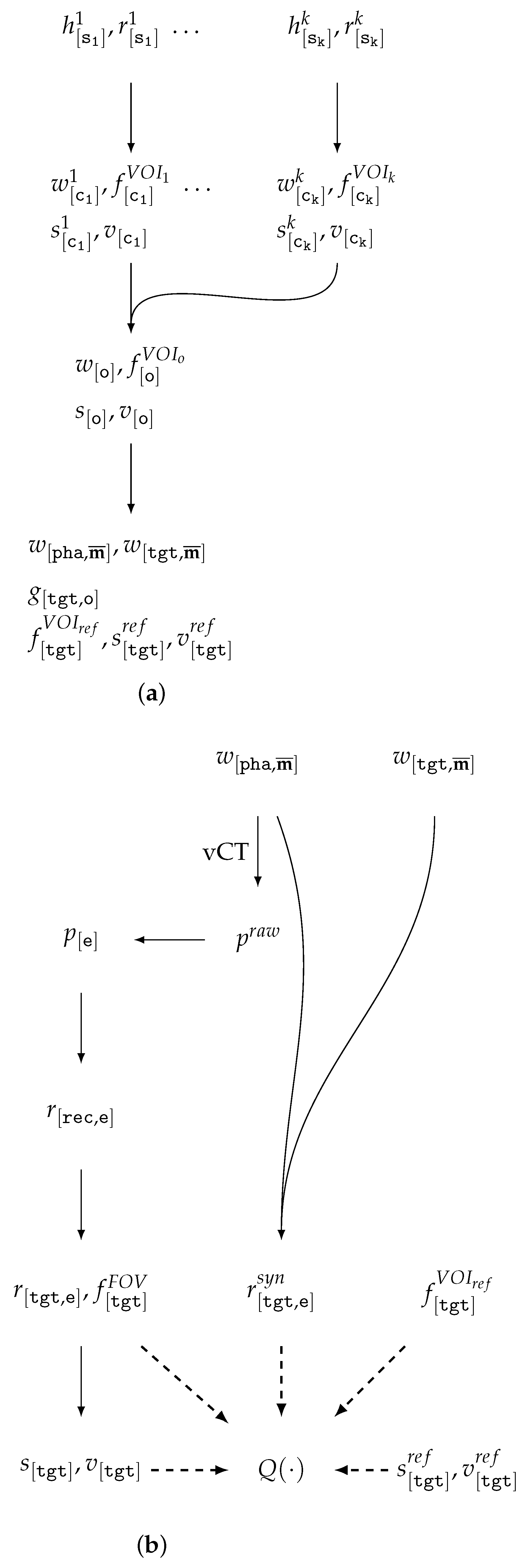
| Id | Type | Description |
|---|---|---|
| L0 | non-repeatability | different runs give different results with the same experimental setup |
| L1 | repeatability | the same team can obtain consistent results using the same experimental setup |
| L2 | reproducibility | external researchers are able to validate the correctness of the original experiment’s findings by following the documented experimental setup |
| L3 | direct replicability | an independent team intentionally varies the implementation of the experiment—while keeping the hypothesis and experimental design consistent with the original study—to verify the results |
| L4 | conceptual replicability | an independent team tests the same hypothesis through a fundamentally new experimental approach |
| Dataset | Year | Data | CT Scheme | Detector | Target Data | Variation | Spectrum | BHC | GT |
|---|---|---|---|---|---|---|---|---|---|
| LoDoPaB-CT [59] | 2019 | [60] | parallel | line | slice | dose | mono | – | normal dose reconstruction |
| SynDeepLesion [61,62] | 202? 1 | [63] 2 | fan | line | slice | metal | poly | no [61] yes [64] | metal-free reconstruction |
| AAPM TrueCT [65] | 2022 | ask 3 | helical | curved | volume | dose | poly | yes | effective energy phantom equivalent |
| AAPM CT-MAR [66] | 2023 | [67] 4 | fan (cone) | line (curved) | slice | metal | poly | yes | metal-free reconstruction |
| ICASSP CBCT [68] | 2024 | [69] | cone | flat | volume | dose | mono | – | normal dose reconstruction |
| Id | Transition | Level | Description |
|---|---|---|---|
| det | windowing | ||
| det|rnd | dequantifying tissue density from HU to LAC | ||
| var | reconstruction | ||
| det | quantifying tissue density in HU units | ||
| var | reconstruction segmentation | ||
| var | reconstruction vectorization | ||
| var | material separation | ||
| var | vectorization of a segmentation mask | ||
| det | material mapping | ||
| rnd | vCT projection of a vector phantom | ||
| det | voxelization of a vector model into a segmentation mask | ||
| det | voxelization of a vector model into a material weight mask | ||
| var|rnd | vCT projection of a voxel phantom | ||
| det | material-based LAC synthesis | ||
| var | segmentation/binarization of material weights | ||
| var | correction of sinograms for BHC | ||
| var | correction of sinograms, including BHC, ring suppression, and others | ||
| rnd | noise contamination of sinograms (low photon counting) | ||
| det | deterministic sinogram subsampling (sparse, limited angle and any-time CT) | ||
| rnd | randomized sinogram subsampling (any-time CT) | ||
| var | denoising | ||
| var | volume-based data resampling betweem CSs and | ||
| det | binary FOV mask for reconstruction |
| Material | ||||||
|---|---|---|---|---|---|---|
| air | 0.000200 | 0.000154 | −1000.0 | −1000.0 | −998.9 | −998.9 |
| lung | 0.047451 | 0.036553 | −742.3 | −742.9 | −741.5 | −742.1 |
| water | 0.183566 | 0.141741 | 0.0 | 0.0 | 0.0 | 0.0 |
| pancreas | 0.189531 | 0.146516 | 32.5 | 33.7 | 32.5 | 33.7 |
| skull | 0.341355 | 0.222230 | 860.5 | 568.5 | 859.6 | 567.9 |
| aluminum | 0.544019 | 0.343439 | 1965.8 | 1424.6 | 1963.6 | 1423.0 |
| titanium | 1.835591 | 0.640721 | 9009.5 | 3524.2 | 8999.6 | 3520.4 |
| Class Id | r | s v | Examples | Description | ||
|---|---|---|---|---|---|---|
| + | + | + | 1 | task-specific with image reference | ||
| + | + | task-specific without image reference | ||||
| + | + | 2 3 | task-specific downstream application | |||
| + | + | generic with image reference (FR-IQA) | ||||
| + | 4, CT-NR-IQA 5 | no reference (NR-IQA) |
| n | GT | Description |
|---|---|---|
| 1 | classification | |
| 2 | s | segmentation (including semantic segmentation such as material decomposition, as well as instance and panoptic segmentation) |
| 3 | v | vectorization |
| 4 | v | object detection |
| 5 | direct estimation of volume characteristics (without explicit use of items 1–4) | |
| 6 | prediction (e.g., survival prediction in medicine) | |
| 7 | r | image harmonization and normalization (i.e., rescaling to a standard spatial resolution and intensity range, including super-resolution techniques) |
| 8 | registration | |
| 8.1 | CT image registration | |
| 8.2 | limited-overlap region registration (image stitching) | |
| 8.3 | multi-modal (tomographic) image registration | |
| 8.4 | multi-scale (tomographic) image registration | |
| 8.5 | vector-model to tomographic image registration |
| n | Level | xCT Section 5.6 | vCT Section 5.9 | Description |
|---|---|---|---|---|
| 1 | L1 | + | + | deterministic implementation (CPU vs GPU, libraries, etc.) |
| 2 | L1 | + | + | specified sinogram subsampling |
| 3 | L1 | + | fixed random seed in the simulation of stochastic processes | |
| 4 | L2 | + | + | dataset includes data (sinograms + GT) of the calibration and validation objects |
| 5 | L2 | + | + | dataset includes masks |
| 6 | L2 | + | + | dataset includes masks |
| 7 | L2 | + | + | dataset includes raw sinograms (raw scan data) as input into the sinogram preprocessing stage |
| 8 | L2 | + | + | dataset includes intermediate sinograms obtained during the sinogram preprocessing stage |
| 9 | L2 | + | + | dataset includes reconstruction-ready sinograms as output of the sinogram preprocessing stage |
| 10 | L2 | + | + | dataset includes volumes reconstructed using a baseline method (specified method with fixed parameters) |
| 11 | L2 | + | + | specified method with fixed parameters for dequantifying tissue density |
| 12 | L2 | + | + | specified method with fixed parameters for quantifying tissue density |
| 13 | L2 | + | + | specified method with fixed parameters for resampling |
| 14 | L2 | + | + | quality is assessed using functions with a specified implementation and fixed parameters (including the required normalization of reconstruction value ranges) |
| 15 | L2 | + | + | quality is assessed in the specified fixed CS |
| 16 | L2 | + | + | quality is assessed along with the computation of uncertainty measures for the obtained estimates |
| 17 | L2 | + | + | quality is assessed within the specified |
| 18 | L2 | + | + | specified method with fixed parameters for sinogram preprocessing , including BHC |
| 19 | L2 | + | dataset includes analytical GT for the reconstructions | |
| 20 | L2 | + | quality is assessed using analytical GT | |
| 21 | L2 | + | vCT specified method with fixed material decomposition parameters used to design phantoms | |
| 22 | L2 | + | vCT specified method with fixed parameters for noise modeling | |
| 23 | L2 | + | vCT specified method for simulating the polychromatic spectrum of the probing radiation with determined parameters (including filters) | |
| 24 | L2 | + | vCT specified method with fixed parameters for scattering modeling | |
| 25 | L2 | + | vCT specified method with fixed parameters for X-ray absorption modeling (with material-specific reference LAC values also provided) | |
| 26 | L2 | + | vCT specified method with fixed parameters for modeling projection registration | |
| 27 | L3 | + | + | dataset includes composite objects with varying configurations |
| 28 | L3 | + | + | dataset includes objects in multiple geometric positions, together with information on these positions (intended for registration) |
| 29 | L3 | + | + | dataset includes objects scanned under different acquisition protocols |
| 30 | L3 | + | + | dataset includes objects equipped with reference features (intended for registration tasks) |
| 31 | L3 | + | + | dataset includes digital models of objects (digital twins), either segmentation-based and/or vector-based |
| 32 | L3 | + | + | quality is assessed using various task-specific ranking methods |
| 33 | L3 | + | + | quality assessment functions’ sensitivity to the selected reference reconstruction method, is examined |
| 34 | L3 | + | published pipeline for benchmark data generation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polevoy, D.; Kazimirov, D.; Gilmanov, M.; Nikolaev, D. No Reproducibility, No Progress: Rethinking CT Benchmarking. J. Imaging 2025, 11, 344. https://doi.org/10.3390/jimaging11100344
Polevoy D, Kazimirov D, Gilmanov M, Nikolaev D. No Reproducibility, No Progress: Rethinking CT Benchmarking. Journal of Imaging. 2025; 11(10):344. https://doi.org/10.3390/jimaging11100344
Chicago/Turabian StylePolevoy, Dmitry, Danil Kazimirov, Marat Gilmanov, and Dmitry Nikolaev. 2025. "No Reproducibility, No Progress: Rethinking CT Benchmarking" Journal of Imaging 11, no. 10: 344. https://doi.org/10.3390/jimaging11100344
APA StylePolevoy, D., Kazimirov, D., Gilmanov, M., & Nikolaev, D. (2025). No Reproducibility, No Progress: Rethinking CT Benchmarking. Journal of Imaging, 11(10), 344. https://doi.org/10.3390/jimaging11100344







