Fast Linde–Buzo–Gray (FLBG) Algorithm for Image Compression through Rescaling Using Bilinear Interpolation
Abstract
1. Introduction
2. Recent Algorithms for Codebook Generation
2.1. Vector Quantization Using LBG
| Algorithm 1: LBG Algorithm |
Rk→CB Initialize X = (, …) as initial training vectors. The Euclidean Distance (D) among the two vector is . Step 1: Initial codebook , which is generated randomly. Step 2: Initialize i = 0. Step 3: Execute the given steps for each training vector. Calculate the distances among the codewords in CBi and training vector as D(X; C) = (xt − ct). Find the closest codeword in CBi. Step 4: Divide the codebook in clusters of N number of blocks. Step 5: Calculate the centroid of each block for obtaining the new codebook CBi + 1. Step 6: Calculate the average distortion of CBi + 1. If no improvement in last iteration, the codebook is finalized and execution stops. Otherwise, i = i + 1, and go to Step 3. |
2.2. Particle Swarm Optimization Vector Quantization Algorithm
| Algorithm 2: PSO-LBG Algorithm |
Step 1: Implement the LBG algorithm to discover the codebook and designate as the global best (gbest) codebook. Step 2: Randomly generate additional codebooks. Step 3: Compute the fitness values for each codebook.
Step 4: Upon observing an enhancement in the fitness of the codebook compared to the previous fitness (pbest), assign the new fitness value as pbest. Step 5: Identify the codebook with the highest fitness value; if the fitness surpasses that of gbest, update gbest with the new value. Step 6: Update velocities and elements to transition to a new position.
The variable K denotes the total number of solutions, where “i” denotes the position of a particle, and and represent random numbers, while and signify the rates of social and cognitive influences, respectively. Step 7: Until max iteration or stopping criteria are met, repeat Steps 3–7. |
2.3. Quantum-Inspired Particle Swarm Optimization Vector Quantization Algorithm
2.4. Firefly Vector Quantization Algorithm
| Algorithm 3: QPSO-LBG Algorithm |
Step 1: Initialization of the LBG algorithm involves assigning the global best codebook (gbest) and initializing the remaining codebooks and velocities randomly. Step 2: The fitness of each codebook is computed. Step 3: If the newly computed fitness surpasses the previous best fitness (pbest), the new fitness value replaces pbest. Step 4: The largest fitness value among all particles is taken, and, if an improvement is detected in gbest, it is updated with the new value. Step 5: Random values, , , and u are chosen within the range of 0 to 1, and the local point Pi is calculated using Equations (8) and (9). Step 6: The elements of the codebook Xi are updated according to Equations (11)–(13).
In this context, the constant ‘z’ is maintained such that it satisfies the condition z < , where ‘t’ represents the iterations. Step 7: Steps (3) to (7) are iterated until reaching the maximum allowable number of iterations. |
| Algorithm 4: FA-LBG Algorithm |
Step 1: Implement the LBG algorithm and designate its output as the brighter firefly (codebook). Step 2: Initialize the parameters alpha (), beta (), and gamma coefficients (). Step 3: Randomly initialize codebooks; select maximum iteration count j. Step 4: Start count . Step 5: Evaluate the fitness of all codebooks using Equation (6). Choose a codebook randomly based on its fitness value and commence moving codebooks toward the brighter fireflies using Equations (14)–(17).
Step 6: If brighter fireflies cannot be located, begin moving randomly within the search space in pursuit of brighter ones using
Step 7: If (m = j), execution stops. Step 8: Increment m = m + 1. Step 9: Jump to step 5. |
2.5. BA Vector Quantization Algorithm
| Algorithm 5: BA-LBG Algorithm |
Step 1: Begin by allocating N codebooks, represented as bats, and defining parameters ‘A’ as (loudness), ‘V’ as (velocity), ‘R’ as (pulse rate), ‘Qmin’ as (minimum frequency), and ‘Qmax’ as (maximum frequency). Step 2: Implement the LBG algorithm to establish the initial codebook. Randomly select the remaining codebooks, denoted as (where i = 1, 2, 3,...N− 1). Step 3: Set the iteration counter m to 1 and define the maximum count as j. Step 4: Evaluate all codebooks’ fitness values using Equation (6). Identify as the best-performing codebook. Step 5: Update the positions of the codebooks by adjusting their frequency and velocity according to Equations (18) through (20).
Step 6: Select the size of the step between 0 and 1 for the random walk (W). Step 7: If the step size exceeds the pulse rate (R), the codebook is shifted using Equation (21).
Step 8: Produce a randomized value, and, if its magnitude is below the threshold of loudness, incorporate it into the codebook. Step 9: Perform sorting the codebooks with respect to fitness value . Step 10: If the condition (m = j) is satisfied, the execution halts. Otherwise, the value of m is incremented by 1. |
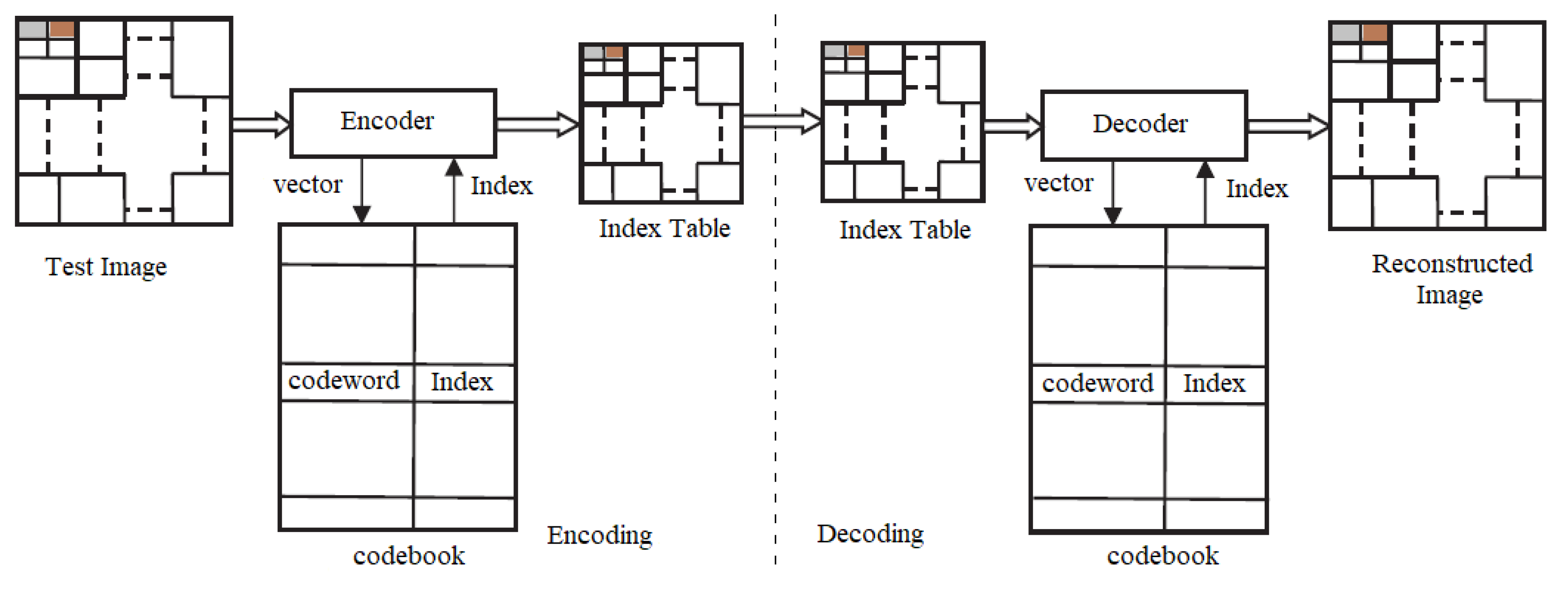
3. Proposed Fast-LBG Algorithm
Bilinear Interpolation for Codebook Rescaling
| Algorithm 6: Proposed FLBG Algorithm |
Step 1: Resize the image using bilinear interpolation using Equations (25) and (26). Step 2: Find the Euclidean Distance “D” between the two vectors as D(x,y). Step 3: Initial codebook , which is generated randomly. Step 4: i = 0. Step 5: Execute the given steps for each training vector. Calculate the distances among the codewords in CBi and the training vector as D(X; C) = (xt − ct). Find the closest codeword in CBi. Step 6: Divide the codebook into clusters of N number of blocks. Step 7: Calculate the centroid of each block for obtaining the new codebook CBi + 1. Step 8: Calculate the average distortion of CBi + 1. If no improvement in last iteration, the codebook is finalized and execution stops, or else i = i + 1, and go to Step 4. |
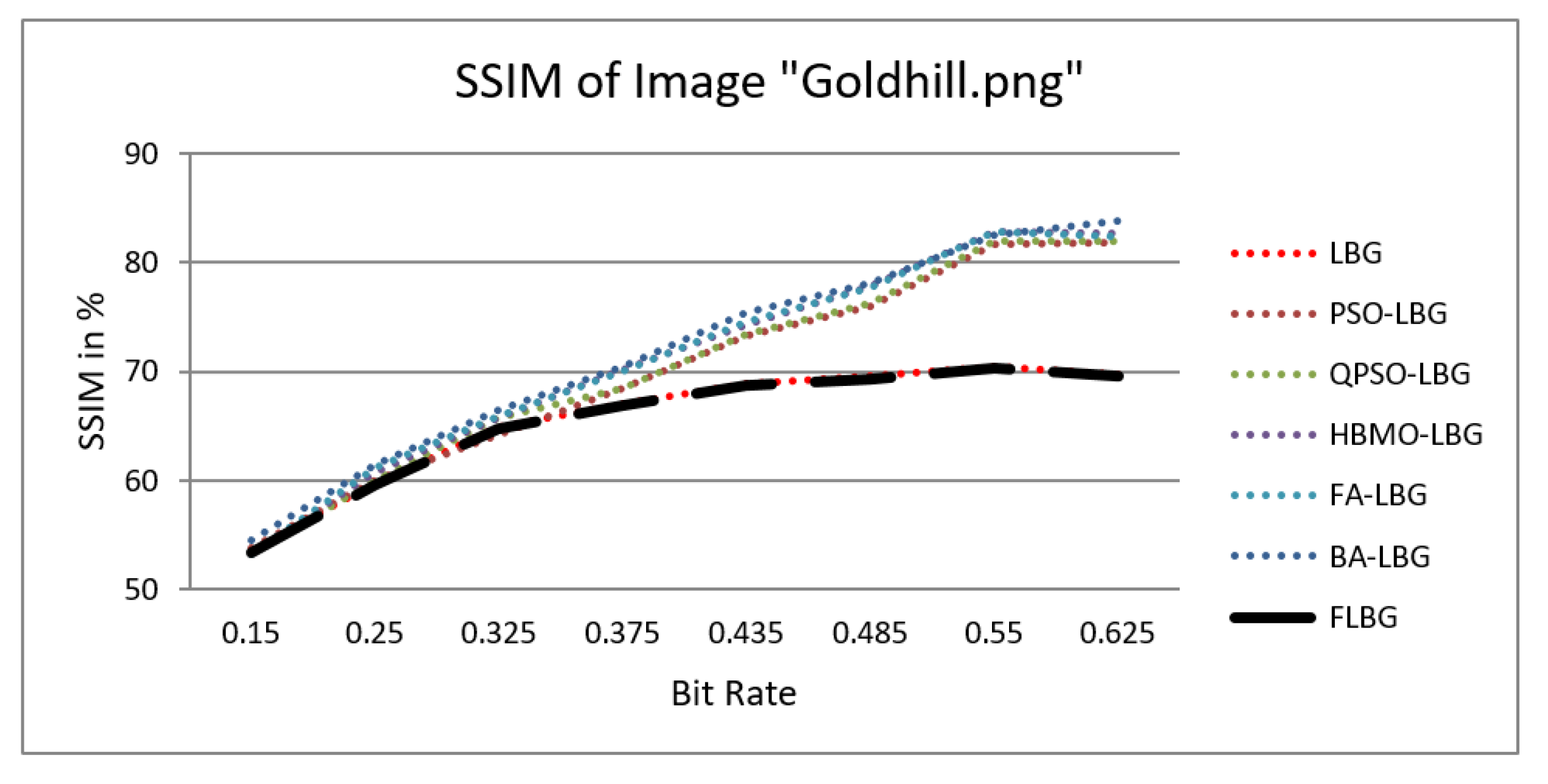
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bilal, M.; Ullah, Z.; Islam, I.U. Fast codebook generation using pattern based masking algorithm for image compression. IEEE Access 2021, 9, 98904–98915. [Google Scholar] [CrossRef]
- Wang, M.; Xie, W.; Zhang, J.; Qin, J. Industrial Applications of Ultrahigh Definition Video Coding With an Optimized Supersample Adaptive Offset Framework. IEEE Trans. Ind. Inform. 2020, 16, 7613–7623. [Google Scholar] [CrossRef]
- Chen, Z.; Bodenheimer, B.; Barnes, J.F. Robust transmission of 3D geometry over lossy networks. In Proceedings of the Eighth International Conference on 3D Web Technology, Saint Malo, France, 9–12 March 2003; p. 161-ff. [Google Scholar]
- Garcia, N.; Munoz, C.; Sanz, A. Image compression based on hierarchical encoding. Image Coding 1986, 594, 150–157. [Google Scholar]
- Huffman, D.A. A method for the construction of minimum-redundancy codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Wallace, G.K. The JPEG still picture compression standard. Commun. ACM 1991, 34, 30–44. [Google Scholar] [CrossRef]
- Howard, P.G.; Vitter, J.S. New methods for lossless image compression using arithmetic coding. Inf. Process. Manag. 1992, 28, 765–779. [Google Scholar] [CrossRef]
- Khalaf, W.; Mohammad, A.S.; Zaghar, D. Chimera: A New Efficient Transform for High Quality Lossy Image Compression. Symmetry 2020, 12, 378. [Google Scholar] [CrossRef]
- Nam, J.H.; Sim, D. Lossless video coding based on pixel-wise prediction. Multimed. Syst. 2008, 14, 291–298. [Google Scholar] [CrossRef]
- Rahman, M.A.; Hamada, M. Lossless image compression techniques: A state-of-the-art survey. Symmetry 2019, 11, 1274. [Google Scholar] [CrossRef]
- Magli, E.; Olmo, G. Lossy predictive coding of SAR raw data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 977–987. [Google Scholar] [CrossRef]
- Wohlberg, B.; De Jager, G. A review of the fractal image coding literature. IEEE Trans. Image Process. 1999, 8, 1716–1729. [Google Scholar] [CrossRef]
- Abbas, H.; Fahmy, M. Neural model for Karhunen-Loeve transform with application to adaptive image compression. IEE Proc. I (Commun. Speech Vis.) 1993, 140, 135–143. [Google Scholar]
- Otto, J.K. Image Reconstruction for Discrete Cosine Transform Compression Schemes; Oklahoma State University: Stillwater, OK, USA, 1993. [Google Scholar]
- Kajiwara, K. JPEG compression for PACS. Comput. Methods Programs Biomed. 1992, 37, 343–351. [Google Scholar] [CrossRef] [PubMed]
- Oehler, K.L.; Gray, R.M. Combining image compression and classification using vector quantization. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 461–473. [Google Scholar] [CrossRef]
- Mitra, S.K.; Murthy, C.; Kundu, M.K. Technique for fractal image compression using genetic algorithm. IEEE Trans. Image Process. 1998, 7, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Shivashetty, V.; Rajput, G. Adaptive Lifting Based Image Compression Scheme Using Interactive Artificial Bee Colony Algorithm. Csity Sigpro Dtmn 2015, 9–21. [Google Scholar] [CrossRef]
- Gray, R. Vector quantization. IEEE Assp Mag. 1984, 1, 4–29. [Google Scholar] [CrossRef]
- Nag, S. Vector quantization using the improved differential evolution algorithm for image compression. Genet. Program. Evol. Mach. 2019, 20, 187–212. [Google Scholar] [CrossRef]
- Linde, Y.; Buzo, A.; Gray, R. An Algorithm for Vector Quantizer Design. IEEE Trans. Commun. 1980, 28, 84–95. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, X.Y.; Huang, Y.X.; Pu, D.B.; Zhou, W.G.; Liang, Y.C.; Zhou, C.G. A novel quantum swarm evolutionary algorithm and its applications. Neurocomputing 2007, 70, 633–640. [Google Scholar] [CrossRef]
- Horng, M.H. Vector quantization using the firefly algorithm for image compression. Expert Syst. Appl. 2012, 39, 1078–1091. [Google Scholar] [CrossRef]
- Karri, C.; Jena, U. Fast vector quantization using a Bat algorithm for image compression. Eng. Sci. Technol. Int. J. 2016, 19, 769–781. [Google Scholar] [CrossRef]
- Rini, D.P.; Shamsuddin, S.M.; Yuhaniz, S.S. Particle swarm optimization: Technique, system and challenges. Int. J. Comput. Appl. 2011, 14, 19–26. [Google Scholar] [CrossRef]
- Sekhar, G.C.; Sahu, R.K.; Baliarsingh, A.; Panda, S. Load frequency control of power system under deregulated environment using optimal firefly algorithm. Int. J. Electr. Power Energy Syst. 2016, 74, 195–211. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]



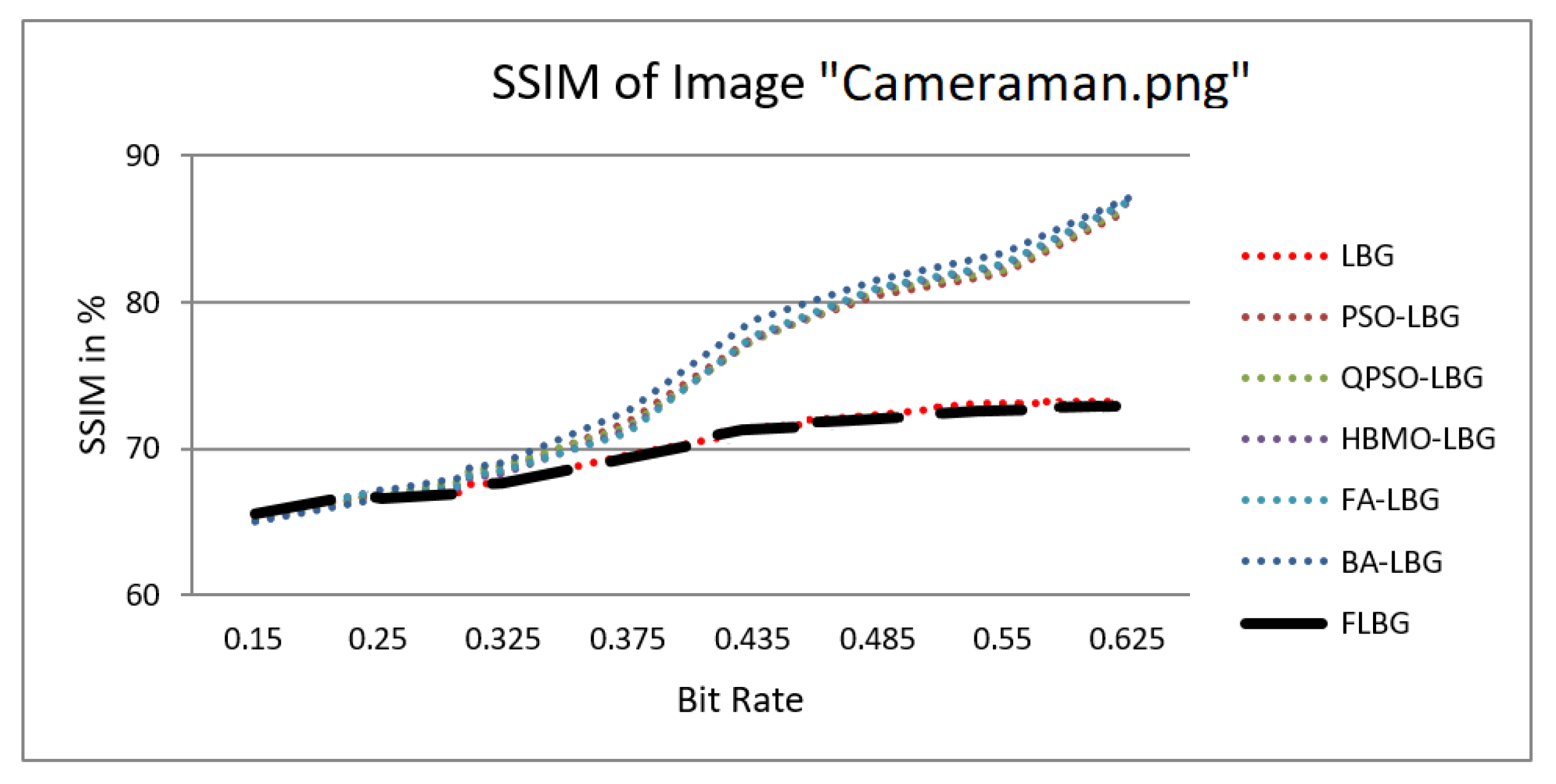
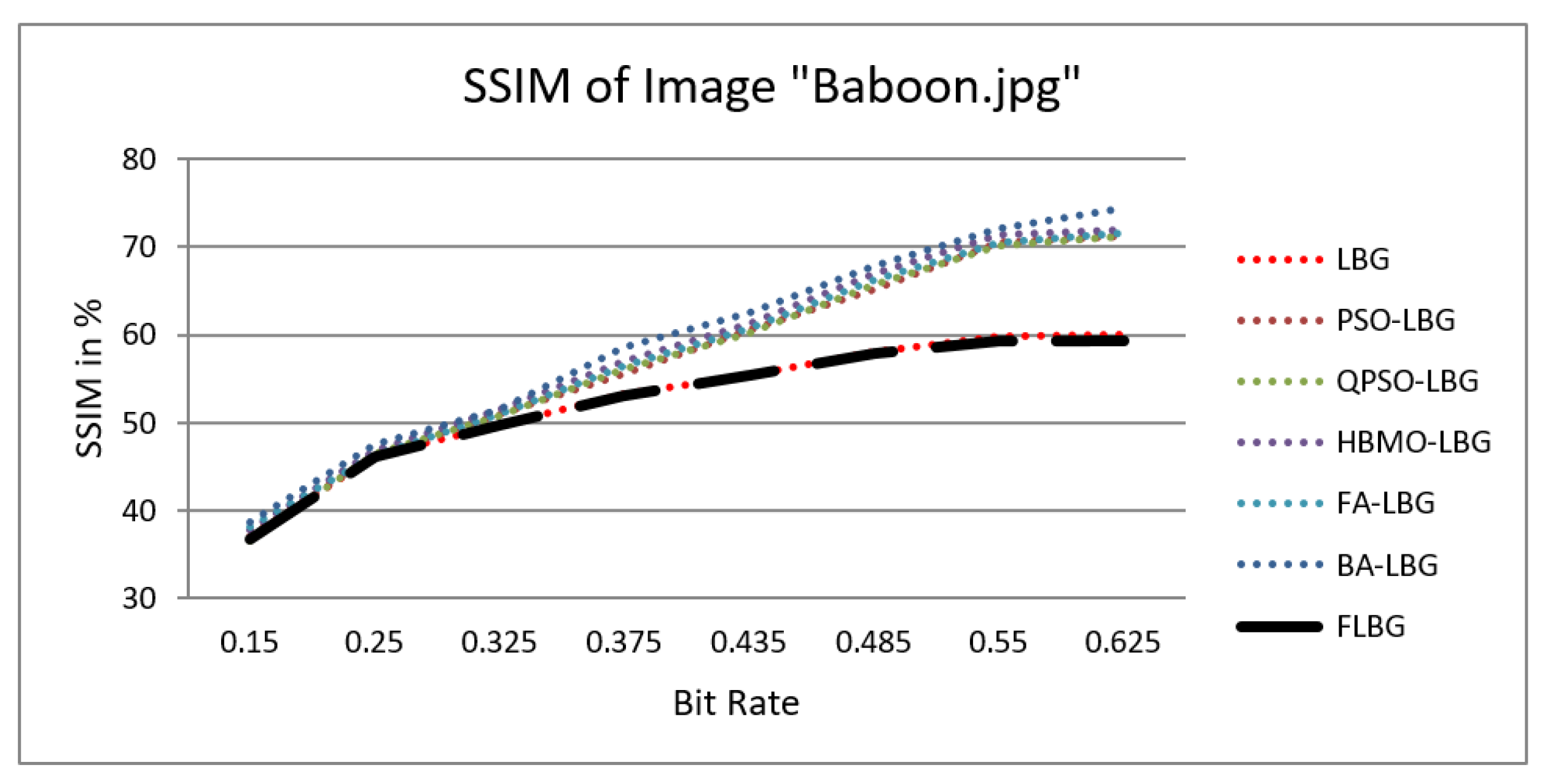

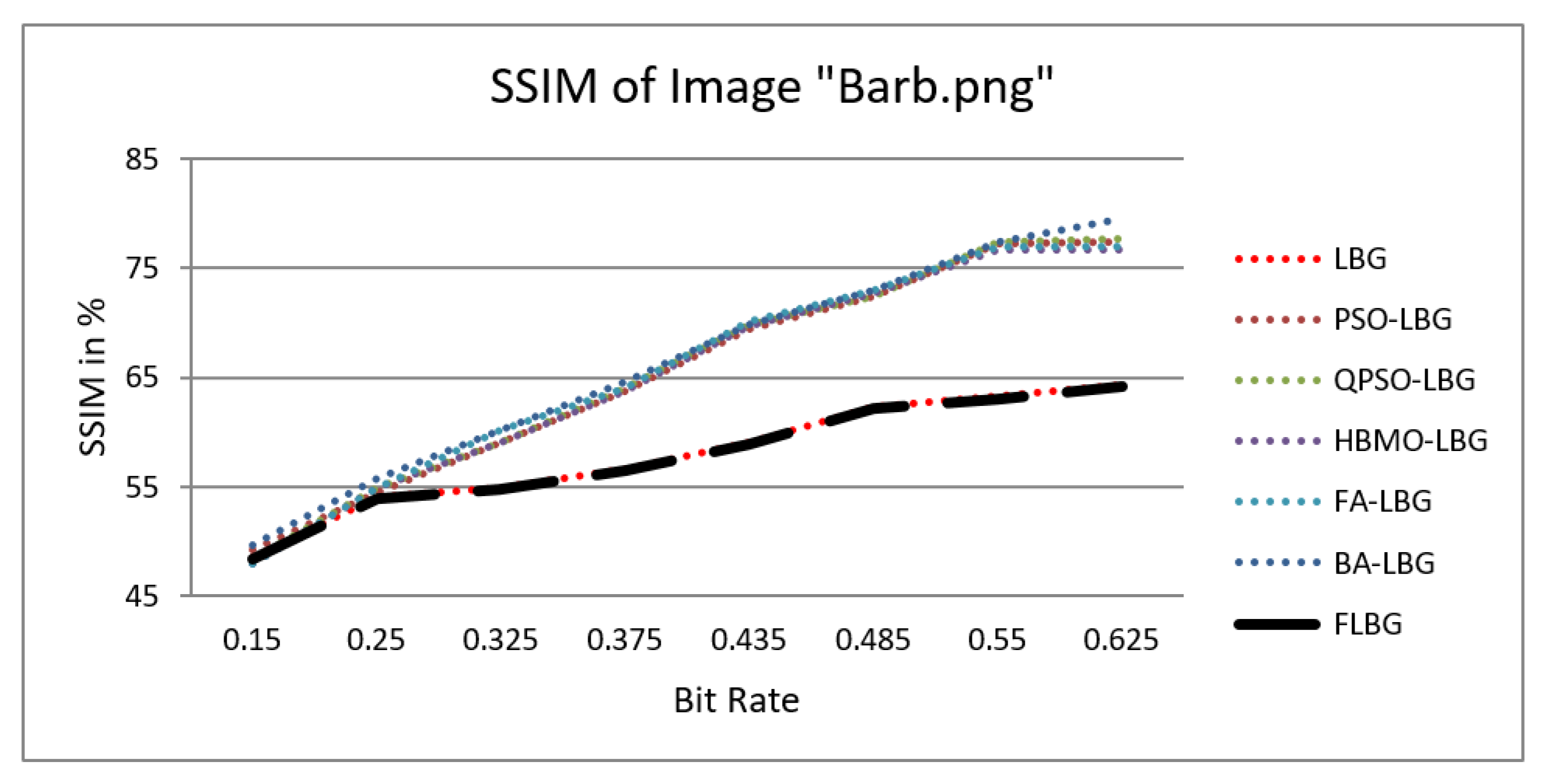



| Bpp | PSNR in Decibels | ||||||
|---|---|---|---|---|---|---|---|
| LBG | PSO | QPSO | HBMO | FA | BA | FLBG | |
| 0.15 | 25.2 | 25.4 | 25.2 | 25.4 | 25.3 | 25.5 | 25.3 |
| 0.25 | 26.4 | 26.3 | 26.4 | 26.5 | 26.4 | 26.5 | 26.3 |
| 0.325 | 26.4 | 26.5 | 26.5 | 26.6 | 26.4 | 26.5 | 26.4 |
| 0.375 | 26.2 | 26.7 | 27.2 | 26.9 | 26.8 | 27.35 | 26.2 |
| 0.435 | 26.3 | 28.6 | 28.6 | 28.5 | 28.7 | 29.2 | 26.5 |
| 0.485 | 26.5 | 29.8 | 29.4 | 29.5 | 29.7 | 29.9 | 26.6 |
| 0.55 | 26.7 | 30.2 | 30.2 | 30.2 | 30.1 | 30.5 | 26.8 |
| 0.625 | 26.7 | 31.4 | 31.5 | 31.6 | 31.6 | 31.8 | 26.8 |
| Bpp | PSNR in Decibels | ||||||
|---|---|---|---|---|---|---|---|
| LBG | PSO | QPSO | HBMO | FA | BA | FLBG | |
| 0.15 | 18.2 | 18.3 | 18.1 | 18.7 | 19.1 | 19.1 | 18.1 |
| 0.25 | 19.6 | 19.6 | 19.7 | 19.8 | 19.6 | 20.1 | 19.3 |
| 0.325 | 19.5 | 20.2 | 20.2 | 20.1 | 20.2 | 20.2 | 19.4 |
| 0.375 | 19.6 | 20.5 | 20.7 | 21.2 | 20.8 | 21.6 | 19.2 |
| 0.435 | 19.7 | 21.5 | 21.4 | 21.8 | 21.6 | 22.2 | 19.1 |
| 0.485 | 19.7 | 22.1 | 22.3 | 22.7 | 22.5 | 23 | 19.3 |
| 0.55 | 19.6 | 23.1 | 23.2 | 23.4 | 23.1 | 23.6 | 19.4 |
| 0.625 | 19.7 | 23.4 | 23.4 | 23.6 | 23.5 | 24.4 | 19.4 |
| Bpp | PSNR in Decibels | ||||||
|---|---|---|---|---|---|---|---|
| LBG | PSO | QPSO | HBMO | FA | BA | FLBG | |
| 0.15 | 24.2 | 24.3 | 24.4 | 24.4 | 24.4 | 24.6 | 24.1 |
| 0.25 | 25.1 | 25.3 | 25.4 | 25.2 | 25.2 | 25.5 | 24.8 |
| 0.325 | 25.2 | 26.2 | 26.4 | 26.3 | 26.1 | 26.3 | 25.1 |
| 0.375 | 25.2 | 27.1 | 27.2 | 27.4 | 27.6 | 28.4 | 25.1 |
| 0.435 | 25.2 | 29.1 | 29.4 | 29.4 | 29.6 | 30.2 | 24.7 |
| 0.485 | 25.3 | 30.1 | 30.3 | 30.4 | 30.5 | 30.7 | 25.2 |
| 0.55 | 25.4 | 31.2 | 31.4 | 31.5 | 31.6 | 31.8 | 24.7 |
| 0.625 | 25.3 | 32.4 | 32.5 | 32.6 | 32.7 | 32.5 | 25.2 |
| Bpp | PSNR in Decibels | ||||||
|---|---|---|---|---|---|---|---|
| LBG | PSO | QPSO | HBMO | FA | BA | FLBG | |
| 0.15 | 23.7 | 24.2 | 23.6 | 23.4 | 23.4 | 24.2 | 23.2 |
| 0.25 | 23.7 | 24.1 | 24.1 | 24.1 | 24.1 | 24.5 | 23.2 |
| 0.325 | 24.1 | 25.7 | 25.7 | 25.7 | 26.2 | 26.2 | 23.7 |
| 0.375 | 24.1 | 27.1 | 27.2 | 27.1 | 27.2 | 27.5 | 24.2 |
| 0.435 | 24.1 | 28.1 | 28.3 | 28.2 | 28.4 | 28.3 | 23.8 |
| 0.485 | 24.7 | 28.7 | 28.7 | 28.8 | 29.1 | 29.1 | 24.5 |
| 0.55 | 24.5 | 30.1 | 30.2 | 29.7 | 29.8 | 30.2 | 24.1 |
| 0.625 | 25.1 | 30.2 | 30.1 | 29.7 | 29.8 | 30.8 | 24.8 |
| Bpp | PSNR in Decibels | ||||||
|---|---|---|---|---|---|---|---|
| LBG | PSO | QPSO | HBMO | FA | BA | FLBG | |
| 0.15 | 24.4 | 24.5 | 24.2 | 24.2 | 24.2 | 24.8 | 23.6 |
| 0.25 | 25.1 | 25.2 | 25.2 | 25.5 | 25.7 | 25.8 | 24.7 |
| 0.325 | 25.5 | 25.2 | 25.8 | 25.8 | 26.1 | 26.1 | 25.1 |
| 0.375 | 25.6 | 26.1 | 26.1 | 26.8 | 26.7 | 27.1 | 25.1 |
| 0.435 | 25.6 | 27.2 | 27.3 | 27.6 | 27.7 | 28.2 | 25.2 |
| 0.485 | 25.6 | 28.2 | 28.1 | 28.7 | 28.6 | 28.8 | 24.8 |
| 0.55 | 25.6 | 29.7 | 29.8 | 30.1 | 30.1 | 30.2 | 24.7 |
| 0.625 | 25.6 | 30.1 | 30.1 | 30.4 | 30.3 | 30.8 | 24.8 |
| Size of Codebook: 16 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Image | Average Time Taken for Computation (seconds) at Bitrate = 0.25 | |||||||
| LBG | PSO-LBG | QPSO-LBG | HBMO-LBG | FA-LBG | BA-LBG | CS-LBG | FLBG | |
| CAMERAMAN | 8.13 | 591.11 | 618.56 | 1232.22 | 1173.37 | 599.61 | 2521.45 | 3.12 |
| PEPPER | 8.92 | 487.57 | 493.45 | 1105.28 | 1040.34 | 630.44 | 3326.92 | 3.33 |
| BABOON | 9.44 | 669.84 | 695.21 | 1983.12 | 1964.46 | 698.98 | 3031.06 | 4.13 |
| GOLDHILL | 9.64 | 625.37 | 740.91 | 1158.50 | 1130.75 | 513.28 | 2480.95 | 4.66 |
| BARB | 9.21 | 555.67 | 656.91 | 1567.51 | 1549.53 | 690.42 | 2811.53 | 4.87 |
| Average | 9.07 | 585.91 | 641.01 | 1409.33 | 1371.69 | 626.55 | 2834.38 | 4.02 |
| Percentage Improvement | 55.65 | 99.31 | 99.37 | 99.71 | 99.71 | 99.36 | 99.86 | |
| Size of Codebook: 32 | ||||||||
| Image | Average Time Taken for Computation (seconds) at Bitrate = 0.3125 | |||||||
| LBG | PSO-LBG | QPSO-LBG | HBMO-LBG | FA-LBG | BA-LBG | CS-LBG | FLBG | |
| CAMERAMAN | 9.16 | 521.32 | 554.42 | 1291.34 | 1298.46 | 593.81 | 2209.83 | 4.12 |
| PEPPER | 9.82 | 532.17 | 428.92 | 898.76 | 934.76 | 546.91 | 1713.63 | 4.59 |
| BABOON | 8.88 | 468.12 | 497.96 | 1249.01 | 1243.71 | 549.34 | 2715.31 | 3.93 |
| GOLDHILL | 7.72 | 476.64 | 538.46 | 1340.21 | 1299.82 | 480.45 | 2625.02 | 3.06 |
| BARB | 10.03 | 423.93 | 474.92 | 1349.01 | 1320.15 | 422.78 | 2025.72 | 5.23 |
| Average | 9.12 | 484.44 | 498.94 | 1225.67 | 1219.38 | 518.66 | 2257.90 | 4.19 |
| Percentage Improvement | 54.11 | 99.14 | 99.16 | 99.66 | 99.66 | 99.19 | 99.81 | |
| Size of Codebook: 64 | ||||||||
| Image | Average Time Taken for Computation (seconds) at Bitrate = 0.3750 | |||||||
| LBG | PSO-LBG | QPSO-LBG | HBMO-LBG | FA-LBG | BA-LBG | CS-LBG | FLBG | |
| CAMERAMAN | 11.31 | 665.23 | 685.12 | 1563.76 | 1491.62 | 671.45 | 2982.76 | 5.41 |
| PEPPER | 11.31 | 597.42 | 599.24 | 1247.54 | 1278.45 | 636.77 | 4468.23 | 5.63 |
| BABOON | 12.25 | 573.61 | 590.12 | 1412.32 | 1437.11 | 740.02 | 3984.18 | 6.12 |
| GOLDHILL | 14.31 | 622.21 | 637.74 | 1577.14 | 1181.33 | 498.56 | 4305.03 | 7.11 |
| BARB | 16.73 | 460.21 | 466.24 | 1306.21 | 854.17 | 398.74 | 2721.12 | 8.32 |
| Average | 13.18 | 583.74 | 595.69 | 1421.39 | 1248.54 | 589.11 | 3692.26 | 6.52 |
| Percentage Improvement | 50.55 | 98.88 | 98.91 | 99.54 | 99.48 | 98.89 | 99.82 | |
| Size of Codebook: 128 | ||||||||
| Image | Average Time Taken for Computation (seconds) at Bitrate = 0.4375 | |||||||
| LBG | PSO-LBG | QPSO-LBG | HBMO-LBG | FA-LBG | BA-LBG | CS-LBG | FLBG | |
| CAMERAMAN | 16.28 | 645.34 | 657.54 | 1080.44 | 1054.19 | 628.82 | 1932.31 | 8.94 |
| PEPPER | 19.41 | 600.32 | 675.32 | 1132.68 | 1081.51 | 623.62 | 2220.82 | 10.71 |
| BABOON | 22.61 | 467.57 | 536.07 | 1112.14 | 1060.77 | 963.91 | 2785.66 | 11.11 |
| GOLDHILL | 18.21 | 835.27 | 860.38 | 1413.08 | 1343.73 | 502.21 | 1962.02 | 9.92 |
| BARB | 30.34 | 579.21 | 589.54 | 1291.81 | 1271.32 | 562.24 | 2438.01 | 12.12 |
| Average | 21.37 | 625.54 | 663.77 | 1206.03 | 1162.30 | 656.16 | 2267.76 | 10.56 |
| Percentage Improvement | 50.58 | 98.31 | 98.41 | 99.12 | 99.09 | 98.39 | 99.53 | |
| Size of Codebook: 256 | ||||||||
| Image | Average Time Taken for Computation (seconds) at Bitrate = 0.50 | |||||||
| LBG | PSO-LBG | QPSO-LBG | HBMO-LBG | FA-LBG | BA-LBG | CS-LBG | FLBG | |
| CAMERAMAN | 23.15 | 898.23 | 922.46 | 824.23 | 816.44 | 696.46 | 1627.23 | 13.24 |
| PEPPER | 18.33 | 760.12 | 760.12 | 1010.65 | 984.54 | 574.41 | 1750.66 | 13.98 |
| BABOON | 28.25 | 599.51 | 568.24 | 1019.86 | 1040.91 | 572.32 | 2039.75 | 14.13 |
| GOLDHILL | 29.92 | 931.61 | 560.64 | 850.06 | 834.32 | 981.93 | 2978.06 | 14.33 |
| BARB | 27.84 | 689.71 | 698.66 | 847.23 | 837.72 | 596.06 | 2598.43 | 13.82 |
| Average | 25.50 | 775.84 | 702.02 | 910.41 | 902.79 | 684.24 | 2198.83 | 13.90 |
| Percentage Improvement | 45.49 | 98.21 | 98.02 | 98.47 | 98.46 | 97.97 | 99.37 | |
| Size of Codebook: 512 | ||||||||
| Image | Average Time Taken for Computation (seconds) at Bitrate = 0.5625 | |||||||
| LBG | PSO-LBG | QPSO-LBG | HBMO-LBG | FA-LBG | BA-LBG | CS-LBG | FLBG | |
| CAMERAMAN | 36.84 | 731.32 | 758.23 | 1125.23 | 1078.35 | 849.45 | 1643.64 | 19.13 |
| PEPPER | 39.31 | 934.72 | 887.53 | 665.21 | 650.81 | 533.07 | 1371.76 | 19.12 |
| BABOON | 20.71 | 657.02 | 715.02 | 712.05 | 723.12 | 803.57 | 1158.42 | 16.32 |
| GOLDHILL | 35.14 | 582.97 | 601.74 | 955.58 | 960.07 | 885.02 | 1253.42 | 18.33 |
| BARB | 72.52 | 815.84 | 706.91 | 878.68 | 872.67 | 693.68 | 1805.61 | 36.23 |
| Average | 40.90 | 744.37 | 733.89 | 867.35 | 857.00 | 752.96 | 1446.57 | 21.83 |
| Percentage Improvement | 46.64 | 97.07 | 97.03 | 97.48 | 97.45 | 97.10 | 98.49 | |
| Size of Codebook: 1024 | ||||||||
| Image | Average Time Taken for Computation (seconds) at Bitrate = 0.625 | |||||||
| LBG | PSO-LBG | QPSO-LBG | HBMO-LBG | FA-LBG | BA-LBG | CS-LBG | FLBG | |
| CAMERAMAN | 66.74 | 1532.32 | 1572.27 | 1918.71 | 2013.43 | 1576.42 | 3679.84 | 35.46 |
| PEPPER | 63.44 | 1022.78 | 1156.53 | 1254.02 | 1231.37 | 855.74 | 2059.35 | 32.13 |
| BABOON | 66.55 | 1435.45 | 1439.54 | 1664.23 | 1636.13 | 1665.13 | 2396.33 | 34.13 |
| GOLDHILL | 94.67 | 1353.84 | 1369.65 | 1489.71 | 1483.25 | 775.30 | 2340.92 | 48.36 |
| BARB | 112.32 | 1515.02 | 1503.81 | 1199.27 | 1181.88 | 1133.72 | 2400.28 | 58.23 |
| Average | 80.74 | 1371.88 | 1408.36 | 1505.19 | 1509.21 | 1201.26 | 2575.34 | 41.66 |
| Percentage Improvement | 48.40 | 96.96 | 97.04 | 97.23 | 97.24 | 96.53 | 98.38 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilal, M.; Ullah, Z.; Mujahid, O.; Fouzder, T. Fast Linde–Buzo–Gray (FLBG) Algorithm for Image Compression through Rescaling Using Bilinear Interpolation. J. Imaging 2024, 10, 124. https://doi.org/10.3390/jimaging10050124
Bilal M, Ullah Z, Mujahid O, Fouzder T. Fast Linde–Buzo–Gray (FLBG) Algorithm for Image Compression through Rescaling Using Bilinear Interpolation. Journal of Imaging. 2024; 10(5):124. https://doi.org/10.3390/jimaging10050124
Chicago/Turabian StyleBilal, Muhammmad, Zahid Ullah, Omer Mujahid, and Tama Fouzder. 2024. "Fast Linde–Buzo–Gray (FLBG) Algorithm for Image Compression through Rescaling Using Bilinear Interpolation" Journal of Imaging 10, no. 5: 124. https://doi.org/10.3390/jimaging10050124
APA StyleBilal, M., Ullah, Z., Mujahid, O., & Fouzder, T. (2024). Fast Linde–Buzo–Gray (FLBG) Algorithm for Image Compression through Rescaling Using Bilinear Interpolation. Journal of Imaging, 10(5), 124. https://doi.org/10.3390/jimaging10050124






