Abstract
Testing an intricate plexus of advanced software system architecture is quite challenging due to the absence of test oracle. Metamorphic testing is a popular technique to alleviate the test oracle problem. The effectiveness of metamorphic testing is dependent on metamorphic relations (MRs). MRs represent the essential properties of the system under test and are evaluated by their fault detection rates. The existing techniques for the evaluation of MRs are not comprehensive, as very few mutation operators are used to generate very few mutants. In this research, we have proposed six new MRs for dilation and erosion operations. The fault detection rate of six newly proposed MRs is determined using mutation testing. We have used eight applicable mutation operators and determined their effectiveness. By using these applicable operators, we have ensured that all the possible numbers of mutants are generated, which shows that all the faults in the system under test are fully identified. Results of the evaluation of four MRs for edge detection show an improvement in all the respective MRs, especially in MR1 and MR4, with a fault detection rate of 76.54% and 69.13%, respectively, which is 32% and 24% higher than the existing technique. The fault detection rate of MR2 and MR3 is also improved by 1%. Similarly, results of dilation and erosion show that out of 8 MRs, the fault detection rates of four MRs are higher than the existing technique. In the proposed technique, MR1 is improved by 39%, MR4 is improved by 0.5%, MR6 is improved by 17%, and MR8 is improved by 29%. We have also compared the results of our proposed MRs with the existing MRs of dilation and erosion operations. Results show that the proposed MRs complement the existing MRs effectively as the new MRs can find those faults that are not identified by the existing MRs.
1. Introduction
In the domain of computer graphics, the importance of Image Processing Applications (IPAs) is growing fast in our daily lives [1]. IPAs utilize algorithms to analyze the characteristics of an image using various methods and techniques. Digital images can be rotated, scaled, translated, and sheared by using geometric transformation. Also, in binary and grayscale images, different morphological operations such as erosion, dilation, skeletonization, and opening and closing operations are used for filtering, thinning, and pruning of the images [2].
Nowadays, IPAs are widely used in safety and mission-critical systems such as medical radiology, biometric systems, surveillance systems, etc. [1]. In medical radiology, machine learning and deep learning approaches are frequently used for automated diagnostics for patients using medical images such as MRI, CT Scan, ultrasound, etc. This diagnostic process involves some pre-processing steps, such as edge detection, and post-processing steps, such as dilation and erosion operations. Any defects in these operations will materially affect the diagnostics results. Testing of the software used in these critical systems is vital to ascertain the credibility of the results produced by these systems. Software testing is a common method to test and verify the quality of IPA software [3]. In software testing, an oracle is a mechanism that ascertains whether the software has been successfully executed for a test case or not. The Software is run for a specific test case, and the result (actual output) is compared with the anticipated result (expected output). If the output differs from what was anticipated, the program is said to be faulty [4]. Testing of IPAs is especially challenging due to the test oracle problem. For example, in image processing, edge detection is an operation that is used to compute the edges of the image. If we want to check whether the edges computed by the edge detection operator are correct or not, then we do not have the reference image (expected output) for comparison. This is the well-known oracle problem where the expected results are not obvious.
Among many solutions to test the oracle problem, metamorphic testing (MT) is the most popular technique that tackles the oracle problem in software testing of IPAs [5]. MT was first proposed by Chen et al. in 1998 [6]. In MT, we need source test cases that manifest the unexpected behavior in the system under test (SUT) [7]. The source test cases are generated through traditional test case generation techniques such as random test case generation, coverage criterion, etc. From these source test cases, a set of new test cases known as follow-up test cases are constructed using metamorphic relations (MR) [8]. MT defines some MRs, which consist of an input relation and an output relation. If the output results of the source and follow-up test cases obtained from SUT satisfy the output relation, then the program is highly reliable. Otherwise, the program will have logical errors [9]. The steps involved in MT are shown in Figure 1.
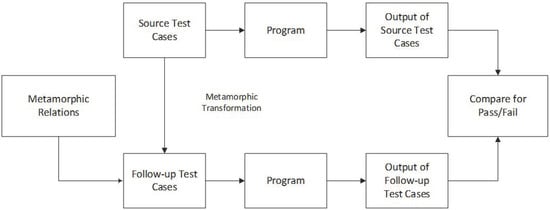
Figure 1.
Process of metamorphic testing.
The reliability of our test results is a function of the efficacy of MT, which is dependent on the effectiveness of MRs. One of the important metrics used to evaluate MRs is the fault detection rate of that particular MR. The fault detection rate shows that either the selected test cases are able to detect faults or not (can we find violations of MRs for the corresponding test cases?) [10]. The fault detection rate is measured as the number of faults detected by the selected source test cases divided by the number of faults detected by the total number of test cases [11].
In our proposed framework, we have studied the fault detection capabilities of MRs. For the evaluation of MRs, we have initially selected four existing MRs of edge detection operation proposed by Sim et al. [12]. We have proposed six MRs for dilation and erosion operationsWe have also ascertained the fault detection capabilities of our proposed MRs (four general and two specific) for dilation and erosion operations.
The existing literature shows that Mayer and Guderlei [13] first proposed four general MRs for Euclidean distance transform. These four MRs (rotation at 90 degrees, transposition, reflection at ordinate, and reflection at abscissa) are generally applicable to all image processing operations. Furthermore, Jameel et al. [14] furthered the research by using two of these four to ascertain the fault detection rate of dilation and erosion MRs. In total, these authors have presented eight MRs (two general and six specific) for dilation and erosion operation. Jameel et al. [14] used only two general MRs, i.e., reflection at ordinate and reflection at abscissa. However, the fault detection rate of the remaining two MRs (rotation and transposition) is not determined. Therefore, we have proposed rotation and transposition MRs for dilation and erosion operations to ascertain the fault detection rate of these two MRs. The associative property is specific to the dilation operation. We have changed the order of associative property to check whether the new arrangement satisfies the dilation operation or not. This result leads us to present a new MR for dilation operation. Image translation is an operation of image processing. We have checked this operation on both dilation and erosion and come to know that it only satisfies the erosion operation. In this way, we have proposed a new MR for erosion operation.
After the selection and identification of MRs, we generated the source test cases through a criterion proposed by Jafari et al. [15]. In the paper, we (the authors) have discussed in detail how source test cases are generated using the black box testing technique (equivalence class testing) and the white box testing technique (coverage criterion). We have used 95 test cases of MRI brain images for our experiments taken from www.kaggle.com. Later, follow-up test cases are generated using source test cases and MRs. Both the source and follow-up test cases are given to the SUT. In this paper, we have the following three SUTs, i.e., edge detection, dilation, and erosion. The relation between the outputs of both the source and follow-up test cases is checked. If the MR holds between the outputs of two test cases, then the SUT has no faults; otherwise, the SUT is faulty.
Afterward, mutation testing is performed to evaluate MRs. Mutation operators always play an important role in generating the mutants. In existing literature [12,14,16,17], only a few mutation operators are used that have generated a very small number of mutants. The authors did not discuss the effectiveness of mutation operators or which operator is effective enough to generate and kill a maximum number of mutants. We have used nine mutation operators and evaluated which operator is most effective in generating and killing a maximum number of mutants.
In the mutation process, we ran the original program on source test cases and then ran the original program on the follow-up test cases. The outputs of both the test cases are recorded for comparison. In the second phase of testing, we ran the same two test cases on the mutated program. The outputs of these test cases are also recorded for comparison. If outputs of both original and mutated test cases satisfy their related MR, then it shows that the mutant is not killed; otherwise, the mutant is killed. Afterward, the mutation score is calculated to check the fault detection rate of each MR. If the mutation score is near 1, then it shows that the MR is strong, or else the MR is weak enough to find the violation.
This paper makes the following contributions:
- We have proposed six new MRs for dilation and erosion operations and ascertain the effectiveness of these MRs while also assessing improvements in them using mutation testing.
- We have compared our six proposed MRs with the eight existing MRs for dilation and erosion operations.
- In existing literature, only two mutation operators are used for the evaluation of edge detection and morphological image operations. We have used nine mutation operators to improve the effectiveness of edge detection and morphological image operation (dilation and erosion) MRs. We have also compared the result of our proposed framework with the existing techniques.
- We have also checked the effectiveness of mutation operators to determine which operator is more effective in generating and killing a maximum number of mutants.
This paper is organized as follows; Section 2 discusses the related work. Section 3 describes the existing and newly proposed MRs. Section 4 discusses the proposed framework for the evaluation of MRs. In Section 5 experiment design is narrated. Section 6 discusses the results and discussion whereas Section 7 describes the conclusion.
2. Related Work
In literature review, we have covered those papers where MRs are evaluated to improve the effectiveness of MT. MT is a common technique to improve the test oracle problem where it is hard to assess the output correctly when an arbitrary input has been given to the SUT [18].
Many researchers have used different image processing operators, such as edge detection, image region growth, dilation and erosion, and used their properties as metamorphic relations. The effectiveness of these MRs is checked through mutation testing. Sim et al. [12] proposed a framework to determine the effectiveness of MT. To conduct the experiments, collections of images are needed for the generation of test inputs. Unlike model-generated images, camera-captured images (real images) from published image libraries are selected randomly. Mutation testing is used to evaluate the fault detection rate of MT. Single operator faults and stride implementation faults are seeded into the Sobel edge detection program. In single-operator faults, two types of operators are used: logical operator replacement (LOR) and relational operator replacement (ROR). Results show that MT is capable of detecting faulty edge detection programs up to 90%. Jameel et al. [14] discussed the oracle problem in IPAs and showed how SUT properties could be used as MR. The authors have studied some properties of morphological image operations. The effectiveness of MRs can be analyzed through mutation testing. In order to conduct the experiments, input images are selected randomly. Mutation testing is used to show the effectiveness of the above-mentioned MRs. Therefore, errors are deliberately added to the Mex C code. The mutation score tells the number of killed mutants. The mutant is said to be killed if an MR is able to detect the bug. It is concluded that for bug identification, specific images are needed instead of general input images such as Lena. Jiang et al. [19] applied MT to the image region growth program. Mutation testing is used to find the effectiveness of MRs. In this paper, MT is applied to test the aerospace image processing software. A segmental symbolic evaluation method is used to generate the input data. The original program implemented in C language is executed sequentially with three mutant programs. The program is said to be faulty if an MR violation can be seen after the validation of output relations.
Many researchers have been fascinated by the use of MT techniques in machine learning algorithms as well. Jameel et al. [20] used support vector machine (SVM) to automate the interpretation of the output results of test oracle requirements. These authors have designed a comparative study to gauge the effectiveness of their proposed scheme against the latest MT oracle technique and the traditional statistical oracle method. Thirty-five distinctive errors are introduced to the original program written in C language to create 35 unique resultant programs. For evaluation purposes, these authors have created the output images from these 35 versions of the image dilation program for pass or fail criteria. Half of the selected images are used to train SVM using various features (wavelet features, binary features, hough features, statistical features) of dilated images to analyze their effectiveness. The results confirmed that SVM was better in terms of the lowest classification error than the other two techniques. Chan et al. [21] integrated the pattern classification technique with MT. A trained classifier (C4.5) is employed for the test oracle by labeling pass/fail. The passed test outputs may also show false positive/negative failures, which are then processed for additional testing. This proposal has proven to be efficient and effective.
MT techniques have also been used with structural testing. Ding et al. [17] used a discrete dipole approximation program (ADDA) implemented in FORTRAN and C++ to check the effectiveness of MT. In this paper, statement coverage is used to check the effectiveness of test cases, whereas mutation testing is used to check the effectiveness of MT. Due to the unknown test output relations, the MRs of this program are considered weak and inadequate. Ding and Hu [16] developed a method for the adequacy of MRs. Coverage criterion, mutation analysis, and mutation tests for testing MRs are critical factors in evaluating the adequacy of MRs. An image processing program that is used to reconstruct a 3D biological cell is used to explain the author’s proposed theory. A case study is performed using a complex Monte Carlo program to gauge the effectiveness of this proposed framework. The results prove the utility of their proposed method for the testing of other scientific software as well. Table 1 shows the summary of related work.

Table 1.
Summary of related work.
After studying the literature, some of the research gaps are identified and are given below:
- In literature, test cases are selected and generated randomly. Random selection leads to an unfair distribution of parametric values, which ultimately affects the testing process.
- In existing techniques, MR evaluation is conducted through mutation testing. This evaluation is not comprehensive, as only a few mutation operators are used to check the fault detection rate of MRs. The total number of mutants generated through these mutation operators is quite low which makes the testing weak.
- In existing literature, no work has been conducted to check the effectiveness of mutation operators. It is not highlighted that which operator is more valuable to generate and kill maximum number of mutants.
3. Metamorphic Relations
In MT, the central element is the set of MRs, which are the necessary properties of the SUT or the algorithm [22]. MR plays a significant role in MT as it validates the relations between the test outputs of a program having a test oracle problem. Generally, MR is the property of a function (f) having inputs x1, x2, x3, … xn, where n is greater than 1. Their corresponding outputs are f(x1), f(x2), f(x3), … f(xn) [23]. The identification of MRs requires expert knowledge in the field of Image Processing (IP) as well as guidance provided by the experiences (Mayer et al. [13], Jameel et al. [14]).
In this paper, we have worked on the MRs of edge detection and two morphological image operations, i.e., dilation and erosion.
3.1. MRs for Edge Detection
We have used the MRs of edge detection proposed by Sim et al. [12]. The complete details of these MRs are given in [12,15]. The MRs are shown in Table 2.

Table 2.
MRs for edge detection.
Table 2 shows the MRs for edge detection where E is the Sobel edge detection, and Im is the input image.
3.2. MRs for Dilation and Erosion
In this section, we have described the existing and proposed MRs for the dilation and erosion operations.
3.2.1. Existing MRs for Dilation and Erosion
The existing MRs proposed by Jameel et al. [14] for dilation and erosion operations are given in Table 3.

Table 3.
Existing MRs for dilation and erosion.
Table 3 shows the MRs for dilation and erosion operations. The details of these MRs are given in [14].
3.2.2. Proposed MRs for Dilation and Erosion
We have proposed six new MRs for dilation and erosion operations. Our proposal consists of four general and two specific MRs of dilation and erosion. In Table 4, we have discussed our proposed MRs with their mathematical properties. The details of these MRs are given below:

Table 4.
Proposed MRs for dilation and erosion.
4. Evaluation of Metamorphic Relations
In this section, we have discussed the historical evaluations of MRs from the existing literature. We have also suggested a new method to evaluate MRs in our proposed framework.
The evaluation of MRs in MT involves assessing how well these relations can effectively guide the generation of additional test cases and help verify the correctness of a software system. The source and follow-up test cases are executed, and their outputs are verified against the relevant MRs, of which any violation implies that the software under test is faulty. The MRs are considered strong and do not satisfy the relation easily. The higher the number of test cases that satisfy the MR, the weaker the MR. Suppose we have a program P that computes the sin function. There are two MRs to compute the sin function.
MR1: sin x = sin (180 − x)
MR2: sin x = sin (x + 360)
The MR that satisfies the relation on maximum test cases is considered weak and vice versa. For all positive values of x, MR1 is better than MR2 as MR2 satisfies the relation for all positive values, and thus, MR2 will always be a weak MR.
The evaluations of MRs based on a random selection of source test cases using existing techniques are not comprehensive with respect to the truly random generation of source test cases. The available sample population from which random source test cases are selected is missing many types of image characteristics such as dimension, resolution, bit depth, type of image, etc.
Sim et al. [12] and Jameel et al. [14] selected the images randomly from various published image libraries available online. Each library has a set of images with only one or two image characteristics. If we create a new library using all the images from these libraries, many image properties will still be missing. By selecting the test cases randomly from these libraries, it is probable that all the selected test cases may cover only one property of the image while ignoring the others. This will definitely affect the testing process because of the lack of diversity in test images.
Furthermore, in existing literature, mutation testing is used for the evaluation of MRs. As discussed earlier, mutation operators play a dominant role in generating a significant number of mutants. In existing techniques, Sim et al. [12] used two mutation operators, i.e., ROR and LOR, whereas Jameel et al. [14] used only one mutation operator (ROR) for the generation of mutants. These two operators only produce a maximum of 33 mutants, which is not a significant number for the purpose of evaluation. So, more mutation operators should be needed for the extensive evaluation of MRs. Figure 2 shows the evaluation process of our proposed framework.
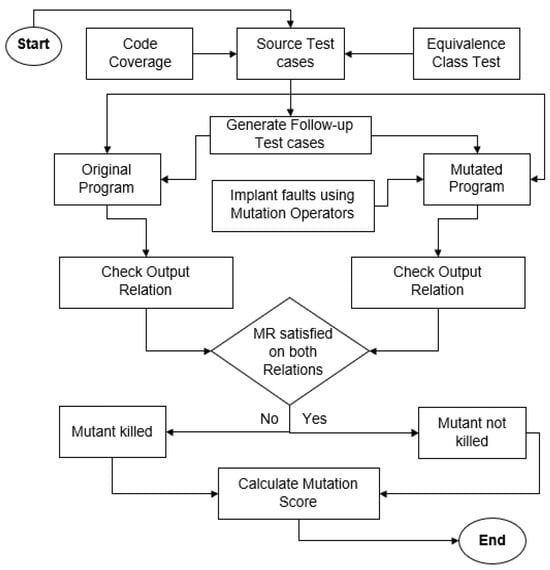
Figure 2.
Evaluation process of MRs.
4.1. Source Test Case Generation
The foremost step is the generation of source test cases (original test cases). In literature, source test cases are generated either through some traditional test case generation techniques as discussed earlier or through some tool such as EvoSuite (it generates source test cases automatically through coverage criterion) [5]. Nowadays, few researches are emerged in the direction of generation and selection of source test cases that are effective in fault detection [24].
As discussed in the literature, the general source test case generation criterion is to generate the test cases randomly. It is a probability that randomly generated test cases may cover only one characteristic of the image while ignoring the other ones. Sim et al. [12] also suggested that considering the characteristics of the image can improve the mutation score of MRs. Keeping this in mind, we have proposed a source test case generation criterion in our previous paper. In this criterion, we have generated the source test cases through equivalence class testing and coverage criterion. In equivalence class testing, we have considered the attributes of images and grouped them into five distinct classes such as horizontal dimension, vertical dimension, resolution, bit depth, and image type. The details of the formation of source test cases are given in [15]. We have used the same (95) test cases for our experiments. Afterward, the adequacy of source test cases is checked through program coverage (statement coverage and branch coverage). If the test cases (accumulatively) do not achieve 100% coverage, then we need more test cases to achieve 100% branch coverage.
4.2. Metamorphic Testing
In IP, it is hard to test a program without a test oracle, as the outcome is not predictable. In MT, we can detect that either the test case has passed or failed by generating new test cases for further evaluation. The steps of MT are discussed in Figure 1. In MT, MR transforms the existing source test cases into new test cases known as follow-up test cases [25]. When the follow-up test cases are generated, both test cases are given to the SUT. By executing the SUT, the output data is generated for each test case [23]. Processing of SUT is conducted by comparing the output relation of source and follow-up test cases. The satisfaction of MR shows that the SUT is not faulty, whereas the dissatisfaction of MR shows that the SUT is faulty.
4.3. MR Evaluation Using Mutation Testing
Evaluation of MRs is an indication of their fault detection capabilities. The greater the fault detection capabilities, the greater the ability to detect more faults from a program. We have checked the fault detection rate of these MRs through mutation testing.
Mutation operators play an important role in generating mutants in mutation testing. Previously, very few mutation operators were used, which did not even highlight the effectiveness of these operators. We have used nine mutation operators to check which operator is most effective for generating and killing a significant number of mutants. Our work is relevant to [12,14], so we have compared the mutation operators used in our proposed framework with these two techniques. The mutation operators used in the existing techniques [12,14] and in the proposed framework are given in Table 5.

Table 5.
Mutation operators are used in existing techniques and in the proposed framework.
If the output of source and follow-up test cases satisfies the relation, then mutation testing can be performed by seeding the faults into the original program to check for MR violation. The process of checking the original and mutated program is explained through an example. Suppose we have two test cases, t1 (source test case) and t′1 (follow-up test case), that have to be tested under the original program p. The outputs of tests t1 and t′1 can be recorded as r1 and r′1. Afterward, the same test cases, t1 and t′1, can be run on the mutated program p′ with mutant m. Record the outputs as r2 and r′2. If both (r1, r′1) and (r2, r′2) satisfy their related MR, then the mutant m is not killed [19]. Otherwise, the mutant is killed. After mutation testing, the mutation score is to be calculated. The mutation score indicates the fault detection rate of each MR. In the existing literature, i.e., [12,14,16,19], all the MRs are evaluated by seeding faults manually in the code or through a tool that calculates the mutation score automatically through the traditional mutation testing approach. We have seeded the faults manually and checked the relation manually on both the programs (original and mutated) for the calculation of the mutation score.
The mutation score indicates the fault detection rate (FDR) of MR. For the calculation of the mutation score, we have examined the mutants manually and have removed all the equivalent mutants. The formula for the mutation score is given below:
According to the formula, if the mutation score is 1 then it means that MR is strong (high fault detection rate) whereas a 0 score would show MR is weak (low fault detection rate). We can also say that if the mutation score is near 0, the MR is weak enough to find the violation, while on the other hand, if the mutation score is near 1, the MR is strong.
4.4. Advantages of Proposed Framework
- In the proposed fraework, we have used nine applicable mutation operators to ascertain the effectiveness of MRs. The higher the number of mutation operators used, the higher the number of faults detected. The use of these operators contribute to the improvement of software quality, the effectiveness of test suites, and improvement in test coverage.
- We have proposed new MRs in the field of IP. Overall, proposing new metamorphic relations in image processing contributes to the advancement of testing methodologies, algorithm validation techniques, and research practices, ultimately leading to more reliable, robust, and efficient image processing systems and applications.
5. Experiment Design
In this section, we have discussed the details of SUT used for our experiment: source code, dataset, original test cases, coverage criterion, and mutation operators used.
5.1. Proposed Evaluation
The subject programs in this paper consist of the following:
- Sobel edge detection program
- Dilation and erosion programs
The properties of edge detection and morphological operations are used as MRs. In IP, edge detection plays a vital role in identifying the immediate changes in grayscale images. Identifying the edges of the images can be invaluable for different real-world applications [26]. Similarly, dilation and erosion are the main morphological operations that increase or decrease the region of the image according to the structuring element [2]. The inputs and outputs of the edge detection program, a dilation and erosion program, are given in Figure 3.
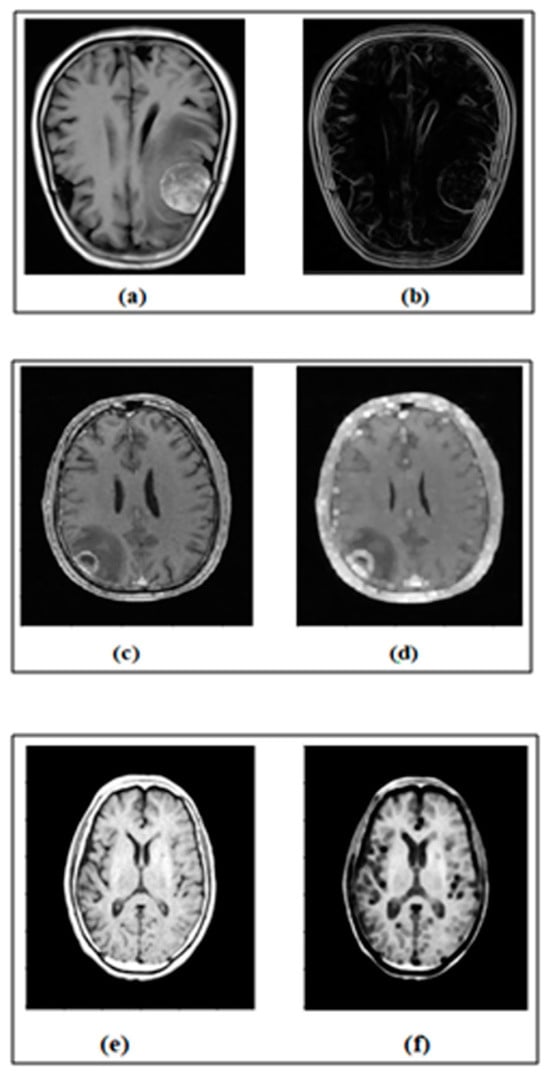
Figure 3.
(a) Input image. (b) Output of edge detection. (c) Input image. (d) Output of dilation. (e) Input image. (f) Output of erosion.
Figure 3 shows the sample inputs of MRI brain images and their expected output images after performing edge detection, dilation operation and erosion operation.
5.2. Source Code
We have used a well-structured code of Sobel edge detection and dilation and erosion operations written in Python version 3.8.3 for our implementation. The code of edge detection consists of 41 statements and 10 branches. Similarly, the code of dilation and erosion consists of 46 statements and 12 branches, respectively. The sources of the above codes are given in Table 6.

Table 6.
Sources of source code.
5.2.1. Pseudocode of Dilation/Erosion Operation
- FUNCTION dilation(image, kernel_size, kernel):
- n, m = shape_of(image)
- transpose_kernel = transpose(kernel)
- create empty array edges_img with shape (n, m)
- x = y = 0
- WHILE y < m + 1 − kernel_size DO
- IF x < n + 1 − kernel_size THEN
- local_pixels = get_subarray(image, x, y, kernel_size)
- val = minimum(local_pixels + kernel)
- IF val > 255 THEN
- set edges_img[x + (kernel_size//2), y + (kernel_size//2)] = 255
- ELSE IF val < 0 THEN
- set edges_img[x + (kernel_size//2), y + (kernel_size//2)] = 0
- ELSE
- set edges_img[x + (kernel_size//2), y + (kernel_size//2)] = maximum/minimum(local_pixels)
- END IF
- increment x by 1
- ELSE
- increment y by 1
- set x to 0
- END IF
- END WHILE
- Convert edges_img to uint8 data type
- RETURN edges_img
- END FUNCTION
- FUNCTION display(images):
- titles = [‘original’, ‘After Dilation’]
- FOR i FROM 1 TO length_of(images) DO
- CREATE a new figure
- SET title of the figure to titles[i]
- DISPLAY the i-th image with gray colormap
- END FOR
- SHOW all figures
- END FUNCTION
- SET path to image file path
- LOAD image from path
- images = [image]
- APPEND dilation(image, 5, ones(5,5)) to images
- DISPLAY images
5.2.2. Pseudocode of Edge Detection Operation
- FUNCTION sad():
- vertical_filter = [[−1,−2,−1], [0,0,0], [1,2,1]]
- horizontal_filter = [[−1,0,1], [−2,0,2], [−1,0,1]]
- path = “path_to_image.jpg”
- img = read_image(path)
- n, m, = dimensions_of_image(img)
- edges_img = copy_of(img)
- x = y = 0
- WHILE y < m + 1 − 3 DO:
- IF x < n + 1 − 3 THEN:
- local_pixels = get_local_pixels(img, x, y)
- vertical_transformed_pixels = vertical_filter * local_pixels
- vertical_score = sum_of_elements(vertical_transformed_pixels)/4
- horizontal_transformed_pixels = horizontal_filter * local_pixels
- horizontal_score = sum_of_elements(horizontal_transformed_pixels)/4
- edge_score = square_root_of((vertical_score^2) + (horizontal_score^2))
- edges_img[x + 1, y + 1] = [edge_score] * 3
- x = x + 1
- ELSE:
- y = y + 1
- x = 0
- END IF
- END WHILE
- edges_img = edges_img/edges_img.max()
- display_image(edges_img)
- save_image(‘output_path.jpg’, edges_img)
- IF _name_ == “_main_”:
- sad()
5.3. Dataset
For our study, a diversified collection of MRI brain images is taken from https://www.kaggle.com/datasets/abhranta/brain-tumor-detection-mri?resource=download (access on 17 February 2024). The dataset consists of 1500 images having brain tumors and 1500 images having no brain tumors. The basic three types of images used as test cases are shown in Figure 4.
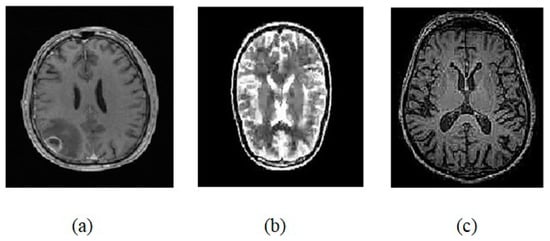
Figure 4.
(a) T1 Weighted image. (b) T2 Weighted image. (c) Flair image.
5.4. Source Test Cases
We have selected 95 source test cases through black box testing technique (strong equivalence class testing) and coverage criteria (statement coverage and branch coverage); a criterion proposed in our previous paper [15].
5.5. Source Test Cases
The coverage of source test cases is checked through statement coverage and branch coverage, respectively. The coverage detail is given in Table 7.

Table 7.
Coverage details.
As shown in Table 7, 95 test cases (accumulatively) cover 100% code coverage in all three programs, so we do not need more test cases for our test suite.
5.6. Mutation Operators
Mutation operators cover a wide range of potential faults or mutations that can occur in the code. They encompass various types of changes that may affect the behavior of the program. Each mutation operator targets a specific kind of fault. For example, some operators might mutate arithmetic operators, while others might mutate relational operators or logical operators. For our study, the mutation operators used in Python language are taken from GitHub—mutpy/mutpy: MutPy is a mutation testing tool for Python 3.x source code. There are twenty traditional and seven experimental operators. The list of traditional and experimental operators is as follows:
- AOD—arithmetic operator deletion
- AOR—arithmetic operator replacement
- ASR—assignment operator replacement
- BCR—break continue replacement
- COD—conditional operator deletion
- COI—conditional operator insertion
- CRP—constant replacement
- DDL—decorator deletion
- EHD—exception handler deletion
- EXS—exception swallowing
- IHD—hiding variable deletion
- IOD—overriding method deletion
- IOP—overridden method calling position change
- LCR—logical connector replacement
- LOD—logical operator deletion
- LOR—logical operator replacement
- ROR—relational operator replacement
- SCD—super calling deletion
- SCI—super calling insert
- SIR—slice index remove
Experimental mutation operators:
- CDI—class method decorator insertion
- OIL—one iteration loop
- RIL—reverse iteration loop
- SDI—static method decorator insertion
- SDL—statement deletion
- SVD—self variable deletion
- ZIL—zero iteration loop
The use of mutation operators is dependent on the source code of a program. We have used all the mutation operators that are applicable according to our source code. The mutation operators used in this research are given below:
- AOD → Unary arithmetic operator deletion
- AOR → Arithmetic operation replacement
- LOR → Logical operator replacement
- ROR → Relational operator Replacement
- OIL → One iteration loop
- RIL → Reverse iteration loop
- SIR → Slice index remove
- SDL → Statement deletion
- ZIL → Zero iteration loop
6. Results and Discussions
In this section, we will discuss the MR evaluation results of our testing methodology in detail.
6.1. Effectiveness of Mutation Operators
In this section we have assessed the effectiveness of mutation operators by calculating the percentage of mutants generated and mutants killed. Mutation score of each operator shows the FDR of each mutation operator. The formula of mutation score depicted in Equation (1) is used to calculate the fault detection rate of each mutation operator. The percentage of generated mutants is calculated by the formula given in Equation (2).
In Equation (2), mutant is denoted by “M” and mutation operator is denoted by “op”.
6.1.1. Effectiveness of Mutation Operators Used in Edge Detection
Table 8 shows the effectiveness of mutation operators in terms of mutants generated and mutants killed by each operator for edge detection.

Table 8.
Effectiveness of Mutation Operators Used in Edge Detection.
In the existing technique of Sim et al. [12], a total of 31 mutants have been generated by using only two mutation operators, i.e., ROR and LOR. In our proposed framework, we have employed nine mutation operators to generate a total of 162 mutants. It is observed that mutation operators such as AOD, COI, ZIL, and SIR have shown 100% mutation scores in all four MRs. But their percentage with respect to generated mutants is very low, i.e., 3.70%, 1.23%, 2.46%, and 1.23%, respectively. The effectiveness is dependent on two factors, i.e., mutation score and number of mutants generated. The operator that scores a high percentage in one of the two factors and scores very low in the other is not as effective as the one having moderate scores in both factors. So, the AOR operator is the most effective operator because its lowest mutation score is 63% (MR4), and the highest mutation score is 74% (MR1), whereas its percentage to generate mutants is 60.49%. RIL is the least effective operator because its lowest mutation score is 0% (MR4), and the highest mutation score is 100% (MR2), whereas its percentage to generate mutants is only 1.23%. SDL operator has achieved a good mutation score of 81.25%, followed by ROR having a mutation score of 73.33% against each MR, whereas their percentage to generate mutants is 9.87% and 18.51%, respectively. The effectiveness of SDL and ROR is almost similar because the mutation score of SDL is 12% higher than ROR, whereas the percentage of the ROR operator in terms of mutation generation is 10% higher than the SDL operator.
6.1.2. Effectiveness of Mutation Operators Used in Dilation and Erosion
Now, we will discuss the effectiveness of mutation operators used in dilation and erosion operations for the proposed MRs. Table 9 shows the FDR (mutation score) and percentage of mutants generated by each mutation operator used in dilation and erosion operations.

Table 9.
Effectiveness of mutation operators used in dilation and erosion operations for proposed MRs.
In the literature, Jameel et al. [14] used only one mutation operator for the generation of mutants and created only 33 mutants, whereas we used eight mutation operators and produced 130 mutants in total. It is observed from Table 9 that the AOR operator is the most effective operator because it has generated a maximum number of mutants, i.e., 95, and its fault detection rate is greater than 50% against each MR. While the FDR of the ZIL operator is 100%, it has generated only one mutant and has a percentage of 0.76. ROR has a better percentage of generating the mutants, i.e., 15% and also, a mutation score lies between 15 to 30%. It is concluded from this section that the AOR operator is the most effective operator in terms of mutants killed and mutants generated in both the subject programs of edge detection and dilation and erosion.
6.2. Effectiveness of Metamorphic Relations
The effectiveness of MRs is determined through mutation testing. FDR depicted in Equation (1) shows the effectiveness of each MR. We have assessed the effectiveness of existing MRs (edge detection and dilation and erosion) and proposed MRs (dilation and erosion).
6.2.1. Effectiveness of Edge Detection MRs
The fault detection rate (mutation score) defines the strength of each MR. FDR is calculated through mutation testing. The FDR of edge detection MRs is given in Table 10.

Table 10.
Fault detection rate of edge detection MRs.
We have generated a total of 162 mutants for edge detection manually by introducing one fault at a time. It is observed from Table 10 that MR2 has killed a maximum number of mutants, i.e., 126, followed by MR1, which has killed 124 mutants. MR3 and MR4 have killed the same number of mutants, i.e., 112 mutants each. The last column in Table 10 shows the FDR (in percentage) of each MR.
6.2.2. Effectiveness of Dilation and Erosion MRs
The FDR of existing operations of dilation and erosion using our proposed framework are given in Table 11.

Table 11.
Fault detection rate of dilation and erosion MRs.
We have generated a total of 130 mutants for dilation and erosion operation. Table 11 shows that R1 has killed a maximum number of mutants, i.e., 70, followed by R2 and R7, with 68 killed mutants each. R6 has killed the least number of mutants, i.e., 45. After calculating the FDR, it is observed that R1 has the highest FDR of 53.84%, thus making R1 the most effective MR. R2 and R7 have the second-highest FDR of 52.30% each. R6 has the lowest FDR of 34.61%, thus making this MR least effective.
6.2.3. Effectiveness of Proposed MRs
As discussed earlier, for the dilation and erosion operation, we have suggested six MRs. Four of the six MRs are general and can be used for the majority of IP operations, while the remaining two MRs are particular to dilation and erosion operations. We have also assessed the effectiveness of our proposed MRs using our proposed framework. The FDR of proposed MRs are given in Table 12.

Table 12.
Fault detection rate of proposed MRs.
Table 12 shows that we have generated a total of 130 mutants. It is observed that MR6 has the highest FDR, killing 68 mutants, followed by MR4, which killed 65 mutants. MR1 and MR3 have killed 59 mutants each. The FDR of MR2 is the lowest because it has killed 57 mutants. It is observed that the FDR of our proposed MRs are neither too high nor too low but are significant enough to find the violations in all the respective MRs. However, the most effective MR among the proposed MRs is MR6 (image translation), which has the highest FDR of 52.30%, followed by MR4 (transposition in erosion operation) with an FDR of 50%. MR2 (counterclockwise rotation at 90 degrees in erosion operation) is the least effective, with an FDR of 43.84%.
6.3. Comparison of Proposed Framework with Existing Techniques
We have compared the results of our proposed framework with Sim et.al [12] and Jameel et al. [14]. Table 13 shows the statistics of existing techniques and proposed framework.

Table 13.
Statistics of existing technique and proposed framework.
According to the statistics given in Table 13, Sim et al. [12] selected 30 images as source test cases from different image libraries given in [12]. The images used by the authors are very limited and not diverse in nature. The Kodak site has 24 images, and the image compression site has only 15 images. All the images have the same bit depth of 24 and resolution of 96 dpi. All the images have only two dimensions, 768 by 512 or 512 by 768 (Kodak site) and a single dimension of 700 by 525. Jameel et al. [14] have not mentioned the source as well as the number of test cases selected for their experiments. We have used the data set of MRI brain images taken from Kaggle.com. The dataset is comprised of 3000 images with diverse image properties. From 3000 images, we have selected 95 images using equivalence class testing and code coverage. Sim et al. [12] used two mutation operators and generated only 31 mutants. Jameel et al. [14] used only one operator and generated 33 mutants. We have used nine mutation operators in the edge detection program and eight operators in the dilation and erosion program to generate 162 and 130 mutants, respectively.
6.3.1. Comparison Results of Edge Detection
We have compared the results of our proposed framework with Sim et al. [12]. The comparison results are given in Table 14.

Table 14.
Comparison of existing technique and proposed framework.
Table 14 shows that in the existing technique of Sim et al. [12], MR2 has the highest FDR followed by MR3, whereas in the proposed framework, MR2 has the highest FDR followed by MR1. In the existing technique, the FDR of MR1 and MR4 are the same, i.e., 45%, whereas in the proposed framework, the FDR of MR3 and MR4 are the same, i.e., 69.13%. In the proposed framework, the FDR of MR1 and MR4 is far better than the existing technique, i.e., 76.54% and 69.13%, respectively. The FDR of MR2 and MR3 is also improved by 1%.
6.3.2. Comparison Results of Dilation and Erosion
Jameel et al. [14] evaluated eight MRs of dilation and erosion operation. We have also evaluated the same MRs using our proposed framework. The comparison results are given in Table 15.

Table 15.
Comparison of existing technique and proposed framework.
Table 15 shows that out of eight MRs, four MRs, i.e., R1, R4, R6, and R8, have improved FDR using our proposed framework. The FDR of R1 (53.84%), R6 (34.61%), and R8 (50%) are far better than the existing technique, having a FDR of 15%, 18%, and 21%, respectively. In existing techniques, R2, R3, R5, and R7 have high FDR, i.e., 58%, 97%, 50% and 73%, because they have used only one mutation operator and considered only one type of fault. In the proposed framework, the FDR of all the MRs is moderate, neither too high nor too low, thus making it effective to find the violations in all respective MRs. In the proposed framework, R1 is improved by 39%, R4 is improved by 0.5%, R6 is improved by 17%, and R8 is improved by 29%. The FDR of some of the MRs in the existing technique is high because the number of mutants generated is just 31.
6.4. Comparison Results of Proposed MRs with Existing MRs of Dilation and Erosion
In this section, we compare the results of our proposed MRs with those of the existing MRs. As described earlier, we have used eight mutation operators for the evaluation of dilation and erosion MRs and have generated 130 mutants in total. The number of mutants against each mutation operator is depicted in Table 16.

Table 16.
Mutants Generated Against Each Mutation Operator.
In mutation testing, we have used eight mutation operators for the evaluation of dilation and erosion MRs. In the AOR operator, we have used six types of faults such as addition (+), subtraction (−), multiplication (*), division (/), exponent/power (**), and floor division (//). It is observed that there are nine arithmetic faults (collectively) that are identified by the proposed MRs and are not identified by any of the existing MRs. Among these faults, eight faults are identified by MR4, five faults are identified by MR5, and nine faults are identified by MR6. So, we can say that MR4, MR5, and MR6 are more effective operators than MR1, MR2, and MR3 because they have identified additional faults not identified by any of the existing MRs. We have observed the presence of alive mutants in both existing and proposed MRs. So, by combining both the MRs, the total number of alive mutants was reduced. Hence, it is concluded that the proposed MRs complement the existing MRs effectively.
7. Conclusions
Testing of Image Processing Applications (IPAs), of course, is a challenging task because of the absence of test oracle. Metamorphic testing is an efficient method to deal with the applications with a test oracle problem. Metamorphic relations play an important role in metamorphic testing. A metamorphic relation relates two or more inputs with their expected outputs after execution of the properties of the target program. Properties of different image processing operations can also be used as metamorphic relations.
In this research, we have proposed six new MRs for morphological image operations (dilation and erosion). The fault detection rate of newly proposed MRs, along with existing MRs, is determined through mutation testing. The effectiveness of mutation operators is also determined by which operator is more effective in generating a maximum number of mutants and through which operator a maximum number of mutants are killed. AOR is considered the best operator in both the subject programs as it generates and kills a maximum number of mutants. We have compared the results of our proposed approach with the existing techniques of edge detection and morphological image operations. Our results demonstrate that the mutation score of all the MRs of edge detection has improved, whereas the MRs of dilation and erosion have shown improvement in four MRs (out of 8). While comparing our proposed MRs with the existing MRs of dilation and erosion operations, we have come to the conclusion that the proposed MRs complement the existing MRs effectively as the proposed MRs are able to find those faults that are not identified by the existing MRs.
Some of the limitations of this study are:
- In this research, we have used only one dataset for the experiments. We can use more datasets for convincing testing.
- One of the limitations of this research is the use of only one algorithm for edge detection. There are several other edge detection algorithms that can be used to make the experiments more substantial.
- We have used only one programming language, i.e., Python. We could use more languages, such as Java, C++, etc., so that more mutation operators can be used.
The future directions of this research are:
- In this research, statement coverage and branch coverage are used for code coverage. In the future, the proposed research for the evaluation of MRs can be strengthened by using more coverage criteria for improved coverage. The future work involving coverage criterion may include multiple condition coverage (MCC), where every combination of conditions’ outcomes is tested at least once in a decision; modified condition/decision coverage (MCDC) where a decision’s potential outcomes are determined by each condition contained within the decision, all def-use (definition usage) coverage where all-def coverage is attained when all defs of any variable are covered and all-uses coverage is attained when a path from each def to each use of that def has been exercised, etc.
- The research can also be strengthened by using additional mutation operators that will cover the fault types not used in the proposed research, such as logical connector replacement (LCR), break continues replacement (BCR), constant replacement (CRP), class method decorator insertion (CDI), etc.
Author Contributions
Conceptualization, F.J. and A.N.; methodology, F.J. and A.N.; software, F.J.; validation, F.J.; formal analysis, A.N.; investigation, F.J.; resources, F.J.; data curation, A.N.; writing—original draft preparation, F.J.; writing—review and editing, F.J. and A.N.; visualization, A.N.; supervision, A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset used in this research is public and is taken from https://www.kaggle.com/datasets/abhranta/brain-tumor-detection-mri?resource=download (accessed on 22 February 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bolchini, C.; Cassano, L.; Mazzeo, A.; Miele, A. Usability-based Cross-Layer Reliability Evaluation of Image Processing Applications. In Proceedings of the IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFT) 2021, Athens, Greece, 6–8 October 2021. [Google Scholar]
- Raid, A.M.; Khedr, W.M.; El-dosuky, M.A.; Aoud, M. Image Restoration Based on Morphological Operations. Int. J. Comput. Sci. Eng. Inf. Technol. (IJCSEIT) 2014, 4, 3. [Google Scholar] [CrossRef]
- Ur Rehman, F.; Izurieta, C. An Approach For Verifying And Validating Clustering Based Anomaly Detection Systems Using Metamorphic Testing. In Proceedings of the IEEE International Conference On Artificial Intelligence Testing (AITest) 2022, Newark, CA, USA, 15–18 August 2022. [Google Scholar]
- Memon, A.; Banerjee, I.; Nagarajan, A. What Test Oracle Should I Use for effective GUI Testing. In Proceedings of the 18th IEEE International Conference on Automated Software Engineering, Montreal, QC, Canada, 6–10 October 2003. [Google Scholar]
- Saha, P.; Kanewala, U. Fault Detection Effectiveness of Source Test Case Generation Strategies for Metamorphic Testing. In Proceedings of the MET ’18: Proceedings of the 3rd International Workshop on Metamorphic Testing, Gothenburg, Sweden, 27 May 2018. [Google Scholar]
- Chen, T.Y.; Cheung, S.C.; Yiu, S.M. Metamorphic testing: A new approach for generating next test cases. In Proceedings of the AST ‘15: Proceedings of the 10th International Workshop on Automation of Software Test, Florence, Italy, 16–24 May 2015. [Google Scholar]
- Segura, S.; Troya, J.; Duran, A.; Cortes, A.R. Performance Metamorphic Testing: Motivation and Challenges. In Proceedings of the IEEE/ACM 39th International Conference on Software Engineering: New Ideas and Emerging Technologies Results Track (ICSE-NIER), Buenos Aires, Argentina, 20–28 May 2017. [Google Scholar]
- Luu, Q.H.; Liu, H.; Chen, T.Y.; Vu, L.H. Testing Ocean Software with Metamorphic Testing. In Proceedings of the 7th International Workshop on Metamorphic Testing 2022, Pittsburgh, PA, USA, 9 May 2022. [Google Scholar]
- Hong, T.P.; Chiu, C.C.; Su, J.H.; Chen, C.H. Applicable Metamorphic Testing for Erasable-Itemset Mining. IEEE Access 2022, 10, 38545–38554. [Google Scholar] [CrossRef]
- Niu, X.; Sun, Y.; Wu, H.; Li, G.; Nie, C.; Yu, L.; Wang, X. Enhance Combinatorial Testing with Metamorphic Relations. J. Latex Cl. Files 2015, 14, 8. [Google Scholar] [CrossRef]
- Arrieta, A. Multi-Objective Metamorphic Follow-up Test Case Selection for Deep Learning Systems. In Proceedings of the Genetic and Evolutionary Computation Conference 2022, Boston, MA, USA, 9–13 July 2022. [Google Scholar]
- Sim, K.Y.; Wong, D.M.L.; Hii, T.Y. Evaluating the Effectiveness of Metamorphic Testing on Edge Detection Programs. Int. J. Innov. Manag. Technol. 2013, 4, 6–10. [Google Scholar]
- Mayer, J.; Guderlei, R. On Random Testing of Image Processing Applications. In Proceedings of the Sixth International Conference on Quality Software (QSIC’06), Beijing, China, 27–28 October 2006. [Google Scholar]
- Jameel, T.; Chao, L. Test Oracles Based on Metamorphic Relations for Image Processing Applications. In Proceedings of the IEEE 16th International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Takamatsu, Japan, 1–3 June 2015. [Google Scholar]
- Jafari, F.; Nadeem, A.; Zaman, Q. Evaluation of Metamorphic Testing for Edge Detection in MRI Brain Diagnostics. Appl. Sci. 2022, 12, 8684. [Google Scholar] [CrossRef]
- Ding, j.; Hu, X.H. Application of Metamorphic Testing Monitored by Test Adequacy in a Monte Carlo Simulation Program. Softw. Qual. J. 2017, 25, 3. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, D.; Hu, X. An Application of Metamorphic Testing for Testing Scientific Software. In Proceedings of the 1st International Workshop on Metamorphic Testing, Austin, TX, USA, 14–22 May 2016. [Google Scholar]
- Jiang, M.; Chen, Y.T.; Kuo, F.C.; Towey, D.; Ding, Z. A metamorphic testing approach for supporting program repair without the need for a test oracle. J. Syst. Softw. 2017, 126, 127–140. [Google Scholar] [CrossRef]
- Jiang, C.; Huang, S.; Hui, Z. Metamorphic Testing of Image Region Growth Programs in Image Processing Applications. In Proceedings of the IEEE International Conference on Software Quality, Reliability and Security Companion, Lisbon, Portugal, 16–20 July 2018. [Google Scholar]
- Jameel, T.; Mengxiang, L.; Chao, L. Automatic Test Oracle for Image Processing Applications Using Support Vector Machines. In Proceedings of the 6th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 September 2015; pp. 1110–1113. [Google Scholar]
- Chan, W.K.; Ho, J.C.F.; Tse, T.H. Piping Classification to Metamorphic Testing: An Empirical Study towards Better Effectiveness for the Identification of Failures in Mesh Simplification Programs. In Proceedings of the 31st Annual International Computer Software and Applications Conference (COMPSAC), Beijing, China, 24–27 July 2007. [Google Scholar]
- Chen, T.Y.; Kuo, F.C.; Liu, H.; Poon, P.L.; Towey, D.; Tse, T.H.; Zhou, Z.Q. Metamorphic Testing: A Review of Challenges and Opportunities. ACM Comput. Surv. 2017, 51, 1–27. [Google Scholar] [CrossRef]
- Ding, J.; Wu, T.; Lu, J.Q.; Hu, X.H. Self-Checked Metamorphic Testing of an Image Processing Program. In Proceedings of the Fourth IEEE International Conference on Secure Software Integration and Reliability Improvement, Singapore, 9–11 June 2010; pp. 190–197. [Google Scholar]
- Sun, C.; Liu, B.; Fu, A.; Liu, Y.; Liu, H. Path-directed source test case generation and prioritization in metamorphic testing. J. Syst. Softw. 2022, 183, 111091. [Google Scholar] [CrossRef]
- Segura, S.; Towey, D.; Zhou, Z.Q.; Chen, T.Y. Metamorphic Testing: Testing the Untestable. IEEE Softw. 2019, 37, 46–53. [Google Scholar] [CrossRef]
- Swathika, R.; Sharmila, T.S.; Bhattacharya, D. Edge Detection Using Simple Image Arithmetic. In Proceedings of the International Conference on Computer, Communication, and Signal Processing (ICCCSP), Chennai, India, 22–23 February 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).