Multi-Modal Convolutional Parameterisation Network for Guided Image Inverse Problems
Abstract
1. Introduction
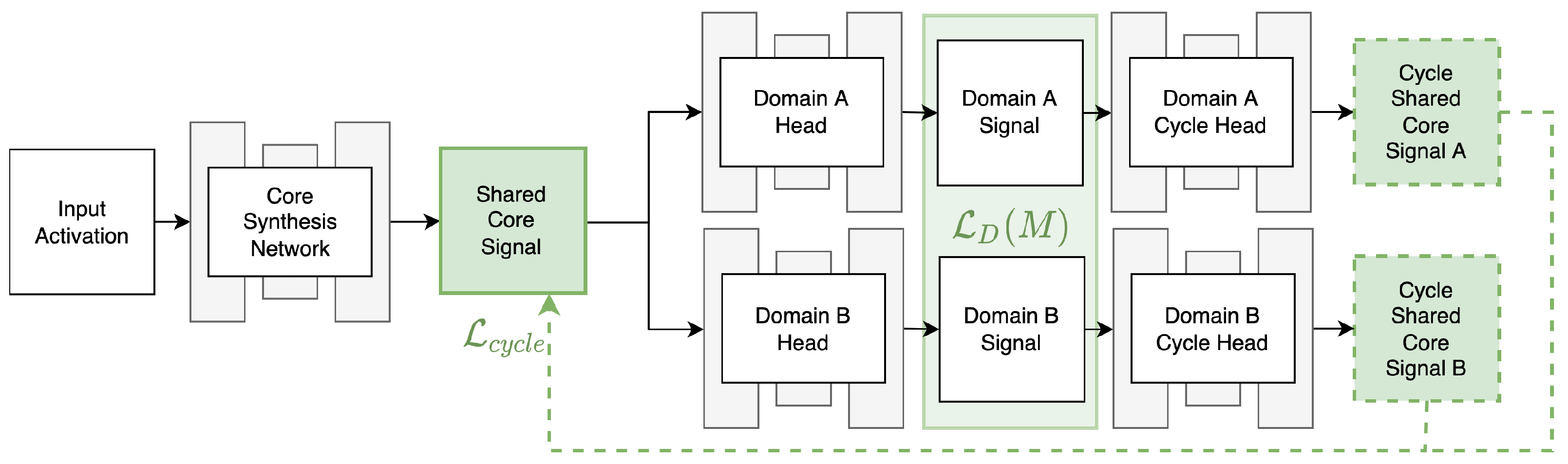
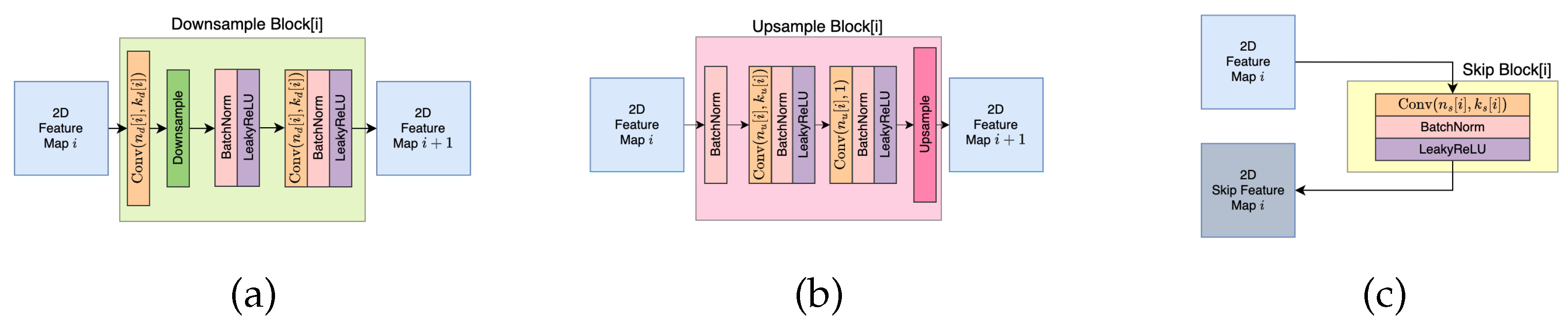
2. Method Description
2.1. Framework Configuration
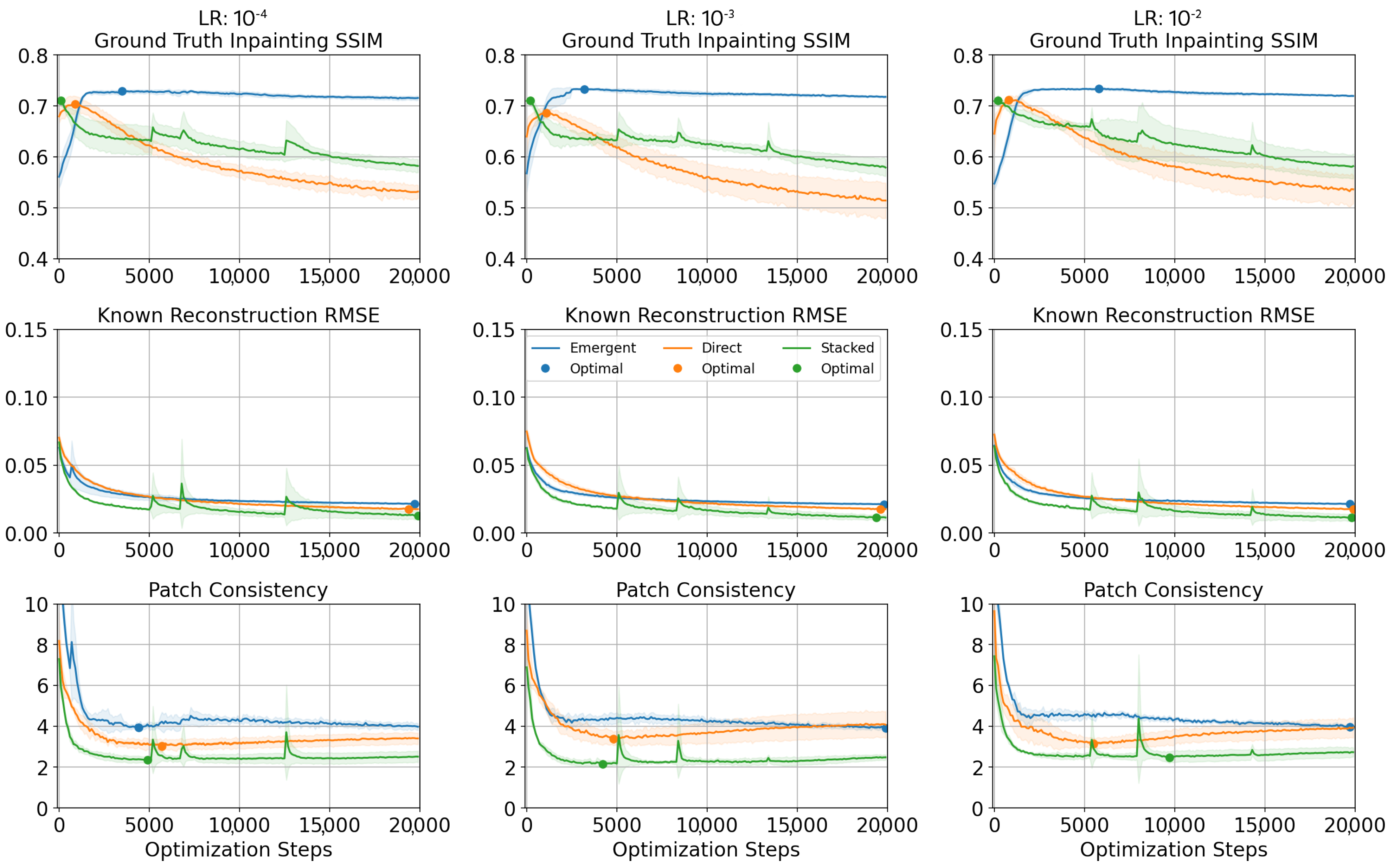
2.2. Convergence Detection
3. Evaluation
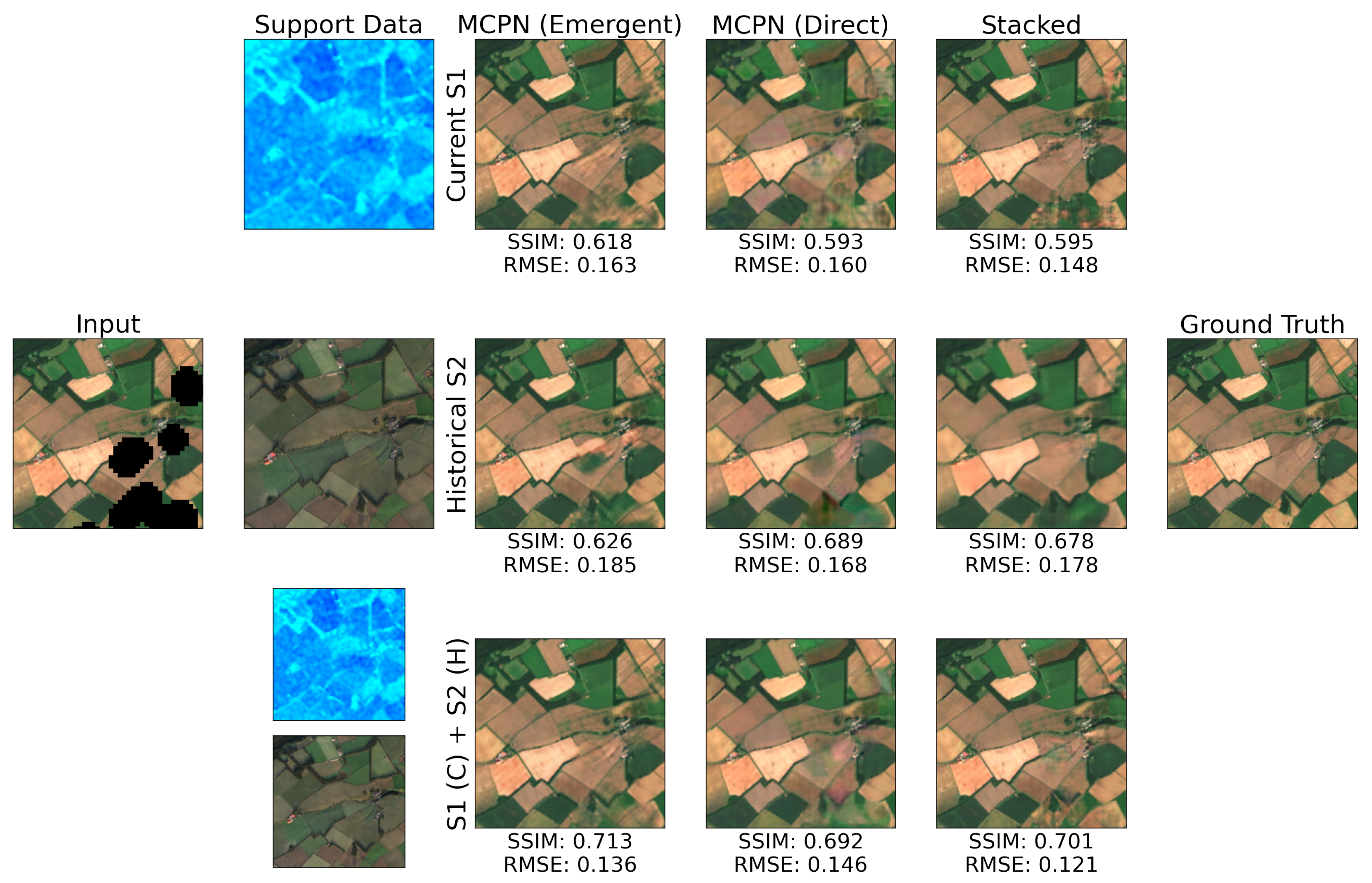
3.1. Guided Satellite Image Inpainting
3.2. Guided Satellite Image Super-Resolution
3.3. Guided Image Inpainting in Other Domains
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MCPN | Multi-modal Convolutional Parameterisation Network |
| SAR | Synthetic Aperture Radar |
| DIP | Deep Image Prior |
Appendix A. Convergence Detection
Appendix A.1. Satellite Inpainting
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Current Sentinel-1 | Whole | SSIM ↑ | 0.833 ± 0.065 | 0.824 ± 0.045 | 0.837 ± 0.063 |
| RMSE ↓ | 0.113 ± 0.104 | 0.081 ± 0.033 | 0.086 ± 0.050 | ||
| Inpainting | SSIM ↑ | 0.604 ± 0.170 | 0.601 ± 0.068 | 0.576 ± 0.080 | |
| RMSE ↓ | 0.203 ± 0.186 | 0.140 ± 0.055 | 0.149 ± 0.071 | ||
| Historical Sentinel-2 | Whole | SSIM ↑ | 0.857 ± 0.070 | 0.864 ± 0.041 | 0.875 ± 0.063 |
| RMSE ↓ | 0.119 ± 0.106 | 0.075 ± 0.028 | 0.086 ± 0.059 | ||
| Inpainting | SSIM ↑ | 0.654 ± 0.191 | 0.692 ± 0.075 | 0.703 ± 0.105 | |
| RMSE ↓ | 0.217 ± 0.190 | 0.131 ± 0.044 | 0.147 ± 0.089 | ||
| Current Sentinel-1 + Historical Sentinel-2 | Whole | SSIM ↑ | 0.855 ± 0.060 | 0.861 ± 0.039 | 0.879 ± 0.055 |
| RMSE ↓ | 0.091 ± 0.095 | 0.071 ± 0.032 | 0.074 ± 0.049 | ||
| Inpainting | SSIM ↑ | 0.700 ± 0.169 | 0.679 ± 0.070 | 0.713 ± 0.100 | |
| RMSE ↓ | 0.158 ± 0.170 | 0.124 ± 0.054 | 0.128 ± 0.076 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Current Sentinel-1 | Whole | SSIM ↑ | 0.850 ± 0.051 | 0.830 ± 0.050 | 0.839 ± 0.059 |
| RMSE ↓ | 0.089 ± 0.071 | 0.081 ± 0.032 | 0.084 ± 0.047 | ||
| Inpainting | SSIM ↑ | 0.621 ± 0.108 | 0.588 ± 0.069 | 0.564 ± 0.082 | |
| RMSE ↓ | 0.159 ± 0.124 | 0.141 ± 0.053 | 0.149 ± 0.077 | ||
| Historical Sentinel-2 | Whole | SSIM ↑ | 0.874 ± 0.054 | 0.872 ± 0.052 | 0.887 ± 0.050 |
| RMSE ↓ | 0.089 ± 0.077 | 0.076 ± 0.031 | 0.079 ± 0.055 | ||
| Inpainting | SSIM ↑ | 0.689 ± 0.135 | 0.690 ± 0.082 | 0.706 ± 0.105 | |
| RMSE ↓ | 0.158 ± 0.133 | 0.133 ± 0.046 | 0.139 ± 0.093 | ||
| Current Sentinel-1 + Historical Sentinel-2 | Whole | SSIM ↑ | 0.873 ± 0.048 | 0.867 ± 0.053 | 0.887 ± 0.047 |
| RMSE ↓ | 0.077 ± 0.069 | 0.073 ± 0.036 | 0.070 ± 0.044 | ||
| Inpainting | SSIM ↑ | 0.721 ± 0.122 | 0.669 ± 0.071 | 0.713 ± 0.093 | |
| RMSE ↓ | 0.134 ± 0.120 | 0.128 ± 0.054 | 0.123 ± 0.071 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Current Sentinel-1 | Whole | SSIM ↑ | 0.859 ± 0.041 | 0.834 ± 0.061 | 0.849 ± 0.060 |
| RMSE ↓ | 0.079 ± 0.048 | 0.086 ± 0.034 | 0.080 ± 0.045 | ||
| Inpainting | SSIM ↑ | 0.638 ± 0.081 | 0.532 ± 0.071 | 0.538 ± 0.079 | |
| RMSE ↓ | 0.141 ± 0.082 | 0.153 ± 0.050 | 0.146 ± 0.073 | ||
| Historical Sentinel-2 | Whole | SSIM ↑ | 0.880 ± 0.043 | 0.885 ± 0.048 | 0.896 ± 0.048 |
| RMSE ↓ | 0.079 ± 0.051 | 0.080 ± 0.029 | 0.075 ± 0.050 | ||
| Inpainting | SSIM ↑ | 0.698 ± 0.107 | 0.670 ± 0.079 | 0.701 ± 0.094 | |
| RMSE ↓ | 0.142 ± 0.089 | 0.143 ± 0.040 | 0.133 ± 0.080 | ||
| Current Sentinel-1 + Historical Sentinel-2 | Whole | SSIM ↑ | 0.882 ± 0.036 | 0.882 ± 0.045 | 0.896 ± 0.046 |
| RMSE ↓ | 0.069 ± 0.048 | 0.073 ± 0.031 | 0.068 ± 0.042 | ||
| Inpainting | SSIM ↑ | 0.735 ± 0.096 | 0.654 ± 0.064 | 0.703 ± 0.091 | |
| RMSE ↓ | 0.120 ± 0.087 | 0.132 ± 0.049 | 0.122 ± 0.067 |
Appendix A.2. Guided Super-Resolution
| Factor | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | PixTransform [34] | EDSR | |
|---|---|---|---|---|---|---|
| ×16 | SSIM ↑ | 0.641 ± 0.090 | 0.735 ± 0.068 | 0.731 ± 0.066 | 0.718 ± 0.060 | 0.699 ± 0.055 |
| RMSE ↓ | 0.140 ± 0.064 | 0.085 ± 0.047 | 0.090 ± 0.052 | 0.094 ± 0.046 | 0.098 ± 0.045 | |
| ×8 | SSIM ↑ | 0.716 ± 0.088 | 0.782 ± 0.049 | 0.783 ± 0.072 | 0.758 ± 0.052 | 0.727 ± 0.050 |
| RMSE ↓ | 0.098 ± 0.057 | 0.064 ± 0.029 | 0.071 ± 0.050 | 0.076 ± 0.039 | 0.080 ± 0.040 | |
| ×4 | SSIM ↑ | 0.783 ± 0.085 | 0.848 ± 0.029 | 0.840 ± 0.070 | 0.815 ± 0.044 | 0.789 ± 0.038 |
| RMSE ↓ | 0.075 ± 0.047 | 0.047 ± 0.017 | 0.055 ± 0.044 | 0.061 ± 0.031 | 0.061 ± 0.031 |
| Factor | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | PixTransform [34] | EDSR | |
|---|---|---|---|---|---|---|
| ×16 | SSIM ↑ | 0.487 ± 0.137 | 0.710 ± 0.062 | 0.719 ± 0.072 | 0.718 ± 0.060 | 0.699 ± 0.055 |
| RMSE ↓ | 0.184 ± 0.057 | 0.091 ± 0.047 | 0.094 ± 0.060 | 0.094 ± 0.046 | 0.098 ± 0.045 | |
| ×8 | SSIM ↑ | 0.584 ± 0.168 | 0.748 ± 0.047 | 0.771 ± 0.085 | 0.758 ± 0.052 | 0.727 ± 0.050 |
| RMSE ↓ | 0.135 ± 0.067 | 0.071 ± 0.032 | 0.076 ± 0.061 | 0.076 ± 0.039 | 0.080 ± 0.040 | |
| ×4 | SSIM ↑ | 0.685 ± 0.137 | 0.809 ± 0.031 | 0.825 ± 0.084 | 0.815 ± 0.044 | 0.789 ± 0.038 |
| RMSE ↓ | 0.104 ± 0.068 | 0.054 ± 0.019 | 0.062 ± 0.057 | 0.061 ± 0.031 | 0.061 ± 0.031 |
| Factor | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | PixTransform [34] | EDSR | |
|---|---|---|---|---|---|---|
| ×16 | SSIM ↑ | 0.410 ± 0.169 | 0.728 ± 0.068 | 0.695 ± 0.078 | 0.718 ± 0.060 | 0.699 ± 0.055 |
| RMSE ↓ | 0.212 ± 0.075 | 0.087 ± 0.047 | 0.102 ± 0.071 | 0.094 ± 0.046 | 0.098 ± 0.045 | |
| ×8 | SSIM ↑ | 0.605 ± 0.137 | 0.780 ± 0.049 | 0.758 ± 0.086 | 0.758 ± 0.052 | 0.727 ± 0.050 |
| RMSE ↓ | 0.131 ± 0.072 | 0.065 ± 0.029 | 0.080 ± 0.065 | 0.076 ± 0.039 | 0.080 ± 0.040 | |
| ×4 | SSIM ↑ | 0.720 ± 0.160 | 0.845 ± 0.030 | 0.830 ± 0.091 | 0.815 ± 0.044 | 0.789 ± 0.038 |
| RMSE ↓ | 0.104 ± 0.115 | 0.047 ± 0.017 | 0.059 ± 0.053 | 0.061 ± 0.031 | 0.061 ± 0.031 |
| Factor | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | PixTransform [34] | EDSR | |
|---|---|---|---|---|---|---|
| ×16 | SSIM ↑ | 0.389 ± 0.180 | 0.733 ± 0.068 | 0.695 ± 0.078 | 0.718 ± 0.060 | 0.699 ± 0.055 |
| RMSE ↓ | 0.213 ± 0.081 | 0.085 ± 0.047 | 0.102 ± 0.071 | 0.094 ± 0.046 | 0.098 ± 0.045 | |
| ×8 | SSIM ↑ | 0.541 ± 0.201 | 0.782 ± 0.049 | 0.759 ± 0.089 | 0.758 ± 0.052 | 0.727 ± 0.050 |
| RMSE ↓ | 0.150 ± 0.081 | 0.064 ± 0.029 | 0.081 ± 0.070 | 0.076 ± 0.039 | 0.080 ± 0.040 | |
| ×4 | SSIM ↑ | 0.674 ± 0.154 | 0.847 ± 0.029 | 0.829 ± 0.096 | 0.815 ± 0.044 | 0.789 ± 0.038 |
| RMSE ↓ | 0.100 ± 0.068 | 0.047 ± 0.017 | 0.060 ± 0.056 | 0.061 ± 0.031 | 0.061 ± 0.031 |
Appendix A.3. Other Tasks
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Facades (Segmentation → Building) | Whole | SSIM ↑ | 0.754 ± 0.062 | 0.761 ± 0.100 | 0.702 ± 0.115 |
| RMSE ↓ | 0.107 ± 0.030 | 0.106 ± 0.034 | 0.109 ± 0.035 | ||
| Inpainting | SSIM ↑ | 0.496 ± 0.104 | 0.532 ± 0.128 | 0.532 ± 0.123 | |
| RMSE ↓ | 0.169 ± 0.050 | 0.166 ± 0.050 | 0.158 ± 0.049 | ||
| Maps (Map → Aerial) | Whole | SSIM ↑ | 0.792 ± 0.069 | 0.733 ± 0.118 | 0.607 ± 0.152 |
| RMSE ↓ | 0.082 ± 0.031 | 0.084 ± 0.030 | 0.111 ± 0.041 | ||
| Inpainting | SSIM ↑ | 0.533 ± 0.173 | 0.540 ± 0.168 | 0.499 ± 0.184 | |
| RMSE ↓ | 0.131 ± 0.051 | 0.124 ± 0.047 | 0.147 ± 0.062 | ||
| Night-to-Day (Day → Night) | Whole | SSIM ↑ | 0.868 ± 0.076 | 0.753 ± 0.116 | 0.807 ± 0.115 |
| RMSE ↓ | 0.072 ± 0.040 | 0.094 ± 0.035 | 0.081 ± 0.042 | ||
| Inpainting | SSIM ↑ | 0.727 ± 0.161 | 0.668 ± 0.141 | 0.729 ± 0.158 | |
| RMSE ↓ | 0.114 ± 0.064 | 0.129 ± 0.053 | 0.112 ± 0.065 | ||
| Cityscapes (Segmentation → Street) | Whole | SSIM ↑ | 0.830 ± 0.031 | 0.743 ± 0.050 | 0.747 ± 0.055 |
| RMSE ↓ | 0.086 ± 0.028 | 0.088 ± 0.018 | 0.083 ± 0.019 | ||
| Inpainting | SSIM ↑ | 0.625 ± 0.075 | 0.649 ± 0.066 | 0.672 ± 0.065 | |
| RMSE ↓ | 0.138 ± 0.046 | 0.120 ± 0.029 | 0.110 ± 0.030 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Facades (Segmentation → Building) | Whole | SSIM ↑ | 0.763 ± 0.044 | 0.700 ± 0.076 | 0.720 ± 0.100 |
| RMSE ↓ | 0.108 ± 0.031 | 0.129 ± 0.035 | 0.118 ± 0.038 | ||
| Inpainting | SSIM ↑ | 0.476 ± 0.109 | 0.447 ± 0.132 | 0.453 ± 0.130 | |
| RMSE ↓ | 0.172 ± 0.051 | 0.200 ± 0.058 | 0.184 ± 0.061 | ||
| Maps (Map → Aerial) | Whole | SSIM ↑ | 0.759 ± 0.069 | 0.768 ± 0.074 | 0.744 ± 0.076 |
| RMSE ↓ | 0.112 ± 0.056 | 0.085 ± 0.030 | 0.113 ± 0.038 | ||
| Inpainting | SSIM ↑ | 0.472 ± 0.167 | 0.510 ± 0.175 | 0.404 ± 0.169 | |
| RMSE ↓ | 0.180 ± 0.093 | 0.134 ± 0.050 | 0.183 ± 0.061 | ||
| Night-to-Day (Day → Night) | Whole | SSIM ↑ | 0.804 ± 0.103 | 0.767 ± 0.092 | 0.823 ± 0.082 |
| RMSE ↓ | 0.157 ± 0.124 | 0.103 ± 0.038 | 0.113 ± 0.060 | ||
| Inpainting | SSIM ↑ | 0.570 ± 0.245 | 0.552 ± 0.171 | 0.605 ± 0.199 | |
| RMSE ↓ | 0.254 ± 0.205 | 0.164 ± 0.063 | 0.183 ± 0.100 | ||
| Cityscapes (Segmentation → Street) | Whole | SSIM ↑ | 0.822 ± 0.031 | 0.793 ± 0.041 | 0.802 ± 0.047 |
| RMSE ↓ | 0.093 ± 0.030 | 0.092 ± 0.023 | 0.093 ± 0.028 | ||
| Inpainting | SSIM ↑ | 0.613 ± 0.077 | 0.610 ± 0.071 | 0.608 ± 0.077 | |
| RMSE ↓ | 0.150 ± 0.050 | 0.143 ± 0.037 | 0.147 ± 0.047 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Facades (Segmentation → Building) | Whole | SSIM ↑ | 0.764 ± 0.043 | 0.784 ± 0.058 | 0.771 ± 0.058 |
| RMSE ↓ | 0.112 ± 0.029 | 0.113 ± 0.040 | 0.110 ± 0.037 | ||
| Inpainting | SSIM ↑ | 0.446 ± 0.106 | 0.505 ± 0.144 | 0.437 ± 0.145 | |
| RMSE ↓ | 0.182 ± 0.048 | 0.183 ± 0.067 | 0.180 ± 0.061 | ||
| Maps (Map → Aerial) | Whole | SSIM ↑ | 0.791 ± 0.070 | 0.798 ± 0.069 | 0.756 ± 0.077 |
| RMSE ↓ | 0.085 ± 0.031 | 0.082 ± 0.029 | 0.098 ± 0.036 | ||
| Inpainting | SSIM ↑ | 0.512 ± 0.174 | 0.505 ± 0.172 | 0.389 ± 0.195 | |
| RMSE ↓ | 0.137 ± 0.051 | 0.134 ± 0.048 | 0.160 ± 0.059 | ||
| Night-to-Day (Day → Night) | Whole | SSIM ↑ | 0.870 ± 0.068 | 0.751 ± 0.080 | 0.842 ± 0.079 |
| RMSE ↓ | 0.075 ± 0.041 | 0.121 ± 0.040 | 0.097 ± 0.057 | ||
| Inpainting | SSIM ↑ | 0.709 ± 0.167 | 0.464 ± 0.159 | 0.620 ± 0.197 | |
| RMSE ↓ | 0.121 ± 0.067 | 0.196 ± 0.066 | 0.159 ± 0.094 | ||
| Cityscapes (Segmentation → Street) | Whole | SSIM ↑ | 0.831 ± 0.030 | 0.821 ± 0.029 | 0.825 ± 0.028 |
| RMSE ↓ | 0.088 ± 0.027 | 0.094 ± 0.021 | 0.084 ± 0.020 | ||
| Inpainting | SSIM ↑ | 0.604 ± 0.076 | 0.593 ± 0.069 | 0.569 ± 0.071 | |
| RMSE ↓ | 0.143 ± 0.045 | 0.153 ± 0.035 | 0.138 ± 0.033 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Facades (Segmentation → Building) | Whole | SSIM ↑ | 0.759 ± 0.046 | 0.734 ± 0.091 | 0.740 ± 0.089 |
| RMSE ↓ | 0.113 ± 0.029 | 0.121 ± 0.039 | 0.122 ± 0.042 | ||
| Inpainting | SSIM ↑ | 0.450 ± 0.103 | 0.478 ± 0.138 | 0.442 ± 0.138 | |
| RMSE ↓ | 0.182 ± 0.048 | 0.189 ± 0.061 | 0.194 ± 0.065 | ||
| Maps (Map → Aerial) | Whole | SSIM ↑ | 0.774 ± 0.064 | 0.771 ± 0.088 | 0.751 ± 0.074 |
| RMSE ↓ | 0.102 ± 0.060 | 0.086 ± 0.030 | 0.101 ± 0.035 | ||
| Inpainting | SSIM ↑ | 0.478 ± 0.161 | 0.506 ± 0.170 | 0.392 ± 0.180 | |
| RMSE ↓ | 0.164 ± 0.099 | 0.134 ± 0.048 | 0.164 ± 0.058 | ||
| Night-to-Day (Day → Night) | Whole | SSIM ↑ | 0.851 ± 0.069 | 0.769 ± 0.093 | 0.828 ± 0.103 |
| RMSE ↓ | 0.085 ± 0.042 | 0.100 ± 0.038 | 0.096 ± 0.055 | ||
| Inpainting | SSIM ↑ | 0.672 ± 0.166 | 0.576 ± 0.148 | 0.644 ± 0.178 | |
| RMSE ↓ | 0.137 ± 0.069 | 0.157 ± 0.060 | 0.150 ± 0.076 | ||
| Cityscapes (Segmentation → Street) | Whole | SSIM ↑ | 0.825 ± 0.028 | 0.801 ± 0.034 | 0.820 ± 0.032 |
| RMSE ↓ | 0.094 ± 0.030 | 0.090 ± 0.020 | 0.093 ± 0.026 | ||
| Inpainting | SSIM ↑ | 0.598 ± 0.069 | 0.609 ± 0.067 | 0.592 ± 0.067 | |
| RMSE ↓ | 0.153 ± 0.050 | 0.142 ± 0.034 | 0.150 ± 0.042 |
References
- Gandelsman, Y.; Shocher, A.; Irani, M. “Double-DIP”: Unsupervised Image Decomposition via Coupled Deep-Image-Priors. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11018–11027. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep Image Prior. Int. J. Comput. Vis. 2020, 128, 1867–1888. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J. Remote Sensing Image Fusion With Deep Convolutional Neural Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Bermudez, J.D.; Happ, P.N.; Oliveira, D.A.; Feitosa, R.Q. SAR to Optical Image Synthesis for Cloud Removal with Generative Adversarial Networks. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 5–11. [Google Scholar] [CrossRef]
- Singh, P.; Komodakis, N. Cloud-Gan: Cloud Removal for Sentinel-2 Imagery Using a Cyclic Consistent Generative Adversarial Networks. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1772–1775. [Google Scholar] [CrossRef]
- Meraner, A.; Ebel, P.; Zhu, X.X.; Schmitt, M. Cloud removal in Sentinel-2 imagery using a deep residual neural network and SAR-optical data fusion. ISPRS J. Photogramm. Remote Sens. 2020, 166, 333–346. [Google Scholar] [CrossRef] [PubMed]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Zeng, C.; Li, X.; Wei, Y. Missing data reconstruction in remote sensing image with a unified spatial-temporal-spectral deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef]
- Kang, S.H.; Choi, Y.; Choi, J.Y. Restoration of missing patterns on satellite infrared sea surface temperature images due to cloud coverage using deep generative inpainting network. J. Mar. Sci. Eng. 2021, 9, 310. [Google Scholar] [CrossRef]
- Gao, J.; Yuan, Q.; Li, J.; Su, X. Unsupervised missing information reconstruction for single remote sensing image with Deep Code Regression. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102599. [Google Scholar] [CrossRef]
- Ebel, P.; Schmitt, M.; Zhu, X.X. Internal Learning for Sequence-to-Sequence Cloud Removal via Synthetic Aperture Radar Prior Information. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2691–2694. [Google Scholar] [CrossRef]
- Ebel, P.; Xu, Y.; Schmitt, M.; Zhu, X.X. SEN12MS-CR-TS: A Remote Sensing Data Set for Multi-modal Multi-temporal Cloud Removal. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5222414. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, C.; Wu, Y.; Luo, J. Remote sensing image cloud removal by deep image prior with a multitemporal constraint. Opt. Contin. 2022, 1, 215–226. [Google Scholar] [CrossRef]
- Czerkawski, M.; Upadhyay, P.; Davison, C.; Werkmeister, A.; Cardona, J.; Atkinson, R.; Michie, C.; Andonovic, I.; Macdonald, M.; Tachtatzis, C. Deep Internal Learning for Inpainting of Cloud-Affected Regions in Satellite Imagery. Remote Sens. 2022, 14, 1342. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, Q. Information Content Weighting for Perceptual Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 1185–1198. [Google Scholar] [CrossRef] [PubMed]
- Golestaneh, S.A.; Dadsetan, S.; Kitani, K.M. No-Reference Image Quality Assessment via Transformers, Relative Ranking, and Self-Consistency. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 3209–3218. [Google Scholar]
- Zhang, W.; Ma, K.; Zhai, G.; Yang, X. Uncertainty-aware blind image quality assessment in the laboratory and wild. IEEE Trans. Image Process. 2021, 30, 3474–3486. [Google Scholar] [CrossRef] [PubMed]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Shaham, T.R.; Dekel, T.; Michaeli, T. SinGAN: Learning a Generative Model From a Single Natural Image. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4569–4579. [Google Scholar] [CrossRef]
- Upadhyay, P.; Czerkawski, M.; Davison, C.; Cardona, J.; Macdonald, M.; Andonovic, I.; Michie, C.; Atkinson, R.; Papadopoulou, N.; Nikas, K.; et al. A Flexible Multi-Temporal and Multi-Modal Framework for Sentinel-1 and Sentinel-2 Analysis Ready Data. Remote Sens. 2022, 14, 1120. [Google Scholar] [CrossRef]
- Zaytar, M.A.; Amrani, C.E. Satellite image inpainting with deep generative adversarial neural networks. IAES Int. J. Artif. Intell. 2021, 10, 121–130. [Google Scholar] [CrossRef]
- Deng, Y.; Hui, S.; Wang, J. Image Inpainting with Bilateral Convolution. Remote Sens. 2022, 14, 6410. [Google Scholar]
- Suvorov, R.; Logacheva, E.; Mashikhin, A.; Remizova, A.; Ashukha, A.; Silvestrov, A.; Kong, N.; Goka, H.; Park, K.; Lempitsky, V. Resolution-robust Large Mask Inpainting with Fourier Convolutions. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision, WACV 2022, Waikoloa, HI, USA, 3–8 January 2022; pp. 3172–3182. [Google Scholar] [CrossRef]
- Saharia, C.; Chan, W.; Chang, H.; Lee, C.; Ho, J.; Salimans, T.; Fleet, D.; Norouzi, M. Palette: Image-to-Image Diffusion Models. Proc. ACM SIGGRAPH 2022, 1, 1–10. [Google Scholar] [CrossRef]
- Lugmayr, A.; Danelljan, M.; Romero, A.; Yu, F.; Timofte, R.; Van Gool, L. RePaint: Inpainting using Denoising Diffusion Probabilistic Models. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11451–11461. [Google Scholar] [CrossRef]
- Conover, W.J. Practical Nonparametric Statistics, 3rd ed.; Wiley series in probability and statistics Applied probability and statistics; Wiley: New York, NY, USA, 1999. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. In Proceedings of the 11th European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 1–14. [Google Scholar] [CrossRef]
- Barron, J.T.; Poole, B. The Fast Bilateral Solver. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 617–632. [Google Scholar]
- Hui, T.W.; Loy, C.C.; Tang, X. Depth Map Super-Resolution by Deep Multi-Scale Guidance. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 353–369. [Google Scholar]
- Ham, B.; Cho, M.; Ponce, J. Robust Guided Image Filtering Using Nonconvex Potentials. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 192–207. [Google Scholar] [CrossRef] [PubMed]
- Lutio, R.D.; D’Aronco, S.; Wegner, J.D.; Schindler, K. Guided super-resolution as pixel-to-pixel transformation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8828–8836. [Google Scholar] [CrossRef]
- Lutio, R.D.; Becker, A.; DAronco, S.; Russo, S.; Wegner, J.D.; Schindler, K. Learning Graph Regularisation for Guided Super-Resolution. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 1969–1978. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Los Alamitos, CA, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Core Network Base | [16, 32, 64, 128, 128, 128] |
| Core Network Skip | [4, 4, 4, 4, 4, 4] |
| Head Network Base | [32, 32] |
| Head Network Skip | [32, 32] |
| Head Kernel Size | 3 × 3 |
| Head Activation | None |
| Method | LR | Inpainting SSIM (GT) ↑ | Known RMSE ↓ | Patch Consistency ↓ |
|---|---|---|---|---|
| 10−4 | 0.732 at 3600 ± 1579 | 0.022 at 19,325 ± 491 | 3.782 at 8600 ± 5839 | |
| MCPN Emergent | 10−3 | 0.735 at 3725 ± 914 | 0.021 at 19,575 ± 449 | 3.805 at 15,275 ± 7553 |
| 10−2 | 0.735 at 3575 ± 1380 | 0.021 at 19,525 ± 363 | 3.875 at 15,000 ± 7510 | |
| 10−4 | 0.706 at 800 ± 254 | 0.017 at 19,400 ± 494 | 2.989 at 5375 ± 1028 | |
| MCPN Direct | 10−3 | 0.689 at 1350 ± 390 | 0.018 at 19,600 ± 212 | 3.322 at 6425 ± 1987 |
| 10−2 | 0.714 at 1000 ± 158 | 0.017 at 19,850 ± 50 | 3.025 at 5750 ± 1425 | |
| 10−4 | 0.713 at 75 ± 43 | 0.011 at 17,650 ± 3332 | 2.261 at 9700 ± 5980 | |
| Stacked | 10−3 | 0.712 at 1400 ± 2136 | 0.011 at 19,450 ± 384 | 2.032 at 9025 ± 4935 |
| 10−2 | 0.716 at 3450 ± 3377 | 0.011 at 16,525 ± 5063 | 2.367 at 8675 ± 4246 |
| Method | LR | Ideal (GT) | 4000 Steps | Known RMSE | Patch Consistency |
|---|---|---|---|---|---|
| MCPN Emergent | 10−3 | 0.677 ± 0.071 | 0.626 ± 0.160 | 0.669 ± 0.066 | 0.637 ± 0.098 |
| MCPN Direct | 10−2 | 0.663 ± 0.069 | 0.611 ± 0.070 | 0.521 ± 0.080 | 0.601 ± 0.074 |
| Stacked | 10−2 | 0.650 ± 0.079 | 0.573 ± 0.090 | 0.545 ± 0.078 | 0.570 ± 0.087 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Current Sentinel-1 | Whole | SSIM ↑ | 0.854 ± 0.041 | 0.760 ± 0.052 | 0.743 ± 0.053 |
| RMSE ↓ | 0.079 ± 0.053 | 0.088 ± 0.029 | 0.092 ± 0.041 | ||
| Inpainting | SSIM ↑ | 0.665 ± 0.082 | 0.657 ± 0.072 | 0.661 ± 0.077 | |
| RMSE ↓ | 0.137 ± 0.090 | 0.130 ± 0.053 | 0.131 ± 0.063 | ||
| Historical Sentinel-2 | Whole | SSIM ↑ | 0.879 ± 0.044 | 0.853 ± 0.069 | 0.879 ± 0.062 |
| RMSE ↓ | 0.081 ± 0.062 | 0.072 ± 0.026 | 0.071 ± 0.046 | ||
| Inpainting | SSIM ↑ | 0.719 ± 0.113 | 0.714 ± 0.068 | 0.738 ± 0.090 | |
| RMSE ↓ | 0.142 ± 0.108 | 0.120 ± 0.039 | 0.120 ± 0.069 | ||
| Current Sentinel-1 + Historical Sentinel-2 | Whole | SSIM ↑ | 0.876 ± 0.036 | 0.838 ± 0.056 | 0.869 ± 0.065 |
| RMSE ↓ | 0.071 ± 0.055 | 0.071 ± 0.030 | 0.066 ± 0.038 | ||
| Inpainting | SSIM ↑ | 0.743 ± 0.098 | 0.694 ± 0.064 | 0.741 ± 0.083 | |
| RMSE ↓ | 0.121 ± 0.101 | 0.117 ± 0.050 | 0.111 ± 0.059 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Known RMSE | 4000 Steps | 4000 Steps | |||
| Current Sentinel-1 | Whole | SSIM ↑ | 0.859 ± 0.041 | 0.824 ± 0.045 | 0.837 ± 0.063 |
| RMSE ↓ | 0.079 ± 0.048 | 0.081 ± 0.033 | 0.086 ± 0.050 | ||
| Inpainting | SSIM ↑ | 0.638 ± 0.081 | 0.601 ± 0.068 | 0.576 ± 0.080 | |
| RMSE ↓ | 0.141 ± 0.082 | 0.140 ± 0.055 | 0.149 ± 0.071 | ||
| Historical Sentinel-2 | Whole | SSIM ↑ | 0.880 ± 0.043 | 0.864 ± 0.041 | 0.875 ± 0.063 |
| RMSE ↓ | 0.079 ± 0.051 | 0.075 ± 0.028 | 0.086 ± 0.059 | ||
| Inpainting | SSIM ↑ | 0.698 ± 0.107 | 0.692 ± 0.075 | 0.703 ± 0.105 | |
| RMSE ↓ | 0.142 ± 0.089 | 0.131 ± 0.044 | 0.147 ± 0.089 | ||
| Current Sentinel-1 + Historical Sentinel-2 | Whole | SSIM ↑ | 0.882 ± 0.036 | 0.861 ± 0.039 | 0.879 ± 0.055 |
| RMSE ↓ | 0.069 ± 0.048 | 0.071 ± 0.032 | 0.074 ± 0.049 | ||
| Inpainting | SSIM ↑ | 0.735 ± 0.096 | 0.679 ± 0.070 | 0.713 ± 0.100 | |
| RMSE ↓ | 0.120 ± 0.087 | 0.124 ± 0.054 | 0.128 ± 0.076 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Known RMSE | 4000 Steps | 4000 Steps | |||
| Current Sentinel-1 | Whole | SSIM ↑ | +0.900 ✓ | −0.993 ✗ | +0.094 |
| RMSE ↓ | −0.555 ✓ | +0.417 ✗ | +0.138 | ||
| Inpainting | SSIM ↑ | +0.900 ✓ | −0.168 ✓ | −0.732 | |
| RMSE ↓ | −0.488 ✓ | +0.175 ✓ | +0.313 | ||
| Historical Sentinel-2 | Whole | SSIM ↑ | +0.207 ✗ | −0.652 ✗ | +0.445 |
| RMSE ↓ | −0.100 ✓ | +0.139 ✗ | −0.039 | ||
| Inpainting | SSIM ↑ | −0.031 ✗ | −0.212 ✗ | +0.243 | |
| RMSE ↓ | −0.032 ✗ | +0.056 ✓ | −0.024 | ||
| Current Sentinel-1 + Historical Sentinel-2 | Whole | SSIM ↑ | +0.405 ✗ | −0.953 ✗ | +0.548 |
| RMSE ↓ | −0.452 ✓ | +0.526 ✗ | −0.074 | ||
| Inpainting | SSIM ↑ | +0.738 ✓ | −0.823 ✗ | +0.085 | |
| RMSE ↓ | −0.521 ✓ | +0.489 ✗ | +0.032 |
| Factor | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | PixTransform [34] | EDSR [36] | |
|---|---|---|---|---|---|---|
| 4000 Steps | Known RMSE | 4000 Steps | ||||
| ×16 | SSIM ↑ | 0.487 ± 0.137 | 0.733 ± 0.068 | 0.719 ± 0.072 | 0.718 ± 0.060 | 0.699 ± 0.055 |
| RMSE ↓ | 0.184 ± 0.057 | 0.085 ± 0.047 | 0.094 ± 0.060 | 0.094 ± 0.046 | 0.098 ± 0.045 | |
| ×8 | SSIM ↑ | 0.584 ± 0.168 | 0.782 ± 0.049 | 0.771 ± 0.085 | 0.758 ± 0.052 | 0.727 ± 0.050 |
| RMSE ↓ | 0.135 ± 0.067 | 0.064 ± 0.029 | 0.076 ± 0.061 | 0.076 ± 0.039 | 0.080 ± 0.040 | |
| ×4 | SSIM ↑ | 0.685 ± 0.137 | 0.847 ± 0.029 | 0.825 ± 0.084 | 0.815 ± 0.044 | 0.789 ± 0.038 |
| RMSE ↓ | 0.104 ± 0.068 | 0.047 ± 0.017 | 0.062 ± 0.057 | 0.061 ± 0.031 | 0.061 ± 0.031 |
| Guidance | MCPN (Emergent Core) | MCPN (Direct Core) | Stacked | ||
|---|---|---|---|---|---|
| Facades (Segmentation → Building) | Whole | SSIM ↑ | 0.763 ± 0.044 § | 0.784 ± 0.058 † | 0.720 ± 0.100 † |
| RMSE ↓ | 0.108 ± 0.031 § | 0.113 ± 0.040 † | 0.118 ± 0.038 † | ||
| Inpainting | SSIM ↑ | 0.476 ± 0.109 § | 0.505 ± 0.144 † | 0.453 ± 0.130 † | |
| RMSE ↓ | 0.172 ± 0.051 § | 0.183 ± 0.067 † | 0.184 ± 0.061 † | ||
| Maps (Map → Aerial) | Whole | SSIM ↑ | 0.791 ± 0.070 † | 0.768 ± 0.074 § | 0.744 ± 0.076 § |
| RMSE ↓ | 0.085 ± 0.031 † | 0.085 ± 0.030 § | 0.113 ± 0.038 § | ||
| Inpainting | SSIM ↑ | 0.512 ± 0.174 † | 0.510 ± 0.175 § | 0.404 ± 0.169 § | |
| RMSE ↓ | 0.137 ± 0.051 † | 0.134 ± 0.050 § | 0.183 ± 0.061 § | ||
| Night-to-Day (Day → Night) | Whole | SSIM ↑ | 0.870 ± 0.068 † | 0.769 ± 0.093 ‡ | 0.828 ± 0.103 ‡ |
| RMSE ↓ | 0.075 ± 0.041 † | 0.100 ± 0.038 ‡ | 0.096 ± 0.055 ‡ | ||
| Inpainting | SSIM ↑ | 0.709 ± 0.167 † | 0.576 ± 0.148 ‡ | 0.644 ± 0.178 ‡ | |
| RMSE ↓ | 0.121 ± 0.067 † | 0.157 ± 0.060 ‡ | 0.150 ± 0.076 ‡ | ||
| Cityscapes (Segmentation → Street) | Whole | SSIM ↑ | 0.822 ± 0.031 § | 0.793 ± 0.041 § | 0.802 ± 0.047 § |
| RMSE ↓ | 0.093 ± 0.030 § | 0.092 ± 0.023 § | 0.093 ± 0.028 § | ||
| Inpainting | SSIM ↑ | 0.613 ± 0.077 § | 0.610 ± 0.071 § | 0.608 ± 0.077 § | |
| RMSE ↓ | 0.150 ± 0.050 § | 0.143 ± 0.037 § | 0.147 ± 0.047 § |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czerkawski, M.; Upadhyay, P.; Davison, C.; Atkinson, R.; Michie, C.; Andonovic, I.; Macdonald, M.; Cardona, J.; Tachtatzis, C. Multi-Modal Convolutional Parameterisation Network for Guided Image Inverse Problems. J. Imaging 2024, 10, 69. https://doi.org/10.3390/jimaging10030069
Czerkawski M, Upadhyay P, Davison C, Atkinson R, Michie C, Andonovic I, Macdonald M, Cardona J, Tachtatzis C. Multi-Modal Convolutional Parameterisation Network for Guided Image Inverse Problems. Journal of Imaging. 2024; 10(3):69. https://doi.org/10.3390/jimaging10030069
Chicago/Turabian StyleCzerkawski, Mikolaj, Priti Upadhyay, Christopher Davison, Robert Atkinson, Craig Michie, Ivan Andonovic, Malcolm Macdonald, Javier Cardona, and Christos Tachtatzis. 2024. "Multi-Modal Convolutional Parameterisation Network for Guided Image Inverse Problems" Journal of Imaging 10, no. 3: 69. https://doi.org/10.3390/jimaging10030069
APA StyleCzerkawski, M., Upadhyay, P., Davison, C., Atkinson, R., Michie, C., Andonovic, I., Macdonald, M., Cardona, J., & Tachtatzis, C. (2024). Multi-Modal Convolutional Parameterisation Network for Guided Image Inverse Problems. Journal of Imaging, 10(3), 69. https://doi.org/10.3390/jimaging10030069











