Neural Radiance Field-Inspired Depth Map Refinement for Accurate Multi-View Stereo †
Abstract
1. Introduction
2. Related Work
2.1. MVS-Based Approaches
2.1.1. COLMAP
2.1.2. Deep Learning
2.2. NeRF-Based Approaches
2.2.1. NeRF
2.2.2. DS-NeRF
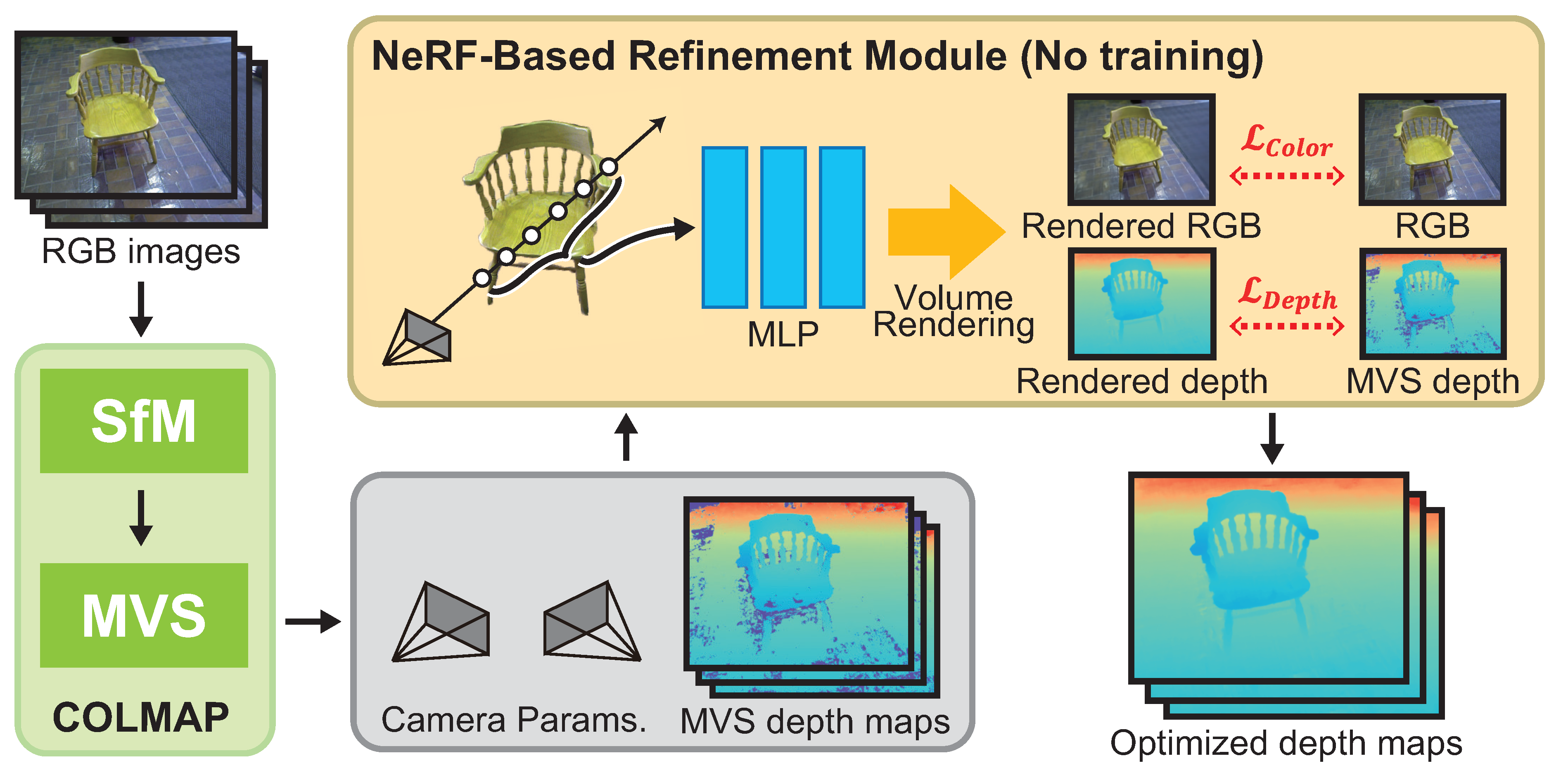
3. NeRF-Inspired Depth Map Refienment
3.1. Overview
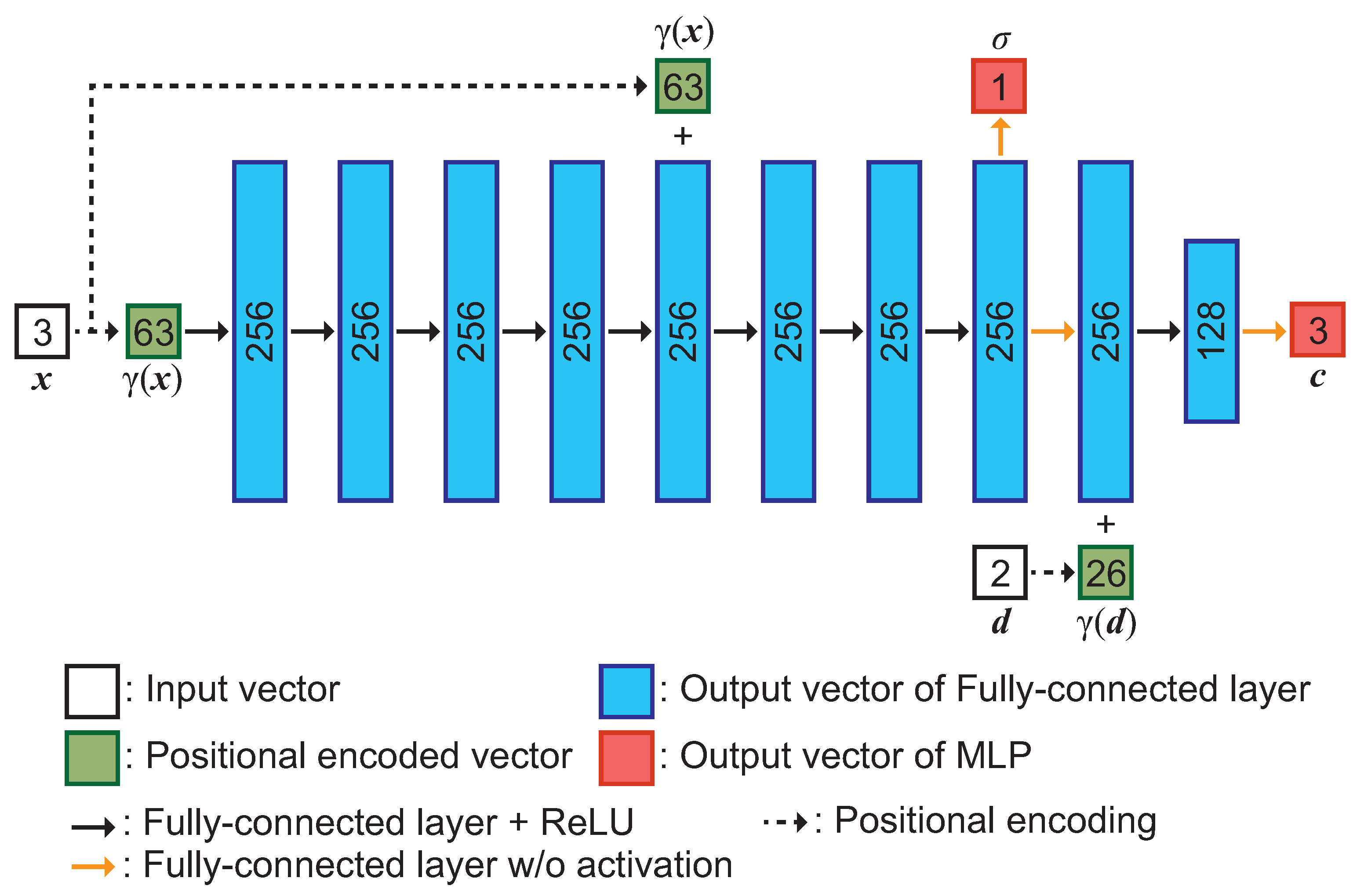
3.2. Network Architecture of an MLP
3.3. Objective Functions
3.3.1. Color Reconstruction
3.3.2. Depth Reconstruction
4. Experiments and Discussion
4.1. Dataset
4.1.1. Redwood-3d Scan Dataset (Redwood)
4.1.2. DTU Dataset (DTU)
4.2. Experimental Condition
4.3. Evaluation Metrics
4.4. Ablation Study of Depth Loss
4.4.1. Threshold of Huber Loss
4.4.2. Hyper Parameter of Objective Function
4.4.3. Difference between Other Depth Loss
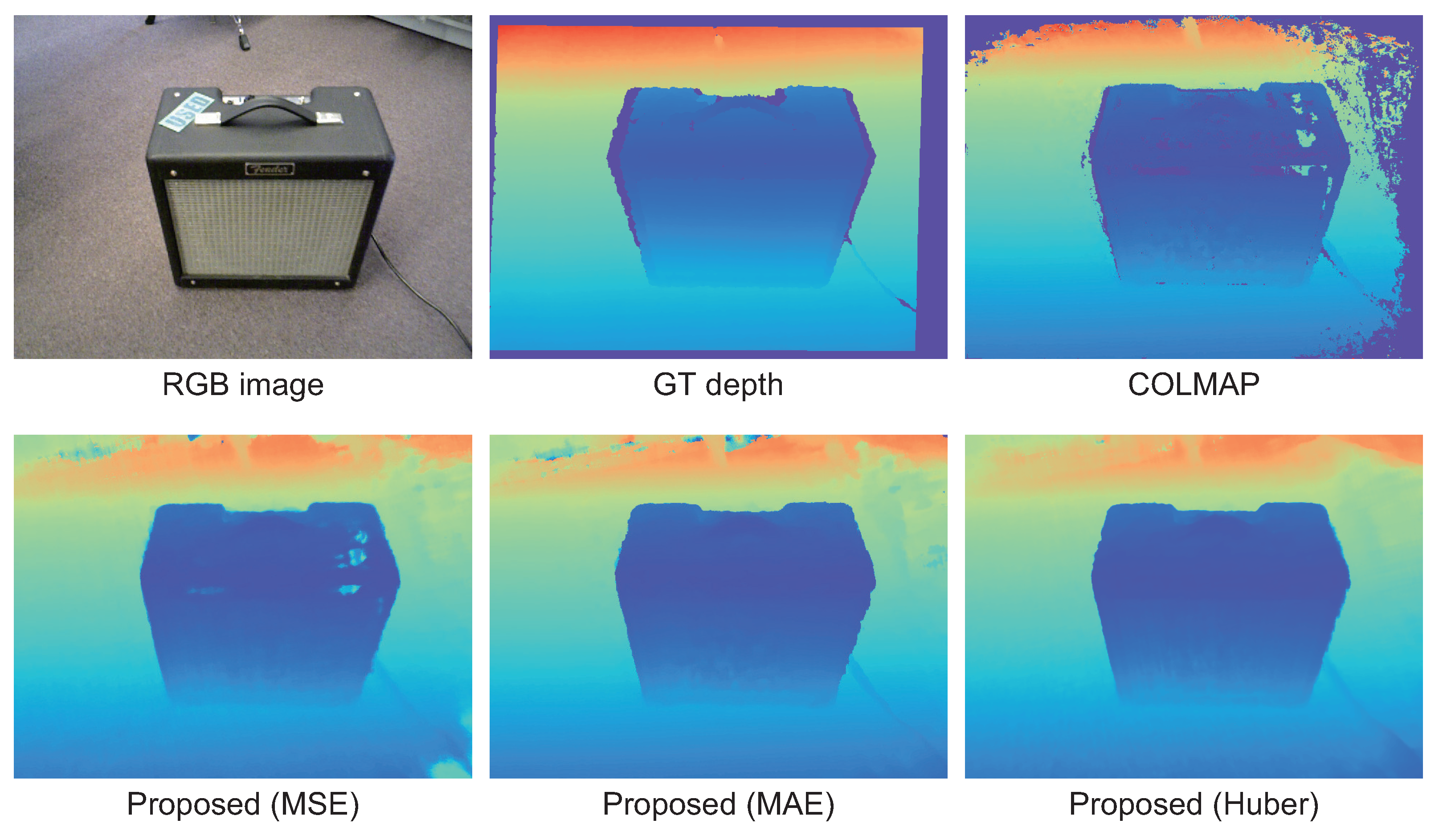
4.5. Comparison with Conventional Methods
4.6. 3D Reconstruction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Seitz, S.M.; Curless, B.; Diebe, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of Multi-View Stereo reconstruction algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 519–528. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Pollefeys, M.; Frahm, J. Pixelwise view selection for unstructured Multi-View Stereo. In Proceedings of the European Conference Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 501–518. [Google Scholar]
- Collins, R.T. A space-sweep approach to true multi-image matching. In Proceedings of the CVPR IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 358–363. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Shen, T.; Fang, T.; Quan, L. Recurrent MVSNet for high-resolution multi-view stereo depth inference. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 6–20 June 2019; pp. 5525–5534. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Respresenting scenes as neural radiance fields for view synthesis. In Proceedings of the 16th European Conference Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 405–421. [Google Scholar]
- Ito, K.; Ito, T.; Aoki, T. PM-MVS: Patchmatch multi-view stereo. Mach. Vis. Appl. 2023, 34, 32–47. [Google Scholar] [CrossRef]
- Gallup, D.; Frahm, J.M.; Mordohai, P.; Yang, Q.; Pollefeys, M. Real-time plane-sweeping stereo with multiple sweeping directions. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Barnes, C.; Shechtman, E.; Flinkelstein, A.; Goldman, B.D. PatchMatch: A randomized correspondence algorithm for structural image editing. ACM Trans. Graph. 2009, 28, 24. [Google Scholar] [CrossRef]
- Bleyer, M.; Rhemann, C.; Rother, C. PatchMatch Stereo-Stereo matching with slanted support windows. In Proceedings of the British Machine Vision Conference, Dundee, UK, 29 August–2 September 2011; pp. 1–11. [Google Scholar]
- Zhang, E.; Dunn, E.; Joic, V.; Frahm, J.M. PatchMatch based joint view selection a nd depthmap estimation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1510–1517. [Google Scholar]
- Hiradate, K.; Ito, K.; Aoki, T.; Watanabe, T.; Unten, H. An extension of PatchMatch stereo for 3D reconstruction from multi-view images. In Proceedings of the 2015 3rd IAPR Asian Conference on Pattern Recognition (ACPR), Kuala Lumpur, Malaysia, 3–6 November 2015; pp. 61–65. [Google Scholar]
- Schönberger, J.L.; Frahm, J. Structure-from-Motion revisited. In Proceedings of the IEEE Conference Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Deepmvs: Learning multi-view stereopsis. In Proceedings of the IEEE Conference Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2821–2830. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. MVSNet: Depth inference for unstructured Multi-View Stereo. In Proceedings of the European Conference Computer Vision, Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Wang, F.; Galliani, S.; Vogel, C.; Speciale, P.; Pollefeys, M. PatchmatchNet: Learned multi-view patchmatch stereo. In Proceedings of the IEEE Conference Computer Vision and Patter Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14194–14203. [Google Scholar]
- Chang, D.; Božič, A.; Zhang, T.; Yan, Q.; Chen, Y.; Süsstrunk, S.; Nießner, M. RC-MVSNet: Unsupervised multi-view stereo with neural rendering. In Proceedings of the European Conference Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 665–680. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Choi, S.; Zhou, Q.; Miller, S.; Koltun, V. A large dataset of object scans. arXiv 2016, arXiv:1602.02481. [Google Scholar]
- Jensen, R.; Dahl, A.; Vogiatzis, G.; Tola, E.; Aanæs, H. Large scale multi-view stereopsis evaluation. In Proceedings of the IEEE Conference Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 406–413. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1–9. [Google Scholar]
- Gu, X.; Fan, Z.; Zhu, S.; Dai, Z.; Tan, F.; Tan, P. Cascade cost volume for high-resolution multi-view stereo and stereo matching. In Proceedings of the IEEE/CVF Conference Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2495–2504. [Google Scholar]
- Deng, K.; Liu, A.; Zhu, J.Y.; Ramanan, D. Depth-supervised NeRF: Fewer views and faster training for free. In Proceedings of the IEEE/CVF Conference Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12882–12891. [Google Scholar]
- Kajiya, J.T.; Herzen, B.P.V. Ray tracing volume densities. In Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques, Minneapolis, MN, USA, 23–27 July 1984; Volume 18, pp. 165–174. [Google Scholar]
- Roessle, B.; Barron, J.T.; Mildenhall, B.; Srinivasan, P.P.; Nießner, M. Dense depth priors for neural radiance fields from sparse input views. In Proceedings of the IEEE/CVF Conference Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12892–12901. [Google Scholar]
- Wei, Y.; Liu, S.; Rao, Y.; Zhao, W.; Lu, J.; Zhou, J. Nerfingmvs: Guided optimization of neural radiance fields for indoor multi-view stereo. In Proceedings of the IEEE/CVF International Conference Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5610–5619. [Google Scholar]
- Rematas, K.; Liu, A.; Srinivasan, P.; Barron, J.; Tagliasacchi, A.; Funkhouser, T.; Ferrari, V. Urban radiance fields. In Proceedings of the IEEE/CVF Conference Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12932–12942. [Google Scholar]
- Toshi, F.; Tonioni, A.; Gregorio, D.D.; Poggi, M. NeRF-supervised deep stereo. In Proceedings of the IEEE/CVF Conference Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 855–866. [Google Scholar]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Statist. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Yodokawa, K.; Ito, K.; Aoki, T.; Sakai, S.; Watanabe, T.; Masuda, T. Outlier and artifact removal filters for multi-view stereo. In Proceedings of the International Conference Image Processing, Quebec City, QC, Canada, 27–30 September 2015; pp. 3638–3642. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, C.A.; Lo, W.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference Computer Vision, Paris, France, 2–3 October 2023; pp. 4015–4026. [Google Scholar]
- Weibel, J.B.; Sebeto, P.; Thalhammer, S.; Vincze, M. Challenges of Depth Estimation for Transparent Objects. In Proceedings of the International Symposium Visual Computing (LNCS 14361), Lake Tahoe, NV, USA, 16–18 October 2023; pp. 277–288. [Google Scholar]
- Kaya, B.; Kumar, S.; Oliveira, C.; Ferrari, V.; Gool, L.V. Multi-View Photometric Stereo Revisited. In Proceedings of the IEEE/CVF Winter Conf. Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 3126–3135. [Google Scholar]







| Method | # of Iterations | Batch Size | Ratio of Depth Rays | ||
|---|---|---|---|---|---|
| Redwood [19] | DTU [20] | ||||
| [Times] | [Times] | [Rays] | [Rays/Batch Size] | ||
| COLMAP [3] | – | – | – | – | – |
| NeRF [6] | 15,000 | 100,000 | 5120 | – | – |
| DS-NeRF [23] | 15,000 | 100,000 | 5120 | 0.5 | 0.1 |
| Proposed | 15,000 | 100,000 | 5120 | 0.2 | 0.1 |
| s | Error↓ | Accuracy ↑ | |||
|---|---|---|---|---|---|
| SILog [log(mm) × 100] | AbsRel [%] | SqRel [%] | RMSE (log) [log(mm)] | [%] | |
| 0.1 | 0.0804 | 3.135 | 0.1097 | 97.61 | |
| 0.5 | 0.5787 | 98.51 | |||
| 1.0 | 0.5759 | 2.992 | 0.1095 | 98.53 | |
| 2.0 | 0.5970 | 0.0779 | 2.988 | 0.1099 | |
| Error↓ | Accuracy ↑ | ||||
|---|---|---|---|---|---|
| SILog [log(mm) × 100] | AbsRel [%] | SqRel [%] | RMSE (log) [log(mm)] | [%] | |
| 0.05 | 0.5822 | 0.0789 | 3.008 | 0.1099 | 98.45 |
| 0.1 | 0.5759 | 0.0786 | 2.992 | 0.1095 | 98.53 |
| 0.2 | 0.6086 | 0.0791 | 3.032 | 0.1115 | 98.44 |
| 0.5 | 0.6180 | 0.0786 | 3.040 | 0.1115 | 98.41 |
| Depth Loss | Error↓ | Accuracy ↑ | |||
|---|---|---|---|---|---|
| SILog [log(mm) × 100] | AbsRel [%] | SqRel [%] | RMSE (log) [log(mm)] | [%] | |
| MSE | 0.6413 | 3.025 | 98.05 | ||
| MAE | 0.6623 | 0.0790 | 3.107 | 0.1139 | 98.24 |
| Huber (Proposed) | 0.0791 | 0.1099 | |||
| Datasets | Method | Error↓ | Accuracy ↑ | |||
|---|---|---|---|---|---|---|
| SILog [log(mm) × 100] | AbsRel [%] | SqRel [%] | RMSE (log) [log(mm)] | [%] | ||
| amp #05668 | COLMAP [3] | 6.533 | 0.0906 | 4.248 | 0.2711 | 97.64 |
| NeRF [6] | 8.313 | 0.2087 | 9.784 | 0.3913 | 84.64 | |
| DS-NeRF [23] | 0.7120 | 0.0794 | 3.289 | 0.1146 | 99.40 | |
| RC-MVSNet [17] | 4.637 | 0.0857 | 3.175 | 0.1678 | 98.64 | |
| Proposed | 0.5759 | 0.0786 | 2.992 | 0.1095 | 99.18 | |
| chair #04786 | COLMAP [3] | 12.86 | 0.1745 | 8.686 | 0.3982 | 95.94 |
| NeRF [6] | 27.22 | 0.5636 | 24.51 | 1.252 | 40.91 | |
| DS-NeRF [23] | 2.895 | 0.1795 | 8.638 | 0.2523 | 97.22 | |
| RC-MVSNet [17] | 0.9583 | 0.1595 | 6.554 | 0.1974 | 98.81 | |
| Proposed | 1.315 | 0.1556 | 6.785 | 0.1982 | 98.62 | |
| chair #05119 | COLMAP [3] | 17.45 | 0.1016 | 8.400 | 0.4359 | 95.28 |
| NeRF [6] | 16.41 | 0.3130 | 19.53 | 0.5966 | 71.09 | |
| DS-NeRF [23] | 1.098 | 0.0754 | 5.089 | 0.1167 | 99.51 | |
| RC-MVSNet [17] | 0.8361 | 0.0656 | 4.396 | 0.1054 | 99.35 | |
| Proposed | 1.026 | 0.0663 | 4.507 | 0.1130 | 99.21 | |
| childseat #04134 | COLMAP [3] | 4.151 | 0.0539 | 2.674 | 0.2009 | 99.25 |
| NeRF [6] | 3.328 | 0.1345 | 5.598 | 0.1900 | 99.99 | |
| DS-NeRF [23] | 0.1874 | 0.0527 | 1.890 | 0.0624 | 100.0 | |
| RC-MVSNet [17] | 0.1023 | 0.0481 | 1.692 | 0.0554 | 100.0 | |
| Proposed | 0.1280 | 0.0488 | 1.670 | 0.0563 | 100.0 | |
| garden #02161 | COLMAP [3] | 3.916 | 0.0928 | 5.647 | 0.2174 | 98.47 |
| NeRF [6] | 9.752 | 0.2282 | 14.92 | 0.4288 | 83.19 | |
| DS-NeRF [23] | 0.8502 | 0.0892 | 5.165 | 0.1272 | 99.33 | |
| RC-MVSNet [17] | 0.4220 | 0.0824 | 4.139 | 0.1032 | 99.73 | |
| Proposed | 0.8336 | 0.0883 | 4.969 | 0.1269 | 99.09 | |
| mischardware #05645 | COLMAP [3] | 16.25 | 0.1213 | 14.77 | 0.4189 | 95.09 |
| NeRF [6] | 7.251 | 0.2172 | 12.80 | 0.3726 | 90.79 | |
| DS-NeRF [23] | 1.913 | 0.1001 | 5.966 | 0.1700 | 99.73 | |
| RC-MVSNet [17] | 2.886 | 0.0656 | 3.837 | 0.1327 | 99.37 | |
| Proposed | 0.8973 | 0.0664 | 4.030 | 0.1137 | 99.74 | |
| Datasets | Method | Error↓ | Accuracy ↑ | |||
|---|---|---|---|---|---|---|
| SILog [log(mm) × 100] | AbsRel [%] | SqRel [%] | RMSE (log) [log(mm)] | [%] | ||
| radio #09655 | COLMAP [3] | 7.308 | 0.0606 | 14.98 | 0.2666 | 98.07 |
| NeRF [6] | 3.968 | 0.1430 | 6.854 | 0.2345 | 98.497 | |
| DS-NeRF [23] | 1.501 | 0.0596 | 4.134 | 0.1233 | 99.81 | |
| RC-MVSNet [17] | 7.078 | 0.0350 | 2.521 | 0.1702 | 98.25 | |
| Proposed | 0.2654 | 0.0235 | 1.730 | 0.0520 | 99.99 | |
| sculpture #06287 | COLMAP [3] | 31.79 | 0.3789 | 10.38 | 0.7903 | 86.08 |
| NeRF [6] | 6.3333 | 0.5077 | 13.431 | 0.7880 | 44.12 | |
| DS-NeRF [23] | 1.136 | 0.3292 | 8.511 | 0.4179 | 97.58 | |
| RC-MVSNet [17] | 5.573 | 0.3340 | 8.103 | 0.4584 | 96.64 | |
| Proposed | 0.8592 | 0.3230 | 8.280 | 0.4037 | 98.08 | |
| table #02169 | COLMAP [3] | 5.456 | 0.1145 | 8.168 | 0.2391 | 97.53 |
| NeRF [6] | 23.94 | 0.1973 | 20.15 | 0.5058 | 87.62 | |
| DS-NeRF [23] | 5.005 | 0.1320 | 10.358 | 0.2251 | 95.90 | |
| RC-MVSNet [17] | 2.106 | 0.1091 | 5.761 | 0.1517 | 99.03 | |
| Proposed | 1.920 | 0.1091 | 6.927 | 0.1572 | 98.50 | |
| telephone #06133 | COLMAP [3] | 13.98 | 0.1245 | 7.174 | 0.3890 | 94.29 |
| NeRF [6] | 16.52 | 0.2938 | 13.25 | 0.5518 | 75.79 | |
| DS-NeRF [23] | 2.935 | 0.1196 | 5.848 | 0.1949 | 97.87 | |
| RC-MVSNet [17] | 7.957 | 0.0962 | 4.651 | 0.2602 | 97.07 | |
| Proposed | 2.412 | 0.0915 | 4.909 | 0.1676 | 98.19 | |
| trashcontainer #07226 | COLMAP [3] | 22.14 | 0.1117 | 6.877 | 0.4908 | 94.15 |
| NeRF [6] | 2.085 | 0.1083 | 6.027 | 0.1874 | 99.03 | |
| DS-NeRF [23] | 0.2313 | 0.0563 | 2.481 | 0.0716 | 99.99 | |
| RC-MVSNet [17] | 0.0332 | 0.0566 | 1.930 | 0.0611 | 99.99 | |
| Proposed | 0.1365 | 0.0564 | 2.159 | 0.0672 | 99.98 | |
| travelingbag #01991 | COLMAP [3] | 12.18 | 0.0800 | 7.401 | 0.347 | 95.85 |
| NeRF [6] | 1.401 | 0.0760 | 5.071 | 0.1231 | 98.86 | |
| DS-NeRF [23] | 0.9334 | 0.0540 | 3.691 | 0.090 | 99.06 | |
| RC-MVSNet [17] | 29.25 | 0.1075 | 7.537 | 0.4499 | 92.53 | |
| Proposed | 0.9091 | 0.0487 | 3.497 | 0.087 | 99.06 | |
| Scene | Method | Error↓ | Accuracy ↑ | |||
|---|---|---|---|---|---|---|
| SILog [log(mm) × 100] | AbsRel [%] | SqRel [%] | RMSE (log) [log(mm)] | [%] | ||
| scan9 | COLMAP [3] | 6.039 | 0.3602 | 9.059 | 0.5097 | 98.10 |
| NeRF [6] | 0.8856 | 0.3528 | 8.793 | 0.4324 | 99.72 | |
| DS-NeRF [23] | 0.7815 | 0.3529 | 8.784 | 0.4327 | 99.74 | |
| RC-MVSNet [17] | 13.83 | 0.3785 | 9.6952 | 0.6160 | 93.40 | |
| Proposed | 0.7280 | 0.3530 | 8.783 | 0.4330 | 99.74 | |
| scan33 | COLMAP [3] | 14.68 | 0.1064 | 4.428 | 0.3971 | 96.76 |
| NeRF [6] | 1.115 | 0.0840 | 3.230 | 0.1251 | 99.70 | |
| DS-NeRF [23] | 1.034 | 0.0837 | 3.093 | 0.1231 | 99.71 | |
| RC-MVSNet [17] | 7.376 | 0.0935 | 3.646 | 0.2886 | 97.71 | |
| Proposed | 0.9809 | 0.0837 | 3.002 | 0.1219 | 99.72 | |
| scan118 | COLMAP [3] | 6.932 | 0.0372 | 2.968 | 0.2629 | 98.61 |
| NeRF [6] | 0.9723 | 0.0342 | 3.004 | 0.0984 | 99.38 | |
| DS-NeRF [23] | 0.7852 | 0.0302 | 2.490 | 0.0888 | 99.43 | |
| RC-MVSNet [17] | 7.091 | 0.0421 | 2.996 | 0.2476 | 97.69 | |
| Proposed | 0.7282 | 0.0296 | 2.318 | 0.0855 | 99.45 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ito, S.; Miura, K.; Ito, K.; Aoki, T. Neural Radiance Field-Inspired Depth Map Refinement for Accurate Multi-View Stereo. J. Imaging 2024, 10, 68. https://doi.org/10.3390/jimaging10030068
Ito S, Miura K, Ito K, Aoki T. Neural Radiance Field-Inspired Depth Map Refinement for Accurate Multi-View Stereo. Journal of Imaging. 2024; 10(3):68. https://doi.org/10.3390/jimaging10030068
Chicago/Turabian StyleIto, Shintaro, Kanta Miura, Koichi Ito, and Takafumi Aoki. 2024. "Neural Radiance Field-Inspired Depth Map Refinement for Accurate Multi-View Stereo" Journal of Imaging 10, no. 3: 68. https://doi.org/10.3390/jimaging10030068
APA StyleIto, S., Miura, K., Ito, K., & Aoki, T. (2024). Neural Radiance Field-Inspired Depth Map Refinement for Accurate Multi-View Stereo. Journal of Imaging, 10(3), 68. https://doi.org/10.3390/jimaging10030068






