Addressing Once More the (Im)possibility of Color Reconstruction in Underwater Images
Abstract
:1. Introduction
- Light scattering was ignored;
- Constant illumination was assumed for all wavelengths;
- The quantum efficiency curves of the sensor were approximated by means of Gaussians using the same parameters;
- The reflectance spectra were represented as three rectangles—each in one of the three main parts of the visible spectrum (red, green, and blue)—except for the maximum wavelength.
2. Image Formation Model
- Quantum efficiency (QE) curves were assumed to have a Gaussian shape;
- The spectra of reflectors were represented by piece-wise functions, as explained in the articles cited above.
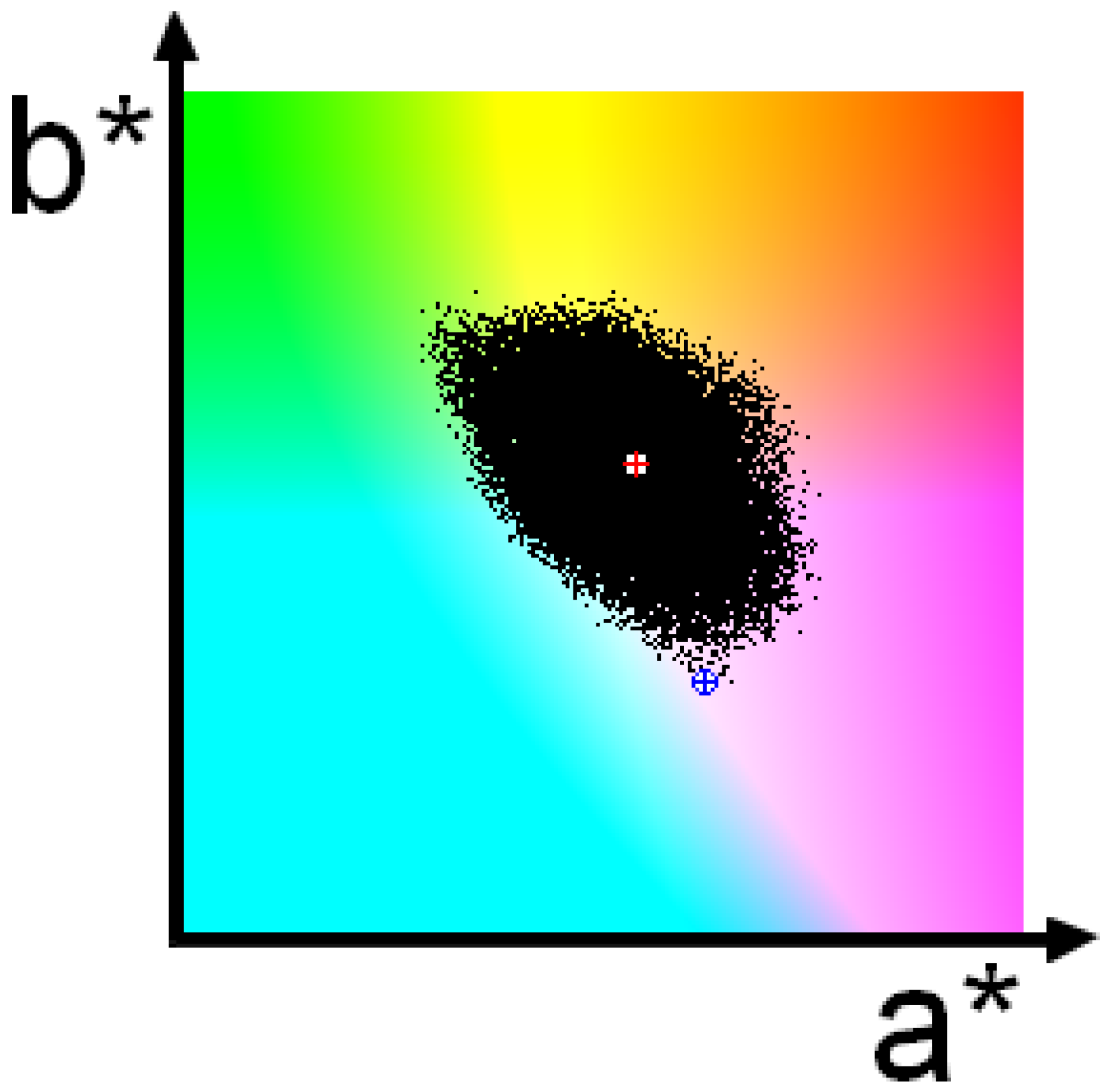
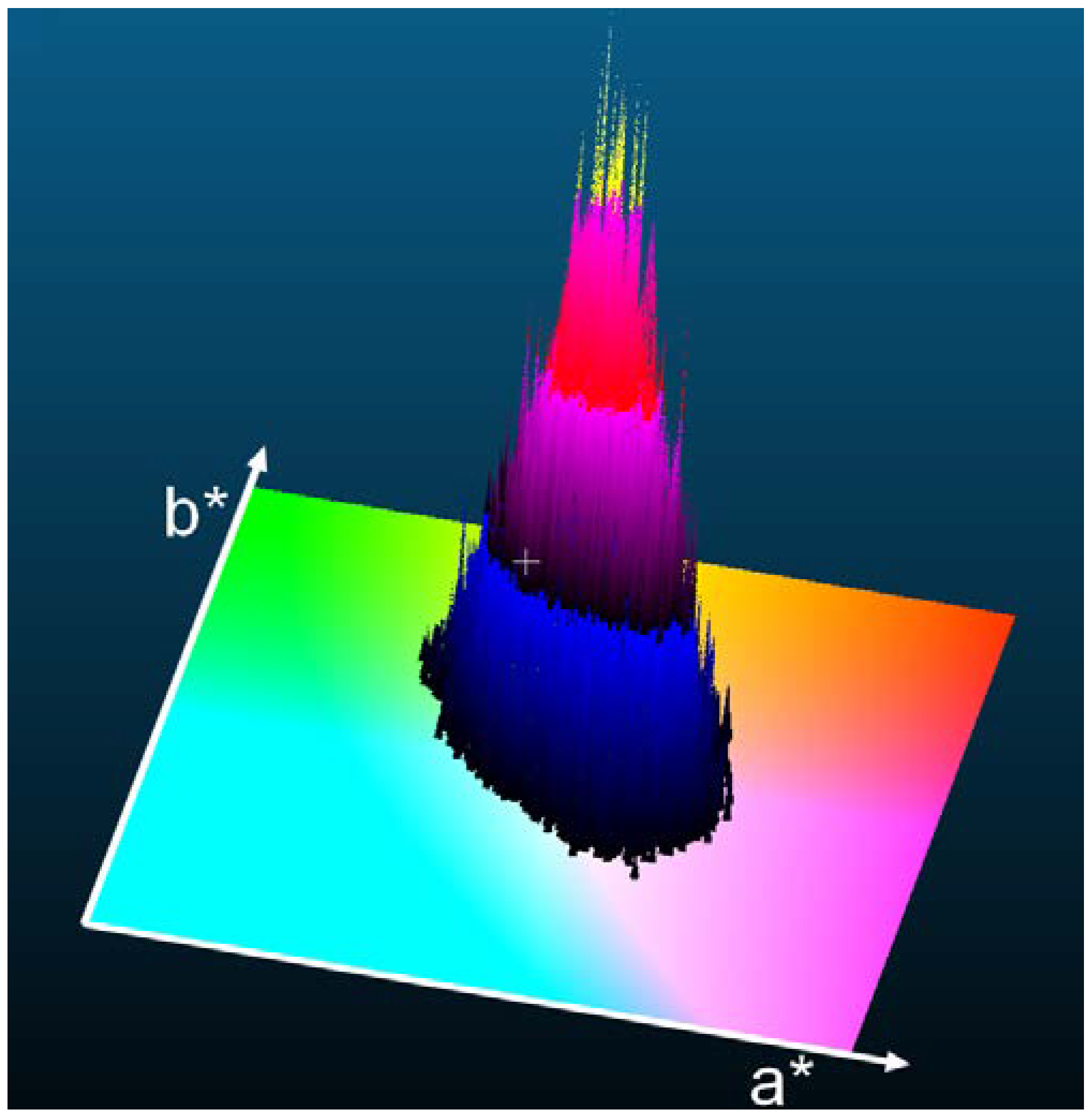
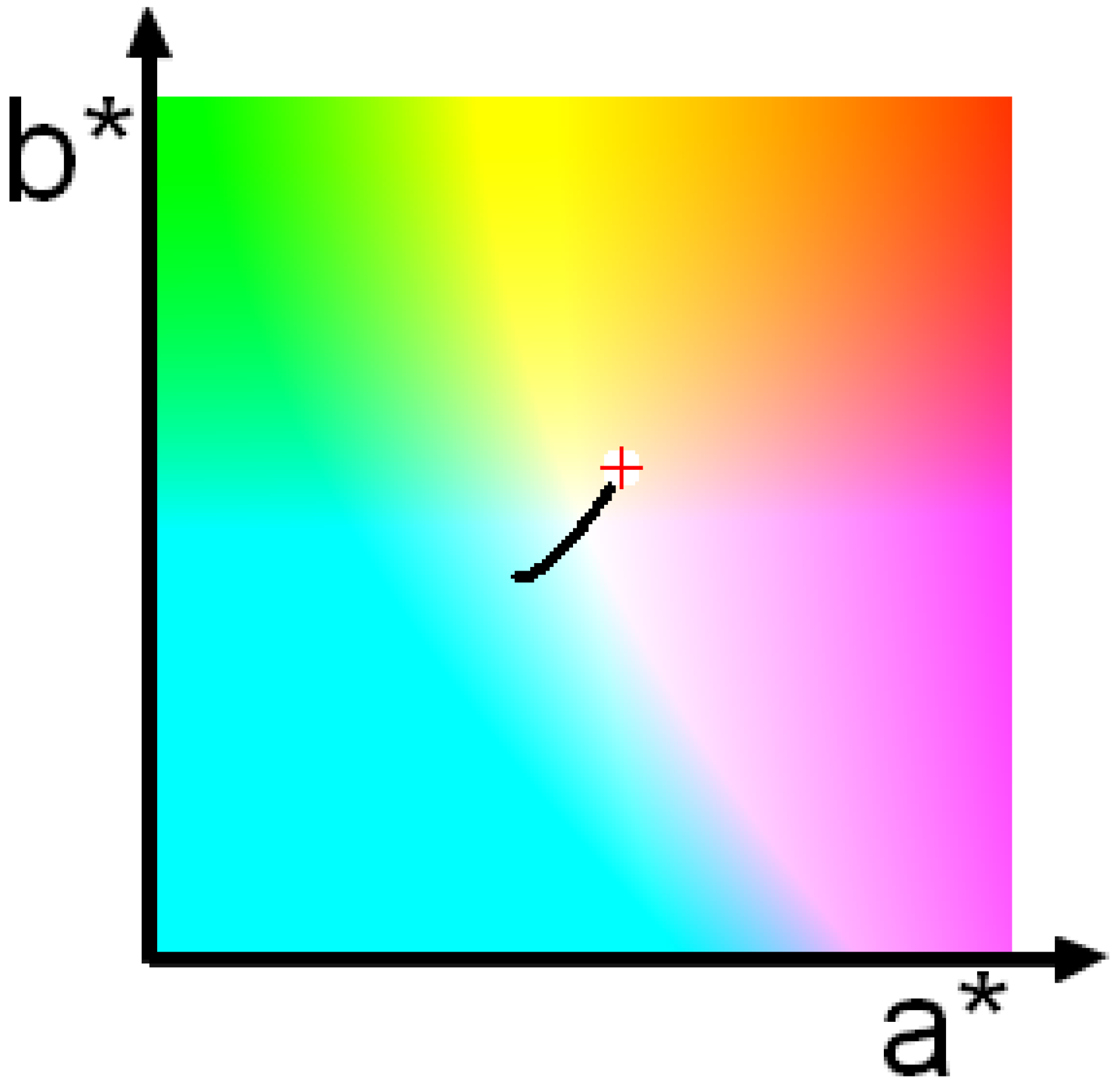
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Åhlén, J.; Bengtsson, E.; Sundgren, D. Evaluation of Underwater Spectral Data for Colour Correction, Applications. In Proceedings of the 5th WSEAS International Conference on Circuits, Systems, Electronics, Control and Signal Processing, Dallas, TX, USA, 1–3 November 2006; pp. 321–326. [Google Scholar]
- Åhlén, J.; Sundgren, D.; Bengtsson, E. Application of Underwater Hyperspectral Data for Color Correction Purposes. Pattern Recognit. Image Anal. 2007, 17, 170–173. [Google Scholar] [CrossRef]
- Finlayson, G.; Hubel, P.M.; Hordley, S. Color by Correlation: A Simple, Unifying Framework for Color Constancy. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 11, 1209–1221. [Google Scholar] [CrossRef]
- Afifi, M.; Price, B.; Cohen, S.; Brown, M.S. When Color Constancy Goes Wrong: Correcting Improperly White-balanced Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 1535–1544, ISBN 978-1-7281-3293-8. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar] [CrossRef] [PubMed]
- Drews, P., Jr.; Erickson, R.N.; Botelho, S.S.C.; Campos, M.F.M. Underwater Depth Estimation and Image Restoration Based on Single Images. IEEE Comput. Graph. Appl. 2016, 2, 24–35. [Google Scholar] [CrossRef] [PubMed]
- Ancuti, C.O.; Ancuti, C.; De Vleeschouwer, C.; Neumann, L.; Garcia, R. Color Transfer for Underwater Dehazing and Depth Estimation. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 695–699. [Google Scholar] [CrossRef]
- Vasilescu, I.; Detweiler, C.; Rus, D. Color-accurate Underwater Imaging Using Perceptual Adaptive Illumination. Auton. Robot. 2011, 31, 285–296. [Google Scholar] [CrossRef]
- Bongiorno, D.L.; Bryson, M.; Williams, S.B. Dynamic Spectral-Based Underwater Colour Correction. In Proceedings of the MTS/IEEE OCEANS, Bergen, Norway, 10–14 June 2013. [Google Scholar] [CrossRef]
- Bryson, M.; Johnson-Roberson, M.; Pizarro, O.; Williams, S.B. True Color Correction of Autonomous Underwater Vehicle Imagery. J. Field Robot. 2016, 33, 853–874. [Google Scholar] [CrossRef]
- Li, J.; Skinner, K.A.; Eustice, R.M.; Johnson-Roberson, M. WaterGAN: Unsupervised Generative Network to Enable Real-time Color Correction of Monocular Underwater Images. IEEE Robot. Autom. Lett. 2017, 3, 1–8. [Google Scholar] [CrossRef]
- Li, C.; Guo, J.; Guo, C. Emerging from Water: Underwater Image Color Correction Based on Weakly Supervised Color Transfer. arXiv 2018, arXiv:1710.07084v3. [Google Scholar] [CrossRef]
- Bianco, G.; Muzzupappa, M.; Bruno, F.; Garcia, R.; Neumann, L. A New Color Correction Method for Underwater Imaging. In Proceedings of the ISPRS/CIPA Workshop “Underwater 3D Recording and Modeling”, Piano di Sorrento, Italy, 16–17 April 2015. [Google Scholar] [CrossRef]
- Rzhanov, Y.; Pe’eri, S.; Shashkov, A. Probabilistic Reconstruction of Color for Species’ Classification Underwater. In Proceedings of the Oceans’15, Genova, Italy, 18–21 May 2015. [Google Scholar] [CrossRef]
- Rzhanov, Y.; Pe’eri, S.; Shashkov, A. Ambiguity of Underwater Color Measurement and Color-based Habitat Classification. In Proceedings of the 4th Topical Meeting on Blue Photonics, Barcelona, Spain, 11–13 May 2015. [Google Scholar]
- Ancuti, C.; Ancuti, C.O.; Haber, T.; Bekaert, P. Enhancing Underwater Images and Videos by Fusion. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 81–88. [Google Scholar] [CrossRef]
- Fabbri, C.; Islam, M.J.; Sattar, J. Enhancing Underwater Imagery Using Generative Adversarial Networks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7159–7165. [Google Scholar] [CrossRef]
- Mangeruga, M.; Bruno, F.; Cozza, M.; Agrafiotis, P.; Skarlatos, D. Guidelines for Underwater Image Enhancement Based on Benchmarking of Different Methods. Remote Sens. 2018, 10, 1652. [Google Scholar] [CrossRef]
- Li, C.; Guo, C.; Ren, W.; Cong, R.; Hou, J.; Kwong, S.; Tao, D. An Underwater Image Enhancement Benchmark Dataset and Beyond. IEEE Trans. Image Process. 2019, 29, 4376–4389. [Google Scholar] [CrossRef] [PubMed]
- Uplavikar, P.M.; Wu, Z.; Wang, Z. All-in-One Underwater Image Enhancement Using Domain-Adversarial Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 15–20 June 2019; pp. 1–8. [Google Scholar]
- Liu, R.; Fan, X.; Zhu, M.; Hou, M.; Luo, Z. Real-world Underwater Enhancement: Challenges, Benchmarks, and Solutions. arXiv 2019, arXiv:1901.05320v2. [Google Scholar]
- Islam, M.J.; Xia, Y.; Sattar, J. Fast Underwater Image Enhancement for Improved Visual Perception. IEEE Robot. Autom. Lett. 2020, 2, 3227–3234. [Google Scholar] [CrossRef]
- Li, C.; Anwar, S.; Hou, J.; Cong, R.; Guo, C.; Ren, W. Underwater Image Enhancement via Medium Transmission-guided Multi-color Space Embedding. IEEE Trans. Image Process. 2021, 30, 4985–5000. [Google Scholar] [CrossRef] [PubMed]
- Peng, L.; Zhu, C.; Bian, L. U-shape Transformer for Underwater Image Enhancement. arXiv 2021, arXiv:2111.11843. [Google Scholar]
- Zhang, W.; Dong, L.; Pan, X.; Zou, P.; Qin, L.; Xu, W. A Survey of Restoration and Enhancement for Underwater Images. IEEE Access 2019, 7, 182259–182279. [Google Scholar] [CrossRef]
- Zhuang, P.; Wu, J.; Porikli, F.; Li, C. Underwater Image Enhancement with Hyper-Laplacian Reflectance Priors. IEEE Trans. Image Process. 2022, 31, 5442–5455. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Jiang, Z.; Yang, S.; Fan, X. Twin Adversarial Contrastive Learning for Underwater Image Enhancement and Beyond. IEEE Trans. Image Process. 2022, 31, 4922–4936. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Kawasaki, H.; Iwaguchi, T. Underwater Image Enhancement by Transformer-based Diffusion Model with Non-uniform Sampling for Skip Strategy. In Proceedings of the CAN international Conference on Multimedia, MM’23, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 5419–5427. [Google Scholar] [CrossRef]
- Schettini, R.; Corchs, S. Underwater Image Processing: State of the Art of Restoration and Image Enhancement Methods. EURASIP J. Adv. Signal Process. 2010, 2010, 746052. [Google Scholar] [CrossRef]
- Rzhanov, Y.; Lowell, K. On the (Im)possibility of Color Reconstruction in Underwater Images. In Proceedings of the Oceans’19, Seattle, WA, USA, 27–31 October 2019. [Google Scholar] [CrossRef]
- Vorobyev, M. Coloured Oil Droplets Enhance Colour Discrimination. Proc. R. Soc. Lond. B 2003, 270, 1255–1261. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, S. Computer Modeling and the Design of Optimal Underwater Imaging Systems. IEEE J. Ocean. Eng. 1990, 15, 101–111. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Akkaynak, D.; Treibitz, T. A Revised Underwater Image Formation Model. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Akkaynak, D.; Treibitz, T. Sea-thru: A Method For Removing Water From Underwater Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Auger, A.; Hansen, N. Performance Evaluation of an Advanced Local Search Evolutionary Algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; pp. 1769–1776. [Google Scholar] [CrossRef]


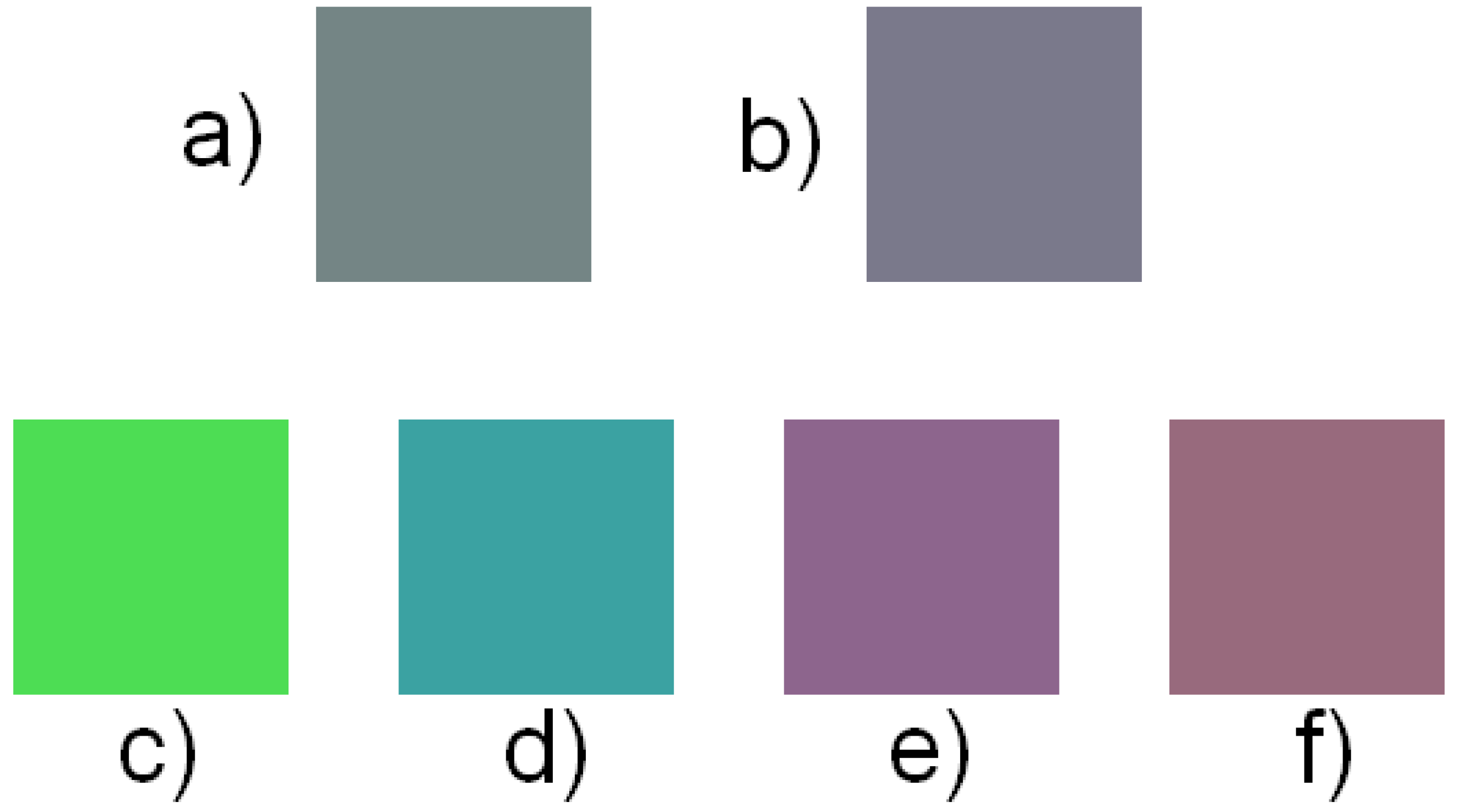
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rzhanov, Y.; Lowell, K. Addressing Once More the (Im)possibility of Color Reconstruction in Underwater Images. J. Imaging 2024, 10, 247. https://doi.org/10.3390/jimaging10100247
Rzhanov Y, Lowell K. Addressing Once More the (Im)possibility of Color Reconstruction in Underwater Images. Journal of Imaging. 2024; 10(10):247. https://doi.org/10.3390/jimaging10100247
Chicago/Turabian StyleRzhanov, Yuri, and Kim Lowell. 2024. "Addressing Once More the (Im)possibility of Color Reconstruction in Underwater Images" Journal of Imaging 10, no. 10: 247. https://doi.org/10.3390/jimaging10100247
APA StyleRzhanov, Y., & Lowell, K. (2024). Addressing Once More the (Im)possibility of Color Reconstruction in Underwater Images. Journal of Imaging, 10(10), 247. https://doi.org/10.3390/jimaging10100247






