Classification of Black Plastics Waste Using Fluorescence Imaging and Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Used Black Plastics
- high-density polyethylene (HDPE, 399 particles);
- polypropylene (PP, 399 particles);
- polyoxymethylene (POM, 399 particles);
- polyphenylene sulfide (PPS, 400 particles);
- polyamide 6 and polyamide 6 (PA6) with glass fibre /without glass fibre (798 particles);
- polyamide 66 and polyamide 66 (PA66) with glass fibre /without glass fibre (756 particles);
- polyamide 66 with flame retardant (PA66 V0, 396 particles);
- styrene-butadiene rubber (SBR, 390 particles);
- polybutylene terephthalate (PBT, 399 particles);
- thermoplastic elastomers (TPE, 397 particles);
- thermoplastic polyurethanes (TPU, 392 particles);
- thermoplastic copolyester (TEEE, 402 particles).
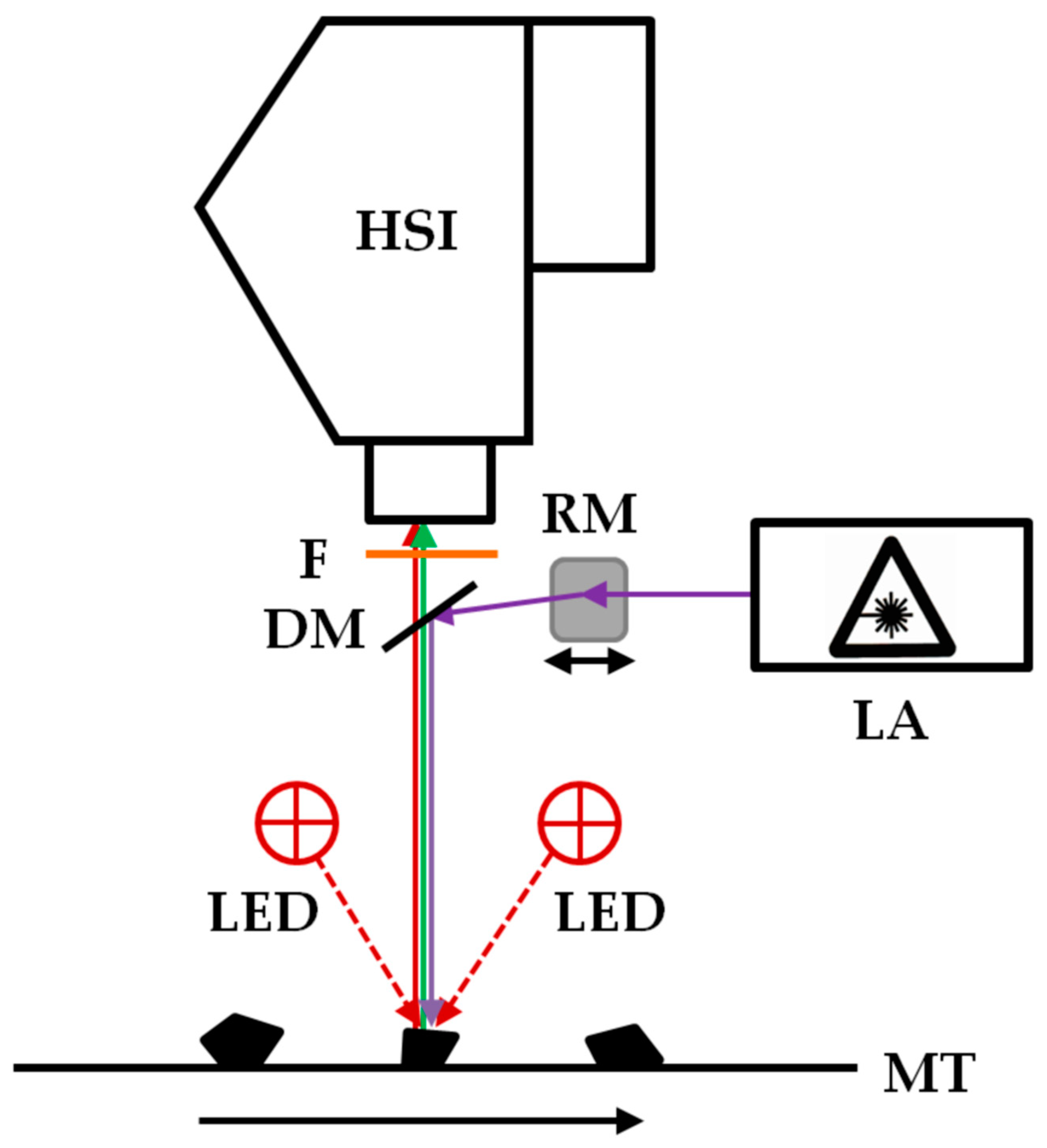
2.2. Imaging Fluorescence Spectrometer
2.3. Data Acquisition and Preprocessing
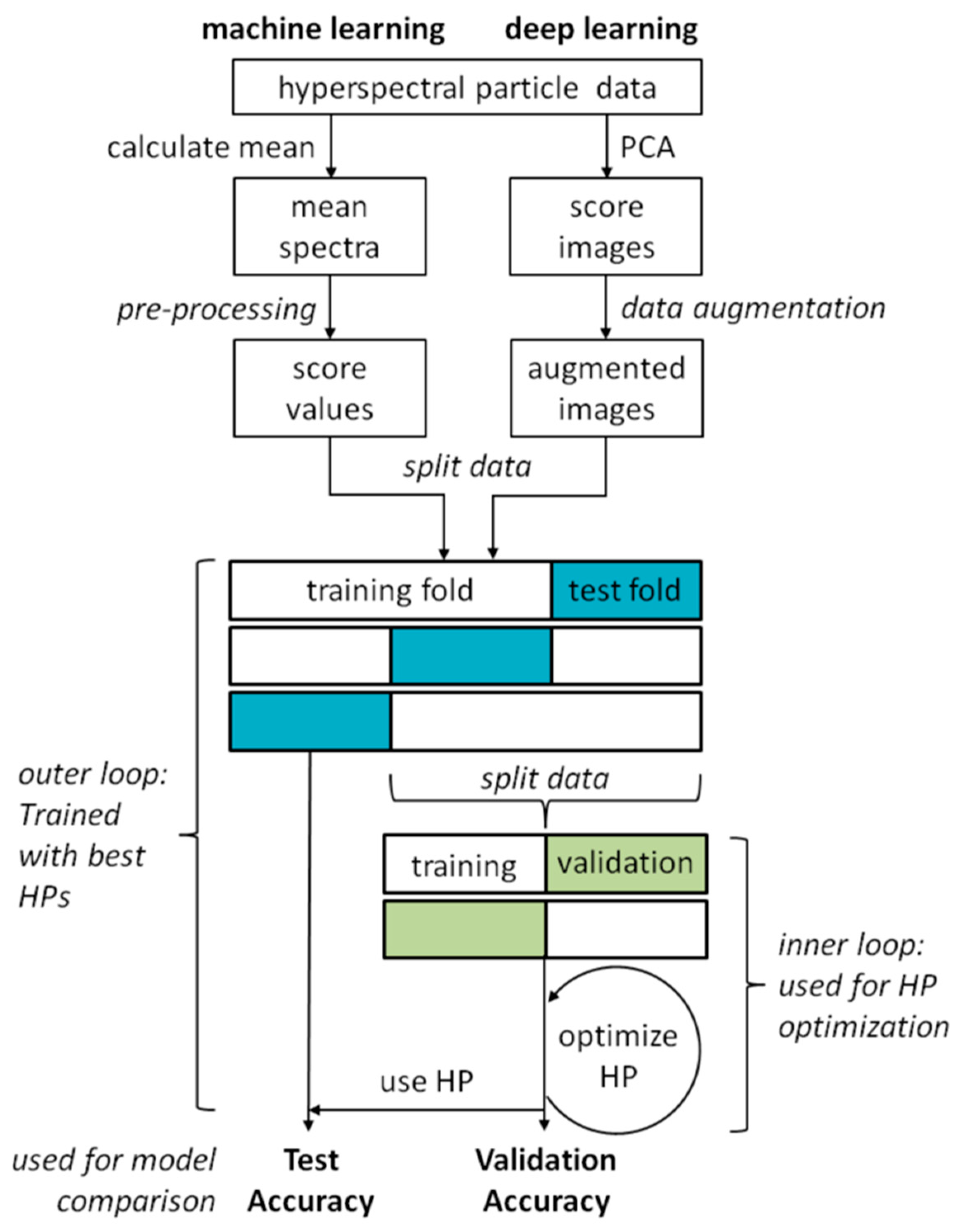
2.4. Classification Experiments
2.4.1. Machine Learning
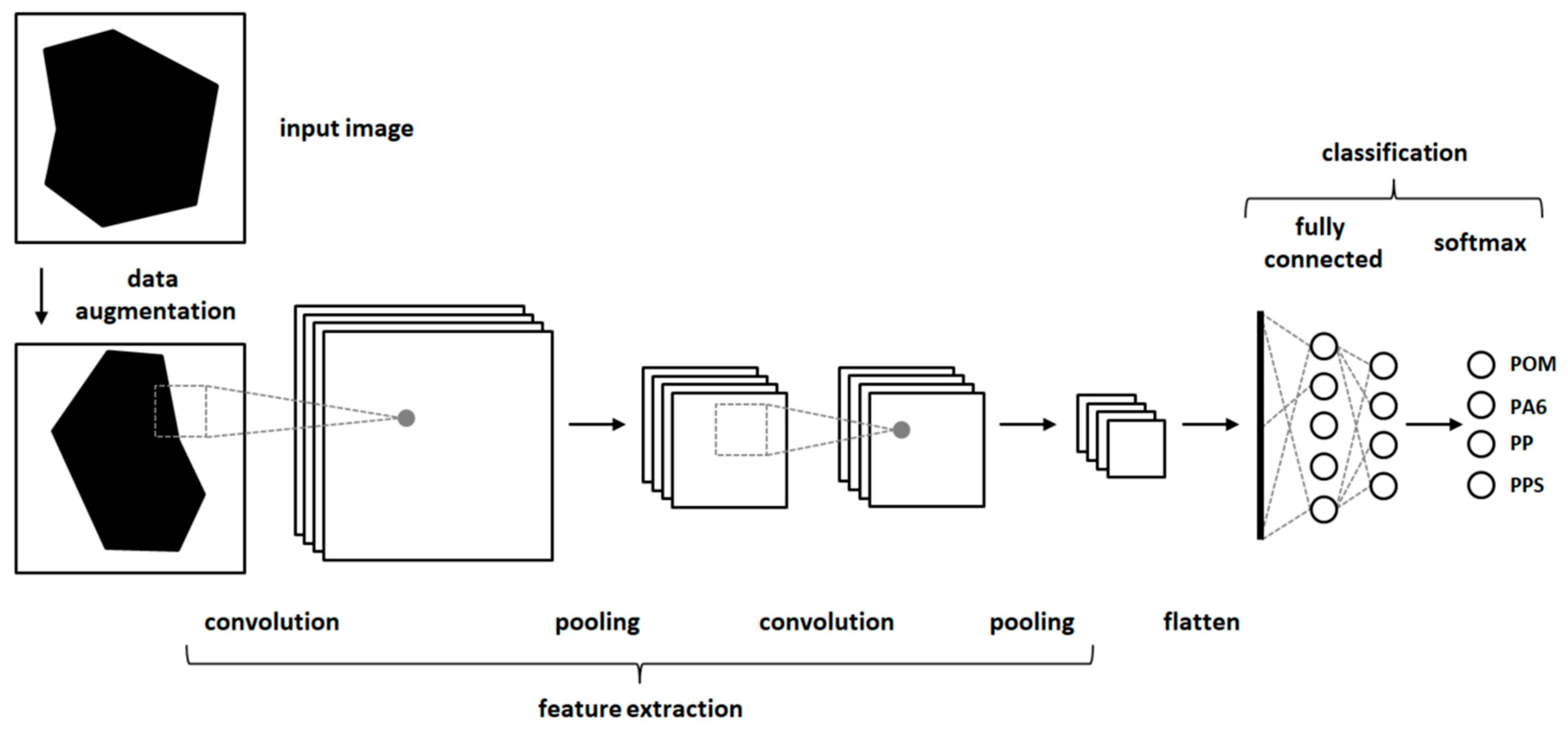
2.4.2. Deep Learning
2.4.3. Hyperparameter Optimization
2.4.4. Model Comparison
3. Results and Discussion
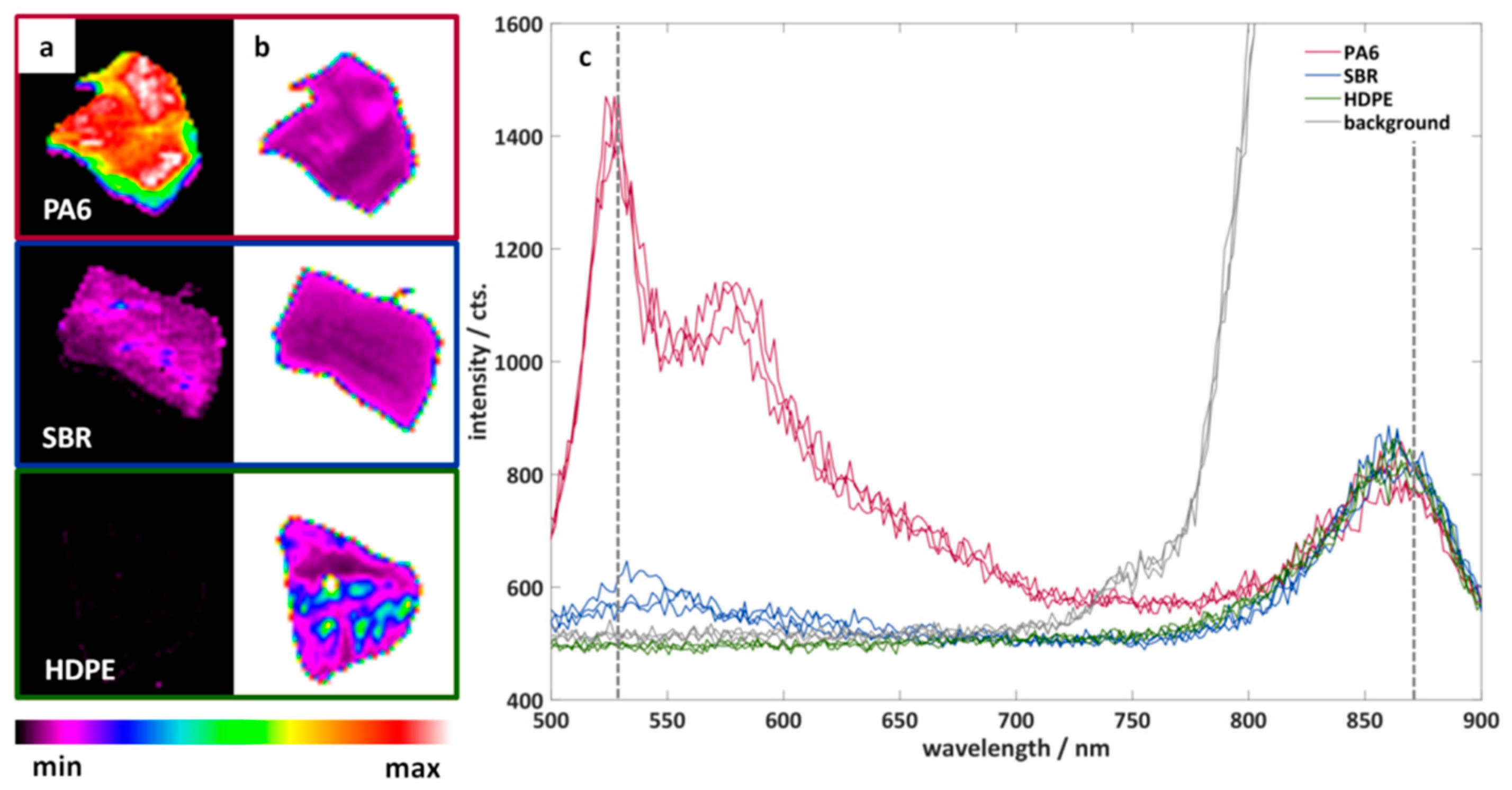
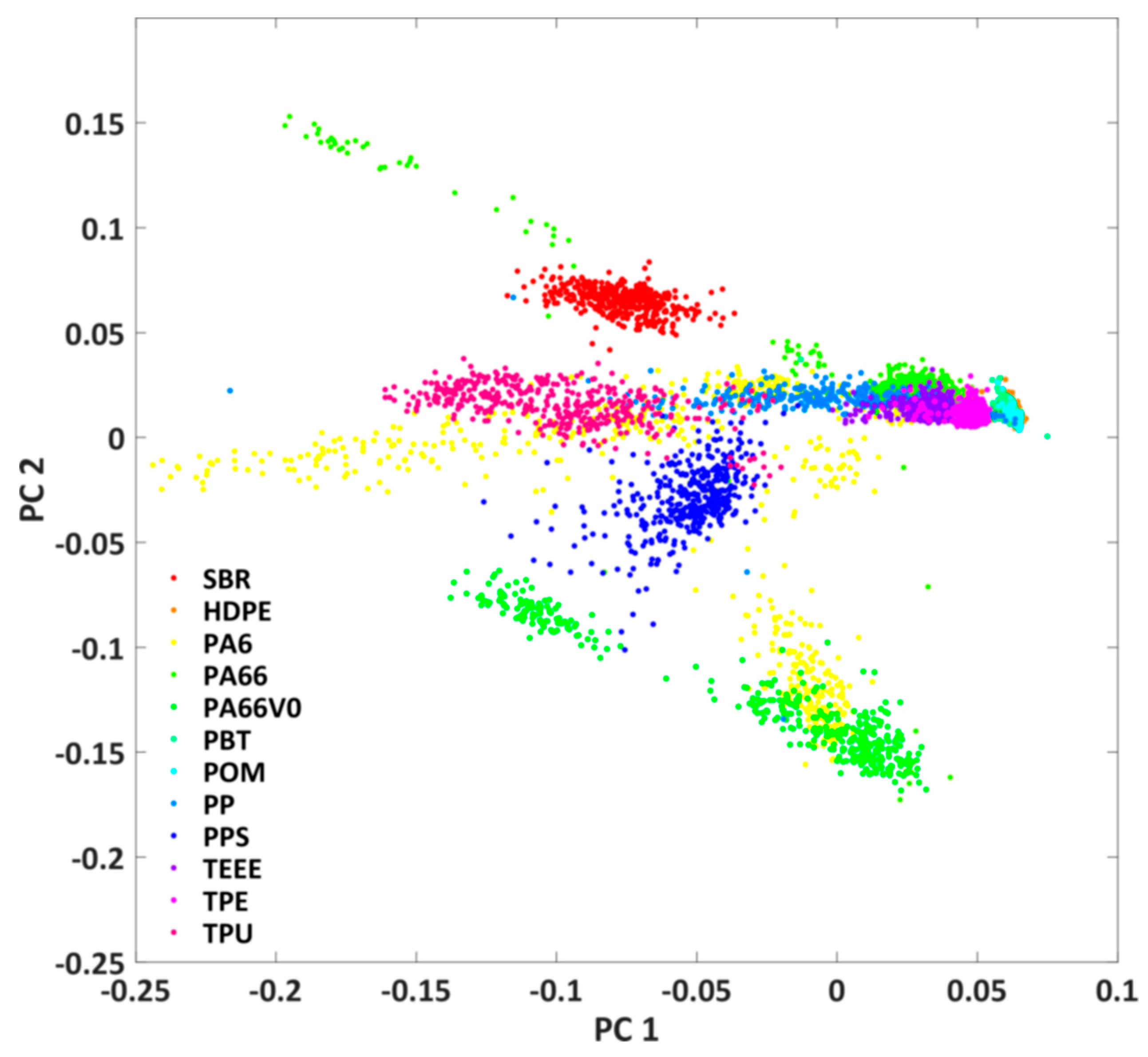
3.1. Imaging Fluorescence Measurements
3.2. Classification Experiments
3.2.1. Classification of all Plastics by a Single Prediction Model
3.2.2. Classification of Relevant Plastic Mixtures by Individual Prediction Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Hyperparameter | Standard Value | Optimization Range | |
|---|---|---|---|
| for all algorithms | Savitzky-Golay smoothing | no | yes/no |
| polynomial degree for Savitzky-Golay smoothing | - | 1–5 | |
| data points for Savitzky-Golay smoothing | - | 3–21 | |
| normalization | none | none/L1/L2/Linf/SNV/min-max | |
| No. of PCs used | 10 | 2–20 | |
| discriminant analysis (DA) [35] | delta | 0 | 0–1 |
| gamma | 0 | 0–1 | |
| k-nearest neighbours (kNN) [36] | number of neighbors | 3 | 1–11 |
| distance metric | euclidean | euclidean/cityblock/cosine | |
| distance weight | equal | equal/invers/quadratic-invers | |
| ensemble learning with decision trees (ENSEMBLE) [37] | ensemble method | AdaBoost | Bag / RusBoost / AdaBoost |
| No. of decision trees | 100 | 10–500 | |
| learnrate | 1 | 0.001–1 | |
| max. number of decision splits | 1 | 1–100 | |
| min. leaf size | 1 | 1–100 | |
| support vector machines (SVM) [38] | kernel | rbf | rbf/linear |
| box-constraint | 1 | 0.001–1000 | |
| kernel-scale | 1 | 0.001–1000 |
| Hyperparameter | Standard Value | Optimization Range | |
|---|---|---|---|
| data augmentation [39] | reflexion | no | yes/no |
| rotation | 0 | 0–360° | |
| translation | 0 | 0–16 pixel | |
| scaling | 1 | 1–1.25 | |
| shearing | 0 | 0–25% | |
| network topologie [40] | No. of convolution blocks | 4 | 2–4 |
| convolution layer per block | 1 | 1–3 | |
| No. of filters of the 1st convolution layer 1 | 16 | 8–48 | |
| size of the convolution kernel | 3 × 3 | 1 × 1; 3 × 3; 5 × 5; 7 × 7 | |
| pooling mode | max-pooling | average-pooling; max-pooling | |
| No. of fully connected layer | 1 | 1–3 | |
| No. of neurons per fully connected layer | 50 | 25; 50; 75; 100; 150; 200 | |
| dropout possibility after last pooling layer 2 | 0 | 0–50% | |
| training parameter [41] | momentum | 0.95 | 0.5–0.999 |
| learnrate | 0.01 | 0.001–1 | |
| L2 regularisation | 0.0005 | 0.0001–1 |

| Abbreviation | Polymers | Abbreviation | Polymers |
|---|---|---|---|
| M1 | HDPE|PP | M22 | PBT|TEEE |
| M2 | PA6|Gummi | M23 | PA6|TPE-HDPE |
| M3 | PA6|PBT | M24 | PA6|TPE-PBT |
| M4 | PA6|POM | M25 | PA6|TPE-PP |
| M5 | PA6|PPS | M26 | PA6|TPU-POM |
| M6 | PA6|TPE | M27 | PA6|TPU-TPE-TEEE |
| M7 | PA6|TPU | M28 | PA66|TPE-HDPE |
| M8 | PA6|PA66 | M29 | PA66|TPE-PBT |
| M9 | PA6|TEEE | M30 | PA66|TPE-PP |
| M10 | PA66|Gummi | M31 | PA66|TPU-POM |
| M11 | PA66|PBT | M32 | PA66|TPU-TPE-TEEE |
| M12 | PA66|POM | M33 | PBT|TPU-TPE-TEEE |
| M13 | PA66|PPS | M34 | PA6|TPE|HDPE |
| M14 | PA66|TPE | M35 | PA6|TPE|PBT |
| M15 | PA66|TPU | M36 | PA6|TPE|PP |
| M16 | PA66|PA66V0 | M37 | PA6|TPU|POM |
| M17 | PA66|TEEE | M38 | PA66|TPE|HDPE |
| M18 | PBT|Gummi | M39 | PA66|TPE|PBT |
| M19 | PBT|PP | M40 | PA66|TPE|PP |
| M20 | PBT|TPE | M41 | PA66|TPU|POM |
| M21 | PBT|TPU |
References
- Geyer, R.; Jambeck, J.R.; Law, K.L. Production, use, and fate of all plastics ever made. Sci. Adv. 2017, 3, e1700782. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.-Q.; Wang, H.; Fu, J.-G.; Liu, Y.-N. Flotation separation of waste plastics for recycling—A review. Waste Manag. 2015, 41, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Hearn, G.L.; Ballard, J.R. The use of electrostatic techniques for the identification and sorting of waste packaging materials. Resour. Conserv. Recycl. 2005, 44, 91–98. [Google Scholar] [CrossRef]
- Kulcke, A.; Gurschler, C.; Spöck, G.; Leitner, R.; Kraft, M. On-line classification of synthetic polymers using near infrared spectral imaging. J. Near Infrared Spectrosc. 2003, 11, 71–81. [Google Scholar] [CrossRef]
- Serranti, S.; Gargiulo, A.; Bonifazi, G. Hyperspectral imaging for process and quality control in recycling plants of polyolefin flakes. J. Near Infrared Spectrosc. 2012, 20, 573–581. [Google Scholar] [CrossRef]
- Riise, B.L.; Biddle, M.B.; Fisher, M.M. X-Ray Fluorescence Spectroscopy in Plastic Recycling; American Plastics Council: Arlington, VA, USA, 2000. [Google Scholar]
- Rozenstein, O.; Puckrin, E.; Adamowski, J. Development of a new approach based on midwave infrared spectroscopy for post-consumer black plastic waste sorting in the recycling industry. Waste Manag. 2017, 68, 38–44. [Google Scholar] [CrossRef] [PubMed]
- EVK DI KERSCHHAGGL GMBH. Black Polymer Sorting. Available online: http://www.bp-sorting.com/uploads/4/7/5/6/4756078/bp_sorting_-_laymans_report.pdf (accessed on 14 September 2015).
- Küter, A.; Reible, S.; Geibig, T.; Nüßler, D.; Pohl, N. THz imaging for recycling of black plastics. Tech. Mess. 2018, 85, 191–201. [Google Scholar] [CrossRef]
- Mikloweit, M. Sortierung Schwarzer Kunststoffe für Recycling. Available online: http://www.blackvalue.de/ (accessed on 25 June 2019).
- Shameem, K.M.M.; Choudhari, K.S.; Bankapur, A.; Kulkarni, S.D.; Unnikrishnan, V.K.; George, S.D.; Kartha, V.B.; Santhosh, C. A hybrid LIBS-Raman system combined with chemometrics: An efficient tool for plastic identification and sorting. Anal. Bioanal. Chem. 2017, 409, 3299–3308. [Google Scholar] [CrossRef]
- Unnikrishnan, V.K.; Choudhari, K.S.; Kulkarni, S.D.; Nayak, R.; Kartha, V.B.; Santhosh, C. Analytical predictive capabilities of Laser Induced Breakdown Spectroscopy (LIBS) with Principal Component Analysis (PCA) for plastic classification. RSC Adv. 2013, 3, 25872. [Google Scholar] [CrossRef]
- Heckmann, W. Characterization of polymer materials by fluorescence imaging. Microsc. Microanal. 2005, 11, 2036–2037. [Google Scholar] [CrossRef]
- Hawkins, K.R.; Yager, P. Nonlinear decrease of background fluorescence in polymer thin-films—A survey of materials and how they can complicate fluorescence detection in μTAS. Lab Chip 2003, 3, 248–252. [Google Scholar] [CrossRef] [PubMed]
- Soutar, I. The application of luminescence techniques in polymer science. Polym. Int. 1991, 26, 35–49. [Google Scholar] [CrossRef]
- UniSensor Sensorsysteme GmbH. POWERSORT 200. Available online: http://www.unisensor.de/en/products/product-details/recycling-industry-1/powersort-200-1.html (accessed on 1 July 2019).
- Suryanarayana, C. Mechanical alloying and milling. Prog. Mater. Sci. 2001, 46, 1–184. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning, Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Bishop, C.M. Pattern recognition and machine learning, 11. (corr. printing). In Information Science and Statistics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inform. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Support vector machines. In Information Science and Statistics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman & Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Gruber, F.; Wollmann, P.; Grählert, W.; Kaskel, S. Hyperspectral imaging using laser excitation for fast raman and fluorescence hyperspectral imaging for sorting and quality control applications. J. Imaging 2018, 4, 110. [Google Scholar] [CrossRef]
- Gruber, F. Imaging Fluorescence Measurements of Black Plastic Particles Measured with 450 nm Excitation. figshare. Dataset. Available online: https://doi.org/10.6084/m9.figshare.9205292 (accessed on 11 September 2019).
- Jolliffe, I. Principal Component Analysis; Springer: New York, NY, USA, 2011. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 3320–3328. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 2951–2959. [Google Scholar]
- Anderson, T.W.; Darling, D.A. Asymptotic theory of certain “goodness of fit” criteria based on stochastic processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Brown, M.B.; Forsythe, A.B. Robust tests for the equality of variances. J. Am. Stat. Assoc. 1974, 69, 364–367. [Google Scholar] [CrossRef]
- Dietterich, T.G. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput. 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [PubMed]
- The MathWorks, Inc. Fitcdiscr: Fit Discriminant Analysis Classifier. Available online: http://de.mathworks.com/help/stats/fitcdiscr.html (accessed on 5 July 2019).
- The MathWorks, Inc. Ficknn: Fit K-Nearest Neighbor Classifier. Available online: http://de.mathworks.com/help/stats/fitcknn.html?s_tid=doc_ta (accessed on 5 July 2019).
- The MathWorks, Inc. Fitcensemble: Fit Ensemble of Learners for Classification. Available online: http://de.mathworks.com/help/stats/fitcensemble.html?s_tid=doc_ta (accessed on 5 July 2019).
- The MathWorks, Inc. Fitcecoc: Fit Multiclass Models for Support Vector Machines or Other Classifier. Available online: http://de.mathworks.com/help/stats/fitcecoc.html?s_tid=doc_ta (accessed on 5 July 2019).
- The MathWorks, Inc. imageDataAugmenter: Configure Image Data Augmentation. Available online: http://de.mathworks.com/help/deeplearning/ref/imagedataaugmenter.html?s_tid=doc_ta (accessed on 5 July 2019).
- The MathWorks, Inc. List of Deep Learning Layers. Available online: http://de.mathworks.com/help/deeplearning/ug/list-of-deep-learning-layers.html (accessed on 5 July 2019).
- The MathWorks, Inc. TrainNetwork: Train Neural Network for Deep Learning. Available online: http://de.mathworks.com/help/deeplearning/ref/trainnetwork.html (accessed on 5 July 2019).
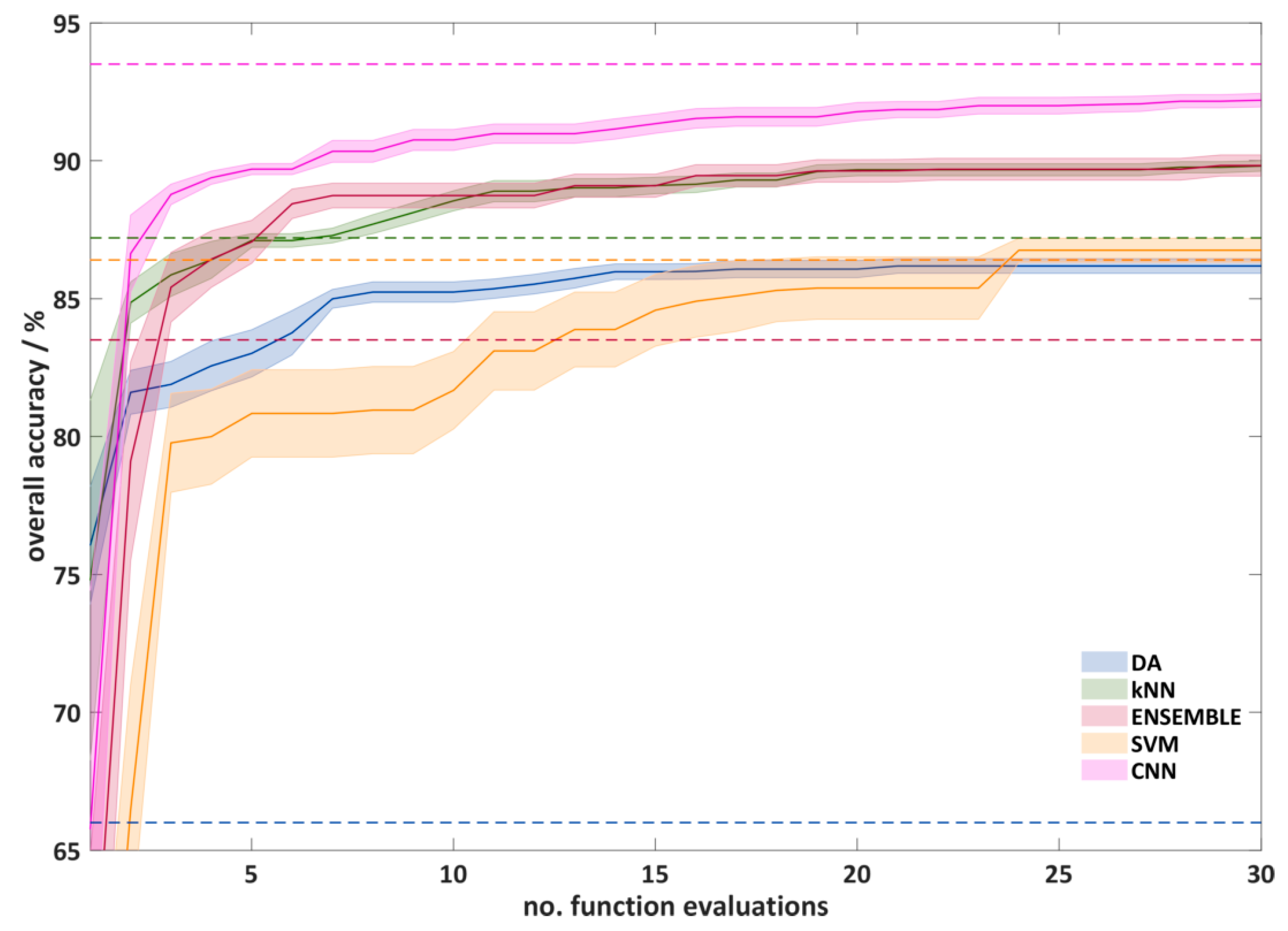
| Overall Accuracy | Kappa Coefficient | |||
|---|---|---|---|---|
| standard parameter | random search | standard parameter | random search | |
| DA | 66.0 ± 1.0 | 86.2 ± 0.6 * | 0.623 ± 0.011 | 0.845 ± 0.006 * |
| kNN | 87.2 ± 0.4 | 89.8 ± 0.4 * | 0.859 ± 0.005 | 0.885 ± 0.006 * |
| ENSEMBLE | 83.5 ± 1.1 | 89.8 ± 0.9* | 0.819 ± 0.012 | 0.874 ± 0.017 * |
| SVM | 86.4 ± 0.8 | 86.8 ± 1.0 | 0.85 ± 0.009 | 0.861 ± 0.01 |
| CNN | 93.5 ± 0.6 | 92.2 ± 0.6 * | 0.916 ± 0.005 | 0.906 ± 0.007 * |
| ENSEMBLE Standard Parameter | ENSEMBLE Random Search | SVM Standard Parameter | SVM Random Search | CNN Standard Parameter | CNN Transfer Learning | |
|---|---|---|---|---|---|---|
| M1 | 99.4 | 99.9 | 93.2 | 100.0 | 77.2 | 100.0 |
| M2 | 100.0 | 100.0 | 99.7 | 100.0 | 87.7 | 100.0 |
| M3 | 99.7 | 99.9 | 97.3 | 100.0 | 75.1 | 100.0 |
| M4 | 86.1 | 90.4 | 84.9 | 89.6 | 70.2 | 89.6 |
| M5 | 99.8 | 100.0 | 99.3 | 100.0 | 87.2 | 100.0 |
| M6 | 98.8 | 99.6 | 97.5 | 99.8 | 71.0 | 99.8 |
| M7 | 99.6 | 100.0 | 99.4 | 100.0 | 83.9 | 100.0 |
| M8 | 98.4 | 99.2 | 98.2 | 98.9 | 87.6 | 98.9 |
| M9 | 98.3 | 99.4 | 97.2 | 99.8 | 75.2 | 99.8 |
| M10 | 99.3 | 100.0 | 99.2 | 99.9 | 83.3 | 99.9 |
| M11 | 99.3 | 99.9 | 98.4 | 100.0 | 70.5 | 100.0 |
| M12 | 100.0 | 100.0 | 98.8 | 100.0 | 71.3 | 100.0 |
| M13 | 99.8 | 99.8 | 98.2 | 100.0 | 80.5 | 100.0 |
| M14 | 98.0 | 99.3 | 98.4 | 99.3 | 66.6 | 99.3 |
| M15 | 99.9 | 100.0 | 98.4 | 100.0 | 75.4 | 100.0 |
| M16 | 99.7 | 99.9 | 99.0 | 99.9 | 75.6 | 99.9 |
| M17 | 97.9 | 98.0 | 94.8 | 99.0 | 66.5 | 99.0 |
| M18 | 99.8 | 99.9 | 99.0 | 100.0 | 86.1 | 100.0 |
| M19 | 98.6 | 99.7 | 94.3 | 99.9 | 83.5 | 99.9 |
| M20 | 100.0 | 100.0 | 97.4 | 100.0 | 81.2 | 100.0 |
| M21 | 99.6 | 99.8 | 96.4 | 100.0 | 81.0 | 100.0 |
| M22 | 98.9 | 99.7 | 93.5 | 99.8 | 78.2 | 99.8 |
| M23 | 98.9 | 99.7 | 98.2 | 99.7 | 83.0 | 99.7 |
| M24 | 99.0 | 99.5 | 98.7 | 99.6 | 86.8 | 99.6 |
| M25 | 99.1 | 99.6 | 99.1 | 99.5 | 93.4 | 99.5 |
| M26 | 89.1 | 92.1 | 88.7 | 91.5 | 82.3 | 91.5 |
| M27 | 99.2 | 99.6 | 98.9 | 99.8 | 79.3 | 99.8 |
| M28 | 98.4 | 99.2 | 98.5 | 98.9 | 84.9 | 98.9 |
| M29 | 98.8 | 99.2 | 98.6 | 98.8 | 86.2 | 98.8 |
| M30 | 98.5 | 99.3 | 98.4 | 98.7 | 88.7 | 98.7 |
| M31 | 99.8 | 100.0 | 99.0 | 99.9 | 89.2 | 99.9 |
| M32 | 98.2 | 99.0 | 97.7 | 98.3 | 74.5 | 98.3 |
| M33 | 99.4 | 99.9 | 99.6 | 99.9 | 75.5 | 99.9 |
| M34 | 98.5 | 99.0 | 97.8 | 99.4 | 61.7 | 99.4 |
| M35 | 98.6 | 99.3 | 97.4 | 99.4 | 67.6 | 99.4 |
| M36 | 99.0 | 99.4 | 97.9 | 99.4 | 71.3 | 99.4 |
| M37 | 88.9 | 92.2 | 88.0 | 92.0 | 71.8 | 92.0 |
| M38 | 98.3 | 98.6 | 97.4 | 98.9 | 57.5 | 98.9 |
| M39 | 98.8 | 99.0 | 98.0 | 99.0 | 63.4 | 99.0 |
| M40 | 98.3 | 98.3 | 97.1 | 98.9 | 64.4 | 98.9 |
| M41 | 99.9 | 100.0 | 99.2 | 100.0 | 71.2 | 100.0 |
| mean | 98.3 | 99.0 | 97.1 | 99.0 | 77.3 | 99.0 |
| ENSEMBLE Random Search | SVM Random Search | CNN Transfer Learning | |
|---|---|---|---|
| /s | 220 | 273 | 54 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gruber, F.; Grählert, W.; Wollmann, P.; Kaskel, S. Classification of Black Plastics Waste Using Fluorescence Imaging and Machine Learning. Recycling 2019, 4, 40. https://doi.org/10.3390/recycling4040040
Gruber F, Grählert W, Wollmann P, Kaskel S. Classification of Black Plastics Waste Using Fluorescence Imaging and Machine Learning. Recycling. 2019; 4(4):40. https://doi.org/10.3390/recycling4040040
Chicago/Turabian StyleGruber, Florian, Wulf Grählert, Philipp Wollmann, and Stefan Kaskel. 2019. "Classification of Black Plastics Waste Using Fluorescence Imaging and Machine Learning" Recycling 4, no. 4: 40. https://doi.org/10.3390/recycling4040040





