Development of Sustainable Composite Sandwich with Wood Waste and Natural Fibers for Circular Economy Applications
Abstract
1. Introduction
2. Materials and Experimental Procedure
2.1. Materials
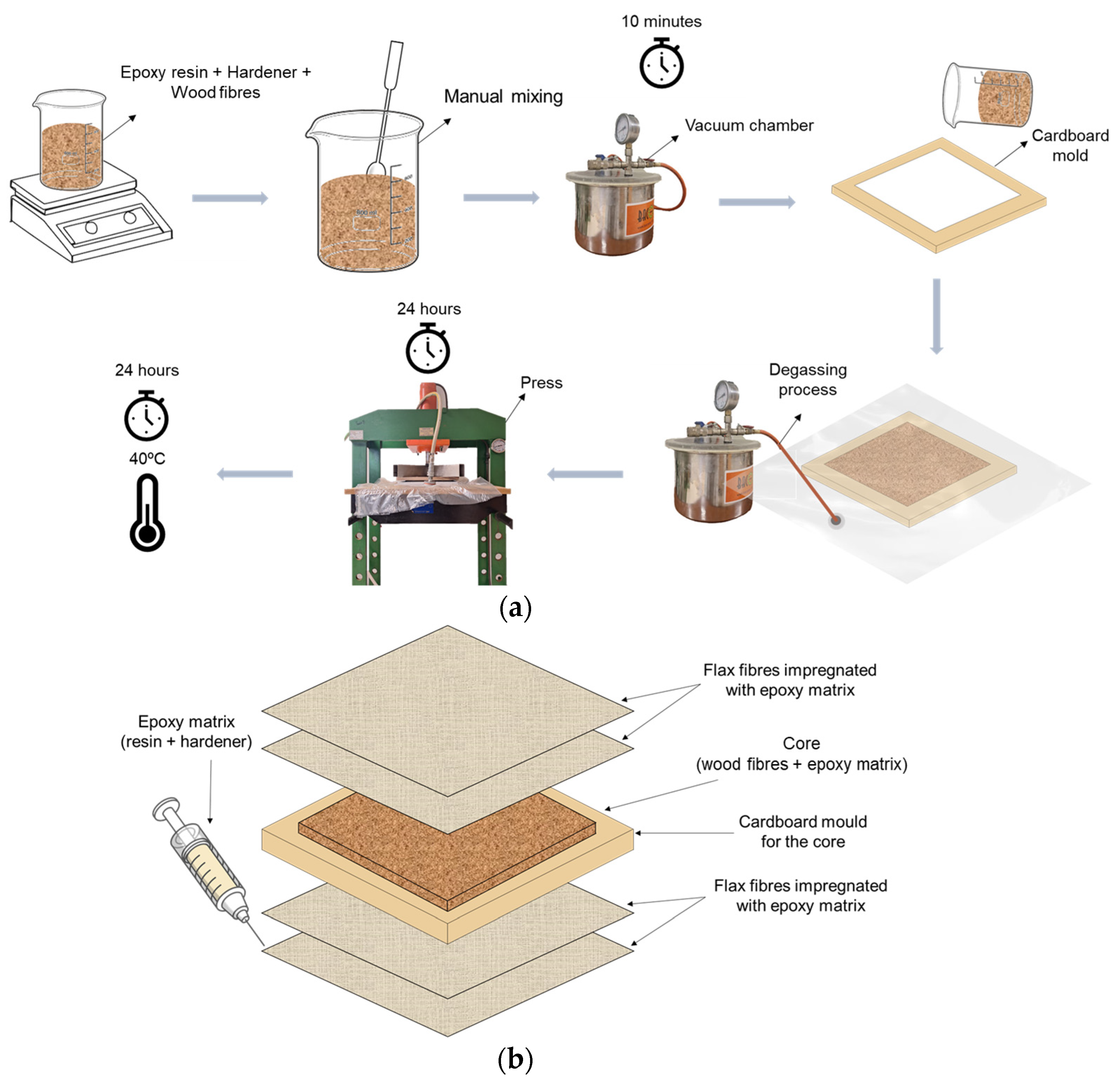
2.2. Manufacture and Experimental Procedure
3. Results
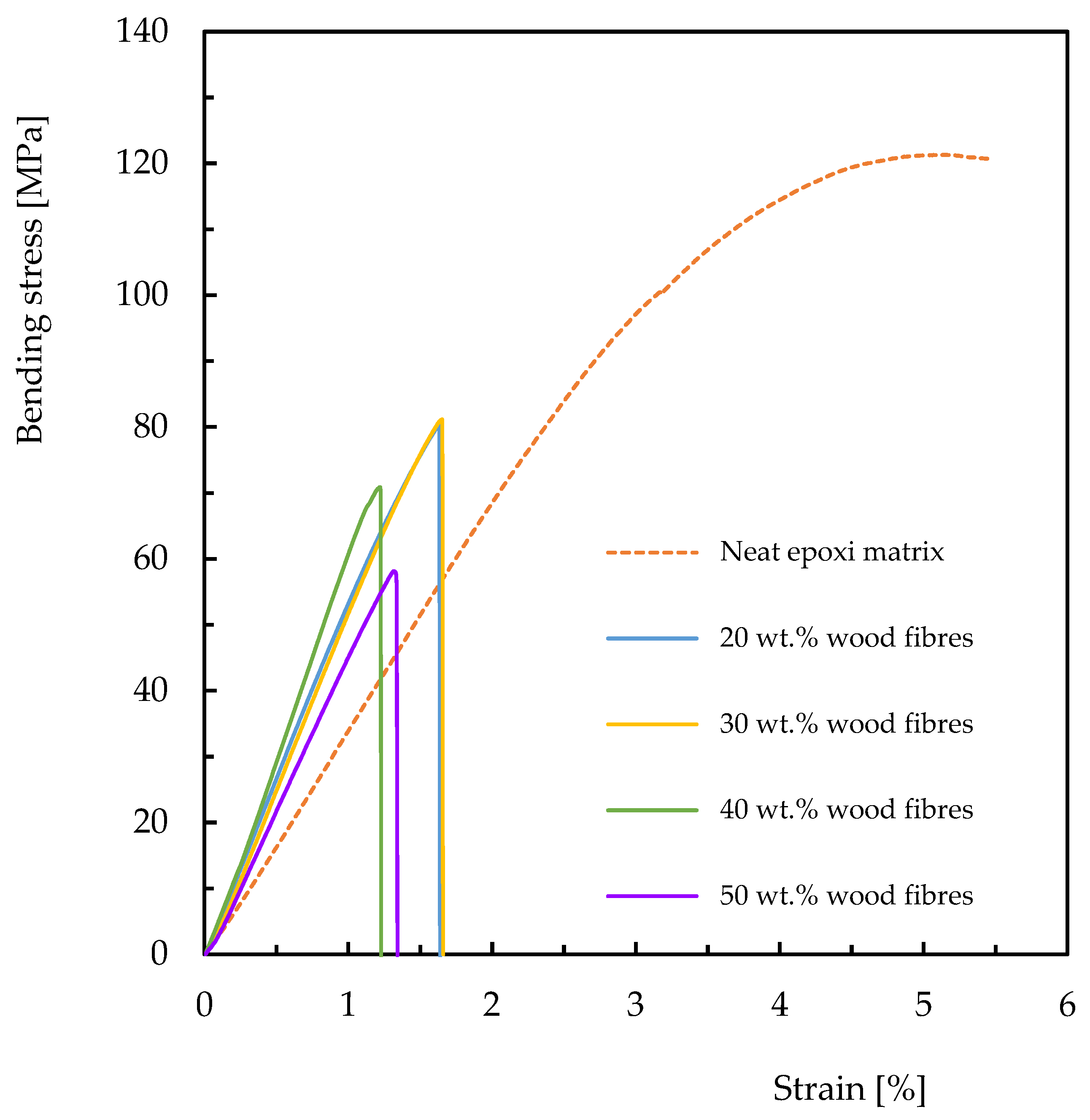
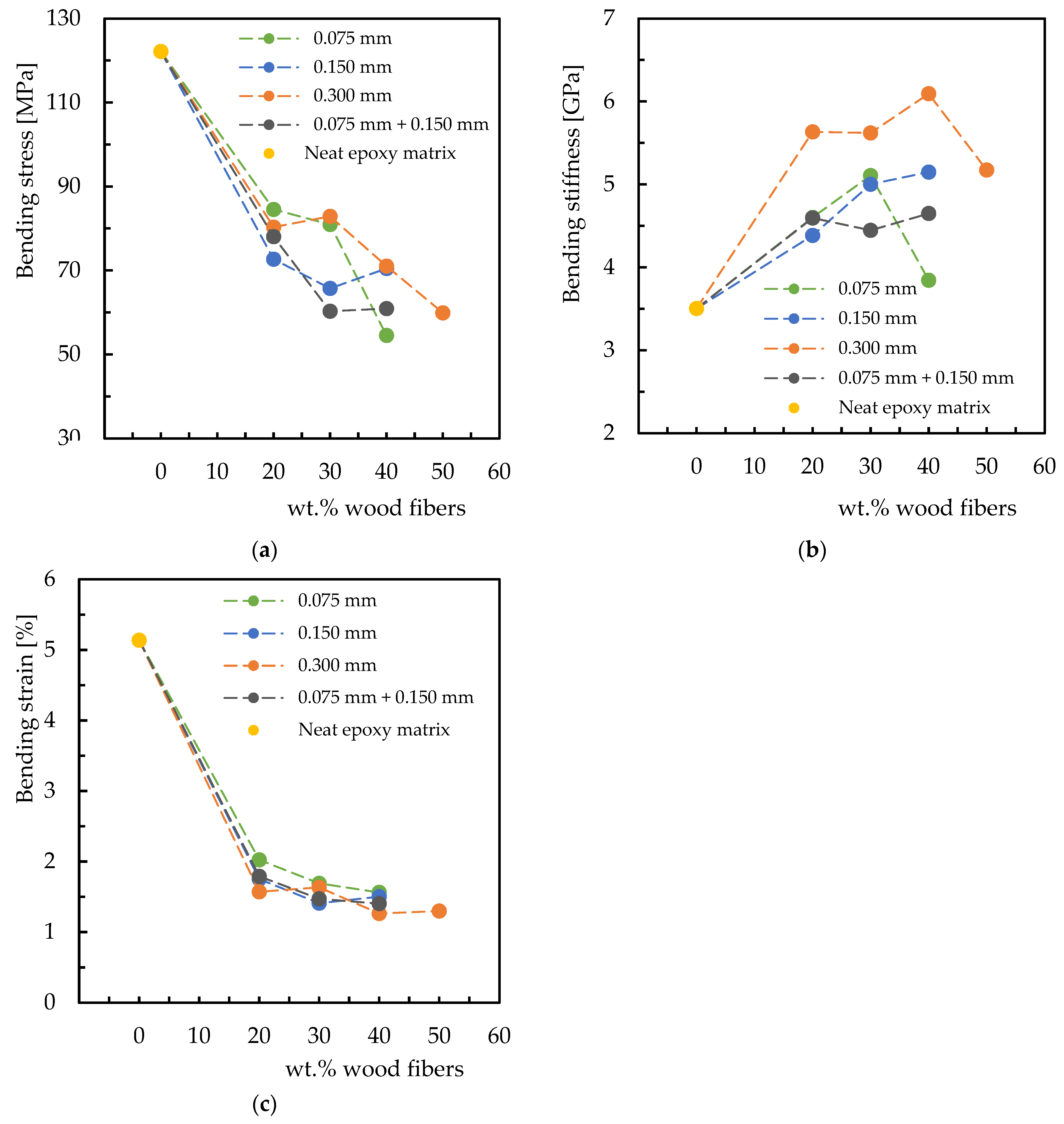
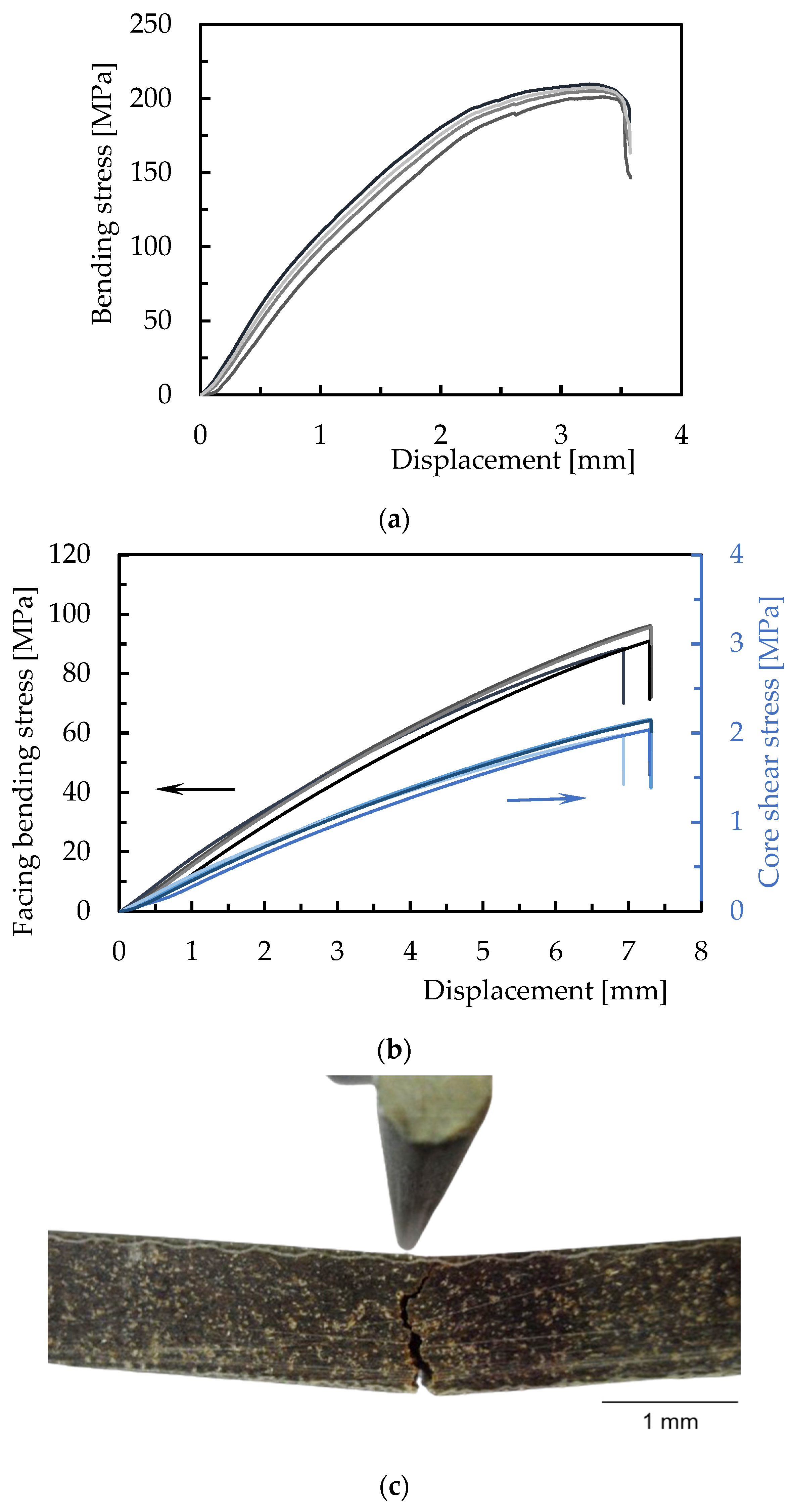
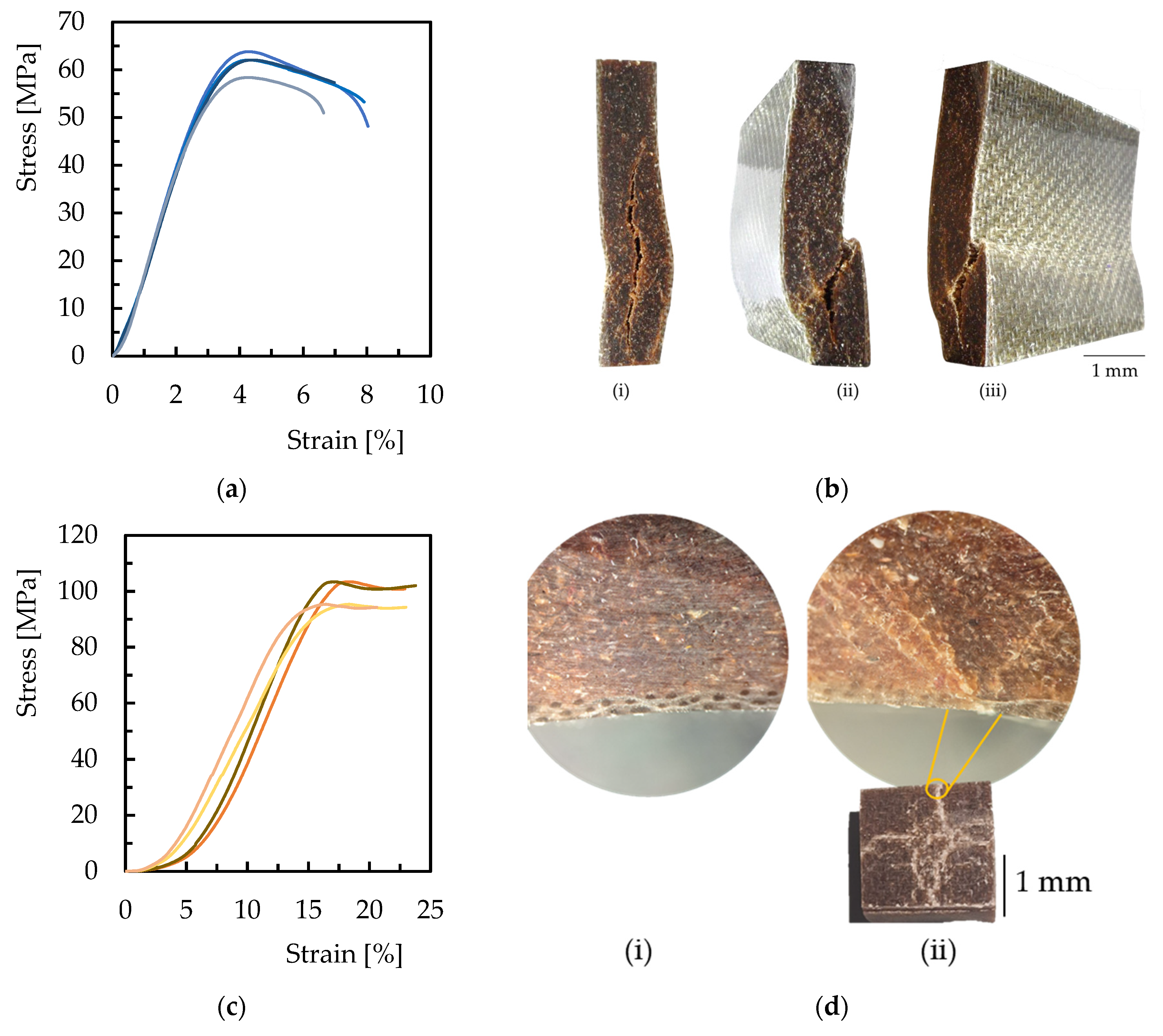
3.1. Static Characterization
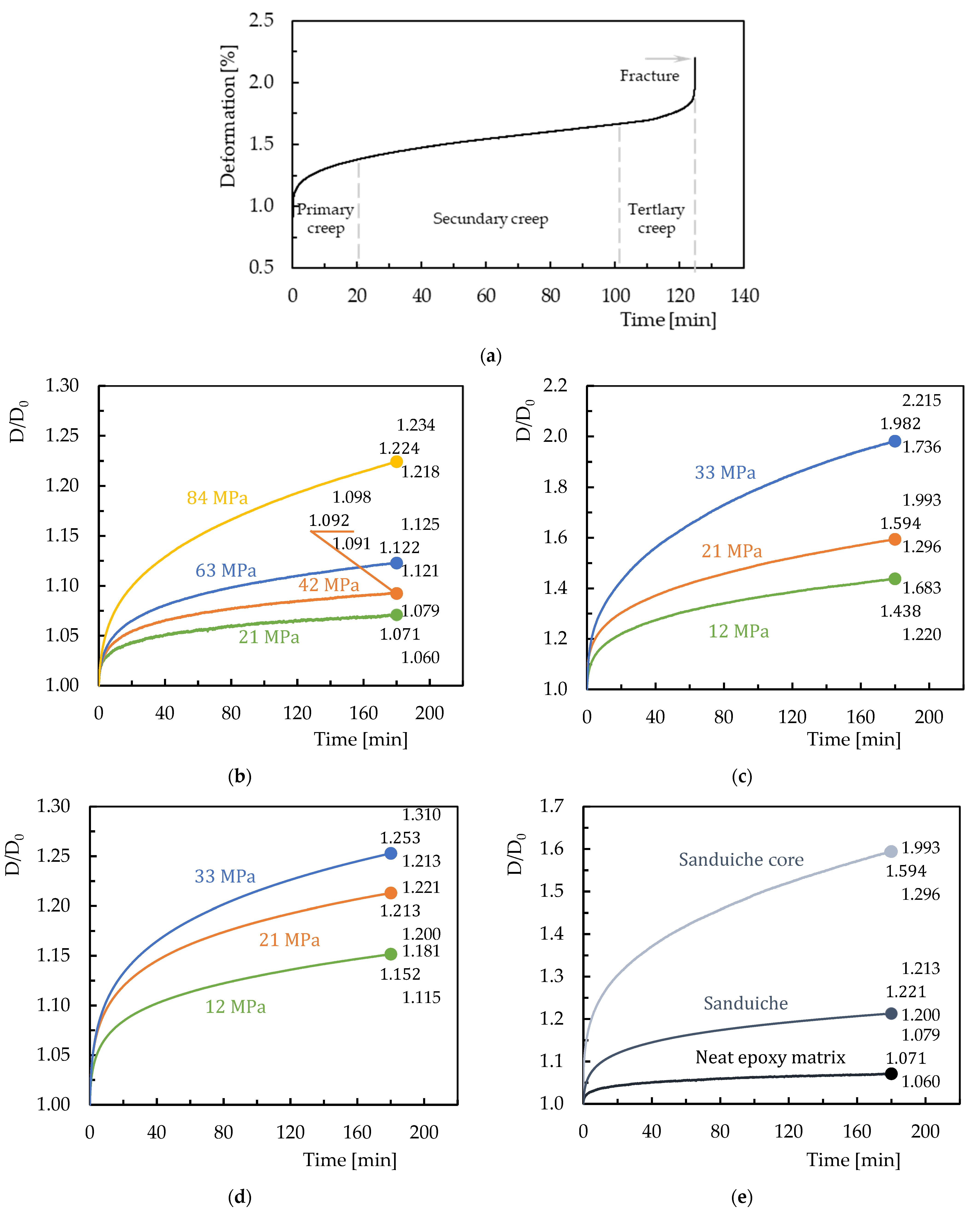
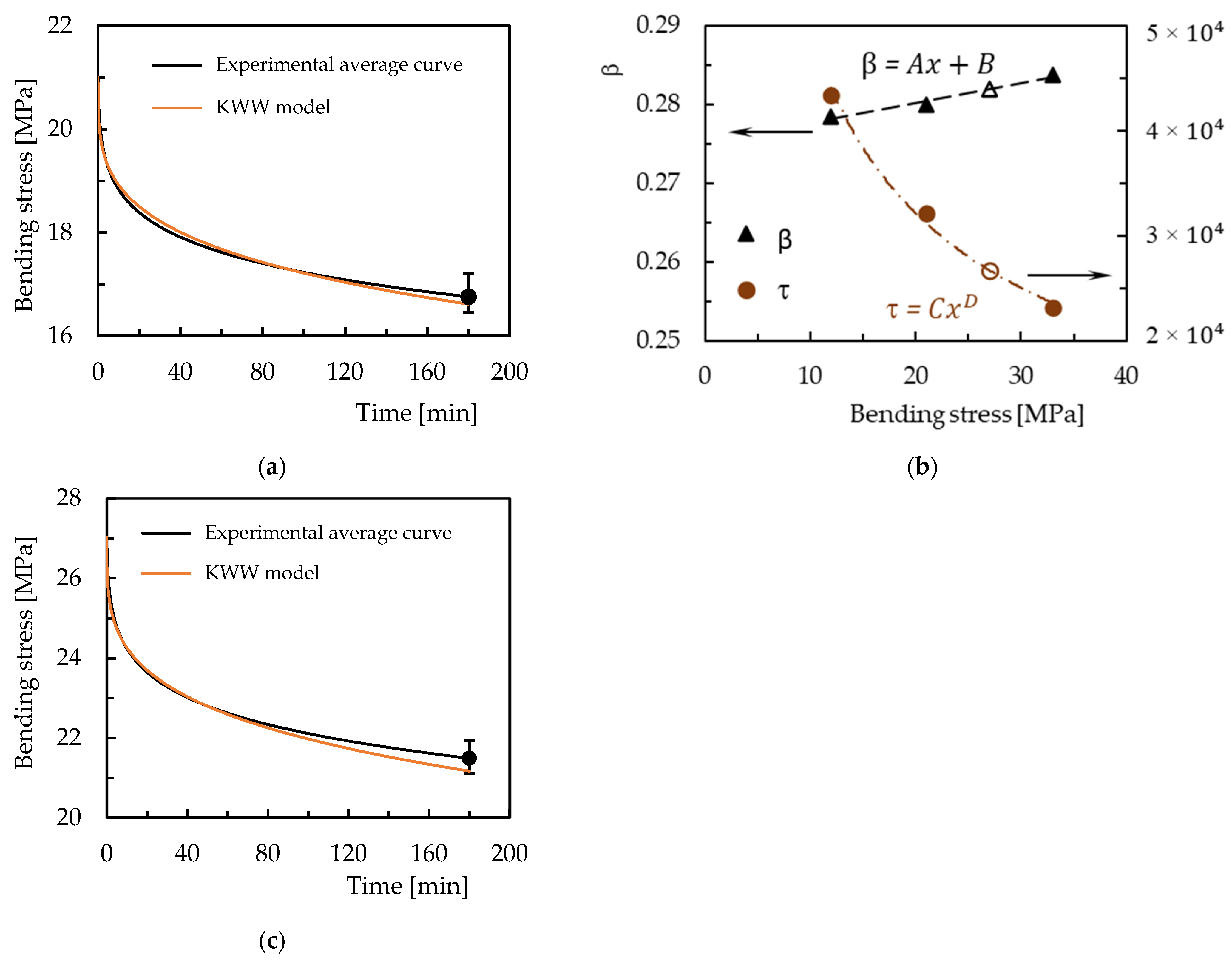
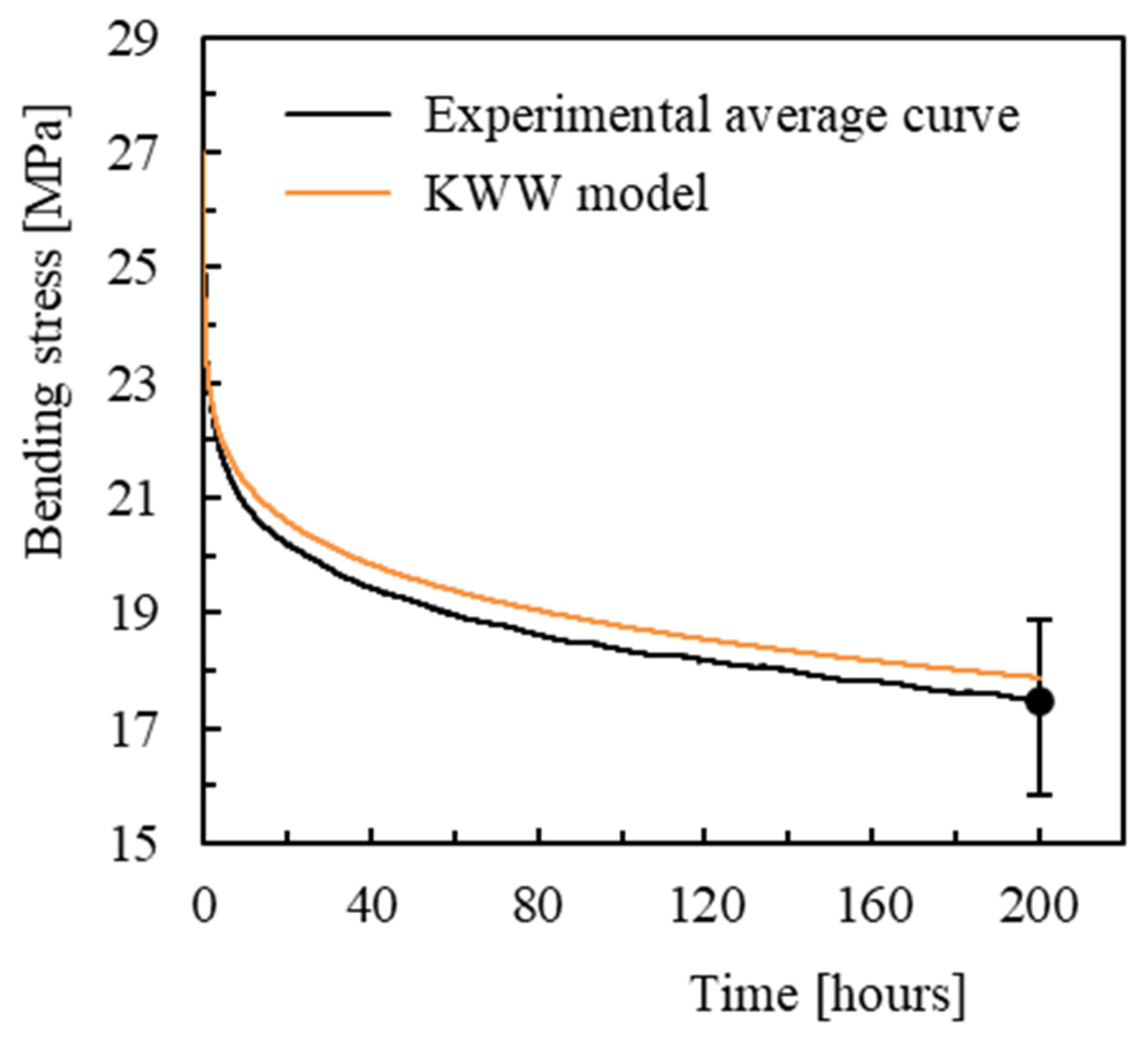
3.2. Creep
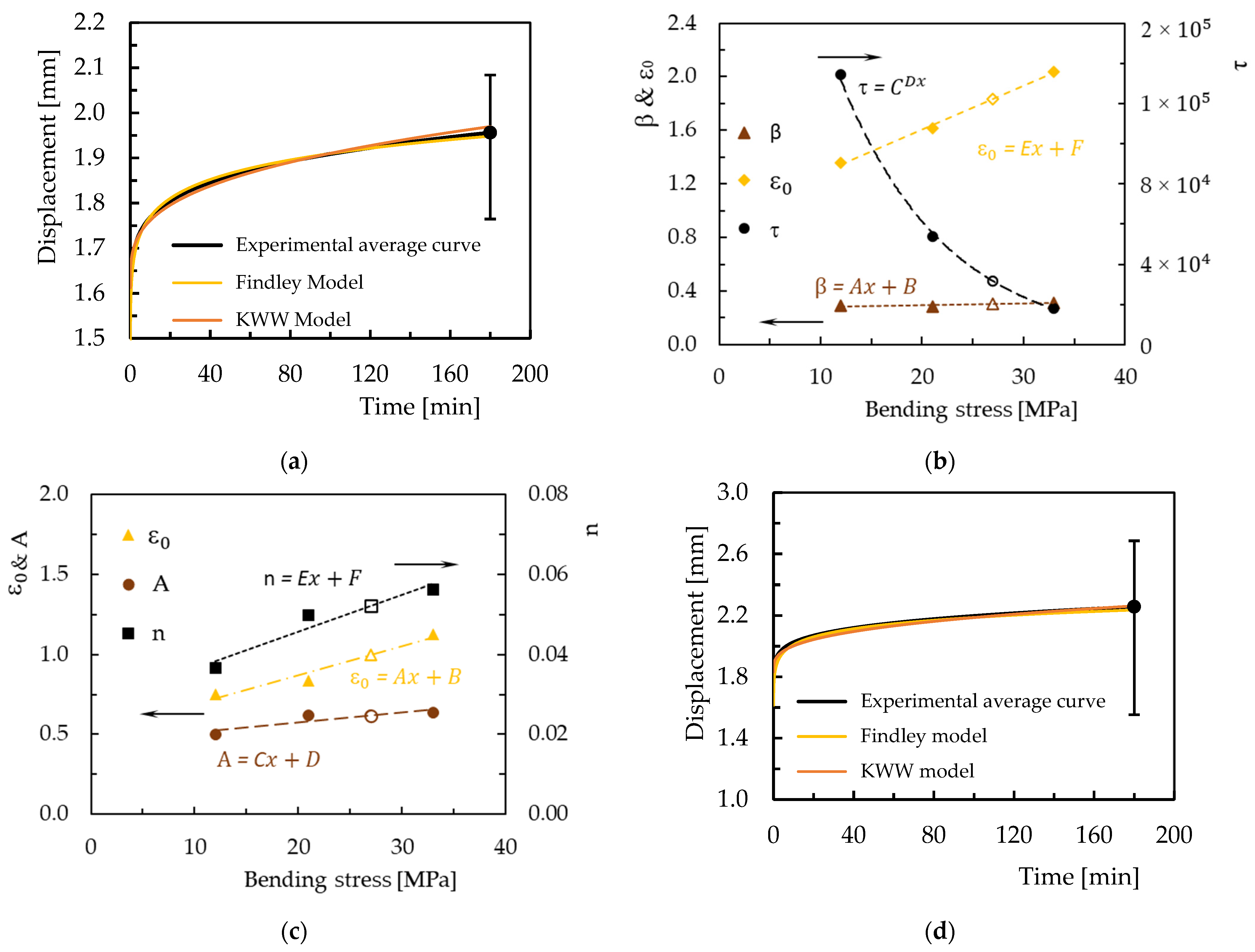
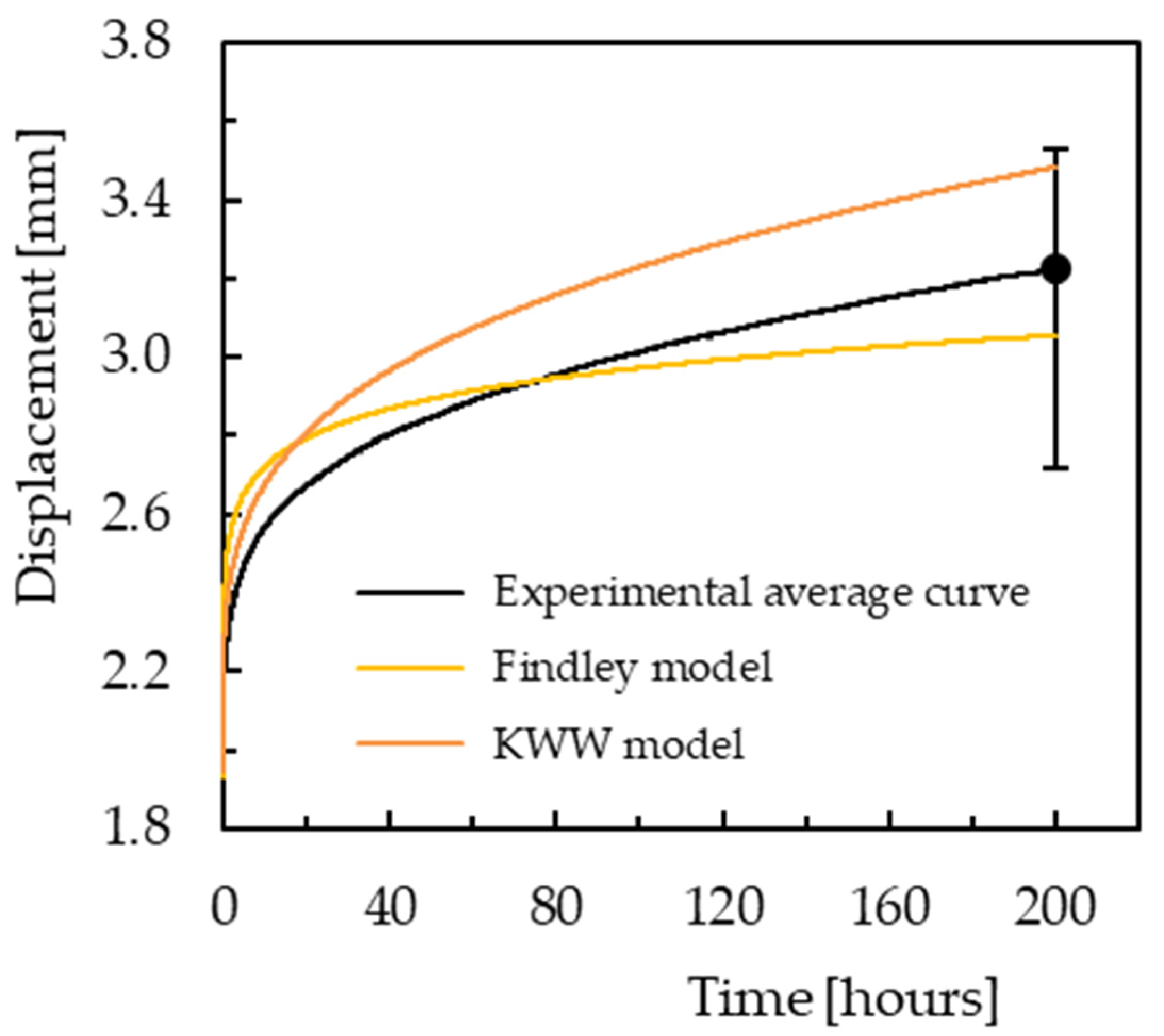
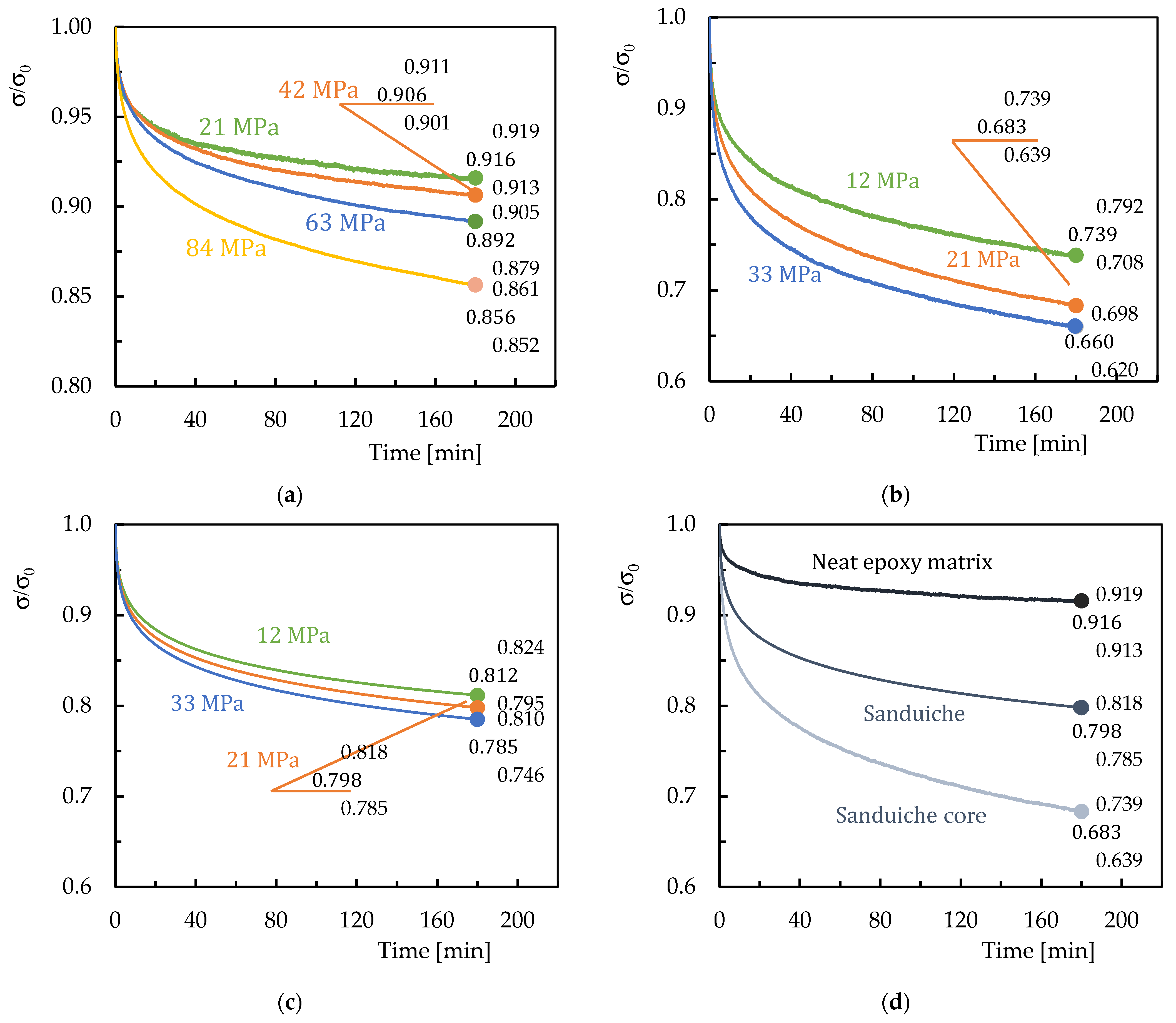
3.3. Stress Relaxation
3.4. Production Costs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuhlman, T.; Farrington, J. What Is Sustainability? Sustainability 2010, 2, 3436–3448. [Google Scholar] [CrossRef]
- Ellen MacArthur Foundation Towards a Circular Economy: Business Rationale for an Accelerated Transition. 2015. Available online: https://content.ellenmacarthurfoundation.org/m/4384c08da576329c/original/Towards-a-circular-economy-Business-rationale-for-an-accelerated-transition.pdf (accessed on 19 June 2023).
- European Parliament Research Service Circular Economy: Definition, Importance and Benefits. Available online: https://www.europarl.europa.eu/news/en/headlines/economy/20151201STO05603/circular-economy-definition-importance-and-benefits (accessed on 19 June 2023).
- Bocken, N.M.P.; de Pauw, I.; Bakker, C.; van der Grinten, B. Product Design and Business Model Strategies for a Circular Economy. J. Ind. Prod. Eng. 2016, 33, 308–320. [Google Scholar] [CrossRef]
- Ho, O.T.-K.; Gajanayake, A.; Iyer-Raniga, U. Transitioning to a State-Wide Circular Economy: Major Stakeholder Interviews. Resour. Conserv. Recycl. Adv. 2023, 19, 200163. [Google Scholar] [CrossRef]
- Le Moigne, R. Waste Watchers. 2021. Available online: https://www.ellenmacarthurfoundation.org/articles/waste-watchers (accessed on 19 June 2023).
- Siva, R.; Valarmathi, T.N.; Palanikumar, K.; Samrot, A.V. Study on a Novel Natural Cellulosic Fiber from Kigelia Africana Fruit: Characterization and Analysis. Carbohydr. Polym. 2020, 244, 116494. [Google Scholar] [CrossRef]
- Mendes, C.P.; Fleming, R.; Goncalves, A.-M.B.; da Silva, M.J.; Prataviera, R.; Cena, C. Mechanical and Microstructural Characterization of Epoxy/Sawdust (Pinus elliottii) Composites. Polym. Polym. Compos. 2021, 29, 1135–1142. [Google Scholar] [CrossRef]
- Siva, R.; Mobithis, M.; Ravichandran, R.; Valarmathi, T.; Jeya Jeevahan, J.; Sangeetha, M. Characterization of Mechanical, Chemical Properties and Microstructure of Untreated and Treated Cissus Quadrangularis Fiber. Mater. Today Proc. 2021, 47, 4479–4483. [Google Scholar] [CrossRef]
- Kumar, N.; Grewal, J.S.; Kumar, S.; Kumar, N.; Kashyap, K. Mechanical and Thermal Properties of NaOH Treated Sisal Natural Fiber Reinforced Polymer Composites: Barium Sulphate Used as Filler. Mater. Today Proc. 2021, 45, 5575–5578. [Google Scholar] [CrossRef]
- Owen, M.M.; Achukwu, E.O.; Romli, A.Z.; Bin Abdullah, A.H.; Ramlee, M.H.; Bin Shuib, S. Thermal and Mechanical Characterization of Composite Materials from Industrial Plastic Wastes and Recycled Nylon Fibers for Floor Paving Tiles Application. Waste Manag. 2023, 166, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, P.R.; dos Santos, J.C.; Ribeiro Filho, S.L.M.; Torres Ferreira, B.; Panzera, T.H.; Scarpa, F. Eco-Friendly Sandwich Panel Based on Recycled Bottle Caps Core and Natural Fibre Composite Facings. Fibers Polym. 2020, 21, 1798–1807. [Google Scholar] [CrossRef]
- Oliveira, P.R.; May, M.; Panzera, T.H.; Scarpa, F.; Hiermaier, S. Improved Sustainable Sandwich Panels Based on Bottle Caps Core. Compos. Part B Eng. 2020, 199, 108165. [Google Scholar] [CrossRef]
- Oliveira, P.R.; Virgen, G.P.G.; Imbert, M.; Beisel, S.; May, M.; Panzera, T.H.; Hiermaier, S.; Balle, F. Ultrasonically Welded Eco-Friendly Sandwich Panels Based on Upcycled Thermoplastic Core: An Eco-Mechanical Characterisation. Resour. Conserv. Recycl. Adv. 2023, 20, 200187. [Google Scholar] [CrossRef]
- McCracken, A.; Sadeghian, P. Corrugated Cardboard Core Sandwich Beams with Bio-Based Flax Fiber Composite Skins. J. Build. Eng. 2018, 20, 114–122. [Google Scholar] [CrossRef]
- Fu, Y.; Sadeghian, P. Bio-Based Sandwich Beams Made of Paper Honeycomb Cores and Flax FRP Facings: Flexural and Shear Characteristics. Structures 2023, 54, 446–460. [Google Scholar] [CrossRef]
- Betts, D.; Sadeghian, P.; Fam, A. Experiments and Nonlinear Analysis of the Impact Behaviour of Sandwich Panels Constructed with Flax Fibre-Reinforced Polymer Faces and Foam Cores. J. Sandw. Struct. Mater. 2021, 23, 3139–3163. [Google Scholar] [CrossRef]
- Fu, Y.; Sadeghian, P. Flexural and Shear Characteristics of Bio-Based Sandwich Beams Made of Hollow and Foam-Filled Paper Honeycomb Cores and Flax Fiber Composite Skins. Thin-Walled Struct. 2020, 153, 106834. [Google Scholar] [CrossRef]
- Dinesh, S.; Kumaran, P.; Mohanamurugan, S.; Vijay, R.; Singaravelu, D.L.; Vinod, A.; Sanjay, M.R.; Siengchin, S.; Bhat, K.S. Influence of Wood Dust Fillers on the Mechanical, Thermal, Water Absorption and Biodegradation Characteristics of Jute Fiber Epoxy Composites. J. Polym. Res. 2020, 27, 9. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Maurya, N.K.; Dwivedi, S.P. Effect of Particle Size and Weight Percent of Different Wood Dust on the Tensile Strength of Glass Fiber Epoxy/Saw Dust Composite Using RSM. Mater. Today Proc. 2021, 47, 3936–3942. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Ou, R.; Wang, Q. The Properties of Flax Fiber Reinforced Wood Flour/High Density Polyethylene Composites. J. For. Res. 2018, 29, 533–540. [Google Scholar] [CrossRef]
- Di, J.; Zuo, H.; Li, Y. Flexural Performance of Glulam Strengthened with Flax-Fiber Reinforced Polymer Composites. Wood Mater. Sci. Eng. 2023, 18, 1014–1023. [Google Scholar] [CrossRef]
- Wang, W.-H.; Huang, H.-B.; Du, H.-H.; Wang, H. Effects of Fiber Size on Short-Term Creep Behavior of Wood Fiber/HDPE Composites. Polym. Eng. Sci. 2015, 55, 693–700. [Google Scholar] [CrossRef]
- Georgiopoulos, P.; Kontou, E.; Christopoulos, A. Short-Term Creep Behavior of a Biodegradable Polymer Reinforced with Wood-Fibers. Compos. Part B Eng. 2015, 80, 134–144. [Google Scholar] [CrossRef]
- Sicomin, S.R. GreenPoxy 56: Système Epoxy Translucide; GreenPoxy: Chateauneuf-les-Martigues, France, 2016; pp. 1–7. [Google Scholar]
- BS EN ISO 178:2003; Plastics—Determination of Flexural Properties. ISO: Geneva, Switzerland, 2003; ISBN 0 580 41324 1.
- C393/C393M-20; ASTM Standard Test Method for Core Shear Properties of Sandwich Constructions by Beam Flexure. ASTM: Washington, DC, USA, 2020.
- C 364/C 364M-07; ASTM Standard Test Method for Edgewise Compressive Strength of Sandwich. ASTM: Washington, DC, USA, 2007; pp. 1–8.
- C 365/C 365M-05; ASTM Standard Test Method for Flatwise Compressive Properties of Sandwich Cores. ASTM: Washington, DC, USA, 2005.
- E328-20; ASTM Standard Test Methods for Stress Relaxation for Materials and Structures. ASTM: Washington, DC, USA, 2020.
- D2990-17; ASTM Standard Test Methods for Tensile, Compressive, and Flexural Creep and Creep-Rupture of Plastics. ASTM: Washington, DC, USA, 2017; p. 8.
- Liu, Y.; Lu, C.; Bian, S.; Hu, K.; Zheng, K.; Sun, Q. Reversible Photo-Responsive Smart Wood with Resistant to Extreme Weather. J. Mater. Sci. 2022, 57, 3337–3347. [Google Scholar] [CrossRef]
- Renner, K.; Móczó, J.; Pukánszky, B. Deformation and Failure of PP Composites Reinforced with Lignocellulosic Fibers: Effect of Inherent Strength of the Particles. Compos. Sci. Technol. 2009, 69, 1653–1659. [Google Scholar] [CrossRef]
- Cho, J.; Joshi, M.S.; Sun, C.T. Effect of Inclusion Size on Mechanical Properties of Polymeric Composites with Micro and Nano Particles. Compos. Sci. Technol. 2006, 66, 1941–1952. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Feng, X.-Q.; Lauke, B.; Mai, Y.-W. Effects of Particle Size, Particle/Matrix Interface Adhesion and Particle Loading on Mechanical Properties of Particulate–Polymer Composites. Compos. Part B Eng. 2008, 39, 933–961. [Google Scholar] [CrossRef]
- Ku, H.; Donald, M.; Cardona, F.; Trada, M. Flexural Properties of Sawdust-Reinforced Epoxy Composites Post-Cured in Microwaves. J. Compos. Mater. 2012, 46, 2879–2890. [Google Scholar] [CrossRef]
- Sombatsompop, N.; Chaochanchaikul, K.; Phromchirasuk, C.; Thongsang, S. Effect of Wood Sawdust Content on Rheological and Structural Changes, and Thermo-mechanical Properties of PVC/Sawdust Composites. Polym. Int. 2003, 52, 1847–1855. [Google Scholar] [CrossRef]
- Santos, P.; Parente, J.P.; Valvez, S.; Silva, M.P.; Reis, P.N.B. Hybridization Effect on the Bending Properties of Flax Composites. Procedia Struct. Integr. 2020, 25, 370–377. [Google Scholar] [CrossRef]
- Benzidane, M.A.; Benzidane, R.; Hamamousse, K.; Adjal, Y.; Sereir, Z.; Poilâne, C. Valorization of Date Palm Wastes as Sandwich Panels Using Short Rachis Fibers in Skin and Petiole “wood” as Core. Ind. Crops Prod. 2022, 177, 114436. [Google Scholar] [CrossRef]
- Kumar, R.; Jha, K.; Sharma, S.; Kumar, V.; Li, C.; Eldin, E.M.T.; Rajkumar, S.; Królczyk, G. Effect of Particle Size and Weight Fraction of SiC on the Mechanical, Tribological, Morphological, and Structural Properties of Al-5.6Zn-2.2Mg-1.3Cu Composites Using RSM: Fabrication, Characterization, and Modelling. Heliyon 2022, 8, e10602. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, Z.; Gong, K.; Zhang, Y. The Effect of Reinforcement Particle Size on the Mechanical and Fracture Properties of Glass Matrix Composites. Heliyon 2023, 9, e21895. [Google Scholar] [CrossRef] [PubMed]
- Phiri, R.; Mavinkere Rangappa, S.; Siengchin, S.; Oladijo, O.P.; Ozbakkaloglu, T. Advances in Lightweight Composite Structures and Manufacturing Technologies: A Comprehensive Review. Heliyon 2024, 10, e39661. [Google Scholar] [CrossRef] [PubMed]
- Sivalingam, P.; Vijayan, K.; Mouleeswaran, S.; Vellingiri, V.; Mayilswamy, S. On the Tensile and Compressive Behavior of a Sandwich Panel Made of Flax Fiber and Agglomerated Cork. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 180–189. [Google Scholar] [CrossRef]
- Fu, Z.; Lu, Y.; Wu, G.; Bai, L.; Barker-Rothschild, D.; Lyu, J.; Liu, S.; Rojas, O.J. Wood Elasticity and Compressible Wood-Based Materials: Functional Design and Applications. Prog. Mater. Sci. 2025, 147, 101354. [Google Scholar] [CrossRef]
- Huang, S.; Fu, Q.; Yan, L.; Kasal, B. Characterization of Interfacial Properties between Fibre and Polymer Matrix in Composite Materials—A Critical Review. J. Mater. Res. Technol. 2021, 13, 1441–1484. [Google Scholar] [CrossRef]
- Matuana, L.M.; Stark, N.M. The Use of Wood Fibers as Reinforcements in Composites; Biofiber Reinforcements in Composite Materials; Woodhead Publishing: Cambridge, UK, 2015; ISBN 9781782421276. [Google Scholar]
- Yin, W.; Zhao, Z.; Lin, H.; Ma, P. Advances in Creep Behaviors of Textile Composites. Appl. Compos. Mater. 2023, 30, 1949–1978. [Google Scholar] [CrossRef]
- Li, X.; Liu, W.; Fang, H.; Huo, R.; Wu, P. Flexural Creep Behavior and Life Prediction of GFRP-Balsa Sandwich Beams. Compos. Struct. 2019, 224, 111009. [Google Scholar] [CrossRef]
- Houshyar, S.; Shanks, R.A.; Hodzic, A. Tensile Creep Behaviour of Polypropylene Fibre Reinforced Polypropylene Composites. Polym. Test. 2005, 24, 257–264. [Google Scholar] [CrossRef]
- Reis, P.N.B.; Silva, M.P.; Santos, P.; Parente, J.M.; Valvez, S.; Bezazi, A. Mechanical Performance of an Optimized Cork Agglomerate Core-Glass Fibre Sandwich Panel. Compos. Struct. 2020, 245, 112375. [Google Scholar] [CrossRef]
- Park, B.; Balatinecz, J.J. Short Term Flexural Creep Behavior of Wood-fiber/Polypropylene Composites. Polym. Compos. 1998, 19, 377–382. [Google Scholar] [CrossRef]
- Almeida, J.H.S.; Ornaghi, H.L.; Lorandi, N.P.; Bregolin, B.P.; Amico, S.C. Creep and Interfacial Behavior of Carbon Fiber Reinforced Epoxy Filament Wound Laminates. Polym. Compos. 2018, 39, E2199–E2206. [Google Scholar] [CrossRef]
- Reis, P.N.B.; Silva, M.P.; Santos, P.; Parente, J.M.; Bezazi, A. Viscoelastic Behaviour of Composites with Epoxy Matrix Filled by Cork Powder. Compos. Struct. 2020, 234, 111669. [Google Scholar] [CrossRef]
- Janeiro-Arocas, J.; Tarrío-Saavedra, J.; López-Beceiro, J.; Naya, S.; López-Canosa, A.; Heredia-García, N.; Artiaga, R. Creep Analysis of Silicone for Podiatry Applications. J. Mech. Behav. Biomed. Mater. 2016, 63, 456–469. [Google Scholar] [CrossRef]
- Gomes, A.S.; Fiadeiro, P.T.; Vieira, A.C.; Vieira, J.C. Viability Study of Serra Da Estrela Dog Wool to Produce Green Composites. Polymers 2024, 16, 718. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, M.; Rahman, R.; Mohammed, A.M.; Adam, T.; Betar, B.O.; Osman, A.F.; Dahham, O.S. Surface Treatment to Improve Water Repellence and Compatibility of Natural Fiber with Polymer Matrix: Recent Advancement. Polym. Test. 2022, 115, 107707. [Google Scholar] [CrossRef]
- Mohammed, M.; Ja’afar Mohamad Jawad, A.; Mohammed, A.M.; Oleiwi, J.K.; Adam, T.; Osman, A.F.; Dahham, O.S.; Betar, B.O.; Gopinath, S.C.B.; Jaafar, M. Challenges and Advancement in Water Absorption of Natural Fiber-Reinforced Polymer Composites. Polym. Test. 2023, 124, 108083. [Google Scholar] [CrossRef]
- Ayrilmis, N.; Jarusombuti, S.; Fueangvivat, V.; Bauchongkol, P. Effect of Thermal-Treatment of Wood Fibres on Properties of Flat-Pressed Wood Plastic Composites. Polym. Degrad. Stab. 2011, 96, 818–822. [Google Scholar] [CrossRef]
- Monticeli, F.M.; Ornaghi, H.L.; Neves, R.M.; Odila Hilário Cioffi, M. Creep/Recovery and Stress-Relaxation Tests Applied in a Standardized Carbon Fiber/Epoxy Composite: Design of Experiment Approach. J. Strain Anal. Eng. Des. 2020, 55, 109–117. [Google Scholar] [CrossRef]
- Varghese, S.; Kuriakose, B.; Thomas, S. Stress Relaxation in Short Sisal-fiber-reinforced Natural Rubber Composites. J. Appl. Polym. Sci. 1994, 53, 1051–1060. [Google Scholar] [CrossRef]
- George, J.; Sreekala, M.S.; Thomas, S.; Bhagawan, S.S.; Neelakantan, N.R. Stress Relaxation Behavior of Short Pineapple Fiber Reinforced Polyethylene Composites. J. Reinf. Plast. Compos. 1998, 17, 651–672. [Google Scholar] [CrossRef]
- Sreekala, M.S.; Kumaran, M.G.; Joseph, R.; Thomas, S. Stress-Relaxation Behaviour in Composites Based on Short Oil-Palm Fibres and Phenol Formaldehyde Resin. Compos. Sci. Technol. 2001, 61, 1175–1188. [Google Scholar] [CrossRef]
- Obaid, N.; Kortschot, M.T.; Sain, M. Understanding the Stress Relaxation Behavior of Polymers Reinforced with Short Elastic Fibers. Materials 2017, 10, 472. [Google Scholar] [CrossRef] [PubMed]
- Vaidyanathan, T.K.; Vaidyanathan, J. Validity of Predictive Models of Stress Relaxation in Selected Dental Polymers. Dent. Mater. 2015, 31, 799–806. [Google Scholar] [CrossRef] [PubMed]
- Sethi, S.; Ray, B.C. Environmental Effects on Fibre Reinforced Polymeric Composites: Evolving Reasons and Remarks on Interfacial Strength and Stability. Adv. Colloid Interface Sci. 2015, 217, 43–67. [Google Scholar] [CrossRef]
- Okolie, O.; Latto, J.; Faisal, N.; Jamieson, H.; Mukherji, A.; Njuguna, J. Manufacturing Defects in Thermoplastic Composite Pipes and Their Effect on the In-Situ Performance of Thermoplastic Composite Pipes in Oil and Gas Applications; Springer: Dordrecht, The Netherlands, 2023; Volume 30, ISBN 0123456789. [Google Scholar]



| Tests | Specimens ID | Dimensions [mm] | Nº of Specimens | |||||
|---|---|---|---|---|---|---|---|---|
| W | L | T | S | |||||
| Core | 3PB tests | Neat epoxy | 10 | 80 | 4 | 60 | 5 × 14 | |
| 20 wt.% 0.075 | ||||||||
| 20 wt.% 0.150 | ||||||||
| 20 wt.% 0.300 | ||||||||
| 20 wt.% (0.075 & 0.150) | ||||||||
| 30 wt.% 0.150 | ||||||||
| 30 wt.% 0.150 | ||||||||
| 30 wt.% 0.300 | ||||||||
| 30 wt.% (0.075 & 0.150) | ||||||||
| 40 wt.% 0.075 | ||||||||
| 40 wt.% 0.150 | ||||||||
| 40 wt.% 0.300 | ||||||||
| 40 wt.% (0.075 & 0.150) | ||||||||
| 50 wt.% 0.300 | ||||||||
| Sandwich Panel | 3PB tests | SD | 75 | 200 | 10 | 150 | 4 | |
| Edgewise compression | SD | 50 ≤ W ≤ (8 × T) | ≤(8 × T) | 10 | - | 4 | ||
| Flatwise compression | SD | >25 | >25 | 10 | - | 4 | ||
| Stress relaxation | SD | 12 MPa | 75 | 200 | 10 | 150 | 4 × 3 | |
| 21 MPa | ||||||||
| 27 MPa | ||||||||
| 33 MPa | ||||||||
| Creep | SD | 12 MPa | 75 | 200 | 10 | 150 | 4 × 3 | |
| 21 MPa | ||||||||
| 27 MPa | ||||||||
| 33 MPa | ||||||||
| KWW model | Initial Bending Stress [MPa] | ε0 | β | τ | Displacement After 3 h [mm] | ||
| Experimental Value | KWW Model Value | Error [%] | |||||
| Neat epoxy matrix | |||||||
| 21 | 0.840 | 0.249 | 7.62 × 106 | 0.899 | 0.901 | 0.161 | |
| 42 | 1.512 | 0.289 | 8.85 × 105 | 1.652 | 1.658 | 0.398 | |
| 63 | 2.284 | 0.327 | 1.14 × 105 | 2.565 | 2.579 | 0.539 | |
| 73.5 | 2.687 | 0.356 | 3.35 × 104 | 3.104 | 3.138 | 1.096 | |
| 84 | 3.095 | 0.386 | 1.03 × 104 | 3.790 | 3.817 | 0.710 | |
| Core | data | ||||||
| 12 | 0.506 | 0.303 | 4.66 × 103 | 0.728 | 0.734 | 0.954 | |
| 21 | 0.822 | 0.261 | 3.31 × 103 | 1.310 | 1.311 | 0.064 | |
| 27 | 0.988 | 0.304 | 1.17 × 103 | 1.610 | 1.741 | 7.577 | |
| 33 | 1.167 | 0.327 | 5.16 × 102 | 2.313 | 3.372 | 2.483 | |
| Sandwich | data | ||||||
| 12 | 1.359 | 0.291 | 1.34 × 105 | 1.565 | 1.572 | 0.449 | |
| 21 | 1.612 | 0.282 | 5.38 × 104 | 1.956 | 1.970 | 0.694 | |
| 27 | 1.833 | 0.302 | 3.15 × 104 | 2.258 | 2.263 | 0.200 | |
| 33 | 2.040 | 0.314 | 1.81 × 104 | 2.555 | 2580 | 0.958 | |
| Findley model | Initial bending stress [MPa] | ε0 | A | n | Displacement after 3 h [mm] | ||
| Experimental value | Findley model value | Error [%] | |||||
| Neat epoxy matrix | |||||||
| 21 | 0.467 | 0.349 | 0.023 | 0.899 | 0.897 | 0.163 | |
| 42 | 0.569 | 0.873 | 0.023 | 1.652 | 1.649 | 0.148 | |
| 63 | 0.731 | 1.374 | 0.031 | 2.565 | 2.557 | 0.316 | |
| 73.5 | 0.747 | 1.591 | 0.042 | 3.104 | 3.103 | 0.007 | |
| 84 | 0.780 | 1.812 | 0.053 | 3.790 | 3.752 | 1.004 | |
| Core | |||||||
| 12 | 0.223 | 0.187 | 0.094 | 0.728 | 0.720 | 0.999 | |
| 21 | 0.380 | 0.270 | 0.094 | 1.310 | 1.291 | 1.416 | |
| 27 | 0.400 | 0.267 | 0.134 | 1.610 | 1.651 | 2.550 | |
| 33 | 0.444 | 0.280 | 0.162 | 2.313 | 2.283 | 1.281 | |
| Sandwich | |||||||
| 12 | 0.752 | 0.503 | 0.037 | 1.565 | 1.559 | 0.408 | |
| 21 | 0.837 | 0.618 | 0.050 | 1.956 | 1.948 | 0.391 | |
| 27 | 0.997 | 0.617 | 0.052 | 2.258 | 2.236 | 0.977 | |
| 33 | 1.128 | 0.638 | 0.056 | 2.555 | 2.542 | 0.541 | |
| KWW Model | Materials | β | ε0 | τ | ||||||
| A | B | R * | C | D | R | E | F | R * | ||
| Neat epoxy matrix | 0.0359 | 0.048 | 0.999 | 0.00218 | 0.196 | 0.990 | 7.06 × 107 | 0.104 | 0.999 | |
| Core | 0.0313 | 0.142 | 0.998 | 0.00136 | 0.267 | 0.432 | 2.13 × 104 | 0.108 | 0.956 | |
| Sandwich | 0.0326 | 0.998 | 0.985 | 0.00117 | 0.270 | 0.753 | 4.12 × 105 | 0.095 | 0.999 | |
| Findley model | Materials | ε0 | A | n | ||||||
| A | B | R * | C | D | R | E | F | R * | ||
| Neat epoxy matrix | 0.0053 | 0.361 | 0.982 | 0.0233 | −0.121 | 0.999 | 4.71 × 10−4 | 0.008 | 0.888 | |
| Core | 0.0102 | 0.124 | 0.948 | 0.0043 | 0.152 | 0.876 | 3.39 × 10−3 | 0.042 | 0.904 | |
| Sandwich | 0.0183 | 0.504 | 0.975 | 0.0062 | 0.451 | 0.889 | 9.17 × 10−4 | 0.027 | 0.963 | |
| Initial Bending Stress [MPa] | β | τ | Bending Stress After 3 h [MPa] | ||
|---|---|---|---|---|---|
| Experimental Value | KWW Model Value | Error [%] | |||
| Neat epoxy matrix | 0.229 | 6.23 × 106 | 19.258 | 19.193 | 0.338 |
| 21 | 0.278 | 6.57 × 105 | 38.093 | 37.929 | 0.432 |
| 42 | 0.310 | 1.69 × 105 | 56.199 | 55.909 | 0.517 |
| 63 | 0.318 | 8.77 × 104 | 64.790 | 63.911 | 1.356 |
| 73.5 | 0.325 | 4.82 × 104 | 71.900 | 71.399 | 0.697 |
| Core | |||||
| 12 | 0.279 | 1.21 × 104 | 8.882 | 8.833 | 0.559 |
| 21 | 0.299 | 4.23 × 103 | 14.356 | 14.233 | 0.860 |
| 27 | 0.282 | 4.22 × 103 | 17.409 | 17.937 | 3.025 |
| 33 | 0.274 | 3.93 × 103 | 21.800 | 21.503 | 1.363 |
| Sandwich | |||||
| 12 | 0.278 | 4.34 × 104 | 9.757 | 9.675 | 0.833 |
| 21 | 0.280 | 3.22 × 104 | 16.759 | 16.617 | 0.848 |
| 27 | 0.282 | 2.32 × 104 | 21.490 | 21.171 | 1.487 |
| 33 | 0.284 | 2.67 × 104 | 25.898 | 25.641 | 0.995 |
| Materials | β | τ | ||||
|---|---|---|---|---|---|---|
| A | B | R | C | D | R * | |
| Neat epoxy matrix | 1.53 × 10−3 | 0.205 | 0.975 | 2.46 × 1011 | 3.455 | 0.998 |
| Core | −3.30 × 10−4 | 0.291 | 0.268 | 1.84 × 105 | 1.146 | 0.925 |
| Sandwich | 2.52 × 10−4 | 0.275 | 0.987 | 2.04 × 105 | 0.617 | 0.996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomes, S.; Santos, P.; Lima, T.M. Development of Sustainable Composite Sandwich with Wood Waste and Natural Fibers for Circular Economy Applications. Recycling 2025, 10, 131. https://doi.org/10.3390/recycling10040131
Gomes S, Santos P, Lima TM. Development of Sustainable Composite Sandwich with Wood Waste and Natural Fibers for Circular Economy Applications. Recycling. 2025; 10(4):131. https://doi.org/10.3390/recycling10040131
Chicago/Turabian StyleGomes, Sofia, Paulo Santos, and Tânia M. Lima. 2025. "Development of Sustainable Composite Sandwich with Wood Waste and Natural Fibers for Circular Economy Applications" Recycling 10, no. 4: 131. https://doi.org/10.3390/recycling10040131
APA StyleGomes, S., Santos, P., & Lima, T. M. (2025). Development of Sustainable Composite Sandwich with Wood Waste and Natural Fibers for Circular Economy Applications. Recycling, 10(4), 131. https://doi.org/10.3390/recycling10040131








