State-of-Charge Estimation of Lithium-Ion Batteries Based on Dual-Coefficient Tracking Improved Square-Root Unscented Kalman Filter
Abstract
1. Introduction
2. Equivalent Circuit Model and State Space Equation of Lithium-Ion Batteries
2.1. Equivalent Circuit Model of the Batteries
2.2. State Space Equation of the Battery Model
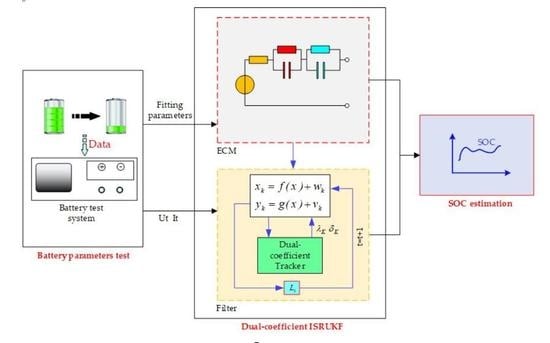
3. SOC Estimation Based on the Dual-Coefficient Tracking ISRUKF
3.1. Improved Square-Root Unscented Kalman Filter (ISRUKF)
3.1.1. Standard SRUKF
- (1)
- Initialize the mean (x0) and the state covariance square root () of the system state:
- (2)
- Assign weights and obtain sampling points:
- (3)
- Time update for the system states:
- a.
- Update the sample point:
- b.
- Estimate the system state:
- c.
- Update the covariance of the estimated state:where is the updated state calculation value; () is the QR decomposition; Sk|k−1 is the state covariance square-root matrix; and () is the Cholesky decomposition.
- (4)
- Measurement update:
- a.
- Attain the measurement:
- b.
- Update the measurement:
- (5)
- Calculate the SRUKF gain matrix L:where is the mutual covariance, as shown in Formula (24), and is the measurement covariance square-root matrix, as shown in Formula (26).where is the updated calculation measurement.
- (6)
- Measurement correction:
- a.
- Update the estimated state:
- b.
- Update the propagated covariance:where is the state covariance square-root optimal estimation matrix.
3.1.2. The ISRUKF Based on the QR Decomposition Method
3.2. The Dual-Coefficient Tracker Based on the Strong Tracking Filter
3.2.1. Strong Tracking Filter
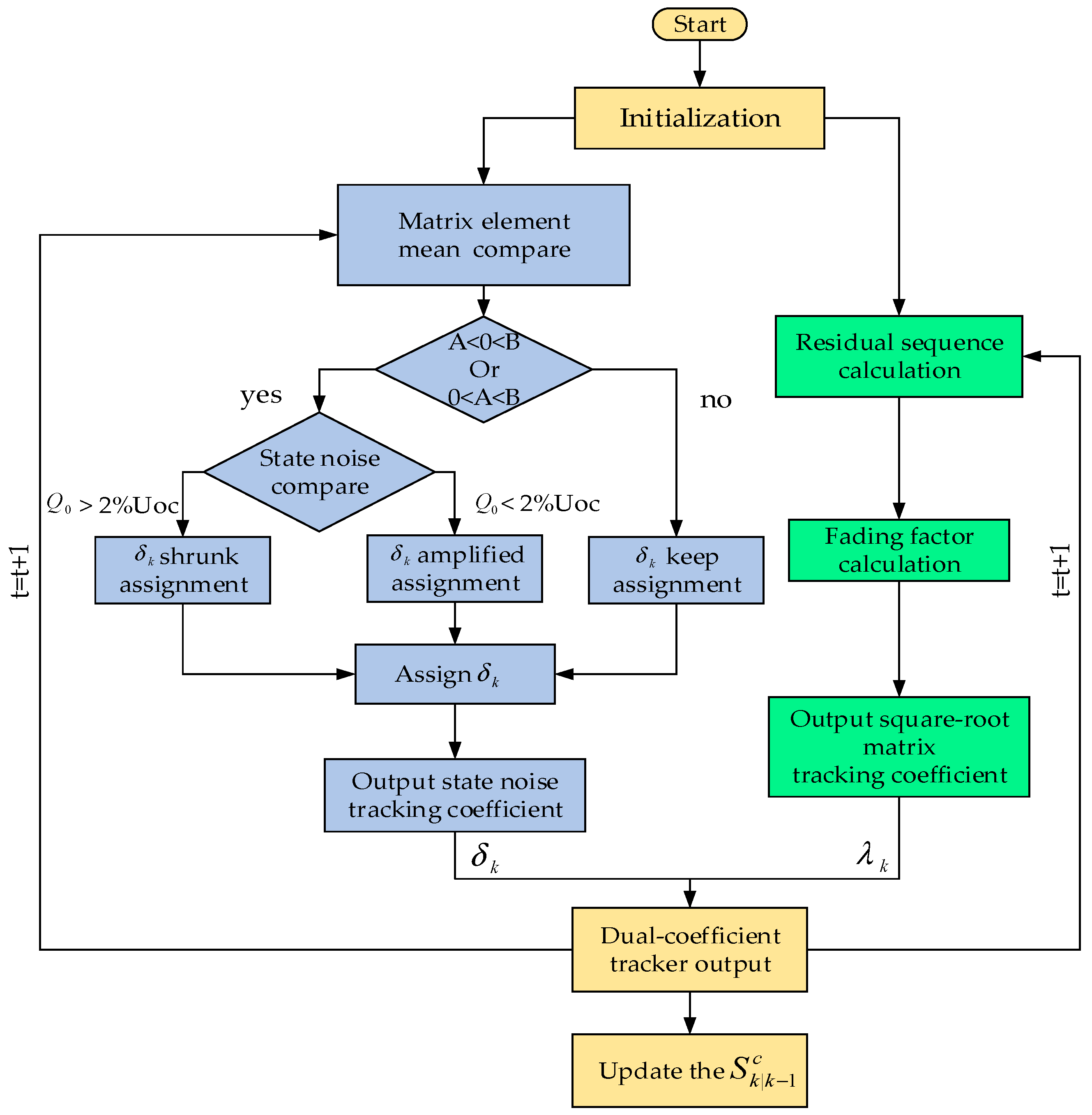
3.2.2. The State Noise Tracking Coefficient
- (1)
- Initialize the and its dimension to n columns.
- (2)
- is set as an element in the row and column of the state covariance square-root matrix at time k. We set the mean of the elements in m adjacent square-root matrices as a parameter and definite A and B as the pairwise comparisons between adjacent parameters, which can be described as
- (3)
- Attain the updated . If the outcome does not match outcome (II) or outcome (V), the should not be modified. If the calculated result matches outcome (II) or outcome (V), the should be reassigned. If the value of is higher than 2% of the , the is judged to be too large, and the state noise tracking coefficient should be shrunk, and then the value should be assigned. If the value is less than 2% of the , the is judged to be too small, and the state noise tracking coefficient should be amplified, and then the value should be assigned, where is the correction coefficient.
- (4)
- According to and Formula (39), we can get the state noise tracking coefficient .
- (5)
- The and are used as inputs to form the dual-coefficient tracker.
- (6)
- The dual-tracking coefficient and are put into the ISRUKF to calculate the updated state covariance square-root matrix , which can be illustrated as
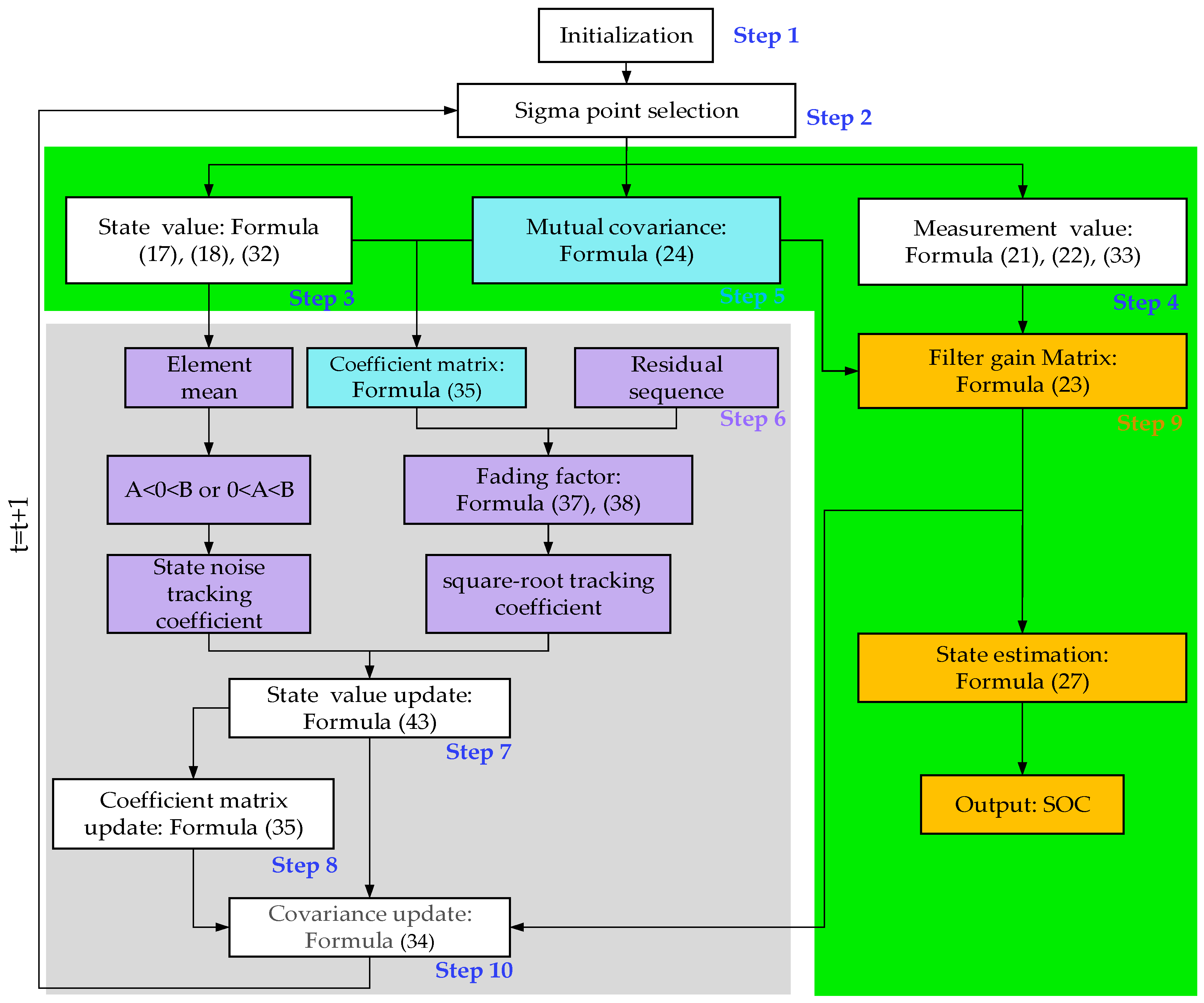
3.3. Battery SOC Estimation Procedure Based on Dual-Coefficient Tracking ISRUKF
4. Simulation and Experimental Results and Analysis
4.1. Test Platform and Experiment Parameters
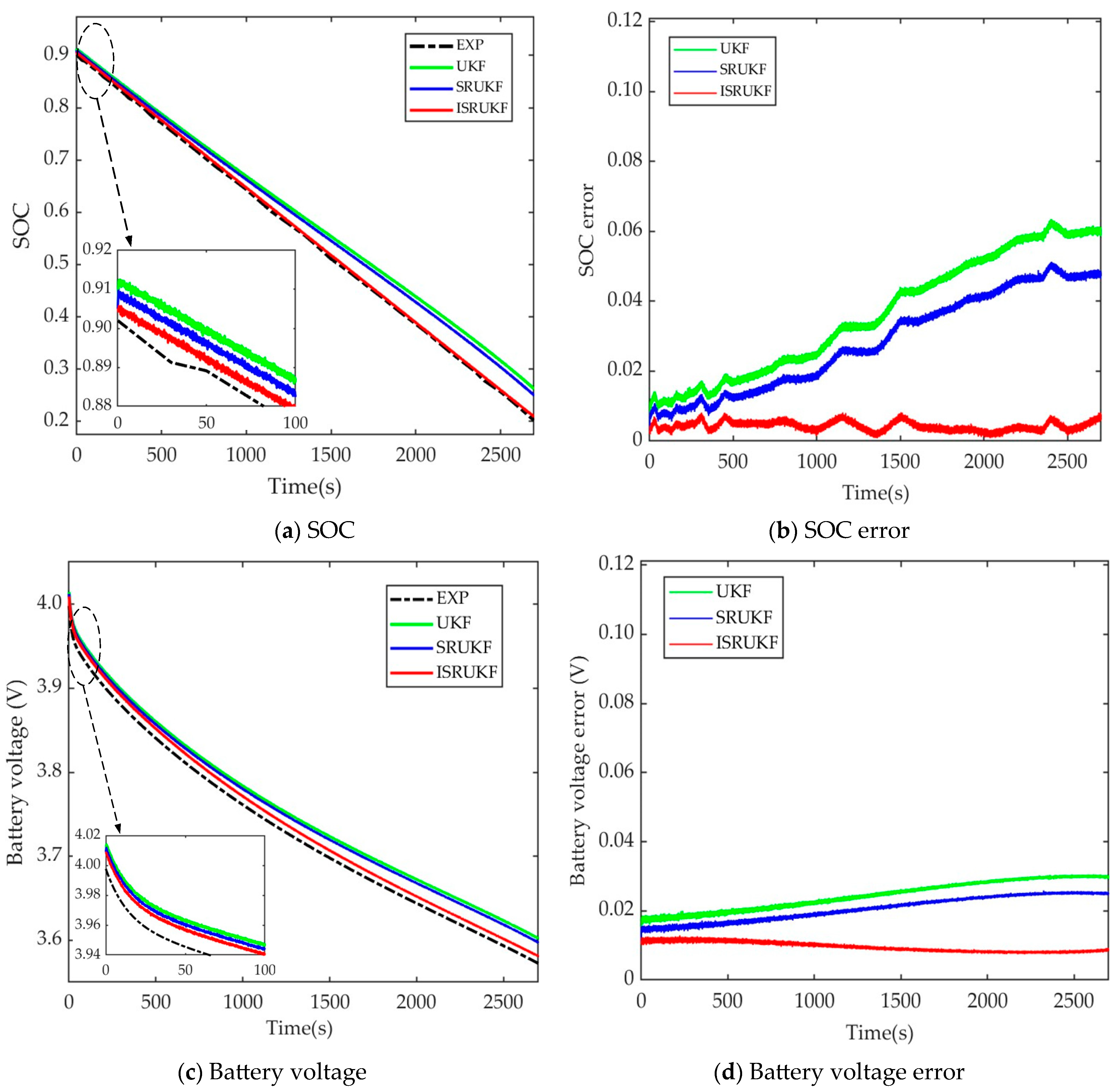
4.2. Comparison of SOC Estimation Accuracy Using the Developed ISRUKF, SRUKF, and UKF with Different Covariance
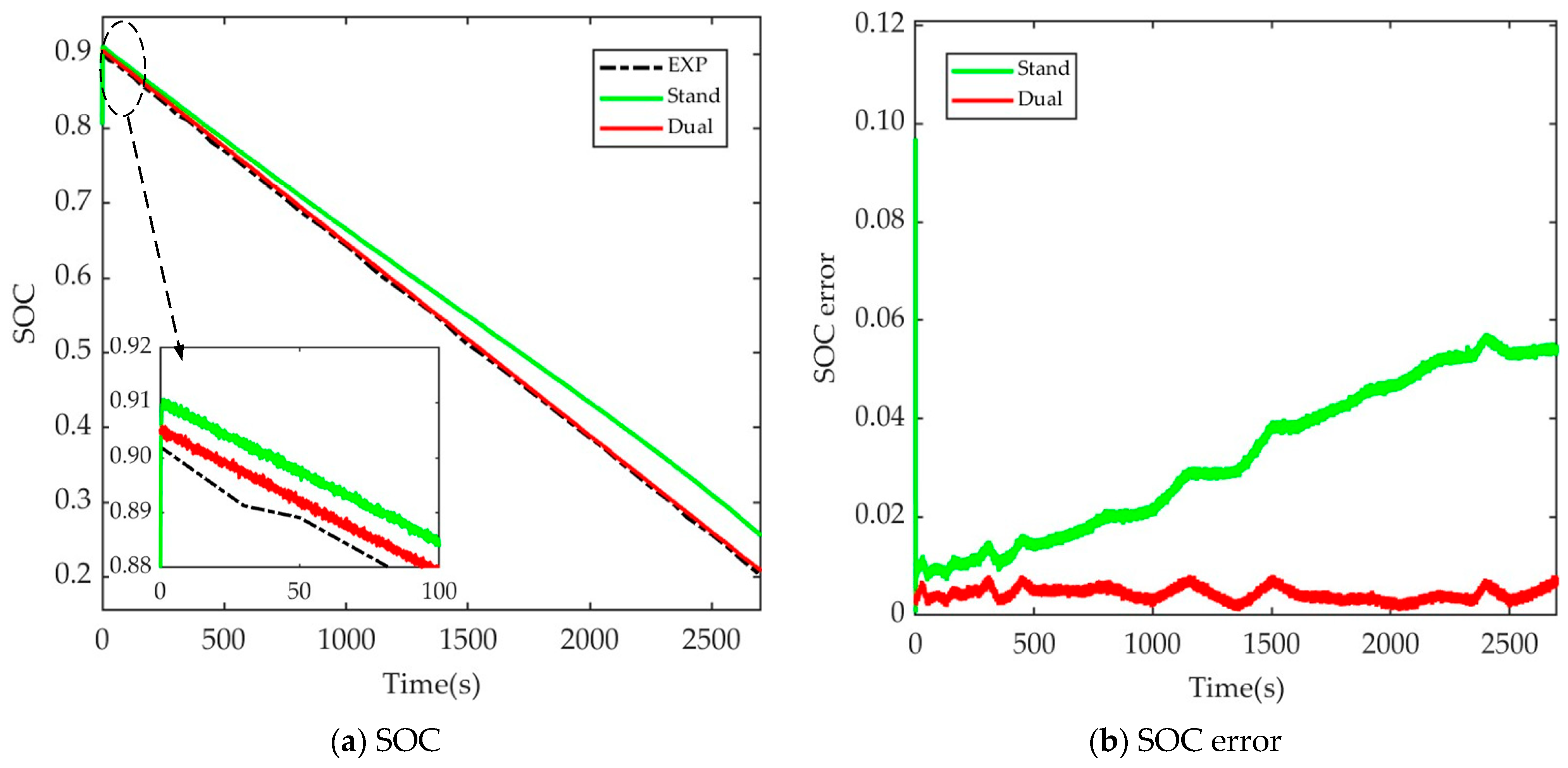
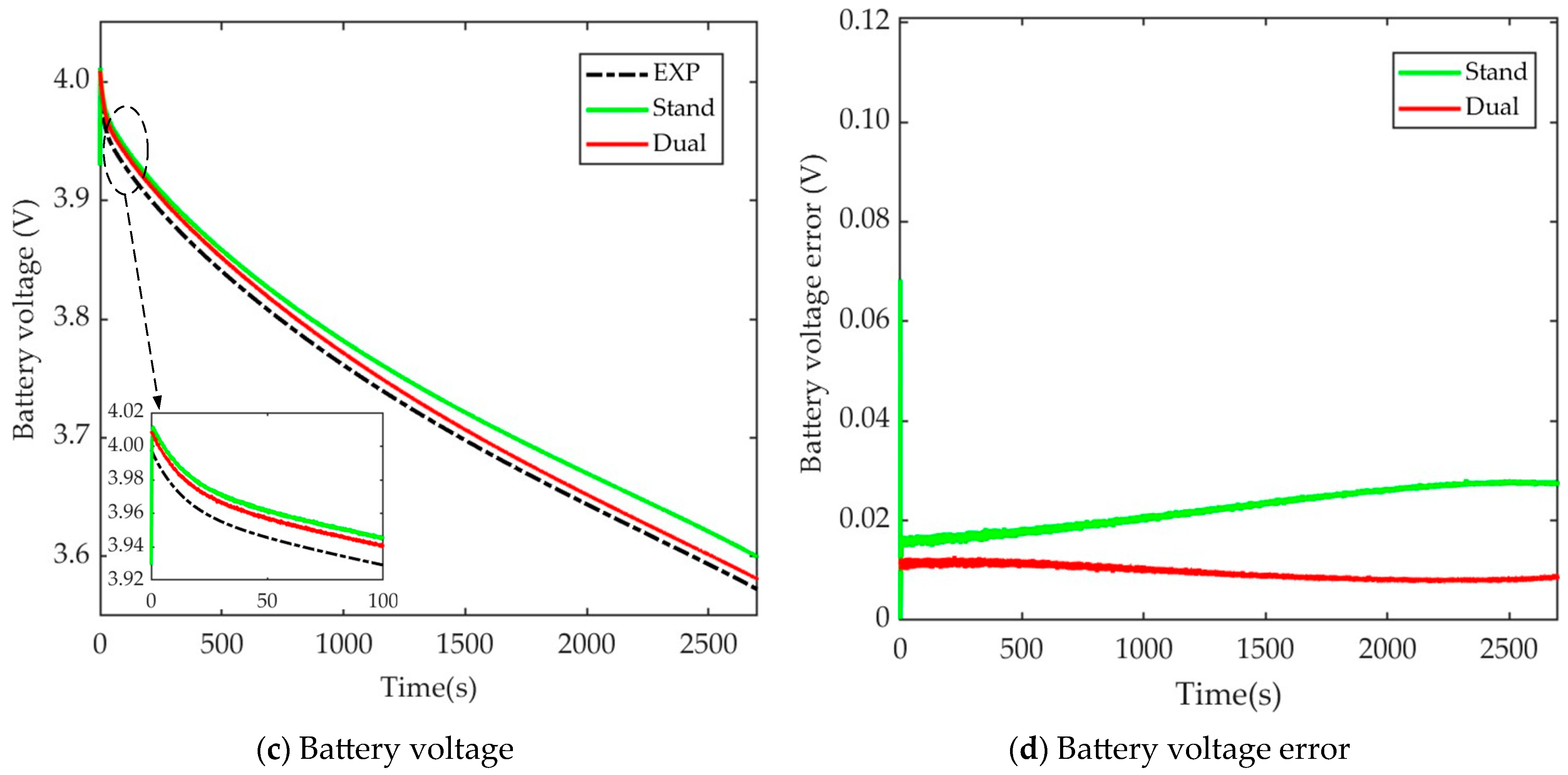
4.3. Comparison of SOC Estimation Results Using Different ISRUKFs, the ISRUKF with Standard STF and the Developed ISRUKF
4.4. SOC Estimation by the Developed ISRUKF with Different Covariance
4.5. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| SOC | state of charge (-) |
| KF | Kalman filter (-) |
| EKF | extended Kalman filter (-) |
| UKF | unscented Kalman filter (-) |
| SRUKF | square-root unscented Kalman filter (-) |
| AUKF | adaptive unscented Kalman filter (-) |
| STF | strong tracking filter (-) |
| OCV | open-circuit voltage (V) |
| ECM | equivalent circuit model (-) |
| UOC | open-circuit voltage of the batteries (V) |
| R0 | internal resistance of the batteries (Ω) |
| RL | concentration resistance of the batteries (Ω) |
| CL | concentration capacitance of the batteries (F) |
| RS | electrochemical resistance (Ω) |
| CS | electrochemical capacitance (F) |
| It | current of the batteries (A) |
| Ut | terminal voltage of the batteries (V) |
| a0~a5 | coefficient of the equation (-) |
| b0~b5 | coefficient of the equation (-) |
| c0~c2 | coefficient of the equation (-) |
| d0~d2 | coefficient of the equation (-) |
| e0~e2 | coefficient of the equation (-) |
| f0~f2 | coefficient of the equation (-) |
| SOC0 | initial value of SOC (-) |
| coulomb efficiency (-) | |
| QN | nominal capacity of the batteries (Wh) |
| US | electrochemical voltage of the batteries (V) |
| UL | concentration voltage of the batteries (V) |
| sampling time (s) | |
| time parameter (s) | |
| time parameter (s) | |
| wk | state noise (-) |
| vk | measurement noise (-) |
| xk | system state vector (-) |
| yk | system measurement vector (-) |
| uk | system input vector (V) |
| f(·) | nonlinear state model (-) |
| g(·) | nonlinear measurement model (-) |
| r | mean of the measurement noise (-) |
| q | mean of the state noise (-) |
| R | covariance value of measurement noise (-) |
| Q | covariance value of state noise (-) |
| x0 | initial mean (-) |
| S0 | initial state covariance square root (-) |
| E(·) | expectation mean value (-) |
| (·)T | matrix transpose operation (-) |
| n | dimension of the state vector (-) |
| scaling parameter (-) | |
| h | column factor (-) |
| wm | variance weight factor (-) |
| wc | mean weight factor (-) |
| error magnitude of the higher-order term (-) | |
| updated state calculation value (-) | |
| () | QR decomposition (-) |
| Sk|k−1 | state covariance square-root matrix (-) |
| () | Cholesky decomposition (-) |
| Pxy | mutual covariance (-) |
| updated calculation measurement | |
| Sz | measurement covariance square-root matrix (-) |
| Sk|k | state covariance square-root optimal estimation matrix (-) |
| Pk|k−1 | state covariance matrix (-) |
| qk | upper triangular matrix (-) |
| rk | orthogonal matrix (-) |
| e | identity matrix of order n (-) |
| Hk | coefficient matrix of the measurement function (-) |
| fading factor (-) | |
| trace() | trace of the corresponding matrix (-) |
| Ck | covariance of the residual sequence of outputs (-) |
| forgetting factor (-) | |
| output residual sequence | |
| corrected state covariance square-root matrix (-) | |
| state noise tracking coefficient (-) |
References
- Renxin, X.; Yanwen, H.; Wei, Z.; Zhaohui, C. A novel approach to estimate the state of charge for lithium-ion battery under different temperatures incorporating open circuit voltage online identification. J. Energy Storage 2023, 67, 107509. [Google Scholar] [CrossRef]
- Meng, J.; Yue, M.; Diallo, D. Nonlinear extension of battery constrained predictive charging control with transmission of Jacobian matrix. Int. J. Electr. Power Energy Syst. 2023, 146, 108762. [Google Scholar] [CrossRef]
- Qiao, J.; Wang, S.; Yu, C.; Yang, X.; Fernandez, C. A chaotic firefly-Particle filtering method of dynamic migration modeling for the state-of-charge and state-of-health co-estimation of a lithium-ion battery performance. Energy 2023, 263, 126164. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, Y.; Long, S.; Jin, X.; Li, J.; Shen, W. A Branch Current Estimation and Correction Method for a Parallel Connected Battery System Based on Dual BP Neural Networks. Green Energy Intell. Transp. 2022, 1, 100029. [Google Scholar] [CrossRef]
- Peng, S.; Zhu, L.; Dou, Z.; Liu, D.; Yang, R.; Pecht, M. Method of Site Selection and Capacity Setting for Battery Energy Storage System in Distribution Networks with Renewable Energy Sources. Energies 2023, 16, 3899. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Yang, R.; Li, H. A novel data-driven method for mining battery open-circuit voltage characterization. J. Green Energy Intell. Transp. 2022, 1, 100001. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, H.; Chen, X.; Li, H. Robust state-of-charge estimation for lithium-ion batteries based on an improved gas-liquid dynamics model. Energy 2022, 238, 122008. [Google Scholar] [CrossRef]
- Xia, L.; Wang, S.; Yu, C.; Fan, Y.; Li, B.; Xie, Y. Joint estimation of the state-of-energy and state-of-charge of lithium-ion batteries under a wide temperature range based on the fusion modeling and online parameter prediction. J. Energy Storage 2022, 52, 105010. [Google Scholar] [CrossRef]
- Wassiliadis, N.; Kriegler, J.; Gamra, K.A.; Lienkamp, M. Model-based health-aware fast charging to mitigate the risk of lithium plating and prolong the cycle life of lithium-ion batteries in electric vehicles. J. Power Sources 2023, 561, 232586. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Z.; Qiu, Y.; Jing, B.; Yang, C. State of charge estimation for Li-ion batteries based on iterative Kalman filter with adaptive maximum correntropy criterion. J. Power Sources 2023, 580, 233282. [Google Scholar] [CrossRef]
- Zhao, X.; Jung, S.; Wang, B.; Xuan, D. State of charge estimation of lithium-ion battery based on improved adaptive boosting algorithm. J. Energy Storage 2023, 71, 108047. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L. Co-estimation of capacity and state-of-charge for lithium-ion batteries in electric vehicles. Energy 2019, 174, 33–44. [Google Scholar] [CrossRef]
- Yu, Q.; Huang, Y.; Tang, A.; Wang, C.; Shen, W. OCV-SOC-Temperature Relationship Construction and State of Charge Estimation for a Series–Parallel Lithium-Ion Battery Pack. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6362–6371. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Yun, X.; Fan, X. A novel hybrid machine learning coulomb counting technique for state of charge estimation of lithium-ion batteries. J. Energy Storage 2023, 63, 107081. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.; Liu, C.; Chang, C.; Li, X. A novel Co-estimation framework of state-of-charge, state-of-power and capacity for lithium-ion batteries using multi-parameters fusion method. Energy 2023, 269, 126820. [Google Scholar] [CrossRef]
- Zhu, R.; Duan, B.; Zhang, J.; Zhang, Q.; Zhang, C. Co-estimation of model parameters and state-of-charge for lithium-ion batteries with recursive restricted total least squares and unscented Kalman filter. Appl. Energy 2020, 277, 115494. [Google Scholar] [CrossRef]
- Xia, B.; Cui, D.; Sun, Z.; Lao, Z.; Zhang, R.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network. Energy 2018, 153, 694–705. [Google Scholar] [CrossRef]
- Song, Q.; Wang, S.; Xu, W.; Shao, Y.; Fernandez, C. A novel joint support vector machine-cubature Kalman filtering method for adaptive state of charge prediction of lithium-ion batteries. Int. J. Electrochem. Sci. 2021, 16, 210823. [Google Scholar] [CrossRef]
- Tagade, P.; Hariharan, K.S.; Gambhire, P.; Kolake, S.M.; Song, T.; Oh, D.; Yeo, T.; Doo, S. Recursive Bayesian filtering framework for lithium-ion cell state estimation. J. Power Sources 2016, 306, 274–288. [Google Scholar] [CrossRef]
- Zhu, W.; Guo, B.; Li, Y.; Yang, Y.; Xie, C.; Jin, J.; Gooi, H.B. Uncertainty quantification of proton-exchange-membrane fuel cells degradation prediction based on Bayesian-Gated Recurrent Unit. eTransportation 2023, 16, 100230. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Wei, X.; Xu, T. Joint estimation of lithium-ion battery state of charge and capacity within an adaptive variable multi-timescale framework considering current measurement offset. Appl. Energy 2019, 253, 113619. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for batteries management systems of LiPB-based HEV batteries packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Chai, H.; Gao, Z.; Jiao, Z.; Yang, C. State of charge estimation for lithium-ion batteries based on an adaptive fractional-order cubature Kalman filter with initial value compensation. J. Energy Storage 2023, 68, 107544. [Google Scholar] [CrossRef]
- Yang, F.; Xing, Y.; Wang, D.; Tsui, K.L. A comparative study of three model-based algorithms for estimating state-of-charge of lithium-ion batteries under a new combined dynamic loading profile. Appl. Energy 2016, 164, 387–399. [Google Scholar] [CrossRef]
- Liu, S.; Deng, D.; Wang, S.; Luo, W.; Takyi-Aninakwa, P.; Qiao, J.; Li, S.; Jin, S.; Hu, C. Dynamic adaptive square-root unscented Kalman filter and rectangular window recursive least square method for the accurate state of charge estimation of lithium-ion batteries. J. Energy Storage 2023, 67, 107603. [Google Scholar] [CrossRef]
- Aung, H.; Low, K.S. Temperature dependent state-of-charge estimation of lithium ion battery using dual spherical unscented Kalman filter. IET Power Electron. 2015, 8, 2026–2033. [Google Scholar] [CrossRef]
- Menegaz, H.M.T.; Ishihara, J.Y. Unscented and square-root unscented Kalman filters for quaternionic systems. Int. J. Robust Nonlinear Control 2018, 28, 4500–4527. [Google Scholar] [CrossRef]
- Wei, W.; Gao, S.; Zhong, Y.; Gu, C.; Hu, G. Adaptive square-root unscented particle filtering algorithm for dynamic navigation. Sensors 2018, 18, 2337. [Google Scholar] [CrossRef]
- Asl, R.M.; Hagh, Y.S.; Simani, S.; Handroos, H. Adaptive square-root unscented Kalman filter: An experimental study of hydraulic actuator state estimation. Mech. Syst. Signal Process. 2019, 132, 670–691. [Google Scholar]
- Zhu, Q.; Xu, M.; Liu, W.; Zheng, M. A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended kalman filter. Energy 2019, 187, 115880. [Google Scholar] [CrossRef]
- Duan, L.; Zhang, X.; Jiang, Z.; Gong, Q.; Wang, Y.; Ao, X. State of charge estimation of lithium-ion batteries based on second-order adaptive extended Kalman filter with correspondence analysis. Energy 2023, 280, 128159. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Xu, X.; Tang, S.; Ren, H.; Han, X.; Wu, Y.; Lu, L.; Feng, X.; Yu, C.; Xie, J.; Ouyang, M.; et al. Joint state estimation of lithium-ion batteries combining improved equivalent circuit model with electrochemical mechanism and diffusion process. J. Energy Storage 2022, 56, 106135. [Google Scholar] [CrossRef]





| Normal Voltage | 3.7 V | Battery Capacity | 860 mAh | ||
|---|---|---|---|---|---|
| Upper Cut-Off Voltage | 4.2 V | Lower Cut-Off Voltage | 3.2 V | ||
| a0 | −0.915 | a1 | 40.867 | a2 | 3.632 |
| a3 | 0.537 | a4 | 0.499 | a5 | 0.522 |
| b0 | 0.1463 | b1 | 30.27 | b2 | 0.1037 |
| b3 | 0.0584 | b4 | 0.1747 | b5 | 0.1288 |
| c0 | 0.1063 | c1 | 62.49 | c2 | 0.0437 |
| d0 | −200 | d1 | 138 | d2 | 300 |
| e0 | 0.0712 | e1 | 61.4 | e2 | 0.0288 |
| f0 | −3083 | f1 | 180 | f2 | 5088 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, S.; Zhang, A.; Liu, D.; Cheng, M.; Kan, J.; Pecht, M. State-of-Charge Estimation of Lithium-Ion Batteries Based on Dual-Coefficient Tracking Improved Square-Root Unscented Kalman Filter. Batteries 2023, 9, 392. https://doi.org/10.3390/batteries9080392
Peng S, Zhang A, Liu D, Cheng M, Kan J, Pecht M. State-of-Charge Estimation of Lithium-Ion Batteries Based on Dual-Coefficient Tracking Improved Square-Root Unscented Kalman Filter. Batteries. 2023; 9(8):392. https://doi.org/10.3390/batteries9080392
Chicago/Turabian StylePeng, Simin, Ao Zhang, Dandan Liu, Mengzeng Cheng, Jiarong Kan, and Michael Pecht. 2023. "State-of-Charge Estimation of Lithium-Ion Batteries Based on Dual-Coefficient Tracking Improved Square-Root Unscented Kalman Filter" Batteries 9, no. 8: 392. https://doi.org/10.3390/batteries9080392
APA StylePeng, S., Zhang, A., Liu, D., Cheng, M., Kan, J., & Pecht, M. (2023). State-of-Charge Estimation of Lithium-Ion Batteries Based on Dual-Coefficient Tracking Improved Square-Root Unscented Kalman Filter. Batteries, 9(8), 392. https://doi.org/10.3390/batteries9080392