Combined State of Charge and State of Energy Estimation for Echelon-Use Lithium-Ion Battery Based on Adaptive Extended Kalman Filter
Abstract
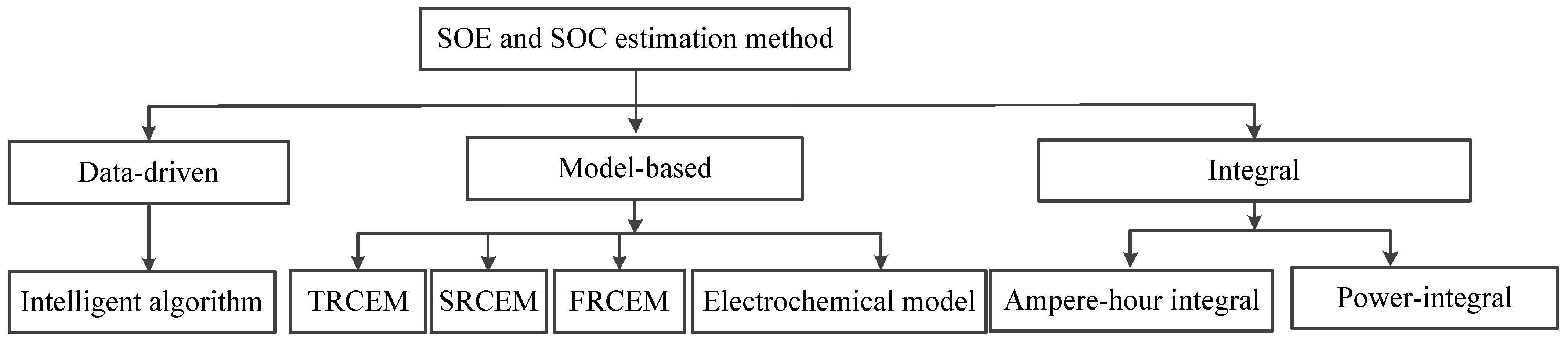
:1. Introduction
2. SOE Estimation
2.1. SOE
2.2. SOC
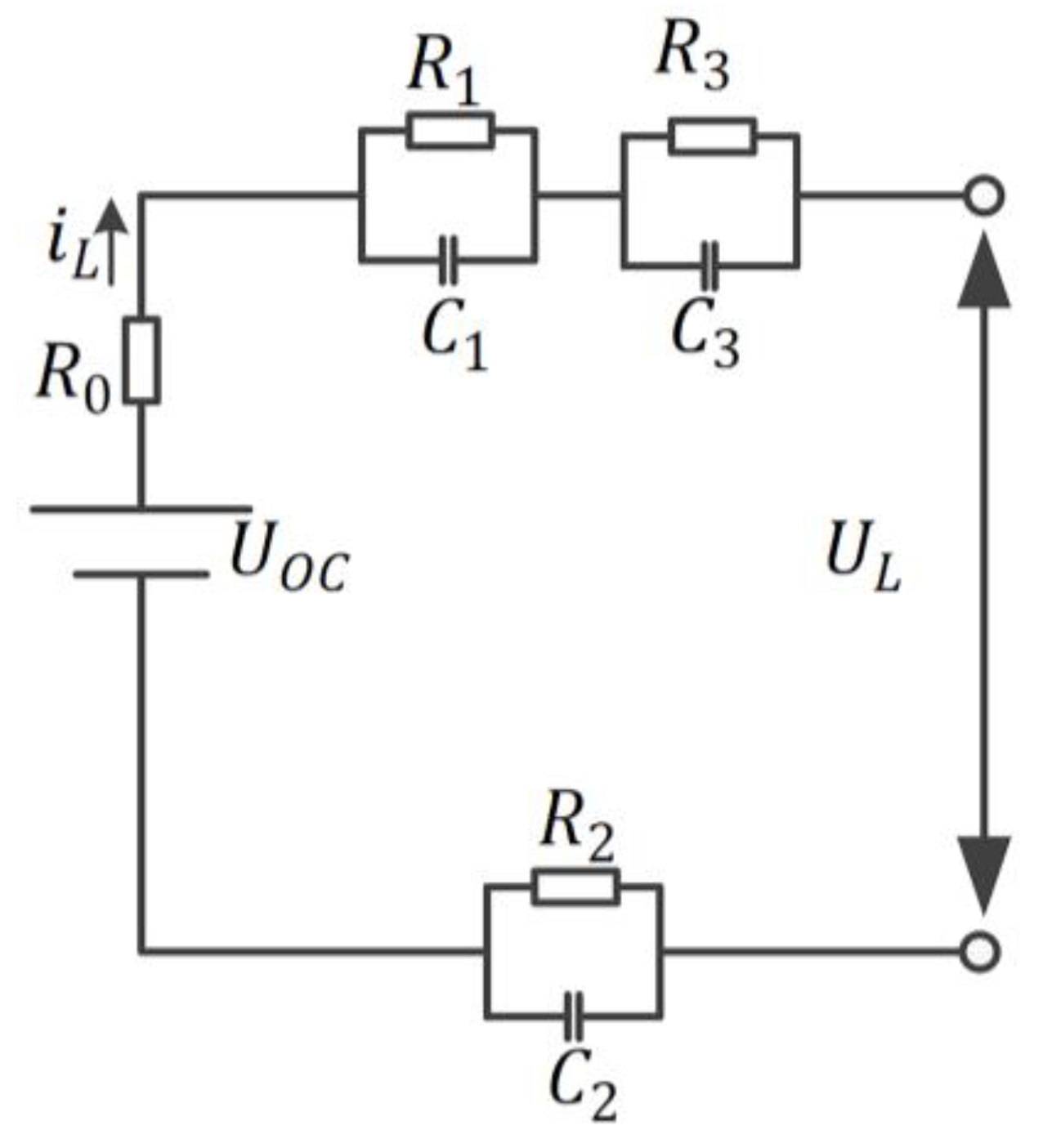
2.3. SOE and SOC Estimation Model Based on TRCEM
2.4. Model Parameter Identification
2.5. SOE and SOC Estimation Based on AEKF
- Step 1: Initialize :
- Step 2: Time update :
- Estimation of the error covariance:
- Step 3: Status update :
- Step 4: Process noise covariance:
- Step 5: Observation noise covariance:
2.6. OIR, AE, and AC Estimation Based on AEKF
- Step 1: Initialize :
- Step 2: Time update :
- Estimation of the error covariance:
- Step 3: Status update :
- Step 4: Process noise mean and covariance:
- Step 5: Observation noise covariance:
2.7. Optimize the OIR, AE, and AC Based on LSTM
2.8. SOE Estimation Based on AEKF and LSTM
3. Simulation
3.1. Experiment
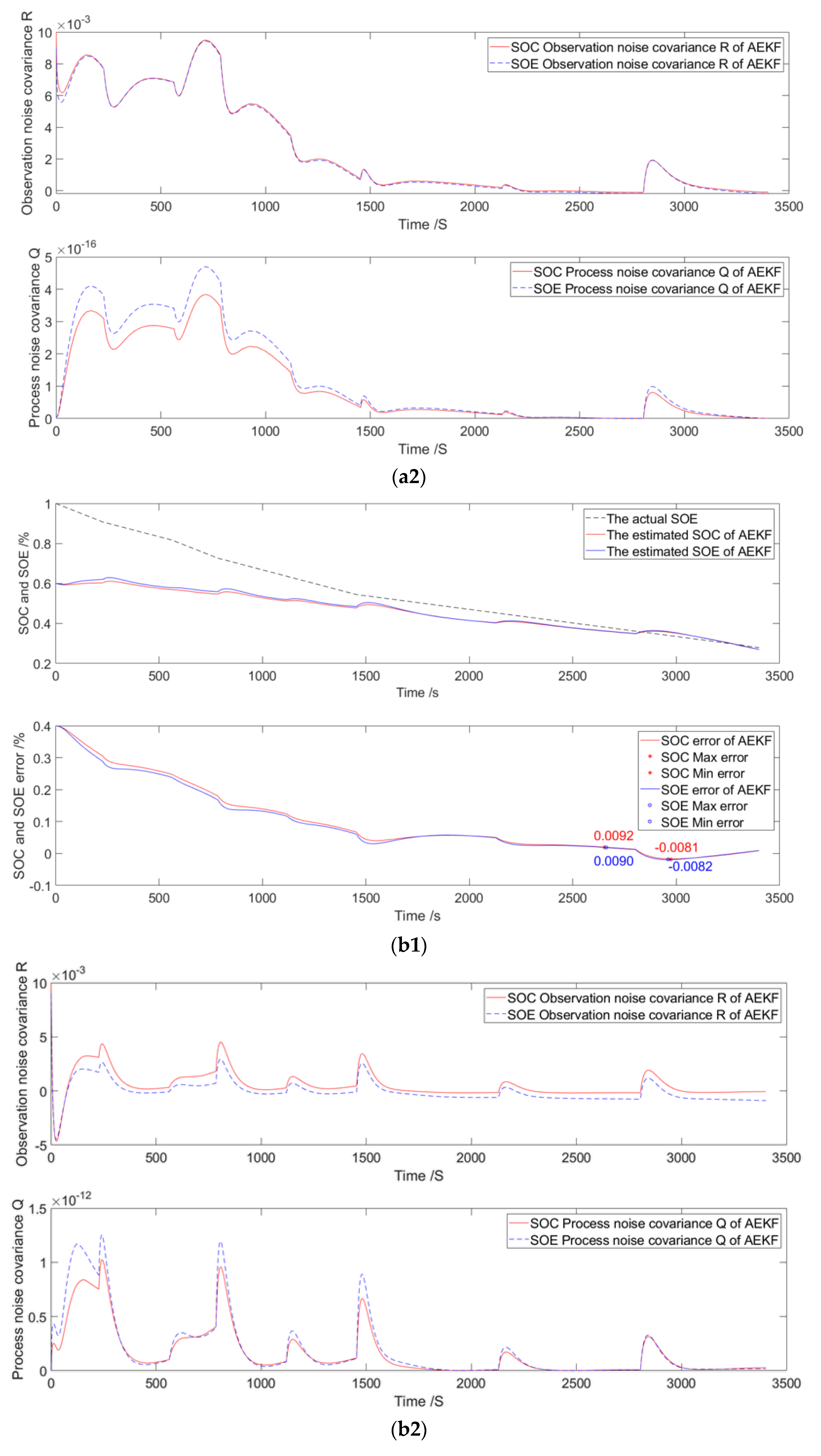
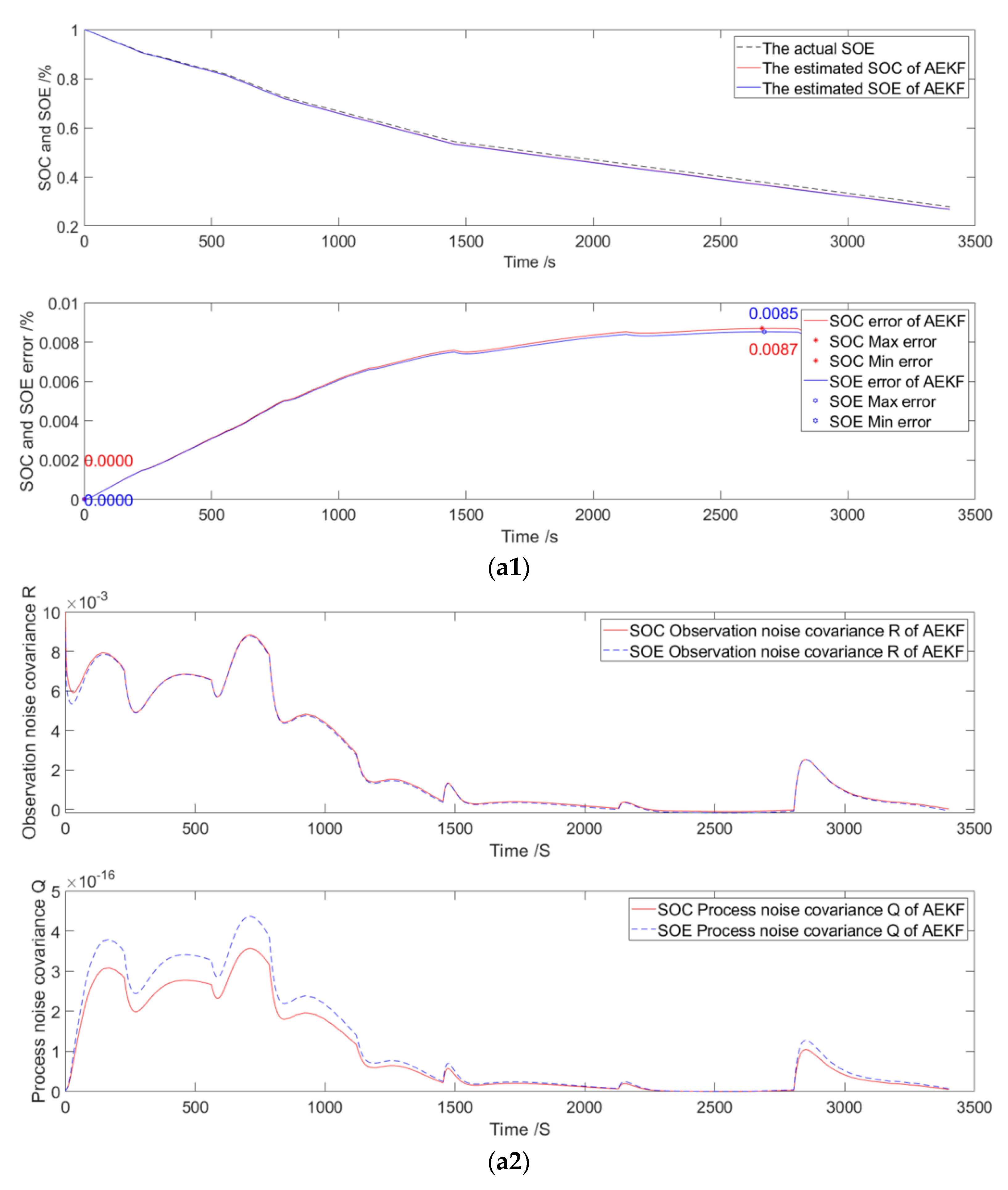
3.2. Decayed to 90%
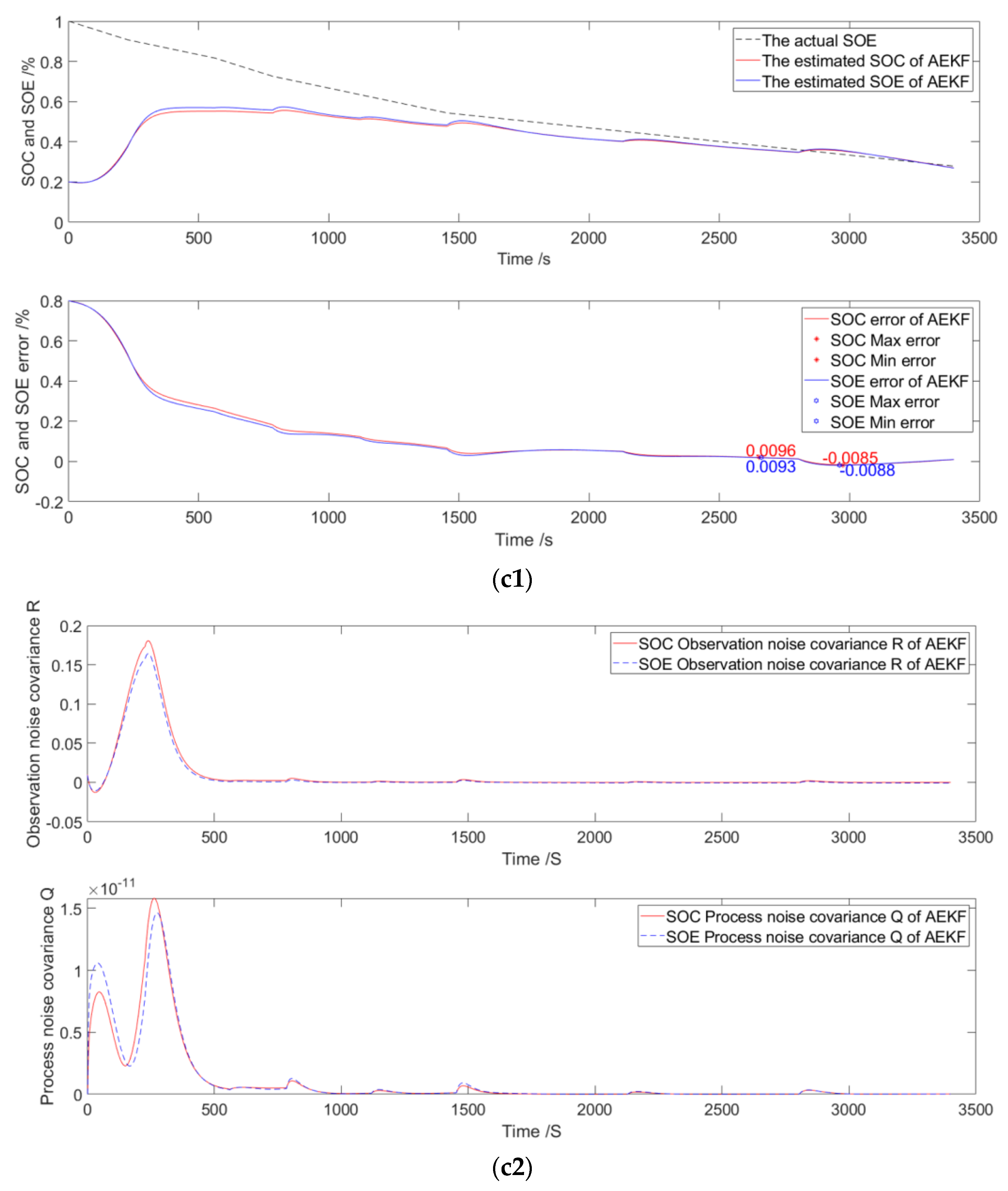
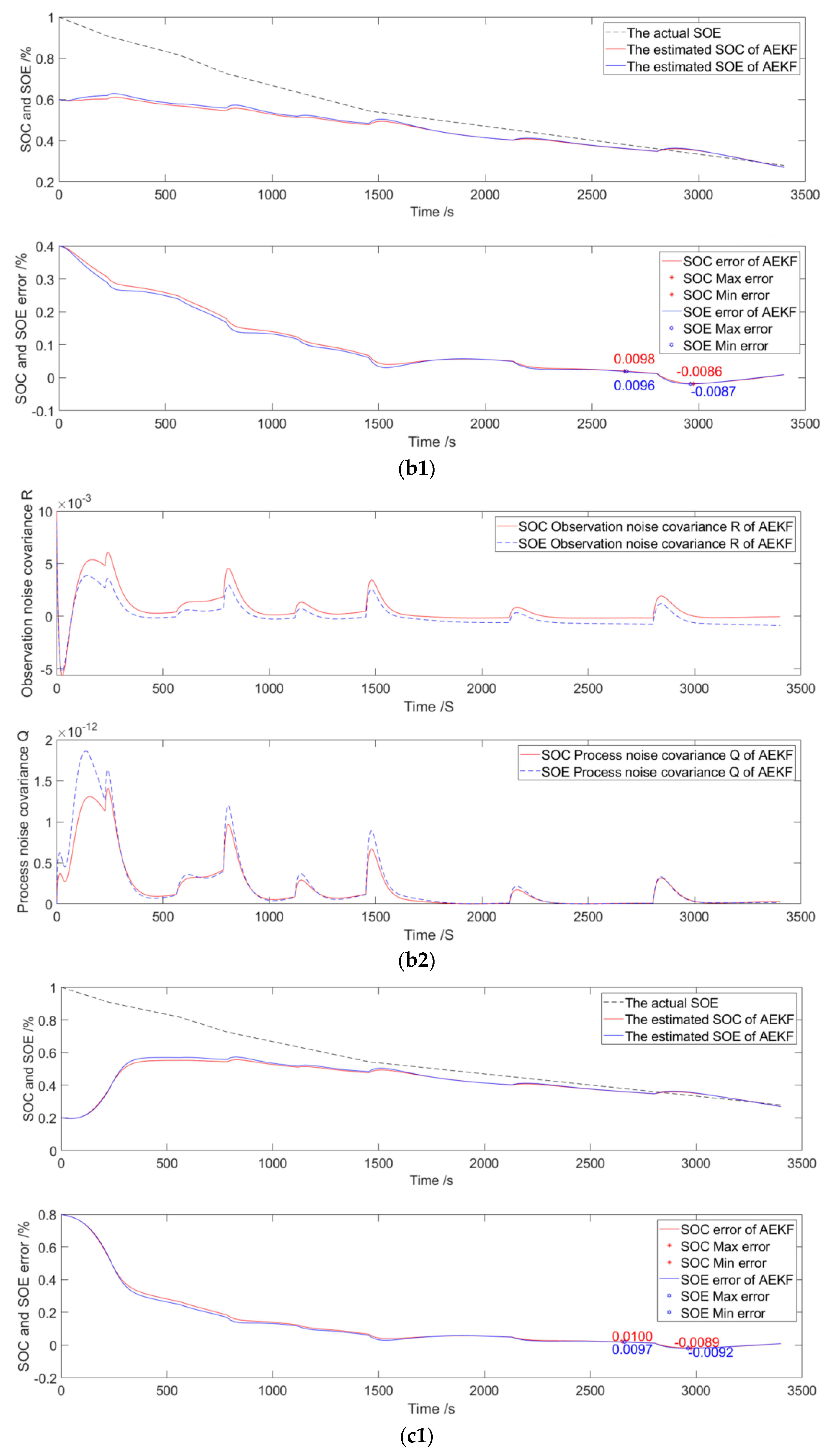
3.3. Decayed to 60%
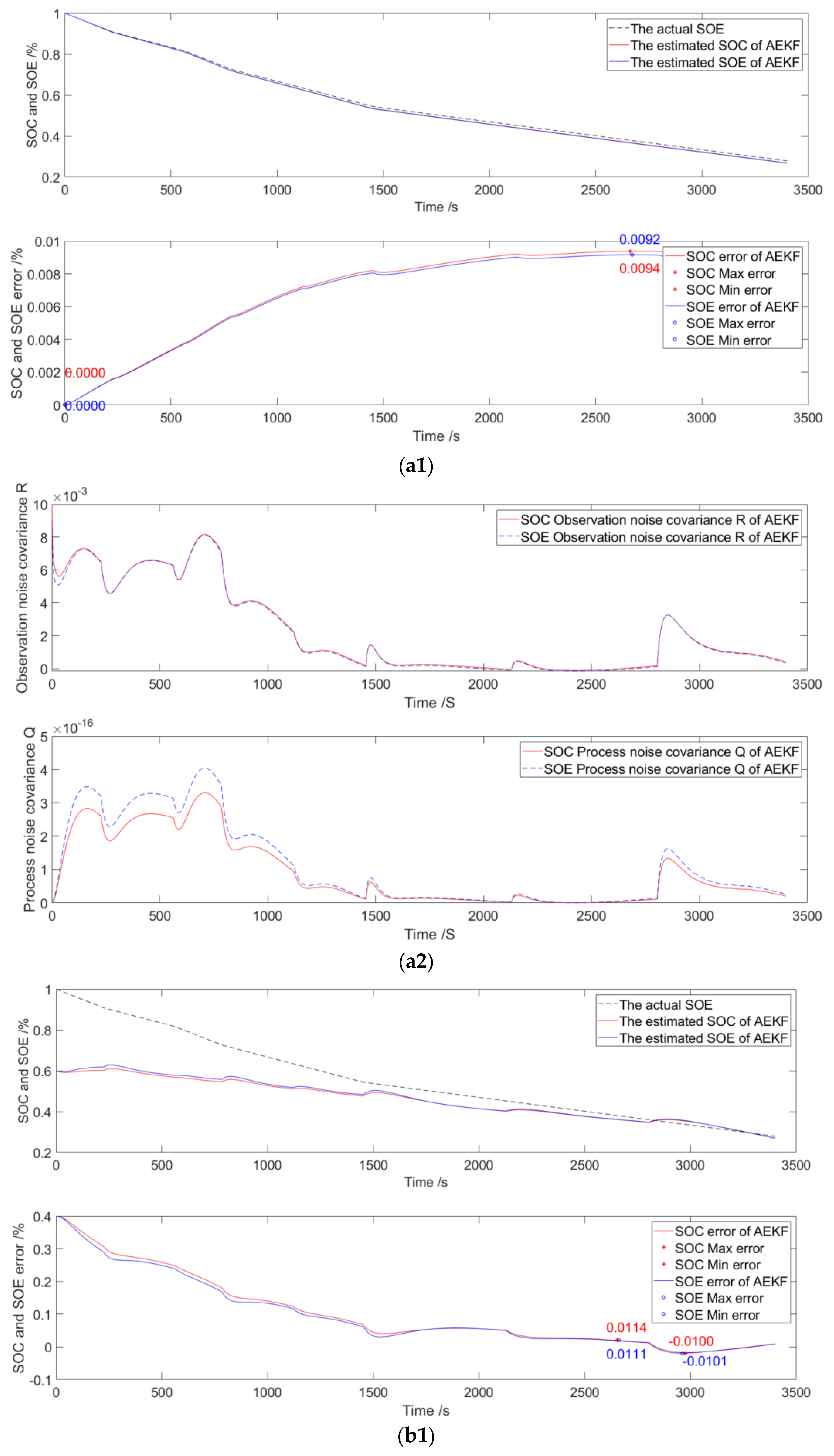
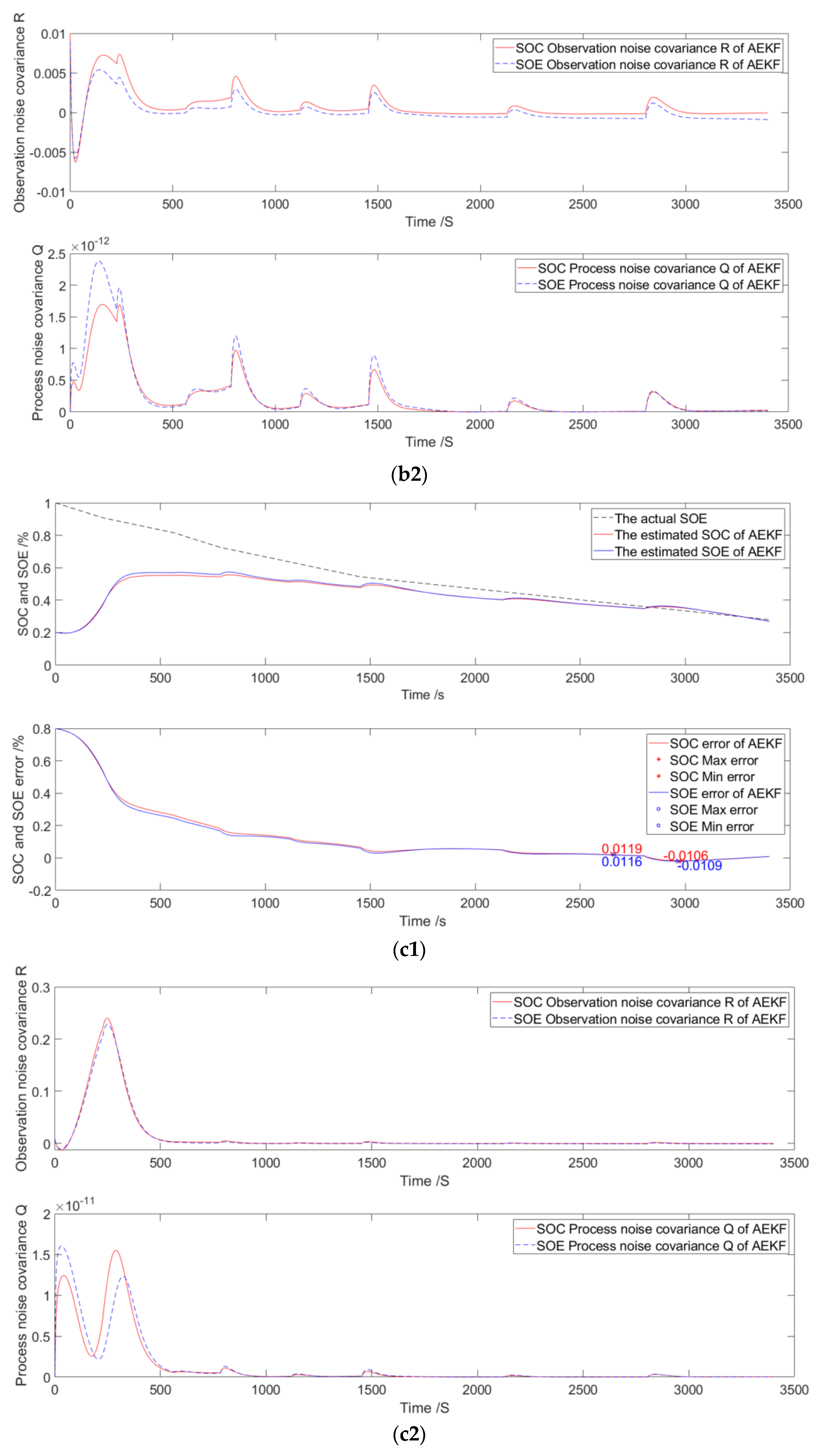
3.4. Decayed to 30%
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiao, X.; Wang, Z.; Hou, E.; Liu, G.; Cai, Y. Online Estimation of Open Circuit Voltage Based on Extended Kalman Filter with Self-Evaluation Criterion. Energies 2022, 15, 4373. [Google Scholar] [CrossRef]
- Hou, E.; Xu, Y.; Qiao, X.; Liu, G.; Wang, Z. Research on State of Power Estimation of Echelon-Use Battery Based on Adaptive Unscented Kalman Filter. Symmetry 2022, 14, 919. [Google Scholar] [CrossRef]
- Xu, W.; Xu, J.; Lang, J.; Yan, X. A Multi-Timescale Estimator for Lithium-Ion Battery state of Charge and State of Energy Estimation Using Dual H infinity Filter. IEEE Access 2019, 7, 181229–181241. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Tao, Y.; Ye, J.; Pan, A.; Li, X.; Liao, Q.; Wang, Z. Performance assessment of retired EV battery modules for echelon use. Energy 2020, 993, 116555. [Google Scholar] [CrossRef]
- Yong, F.; Fan, B.; Chen, X.; Fengling, H. State-of-Charge and State-of-Energy Estimation for Lithium-ion Batteries Using Sliding-Mode Observers. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021. [Google Scholar] [CrossRef]
- Mamadou, K.; Lemaire, E.; Delaille, A.; Riu, D.; Hing, S.E.; Bultel, Y. Definition of a State-of-Energy Indicator (SOE) for Electrochemical Storage Devices: Application for Energetic Availability Forecasting. J. Electrochem. Soc. 2012, 159, A1298–A1307. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Widanalage, W.D.; McGordon, A.; Jennings, P. The effect of average cycling current on total energy of lithium-ion batteries for electric vehicles. J. Power Sources 2016, 303, 81–85. [Google Scholar] [CrossRef]
- Li, X.; Pan, K.; Fan, G.; Lu, R.; Zhu, C.; Rizzoni, G.; Canova, M. A physics-based fractional order model and state of energy estimation for lithium-ion batteries. Part II: Parameter identification and state of energy estimation for LiFePO4 battery. J. Power Sources 2017, 367, 202–213. [Google Scholar] [CrossRef]
- Wu, L.; Pang, H.; Geng, Y.; Liu, X.; Liu, J.; Liu, K. Low-complexity state of charge and anode potential prediction for lithium-ion batteries using a simplified electrochemical model-based observer under variable load condition. Int. J. Energy Res. 2022, 46, 11834–11848. [Google Scholar] [CrossRef]
- Fan, T.E.; Liu, S.M.; Tang, X.; Qu, B. Simultaneously estimating two battery states by combining a long short-term memory network with an adaptive unscented Kalman filter. J. Energy Storage 2022, 50, 104553. [Google Scholar] [CrossRef]
- Zhang, S.; Peng, N.; Zhang, X. An application-oriented multistate estimation framework of lithium-ion battery used in electric vehicles. Int. J. Energy Res. 2021, 45, 18554–18576. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Combined State of Charge and State of Energy Estimation of Lithium-Ion Battery Using Dual Forgetting Factor-Based Adaptive Extended Kalman Filter for Electric Vehicle Applications. IEEE Trans. Veh. Technol. 2021, 70, 1200–1215. [Google Scholar] [CrossRef]
- Gao, T.; Lu, W. Machine learning toward advanced energy storage devices and systems. iScience 2021, 24, 101936. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Li, S.E.; Yang, Y. Advanced Machine Learning Approach for Lithium-Ion Battery State Estimation in Electric Vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 140–149. [Google Scholar] [CrossRef]
- Hossain, L.M.S.; Hannan, M.A.; Hussain, A.; Ayob, A.; Saad, M.H.M.; Karim, T.F.; How, D.N.T. Data-driven state of charge estimation of lithium-ion batteries: Algorithms, implementation factors, limitations and future trends. J. Clean. Prod. 2020, 277, 124110. [Google Scholar] [CrossRef]
- Hu, J.N.; Hu, J.J.; Lin, H.B.; Li, X.P.; Jiang, C.L.; Qiu, X.H.; Li, W.S. State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Sources 2014, 269, 682–693. [Google Scholar] [CrossRef]
- Hossain Lipu, M.; Karim, T.; Ansari, S.; Miah, M.; Rahman, M.; Meraj, S.; Elavarasan, R.; Vijayaraghavan, R. Intelligent SOX Estimation for Automotive Battery Management Systems: State-of-the-Art Deep Learning Approaches, Open Issues, and Future Research Opportunities. Energies 2022, 16, 23. [Google Scholar] [CrossRef]
- Purohit, K.; Srivastava, S.; Nookala, V.; Joshi, V.; Shah, P.; Sekhar, R.; Panchal, S.; Fowler, M.; Fraser, R.; Tran, M.K.; et al. Soft Sensors for State of Charge, State of Energy, and Power Loss in Formula Student Electric Vehicle. Appl. Syst. Innov. 2021, 4, 78. [Google Scholar] [CrossRef]
- Wang, Y.X.; Chen, Z.; Zhang, W. Lithium-ion battery state-of-charge estimation for small target sample sets using the improved GRU-based transfer learning. Energy 2022, 244, 123178. [Google Scholar] [CrossRef]
- Cui, Z.; Kang, L.; Li, L.; Wang, L.; Wang, K. A combined state-of-charge estima-tion method for lithium-ion battery using an improved BGRU network and UKF. Energy 2022, 259, 124933. [Google Scholar] [CrossRef]
- Ma, L.; Hu, C.; Cheng, F. State of Charge and State of Energy Estimation for Lithium-Ion Batteries Based on a Long Short-Term Memory Neural Network. J. Energy Storage 2021, 37, 102440. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Model-based state of X estimation of lithium-ion battery for electric vehicle applications. Int. J. Energy Res. 2022, 46, 10704–10723. [Google Scholar] [CrossRef]
- Chen, L.; Wang, S.; Jiang, H.; Fernandez, C. A novel combined estimation method for state of energy and predicted maximum available energy based on fractional-order modeling. J. Energy Storage 2023, 62, 106930. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Ma, Y.; Shan, C.; Gao, J.; Chen, H. A novel method for state of health estimation of lithium-ion batteries based on improved LSTM and health indicators extraction. Energy 2022, 251, 123973. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, X.; Gao, D.; Li, H.; Yan, L.; Peng, J.; Huang, Z. State-of-health estimation of lithium-ion batteries based on improved long short-term memory algorithm. J. Energy Storage 2022, 53, 105046. [Google Scholar] [CrossRef]
- Takyi-Aninakwa, P.; Wang, S.; Zhang, H.; Li, H.; Xu, W.; Fernandez, C. An optimized relevant long short-term memory-squared gain extended Kalman filter for the state of charge estimation of lithium-ion batteries. Energy 2022, 260, 120043. [Google Scholar] [CrossRef]
- Rahimifard, S.; Ahmed, R.; Habibi, S. Interacting Multiple Model Strategy for Electric Vehicle Batteries State of Charge/Health/Power Estimation. IEEE Access 2021, 9, 109875–109888. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Li, W.; Cheng, W.; Zhu, Q. State of charge estimation for lithium-ion batteries using gated recurrent unit recurrent neural network and adaptive Kal-man filter. J. Energy Storage 2022, 55, 105396. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Hong, J.; Tian, J.; Tian, Y. State of energy estimation for a series-connected lithium-ion battery pack based on an adaptive weighted strategy. Energy 2021, 214, 118858. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.; Luo, D.; Wen, R. Remaining available energy prediction for lithium-ion batteries considering electrothermal effect and energy conversion efficiency. J. Energy Storage 2021, 40, 102728. [Google Scholar] [CrossRef]
- Xia, B.; Chen, C.; Tian, Y.; Sun, W.; Xu, Z.; Zheng, W. A novel method for state of charge es-timation of lithium-ion batteries using a nonlinear observer. J. Power Sources 2014, 270, 359–366. [Google Scholar] [CrossRef]
- Hou, E.; Xu, Y.; Qiao, X.; Liu, G.; Wang, Z. State of Power Estimation of Echelon-Use Battery Based on Adaptive Dual Extended Kalman Filter. Energies 2021, 14, 5579. [Google Scholar] [CrossRef]
- Lu, J.X.; Zhang, Q.P.; Yang, Z.H.; Tu, M.F.; Lu, J.J.; Peng, H. Short-term load forecasting method based on CNN-LSTM hybrid neural network model. Autom.Electr. Power Syst. 2019, 43, 131–137. [Google Scholar] [CrossRef]
- Meng, J.; Yue, M.; Diallo, D. Nonlinear extension of battery constrained predictive charging control with transmission of Jacobian matrix. Int. J. Electr. Power Energy Syst. 2023, 146, 108762. [Google Scholar] [CrossRef]
- Yang, X.; Wang, S.; Xu, W.; Qiao, J.; Yu, C.; Takyi-Aninakwa, P.; Jin, S. A novel fuzzy adaptive cubature Kalman filtering method for the state of charge and state of energy co-estimation of lithium-ion batteries. Electrochim. Acta 2022, 415, 140241. [Google Scholar] [CrossRef]
- Wei, X.; Jun, C.; Yu, G.; Jiachen, M.; Jiaqing, C. Unscented Particle Filter Based State of Energy Estimation for LiFePO4 Batteries Using an Online Updated Model. Int. J. Automot. Technol. 2022, 23, 503–510. [Google Scholar] [CrossRef]




| Items | Parameter | Remarks |
|---|---|---|
| Rated capacity | 60 Ah | 60 A |
| Rated voltage | 3.2 V | |
| Cut-off voltage | 2.5 V | |
| Rated energy | 192 Wh | Watt-Hour |
| Maximum charging voltage | 3.65 V | |
| Maximum continuous charge current | 20 A | 0.3 C |
| Charging/discharging temperature | 25 °C |
| Initial Value | SOE Error | SOC Error | |
|---|---|---|---|
| Decayed to 90% | 100% | 0% to 0.84% | 0% to 0.81% |
| 60% | −0.82% to 0.90% | −0.81% to 0.92% | |
| 20% | −0.88% to 0.93% | −0.85% to 0.96% | |
| Decayed to 60% | 100% | 0% to 0.85% | 0% to 0.87% |
| 60% | −0.87% to 0.96% | −0.86% to 0.98% | |
| 20% | −0.92% to 0.97% | −0.89% to 1.00% | |
| Decayed to 30% | 100% | 0% to 0.92% | 0% to 0.94% |
| 60% | −1.01% to 1.11% | −1.00% to 1.14% | |
| 20% | −1.09% to 1.16% | −1.06% to 1.19% | |
| Reference | Accuracy of Estimation | Adaptability | Method |
|---|---|---|---|
| Method in this paper | 1.19% | Yes | LSTM optimization AEKF |
| [2] | 2.34% | Yes | AUKF |
| [23] | 2% | Yes | Adaptive double fractional-order extended Kalman filter |
| [28] | 2% | No | Interacting multiple model |
| [36] | 1.93% | Yes | Fuzzy adaptive cubature Kalman filtering |
| [37] | 1.8% | No | Unscented particle filter |
| Initial Value | SOE Error | SOC Error | |
|---|---|---|---|
| Decayed to 90% | 60% | −0.82% to 0.90% | −0.81% to 0.92% |
| Decayed to 60% | 60% | −0.87% to 0.96% | −0.86% to 0.98% |
| Decayed to 30% | 60% | −1.01% to 1.11% | −1.00% to 1.14% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, E.; Wang, Z.; Zhang, X.; Wang, Z.; Qiao, X.; Zhang, Y. Combined State of Charge and State of Energy Estimation for Echelon-Use Lithium-Ion Battery Based on Adaptive Extended Kalman Filter. Batteries 2023, 9, 362. https://doi.org/10.3390/batteries9070362
Hou E, Wang Z, Zhang X, Wang Z, Qiao X, Zhang Y. Combined State of Charge and State of Energy Estimation for Echelon-Use Lithium-Ion Battery Based on Adaptive Extended Kalman Filter. Batteries. 2023; 9(7):362. https://doi.org/10.3390/batteries9070362
Chicago/Turabian StyleHou, Enguang, Zhen Wang, Xiaopeng Zhang, Zhixue Wang, Xin Qiao, and Yun Zhang. 2023. "Combined State of Charge and State of Energy Estimation for Echelon-Use Lithium-Ion Battery Based on Adaptive Extended Kalman Filter" Batteries 9, no. 7: 362. https://doi.org/10.3390/batteries9070362
APA StyleHou, E., Wang, Z., Zhang, X., Wang, Z., Qiao, X., & Zhang, Y. (2023). Combined State of Charge and State of Energy Estimation for Echelon-Use Lithium-Ion Battery Based on Adaptive Extended Kalman Filter. Batteries, 9(7), 362. https://doi.org/10.3390/batteries9070362







