Grain Boundary Characterization and Potential Percolation of the Solid Electrolyte LLZO
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Investigations
2.1.1. Synthesis and Fabrication of LLZO Samples
2.1.2. Sample Characterization
2.2. Percolation Models
3. Results and Discussion
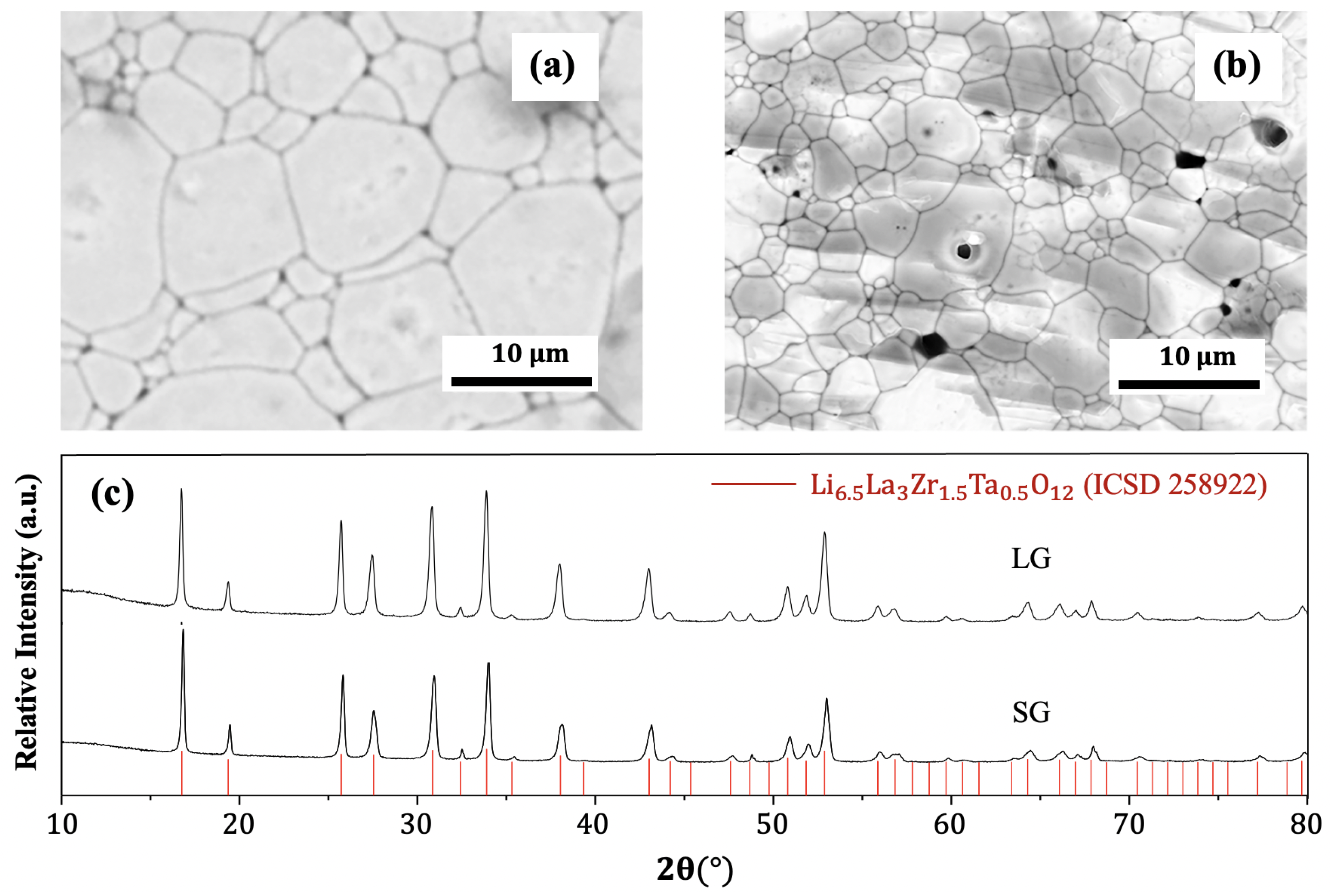
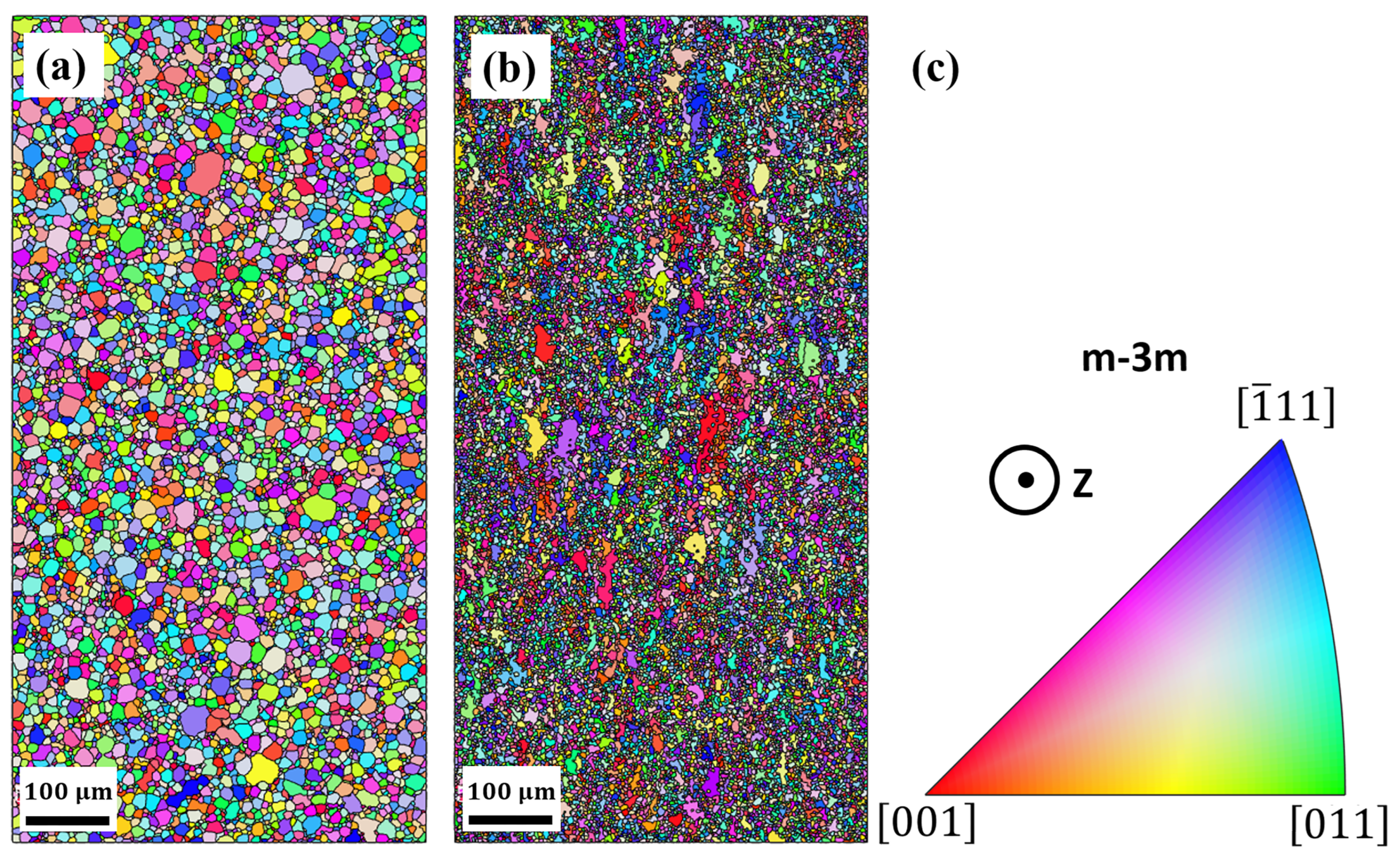
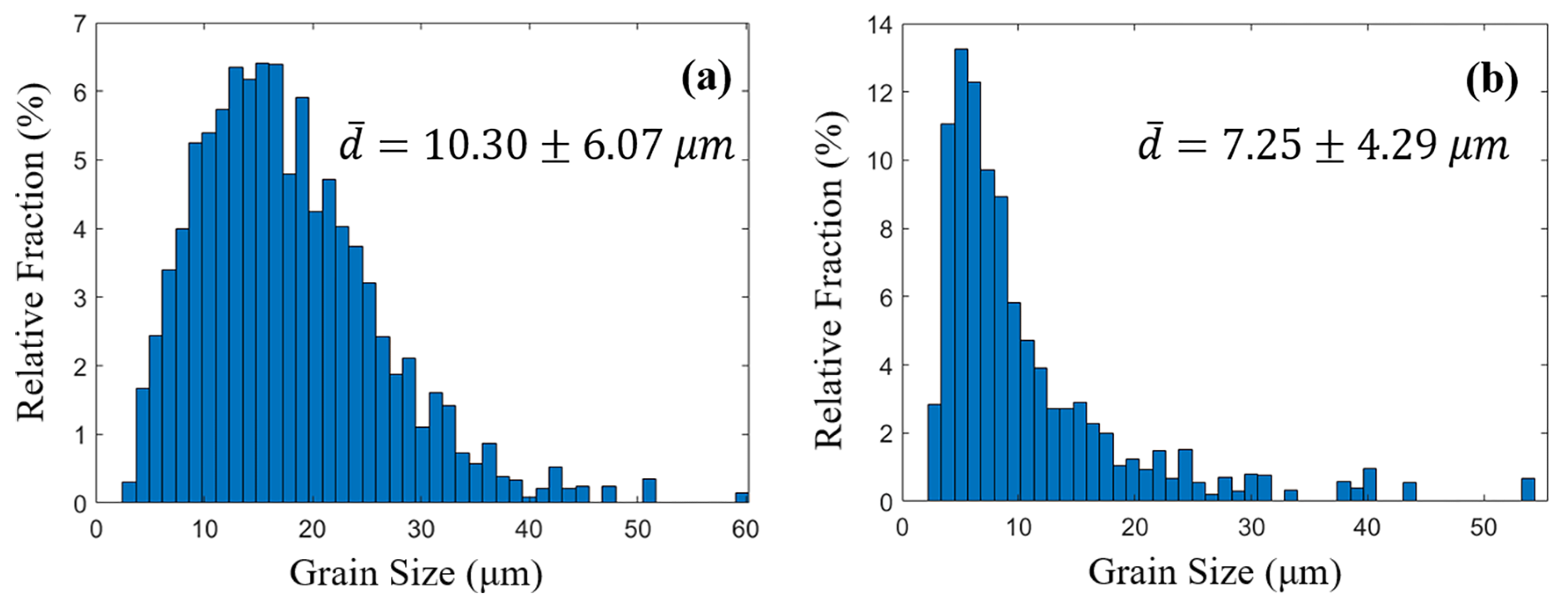
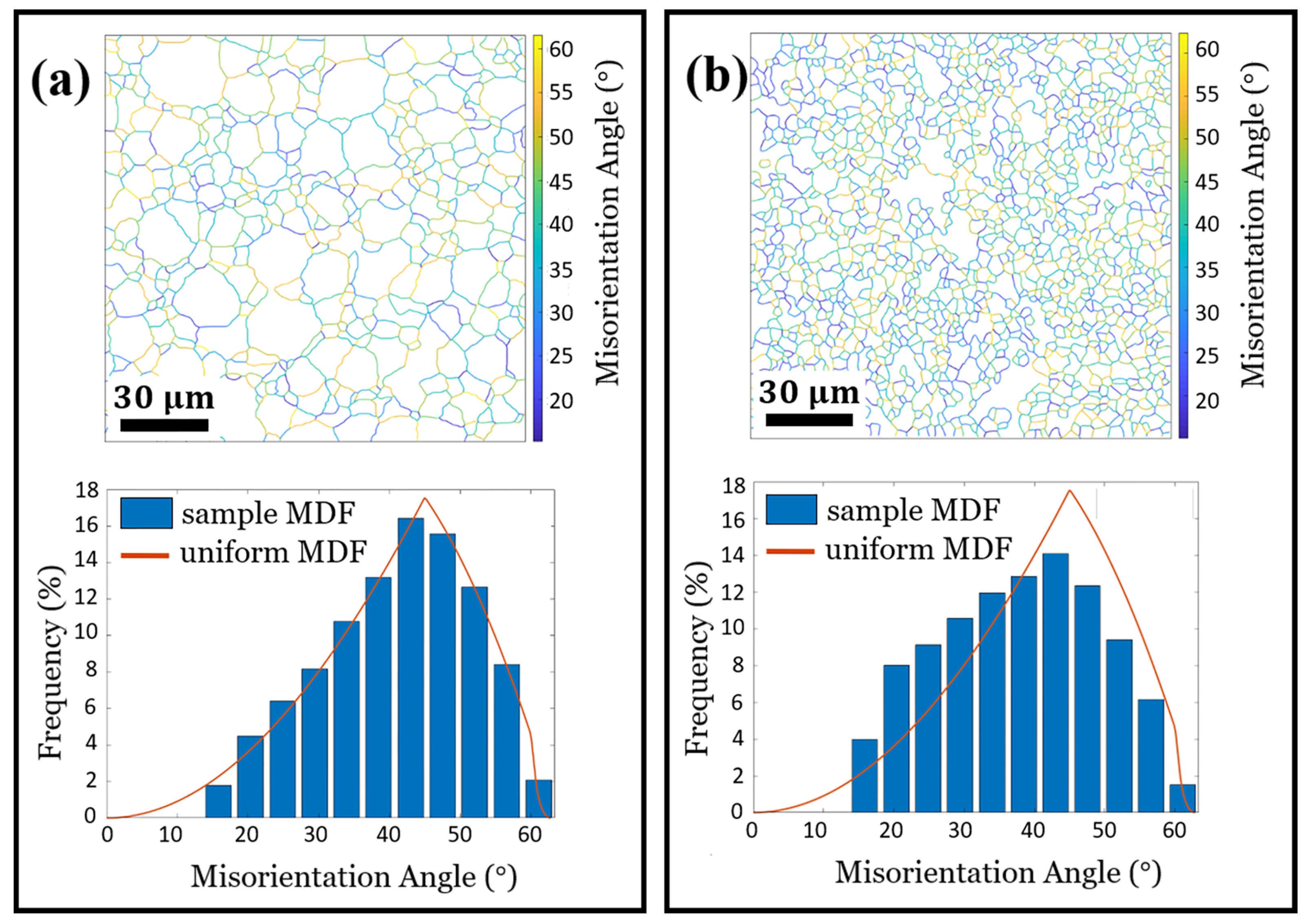
3.1. Microstuctural Analysis
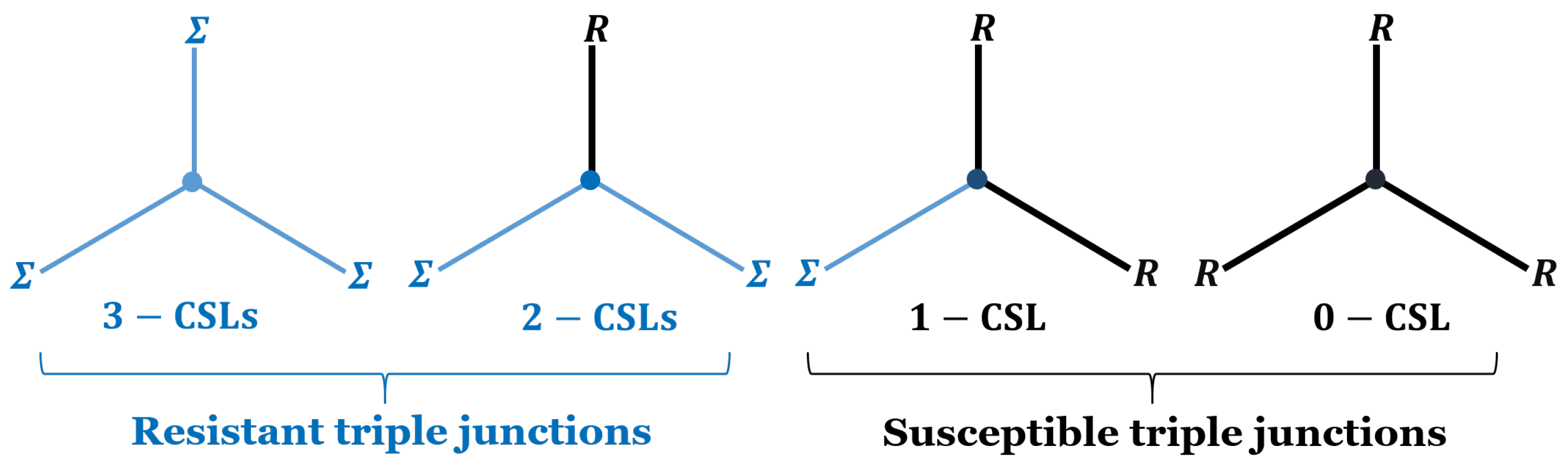
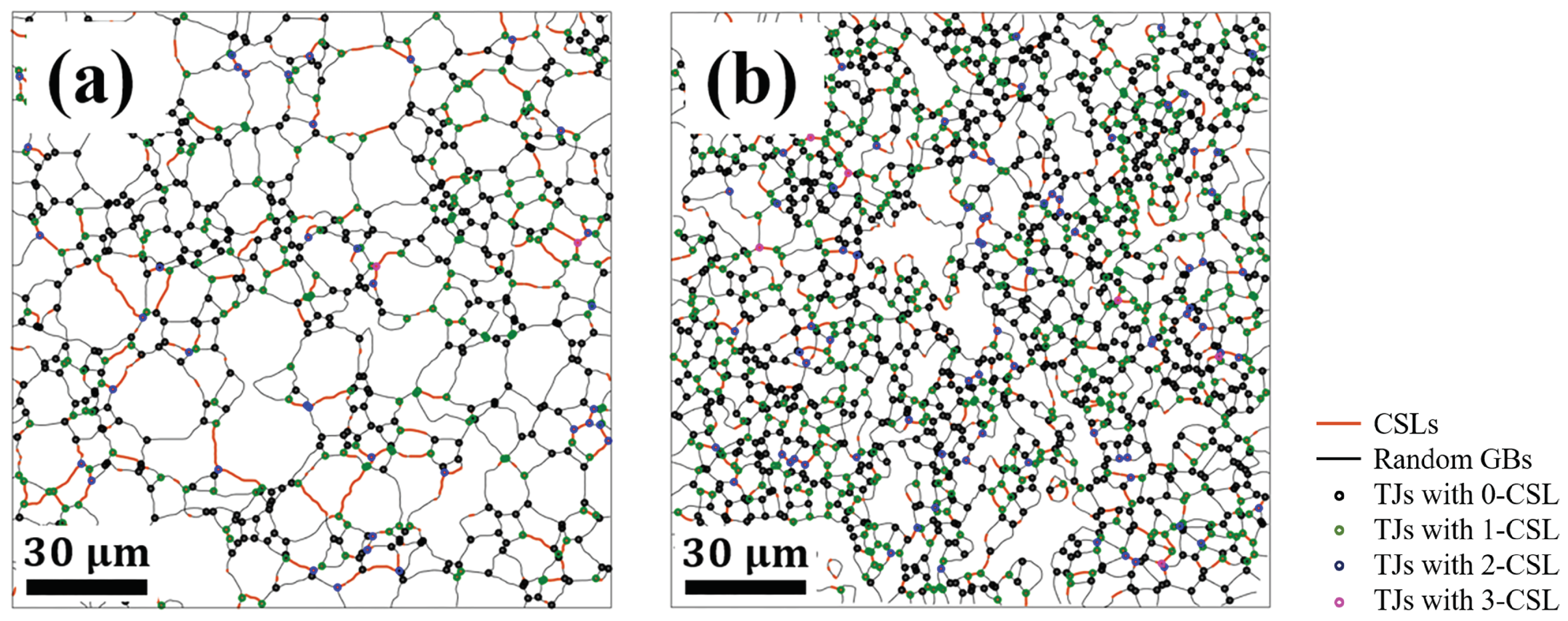
3.2. Grain Boundary and Triple Junction Classification
3.3. Percolation Hypothesis
4. Conclusions
- The synthesis methods of the precursor powder and hot-pressed pellets are successful in producing large amounts of pure cubic phase of Ta:LLZO with very high relative density, the same composition and surface treatment, but with different grain size distributions, namely small grain (SG) and large grain (LG) samples.
- The fraction of CSL grain boundaries are slightly larger in the LG sample than those in the SG sample.
- The fraction of random grain boundaries is significantly higher than in typical metallic materials.
- Our investigations indicate that percolation-based failure criteria, which are successfully used, e.g., for corrosion of austenitic steels, cannot be applied for the prediction of Li plating along grain boundaries in LLZO as solid electrolytes. This conclusion does however not exclude that different grain boundary characteristics can influence the delayed failure after long operation times.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASSB | All-Solid-State Batteries |
| LLZO | LiLaZrO |
| EBSD | Electron Back Scatter Diffraction |
| CSL | Coincidence Site Lattice |
| LAGB | Low Angle Grain Boundary |
| GB | Grain Boundary |
| HP | Hot-Pressing |
| XRD | X-Ray Diffraction |
| ICP-OES | Inductively Coupled Plasma Optical Emission Spectroscopy |
| SEM | Scanning Emission Microscopy |
| MDF | Misorientation Density Function |
| TJ | Triple Junction |
| LG | Large Grain |
| SG | Small Grain |
| SSR | Solid-State Reaction |
| SASSR | Solution-Assisted Solid-State Reaction |
References
- Goodenough, J.B. Rechargeable batteries: Challenges old and new. J. Solid State Electrochem. 2012, 16, 2019–2029. [Google Scholar] [CrossRef]
- Murugan, R.; Thangadurai, V.; Weppner, W. Fast lithium ion conduction in garnet-type Li7La3Zr2O12. Angew. Chem. Int. Ed. 2007, 46, 7778–7781. [Google Scholar] [CrossRef] [PubMed]
- Arinicheva, Y.; Wolff, M.; Lobe, S.; Dellen, C.; Fattakhova-Rohlfing, D.; Guillon, O.; Böhm, D.; Zoller, F.; Schmuch, R.; Li, J.; et al. Ceramics for electrochemical storage. In Advanced Ceramics for Energy Conversion and Storage; Elsevier: Amsterdam, The Netherlands, 2020; pp. 549–709. [Google Scholar]
- Motoyama, M.; Tanaka, Y.; Yamamoto, T.; Tsuchimine, N.; Kobayashi, S.; Iriyama, Y. The Active Interface of Ta-Doped Li7La3Zr2O12 for Li Plating/Stripping Revealed by Acid Aqueous Etching. ACS Appl. Energy Mater. 2019, 2, 6720–6731. [Google Scholar] [CrossRef]
- Manthiram, A.; Yu, X.; Wang, S. Lithium battery chemistries enabled by solid-state electrolytes. Nat. Rev. Mater. 2017, 2, 1–16. [Google Scholar] [CrossRef]
- McConohy, G.; Xu, X.; Cui, T.; Barks, E.; Wang, S.; Kaeli, E.; Melamed, C.; Gu, X.W.; Chueh, W.C. Mechanical regulation of lithium intrusion probability in garnet solid electrolytes. Nat. Energy 2023, 8, 241–250. [Google Scholar] [CrossRef]
- Ren, Y.; Shen, Y.; Lin, Y.; Nan, C.W. Direct observation of lithium dendrites inside garnet-type lithium-ion solid electrolyte. Electrochem. Commun. 2015, 57, 27–30. [Google Scholar] [CrossRef]
- Han, F.; Westover, A.S.; Yue, J.; Fan, X.; Wang, F.; Chi, M.; Leonard, D.N.; Dudney, N.J.; Wang, H.; Wang, C. High electronic conductivity as the origin of lithium dendrite formation within solid electrolytes. Nat. Energy 2019, 4, 187–196. [Google Scholar] [CrossRef]
- Song, Y.; Yang, L.; Zhao, W.; Wang, Z.; Zhao, Y.; Wang, Z.; Zhao, Q.; Liu, H.; Pan, F. Revealing the short-circuiting mechanism of garnet-based solid-state electrolyte. Adv. Energy Mater. 2019, 9, 1900671. [Google Scholar] [CrossRef]
- Cheng, E.J.; Sharafi, A.; Sakamoto, J. Intergranular Li metal propagation through polycrystalline Li6.25Al0.25La3Zr2O12 ceramic electrolyte. Electrochim. Acta 2017, 223, 85–91. [Google Scholar] [CrossRef]
- Sharafi, A.; Haslam, C.; Kerns, R.D.; Wolfenstine, J.; Sakamoto, J.S. Controlling and correlating the effect of grain size with the mechanical and electrochemical properties of Li7La3Zr2O12 solid-state electrolyte. J. Mater. Chem. 2017, 5, 21491–21504. [Google Scholar] [CrossRef]
- Yonemoto, F.; Nishimura, A.; Motoyama, M.; Tsuchimine, N.; Kobayashi, S.; Iriyama, Y. Temperature effects on cycling stability of Li plating/stripping on Ta-doped Li7La3Zr2O12. J. Power Sources 2017, 343, 207–215. [Google Scholar] [CrossRef]
- Tsai, C.L.; Roddatis, V.; Chandran, C.V.; Ma, Q.; Uhlenbruck, S.; Bram, M.; Heitjans, P.; Guillon, O. Li7La3Zr2O12 Interface Modification for Li Dendrite Prevention. ACS Appl. Mater. Interfaces 2016, 8, 10617–10626. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Shen, Y.; Lin, Y.; Nan, C.W. Microstructure Manipulation for Enhancing the Resistance of Garnet-Type Solid Electrolytes to “Short Circuit” by Li Metal Anodes. ACS Appl. Mater. Interfaces 2019, 116, 5928–5937. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, W.; Kunz, M.; Persson, K.A.; Tamura, N.; Chen, G.; Doeff, M.M. Effect of surface microstructure on electrochemical performance of garnet solid electrolytes. ACS Appl. Mater. Interfaces 2015, 7, 2073–2081. [Google Scholar] [CrossRef]
- Wells, D.B.; Stewart, J.; Herbert, A.W.; Scott, P.M.; Williams, D.E. The Use of Percolation Theory to Predict the Probability of Failure of Sensitized, Austenitic Stainless Steels by Intergranular Stress Corrosion Cracking. Corrosion 1989, 45, 649–660. [Google Scholar] [CrossRef]
- Gaudett, M.A.; Scully, J.R. Applicability of bond percolation theory to intergranular stress-corrosion cracking of sensitized AlSI 304 stainless steel. Metall. Trans. 1994, 25, 775–787. [Google Scholar] [CrossRef]
- Perriot, R.; Uberuaga, B.P.; Zamora, R.J.; Perez, D.; Voter, A.F. Evidence for percolation diffusion of cations and reordering in disordered pyrochlore from accelerated molecular dynamics. Nat. Commun. 2017, 8, 618. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Urban, A.; Li, X.; Su, D.; Hautier, G.; Ceder, G. Unlocking the Potential of Cation-Disordered Oxides for Rechargeable Lithium Batteries. Science 2014, 343, 519–522. [Google Scholar] [CrossRef] [PubMed]
- Tsurekawa, S.; Nakamichi, S.; Watanabe, T. Correlation of grain boundary connectivity with grain boundary character distribution in austenitic stainless steel. Acta Mater. 2006, 54, 3617–3626. [Google Scholar] [CrossRef]
- Kobayashi, S.; Kobayashi, R.; Watanabe, T. Control of grain boundary connectivity based on fractal analysis for improvement of intergranular corrosion resistance in SUS316L austenitic stainless steel. Acta Mater. 2016, 102, 397–405. [Google Scholar] [CrossRef]
- Tsai, C.L.; Dashjav, E.; Hammer, E.M.; Finsterbusch, M.; Tietz, F.; Uhlenbruck, S.; Buchkremer, H.P. High conductivity of mixed phase Al-substituted Li7La3Zr2O12. J. Electroceramics 2015, 35, 25–32. [Google Scholar] [CrossRef]
- Mainprice, D.; Hielscher, R.; Schaeben, H. Calculating anisotropic physical properties from texture data using the MTEX open-source package. Geol. Soc. Lond. Spec. Publ. 2011, 360, 175–192. [Google Scholar] [CrossRef]
- Kronberg, M.; Wilson, F. Secondary recrystallization in copper. JOM 1949, 1, 501–514. [Google Scholar] [CrossRef]
- Brandon, D. The structure of high-angle grain boundaries. Acta Metall. 1966, 14, 1479–1484. [Google Scholar] [CrossRef]
- Gottstein, G.; Shvindlerman, L. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications; Engineering & Technology, Physical Sciences, CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Priester, L. Grain Boundaries: From Theory to Engineering; Springer Series in Materials Science; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Fortier, P.; Aust, K.; Miller, W. Effects of symmetry, texture and topology on triple junction character distribution in polycrystalline materials. Acta Metall. Mater. 1995, 43, 339–349. [Google Scholar] [CrossRef]
- Fortier, P.; Miller, W.; Aust, K. Triple junction and grain boundary character distributions in metallic materials. Acta Mater. 1997, 45, 3459–3467. [Google Scholar] [CrossRef]
- Sykes, M.F.; Essam, J.W. Exact Critical Percolation Probabilities for Site and Bond Problems in Two Dimensions. J. Math. Phys. 1964, 5, 1117–1127. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory, 2nd ed.; Taylor & Francis: London, UK, 1992. [Google Scholar]
- Frary, M.; Schuh*, C.A. Connectivity and percolation behaviour of grain boundary networks in three dimensions. Philos. Mag. 2005, 85, 1123–1143. [Google Scholar] [CrossRef]
- Kumar, M.; King, W.E.; Schwartz, A.J. Modifications to the microstructural topology in fcc materials through thermomechanical processing. Acta Mater. 2000, 48, 2081–2091. [Google Scholar] [CrossRef]
- Awaka, J.; Takashima, A.; Kataoka, K.; Kijima, N.; Idemoto, Y.; Akimoto, J. Crystal Structure of Fast Lithium-ion-conducting Cubic Li7La3Zr2O12. Chem. Lett. 2011, 40, 60–62. [Google Scholar] [CrossRef]
- Mackenzie, J.K. Second paper on statistics associated with the random disorientation of cubes. Biometrika 1958, 45, 229–240. [Google Scholar] [CrossRef]
- Don, J.; Majumdar, S. Creep cavitation and grain boundary structure in type 304 stainless steel. Acta Metall. 1986, 34, 961–967. [Google Scholar] [CrossRef]
- Palumbo, G.; Aust, K.T.; Erb, U.; King, P.J.; Brennenstuhl, A.M.; Lichtenberger, P.C. On annealing twins and CSL distributions in F.C.C. polycrystals. Phys. Status Solidi 1992, 131, 425–428. [Google Scholar] [CrossRef]
- Schuh, C.A.; Kumar, M.; King, W.E. Analysis of grain boundary networks and their evolution during grain boundary engineering. Acta Mater. 2003, 51, 687–700. [Google Scholar] [CrossRef]
- Yu, S.; Siegel, D. Grain boundary contributions to Li-ion transport in the solid electrolyte Li7La3Zr 2O12 (LLZO). Chem. Mater. 2017, 29, 9639–9647. [Google Scholar] [CrossRef]
- Zhu, Y. Atomistic Modeling of Solid Interfaces in All-Solid-State Li-ion Batteries. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2018. [Google Scholar]
- Ren, J.; Zhang, L.; Siegmund, S. How Inhomogeneous Site Percolation Works on Bethe Lattices: Theory and Application. Sci. Rep. 2016, 6, 22420. [Google Scholar] [CrossRef]
- Aguesse, F.; Manalastas, W.; Buannic, L.; Lopez del Amo, J.M.; Singh, G.; Llordés, A.; Kilner, J. Investigating the dendritic growth during full cell cycling of garnet electrolyte in direct contact with Li metal. ACS Appl. Mater. Interfaces 2017, 9, 3808–3816. [Google Scholar] [CrossRef]
- Liu, X.; Garcia-Mendez, R.; Lupini, A.R.; Cheng, Y.; Hood, Z.D.; Han, F.; Sharafi, A.; Idrobo, J.C.; Dudney, N.J.; Wang, C.; et al. Local electronic structure variation resulting in Li ‘filament’formation within solid electrolytes. Nat. Mater. 2021, 20, 1485–1490. [Google Scholar] [CrossRef]
- Krause, D.; Thörnig, P. JURECA: Modular supercomputer at Jülich Supercomputing Centre. J. Large-Scale Res. Facil. 2018, 4, 1–9. [Google Scholar] [CrossRef]

| Sample | Powder Synthesis | Surface Roughness | Grain Size |
|---|---|---|---|
| SG | SASSR | nm | µm |
| LG | SSR | nm | µm |
| 3 | 63.43 | 48.19 | 333.44 | 60 | 8.66 |
| 5 | 53.13 | 0 | 0 | 36.87 | 6.71 |
| 7 | 56.31 | 31 | 326.31 | 38.21 | 5.67 |
| 9 | 104.04 | 27.27 | 284.04 | 38.94 | 5 |
| 11 | 108.44 | 35.10 | 288.44 | 50.48 | 4.52 |
| 13a | 22.62 | 0 | 0 | 22.62 | 4.16 |
| 13b | 53.13 | 22.62 | 323.13 | 27.80 | 4.16 |
| 15 | 111.80 | 21.04 | 291.80 | 48.19 | 3.87 |
| 17a | 28.07 | 0 | 0 | 28.07 | 3.64 |
| 17b | 85.24 | 45.10 | 318.37 | 61.93 | 3.64 |
| 19a | 99.46 | 18.67 | 279.46 | 26.53 | 3.44 |
| 19b | 59.04 | 37.86 | 329.04 | 46.83 | 3.44 |
| 21a | 51.34 | 17.75 | 321.34 | 21.79 | 3.27 |
| 21b | 116.57 | 25.21 | 296.57 | 44.42 | 3.27 |
| 23 | 116.57 | 16.96 | 296.57 | 40.46 | 3.13 |
| 25a | 16.26 | 0 | 0 | 16.26 | 3 |
| 25b | 90 | 36.87 | 306.87 | 51.68 | 3 |
| 27a | 105.95 | 15.64 | 285.95 | 35.43 | 2.89 |
| 27b | 101.31 | 22.19 | 281.31 | 31.59 | 2.89 |
| 29 | 79.38 | 34.15 | 312.51 | 46.40 | 2.79 |
| 31 | 113.20 | 29.43 | 293.20 | 52.20 | 2.69 |
| 33a | 97.13 | 14.14 | 277.13 | 20.05 | 2.61 |
| 33b | 119.75 | 14.14 | 299.75 | 33.56 | 2.61 |
| 33c | 68.20 | 40.75 | 338.20 | 58.99 | 2.61 |
| 35 | 50.04 | 19.46 | 329.04 | 34.05 | 2.54 |
| 37a | 18.98 | 0 | 0 | 18.98 | 2.46 |
| 37b | 110.56 | 13.35 | 290.56 | 43.14 | 2.47 |
| 39a | 54.46 | 26.18 | 324.46 | 32.20 | 2.40 |
| 39b | 83.99 | 29.33 | 317.12 | 50.13 | 2.40 |
| 39c | 85.60 | 41.96 | 302.47 | 50.13 | 2.40 |
| 41a | 12.68 | 0 | 0 | 12.68 | 2.34 |
| 41b | 108.44 | 17.97 | 288.44 | 40.88 | 2.34 |
| 43a | 102.53 | 12.38 | 282.53 | 27.91 | 2.29 |
| 43b | 76.87 | 45.76 | 324.25 | 60.77 | 2.29 |
| 45a | 75.96 | 27.27 | 309.09 | 36.87 | 2.24 |
| 45b | 81.87 | 38.94 | 315 | 53.13 | 2.24 |
| 47 | 108.44 | 23.81 | 288.44 | 43.66 | 2.19 |
| 49a | 113.96 | 11.60 | 293.96 | 43.57 | 2.14 |
| 49b | 116.57 | 33.20 | 296.57 | 49.23 | 2.14 |
| Property | SG | LG |
|---|---|---|
| (µm) | 7.25 | 10.30 |
| Grain Boundary Distribution | ||
| CSL% | 12.29 | 13.31 |
| 1.42 | 1.78 | |
| 1.00 | 0.91 | |
| 0.71 | 0.65 | |
| Triple Junction Distribution | ||
| 62.65 | 61.55 | |
| 32.05 | 31.70 | |
| 5.02 | 6.20 | |
| 0.27 | 0.54 | |
| 5.04 | 6.23 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, S.; Arinicheva, Y.; Hüter, C.; Finsterbusch, M.; Spatschek, R. Grain Boundary Characterization and Potential Percolation of the Solid Electrolyte LLZO. Batteries 2023, 9, 222. https://doi.org/10.3390/batteries9040222
Fu S, Arinicheva Y, Hüter C, Finsterbusch M, Spatschek R. Grain Boundary Characterization and Potential Percolation of the Solid Electrolyte LLZO. Batteries. 2023; 9(4):222. https://doi.org/10.3390/batteries9040222
Chicago/Turabian StyleFu, Shuo, Yulia Arinicheva, Claas Hüter, Martin Finsterbusch, and Robert Spatschek. 2023. "Grain Boundary Characterization and Potential Percolation of the Solid Electrolyte LLZO" Batteries 9, no. 4: 222. https://doi.org/10.3390/batteries9040222
APA StyleFu, S., Arinicheva, Y., Hüter, C., Finsterbusch, M., & Spatschek, R. (2023). Grain Boundary Characterization and Potential Percolation of the Solid Electrolyte LLZO. Batteries, 9(4), 222. https://doi.org/10.3390/batteries9040222








