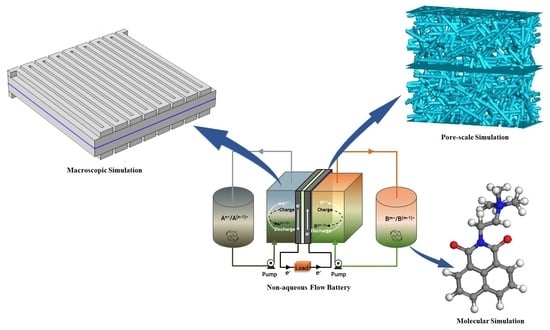
Modeling and Simulation of Non-Aqueous Redox Flow Batteries: A Mini-Review
Abstract
1. Introduction
2. Design and Operation Parameters of Non-Aqueous Flow Batteries
2.1. Redox Couple Design
2.2. Solvent Paring and Supporting Electrolyte Selection
2.3. The Choice of Membrane
3. Non-Aqueous Flow Batteries with Organic Solvents
3.1. Working Principle
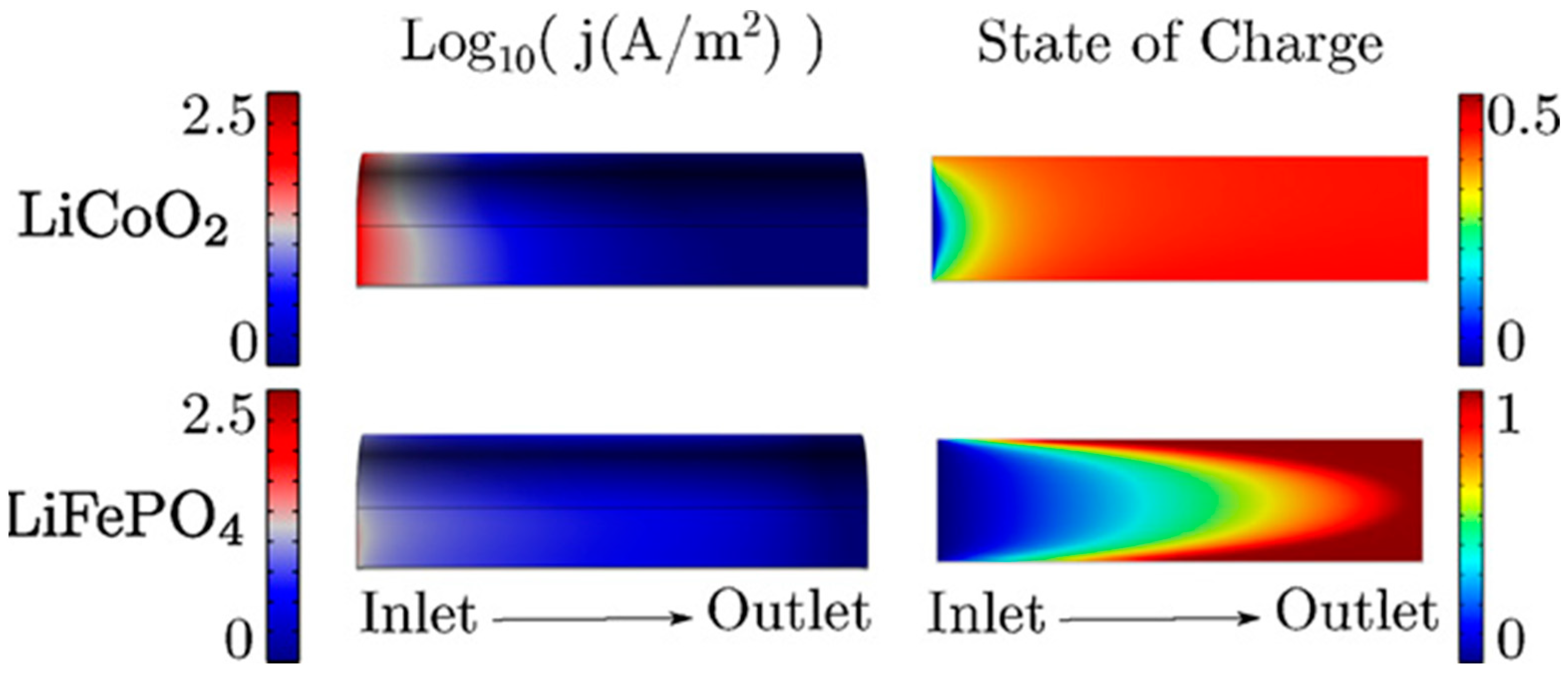
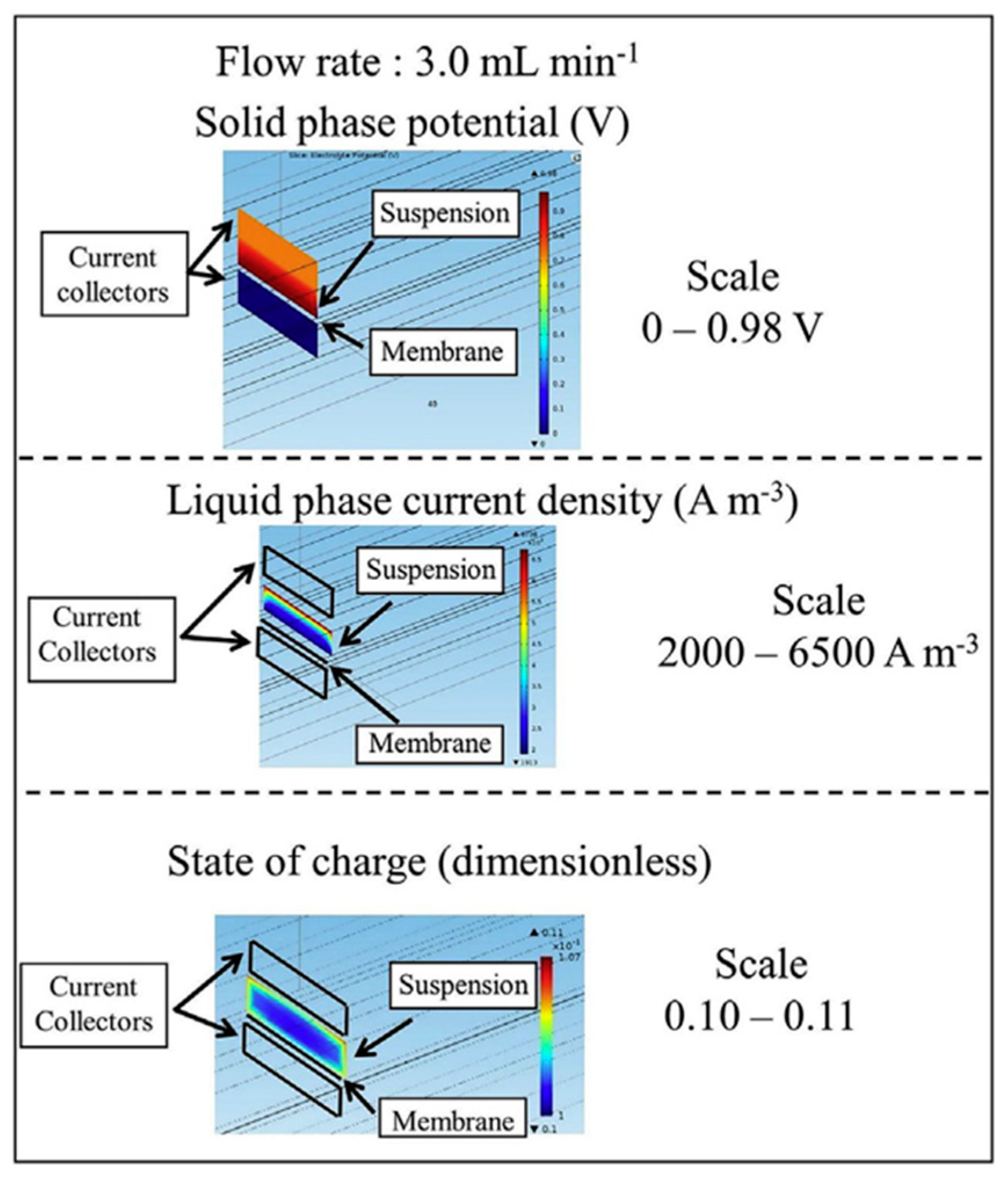
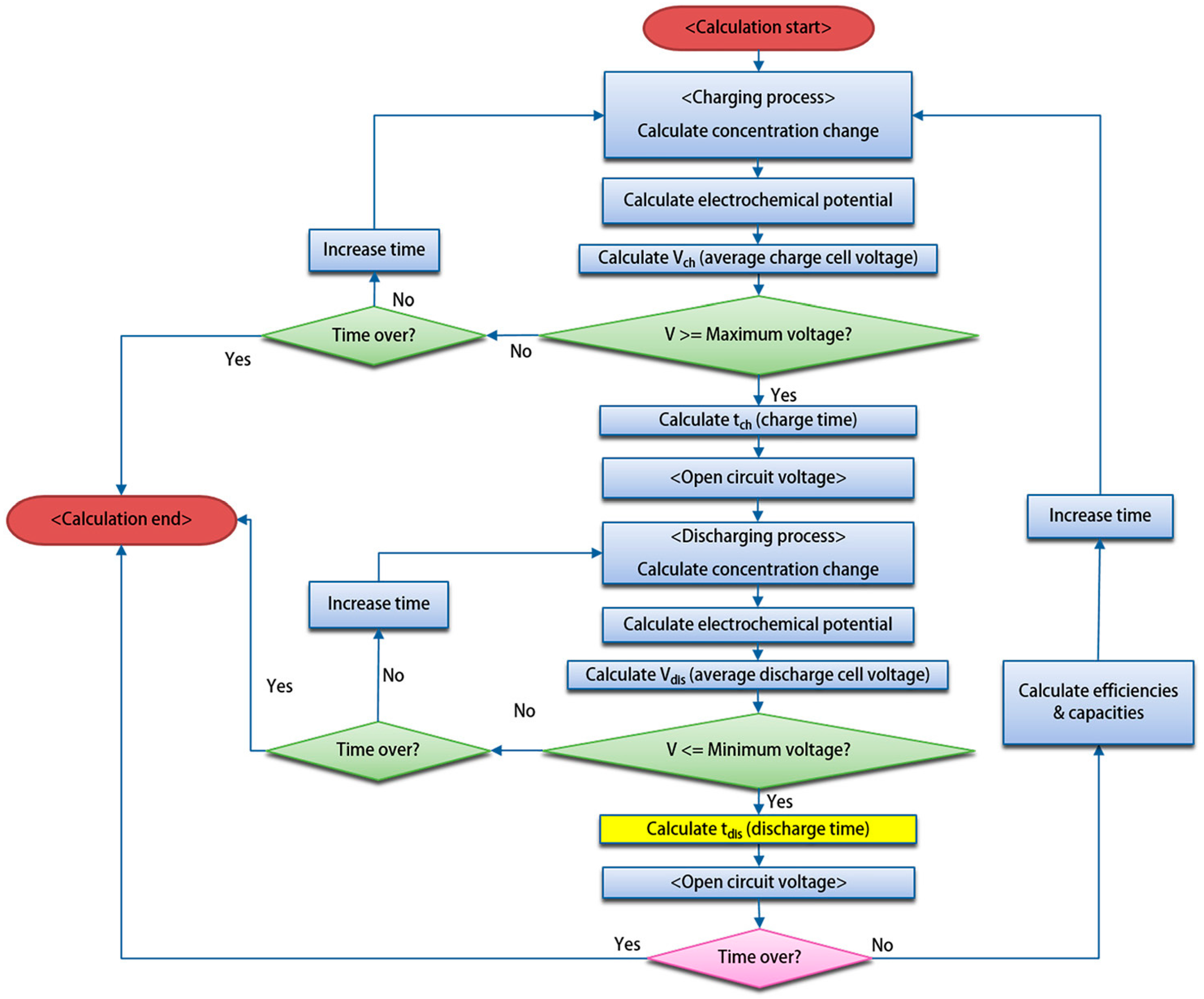
3.2. Modeling Research
- Numerical simulation methods based on multi-physics field coupling. These methods include multi-physics field computational fluid dynamics (MPF-CFD) models, the finite element method (FEM), and multiscale simulation methods.
- In terms of electrochemical reaction models, molecular simulation methods, such as molecular dynamics simulation, can be applied to simulate chemical reactions and diffusion phenomena inside the electrolyte. These methods can provide more accurate reaction mechanisms and reaction kinetics information, thus improving the reliability of simulation results.
- In the flow model aspect, the non-Newtonian flow characteristics of SSFB should receive attention. Some studies have shown that the non-Newtonian flow characteristics of SSFB have a significant impact on battery performance and thus need to be taken into account.
- With the continuous development of machine learning and artificial intelligence technology, these technologies can also be used in SSFB modeling. For example, machine learning methods can accurately predict the potential distribution and ion concentration distribution inside the battery, providing better guidance for optimizing design and operating parameters.
4. Non-Aqueous Flow Batteries with Ionic Liquid Solvents
4.1. Working Principle
4.2. Modeling Research
5. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, H.; Lu, W.; Li, X. Progress and Perspectives of Flow Battery Technologies. Electrochem. Energy Rev. 2019, 2, 492–506. [Google Scholar] [CrossRef]
- Thaller, L.H. Electrically rechargeable redox flow cells. In Proceedings of the 9th Intersociety Energy Conversion Engineering Conference, Chicago, IL, USA, 1 January 1974; pp. 924–928. [Google Scholar]
- Zeng, Y.K.; Zhou, X.L.; An, L.; Wei, L.; Zhao, T.S. A high-performance flow-field structured iron-chromium redox flow battery. J. Power Sources 2016, 324, 738–744. [Google Scholar] [CrossRef]
- Cho, K.T.; Ridgway, P.; Weber, A.Z.; Haussener, S.; Battaglia, V.; Srinivasan, V. High Performance Hydrogen/Bromine Redox Flow Battery for Grid-Scale Energy Storage. J. Electrochem. Soc. 2012, 159, A1806–A1815. [Google Scholar] [CrossRef]
- Wu, M.C.; Zhao, T.S.; Jiang, H.R.; Zeng, Y.K.; Ren, Y.X. High-performance zinc bromine flow battery via improved design of electrolyte and electrode. J. Power Sources 2017, 355, 62–68. [Google Scholar] [CrossRef]
- Li, L.; Kim, S.; Wang, W.; Vijayakumar, M.; Nie, Z.; Chen, B.; Zhang, J.; Xia, G.; Hu, J.; Graff, G.; et al. A Stable Vanadium Redox-Flow Battery with High Energy Density for Large-Scale Energy Storage. Adv. Energy Mater. 2011, 1, 394–400. [Google Scholar] [CrossRef]
- Wills, R.G.A.; Collins, J.; Stratton-Campbell, D.; Low, C.T.J.; Pletcher, D.; Walsh, F.C. Developments in the soluble lead-acid flow battery. J. Appl. Electrochem. 2010, 40, 955–965. [Google Scholar] [CrossRef]
- Hu, B.; DeBruler, C.; Rhodes, Z.; Liu, T.L. Long-Cycling Aqueous Organic Redox Flow Battery (AORFB) toward Sustainable and Safe Energy Storage. J. Am. Chem. Soc. 2017, 139, 1207–1214. [Google Scholar] [CrossRef] [PubMed]
- Skyllas-Kazacos, M.; Chakrabarti, M.H.; Hajimolana, S.A.; Mjalli, F.S.; Saleem, M. Progress in Flow Battery Research and Development. J. Electrochem. Soc. 2011, 158, R55–R79. [Google Scholar] [CrossRef]
- Robb, B.H.; Waters, S.E.; Marshak, M.P. Evaluating aqueous flow battery electrolytes: A coordinated approach. Dalton Trans. 2020, 49, 16047–16053. [Google Scholar] [CrossRef]
- Huang, Y.; Gu, S.; Yan, Y.; Li, S.F.Y. Nonaqueous redox-flow batteries: Features, challenges, and prospects. Curr. Opin. Chem. Eng. 2015, 8, 105–113. [Google Scholar] [CrossRef]
- Kowalski, J.A.; Su, L.; Milshtein, J.D.; Brushett, F.R. Recent advances in molecular engineering of redox active organic molecules for nonaqueous flow batteries. Curr. Opin. Chem. Eng. 2016, 13, 45–52. [Google Scholar] [CrossRef]
- Ortiz-Martínez, V.M.; Gómez-Coma, L.; Pérez, G.; Ortiz, A.; Ortiz, I. The roles of ionic liquids as new electrolytes in redox flow batteries. Sep. Purif. Technol. 2020, 252, 117436. [Google Scholar] [CrossRef]
- Hogue, R.W.; Toghill, K.E. Metal coordination complexes in nonaqueous redox flow batteries. Curr. Opin. Electrochem. 2019, 18, 37–45. [Google Scholar] [CrossRef]
- Winsberg, J.; Hagemann, T.; Janoschka, T.; Hager, M.D.; Schubert, U.S. Redox-Flow Batteries: From Metals to Organic Redox-Active Materials. Angew. Chem.-Int. Ed. 2017, 56, 686–711. [Google Scholar] [CrossRef]
- Bamgbopa, M.O.; Pour, N.; Shao-Horn, Y.; Almheiri, S. Systematic selection of solvent mixtures for non-aqueous redox flow batteries—Vanadium acetylacetonate as a model system. Electrochim. Acta 2017, 223, 115–123. [Google Scholar] [CrossRef]
- Soavi, F.; Brilloni, A.; De Giorgio, F.; Poli, F. Semi-solid lithium/oxygen flow battery: An emerging, high-energy technology. Curr. Opin. Chem. Eng. 2022, 37, 100835. [Google Scholar] [CrossRef]
- Ventosa, E. Semi-solid flow battery and redox-mediated flow battery: Two strategies to implement the use of solid electroactive materials in high-energy redox-flow batteries. Curr. Opin. Chem. Eng. 2022, 37, 100834. [Google Scholar] [CrossRef]
- Li, L.; Yin, Y.J.; Hei, J.P.; Wan, X.J.; Li, M.L.; Cui, Y. Molecular Engineering of Aromatic Imides for Organic Secondary Batteries. Small 2021, 17, e2005752. [Google Scholar] [CrossRef] [PubMed]
- Sheldon, R.A. The greening of solvents: Towards sustainable organic synthesis. Curr. Opin. Green Sustain. Chem. 2019, 18, 13–19. [Google Scholar] [CrossRef]
- Lehmann, M.L.; Tyler, L.; Self, E.C.; Yang, G.; Nanda, J.; Saito, T. Membrane design for non-aqueous redox flow batteries: Current status and path forward. Chem 2022, 8, 1611–1636. [Google Scholar] [CrossRef]
- Moutet, J.; Veleta, J.M.; Gianetti, T.L. Symmetric, Robust, and High-Voltage Organic Redox Flow Battery Model Based on a Helical Carbenium Ion Electrolyte. Acs Appl. Energy Mater. 2021, 4, 9–14. [Google Scholar] [CrossRef]
- Yu, X.; Yu, W.A.; Manthiram, A. A mediator-ion nitrobenzene—Iodine nonaqueous redox flow battery with asymmetric solvents. Energy Storage Mater. 2020, 29, 266–272. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, C.; Zhen, Y.; Zhao, Y.; Li, Y. A high-rate nonaqueous organic redox flow battery. J. Power Sources 2021, 495, 229819. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, K.J.; Park, M.-S.; Lee, N.J.; Hwang, U.; Kim, H.; Kim, Y.-J. Development of metal-based electrodes for non-aqueous redox flow batteries. Electrochem. Commun. 2011, 13, 997–1000. [Google Scholar] [CrossRef]
- Chu, F.M.; Su, M.H.; Xiao, G.Z.; Tan, Z.A.; Yang, G.A. Analysis of Electrode Configuration Effects on Mass Transfer and Organic Redox Flow Battery Performance. Ind. Eng. Chem. Res. 2022, 61, 2915–2925. [Google Scholar] [CrossRef]
- Esan, O.C.; Shi, X.; Pan, Z.; Huo, X.; An, L.; Zhao, T.S. Modeling and Simulation of Flow Batteries. Adv. Energy Mater. 2020, 10, 2000758. [Google Scholar] [CrossRef]
- Yao, S.; Zhou, J.; Zhang, Y.; Hu, J.; Xie, T. Modeling and characterization of the biochar electrodes for vanadium redox flow battery. Electrochim. Acta 2021, 400, 139469. [Google Scholar] [CrossRef]
- Jiao, Y.-H.; Lu, M.-Y.; Yang, W.-W.; Tang, X.-Y.; Ye, M.; Xu, Q. A 3D macro-segment network model for vanadium redox flow battery with serpentine flow field. Electrochim. Acta 2022, 403, 139657. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Hao, L. Three-dimensional modeling study of all-vanadium redox flow batteries with the serpentine and interdigitated flow fields. J. Electroanal. Chem. 2022, 918, 116460. [Google Scholar] [CrossRef]
- Kurilovich, A.A.; Trovò, A.; Pugach, M.; Stevenson, K.J.; Guarnieri, M. Prospect of modeling industrial scale flow batteries—From experimental data to accurate overpotential identification. Renew. Sustain. Energy Rev. 2022, 167, 112559. [Google Scholar] [CrossRef]
- Akhmetov, N.; Ovsyannikov, N.; Gvozdik, N.; Pogosova, M.; Ryazantsev, S.; Lipovskikh, S.; Krasnikova, I.; Stevenson, K. Composite lithium-conductive LATP+PVdF membranes: Development, optimization, and applicability for Li-TEMPO hybrid redox flow batteries. J. Membr. Sci. 2022, 643, 120002. [Google Scholar] [CrossRef]
- Tang, L.A.; Leung, P.; Xu, Q.; Mohamed, M.R.; Dai, S.Y.; Zhu, X.; Flox, C.; Shah, A.A. Future perspective on redox flow batteries: Aqueous versus nonaqueous electrolytes. Curr. Opin. Chem. Eng. 2022, 37, 100833. [Google Scholar] [CrossRef]
- Yuan, J.; Pan, Z.-Z.; Jin, Y.; Qiu, Q.; Zhang, C.; Zhao, Y.; Li, Y. Membranes in non-aqueous redox flow battery: A review. J. Power Sources 2021, 500, 229983. [Google Scholar] [CrossRef]
- Armstrong, C.G.; Toghill, K.E. Stability of molecular radicals in organic non-aqueous redox flow batteries: A mini review. Electrochem. Commun. 2018, 91, 19–24. [Google Scholar] [CrossRef]
- Brunini, V.E.; Chiang, Y.-M.; Carter, W.C. Modeling the hydrodynamic and electrochemical efficiency of semi-solid flow batteries. Electrochim. Acta 2012, 69, 301–307. [Google Scholar] [CrossRef]
- Lacroix, R.; Biendicho, J.J.; Mulder, G.; Sanz, L.; Flox, C.; Morante, J.R.; Da Silva, S. Modelling the rheology and electrochemical performance of Li4Ti5O12 and LiNi1/3Co1/3Mn1/3O2 based suspensions for semi-solid flow batteries. Electrochim. Acta 2019, 304, 146–157. [Google Scholar] [CrossRef]
- Lee, D.; Ryu, S.; Shin, S.-H.; Kim, J.-H.; Moon, S.-H. A model study on effects of vanadium ion diffusion through ion exchange membranes in a non-aqueous redox flow battery. J. Renew. Sustain. Energy 2019, 11, 034701. [Google Scholar] [CrossRef]
- Chakrabarti, M.H.; Mjalli, F.S.; AlNashef, I.M.; Hashim, M.A.; Hussain, M.A.; Bahadori, L.; Low, C.T.J. Prospects of applying ionic liquids and deep eutectic solvents for renewable energy storage by means of redox flow batteries. Renew. Sustain. Energy Rev. 2014, 30, 254–270. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Q.; Xing, L.; Li, H.; Leung, P.; Yang, W.; Su, H.; Xu, Q. Modeling the effect of temperature on performance of an iron-vanadium redox flow battery with deep eutectic solvent (DES) electrolyte. J. Power Sources 2020, 449, 227491. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, Q.; Chen, Q.; Chen, Z.; Su, H.; Zhang, W. Lattice Boltzmann model for complex transfer behaviors in porous electrode of all copper redox flow battery with deep eutectic solvent electrolyte. Appl. Therm. Eng. 2019, 160, 114015. [Google Scholar] [CrossRef]
- Ma, Q.; Zhao, L.; Xu, J.; Su, H.; Zhang, W.; Yang, W.; Xu, Q. Pore-scale investigation of reactive transfer process in a deep eutectic solvent (DES) electrolyte-based vanadium-iron redox flow battery. Electrochim. Acta 2020, 353, 136486. [Google Scholar] [CrossRef]
- Cacciuttolo, Q.; Petit, M.; Pasquier, D. Fast computing flow battery modeling to optimize the choice of electrolytes and operating conditions—Application to aqueous organic electrolytes. Electrochim. Acta 2021, 392, 138961. [Google Scholar] [CrossRef]

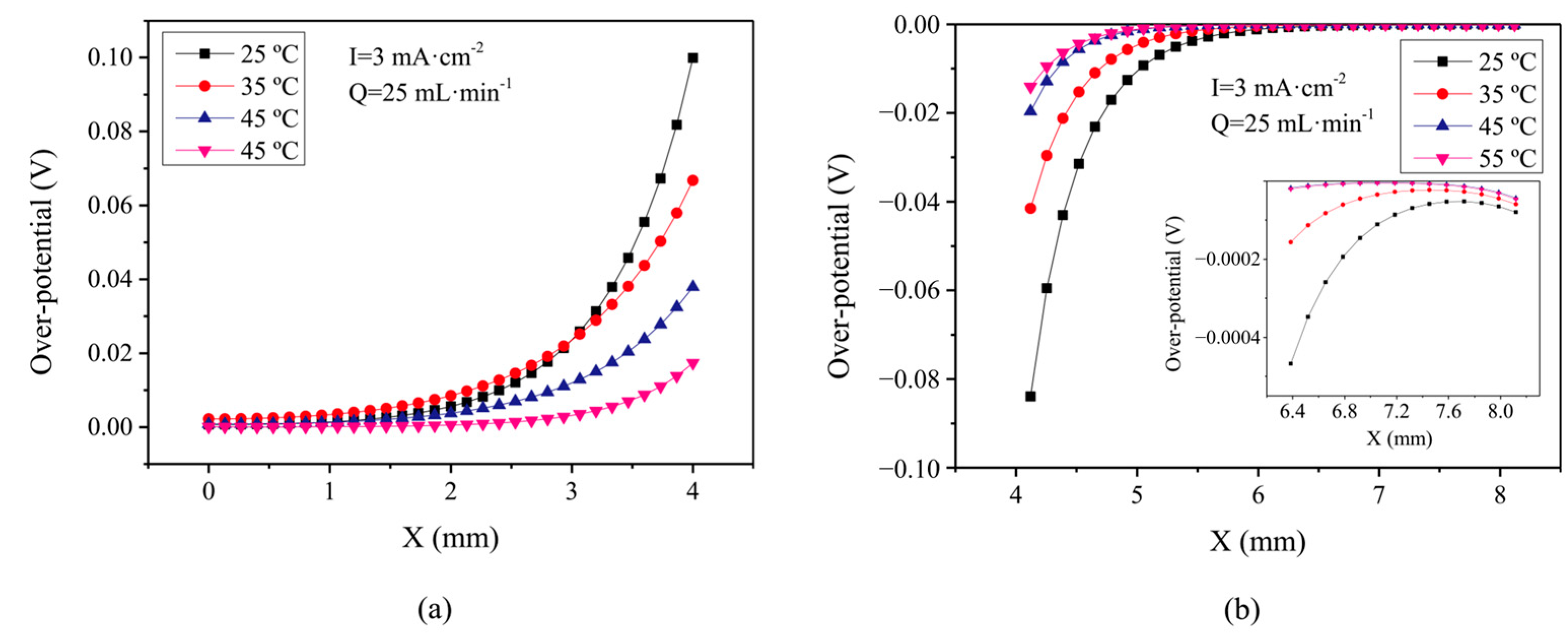
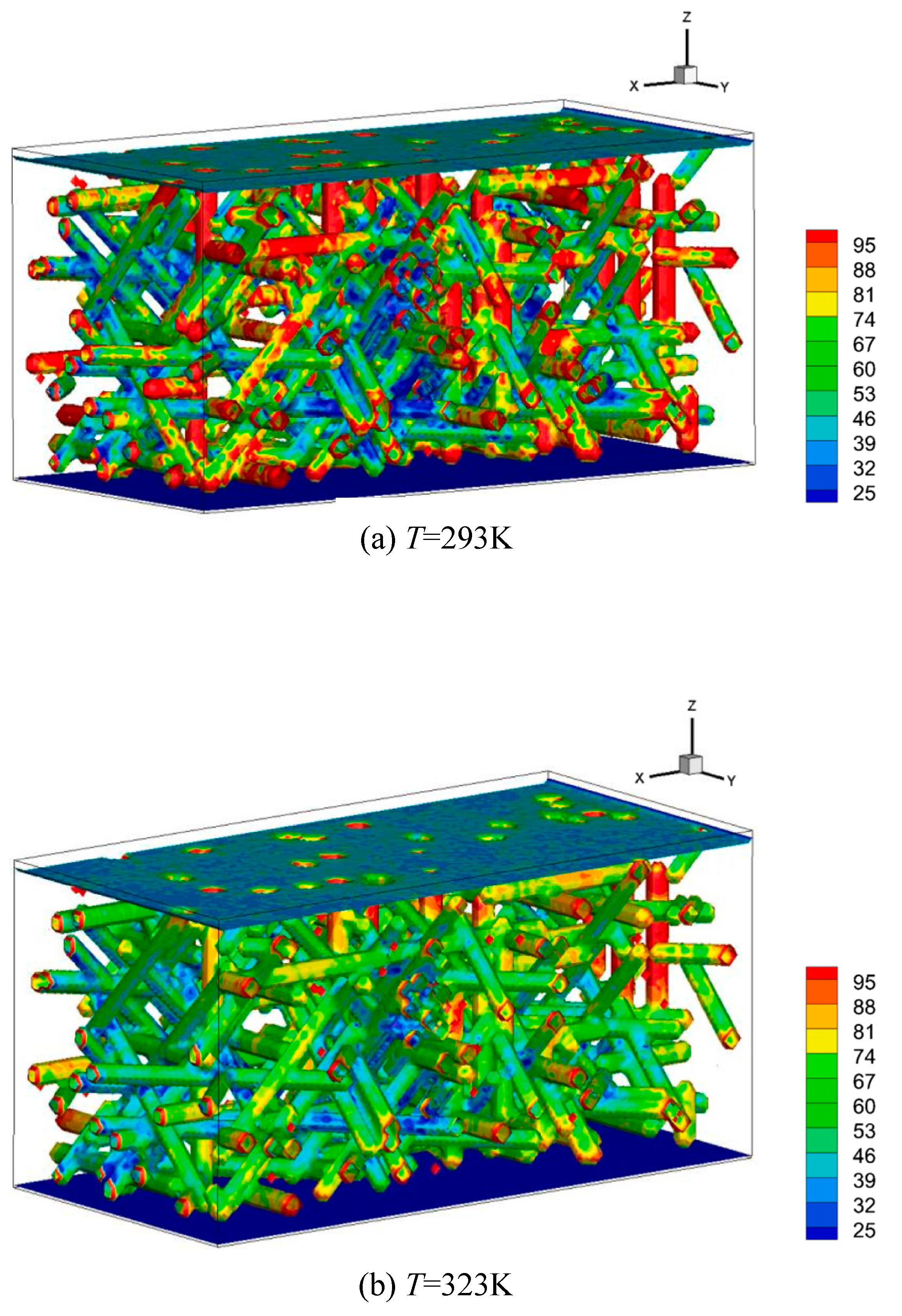
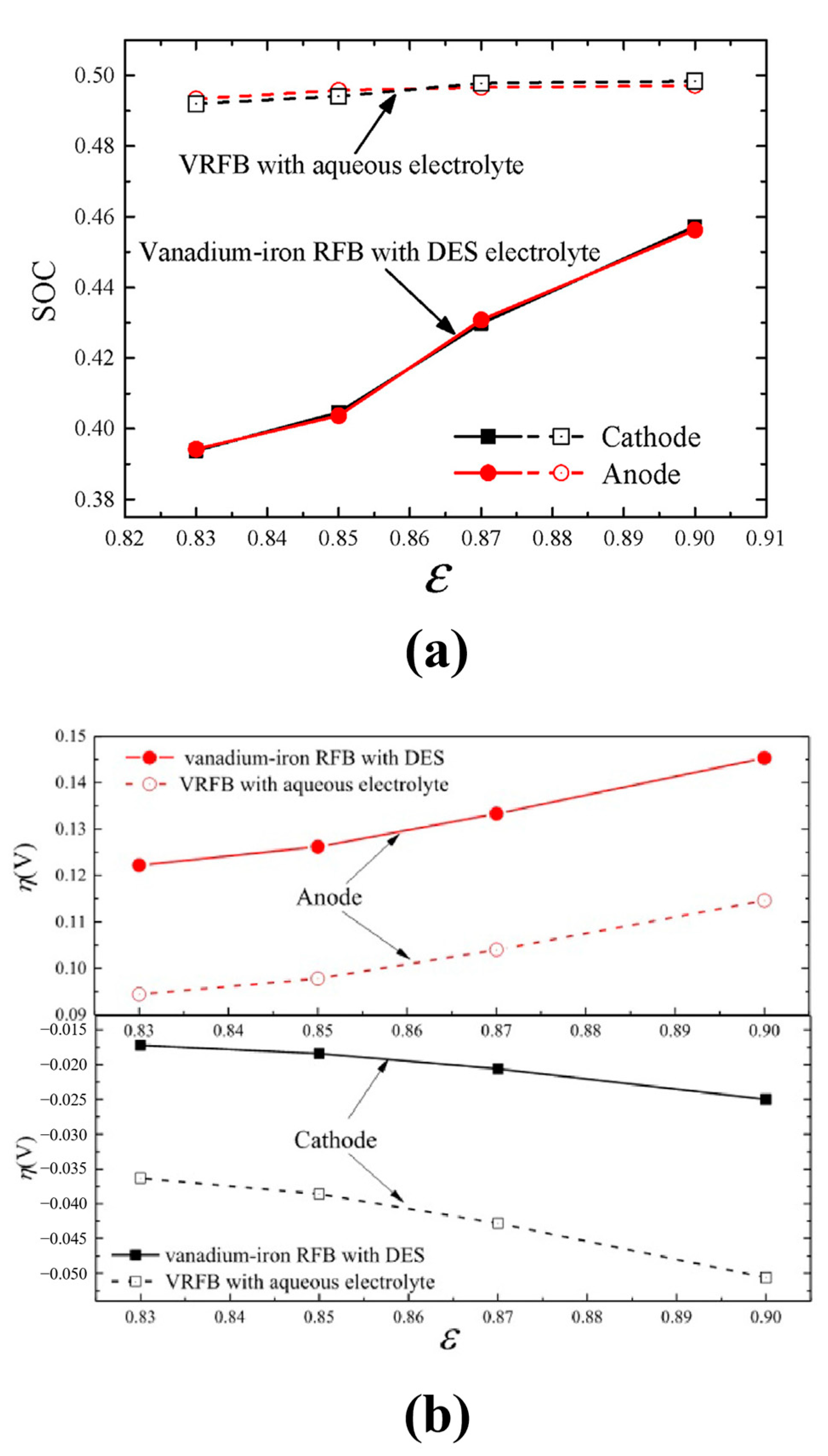
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Zhang, R.; Ma, Q.; Li, Z.; Su, H.; Lu, P.; Yang, W.; Xu, Q. Modeling and Simulation of Non-Aqueous Redox Flow Batteries: A Mini-Review. Batteries 2023, 9, 215. https://doi.org/10.3390/batteries9040215
Zhou H, Zhang R, Ma Q, Li Z, Su H, Lu P, Yang W, Xu Q. Modeling and Simulation of Non-Aqueous Redox Flow Batteries: A Mini-Review. Batteries. 2023; 9(4):215. https://doi.org/10.3390/batteries9040215
Chicago/Turabian StyleZhou, Haotian, Ruiping Zhang, Qiang Ma, Zhuo Li, Huaneng Su, Ping Lu, Weiwei Yang, and Qian Xu. 2023. "Modeling and Simulation of Non-Aqueous Redox Flow Batteries: A Mini-Review" Batteries 9, no. 4: 215. https://doi.org/10.3390/batteries9040215
APA StyleZhou, H., Zhang, R., Ma, Q., Li, Z., Su, H., Lu, P., Yang, W., & Xu, Q. (2023). Modeling and Simulation of Non-Aqueous Redox Flow Batteries: A Mini-Review. Batteries, 9(4), 215. https://doi.org/10.3390/batteries9040215