Abstract
Energy storage systems are key to propelling the current renewable energy revolution. Accurate State-of-Charge estimation of the lithium-ion battery energy storage systems is a critical task to ensure their reliable operations. Multiple advanced battery model-based SOC estimation algorithms have been developed to pursue this objective. Nevertheless, these battery model-based algorithms are sensitive to measurement noises since the measurement noises affect the accuracy of battery model identification, thus leading to inaccurate battery SOC estimation consequently due to modeling error. The Butterworth low-pass filter has proven effectiveness in measurement noise filtering for accurate parameter identification, while the cutoff frequency design relies on prior knowledge of lithium-ion batteries, making its capability limited to general cases. To overcome this issue, this paper proposes an adaptive cutoff frequency design algorithm for the Butterworth low-pass filter. Simulation results show that the low-pass filter functions properly in the presence of multiple scales of measurement noises adopting the proposed work. Consequently, the parameters of the battery model and the SOC of the battery are both identified and estimated accurately, respectively. In detail, the parameters: , , , and the time constant are all identified accurately with low relative identification errors of 0.028%, 11.12%, 6.21%, and 5.94%, respectively, in an extreme case. Furthermore, the SOC of the battery can thus be estimated accurately, leaving a low of 0.081%, 0.97%, and 0.14% in the mean and maximum absolute SOC estimation error and the standard deviation, respectively.
1. Introduction
Energy storage systems crucially contribute to the success of current energy revolutions from fossil fuels to clean energies, which aims at reducing greenhouse emissions [1]. Energy storage systems are developed in power grids to improve the reliability of utilizing renewable energies by mitigating their intermittency in energy generation. Also, energy storage systems are capable of storing surplus energy generation and fulfilling excess energy demand, thus optimizing operations in power grids. Energy storage systems are also adopted in electric vehicles serving as an alternate energy supply from fossil fuels. Among energy storage systems available on the market, lithium-ion battery storage systems are appealing due to their modular capability for various power and energy needs; meanwhile, they are known for swift power demand response, high energy density, and low degradation rate [2]. To safely and reliably employ lithium-ion battery energy storage systems in power grids and electric vehicles is a critical task for energy storage management systems, which depends on accurate real-time battery State-of-Charge (SOC) estimation.
Real-time battery SOC estimation algorithms are roughly categorized as (1) model-free algorithms, (2) data-driven algorithms, and (3) model-based algorithms [3]. The model-free SOC estimation algorithm, i.e., the Coulomb counting approach and the voltage-based approach, estimate the SOC of the battery using the direct measurements of the battery, i.e., current and voltage [4]. The light computation demands allow both algorithms to be applied in real-time estimation. However, their estimation accuracy relies on predetermined variables such as accurate initial SOC value, battery capacity, or the SOC to open-circuit voltage profile [5]. Data-driven algorithms, e.g., to name a few, fuzzy networks, neural networks, and machine learning algorithms, are also gaining attention in real-time estimation. These algorithms estimate the SOC of batteries using pre-trained models. The parameters of the pre-trained models are learned from the battery current and voltage data. However, a huge battery dataset is necessary to avoid biased parameter learning and the computation effort of training is proportional to the model complexity [6].
Model-based SOC estimation algorithms are also appealing in battery SOC estimations. The battery model, i.e., the battery electrochemical model and the battery electric circuit model, are developed based on the battery dynamics, meaning that the battery models are developed with physical meanings. SOC estimation algorithms using the electrochemical model are accurate since the battery dynamics are described in partial differential equations [7]. However, detailed battery modeling is computationally demanding, making their real-time estimation a concern. In comparison, model-based battery SOC estimation algorithms using the electric circuit model are appealing in real-time battery SOC estimation [8]. The battery electric circuit model formulates battery dynamics by constructing an electric circuit with multiple electric components. This linear model is known for its simplicity in equation formulation. The light computation effort allows it to be implemented for real-time battery SOC estimation thus ensuring reliable and safe lithium-ion battery energy storage operation. Along with the ease of implementation, this battery model renders decent battery SOC estimation accuracy, fulfilling most industrial requirements in SOC estimation accuracy [9]. The key to achieving the goal of accurate SOC estimation in various operating cases using the battery SOC estimation algorithms is to model the battery nonlinear dynamics. To do so, parameter identification approaches are adopted along with the SOC estimation algorithms to identify and update the highly nonlinear battery dynamics [10].
Popular parameter identification approaches include the sliding window least-square fitting method and the recursive least-square fitting method [11]. The sliding window least square fitting method outputs the best-fitted battery’s input-to-output relationship with the smallest sum of the squared residuals. To improve the computation efficiency, a sliding-moving window approach is adopted. In detail, the battery parameters are identified using a window of the latest battery data. The performance of this method, however, is limited in the presence of measurement noises [12]. Although increasing the sliding window size helps filter the measurement noises, the large window size can increase the computation complexity in matrix arithmetic, burdening the battery management system with low computation power. The recursive least square fitting method is another popular parameter identification approach. It recursively adapts its identification and minimizes the weighted linear least squares cost function. The performance of this method in general operating conditions relies on carefully selecting the forgetting factor, which increases the algorithm design complexity [13]. The robustness of both parameter identification approaches against measurement noises is an overlooked issue that is worth investigating [14,15].
Improving the capability of the sliding window least-square fitting method against the measurement noises is a key concern of in this paper. The sliding window least square fitting method identifies the battery parameters erroneously in the presence of measurement noises [16]. With the inaccurately identified battery model, the battery model-based SOC estimation algorithm renders inaccurate estimations. Popular measurement filtering algorithms suited to real-time estimation include the sliding average filter, the double sliding average filter, the sliding median filter, and the low-pass filter [17]. The sliding average filter and the sliding median filter smooth the battery data using the mean and median data from a window of battery data, respectively. These filters are effective in smoothing the data, so to achieve the goal of rejecting measurement noises [18]. The smoothing performance can further improve by cascading filters, e.g., double sliding average filter [19]. However, designing the proper window size to filter the measurement noise without affecting the battery dynamics for identification is an issue that requires careful design.
The low-pass filter is an alternative solution to reject measurement noises from battery data. It is designed in the frequency domain attempting to filter high-frequency compound measurement noises. Typical low-pass filters include the Butterworth filter, the Chebyshev I and II filter, the Elliptic filter, and other advanced filters [20]. Among these filters, the Butterworth low-pass filter is well-known for its ease in filter design and no extra ripples in both the passband and stopband. These features make it suit for measurement noise rejection in battery applications. The variables to design this filter are the filter order and the cutoff frequency. Low filter order is usually preferred due to the design simplicity [21]. The cutoff frequency is another key determinant of the filtering performance which requires careful design. The cutoff frequency of the Butterworth low-pass filter can be designed based on the cutoff frequency of the battery system [22]. However, the corner frequency of the battery system is unknown in most cases and can be falsely determined due to the presence of measurement noises, especially for complicated energy storage systems.
To overcome the research issue mentioned above, this paper proposes an adaptive cutoff frequency design. The proposed work made the following contributions.
- The proposed algorithm adapts the cutoff frequency of the Butterworth low-pass filter along with the lithium-ion battery operations thus ensures parameter identification accuracy in various operating conditions.
- The proposed algorithm provides an initial cutoff frequency value for the Butterworth low-pass filter through the cutoff frequency screening procedure, thus fastening the convergence of the cutoff frequency adaption.
- The algorithm proposed in this paper effectively improves the parameter identification outcome in cases with commonly observed measurement noises. The reduced modeling error helps ensure SOC estimation accuracy using model-based algorithms.
The organization of this paper is structured as follows. Section 2 formulates the cutoff frequency issue in this paper. Section 3 proposes an adaptive cutoff frequency design algorithm. The design procedure is explained and summarized. Section 4 examines the performance of the proposed algorithm in various scales of measurement noises. The proposed work is finally concluded in Section 5.
2. Problem Formulation
This Section formulates the cutoff frequency issue of interest. To help formulate the problem, the electric circuit model commonly adopted to model the lithium-ion battery is first formulated. With the transfer function of the battery electric circuit model, the least square regression method is then introduced. The least square regression model is a practical method for parameter identification. However, its parameter identification accuracy can be affected by measurement noises. To reject the measurement noise, the high-frequency compound, specifically the Butterworth low-pass filter, is discussed and its problem determining the cutoff frequency is pinpointed and thoroughly explained.
2.1. Battery Electric Circuit Model
The battery electric circuit model is widely adopted to describe the dynamics of the terminal voltage of the battery in response to the load current injected into the lithium-ion battery, as shown in Figure 1. This model with one RC pair is popular for real-time battery state estimation due to its simplicity and decent modeling accuracy [23,24,25,26]. With the help of the simple model structure, the computation efforts for parameter identification and state observer are greatly reduced, making it preferred for battery management systems performing real-time battery state estimations. To be specific, the battery electric circuit model describes the terminal voltage of the battery as a summation of the open-circuit voltage of the battery , the voltage Ohmic drop/rise , and the exponential voltage dynamic . The terminal voltage formulation can be written as the following equation.
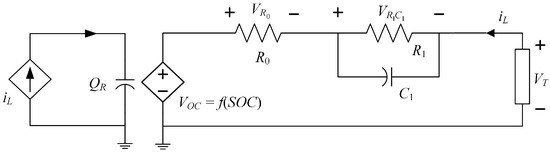
Figure 1.
Battery electric circuit model.
The open-circuit voltage is a nonlinear function with respect to the battery SOC. In order to formulate the nonlinear relationship using a linear battery electric circuit model, a piecewise linearization is adopted using the Taylor series with high-order terms ignored [10].
where and are the intercept and the slope of the ith piecewise linear function.
The voltage Ohmic drop/rise describes the immediate voltage drop/rise in response to the load current change. The voltage drop or rise is determined by the direction of the load current. In the electric circuit model, this formulates the voltage across the internal resistance .
and the exponential voltage dynamic describes the long-term exponential dynamic after the immediate voltage drop/rise. This formulates the voltage across the − pair.
Derived from Equations (1) to (4), the dynamics of the in response to the can be formulated as a second-order transfer function.
where Q is the battery capacity and , , and are variables constructing the electric circuit model, as depicted in Figure 1, and they are variables to be identified. It is worth noting that the multiplication of and is the same as the time constant of the exponential voltage dynamic , as the dynamic described using the - pair.
It is worth noting that the above-mentioned load current to terminal voltage dynamic, as written in Equation (5), is derived in the continuous-time domain (s-domain). Considering that the load current and the terminal voltage of the battery are sampled at a given sampling rate , Equation (5) has to be discretized in practice for parameter identification. The discretization can be achieved using the bilinear transformation. The identified discrete transfer function has to convert back into the continuous t-domain to complete the parameter identification and acquire the variables in the battery circuit model.
2.2. Least Square Regression Method
Least square regression method is an effective approach adopted to fit the input-to-output relationship of the battery model, i.e., the relationship between the load current and the terminal voltage of the lithium-ion battery. The best input-to-output relationship fitting is defined with the lowest sum of the squared residuals. To improve the least square regression method with the real-time calculation feature, only a moving window lengthening l containing the latest data is used in fitting.
To identify the input-to-output relationship of the battery circuit model, the terminal voltage at the k time stamp can be formulated as a summation of a window of previous terminal voltage values from the to the time stamp and the load current values in the window from the to the k time stamp.
Formulating the terminal voltage and the load current as a regression matrix and their coefficients and as a coefficient matrix , the Equation (6) can be rewritten as:
where the coefficient matrix is the coefficients of the battery model in identification. After a window of regression matrix is collected, the least square solution of Equation (7) can be calculated using the least square regression method written in Equation (8):
2.3. Luenberger SOC Observer
Luenberger SOC observer is a typical state observer which estimates the states of the battery based on the measured current and voltage . The Luenberger SOC observer can be formulated in Equation (9).
where L is the observer gain and x represents the states of the battery: [, ]. To estimate the SOC of the battery, one of the states: has to be mapped to SOC using the predetermined SOC- profile as explained in Equation (2).
The A, B, C, and D matrices are the state, input, output, and feedforward matrix, respectively. Considering that the lithium-ion battery is a nonlinear system but the Luenberger SOC observer is a linear observer, the observer A, B, C, and D matrices have to be continuously updated. The A, B, C, and D matrices are formulated as follows and the variables in these matrices are identified using the least square regression method which had been introduced.
3. Adaptive Butterworth Low-Pass Filter Design
This Section proposes an adaptive cutoff frequency design algorithm for the Butterworth low-pass filter. The objective of this algorithm is to determine the cutoff frequency of the Butterworth low-pass filter using “noisy” load current and terminal voltage data with measurement noises that existed. This proposed algorithm contains two critical phases: firstly, to determine the initial cutoff frequency without the prior knowledge of the time constant of the lithium-ion battery; secondly, to adapt the cutoff frequency of the Butterworth low-pass filter along with the operation of the battery.
3.1. Butterworth Low-Pass Filter
Butterworth low-pass filter is famous for its flat filtering performance in both the passband and the stopband with no ripples. The Butterworth low-pass filter also appeals to real implementation due to its simplicity in filter design. In detail, two variables related to the Butterworth low-pass filter that is to be determined, i.e., filter order and cutoff frequency . Other variables related to the typical low-pass filters do not have to be designed, e.g., transition band, passband and stopband frequency, passband ripple, and stopband attenuation. With these features, the Butterworth low-pass filter is ideal to reject the measurement noises of the lithium-ion battery for accurate parameter identification.
The frequency response of the nth Butterworth low-pass filter is formulated as follows.
where n, f, and are the order, the operating frequency, and the cutoff frequency of the Butterworth low-pass filter, respectively, and and are the input and the output data of the Butterworth filter, respectively. The low-pass filter with higher order has a smaller transition band and thus has better filtering performance; however, it will increase the difficulty in hardware implementation. Considering the potential of implementation, a second-order Butterworth low-pass filter is selected in this paper.
The cutoff frequency of the Butterworth low-pass filter is critical to parameter identification by rejecting the high-frequency measurement noises and avoiding inaccurate pair identification [22]. To achieve this objective, the cutoff frequency was suggested to be set greater than half of the time constant of the lithium-ion battery, i.e., the time constant of the exponential voltage dynamic as described as the voltage across the - pair in the battery electric circuit model.
where and are the angular cutoff frequency of the Butterworth low-pass filter and the battery, respectively and is the corner frequency of the lithium-ion battery:
Though the cutoff frequency of the Butterworth low-pass filter can be properly defined based on the time constant of a specific battery, the time constant of this battery is unknown and hard to be determined due to the existence of the measurement noise; therefore, determining a proper cutoff frequency of the filter is the research focus of this paper.
3.2. Initial Cutoff Frequency Screening
A proper cutoff frequency design is critical to the success of the measurement noise rejection. The design setting the cutoff frequency of the filter based on the time constant of the battery can effectively prevent one of the poles in the transfer function: from being wrongly identified. However, the time constant of the lithium-ion battery is unknown in the Butterworth low-pass filter design process. Also, the existence of high-frequency measurement noise can affect the filter design. To overcome this issue, an adaptive cutoff frequency design algorithm is proposed to filter the measurement noises.
The first phase of designing the cut-off frequency of the Butterworth low-pass filter is to determine the initial cutoff frequency . In detail, a fixed window size (from to k) of load current and terminal voltage is used. It is noted that this set of data contains measurement noises since they are measured by sensors. The next step is to filter this set of data by adopting the Butterworth low-pass filter with cutoff frequency screening. After the filtering, the filtered data and is then used to identify the coefficients of the transfer function of the battery electric circuit model, and the fitting performance is analyzed by comparing their mean square error .
where l is the number of the data samples used in the least square regression method, is the measured terminal voltage containing measurement noise in the time stamps ranging from to k, and is the fitted terminal voltage data in the same time window.
To determine the proper initial cutoff frequency for the Butterworth low-pass filter, the mean square error after cutoff frequency screening is compared and the Elbow point is pinpointed. The small cutoff frequency used may filter the battery system dynamics, leaving distorted signals dominated by low frequencies, e.g., DC bias. As a result, the mean square error of the least square method increases. In contrast, the large cutoff frequency used cannot effectively filter the high-frequency measurement noises, resulting in a small mean square error of the least square method but the identification is wrong. Therefore, the Elbow point is an approach to determining the proper initial cutoff frequency for the Butterworth low-pass filter. The Elbow point can be found by calculating the sum of the squared Euclidean distances L to the centroid , as formulated following.
3.3. Adaptive Cutoff Frequency Method
The next phase of the proposed design is to adapt the cutoff frequency along with the battery operation. The cutoff frequency of the Butterworth low-pass filter starts from the initial cutoff frequency determined in phase I. Then the cutoff frequency of the filter is adapted every iteration, and the amount of the adaptation is calculated based on the variation of the latest time constant of the lithium-ion battery identified using the least square regression method. This adaptive cutoff frequency method is designed following Equation (12). This equation explains that the cutoff frequency is closely related to the time constant of the lithium-ion battery; therefore, following this equation, the cut-off frequency of the Butterworth low-pass filter adapts based on the identified time constant of the lithium-ion battery.
where is the correction gain set to adapt the angular cutoff frequency of the Butterworth low-pass filter and is the adaptation factor in the angular cutoff frequency . This adaptation factor is calculated based on the variation in the identified time constant of the lithium-ion battery, as shown in the following equation.
To prevent the adaption from being dominated by the outliers of the identification, the mean of the previous identification in the time constant of the battery is used to calculate the adaptation factor in the angular cutoff frequency .
It is worth noting that the adaptive cutoff frequency method is designed considering the time constant of the battery remains almost constant with respect to the SOC of the battery and the time constant changes slightly as the operating condition changes [27]. Therefore, the adaptive cutoff frequency method can be designed based on the variation in the time constant of the battery. Table 1 summarizes the detailed step-by-step procedure of the proposed algorithm, and the block diagram illustrating the procedure of the proposed algorithm is shown in Figure 2.

Table 1.
Step-by-step procedure of the proposed adaptive cutoff frequency design algorithm for the Butterworth low-pass filter.
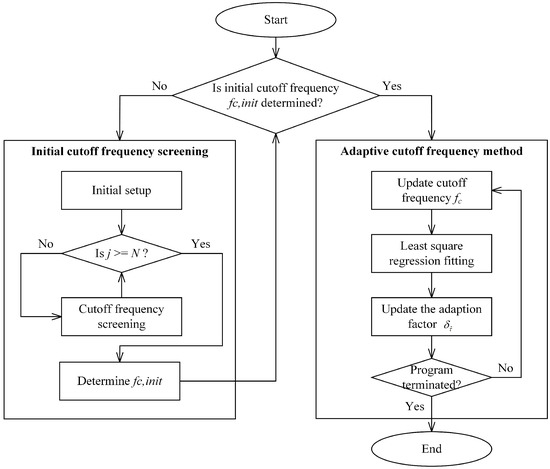
Figure 2.
Block diagram of the proposed adaptive cutoff frequency design for Butterworth low-pass filter.
4. Simulation Result
This section explains the design procedure of the proposed algorithm step-by-step, providing an in-depth insight into the algorithm. To showcase the performance of the cutoff frequency adaptation performance, a case is also studied given a randomly assigned initial cutoff frequency. This section also validates the performance of the proposed algorithm in various operating conditions with different measurement noise presences.
4.1. Simulation Environment
A set of lithium-ion battery simulations are performed to evaluate the performance of the proposed adaptive cutoff frequency design algorithm for the Butterworth low-pass filter. To showcase the performance of the proposed work in improving the parameter identification accuracy, the simulation is performed using MATLAB 2021b and the reference values of the parameters are predefined considering the actual lithium-ion battery dynamics [28,29,30]. The simulation cycles the lithium-ion battery using the urban dynamometer driving schedule (UDDS) profile. This profile is a standard testing protocol simulating real-world battery operations in electric vehicles. To showcase the performance of the proposed algorithm in cases of various measurement noises, the battery load current and terminal voltage data are injected with different measurement noises leveling from 0.1% F.S. measurement noise up to 0.5% F.S. measurement noise. The 0.1% F.S. measurement noise and 0.2% F.S. measurement noise are the typical scales of measurement noises as limited by the sensor hardware setup. To investigate the performance of the proposed work, the scales of measurement noises are increased to an extreme of 0.5% F.S. measurement noise. It is noted that the white Gaussian measurement noise is selected as the measurement noise investigated in this work. The white Gaussian noise is a normally distributed noise with uniform power across the frequency band, making it suitable for simulating the random noise measured in actual operating conditions.
4.2. Performance of the Proposed Algorithm in Parameter Identification
The proposed algorithm adapts the cutoff frequency of the Butterworth low-pass filter aiming at rejecting the high-frequency measurement noises. The first phase of the proposed algorithm is to search for a proper initial cutoff frequency through a screening approach. As illustrated in Figure 3, the mean square error of the least square regression method is compared and the initial cutoff frequency is determined by finding the Elbow point. If a large cutoff frequency is assigned, the fitting may be inaccurate due to the existence of the measurement noises. The fitting error can be reduced by decreasing the value of the assigned cutoff frequency. Although assigning a very small cutoff frequency can help acquire better-fitting results, some of the battery dynamics may be lost; the result will be poorer parameter identifications and SOC estimations. To avoid this issue and determine a proper initial cutoff frequency for adaption, the Elbow point is adopted as pinpointed in Figure 3.
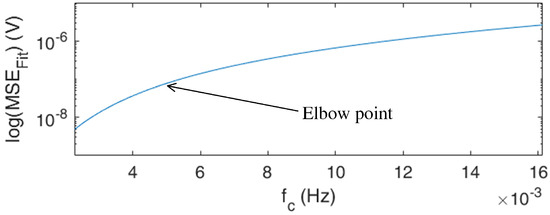
Figure 3.
Phase I: Determine the initial cutoff frequency through cutoff frequency screening.
The second phase of the proposed algorithm adapts the cutoff frequency of the Butterworth low-pass filter as the battery is operated, as shown in Figure 4. The cutoff frequency is adapted based on the time constant identified using the least square regression method. The identification of the time constant can be easily affected by the high-frequency measurement noises. In other words, if the cutoff frequency is not assigned properly, the high-frequency measurement noises are not filtered well, resulting in inaccurate time constant identification. Therefore, the cutoff frequency adapts based on the time constant identification. It is worth noting that the adaptation starts from the initial cutoff frequency determined in phase I; however, adaptation still functions well if the initial cutoff frequency is given improperly. As illustrated in Figure 5, the cutoff frequency is deliberately assigned with a high initial cutoff frequency value, which renders poor parameter identification results. The cutoff frequency adapts and finally converges to the best-suited cutoff frequency.
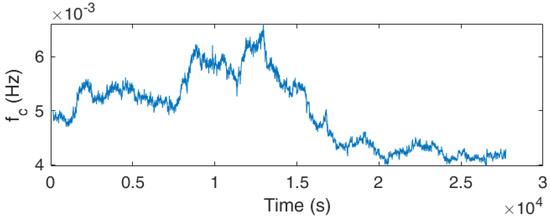
Figure 4.
Phase II: Adapt the cutoff frequency with an initial cutoff frequency given.
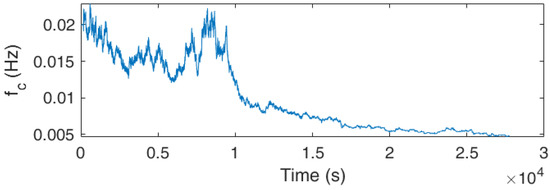
Figure 5.
Adapt the cutoff frequency in the case giving an improper value.
To examine the performance of the algorithm proposed, the parameter identification results are analyzed, and the identification result is compared by adopting cutoff frequency using different cutoff frequencies, as illustrated in Figure 6. The black line is the reference value, the blue line is the parameter identification result without adopting the Butterworth low-pass filter, and the red and orange lines are the results adopting the cutoff frequency 0.02 Hz and 0.04 Hz, respectively. In comparison, the result acquired from the proposed work is shown in purple. In the presence of measurement noises, the parameters are identified erroneously without adopting the filter, leaving only the internal resistance identified okay. This result shows that the least square regression method will erroneously identify the battery dynamics, i.e., the poles of the transfer function. With the help of the Butterworth low-pass filter, the parameters of the battery model can be identified accurately. The identification accuracy is improved as the cutoff frequency is set smaller. The comparison indicates that the parameters are identified as most accurately adopting the proposed algorithm.
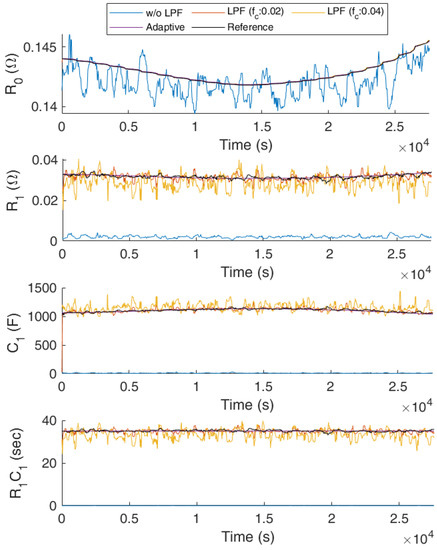
Figure 6.
Parameter identification result comparison.
The detailed parameter identification performance using multiple cutoff frequency design is further investigated in cases of various scales of measurement noises injected, as summarized in Table 2. The four sub-tables listed in Table 2 compare the relative identification error of , , , and time constant to their reference values, respectively. The result shows that without the help of the Butterworth low-pass filter, the parameters of the battery model are identified inaccurately, especially the dynamics. In detail, the battery is identified as a pure resistance when the measurement noise exists, and as a result, the dynamics cannot be identified accurately. This is because of the nature of the least square regression method.

Table 2.
Parameter identification performance comparison in cases of various scales of measurement noises using multiple cutoff frequency design.
Adopting the Butterworth low-pass filter, the parameter identification accuracy is significantly improved. It is noted that the parameter identification accuracy reduces as the scale of the injected measurement error increases. It is also noted that if the selected cutoff frequency is low, the high-frequency compound measurement noises are filtered well, resulting in more accurate parameter identification using the least square regression method, especially in the dynamic. However, selecting low cutoff frequencies does not guarantee better parameter identification. Selecting a small cutoff frequency, i.e., 0.005 Hz cutoff frequency, the identification error is slightly higher than other cutoff frequencies although the rest of the parameters are identified more accurately.
The results listed in Table 2 demonstrate that the parameters are identified more accurately compared to the case with a medium cutoff frequency. Similar results are acquired in cases of various scales of measurement noises injected. In detail, the relative identification error in the , , , and the time constant are 0.028%, 4.16%, 2.73%, and 2.27%, respectively, when 0.1% of full-scale (F.S.) measurement noise is presented, and the relative identification error increases to 0.028%, 11.12%, 6.21%, and 5.94%, respectively, when an extreme of 0.5% of full-scale (F.S.) measurement noise exists. The results well-demonstrate that the proposed work adapts the cutoff frequency of the Butterworth low-pass filter, rendering accurate parameter identification results in various scales of measurement noise presence.
4.3. Performance of the Proposed Algorithm in SOC Estimation
The performance of the proposed work is evaluated one step further in the sense of SOC estimation accuracy. This is because the accuracy of the battery SOC estimation highly relies on accurately identified battery parameters. The battery SOC estimation performance comparison using multiple cutoff frequency design in cases of various scale measurement noises is summarized in Table 3. The typical Luenberger SOC observer is selected in battery SOC estimation due to its simplicity for algorithm validation. The results demonstrate the estimation inaccuracy has a strong relationship with the existence of the measurement noises, leaving about 1.35% mean absolute SOC estimation error in different scales of measurement noises. Although the mean absolute error seems promising, the maximum absolute SOC estimation error is a high of 14.47%, and the standard deviation is close to 1.85%, meaning that the SOC estimation is inaccurate and deviated.

Table 3.
SOC estimation performance comparison in cases of various scale measurement noises using multiple cutoff frequency design.
With the help of the Butterworth low-pass filter in high-frequency measurement noise filtering, the SOC estimation error is reduced and converged. In detail, the mean absolute SOC estimation error is roughly 0.12% if the cutoff frequency is selected carefully, the maximum absolute SOC estimation error is less than 2.51%, and the standard deviation is about 0.22%, meaning the SOC estimation accuracy is significantly improved due to the adoption of the low-pass filter. In comparison, the proposed work renders the best battery SOC estimation performance. The result is acquired since the parameters are identified more accurately in adopting the proposed work, leaving a smaller modeling error. The result shows that the proposed work renders a mean absolute SOC estimation error less than 0.081% in an extreme case of 0.5% full-scale measurement noises existed. In this case, the proposed work renders a 0.97% maximum absolute SOC estimation error with a 0.14% standard deviation. The SOC estimation result demonstrates the effectiveness of the proposed work in filtering measurement noises.
5. Conclusions
Measurement noises on the battery data are a critical but usually overlooked issue that needs to be solved. The measurement noises affect the estimation accuracy of electric circuit model-based SOC estimation algorithms. Specifically, the presence of the measurement noises results in battery modeling errors in inaccurate identifications of the battery parameters. The modeling errors lead to inaccurate battery SOC estimation using model-based estimation algorithms. To overcome this issue, this paper proposes an adaptive cutoff frequency design algorithm. The proposed algorithm first applies a cutoff frequency screening procedure to determine the initial cutoff frequency for the Butterworth low-pass filter. The proposed algorithm then adapts the cutoff frequency along with the battery operations based on the initial value which had been determined.
The performance of the proposed work is examined through simulation results using a standard testing protocol. The results demonstrate that the low-pass filter functions properly due to the adaption of the cutoff frequency. The least square regression method renders a relative error of 0.028%, 11.12%, 6.21%, and 5.94% in the , , , and the time constant identifications, respectively, in an extreme case. The low modeling error then helps the battery SOC estimation accuracy, rendering a 0.081% mean absolute SOC estimation error, a 0.97% maximum absolute estimation error, and a 0.14% standard deviation, which has significantly improved the SOC estimation accuracy compared with other cases studied.
Funding
This work was funded by the National Science and Technology Council under Grant MOST-111-2222-E-027-004-MY2. And the APC was funded by MOST-111-2222-E-027-004-MY2.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, L.; Lian, G.; Hu, S. Research on a real-time control strategy of battery energy storage system based on filtering algorithm and battery state of charge. Sustain. Energy Technol. Assess. 2021, 47, 101524. [Google Scholar] [CrossRef]
- da Silva Lima, L.; Quartier, M.; Buchmayr, A.; Sanjuan-Delmás, D.; Laget, H.; Corbisier, D.; Mertens, J.; Dewulf, J. Life cycle assessment of lithium-ion batteries and vanadium redox flow batteries-based renewable energy storage systems. Sustain. Energy Technol. Assess. 2021, 46, 101286. [Google Scholar] [CrossRef]
- Sarrafan, K.; Muttaqi, K.M.; Sutanto, D. Real-time estimation of model parameters and state-of-charge of li-ion batteries in electric vehicles using a new mixed estimation model. IEEE Trans. Ind. Appl. 2020, 56, 5417–5428. [Google Scholar] [CrossRef]
- Mohammadi, F. Lithium-ion battery State-of-Charge estimation based on an improved Coulomb-Counting algorithm and uncertainty evaluation. J. Energy Storage 2022, 48, 104061. [Google Scholar] [CrossRef]
- Haus, B.; Mercorelli, P. Polynomial augmented extended Kalman filter to estimate the state of charge of lithium-Ion batteries. IEEE Trans. Veh. Technol. 2020, 69, 1452–1463. [Google Scholar] [CrossRef]
- Liu, Y.; He, Y.; Bian, H.; Guo, W.; Zhang, X. A review of lithium-ion battery state of charge estimation based on deep learning: Directions for improvement and future trends. J. Energy Storage 2022, 52, 104664. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, K.; Zhu, C.; Zhang, X.; Zhang, D. Co-estimation of state-of-charge and state-of-health for lithium-ion batteries using an enhanced electrochemical model. IEEE Trans. Ind. Electron. 2022, 69, 2684–2696. [Google Scholar] [CrossRef]
- Kwak, M.; Lkhagvasuren, B.; Park, J.; You, J.H. Parameter identification and SOC estimation of a battery under the hysteresis effect. IEEE Trans. Ind. Electron. 2020, 67, 9758–9767. [Google Scholar] [CrossRef]
- Huang, C.S.; Chow, M.Y. Robust state-of-charge estimation for lithium-ion batteries over full SOC range. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 2, 305–313. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Baronti, F.; Chow, M.Y. Online adaptive parameter identification and state-of-charge coestimation for lithium-polymer battery cells. IEEE Trans. Ind. Electron. 2014, 61, 2053–2061. [Google Scholar] [CrossRef]
- Huang, C.S. An online condition-based parameter identification switching algorithm for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2022, 72, 1701–1709. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, D.; He, H.; Cao, W.; Dong, G. A noise-tolerant model parameterization method for lithium-ion battery management system. Appl. Energy 2020, 268, 114932. [Google Scholar] [CrossRef]
- Shi, J.; Guo, H.; Chen, D. Parameter identification method for lithium-ion batteries based on recursive least square with sliding window difference forgetting factor. J. Energy Storage 2021, 44, 103485. [Google Scholar] [CrossRef]
- Wei, Z.; He, H.; Pou, J.; Tsui, K.L.; Quan, Z.; Li, Y. Signal-disturbance interfacing elimination for unbiased model parameter identification of lithium-ion battery. IEEE Trans. Ind. Inform. 2021, 17, 5887–5897. [Google Scholar] [CrossRef]
- Du, X.; Meng, J.; Zhang, Y.; Huang, X.; Wang, S.; Liu, P.; Liu, T. An information appraisal procedure: Endows reliable online parameter identification to lithium-ion battery model. IEEE Trans. Ind. Electron. 2022, 69, 5889–5899. [Google Scholar] [CrossRef]
- Ouyang, Q.; Chen, J.; Zheng, J. State-of-charge observer design for batteries with online model parameter identification: A robust approach. IEEE Trans. Power Electron. 2020, 35, 5820–5831. [Google Scholar] [CrossRef]
- Syed, M.A.; Khalid, M. Moving regression filtering with battery state of charge feedback control for solar PV firming and ramp rate curtailment. IEEE Access 2021, 9, 13198–13211. [Google Scholar] [CrossRef]
- Wu, X.; Li, S.; Gan, S.; Hou, C. An adaptive energy optimization method of hybrid battery-supercapacitor storage system for uncertain demand. Energies 2022, 15, 1765. [Google Scholar] [CrossRef]
- Pranith, S.; Kumar, S.; Singh, B.; Bhatti, T.S. MAF-DCGI based single-phase uninterrupted PV-battery system under unintentional islanding. IEEE Trans. Energy Convers. 2022, 37, 36–49. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Xie, S.; Feng, X.; Qin, H.; Zhao, C. Current harmonic suppression for permanent-magnet synchronous motor based on notch filter and LADRC. IEEE Trans. Magn. 2022, 8, 175–182. [Google Scholar] [CrossRef]
- Gao, J.T.; Shih, C.H.; Lee, C.W.; Lo, K.Y. An active and reactive power controller for battery energy storage system in microgrids. IEEE Access 2022, 10, 10490–10499. [Google Scholar] [CrossRef]
- Huang, C.S.; Chow, T.W.S.; Chow, M.Y. Li-ion battery parameter identification with low pass filter for measurement noise rejection. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 2075–2080. [Google Scholar]
- Liu, Y.; Huang, Z.; Wu, Y.; Yan, L.; Jiang, F.; Peng, J. An online hybrid estimation method for core temperature of Lithium-ion battery with model noise compensation. Appl. Energy 2022, 327, 120037. [Google Scholar] [CrossRef]
- Xie, Y.; Li, W.; Hu, X.; Tran, M.K.; Panchal, S.; Fowler, M.; Liu, K. Co-estimation of SOC and three-dimensional SOT for lithium-ion batteries based on distributed spatial-temporal online correction. IEEE Trans. Ind. Electron. 2022, 70, 5937–5948. [Google Scholar] [CrossRef]
- Wei, Z.; Dong, G.; Zhang, X.; Pou, J.; Quan, Z.; He, H. Noise-immune model identification and state-of-charge estimation for lithium-ion battery using bilinear parameterization. IEEE Trans. Ind. Electron. 2021, 68, 312–323. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Lund, P.D.; Zhang, Y. Co-estimating the state of charge and health of lithium batteries through combining a minimalist electrochemical model and an equivalent circuit model. Energy 2022, 240, 122815. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Xiong, R.; Dong, G.; Pou, J.; Tseng, K.J. Online estimation of power capacity with noise effect attenuation for lithium-ion battery. IEEE Trans. Ind. Electron. 2019, 66, 5724–5735. [Google Scholar] [CrossRef]
- Bao, Y.; Dong, W.; Wang, D. Online internal resistance measurement application in lithium ion battery capacity and state of charge estimation. Energies 2018, 11, 1073. [Google Scholar] [CrossRef]
- Wu, X.; Li, X.; Du, J. State of charge estimation of lithium-ion batteries over wide temperature range using unscented Kalman filter. IEEE Access 2018, 6, 41993–42003. [Google Scholar] [CrossRef]
- Du, J.; Chen, Z.; Li, F. Multi-objective optimization discharge method for heating lithium-ion battery at Low temperatures. IEEE Access 2018, 6, 44036–44049. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).