Abstract
Fast charging is a key requirement for customer acceptance of battery electric vehicles. Fast charging of lithium-ion batteries is limited by lithium plating, an undesired side reaction that leads to rapid degradation and poses a potential safety hazard. In order to approach but not exceed the lithium plating current limit during fast charging, a variety of analytical tools have been developed to detect lithium plating. In this publication, we propose a new impedance-based method for the time-resolved detection of lithium plating. The proposed method was demonstrated with an integrated cell monitoring circuit capable of measuring the impedance during cell operation, bringing the feasibility of implementation in an automotive target application within reach. Importantly, the proposed method eliminates the temperature dependence which is an intrinsic problem for impedance-based lithium plating detection in automotive lithium-ion cells, thus making on-board plating detection feasible.
1. Introduction
In 2021, weather extremes such as the North American heat wave and unprecedented wildfires in the Mediterranean stressed the urgency to fight global warming. In this endeavor, the decarbonization of the transport sector is of high importance as passenger road vehicles alone were responsible for about 10% of anthropogenic CO2 emissions in 2018 (3.6 out of 36 Gt) [1,2]. Battery electric vehicles (BEVs) are a potential solution as their life-time greenhouse gas emissions are—already in 2021—significantly lower than those of comparable combustion-engine-powered vehicles and their advantage is expected to further increase during the next decades [3]. A key feature to achieve widespread customer acceptance and alleviate “range anxiety” is the fast charge capability of BEVs.
In general, the fast charge capability of a BEV is limited by the lithium-ion battery cell. On cell level, the rate-determining step for fast charging is the plating of metallic lithium on the graphite negative electrode. This undesired side reaction is caused by lithium-ion mass transport limitation in the liquid electrolyte and can cause rapid cell degradation and also poses a potential safety thread due to internal short-circuiting [4,5]. Therefore, lithium plating has been intensively studied in the literature and a variety of lithium plating detection methods have been developed over the last years. There are several excellent reviews on this topic, so we only briefly discuss the most common lithium plating detection techniques, namely (i) analysis of open-circuit voltage (OCV) relaxation or cell impedance relaxation directly after fast charging [4,6,7,8,9,10,11,12,13,14], (ii) high-precision coulombic efficiency (CE) determination [15,16,17,18], (iii) differential charging voltage analysis (DCV) during fast charging [18,19], (iv) measurement of cell expansion via dilatometry [20,21,22,23,24,25], and (v) advanced tomographic and spectroscopic techniques [7,26,27,28,29,30].
These methods have different advantages and can be very useful for the development of fast-charging profiles and benchmarking of the fast-charge capabilities of lithium-ion cells under laboratory conditions. In a recent publication [19], we showed how a combination of several of these methods allows for the rapid assessment of fast-charging profiles for automotive lithium-ion cells, enabling a reduction in test time from months to days. Unfortunately, most of these methods are not suitable for time-resolved detection of lithium plating for on-board vehicle applications for several reasons: lithium plating detection is only possible in retrospect after completing the charging process (relaxation-based techniques, (i) or even the entire charge–discharge-cycle (coulombic efficiency, (ii) and they are not suitable if there is a lack of special test equipment (cell dilatometry and tomography/spectroscopy, (iv) and (v). In theory, DCV (iii) can be used for time-resolved lithium plating detection, but unfortunately, this method only works reliably for simple constant-current charging and fails for realistic fast-charging profiles (high initial C-rate, then stepwise or continuous reduction) as demonstrated in our abovementioned study [19].
An interesting approach for the time-resolved detection of lithium plating via online analysis of cell impedance was recently published by Koleti et al. [31] and Koseoglou et al. [32] and was adapted for pulse-resistance measurements by Dotoli et al. [33,34]. These approaches make use of a reduction of the charge transfer resistance caused by lithium plating in comparison to the expected resistance value in the absence of lithium plating. For a given cell, the charge transfer resistance depends on cell temperature and state of charge (SOC). The temperature dependence of the charge transfer resistance is dominating, making it even possible to derive the cell’s internal temperature via impedance measurement [35]. For the approach of Koleti et al. and Koseoglou et al., this strong temperature dependence is a challenge because knowledge of the cell’s internal temperature is necessary for the interpretation of the measured charge transfer resistance; this is especially problematic during fast charging of large prismatic cells which can exhibit a strong spatial as well as temporal temperature gradient. In another approach, Brown et al. [36] performed electrochemical impedance spectroscopy sweeps during fast charging and compared the evolution of charge transfer and solid electrolyte interphase (SEI) resistance after fitting to normal charging cycles. In this approach, the excitation current is up to 15% of the charging current which is about 40 times higher than the excitation currents used in our approach.
In this publication, which further illuminates the scientific basis of the patent application [37], we suggest a novel impedance-based approach for time-resolved lithium plating detection which exploits the different temperature dependencies of real and imaginary parts of the impedance under plating conditions. This property is a fundamental requirement to be able to eliminate the temperature dependence as an input variable later in the development of the algorithm. As the results were obtained with an impedance measurement circuit that could be implemented in a real-world application, we believe that this novel method might be robust enough for on-board vehicle application.
2. Methods/Experimental
For this study, prismatic hard-case automotive lithium-ion cells from a commercial cell supplier with a cell capacity > 50 Ah, containing an NMC622 cathode and a graphite anode, were used. The cells were mechanically constrained in between metallic pressure plates and the pressure was sensed with a force measurement gauge (K-450, Lorenz Messtechnik, Germany). A more detailed drawing of the setup is given in [18]. Active cooling through a bottom plate was used during fast charging to limit the temperature increase. Each cell was equipped with two external PT-100 temperature sensors, one placed at the center of the front side and one close to the positive terminal. Electrochemical tests were carried out with a battery test system (Basytec HPS, Asselfingen, Germany), and the temperature, volt, age and current were recorded with the test system as well. One battery cell was equipped with a single-cell supervisory circuit and an engineering sample integrated circuit from Infineon (Infineon, Munich, Germany) which facilitates impedance measurement [38]. This setup enabled extremely short wiring with four terminal contacts and thus high-quality impedance measurements up to 8 kHz. Control and recording of the impedance data from the impedance measurement board were performed by a Matlab-GUI program also supplied by Infineon. Data from three different sources (a force measurement gauge, a battery test system, and an impedance measurement board) were merged and evaluated after the test with a program written in Python.
The cells were subjected to various fast-charging profiles of different charging times and profile shapes, namely (i) simple constant current–constant-voltage charging (CCCV), (ii) multi-step constant current profiles (MSCC) in which the current is reduced stairway-like, and (iii) a single constant current–constant anode potential (CCCA) profile in which the current is reduced continuously (see Figure 1).
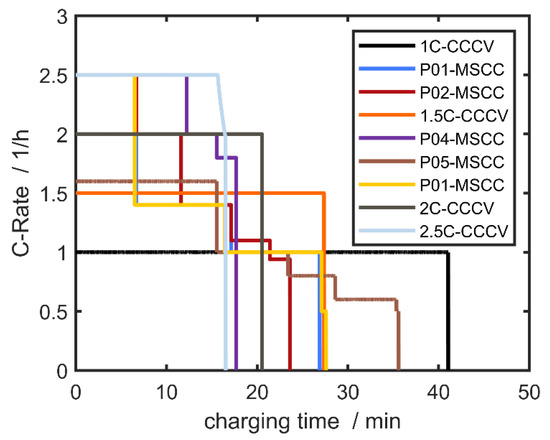
Figure 1.
Overview of the various fast-charging profiles applied in this study: simple constant current–constant voltage charging (CCCV) and multi-step constant current charging (MSCC).
A variety of well-known detection methods (e.g., Coulombic efficiency and swelling force analysis) were used to determine whether lithium plating occurred. These results are discussed in detail in our previous study [17]. Table 1 below summarizes the profile names, types, charging times (for 10 to 80% SOC at a 25 °C start temperature), and whether lithium plating occurred.

Table 1.
Overview of applied fast-charging profiles; charging time for 10 to 80% SOC at a 25 °C initial temperature; lithium plating detection based on several test methods. For details on lithium plating detection, see [19].
The same cell monitoring circuit from Infineon as in [38] was used to measure impedance, which allows for use of the balancing resistor for excitation of the impedance measurement and direct processing of the time-domain voltage and currents measurement to yield the impedance. Compared to typical laboratory impedance measurement devices, the setup enabled extremely short wiring with four terminal contacts and thus high-quality impedance measurements up to 8 kHz and the used components would allow implementation in a target battery system. In contrast to laboratory measurement devices, only galvanostatic excitation with an offset current is possible. The excitation of the cell for impedance measurement was performed galvanostatically with a 500 mA amplitude by modulating the current through the balancing resistor and an integration time of 1 s. Impedance was measured while performing fast-charging cycles and during equilibration of temperature after fast charging at 14 single frequencies within a frequency range from 781 Hz to 8 kHz periodically every second, resulting in impedance data for each frequency with a period of 14 s. This frequency range was selected to minimize cross-sensitivities to current dynamics during driving and to exploit the maximum range of precision of the measurement device, which will be reduced for higher and lower frequencies.
3. Results
Figure 2a shows the current and voltage during a 1C-CCCV charging process as an example of moderate fast charging without lithium plating. Figure 2b shows the real and imaginary parts of the impedance measured with the single-cell supervisory circuit. Figure 2c shows the cell temperature (black line) as measured with the external temperature sensor attached to the cell front. In addition, cell temperatures derived from the cell impedance are also plotted. Temperature determination via cell impedance has been described in detail elsewhere [35,39]. In short, it is based on a simple look-up table for linear regression (see Supporting Material) with the input parameters SOC and real or imaginary parts of the impedance at a single frequency and cell temperature as the output. To increase the robustness of temperature determination one would usually use both the imaginary and real parts of cell impedance, but it is also possible to determine two independent temperatures TRe and TIm based on two individual look-up tables. As Figure 2c shows, TRe and TIm coincide very well, although TRe is more robust due to the stronger sensitivity of the real part on the temperature compared to the imaginary part at the frequency of 3125 Hz (compare the fluctuations of Re and Im in Figure 2b). When comparing TRe and TIm with Tmeas, one has to keep in mind that the former two correspond to a volumetric averaged cell internal temperature whereas the latter is measured externally at one single point. Initially, TRe and TIm are slightly higher than Tmeas because of the temperature gradient along the cell thickness. After 25 min, the decrease and subsequent increase in TRe and TIm compared to the externally measured cell temperature coincide with turning on and off the bottom cooling plate, which is controlled by the external cell temperature (Ton = 28 °C, Toff = 25 °C). In general, TRe and TIm agree within less than 1.5 K in a broad range of temperature and SOC and state of health (SOH) values. For SOH, regular re-calibration of the look-up tables is necessary during the battery (or vehicle’s) lifetime. This is achieved via impedance measurement when the conditions Tmeas < 29 °C and I < 1A are satisfied. Alternatively, a separate temperature sweep with the rest periods at defined temperatures could have been applied, allowing for a completely thermally equilibrated system. However, in the application, it is beneficial to use the existing temperature dynamics and accept a remaining temperature gradient from the inside of the cell to the cell temperature sensors. Thus, we followed this pragmatic approach for re-calibration of the look-up tables during low-power situations under modest temperatures. As we will be exploiting the difference in the model temperatures from the real and imaginary parts of the impedance, the deviation in the look-up table with respect to the remaining temperature gradient is further mitigated.
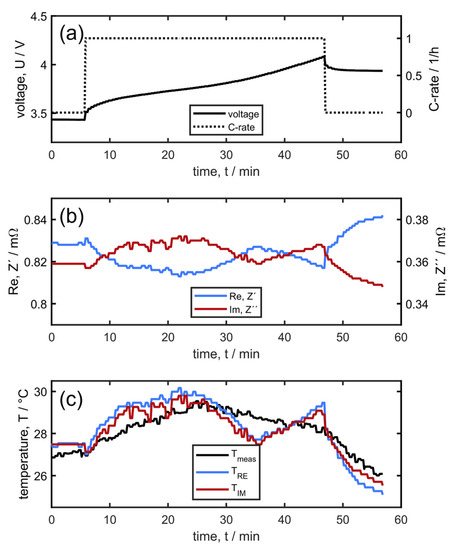
Figure 2.
Moderate fast charging with 1C at a 25 °C initial temperature without lithium plating, (a) cell potential and current, (b) real and imaginary cell impedance measured at 3125 Hz, and (c) cell temperatures measured with an external temperature sensor and derived from the cell impedance.
In addition to Figure 2, the impedance and temperature behavior during a 2.5C-CCCV charging process as an example of critical fast charging with the occurrence of lithium plating can be found in the Supporting Information.
Figure 3 shows fast charging with the above-described fast-charging profiles (Table 1). Let us first consider cell potentials (Figure 3a:) CCCV charging produces a continuous voltage curve (e.g., black line) while MSCC profiles produce characteristic voltage relaxations corresponding to stepwise current reductions (e.g., the orange line); the only CCCA profile (green line) is characterized by a more gradual voltage relaxation in line with the gradual current reduction after the initial constant current phase. As mentioned before, these fast-charging profiles (including the profile names and color coding) are identical to the ones investigated in our previous publication [19].
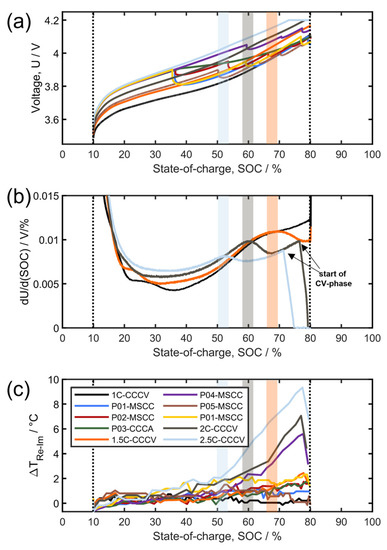
Figure 3.
Fast charging with different profiles at a 25 °C initial temperature, (a) cell potential, (b) differential charging voltage analysis of the CCCV-charging profiles, and (c) respective ΔTRe−Im values.
Figure 2b shows the differential voltage as a function of cell SOC in which a maximum (not present at lower charging rates) indicates lithium plating [19]; accordingly, lithium plating takes place at C-rates of 1.5, 2.0, and 2.5C whereas no lithium plating is detected for 1.0 C. Unfortunately, this lithium plating method only works for constant current charging and not for MSCC and CCCA profiles as discussed in detail in our previous study. The unique advantage of the differential voltage method is the possibility to detect the onset of lithium plating which is around 50% SOC for 2.5C, 60% for 2.0C, and 70% for 1.5C.
In Figure 3c the difference between TRe and TIm (ΔTRe−Im = TRe − TIm) is plotted for all of the different charging profiles. Let us first consider moderate fast charging, namely 1C-CCCV, P01-MSCC (blue line), P02-MSCC, P03-CCCA, and P05-MSCC. For these moderate fast-charging profiles, which do not cause lithium plating (Table 1), ΔTRe−Im is smaller than ≈1.5 K as expected. This demonstrates that the good agreement of TRe − TIm also holds true in the case of rapid and inhomogeneous cell heating; for the three MSCC/CCCA profiles (P01, P02, and P03), the initial temperature increase is between 10 and 15 K within 10 min as measured by the external temperature sensor.
Let us now consider the aggressive fast-charging profiles 2.0-CCCV, 2.5C-CCCV, and P04-MSCC which are known to cause lithium plating (Table 1). For these three charging profiles, the ΔTRe−Im value increases well above 2 K. The onset of plating, detected via the differential voltage method, has been highlighted and it can be observed that:
- For the case of 2.5C-CCCV (light blue), the beginning of a significant increase IN ΔTRe−Im coincides with the onset of plating detected by the differential voltage;
- For the case of 2C-CCCV ΔTRe−Im., even increases before the peak in the differential voltage can be detected;
- For the case of 1.5-CCCV, only minor plating could be observed and ΔTRe−Im seems not to be sensitive enough to detect that degree of plating.
So far, aggressive fast charging with the occurrence of lithium plating has been the only case in which we observed a significant deviation of TRe and TIm. We therefore propose to use ΔTRe−Im as a proxy for time-resolved lithium plating detection. The correlation of ΔTRe−Im increase with lithium plating is further strengthened by considering the observed onset times; the shaded vertical areas in Figure 3b indicate the point in time at which lithium plating was detected by DCV analysis for 2.0-CCCV and 2.5C-CCCV; obviously, the lithium plating onset detected by DCV coincides nicely with the one detected by the ΔTRe−Im increase. Finally, the shape of the ΔTRe−Im curves qualitatively matches the expected amount of lithium plating with an initial delay (build-up of a lithium-ion concentration gradient in the liquid electrolyte), then a steep increase, and a sudden decrease during OCV (re-intercalation into graphite) [28]. As can be seen from the look-up-table data for TRe and TIm given for all of the cycles in the Supplementary Materials, there is also an irreversible change in the temperature-impedance dependence. While Figure 2b indicates an at least semi-quantitative relationship between the amount of plated lithium with ΔTRe−Im, further research is required to elucidate whether real quantification can be achieved.
Let us finally consider 1.5C-CCCV charging which is known to cause slight lithium plating. The ΔTRe−Im value does increase after about 25 min, reaching more than 2K at the end of charging; again, the shaded vertical orange bar indicates the onset of lithium plating as detected via DCV. Nevertheless, we would consider the 1.5C-CCCV case ambiguous and short of clear detection by impedance. In addition, note that the P01-MSCC profile is tested twice (blue and yellow) to check for reproducibility. The second run (yellow) shows increased ΔTRe−Im values despite the absence of lithium plating. This indicates that a recalibration of the look-up tables would have been necessary after the ≈50 previous cycles, especially as P04-MSCC had already caused some cell aging.
4. Discussion
It has been shown by other publications that the volumetric averaged cell temperature can be determined via the real or imaginary part of the impedance, as well as the amplitude or phase angle [40]. The effect we made use of for detecting the onset of plating, as well as the re-intercalation of the plated lithium, is the different change of the function of temperature T in dependence of imaginary TIm = f(Im(Z)) and real part TRe = f(Re(Z)) associated with plating. The underlying physical effects that form the characteristic change, e.g., the evolution of a parallel charge transfer path or modification of the SEI, have been discussed in the previous literature [32]. In our measurements, we can observe a decrease in the real part at 3125 Hz during plating similar to Brown et al. [36], while the imaginary part shows an almost negligible increase, shifting to less inductive values.
As the frequency range was limited from 781 Hz to 8 kHz, the impedance is already dominated by inductive behavior. Thus, the typical shapes of the impedance spectra observed for a wider frequency range and especially for small format cells, exhibiting an inducive part for high frequencies, one or more arcs at lower and medium frequencies and the branch for diffusion and differential capacity, were not observed and are not shown in this manuscript.
For the cell measured, the dependence of estimated temperature from the imaginary part TIm = f(Im(Z)) was observed to be almost not influenced during plating conditions and can therefore be considered as the true internal cell temperature. Hence, a deviation of both estimated internal cell temperatures given with ΔTRe−Im must be the result of a change in the impedance of the real part under plating conditions.
This is qualitatively illustrated in Figure 4. Here, positive changes for the measured impedance during plating are colored blue and negative changes are in red. After processing the data with the look-up tables, the sign of the deviation changes due to the nature of the characteristics—depending on the sign of the coefficient for the linear regression.
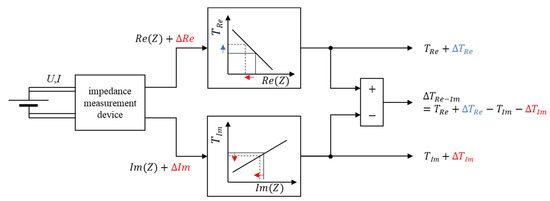
Figure 4.
Block diagram of the method to infer a plating-sensitive signal ΔTRe−Im. Changes in the measured and inferred quantities during plating are given as ΔIm and ΔRe and are colored blue for positive and red for negative deviations.
Because the real part of the impedance is decreased by ΔRe during plating and the linear temperature model for the real part has a negative coefficient, the temperature derived from the real part will be deviating positively by ΔTRe, or put in other words, the underlying linear model for the dependence of cell temperature on the real part cannot reflect the changes due to the plating. Hence, the resulting estimated temperature will be the true temperature TRe plus the model error ΔTRe (compare the upper path of the block diagram in Figure 4). In contrast, the imaginary part is not affected as much during plating conditions and the change in the imaginary part ΔIm is also in the negative direction. As the linear temperature model from the imaginary impedance has a positive coefficient, this less pronounced impedance change in a negative direction leads to a negative deviation of the estimated temperature ΔTIm (compare the lower path of the block diagram in Figure 4). As indicated in Figure 4 with the colors blue and red, the term ΔTRe will be positive and the term ΔTIm will be negative. Due to their different signs, they do not cancel when subtracted and result in an overall deviation ΔTRe−Im. As an intermediate step of the algorithm, the independently derived temperatures under plating conditions are depicted in figure B in the Supplementary Materials.
In contrast, under normal, no plating conditions, the temperatures derived separately from the real and imaginary parts will be identical (TRe = TIm) as the linear temperature models can reflect the behavior correctly and therefore show a resulting difference of zero.
In general, this approach could be applied to other, lower frequencies. We have also measured frequencies down to 781 Hz and evaluated their applicability. However, the dependence of the impedance on SOC and potentially also on the current increases with decreasing frequencies. Thus, the characteristics of TIm = f(Im(Z)) and TRe = f(Re(Z)) become much more complex and sensitive to other parameters such as SOC. From these additional dependencies arise two challenges: (1) already, slight model deviations will lead to strong deviations in the estimated temperature, and (2) the adjustment of the characteristic functions over a lifetime becomes more complex. Considering higher frequencies, it is reasonable to assume that the decreasing sensitivity of the method results from the decreasing excitation of the processes responsible for the impedance change during plating. This sets an upper-frequency limit for the application of the method, but also provides clues for investigating the origins of the underlying effects. Such further investigations, revealing detailed mechanisms for the impedance change during plating, are important to generalize the applicability of the method to a wide variety of cells. Thus, the findings in this paper can be seen as a first step, encouraging more detailed investigations on lab-scale cells and experimental setups, which allow for the separation of potential mechanisms.
Even though it is not possible to finally conclude the root cause of the changes in the characteristics of TRe = f(Re(Z)) and TIm = f(Im(Z)), it is possible to apply that knowledge and implement a function that generates a signal to adapt the fast-charging current online with respect to the individual cell conditions. The only condition that must be fulfilled is that the changes in the characteristics of TIm = f(Im(Z)) and TRe = f(Re(Z)) during lithium plating do not compensate each other.
5. Conclusions
The measurements performed in this study showed a clear correlation of ΔTRe−Im with the degree of plating investigated by other methods and can therefore be applied with reasonable empirical evidence. Though the discussed effects that plating has on the impedance spectra are logically justified and empirically sound, further research is encouraged to improve the understanding of changes to the impedance under non-stationary conditions and especially under lithium plating. We believe that the suggested method is robust enough to detect lithium plating even in a vehicle application as it effectively eliminates the need for knowing the cell’s internal temperature and, if sufficient recalibration is carried out, also the SOH.
The results further highlight that the market introduction of impedance measurement in everyday battery applications seems possible as the measurement results have been obtained by a low-cost implementation with an integrated circuit instead of bulky and expensive laboratory devices.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/batteries9020097/s1, Figure S1: Regression lines to determine the cell temperature for each fast-charging profile based on impedance measurements; Figure S2: Critical fast charging with 2.5C at 25 °C initial temperature with the occurrence of lithium plating; Table S1: Information of the linear regression line to calculate the cell temperature based on impedance data;.
Author Contributions
Conceptualization: J.P.S., A.A. and J.W.; methodology: J.P.S.; investigation: J.P.S. and A.A.; formal analysis: J.P.S. and A.A.; software: J.P.S.; visualization: J.P.S. and A.A.: validation: J.W.; writing—original draft: J.P.S.; writing—review & editing: A.A. and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—491183248 and the Open Access Publishing Fund of the University of Bayreuth.
Data Availability Statement
Additional data is presented in the supplementary material.
Conflicts of Interest
The authors have filed a patent for the method described in this paper [37].
References
- IEA. IEA, Transport Sector CO2 Emissions by Mode in the Sustainable Development Scenario, 2000–2030; IEA: Paris, France, 2020. [Google Scholar]
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global Carbon Budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Bieker, G. A global comparison of the life-cycle greenhouse gas emissions of combustion engine and electric passenger cars. The international council on clean transportation. Communications 2021, 49, 847129–102. [Google Scholar]
- Petzl, M.; Danzer, M.A. Nondestructive detection, characterization, and quantification of lithium plating in commercial lithium-ion batteries. J. Power Sources 2014, 254, 80–87. [Google Scholar] [CrossRef]
- Lin, H.-P.; Chua, D.; Salomon, M.; Shiao, H.-C.; Hendrickson, M.; Plichta, E.; Slane, S. Low-Temperature Behavior of Li-Ion Cells. Electrochem. Solid State Lett. 2001, 4, A71–A73. [Google Scholar] [CrossRef]
- Schindler, S.; Bauer, M.; Petzl, M.; Danzer, M.A. Voltage relaxation and impedance spectroscopy as in-operandomethods for the detection of lithium plating on graphitic anodes incommercial lithium-ion cells. J. Power Sources 2016, 304, 170–180. [Google Scholar] [CrossRef]
- von Lüders, C.; Zinth, V.; Erhard, S.V.; Osswald, P.J.; Hofmann, M.; Gilles, R.; Jossen, A. Lithium plating in lithium-ion batteries investigated by voltage relaxation and in situ neutron diffraction. J. Power Sources 2017, 342, 17–23. [Google Scholar] [CrossRef]
- Smart, M.C.; Ratnakumar, B.V. Effects of Electrolyte Composition on Lithium Plating inLithium-Ion Cells. J. Electrochem. Soc. 2011, 158, 379–389. [Google Scholar] [CrossRef]
- Smart, M.C.; Ratnakumar, B.V.; Whitcanack, L.; Chin, K.; Rodriguez, M.; Surampudi, S. Performance characteristics of lithium ion cells at low temperatures—IEEE Aerospace and Electronics Systems Magazine. IEEE AESS Syst. Mag. 2002, 17, 16–20. [Google Scholar] [CrossRef]
- Uhlmann, C.; Illig, J.; Ender, M.; Schuster, R.; Ivers-Tiffée, E. In situ detection of lithium metal plating on graphite in ex-perimentalcells. J. Power Sources 2015, 279, 428–438. [Google Scholar] [CrossRef]
- Konz, Z.M.; McShane, E.J.; McCloskey, B.D. Detecting the Onset of Lithium Plating and Monitoring Fast Charging Per-formance with Voltage Relaxation. ACS Energy Lett. 2020, 5, 1750–1757. [Google Scholar] [CrossRef]
- Katzer, F.; Jahn, L.; Hahn, M.; Danzer, M.A. Model-based lithium deposition detection method using differential voltage analysis. J. Power Sources 2021, 512, 230449. [Google Scholar] [CrossRef]
- Katzer, F.; Mößle, P.; Schamel, M.; Danzer, M.A. Adaptive fast charging control using impedance-based detection of lith-ium. J. Power Sources 2023, 555, 232354. [Google Scholar] [CrossRef]
- Chen, X.; Li, L.; Liu, M.; Huang, T.; Yu, A. Detection of lithium plating in lithium-ion batteries by distribution of relaxation times. J. Power Sources 2021, 496, 229867. [Google Scholar] [CrossRef]
- Downie, L.E.; Krause, L.J.; Burns, J.C.; Jensen, L.D.; Chevrier, V.; Dahna, J.R. In Situ Detection of Lithium Plating on Graphite Electrodes by Electrochemical Calorimetry. J. Electrochem. Soc. 2013, 160, A588–A594. [Google Scholar] [CrossRef]
- Burns, J.C.; Stevens, D.A.; Dahn, J.R. In-Situ Detection of Lithium Plating Using High Precision Coulometry. J. Electrochem. Soc. 2015, 162, A959–A964. [Google Scholar] [CrossRef]
- Smith, A.J.; Burns, J.C.; Trussler, S.; Dahn, J.R. Precision Measurements of the Coulombic Efficiency of Lithium-Ion Batteries and of Electrode Materials for Lithium-Ion Batteries. J. Electrochem. Soc. 2010, 157, A196–A202. [Google Scholar] [CrossRef]
- Adam, A.; Knobbe, E.; Wandt, J.; Kwade, A. Application of the differential charging voltage analysis to determine the onset of lithium-plating during fast charging of lithium-ion cells. J. Power Sources 2021, 495, 229794. [Google Scholar] [CrossRef]
- Adam, A.; Wandt, J.; Knobbe, E.; Bauer, G.; Kwade, A. Fast-Charging of Automotive Lithium-Ion Cells: In-Situ Lithi-um-Plating Detection and Comparison of Different Cell Designs. J. Electrochem. Soc. 2020, 167, 130503. [Google Scholar] [CrossRef]
- Birkenmaier, C.; Bitzer, B.; Harzheim, M.; Hintennach, A.; Schleid, T. Lithium Plating on Graphite Negative Electrodes: Innovative Qualitative and Quantitative Investigation Methods. J. Electrochem. Soc. 2015, 162, A2646–A2650. [Google Scholar] [CrossRef]
- Bauer, M.; Wachtler, M.; Stöwe, H.; Persson, J.V.; Danzer, M.A. Understanding the dilation and dilation relaxation behavior of graphite-based lithium-ion cells. J. Power Sources 2016, 317, 93–102. [Google Scholar] [CrossRef]
- Rieger, B.; Schuster, S.; Erhard, S.; Osswald, P.; Rheinfeld, A.; Willmann, C.; Jossen, A. Multi-directional laser scanning as innovative method to detect local cell damage during fast charging of lithium-ion cells. J. Energy Storage 2016, 8, 1–5. [Google Scholar] [CrossRef]
- Daubinger, P.; Ebert, F.; Hartmann, S.; Giffin, G.A. Impact of electrochemical and mechanical interactions on lithium-ion battery performance investigated by operando dilatometry. J. Power Sources 2021, 488, 229457. [Google Scholar] [CrossRef]
- Bitzer, B.; Gruhle, A. A new method for detecting lithium plating by measuring the cell thickness. J. Power Sources 2014, 262, 297–302. [Google Scholar] [CrossRef]
- Spingler, F.B.; Wittmann, W.; Sturm, J.; Rieger, B.; Jossen, A. Optimum fast charging of lithium-ion pouch cells based on local volume expansion criteria. J. Power Sources 2018, 393, 152–160. [Google Scholar] [CrossRef]
- Zinth, V.; von Lüders, C.; Hofmann, M.; Hattendorff, J.; Buchberger, I.; Erhard, S.; Rebelo-Kornmeier, J.; Jossen, A.; Gilles, R. Lithium plating in lithium-ion batteries at sub-ambient temperatures investigated by in situ neutron diffraction. J. Power Sources 2014, 271, 152–159. [Google Scholar] [CrossRef]
- McShane, E.J.; Colclasure, A.M.; Brown, D.E.; Konz, Z.M.; Smith, K.; McCloskey, B.D. Quantification of Inactive Lithium and Solid–Electrolyte Interphase Species on Graphite Electrodes after Fast Charging. ACS Energy Lett. 2020, 5, 2045–2051. [Google Scholar] [CrossRef]
- Wandt, J.; Jakes, P.; Granwehr, J.; Eichel, R.-A.; Gasteiger, H.A. Quantitative and time-resolved detection of lithium plating on graphite anodes in lithium ion batteries. Mater. Today 2017, 21, 231–240. [Google Scholar] [CrossRef]
- Wandt, J.; Marino, C.; Gasteiger, H.A.; Jakes, P.; Eichel, R.-A.; Granwehr, J. Operando electron paramagnetic resonance spectroscopy—Formation of mossy lithium on lithium anodes during charge–discharge cycling. Energy Environ. Sci. 2015, 8, 1358–1367. [Google Scholar] [CrossRef]
- Niemöller, A.; Jakes, P.; Eichel, R.-A.; Granwehr, J. EPR Imaging of Metallic Lithium and its Application to Dendrite Lo-calisation in Battery Separators. Sci. Rep. 2018, 8, 14331. [Google Scholar] [CrossRef]
- Koleti, U.R.; Dinh, T.Q.; Marco, J. A new on-line method for lithium plating detection in lithium-ion batteries. J. Power Sources 2020, 451, 227798. [Google Scholar] [CrossRef]
- Koseoglou, M.; Tsioumas, E.; Ferentinou, D.; Jabbour, N.; Papagiannis, D.; Mademlis, C. Lithium plating detection using dynamic electrochemical impedance spectroscopy in lithium-ion batteries. J. Power Sources 2021, 512, 230508. [Google Scholar] [CrossRef]
- Dotoli, M.; Milo, E.; Giuliano, M.; Rocca, R.; Nervi, C.; Baricco, M.; Ercole, M.; Sgroi, M.F. Detection of Lithium Plating in Li-Ion Cell Anodes Using Realistic Automotive Fast-Charge Profiles. Batteries 2021, 7, 46. [Google Scholar] [CrossRef]
- Dotoli, M.; Milo, E.; Giuliano, M.; Tiozzo, A.; Baricco, M.; Nervi, C.; Ercole, M.; Sgroi, M.F. Development of an Innovative Procedure for Lithium Plating. Batteries 2022, 8, 88. [Google Scholar] [CrossRef]
- Haussmann, P.; Melbert, J. Internal Cell Temperature Measurement and Thermal Modeling of Lithium Ion Cells for Au-tomotive Applications by Means of Electrochemical Impedance Spectroscopy. SAE Int. J. Altern. Powertrains 2017, 6, 261–270. [Google Scholar] [CrossRef]
- Brown, D.E.; McShane, E.J.; Konz, Z.M.; Knudsen, K.B.; McCloskey, B.D. Detecting onset of lithium plating during fast charging of Li-ion batteries using operando electrochemical impedance spectroscopy. Cell Rep. Phys. Sci. 2021, 2, 100589. [Google Scholar] [CrossRef]
- Wandt, J.; Adam, A.; Schardax, C.; Schmidt, J.P. Verfahren zum Detektieren von Lithium-Plating in Einer Lithiumionenzelle Sowie Lithiumionenbatterie. Germany Patent DE102021103949A, 25 August 2022. [Google Scholar]
- Landinger, T.; Schwarzberger, G.; Hofer, G.; Rose, M.; Jossen, A. Power Line Communications for Automotive High Voltage Battery Systems: Channel Modeling and Coexistence Study with Battery Monitoring. Energies 2021, 14, 1851. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Arnold, S.; Loges, A.; Werner, D.; Wetzel, T.; Ivers-Tiffée, E. Measurement of the internal cell temperature via impedance: Evaluation and application of a new method. J. Power Sources 2013, 243, 110–117. [Google Scholar] [CrossRef]
- Beelen, H.; Raijmakers, L.; Donkers, M.; Notten, P.; Bergveld, H. A comparison and accuracy analysis of impedance-based temperature estimation methods for Li-ion batteries. Appl. Energy 2016, 175, 128–140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).