Review and Stress Analysis on the Lithiation Onset of Amorphous Silicon Films
Abstract
1. Introduction
2. Literature Survey
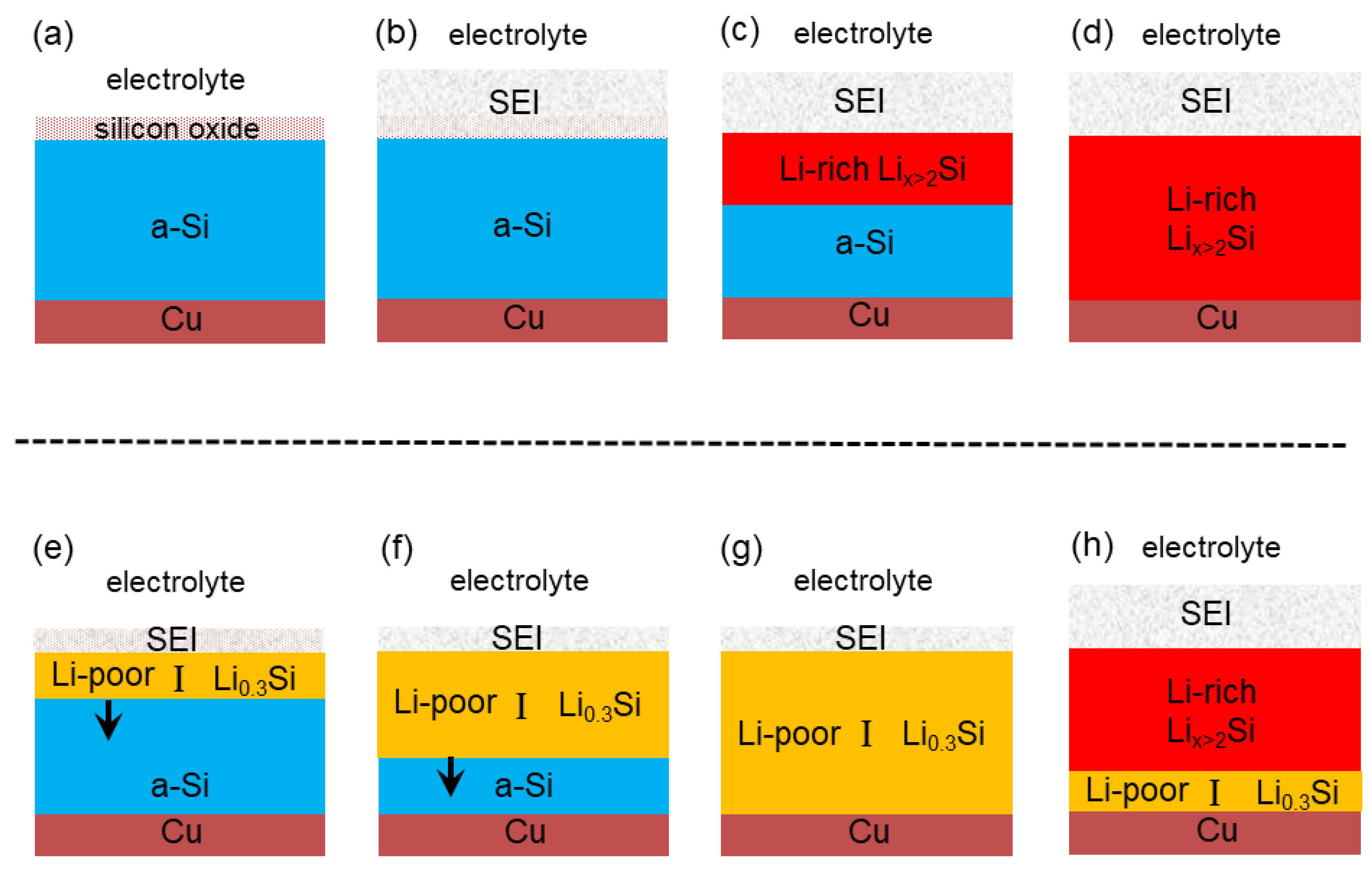
2.1. Description of the Lithiation Onset of Amorphous Silicon
2.2. Changes in Physical Properties of Silicon during the Lithiation Onset

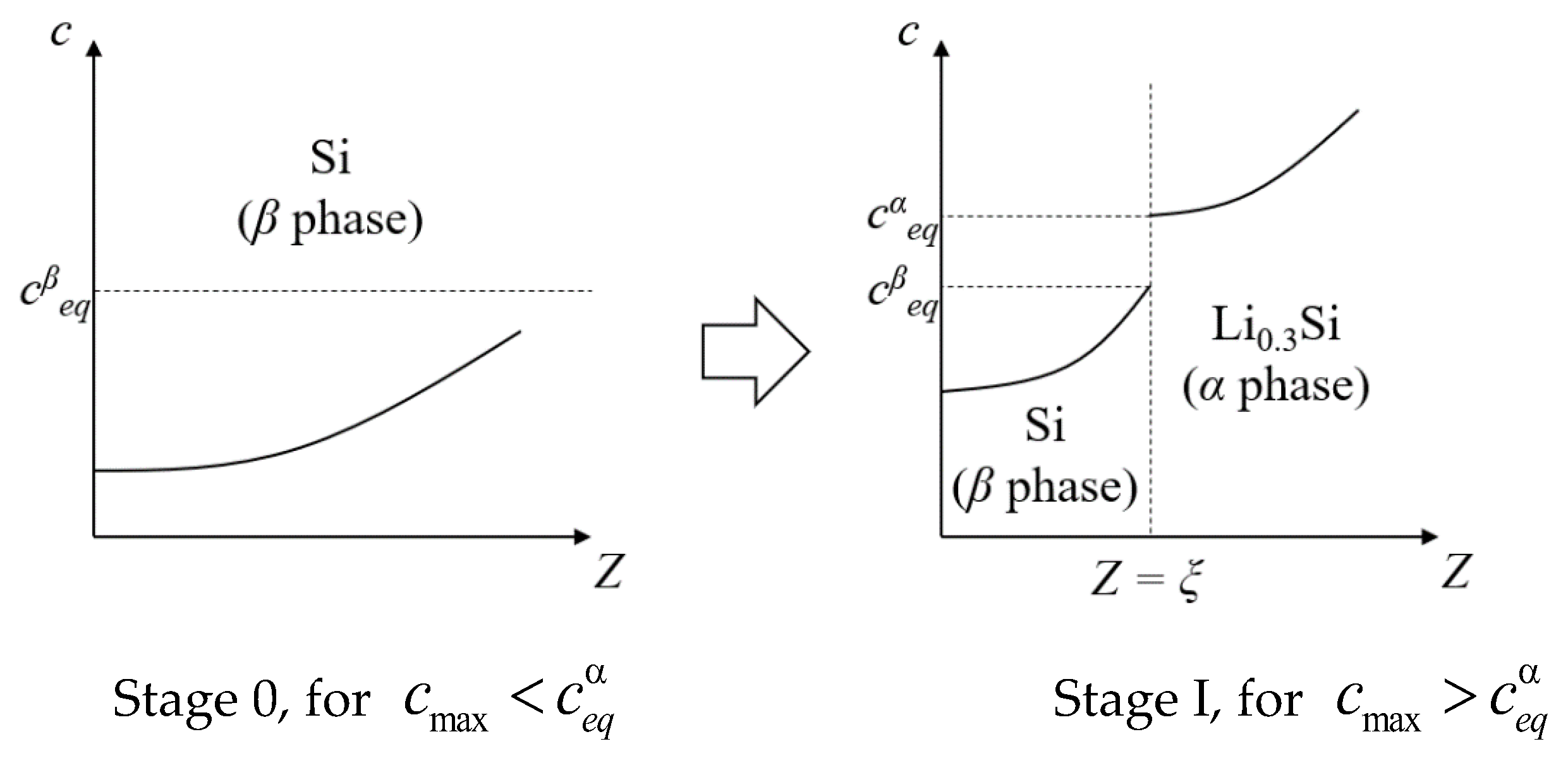
2.3. Reasons for the Appearance of the Phase Front Delimiting Li0.3Si from a-Silicon
3. Numerical Investigation
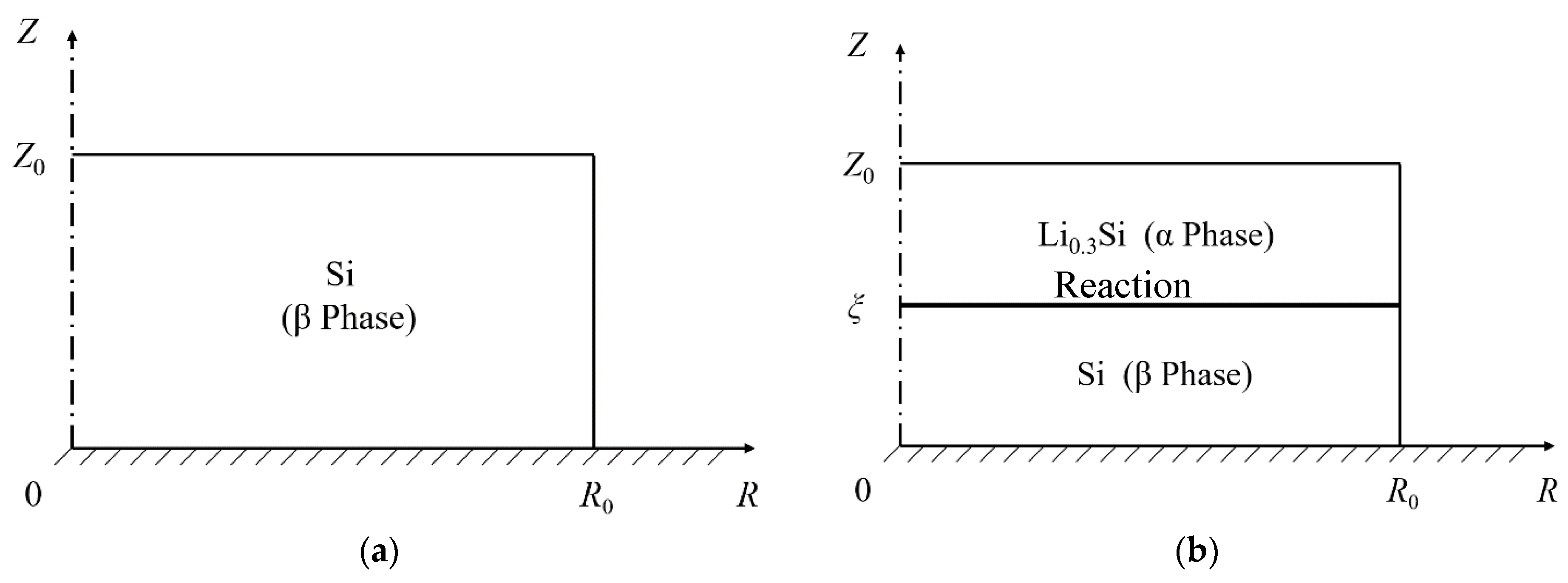
3.1. Mechanochemical Model
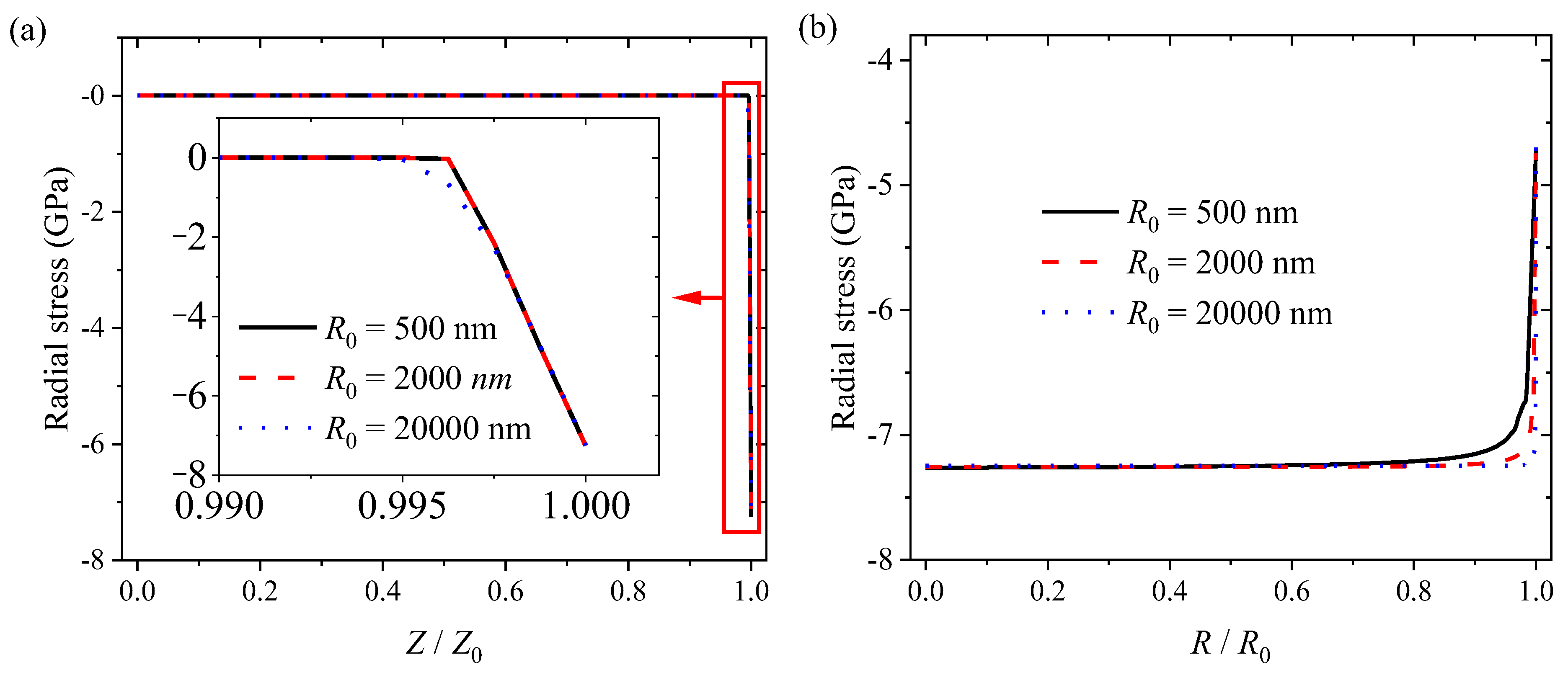
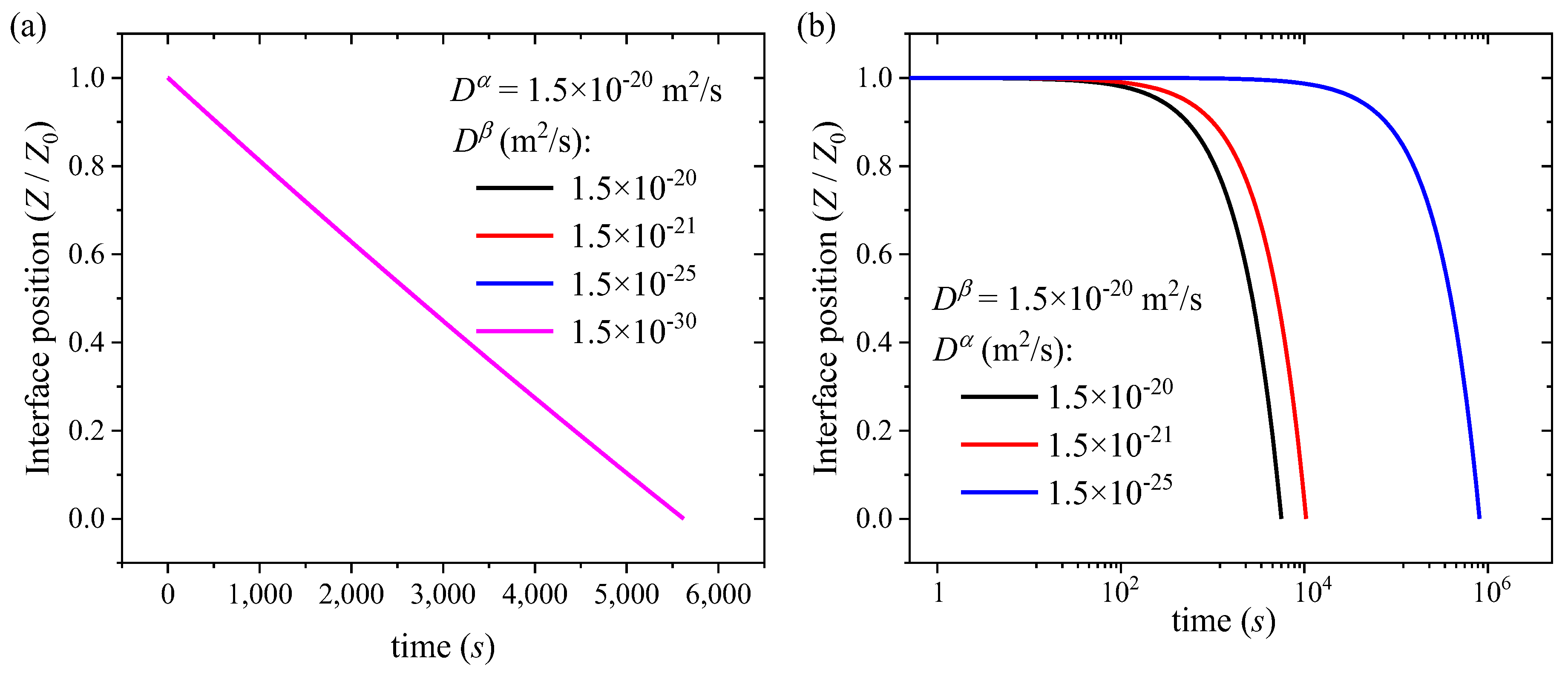
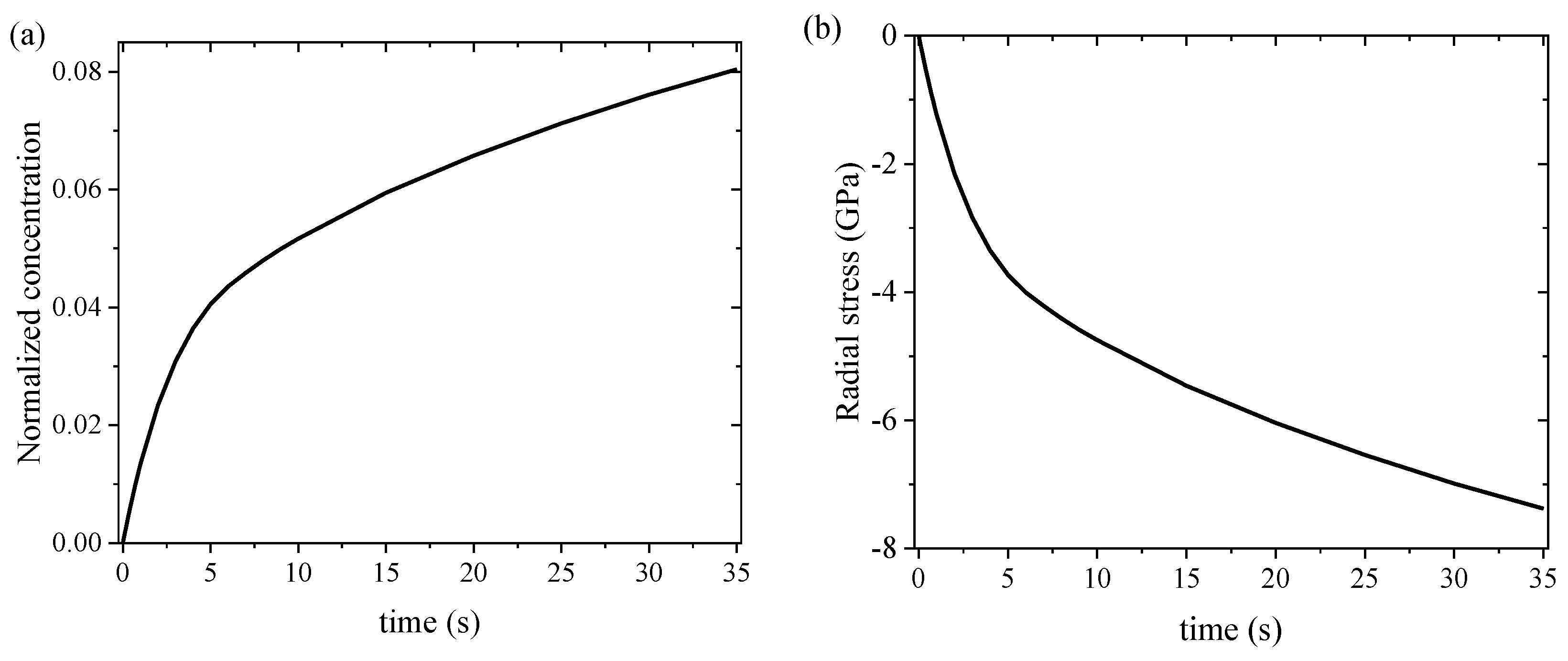
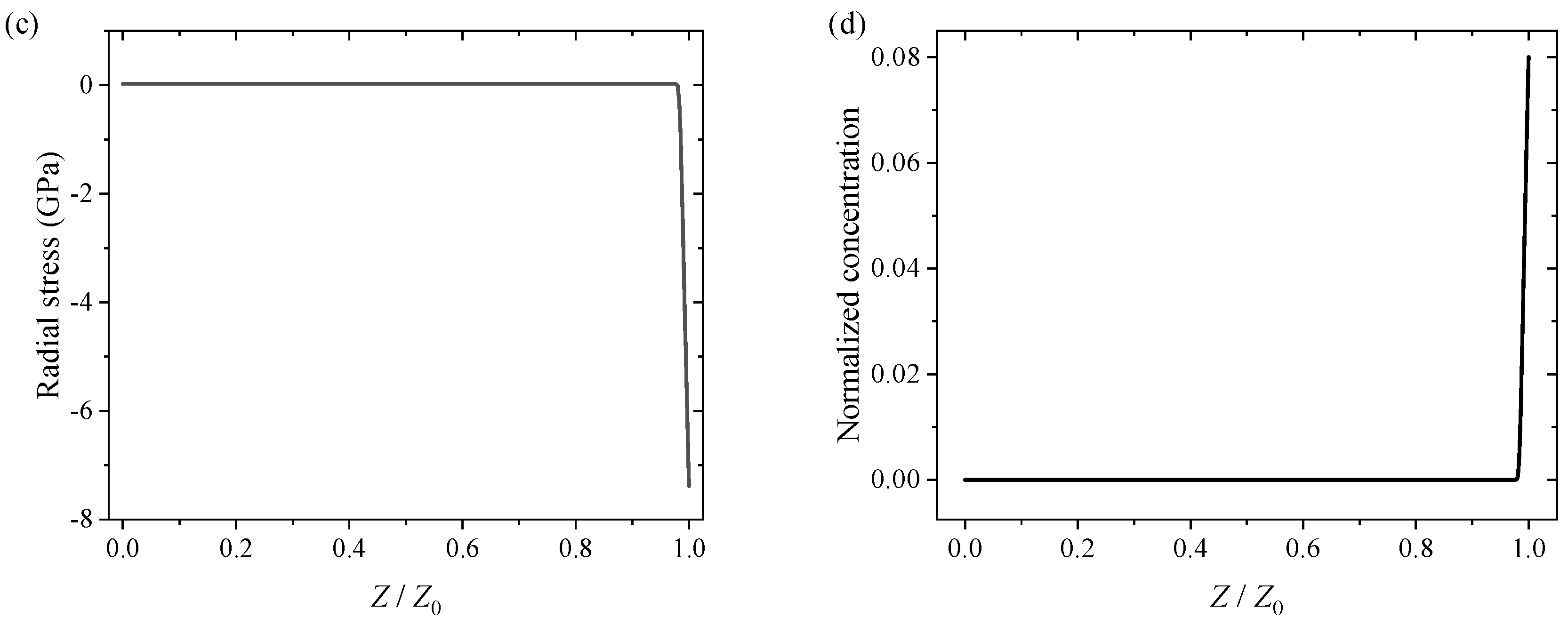
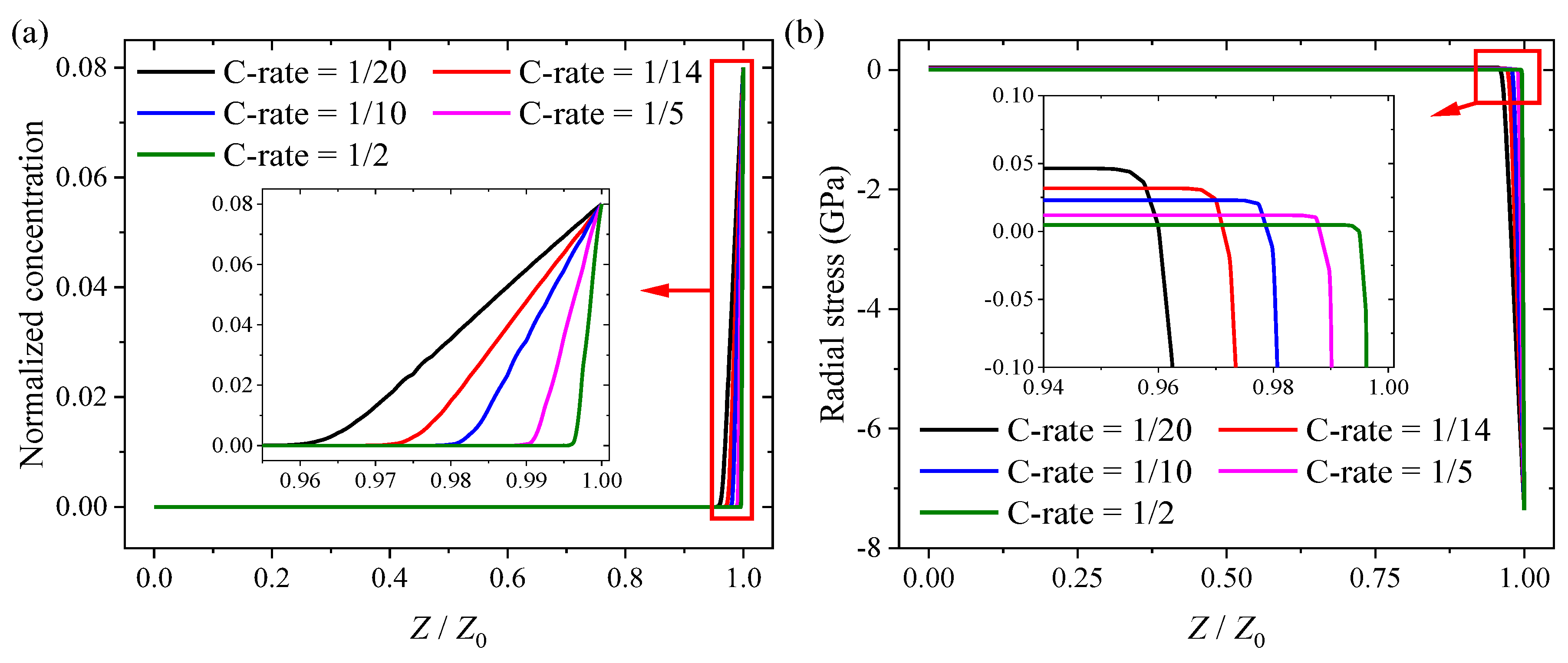
3.2. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Experimental Procedure
Appendix A.2. Additional Figures and Information on the Mechanochemical Simulation
References
- Hüger, E.; Uxa, D.; Yang, F.; Schmidt, H. The lithiation onset of amorphous silicon thin-film electrodes. Appl. Phys. Lett. 2022, 121, 133901. [Google Scholar] [CrossRef]
- Hüger, E.; Jin, C.; Schmidt, H. Electrochemical investigation of ion-beam sputter-deposited carbon thin films for Li-ion batteries. J. Appl. Electrochem. 2022, 52, 1715–1732. [Google Scholar] [CrossRef]
- Wu, B.; Chen, C.; Danilov, D.L.; Jiang, M.; Raijmakers, L.H.; Eichel, R.d.-A.; Notten, P.H. Influence of the SEI formation on the stability and lithium diffusion in Si electrodes. ACS Omega 2022, 7, 32740–32748. [Google Scholar] [CrossRef]
- Phan, V.P.; Pecquenard, B.; Le Cras, F. High-Performance all-solid-state cells fabricated with silicon electrodes. Adv. Funct. Mater. 2012, 22, 2580–2584. [Google Scholar] [CrossRef]
- Cao, C.; Abate, I.I.; Sivonxay, E.; Shyam, B.; Jia, C.; Moritz, B.; Devereaux, T.P.; Persson, K.A.; Steinrück, H.-G.; Toney, M.F. Solid electrolyte interphase on native oxide-terminated silicon anodes for Li-ion batteries. Joule 2019, 3, 762–781. [Google Scholar] [CrossRef]
- Browning, K.L.; Browning, J.F.; Doucet, M.; Yamada, N.L.; Liu, G.; Veith, G.M. Role of conductive binder to direct solid–electrolyte interphase formation over silicon anodes. Phys. Chem. Chem. Phys. 2019, 21, 17356–17365. [Google Scholar] [CrossRef]
- Philippe, B.; Dedryvère, R.M.; Allouche, J.; Lindgren, F.; Gorgoi, M.; Rensmo, H.K.; Gonbeau, D.; Edström, K. Nanosilicon electrodes for lithium-ion batteries: Interfacial mechanisms studied by hard and soft X-ray photoelectron spectroscopy. Chem. Mater. 2012, 24, 1107–1115. [Google Scholar] [CrossRef]
- Schroder, K.W.; Celio, H.; Webb, L.J.; Stevenson, K.J. Examining solid electrolyte interphase formation on crystalline silicon electrodes: Influence of electrochemical preparation and ambient exposure conditions. J. Phys. Chem. C 2012, 116, 19737–19747. [Google Scholar] [CrossRef]
- Yin, Y.; Arca, E.; Wang, L.; Yang, G.; Schnabel, M.; Cao, L.; Xiao, C.; Zhou, H.; Liu, P.; Nanda, J. Nonpassivated silicon anode surface. ACS Appl. Mater. Interfaces 2020, 12, 26593–26600. [Google Scholar] [CrossRef]
- Schnabel, M.; Harvey, S.P.; Arca, E.; Stetson, C.; Teeter, G.; Ban, C.; Stradins, P. Surface SiO2 thickness controls uniform-to-localized transition in lithiation of silicon anodes for lithium-ion batteries. ACS Appl. Mater. Interfaces 2020, 12, 27017–27028. [Google Scholar] [CrossRef]
- Schnabel, M.; Arca, E.; Ha, Y.; Stetson, C.; Teeter, G.; Han, S.-D.; Stradins, P. Enhanced interfacial stability of Si anodes for Li-ion batteries via surface SiO2 coating. ACS Appl. Energy Mater. 2020, 3, 8842–8849. [Google Scholar] [CrossRef]
- Hasa, I.; Haregewoin, A.M.; Zhang, L.; Tsai, W.-Y.; Guo, J.; Veith, G.M.; Ross, P.N.; Kostecki, R. Electrochemical reactivity and passivation of silicon thin-film electrodes in organic carbonate electrolytes. ACS Appl. Mater. Interfaces 2020, 12, 40879–40890. [Google Scholar] [CrossRef]
- Stetson, C.; Schnabel, M.; Li, Z.; Harvey, S.P.; Jiang, C.-S.; Norman, A.; DeCaluwe, S.C.; Al-Jassim, M.; Burrell, A. Microscopic observation of solid electrolyte interphase bilayer inversion on silicon oxide. ACS Energy Lett. 2020, 5, 3657–3662. [Google Scholar] [CrossRef]
- Huang, W.; Wang, J.; Braun, M.R.; Zhang, Z.; Li, Y.; Boyle, D.T.; McIntyre, P.C.; Cui, Y. Dynamic structure and chemistry of the silicon solid-electrolyte interphase visualized by cryogenic electron microscopy. Matter 2019, 1, 1232–1245. [Google Scholar] [CrossRef]
- Steinrück, H.-G.; Cao, C.; Veith, G.M.; Toney, M.F. Toward quantifying capacity losses due to solid electrolyte interphase evolution in silicon thin film batteries. J. Chem. Phys. 2020, 152, 084702. [Google Scholar] [CrossRef] [PubMed]
- Kohler, T.; Hadjixenophontos, E.; Joshi, Y.; Wang, K.; Schmitz, G. Reversible oxide formation during cycling of Si anodes. Nano Energy 2021, 84, 105886. [Google Scholar] [CrossRef]
- Cao, C.; Steinrück, H.-G.; Shyam, B.; Stone, K.H.; Toney, M.F. In situ study of silicon electrode lithiation with X-ray reflectivity. Nano Lett. 2016, 16, 7394–7401. [Google Scholar] [CrossRef] [PubMed]
- Stournara, M.E.; Xiao, X.C.; Qi, Y.; Johari, P.; Lu, P.; Sheldon, B.W.; Gao, H.J.; Shenoy, V.B. Li segregation induces structure and strength changes at the amorphous Si/Cu interface. Nano Lett. 2013, 13, 4759–4768. [Google Scholar] [CrossRef]
- Guo, M.Q.; Meng, W.J.; Zhang, X.G.; Bai, Z.C.; Wang, G.W.; Wang, Z.H.; Yang, F.Q. Structural degradation of Cu current collector during electrochemical cycling of Sn-based lithium-ion batteries. J. Electron. Mater. 2019, 48, 7543–7550. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, J.B. Wadsley-roth crystallographic shear structure niobium-based oxides: Promising anode materials for high-safety lithium-ion batteries. Adv. Sci. 2021, 8, 2004855. [Google Scholar] [CrossRef]
- Al-Maghrabi, M.; Suzuki, J.; Sanderson, R.; Chevrier, V.; Dunlap, R.; Dahn, J. Combinatorial studies of Si1-xOx as a potential negative electrode material for Li-ion battery applications. J. Electrochem. Soc. 2013, 160, A1587. [Google Scholar] [CrossRef]
- Cao, Y.; Bennett, J.C.; Dunlap, R.; Obrovac, M. A simple synthesis route for high-capacity SiOx anode materials with tunable oxygen content for lithium-ion batteries. Chem. Mater. 2018, 30, 7418–7422. [Google Scholar] [CrossRef]
- Cao, Y.; Dunlap, R.; Obrovac, M. Electrochemistry and thermal behavior of SiOx made by reactive gas milling. J. Electrochem. Soc. 2020, 167, 110501. [Google Scholar] [CrossRef]
- Uxa, D.; Jerliu, B.; Hüger, E.; Dörrer, L.; Horisberger, M.; Stahn, J.; Schmidt, H. On the lithiation mechanism of amorphous silicon electrodes in Li-ion batteries. J. Phys. Chem. C 2019, 123, 22027–22039. [Google Scholar] [CrossRef]
- Seidlhofer, B.-K.; Jerliu, B.; Trapp, M.; Hüger, E.; Risse, S.; Cubitt, R.; Schmidt, H.; Steitz, R.; Ballauff, M. Lithiation of crystalline silicon as analyzed by operando neutron reflectivity. ACS Nano 2016, 10, 7458–7466. [Google Scholar] [CrossRef]
- Sheldon, B.W.; Soni, S.K.; Xiao, X.; Qi, Y. Stress contributions to solution thermodynamics in Li-Si alloys. Electrochem. Solid-State Lett. 2011, 15, A9. [Google Scholar] [CrossRef]
- Sethuraman, V.A.; Srinivasan, V.; Bower, A.F.; Guduru, P.R. In situ measurements of stress-potential coupling in lithiated silicon. J. Electrochem. Soc. 2010, 157, A1253. [Google Scholar] [CrossRef]
- Jerliu, B.; Hüger, E.; Dorrer, L.; Seidlhofer, B.-K.; Steitz, R.; Oberst, V.; Geckle, U.; Bruns, M.; Schmidt, H. Volume expansion during lithiation of amorphous silicon thin film electrodes studied by in-operando neutron reflectometry. J. Phys. Chem. C 2014, 118, 9395–9399. [Google Scholar] [CrossRef]
- Beaulieu, L.; Hatchard, T.; Bonakdarpour, A.; Fleischauer, M.; Dahn, J. Reaction of Li with alloy thin films studied by in situ AFM. J. Electrochem. Soc. 2003, 150, A1457. [Google Scholar] [CrossRef]
- Soni, S.K.; Sheldon, B.W.; Xiao, X.; Tokranov, A. Thickness effects on the lithiation of amorphous silicon thin films. Scr. Mater. 2011, 64, 307–310. [Google Scholar] [CrossRef]
- Nadimpalli, S.P.; Sethuraman, V.A.; Bucci, G.; Srinivasan, V.; Bower, A.F.; Guduru, P.R. On plastic deformation and fracture in Si films during electrochemical lithiation/delithiation cycling. J. Electrochem. Soc. 2013, 160, A1885. [Google Scholar] [CrossRef]
- Sethuraman, V.A.; Chon, M.J.; Shimshak, M.; Srinivasan, V.; Guduru, P.R. In situ measurements of stress evolution in silicon thin films during electrochemical lithiation and delithiation. J. Power Sources 2010, 195, 5062–5066. [Google Scholar] [CrossRef]
- Pharr, M.; Suo, Z.; Vlassak, J.J. Measurements of the fracture energy of lithiated silicon electrodes of Li-ion batteries. Nano Lett. 2013, 13, 5570–5577. [Google Scholar] [CrossRef]
- Wang, X.; Fan, F.; Wang, J.; Wang, H.; Tao, S.; Yang, A.; Liu, Y.; Beng Chew, H.; Mao, S.X.; Zhu, T.; et al. High damage tolerance of electrochemically lithiated silicon. Nat. Commun. 2015, 6, 8417. [Google Scholar] [CrossRef] [PubMed]
- Housel, L.M.; Li, W.Z.; Quilty, C.D.; Vila, M.N.; Wang, L.; Tang, C.R.; Bock, D.C.; Wu, Q.Y.; Tong, X.; Head, A.R.; et al. Insights into reactivity of silicon negative electrodes: Analysis using isothermal microcalorimetry. ACS Appl. Mater. Interfaces 2019, 11, 37567–37577. [Google Scholar] [CrossRef]
- Yang, F.Q. Cycling-induced structural damage/degradation of electrode materials—Microscopic viewpoint. Nanotechnology 2022, 33, 065405. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Kozlov, A.; Thomas, D.; Mertens, F.; Schmid-Fetzer, R. Thermodynamic analysis of the Li–Si phase equilibria from 0 K to liquidus temperatures. Intermetallics 2013, 42, 137–145. [Google Scholar] [CrossRef]
- Zeilinger, M.; Kurylyshyn, I.M.; Haussermann, U.; Fässler, T.F. Revision of the Li–Si phase diagram: Discovery and single-crystal X-ray structure determination of the high-temperature phase Li4.11Si. Chem. Mater. 2013, 25, 4623–4632. [Google Scholar] [CrossRef]
- Morris, A.J.; Grey, C.; Pickard, C.J. Thermodynamically stable lithium silicides and germanides from density functional theory calculations. Phys. Rev. B 2014, 90, 054111. [Google Scholar] [CrossRef]
- Braga, M.H.; Dębski, A.; Gąsior, W. Li–Si phase diagram: Enthalpy of mixing, thermodynamic stability, and coherent assessment. J. Alloys Compd. 2014, 616, 581–593. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Yang, G.; Ma, Y. Silicon framework-based lithium silicides at high pressures. ACS Appl. Mater. Interfaces 2016, 8, 16761–16767. [Google Scholar] [CrossRef]
- Chiang, H.-H.; Lu, J.-M.; Kuo, C.-L. First-principles study of the structural and dynamic properties of the liquid and amorphous Li–Si alloys. J. Chem. Phys. 2016, 144, 034502. [Google Scholar] [CrossRef] [PubMed]
- Yang, F. Interaction between diffusion and chemical stresses. Mater. Sci. Eng. A 2005, 409, 153–159. [Google Scholar] [CrossRef]
- Strauß, F.; Hüger, E.; Julin, J.; Munnik, F.; Schmidt, H. Lithium diffusion in ion-beam sputter-deposited lithium–silicon layers. J. Phys. Chem. C 2020, 124, 8616–8623. [Google Scholar] [CrossRef]
- Hüger, E.; Dörrer, L.; Schmidt, H. Permeation, solubility, diffusion and segregation of lithium in amorphous silicon layers. Chem. Mater. 2018, 30, 3254–3264. [Google Scholar] [CrossRef]
- Strauß, F.; Dörrer, L.; Bruns, M.; Schmidt, H. Lithium tracer diffusion in amorphous LixSi for low Li concentrations. J. Phys. Chem. C 2018, 122, 6508–6513. [Google Scholar] [CrossRef]
- Chevrier, V.L.; Dahn, J.R. First principles model of amorphous silicon lithiation. J. Electrochem. Soc. 2009, 156, A454–A458. [Google Scholar] [CrossRef]
- Artrith, N.; Urban, A.; Ceder, G. Constructing first-principles phase diagrams of amorphous LixSi using machine-learning-assisted sampling with an evolutionary algorithm. J. Chem. Phys. 2018, 148, 241711. [Google Scholar] [CrossRef] [PubMed]
- Bucci, G.; Swamy, T.; Bishop, S.; Sheldon, B.W.; Chiang, Y.M.; Carter, W.C. The effect of stress on battery-electrode capacity. J. Electrochem. Soc. 2017, 164, A645–A654. [Google Scholar] [CrossRef]
- Stournara, M.E.; Kumar, R.; Qi, Y.; Sheldon, B.W. Ab initio diffuse-interface model for lithiated electrode interface evolution. Phys. Rev. E 2016, 94, 012802. [Google Scholar] [CrossRef]
- Hirai, K.; Ichitsubo, T.; Uda, T.; Miyazaki, A.; Yagi, S.; Matsubara, E. Effects of volume strain due to Li–Sn compound formation on electrode potential in lithium-ion batteries. Acta Mater. 2008, 56, 1539–1545. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, K.; Zheng, B.; Yang, F. Effect of local deformation on the coupling between diffusion and stress in lithium-ion battery. Int. J. Solids Struct. 2016, 87, 81–89. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, J.; Liu, S.; Du, Y. Effects of the volume changes and elastic-strain energies on the phase transition in the Li-Sn battery. J. Power Sources 2016, 330, 111–119. [Google Scholar] [CrossRef]
- Selvi, G.T.; Jha, S.K. Anomalous interfacial stress generation and role of elasto-plasticity in mechanical failure of Si-based thin film anodes of Li-ion batteries. Bull. Mater. Sci. 2022, 45, 23. [Google Scholar] [CrossRef]
- Li, J.; Fang, Q.; Wu, H.; Liu, Y.; Wen, P. Investigation into diffusion induced plastic deformation behavior in hollow lithium ion battery electrode revealed by analytical model and atomistic simulation. Electrochim. Acta 2015, 178, 597–607. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Zhang, K.; Zheng, B.; Yang, F. A defect-based viscoplastic model for large-deformed thin film electrode of lithium-ion battery. Int. J. Plast. 2019, 115, 293–306. [Google Scholar] [CrossRef]
- Bagheri, A.; Arghavani, J.; Naghdabadi, R.; Brassart, L. A theory for coupled lithium insertion and viscoplastic flow in amorphous anode materials for Li-ion batteries. Mech. Mater. 2021, 152, 103663. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, J.; Yang, F.; Zhang, Y.; Pan, Y.; Zheng, B.; Li, Y.; Yang, F. A stress-control charging method with multi-stage currents for silicon-based lithium-ion batteries: Theoretical analysis and experimental validation. J. Energy Storage 2022, 56, 105985. [Google Scholar] [CrossRef]
- Zuo, P.; Zhao, Y.-P. A phase field model coupling lithium diffusion and stress evolution with crack propagation and application in lithium ion batteries. Phys. Chem. Chem. Phys. 2015, 17, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Wagner, G.J.; Muller, R.P. Phase field modeling of solid electrolyte interface formation in lithium ion batteries. J. Electrochem. Soc. 2013, 160, A487. [Google Scholar] [CrossRef]
- Liu, Z.; Cai, R.; Chen, B.; Liu, T.; Zhou, J. Effect of electrochemical reaction on diffusion-induced stress in hollow spherical lithium-ion battery electrode. Ionics 2017, 23, 617–625. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, Z.; Wang, Y.; Zhu, J. Effect of reversible electrochemical reaction on Li diffusion and stresses in cylindrical Li-ion battery electrodes. J. Appl. Phys. 2014, 115, 083504. [Google Scholar] [CrossRef]
- Suo, Y.; Yang, F. Transient analysis of diffusion-induced stress: Effect of solid reaction. Acta Mech. 2019, 230, 993–1002. [Google Scholar] [CrossRef]
- Yang, F. Effect of local solid reaction on diffusion-induced stress. J. Appl. Phys. 2010, 107, 103516. [Google Scholar] [CrossRef]
- Hüger, E.; Jerliu, B.; Dörrer, L.; Bruns, M.; Borchardt, G.; Schmidt, H. A secondary ion mass spectrometry study on the mechanisms of amorphous silicon electrode lithiation in Li-ion batteries. Z. Phys. Chem. 2015, 229, 1375–1385. [Google Scholar] [CrossRef]
- Li, J.C.-M. Physical chemistry of some microstructural phenomena. Metall. Trans. A 1978, 9, 1353–1380. [Google Scholar]
- Zang, J.-L.; Zhao, Y.-P. A diffusion and curvature dependent surface elastic model with application to stress analysis of anode in lithium ion battery. Int. J. Eng. Sci. 2012, 61, 156–170. [Google Scholar] [CrossRef]
- Uxa, D.; Hüger, E.; Schmidt, H. Li diffusion in thin-film LiySi electrodes: Galvanostatic intermittent titration technique and tracer diffusion experiments. J. Phys. Chem. C 2020, 124, 27894–27899. [Google Scholar] [CrossRef]
- Hertzberg, B.; Benson, J.; Yushin, G. Ex-situ depth-sensing indentation measurements of electrochemically produced Si–Li alloy films. Electrochem. Commun. 2011, 13, 818–821. [Google Scholar] [CrossRef]
- Kuznetsov, V.; Zinn, A.-H.; Zampardi, G.; Borhani-Haghighi, S.; La Mantia, F.; Ludwig, A.; Schuhmann, W.; Ventosa, E. Wet nanoindentation of the solid electrolyte interphase on thin film Si electrodes. ACS Appl. Mater. Interfaces 2015, 7, 23554–23563. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Hong, W. Phase-field model for the two-phase lithiation of silicon. J. Mech. Phys. Solids 2016, 94, 18–32. [Google Scholar] [CrossRef]
- Ronneburg, A.; Silvi, L.; Cooper, J.; Harbauer, K.; Ballauff, M.; Risse, S. Solid Electrolyte Interphase Layer Formation during Lithiation of Single-Crystal Silicon Electrodes with a Protective Aluminum Oxide Coating. ACS Appl. Mater. Interfaces 2021, 13, 21241–21249. [Google Scholar] [CrossRef] [PubMed]
- Strafela, M.; Fischer, J.; Music, D.; Chang, K.; Schneider, J.; Leiste, H.; Rinke, M.; Bergfeldt, T.; Seifert, H.; Ulrich, S. Dependence of the constitution, microstructure and electrochemical behaviour of magnetron sputtered Li–Ni–Mn–Co–O thin film cathodes for lithium-ion batteries on the working gas pressure and annealing conditions. Int. J. Mater. Res. 2017, 108, 879–886. [Google Scholar] [CrossRef]

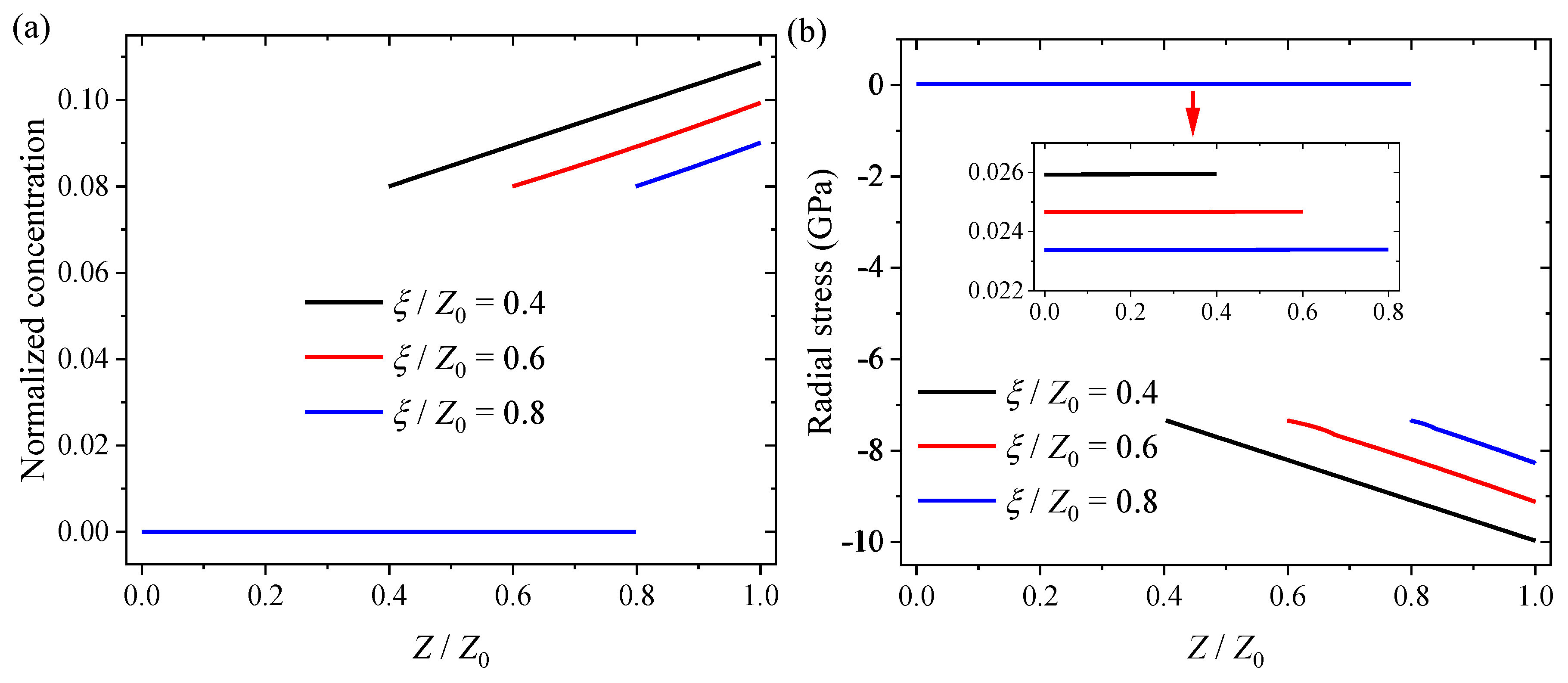
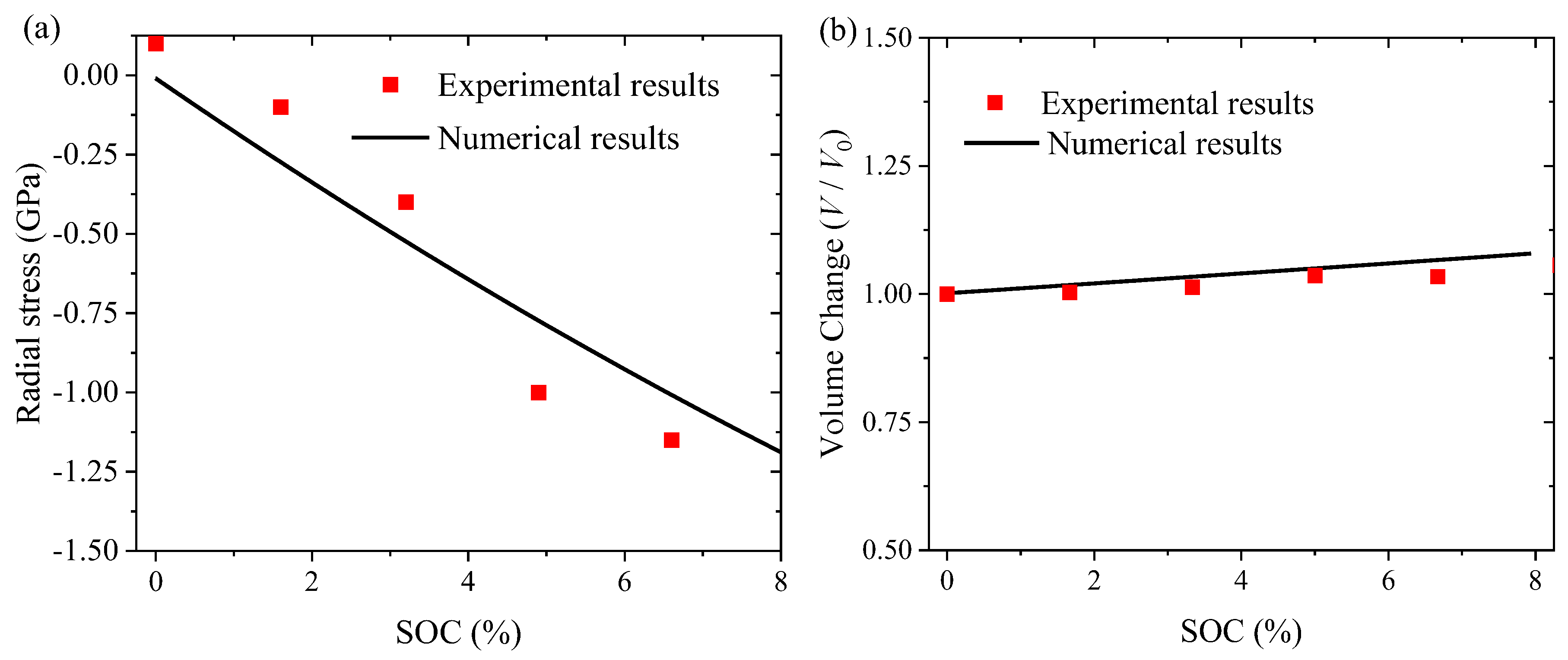
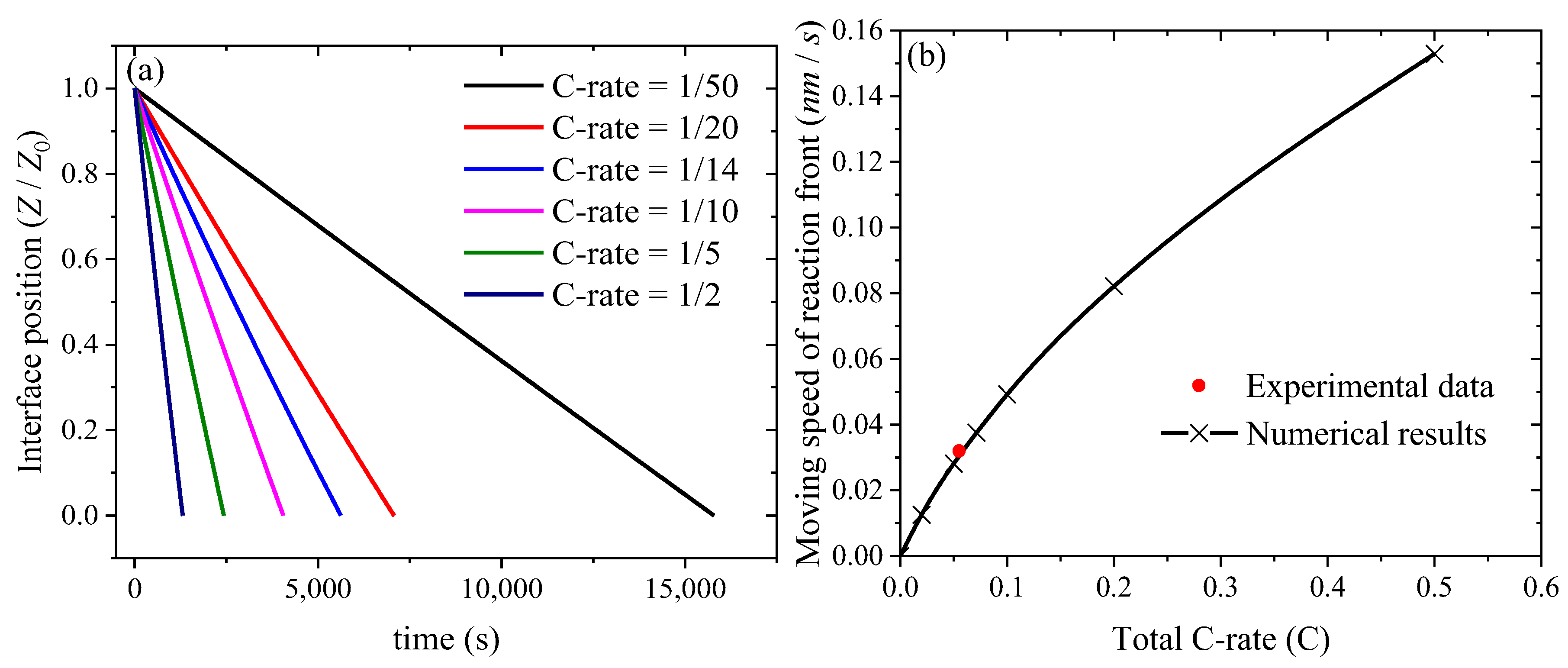
| Symbol | Parameter | Numerical Value |
|---|---|---|
| Dα | Diffusion coefficient in α phase | 1.5 × 10−20 m2·s−1 |
| Dβ | Diffusion coefficient in β phase | 1.5 × 10−20 m2·s−1 |
| Z0 | Initial thickness of the silicon thin film | 200 × 10−9 m |
| Normalized equilibrium value of α phase | 0.08 | |
| Normalized equilibrium value of β phase | 0 | |
| E | Elastic modulus | 92 GPa [69] |
| ν | Poisson’s ratio | 0.28 [70] |
| Ω | Partial molar volume | 8.18 × 10−6 m3·mol−1 [71] |
| Cmax | Maximum concentration | 3.67 × 10−5 mol·m−3 [33] |
| R | Gas constant | 8.314 J·mol−1·K−1 |
| T | Absolut temperature | 300 K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Hüger, E.; Li, Y.; Schmidt, H.; Yang, F. Review and Stress Analysis on the Lithiation Onset of Amorphous Silicon Films. Batteries 2023, 9, 105. https://doi.org/10.3390/batteries9020105
Zhang K, Hüger E, Li Y, Schmidt H, Yang F. Review and Stress Analysis on the Lithiation Onset of Amorphous Silicon Films. Batteries. 2023; 9(2):105. https://doi.org/10.3390/batteries9020105
Chicago/Turabian StyleZhang, Kai, Erwin Hüger, Yong Li, Harald Schmidt, and Fuqian Yang. 2023. "Review and Stress Analysis on the Lithiation Onset of Amorphous Silicon Films" Batteries 9, no. 2: 105. https://doi.org/10.3390/batteries9020105
APA StyleZhang, K., Hüger, E., Li, Y., Schmidt, H., & Yang, F. (2023). Review and Stress Analysis on the Lithiation Onset of Amorphous Silicon Films. Batteries, 9(2), 105. https://doi.org/10.3390/batteries9020105






