Abstract
Overcharging due to an abnormal charging capacity is one of the most common causes of thermal runaway (TR). This study proposes a method for diagnosing abnormal battery charging capacity based on electric vehicle (EV) data. The proposed method can obtain the fault frequency and output the corresponding state of charge (SOC) when a fault occurs. First, a machine-learning-based data cleaning framework is developed to overcome the limitations of the interpolation method. Then, offline training is implemented, based on big vehicle operation data and an improved Gaussian process regression (GPR). Thereafter, online monitoring of the discrete capacity increment (DCI) is used to identify the abnormal charging capacity. The abnormal charging capacity fault is identified by the absolute error between the GPR outputs and the true DCI, and the thresholds are determined using a Box–Cox transformation with a value of 3. The diagnostic results indicate that the abnormal charging capacity of the TR vehicle is identified two months in advance, and the fault frequency of the abnormal and normal vehicles is 0.5221 and 0.0311, respectively. EV operation data and various methods are used to validate the robustness and applicability of the proposed method.
1. Introduction
The widespread use of vehicles powered by traditional fuels has contributed to severe problems, such as the current fossil fuel energy crisis and air pollution. Several nations are promoting electric vehicles (EVs) as a key solution for the aforementioned issues [1]. Owing to their high energy density, low self-discharge rate, and long cycle-life, lithium-ion batteries (LIBs) have gradually become the standard energy storage components for EVs [2]. Battery modules are composed of cells in series and parallel [3,4]. However, the abnormal capacity of power batteries causes a rapid degradation of the power and dependability of EVs. The calibration of the battery’s state of charge (SOC) is inaccurate because of the inability of the battery management system (BMS) to accurately evaluate the aging of all cells. This leads to the overcharging of cells, which is one of the most common real-world causes of thermal runaway (TR) in batteries [5]. By establishing a diagnostic method based on actual vehicle data, an early abnormal power battery capacity was identified. This diagnostic method can provide feedback for the manufacturer to improve the BMS, in addition to enhancing the safety of power batteries to protect people’s lives and properties [6].
The estimation of the battery parameters and fault-tolerant control algorithm of the BMS rely on the precise estimation of the battery capacity [7]. In the past, researchers have emphasised the precise estimation of the battery capacity. Several research findings have been translated to the real world. Wang et al. [8] implemented an online estimation of battery health based on the extraction of health factors during constant-voltage charging under experimental conditions. Combined with regression models, an incremental capacity analysis (ICA) [9,10] is widely used for battery capacity estimation. However, it is difficult to guarantee the accuracy of the capacity estimation model established under a real-world test or simulation conditions. She et al. [11] applied ICA to estimate the actual vehicle capacity while accounting for battery inconsistencies. Using a feed-forward neural network, Song et al. [12] extracted features from the historical operation data of EVs and described battery degradation. However, few studies have focused on the abnormal capacity change fault diagnosis and parameter calibration. Despite the existence of several charging protection measures, the abnormal charging capacity of the power battery leads to overcharging, which inevitably results in TR accidents [13,14].
Various methods for diagnosing power battery faults have been proposed, including knowledge-based, model-based, and data-driven approaches. Knowledge-based fault-diagnosis methods identify faults using prior knowledge. Both fault trees [15] and expert systems [16] have been used for power battery fault diagnosis. However, knowledge-based fault diagnosis methods have a limited ability to identify fault types, locate specific faults, and quantify fault levels. A model-based fault diagnosis identifies faults by constructing a battery model and comparing the deviations between the sensor measurements and models (called residuals). Tian et al. [17] accurately isolated electrical and temperature faults using Thevenin equivalent circuit and radial equivalent thermal models. Feng et al. [18] proposed a fault diagnosis method for internal short circuits that converts the measured value to an electrochemical state, which reflects typical internal short-circuit characteristics. The real-world diagnostic capabilities of simulation- or experiment-based battery models remain unknown, and the parameter identification of some models limits their practical applications. Data-driven fault diagnosis methods combined with big data from vehicles have achieved outstanding performance in fault diagnosis and early warnings. Zhao et al. [19] proposed a 3 multilevel screening strategy (3-MSS) to identify possible abnormal cells and provide feedback on the upstream of designing. Wang et al. [20] identified two typical subhealth battery states based on statistical principles. Various entropy theories [21,22,23,24] identify abnormal voltage fluctuations and are used to diagnose battery failures and prevent TR. To predict the battery voltage to diagnose faults, Li et al. [25] developed a fault diagnosis model based on a long short-term memory (LSTM) neural network and an equivalent circuit model (ECM) to monitor cell faults based on predictive voltage. The voltage and temperature of the battery were used to develop fault diagnosis models using the data-driven methods described above. Despite this, few studies have been conducted on the diagnosis of abnormal charging capacity, particularly those based on actual vehicle data [26]. Zheng et al. [27] proposed a method based on an Extended Kalman Filter (EKF) for the diagnosis of capacity anomalies. This method can effectively diagnose the low-capacity fault of battery packs. Wang et al. [28] proposed a method for diagnosing the battery charging capacity based on extreme gradient boosting (XGBoost), which is based on the entire charging segment of the EV to determine whether an abnormal charging capacity occurs.
The current research on charging capacity fault can determine only whether a fault occurs based on the entire charging segment, as reported in the literature [28]. Therefore, the motivation of this study is to propose a diagnostic method that can output the corresponding SOC when these charging capacity faults occur. The significance of this work is to rapidly identify charging faults during an actual vehicle operation and provide more information for fault tracking and analysis. In addition, existing data-driven fault diagnosis methods continue to have the limitations of a high workload of tuning hyperparameters and operational complexity, which limits the performance of their practical applications. For the first time, this study proposes an XGBoost-based general data restoration framework for data platforms. Second, the features are extracted from real-world EVs charging data, discrete capacity increment (DCI) is used as the monitoring indicator for abnormal charging capacity, and the fault threshold value is computed using the Box–Cox transformation and 3. This process can diagnose the abnormal charging capacity and the corresponding SOC based on the improved GPR regression model established using EVs operation data without any complex parameter adjustment.
The remainder of this study is structured as follows: Section 2 introduces data collection and the XGBoost-based framework for data restoration. Section 3 describes the methodology and procedure for fault diagnosis, including the development of a capacity prediction model and the determination of the fault threshold. Section 4 presents the results, verifies the effectiveness of the methods, and compares the benefits and limitations of the various methods.
2. Data Acquisition and Pre-Processing
2.1. Data Acquisition
In 2016, the National Monitoring and Management Platform for New Energy Vehicles (NMMP-NEV) was established in Beijing, China. As of 1 July 2022, the NMMP-NEV includes over 9 million new energy vehicles. Figure 1 depicts the collection and transmission of real vehicle data to the NMMP-NEV. The vehicle terminal collects the battery, motor, and electronic control system operation data, and transmits it to the NMMP-NEV via a General Packet Radio Service (GPRS) in real time. Based on big data, the NMMP-NEV enables security management, mileage accounting, and the performance evaluation of new energy vehicles [21]. This study utilises half a year’s worth of data collected by the NMMP-NEV for five EVs of the same brand.
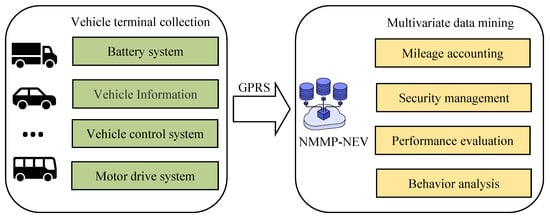
Figure 1.
Real vehicle data collection and transmission to the NMMP-NEV.
2.2. Data Pre-Processing
Owing to building occlusion, sensor failure, signal loss, and other signals during transmission, the data contain a certain number of outliers and missing values. Therefore, data pre-processing primarily consists of outlier detection and restoration. To prevent the identification of failed or pre-failed data as outliers, data outside the valid range of the acquisition protocol or endpoints were eliminated.
References [29,30,31,32] restored the missing data using an alternative interpolation method and the previous value. However, the inherent disadvantage of interpolation is the existence of adjacent numerical requirements for missing values and the loss of precision, which results from restoring the data using previous values. For instance, the mean interpolation method requires the existence of data before and after the missing value, and extrapolation of the Lagrangian or Newton interpolation method requires the existence of multiple numbers (at least two) that precede the missing value. As shown in Figure 2a, the interpolation method is applied to a single line of missing data. However, as shown in Figure 2b, the interpolation method cannot be used when two consecutive lines of data are missing.
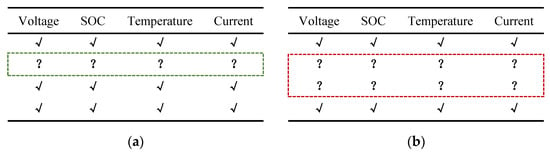
Figure 2.
Different types of missing data. (a) Single line of missing data; (b) continuous missing data.
This study proposes an all-encompassing strategy for restoring the data on big data platforms. To fill in the missing voltage, current, SOC, and temperature values, a regression model was established using XGBoost. XGBoost is an ensemble-learning algorithm based on gradient-boosting decision trees, and its large-scale parallel characteristics make it more suitable for big-data regression.
By selecting the samples and features, XGBoost integrates multiple weak learners. The objective function values of new learners are minimised and aggregated into a model with high precision by learning the residuals of existing learners. The XGBoost prediction results are presented in Equation (1) [33].
where is the predicted value for the ith sample, is the number of trees, is the set space of trees, is the feature vector of the ith sample, and represents the structure and leaf weight of the kth independent tree.
The XGBoost loss function is defined using Equations (2) and (3) as follows.
where is the error between the predicted and true values, and is the regularisation item that represents the complexity of the tree. controls the number of leaf nodes and T is the number of leaf nodes. controls the score of leaf nodes and is the score of leaf nodes.
Each loss function seeks to minimise the objective function as much as possible, and the objective function of the tth round is calculated using Equation (4).
The mathematical derivation was reported in a previous paper [33].
The battery voltage, current, SOC, and the mean temperature are the most intuitive indicators of performance. The changes in the operation and charging parameters of the EVs are shown in Figure 3. Because the SOC and temperature do not change significantly within a short period of time, the previous value is used to fill the missing values. However, during the operation, the voltage and current vary considerably with time, whereas during charging, they exhibit a relatively stable upward trend.
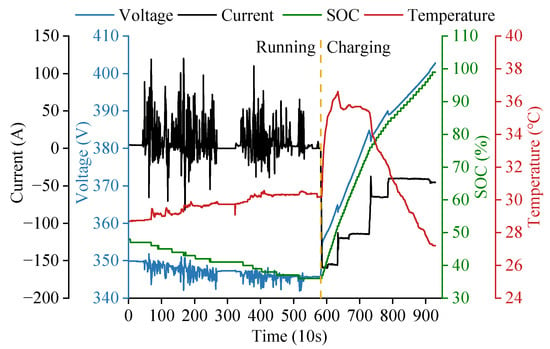
Figure 3.
Variation in different battery parameters during operation.
The following voltage and current regression relationships were established to achieve an accurate and continuous restoration of missing data:
where g is the XGBoost model trained using historical data; , , , and are the voltage, current, SOC, and average temperature of the probe at the ith time, respectively, and is the operating mode of the EV indicating the charging or operation status.
The hyperparameters of XGBoost were tuned using a k-fold cross-validation, with the generalisation error as the optimisation objective. The generalisation error considers bias and variance to ensure the precision and stability of the model [34]. The generalisation error was computed as in Equation (6).
where is the generalisation error, is the bias, is the variance, and is noise.
Figure 4 depicts the data restoration framework. In the offline state, the k-fold cross-validation is applied to the training set. The hyperparameters of XGBoost are sequentially tuned to reduce the generalisation error.
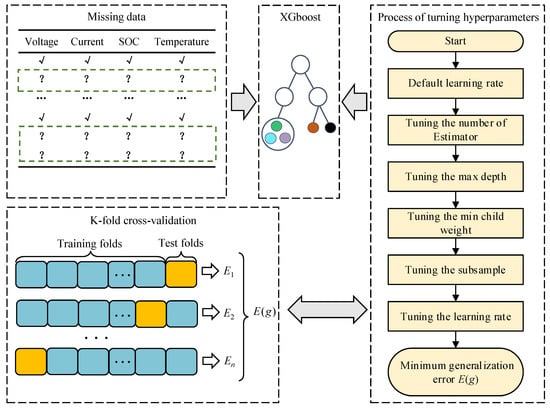
Figure 4.
Data restoration framework based on XGBoost.
3. Diagnostic Method for Abnormal Charging Capacity
3.1. Feature Extraction during Charging State
As shown in Figure 3, the current consistency and stability are observable in the charging state. Consequently, a more precise capacity can be determined during charging. In previous studies, the charging capacity was determined using the current integration method [12] or moving average method [28] to determine the charging capacity corresponding to the SOC at a particular interval. However, the aforementioned studies did not consider the effect of the BMS on SOC correction and cell equalisation. If the SOC intervals of varying lengths are chosen, the BMS will adjust the SOC calibration to some intervals, resulting in an inaccurate capacity calculation. In this study, we propose the calculation of the DCI corresponding to the SOC increases during charging. The DCI is defined as in Equation (7).
where (Ah) is the charging capacity of the SOC as it increases from i % to i + 1%. and are the times when the SOC is i and i + 1, respectively.
Depending on the charging mode and surrounding environment, a number of variables affect the DCI. The following variables affecting the DCI were selected as inputs to the subsequent regression model.
- (1)
- The charging current is an indicator of the DCI according to Equation (7). Consequently, the mean and variance of the charging current were chosen as indicators that, respectively, represent the level and stability of the charging current.
- (2)
- Temperature has a significant impact on battery capacity. For instance, the available capacity of a battery decreases significantly at low temperatures [33]. The average temperature of the battery was determined using a temperature probe within the battery pack.
- (3)
- Considering the impact of the BMS on the real-time SOC correction, the charging capacity varies across the SOC intervals. The start and end SOC in the charging status were selected.
- (4)
- During an EV operation, the actual capacity of the battery degrades nonlinearly, and the accumulated mileage is an effective indicator of the degree of degradation.
According to the preceding assertion, the features selected for the regression model are as presented in Equation (8).
where is the average value of the charging current, is the variance of the charging current, is the initial charging SOC, , is the final charging SOC, represents the average temperature of the probe in the battery pack, and represents the accumulated mileage.
3.2. Gaussian Process Regression
During the driving process of a power battery, the nonlinear degradation of capacity, sampling sparsity, and environmental impact hinder the establishment of regression models. Gaussian process regression (GPR) is a machine learning model based on the Bayesian theory and the kernel function method, which has the capacity for fine nonlinear regression and generalisation.
GPR can be explained using the principle of the function space perspective, and a Gaussian process (GP) is defined as a finite set of variables that conform to a joint Gaussian distribution. For dataset , the GP is defined by the mean and covariance functions, as shown in Equation (9) [35].
where and are the mean and covariance functions, respectively.
and are presented in Equations (10) and (11), respectively:
where is considered an unknown latent function.
Considering the effect of noise , the observed values of and are as follows:
follows the joint Gaussian distribution and consists of a finite number of :
is the mean function of , which represents the expectation of x corresponding to before the observed data. is the covariance function of , which measures the similarity of the sets in the GPR and is often expressed in the form of a kernel function. The selection of the kernel function is presented in Section 3.3.
According to the training sample data, the GPR determines the distribution of the latent function f to realise the regression, as shown in Figure 5.
Figure 5.
Schematic of the GPR.
Noise follows an independent and identically distributed Gaussian distribution . The prior distribution of the latent function with is presented in Equation (14).
The joint prior distribution of y and is defined in Equation (15):
where , , and . is the training set and is the test set. , , and are all positive-definite covariance matrices.
Combined with the prior distribution of GPR, the posterior distribution of is provided in Equation (16).
where is the predicted mean matrix and is the predicted covariance matrix .
Therefore, the GPR can quantify the uncertainty of the output result, and its 95% confidence interval is as follows:
3.3. Enhanced Gaussian Process Regression
The capacity of the power battery degrades continuously as a result of the working process and is influenced by several variables; therefore, it is highly nonlinear and uncertain. The single-covariance kernel function has restricted local approximation and generalisation capabilities [36]. With only a single covariance kernel function, it is impossible to establish a GPR with a high accuracy and excellent generalisation performance. Therefore, this study proposes a modification to the GPR. The neural network covariance kernel function has a strong local approximation ability but a poor generalisation ability, whereas the linear covariance kernel function in the global kernel function exhibits an excellent generalisation performance. As shown in Equation (18), the aforementioned kernel functions and the noise kernel function are combined to form the covariance kernel function of the enhanced GPR.
where , , and are hyperparameters, and is the Kronecker delta function.
The mean kernel function represents the expectation of the prior distribution. For natural and symmetrical considerations, it is generally selected as 0, as shown in Equation (19).
The advantage of the GPR is that there are few hyperparameters to be determined, and the hyperparameters are automatically searched by the maximum likelihood, which significantly reduces the workload associated with the tuning parameter. The procedure for optimising the hyperparameters is as follows:
GPR obtains optimal hyperparameters based on edge-likelihood maximisation. The training-sample-set-based edge-likelihood function is presented in Equation (20).
where represents the hyperparameters of the GPR.
The negative log-edge likelihood function for Equation (21) is
where . To reduce the computational cost, the matrix G is inverted using the Cholesky decomposition:
where L is a lower triangular matrix.
Equation (21) represents the minimal objective function, and the partial derivatives of the hyperparameters are obtained. In Equation (23), the partial derivatives are computed using the conjugate gradient method.
3.4. Abnormal Charging Capacity Diagnosis
A diagnostic flowchart for the abnormal charging capacity is depicted in Figure 6. The data of three EVs of the same brand, which had been in operation for six months, were pre-processed. A GPR model was trained using the DCI of the EV charging state and its corresponding characteristics. The model was validated using charging data from two other EVs of the same brand, one of which experienced severe TR during charging. By comparing the absolute error of the DCI output from the GPR model to that of the actual DCI, the abnormal charging capacity could be identified. In addition, the Box–Cox and 3 were used to determine the threshold of the abnormal charging capacity in the online diagnosis model. The procedure for determining the threshold is comprehensively described below.
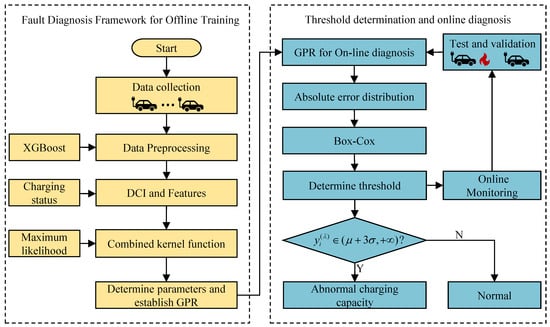
Figure 6.
Flowchart for the diagnosis of charge capacity abnormalities.
Owing to the unique conditions of each EV, the absolute value of the error varies during the online monitoring of each EV. Statistics-based methods can rapidly determine the abnormal threshold of each EV. The 3 [19] principles were applied to the diagnosis of power battery failure, and the outlier threshold can be well-determined in a normal distribution. However, the distribution of the absolute errors did not conform to the normal distribution. The Box–Cox has been proposed to enhance the normality of the data using the following formula:
where , , and are the data before and after the Box–Cox transformation.
The largest is calculated, and is determined by the maximum likelihood method, which is expressed as shown in Equation (25):
where .
For Box–Cox transformed , the distribution follows the Gaussian distribution:
is the mean of and is the standard deviation of .
The abnormal charging capacity threshold is determined based on the 3 principles as follows [19]:
After the inverse Box–Cox transformation, the true abnormal charging capacity threshold is the output, as shown in Equation (28).
4. Results and Discussion
4.1. Data Restoring Results
The validity of the proposed model was evaluated by randomly generating the missing data. The hyperparameters were tuned to reduce the generalisation error based on a 10-fold cross-validation. The learning curve quantified the scores of the training and test sets as the number of training samples that gradually increased. The scores of the training and test sets before and after tuning the parameter for the same estimator in XGBoost are shown in Figure 7. Figure 7a depicts the current restoring learning curve and Figure 7b depicts the voltage-restoring learning curve. The large score difference between the training and test sets prior to tuning the hyperparameters demonstrates that XGBoost overfits the data. After tuning the hyperparameters, the score of the test set increased, and the scores of the training and test sets converged, indicating that the generalisation capability of the model had improved.
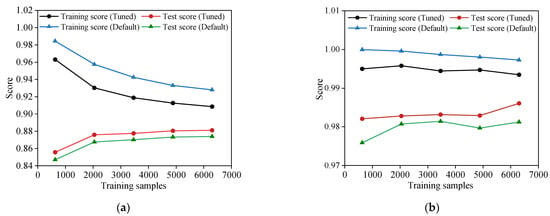
Figure 7.
Learning curve for different parameter restorations. (a) Learning curve of the current restoring model; (b) learning curve of the voltage restoring model.
In this study, the model was evaluated using the mean of absolute value of errors (MAE) and root mean square error (RMSE). The MAE and RMSE are calculated as follows:
where denotes the observed value, denotes the predicted value of the model, and N denotes the number of samples.
Table 1 depicts the MAE and RMSE for restoring the missing current and voltage and compares the method proposed in this study with the previous value restoring the missing value. In the current restoration, the MAE of XGBoost is lower than the previous restoration value, whereas in the voltage restoration, the MAE is slightly higher. Regardless of the current or voltage, the RMSE of XGboost is less than the previous row of values used for restoration. The RMSE penalises the predictive value of the model with a large deviation, demonstrating that the model is more robust.

Table 1.
Performance comparison of XGBoost and the previous value in parameter restoration.
4.2. Abnormal Charging Capacity Diagnosis Results
The distributions and Q-Q plots of the absolute error before and after the Box–Cox transformation are shown in Figure 8. The transformed points coincide with the red line on the Q-Q plot, indicating that the data adhere to a normal distribution [37]. As shown in Figure 8a,b, the original absolute error distribution does not conform to the normal distribution. As shown in Figure 8c,d, the absolute error of V1 is approximately a normal distribution after the Box–Cox transformation.
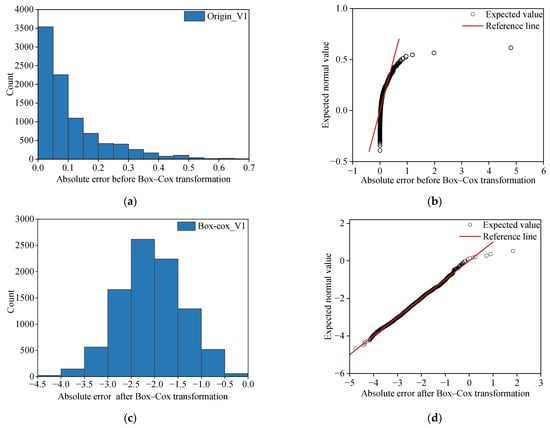
Figure 8.
Distribution and Q-Q plot before and after the Box–Cox transformation. (a) Distribution of the absolute error before the Box–Cox transformation; (b) Q-Q plot of the absolute error before the Box–Cox transformation; (c) distribution of the absolute error after the Box–Cox transformation; (d) Q-Q plot of the absolute error after the Box–Cox transformation.
The value of determines the absolute error threshold for diagnosing charge capacity failures. When the DCI exceeds this threshold, a charging capacity fault occurs. Figure 9 shows the results of the fault diagnosis for various charging segments of the two vehicles. Figure 9a shows the results of the V1 vehicle charging segment diagnosis. Inevitably, an error occurs between the predicted value and actual DCI, but it remains below the threshold. As shown in Figure 9b, both the predicted value and actual DCI for V2 vehicles exceed the threshold at SOC = 97%, which is recorded as an abnormal charging capacity.
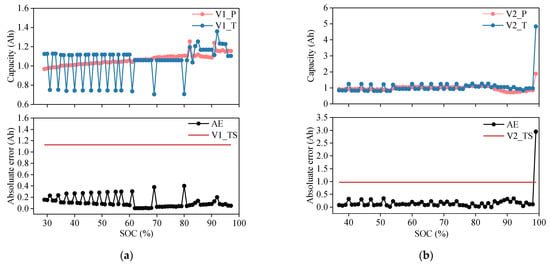
Figure 9.
Diagnostic results of a charging segment of V1 and V2. (a) Diagnostic results of the charging process of V1. (b) Diagnostic results of the charging process of V2.
The frequency of the faults was used to quantify the potential risk of the vehicle. The formula for the fault frequency is defined as follows:
where is the number of charging segments with faults and is the number of all charging segments.
Table 2 displays the frequency of faults for the two test vehicles, with the value for V2 being significantly higher than that for V1. Statistically, among the 161 driving segments over the course of six months, V1 had only five abnormalities. However, V2 tested 113 driving segments over the course of six months, and 59 abnormalities were found across all segments. The normal vehicle V1 also has some charging abnormal capacity faults, but the fault frequency of the abnormal charging capacity is only 0.0311. However, the fault frequency of the V2 vehicle is 0.5221, which is significantly higher than that of V1. It can be clearly determined that V2 vehicles have a greater safety risk.

Table 2.
Fault frequency of the abnormal charging capacity of V1 and V2.
By tallying the SOC values corresponding to the abnormality, as shown in Figure 10, the following results were obtained: For V1, five abnormal charging capacity faults were observed in different SOC regions, three of which occurred in high-SOC regions. However, for V2, the abnormal charging capacity was concentrated entirely in the high-SOC region, i.e., SOC = 96–99%. This demonstrates that the BMS estimation of the SOC under high SOC levels for vehicles of this brand is inaccurate. This may result in overcharging at high SOC levels, which should be considered by manufacturers.
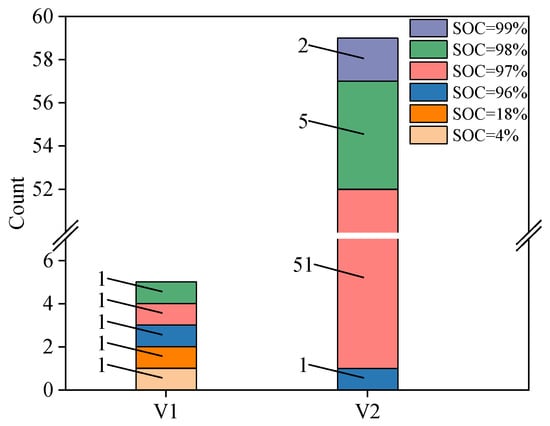
Figure 10.
Column distribution of SOC corresponding to the abnormal charging capacity of V1 and V2.
Figure 11 depicts the abnormal charging capacity counts of V2 over several months. For V2, between 28 April 2020 and 28 October 2020, the first capacity abnormality alarm occurred on 14 June 2022. The number of alarms was tallied by month, as shown in Figure 11, and the number of alarms demonstrates an upward trend with each passing month. The charge capacity warnings are counted by month. The number of warnings was only three in June and 0 in July, but it suddenly increased to 12 during August. Then, the number of warnings in September and October increased to more than 20, and the TR failure occurred in October.
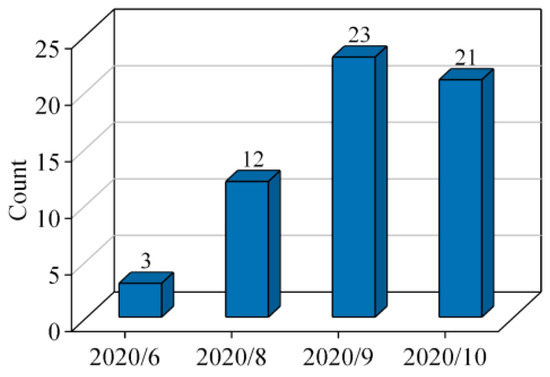
Figure 11.
V2 number of charge capacity warnings in different months.
As depicted in Figure 12, for V2, the SOC was charged from 97% to 98% at 16:00 on 28 October 2020. The SOC then dropped abnormally, resulting in a severe TR failure as a result of the sudden and rapid temperature increase of the probe to over 200 °C. Ultimately, the vehicle’s multiparameter transmission was lost, and the communication connection failed. In the fault statistics in Figure 10, there are up to 51 abnormal charging capacities of V2 when SOC = 97%. According to the definition of DCI in Equation (7), it is confirmed that V2 has a significant risk of failure when the SOC = 97% increases to SOC = 98%, which verifies the effectiveness of this method.
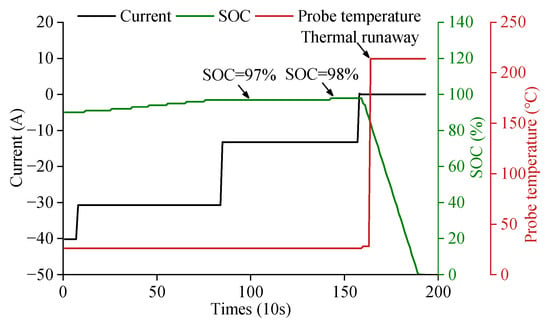
Figure 12.
TR occurs with parameter changes during V2 charging.
4.3. Model Validation
To test the validity of the model, a DCI prediction model was developed using the GPR data from each vehicle. The V1 training set was constructed based on the charging segments in June 2022 and July 2022, with subsequent dates inspected for failure. The training set was constructed using the charging segments of V2 vehicles in the April 2022 to May 2022 period to diagnose abnormal charging capacity faults between June 2022 and October 2022. As depicted in Figure 13, the abnormal DCI and corresponding SOC were tallied. In V1, there were no alarms, whereas in V2, the number of alarms was nearly identical to that in the previous model, and the faulty SOC was between 96% and 99%.
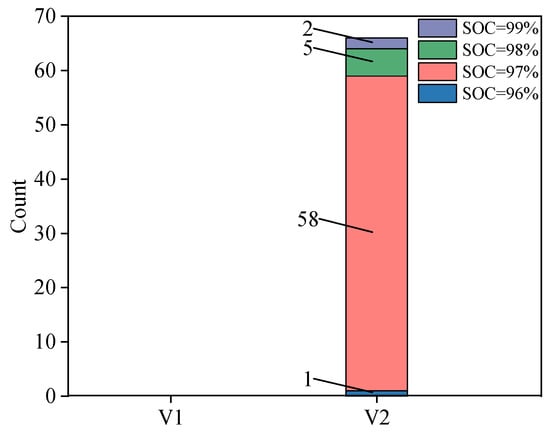
Figure 13.
Column distribution of the SOC corresponding to the abnormal charging capacity of V1 and V2 using GPR for each vehicle.
Table 3 presents the MAE and RMSE of various GPR establishment strategies. The GPR proposed in this study was more precise than the GPR established for each EV. Given that each vehicle must operate for some time, sufficient data can be used to establish regression. Owing to the small size of the training set, the generalisation performance of the model was inadequate.

Table 3.
MAE and RMSE of different strategies for establishing GPR.
The validity of the general model was verified by constructing a GPR model for each vehicle. Two distinct strategies were used to identify both the abnormal charging segments and the corresponding SOC of thermally runaway vehicles. Nevertheless, the GPR established for each vehicle could not be used to monitor the abnormal charging capacity of normal vehicles because it was not sufficiently sensitive. Without sufficient historical data, it is difficult to establish a model with a high accuracy for establishing the GPR for each EV. Moreover, if the historical data of a vehicle contain potentially abnormally charged DCI, it will provide a machine learning model with incorrect training data. More importantly, because the data platform monitors thousands of vehicles, establishing a model for each vehicle presents a challenge for the memory and processing load of the platform. We prefer to find a general and highly robust model; therefore, an offline GPR model based on the vehicle data of a certain brand is developed and used to monitor the charging safety of that brand’s vehicles online.
4.4. Model Comparison
Different kernel function performances were utilised to compare and validate the benefits of an enhanced GPR, including the combined kernel, neural network kernel, and linear kernel functions. Moreover, the relevant vector machine (RVM) and GPR are probability extension models based on the Bayesian framework [38]. The RVM performance was also utilised for this comparison.
The MAE and RMSE of the DCI predicted by the various methods for the two test sample EVs are shown in Figure 14. Figure 14a,b depict the MAE and RMSE of the various methods for V1 and V2, respectively. Because V2 is an abnormal vehicle and some abnormal samples exist, the MAE and RMSE of the GPR are slightly lower than the V1 of normal vehicles. The combination kernel function shows the best performance, and the generalisation performance of the function neural network kernel function is slightly lower than the combination kernel function. Because the capacity estimation is a complex and nonlinear regression task, the linear kernel function does not perform as efficiently as the preceding kernel functions. In this study, the RVM is more suitable for the testing and regression of small sample sets, and its performance is not as good as that of the GPR for the regression of big data.
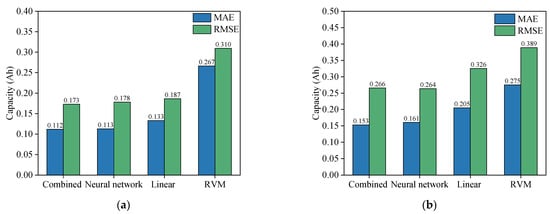
Figure 14.
MAE and RMSE of DCI predicted by different methods in two test sample EVs. (a) The MAE and RMSE of DCI are predicted by different methods in V1. (b) The MAE and RMSE of DCI are predicted by different methods in V2.
A true DCI that exceeds the 95% confidence interval of the GPR indicates a charging capacity fault. The thresholds determined by 3 and the Box–Cox transformation are compared to those determined with this method. Figure 15 depicts the prediction of a charging segment and a 95% confidence interval, with some values exceeding the 95% confidence interval. The method described in this study only activates an alarm for an abnormal charging capacity when SOC = 97%. Because of the 0.1 Hz sampling frequency and the noise in the real world, the variance fluctuates continuously during the GPR training, resulting in the instability of the confidence interval. This leads to a false alarm, as shown in Figure 15, for other points beyond the confidence interval except when SOC = 97%.
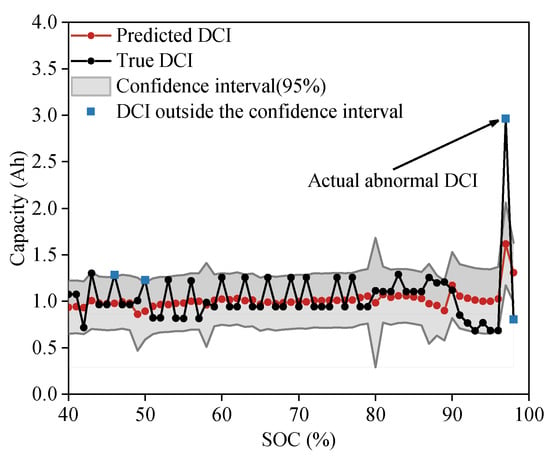
Figure 15.
Prediction and 95% confidence interval of a charging segment.
This section compares the performance of various covariance kernel functions and RVM, with the combined kernel function exhibiting the highest regression precision. The effectiveness of determining failures beyond the 95% confidence interval and Box–Cox failure determination are discussed. Owing to sampling frequency and environmental factors, the Box–Cox transformation results in increased stability and fewer false alarms when determining the charging capacity threshold.
5. Conclusions
A method for diagnosing the abnormal battery charging capacity based on EV operation data was developed in this study. By establishing offline and online diagnosis systems to monitor the charging capacity, the TR caused by overcharging can be effectively identified in time. The following are the most important findings of this study.
- (1)
- The XGBoost framework for data restoration eliminates the limitation that traditional interpolation can only fill a single line. A tuning parameter strategy that reduces the generalisation error of cross-validation improves the performance of the model. The MAE of this framework in recovering critical data of the battery, such as the current and voltage, reached 10.440 A and 0.573 V, respectively.
- (2)
- The abnormal charging capacity fault is identified by the absolute error between the GPR outputs and the true DCI, and the thresholds are determined using the Box–Cox with 3. The method finds vehicles with an abnormal charging capacity two months in advance, and the fault frequencies of the abnormal and normal vehicles are 0.5221 and 0.0311, respectively. In addition, the test vehicle frequently exhibits an abnormal charging capacity at high SOC levels; therefore, to prevent overcharging, it is necessary for manufacturers to focus on the charging strategy for controlling high SOC levels.
- (3)
- In reality, the model proposed in this study can establish a unified diagnosis and monitoring model for a specific brand of power batteries, and it exhibits good potential for application. The results indicate that the failure thresholds determined by Box–Cox with 3 produce fewer false alarms than those determined by confidence intervals. In addition, the tuning parameter workload of the proposed method is acceptable and can be simply and reliably integrated into a big data platform.
Author Contributions
Conceptualisation, F.L. and Y.M.; methodology, F.L.; software, F.L.; validation, Y.Z.; formal analysis, F.L.; investigation, Y.M.; resources, Y.M.; writing—original draft preparation, F.L.; writing—review and editing, Y.Z.; visualisation, F.L. and C.W.; supervision, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
This work is based on data provided by the new energy vehicle digital competition (http://www.ncbdc.top/, accessed on 1 January 2023). The authors thank the National Big Data Alliance of New Energy Vehicles for providing data. (http://www.ndanev.com/, accessed on 1 January 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xia, X.; Li, P. A review of the life cycle assessment of electric vehicles: Considering the influence of batteries. Sci. Total Environ. 2022, 814, 152870. [Google Scholar] [CrossRef]
- Chen, S.; Gao, Z.; Sun, T. Safety challenges and safety measures of Li-ion batteries. Energy Sci. Eng. 2021, 9, 1647–1672. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, W.; Yu, Q.; Sun, F. Research progress, challenges and prospects of fault diagnosis on battery system of electric vehicles. Appl. Energy 2020, 279, 115855. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Qu, C.; Zhou, Y.; Shan, T.; Zhang, J.; Hou, Y. Investigation on overcharge-caused thermal runaway of lithium-ion batteries in real-world electric vehicles. Appl. Energy 2022, 321, 119229. [Google Scholar] [CrossRef]
- Miao, Y.; Hynan, P.; Von Jouanne, A.; Yokochi, A. Current Li-ion battery technologies in electric vehicles and opportunities for advancements. Energies 2019, 12, 1074. [Google Scholar] [CrossRef]
- Dai, H.; Jiang, B.; Hu, X.; Lin, X.; Wei, X.; Pecht, M. Advanced battery management strategies for a sustainable energy future: Multilayer design concepts and research trends. Renew. Sustain. Energy Rev. 2021, 138, 110480. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, S.; Guo, J.; Qin, T. State of health estimation of lithium-ion batteries based on the constant voltage charging curve. Energy 2019, 167, 661–669. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Li, X.; Wang, Z. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression. Energy 2020, 190, 116467. [Google Scholar] [CrossRef]
- Pang, X.; Liu, X.; Jia, J.; Wen, J.; Shi, Y.; Zeng, J.; Zhao, Z. A lithium-ion battery remaining useful life prediction method based on the incremental capacity analysis and Gaussian process regression. Microelectron. Reliab. 2021, 127, 114405. [Google Scholar] [CrossRef]
- She, C.; Zhang, L.; Wang, Z.; Sun, F.; Liu, P.; Song, C. Battery state of health estimation based on incremental capacity analysis method: Synthesizing from cell-level test to real-world application. IEEE J. Emerg. Sel. Top. Power Electron. 2021. [Google Scholar] [CrossRef]
- Song, L.; Zhang, K.; Liang, T.; Han, X.; Zhang, Y. Intelligent state of health estimation for lithium-ion battery pack based on big data analysis. J. Energy Storage 2020, 32, 101836. [Google Scholar] [CrossRef]
- Jiang, L.; Diao, X.; Zhang, Y.; Zhang, J.; Li, T. Review of the Charging Safety and Charging Safety Protection of Electric Vehicles. World Electr. Veh. J. 2021, 12, 184. [Google Scholar] [CrossRef]
- Kurzweil, P.; Frenzel, B.; Scheuerpflug, W. A Novel Evaluation Criterion for the Rapid Estimation of the Overcharge and Deep Discharge of Lithium-Ion Batteries Using Differential Capacity. Batteries 2022, 8, 86. [Google Scholar] [CrossRef]
- Zhang, C.; Fang, W.; Zhao, B.; Xie, Z.; Hu, C.; Wen, H.; Zhong, T. Study on Fault Diagnosis Method and Application of Automobile Power Supply Based on Fault Tree-Bayesian Network. Secur. Commun. Netw. 2022, 2022, 4046966. [Google Scholar] [CrossRef]
- Wang, L.-y.; Wang, L.-f.; Liu, W.; Zhang, Y.-w. Research on Fault Diagnosis System of Electric Vehicle Power Battery Based on OBD Technology. In Proceedings of the 2017 International Conference on Circuits, Devices and Systems (ICCDS), Chengdu, China, 5–8 September 2017; pp. 95–99. [Google Scholar]
- Tian, J.; Wang, Y.; Chen, Z. Sensor fault diagnosis for lithium-ion battery packs based on thermal and electrical models. Int. J. Electr. Power Energy Syst. 2020, 121, 106087. [Google Scholar] [CrossRef]
- Feng, X.; Pan, Y.; He, X.; Wang, L.; Ouyang, M. Detecting the internal short circuit in large-format lithium-ion battery using model-based fault-diagnosis algorithm. J. Energy Storage 2018, 18, 26–39. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, P.; Wang, Z.; Zhang, L.; Hong, J. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Wang, C.; Yu, C.; Guo, W.; Wang, Z.; Tan, J. Identification of Typical Sub-Health State of Traction Battery Based on a Data-Driven Approach. Batteries 2022, 8, 65. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Ma, F.; Yang, J.; Xu, X.; Qu, C.; Zhang, J.; Shan, T.; Hou, Y.; Zhou, Y. Thermal runaway prognosis of battery systems using the modified multiscale entropy in real-world electric vehicles. IEEE Trans. Transp. Electrif. 2021, 7, 2269–2278. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, G.; Kang, Y.; Zhou, Z.; Duan, B.; Zhang, C. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Sources 2020, 446, 227275. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Z.; Chen, Y.; Liu, P.; Wang, S.; Zhang, Z.; Dorrell, D.G. Modified Relative Entropy-Based Lithium-Ion Battery Pack Online Short-Circuit Detection for Electric Vehicle. IEEE Trans. Transp. Electrif. 2021, 8, 1710–1723. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, J.; Liu, P.; Zhang, L. Voltage fault diagnosis and prognosis of battery systems based on entropy and Z-score for electric vehicles. Appl. Energy 2017, 196, 289–302. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Liu, P.; Wang, Z.; Zhang, L. Battery fault diagnosis for electric vehicles based on voltage abnormality by combining the long short-term memory neural network and the equivalent circuit model. IEEE Trans. Power Electron. 2020, 36, 1303–1315. [Google Scholar] [CrossRef]
- Klink, J.; Hebenbrock, A.; Grabow, J.; Orazov, N.; Nylén, U.; Benger, R.; Beck, H.-P. Comparison of Model-Based and Sensor-Based Detection of Thermal Runaway in Li-Ion Battery Modules for Automotive Application. Batteries 2022, 8, 34. [Google Scholar] [CrossRef]
- Zheng, Y.; Luo, Q.; Cui, Y.; Dai, H.; Han, X.; Feng, X. Fault identification and quantitative diagnosis method for series-connected lithium-ion battery packs based on capacity estimation. IEEE Trans. Ind. Electron. 2021, 69, 3059–3067. [Google Scholar] [CrossRef]
- Wang, Z.; Song, C.; Zhang, L.; Zhao, Y.; Liu, P.; Dorrell, D.G. A data-driven method for battery charging capacity abnormality diagnosis in electric vehicle applications. IEEE Trans. Transp. Electrif. 2021, 8, 990–999. [Google Scholar] [CrossRef]
- Bi, J.; Wang, Y.; Sai, Q.; Ding, C. Estimating remaining driving range of battery electric vehicles based on real-world data: A case study of Beijing, China. Energy 2019, 169, 833–843. [Google Scholar] [CrossRef]
- Li, F.; Min, Y.; Zhang, Y. A Novel Method for Lithium-Ion Battery Fault Diagnosis of Electric Vehicle Based on Real-Time Voltage. Wirel. Commun. Mob. Comput. 2022, 2022, 7277446. [Google Scholar] [CrossRef]
- Nan, J.; Deng, B.; Cao, W.; Hu, J.; Chang, Y.; Cai, Y.; Zhong, Z. Big Data-Based Early Fault Warning of Batteries Combining Short-Text Mining and Grey Correlation. Energies 2022, 15, 5333. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, P.; Zhang, X.; Lin, N. Research on Safety of New Energy Vehicles based on Big Data. In Proceedings of the 2022 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 24–26 June 2022; pp. 507–510. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Gan, N.; Sun, Z.; Zhang, Z.; Xu, S.; Liu, P.; Qin, Z. Data-driven fault diagnosis of lithium-ion battery overdischarge in electric vehicles. IEEE Trans. Power Electron. 2021, 37, 4575–4588. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Jin, S.-S. Compositional kernel learning using tree-based genetic programming for Gaussian process regression. Struct. Multidiscip. Optim. 2020, 62, 1313–1351. [Google Scholar] [CrossRef]
- Kazemzadeh, E.; Fuinhas, J.A.; Koengkan, M. The impact of income inequality and economic complexity on ecological footprint: An analysis covering a long-time span. J. Environ. Econ. Policy 2022, 11, 133–153. [Google Scholar] [CrossRef]
- Quinonero-Candela, J. Learning with Uncertainty: Gaussian Processes and Relevance Vector Machines; Technical University of Denmark: Lyngby, Denmark, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).