Equivalent Circuit Model for High-Power Lithium-Ion Batteries under High Current Rates, Wide Temperature Range, and Various State of Charges
Abstract
:1. Introduction
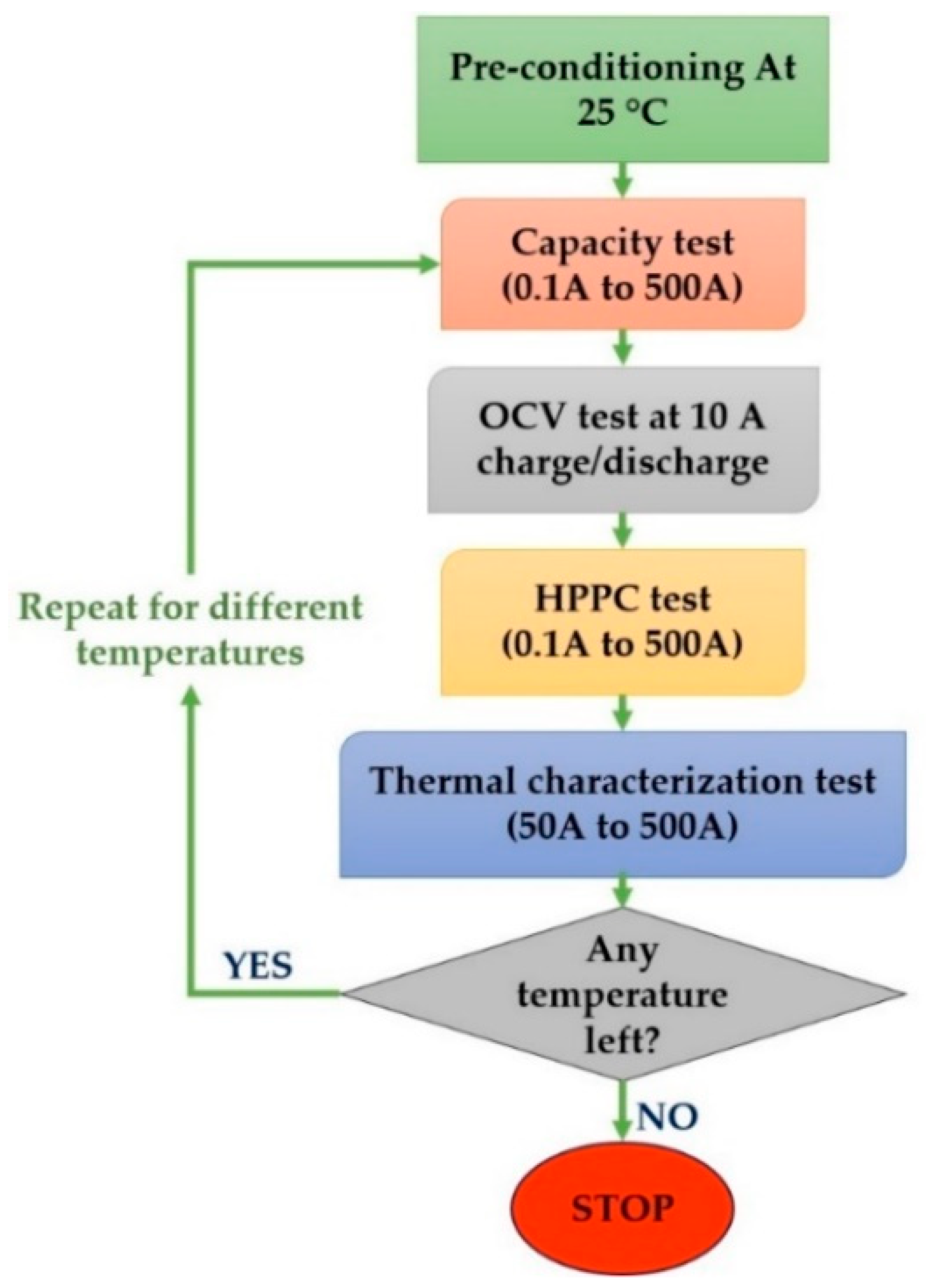
2. Experimental Procedures
3. Equivalent Circuit Model (ECM) Development and Trend Analysis
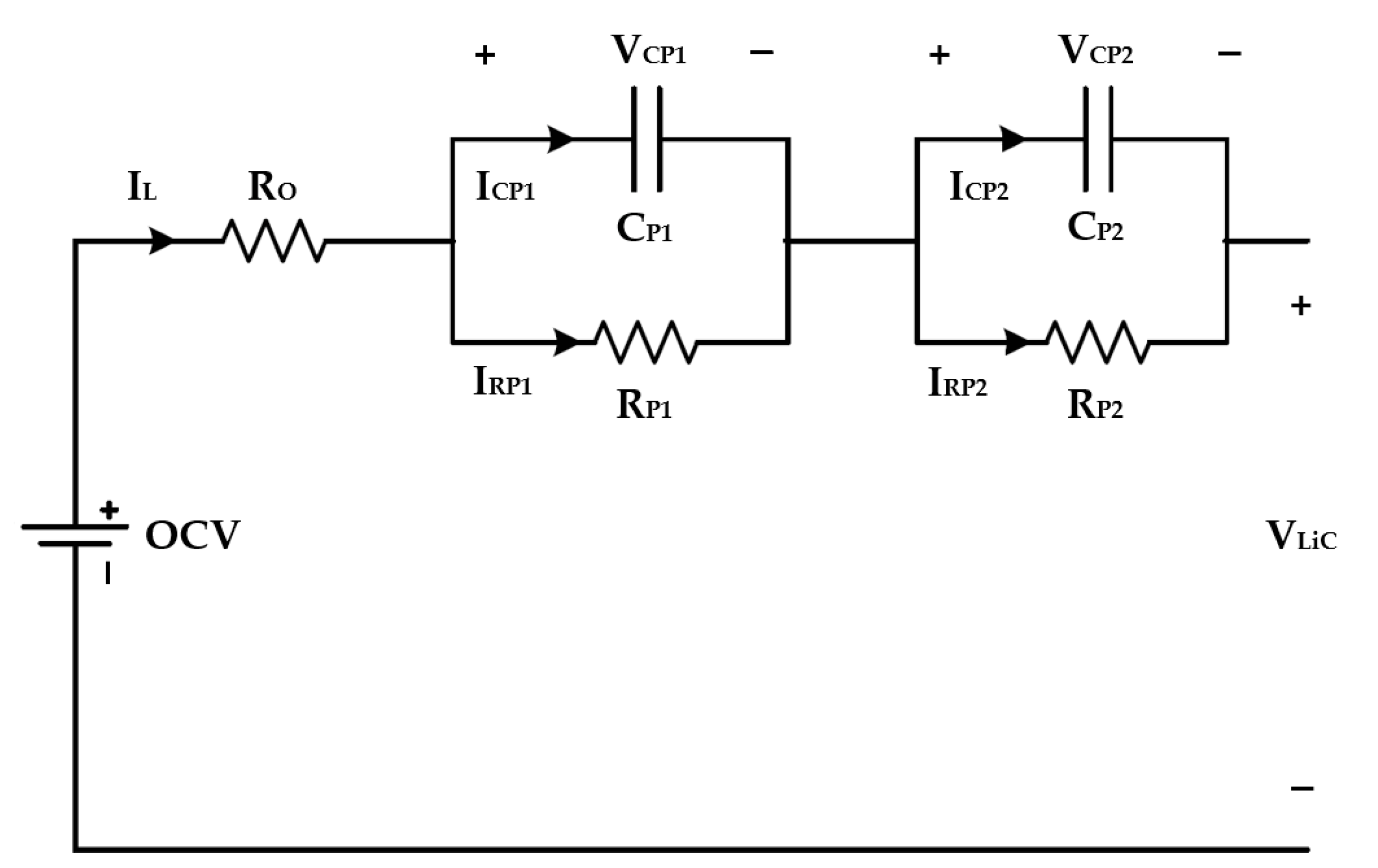
3.1. The Second-Order Equivalent Circuit Model (ECM)
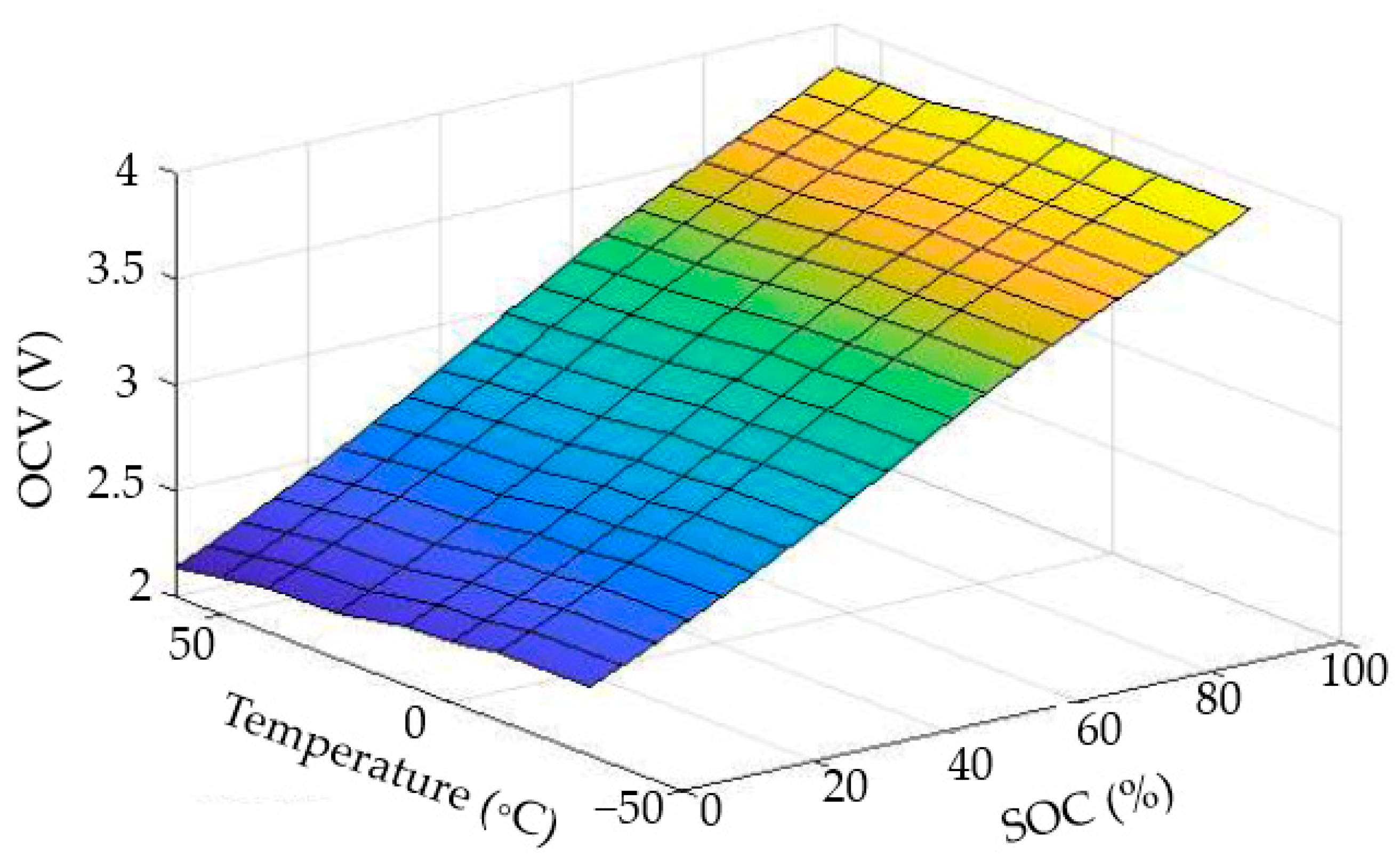
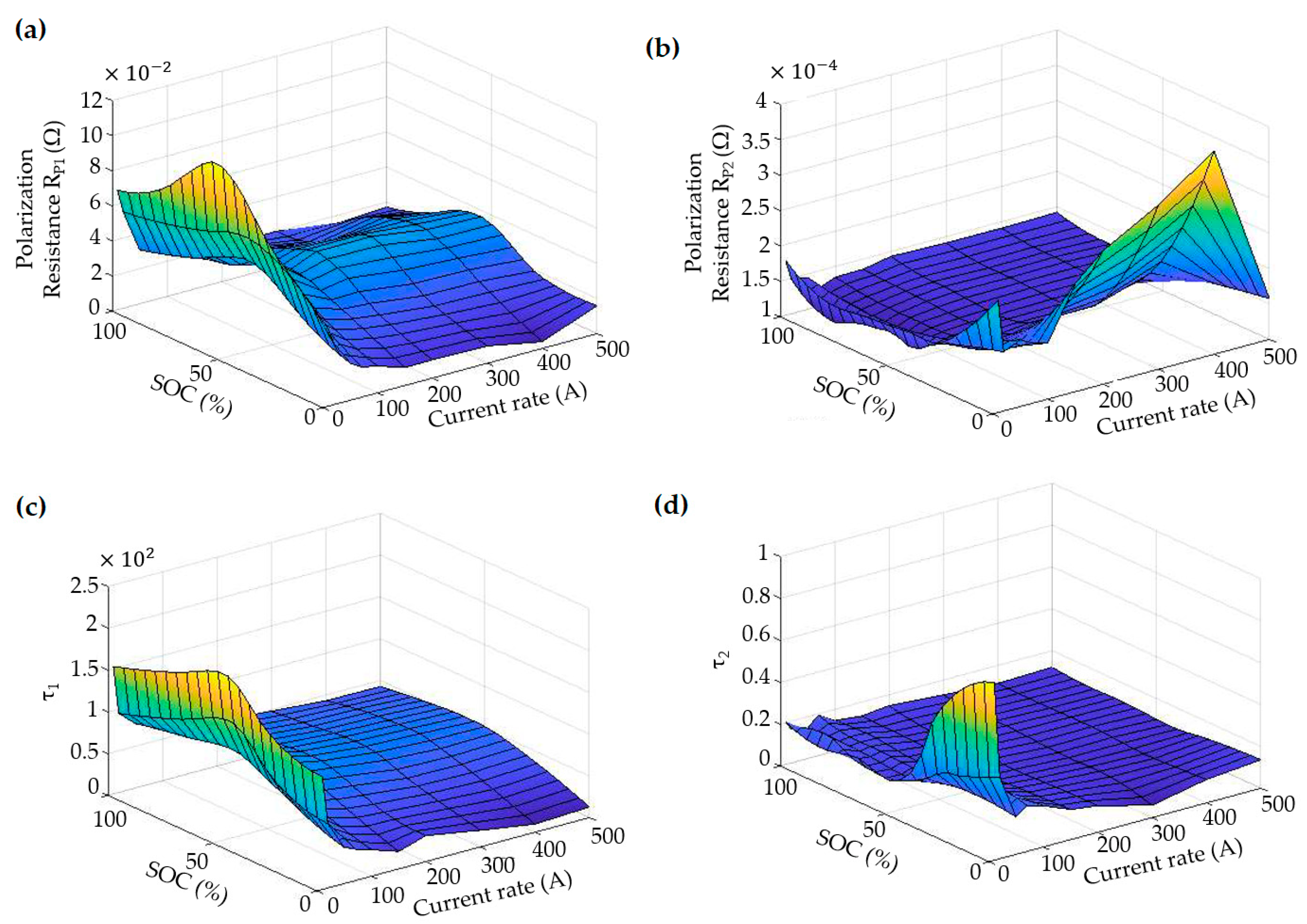
3.2. The LiC Cell Characterization Results and Trend Analysis
4. Validation of the Second-Order ECM
5. Conclusions
- The electrical parameters were generated at other temperatures such as −10 °C, 0 °C, 10 °C, 40 °C, 50 °C, and 60 °C. The table includes the applied current of 10 A, 20 A, 50 A, 70 A, 100 A, 150 A, 200 A, 300 A, 400 A, and 500 A.
- The SOC range was from 0% to 100%, but in this paper, three SOC values have been listed in the table, including 25% SOC, 50% SOC, and 100% SOC, to compare how the electrical parameters differ at different SOC values.
- The results proved that decreasing the temperature increases the ohmic resistance sharply, regardless of the health status of the cell. Moreover, when the LiC was aged, the ohmic resistance was increased. When the ohmic resistance was increased by 200%, the cell is called a dead cell (end-of-life degradation).
- This behavior was even sharper when the operating temperature was too cold, meaning that the ohmic resistance increased faster. This trend was the same for the polarization resistances for both RC branches, which was increased by decreasing the temperature. However, polarization resistance was changed sharply with SOC variation.
- The validation results exhibit that, where the current rate was less than 150 A, the error of the developed ECM was lower than 3%. When the demanded power was high, in current rates above 150 A, the error of the developed model was lower than 5%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Mierlo, J.; Berecibar, M.; El Baghdadi, M.; De Cauwer, C.; Messagie, M.; Coosemans, T.; Jacobs, V.; Hegazy, O. Beyond the State of the Art of Electric Vehicles: A Fact-Based Paper of the Current and Prospective Electric Vehicle Technologies. World Electr. Veh. J. 2021, 12, 20. [Google Scholar] [CrossRef]
- Khaleghi, S.; Hosen, M.; Karimi, D.; Behi, H.; Beheshti, S.; Van Mierlo, J.; Berecibar, M. Developing an online data-driven approach for prognostics and health management of lithium-ion batteries. Appl. Energy. 2022, 308, 118348. [Google Scholar] [CrossRef]
- Kim, G.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources. 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Van Mierlo, J.; Berecibar, M. Novel Hybrid Thermal Management System for High-Power Lithium-Ion Module for Electric Vehicles: Fast Charging Applications. World Electr. Veh. J. 2022, 13, 86. [Google Scholar] [CrossRef]
- Soltani, M.; Berckmans, G.; Jaguemont, J.; Ronsmans, J.; Kakihara, S.; Hegazy, O.; Van Mierlo, J.; Omar, N. Three dimensional thermal model development and validation for lithium-ion capacitor module including air-cooling system. Appl. Therm. Eng. 2019, 153, 264–274. [Google Scholar] [CrossRef]
- Soltani, M.; Beheshti, S. A comprehensive review of lithium ion capacitor: Development, modelling, thermal management and applications. J. Energy Storage 2021, 34, 102019. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Kalogiannis, T.; Jin, L.; Karimi, D.; Van Mierlo, J.; Berecibar, M. Experimental and numerical thermal analysis of a lithium-ion battery module based on a novel liquid cooling plate embedded with phase change material. J. Energy Storage. 2022, 50, 104673. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Van Mierlo, J.; Berecibar, M. A Comprehensive Review of Lithium-Ion Capacitor Technology: Theory, Development, Modeling, Thermal Management Systems, and Applications. Molecules 2022, 27, 3119. [Google Scholar] [CrossRef]
- Soltani, M.; Ronsmans, J.; Kakihara, S.; Jaguemont, J.; Van den Bossche, P.; van Mierlo, J.; Omar, N. Hybrid battery/lithium-ion capacitor energy storage system for a pure electric bus for an urban transportation application. Appl. Sci. 2018, 8, 1176. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Akbarzadeh, M.; Khaleghi, S.; Van Mierlo, J.; Berecibar, M. Optimization of 1D/3D Electro-Thermal Model for Liquid-Cooled Lithium-Ion Capacitor Module in High Power Applications. Electricity 2021, 2, 503–523. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Van Mierlo, J.; Berecibar, M. An Experimental Study on Thermal Performance of Graphite-Based Phase-Change Materials for High-Power Batteries. Energies 2022, 15, 2515. [Google Scholar] [CrossRef]
- Sedlakova, V.; Sikula, J.; Majzner, J.; Sedlak, P.; Kuparowitz, T.; Buergler, B.; Vasina, P. Supercapacitor equivalent electrical circuit model based on charges redistribution by diffusion. J. Power Sources. 2015, 286, 58–65. [Google Scholar] [CrossRef]
- Karimi, D.; Hosen, M.; Behi, H.; Khaleghi, S.; Akbarzadeh, M.; Van Mierlo, J.; Berecibar, M. A hybrid thermal management system for high power lithium-ion capacitors combining heat pipe with phase change materials. Heliyon 2021, 7, e07773. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zhang, C.; Wang, K.; Yu, F.; Xie, J.; Zhang, Q. Multi-thiol-supported dicarboxylate-based metal–organic framework with excellent performance for lithium-ion battery. Chem. Eng. J. 2022, 431, 133234. [Google Scholar] [CrossRef]
- Li, C.; Zhang, C.; Xie, J.; Wang, K.; Li, J.; Zhang, Q. Ferrocene-based metal-organic framework as a promising cathode in lithium-ion battery. Chem. Eng. J. 2021, 404, 126463. [Google Scholar] [CrossRef]
- Wang, H.; Yao, C.; Nie, H.; Wang, K.; Zhong, Y.; Chen, P.; Mei, S.; Zhang, Q. Recent progress in carbonyl-based organic polymers as promising electrode materials for lithium-ion batteries (LIBs). J. Mater. Chem. A 2020, 8, 11906–11922. [Google Scholar] [CrossRef]
- Li, C.; Yang, H.; Xie, J.; Wang, K.; Li, J.; Zhang, Q. Ferrocene-Based Mixed-Valence Metal-Organic Framework as an Efficient and Stable Cathode for Lithium-Ion-Based Dual-Ion Battery. ACS Appl. Mater. Interfaces 2020, 12, 32719–32725. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Kalogiannis, T.; He, J.; Patil, M.; Muller, J.-D.; Haider, A.; Van Mierlo, J.; Berecibar, M. Advanced hybrid thermal management system for LTO battery module under fast charging. Case Stud. Therm. Eng. 2022, 33, 101938. [Google Scholar] [CrossRef]
- Jaguemont, J.; Van Mierlo, J. A comprehensive review of future thermal management systems for battery-electrified vehicles. J. Energy Storage. 2020, 31, 101551. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Akbarzadeh, M.; Van Mierlo, J.; Berecibar, M. A Novel Air-Cooled Thermal Management Approach towards High-Power Lithium-Ion Capacitor Module for Electric Vehicles. Energies 2021, 14, 7150. [Google Scholar] [CrossRef]
- Patel, J.; Rathod, M. Recent developments in the passive and hybrid thermal management techniques of lithium-ion batteries. J. Power Sources 2020, 480, 228820. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Jaguemont, J.; Kalogiannis, T.; Karimi, D.; He, J.; Jin, L.; Xie, P.; Van Mierlo, J.; Berecibar, M. A novel liquid cooling plate concept for thermal management of lithium-ion batteries in electric vehicles. Energy Convers. Manag. 2021, 231, 113862. [Google Scholar] [CrossRef]
- Gandoman, F.; Behi, H.; Berecibar, M.; Jaguemont, J.; Aleem, S.; Behi, M.; Van Mierlo, J. Chapter 16—Reliability evaluation of Li-ion batteries for electric vehicles applications from the thermal perspectives. In Uncertainties in Modern Power Systems; Zobaa, A.F., Abdel Aleem, S.H.E., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 563–587. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Karimi, D.; Berecibar, M.; Van Mierlo, J. Modular Methodology for Developing Comprehensive Active and Passive Thermal Management Systems for Electric Vehicles, Vrije Universiteit Brussel. 2022. Available online: https://researchportal.vub.be/en/publications/modular-methodology-for-developing-comprehensive-active-and-passi (accessed on 13 April 2022).
- Karimi, D.; Behi, H.; Jaguemont, J.; Berecibar, M.; Van Mierlo, J. A refrigerant-based thermal management system for a fast charging process for lithium-ion batteries. In Proceedings of the International Conference on Renewable Energy Systems and Environmental Engineering (IRESE2020), Brussels, Belgium, 18–20 July 2020; Global Publishers: Glendale, WI, USA, 2020; pp. 1–6. [Google Scholar]
- Akbarzadeh, M.; Kalogiannis, T.; Jaguemont, J.; Jin, L.; Behi, H.; Karimi, D.; Beheshti, H.; Van Mierlo, J.; Berecibar, M. A comparative study between air cooling and liquid cooling thermal management systems for a high-energy lithium-ion battery module. Appl. Therm. Eng. 2021, 198, 117503. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Hosen, M.; Jaguemont, J.; Berecibar, M.; Van Mierlo, J. A compact and optimized liquid-cooled thermal management system for high power lithium-ion capacitors. Appl. Therm. Eng. 2021, 185, 116449. [Google Scholar] [CrossRef]
- Giuliani, F.; Delmonte, N.; Cova, P. Thermal-Fluid Dynamic FEM Simulation of Advanced Water Cold Plates for Power Electronics. In Proceedings of the COMSOL Conference, Milan, Italy, 10–12 October 2012. [Google Scholar]
- Behi, H.; Behi, M.; Karimi, D.; Jaguemont, J.; Ghanbarpour, M.; Behnia, M.; Berecibar, M.; Van Mierlo, J. Heat pipe air-cooled thermal management system for lithium-ion batteries: High power applications. Appl. Therm. Eng. 2020, 183, 116240. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Behi, M.; Jaguemont, J.; Ghanbarpour, M.; Behnia, M.; Berecibar, M.; Van Mierlo, J. Thermal management analysis using heat pipe in the high current discharging of lithium-ion battery in electric vehicles. J. Energy Storage 2020, 32, 101893. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Jaguemont, J.; Gandoman, F.; Khaleghi, S.; Van Mierlo, J.; Berecibar, M. Aluminum heat sink assisted air-cooling thermal management system for high current applications in electric vehicles. In Proceedings of the 2020 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 18–20 November 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Behi, H.; Behi, M.; Ghanbarpour, A.; Karimi, D.; Azad, A.; Ghanbarpour, M.; Behnia, M. Enhancement of the Thermal Energy Storage Using Heat-Pipe-Assisted Phase Change Material. Energies 2021, 14, 6176. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Jaguemont, J.; Sokkeh, M.; Kalogiannis, T.; Hosen, M.; Berecibar, M.; Van Mierlo, J. Thermal performance enhancement of phase change material using aluminum-mesh grid foil for lithium-capacitor modules. J. Energy Storage 2020, 30, 101508. [Google Scholar] [CrossRef]
- Möller, S.; Karimi, D.; Vanegas, O.; El Baghdadi, M.; Kospach, A.; Lis, A.; Hegazy, O.; Abart, C.; Offenbach, Â. Application considerations for Double Sided Cooled Modules in Automotive Environment. 2020. Available online: https://ieeexplore.ieee.org/document/9097721 (accessed on 16 November 2020).
- Karimi, D.; Behi, H.; Jaguemont, J.; Berecibar, M.; Van Mierlo, J. Optimized air-cooling thermal management system for high power lithium-ion capacitors. Energy Perspect. 2020, 1, 93. [Google Scholar]
- Karimi, D.; Behi, H.; Jaguemont, J.; Berecibar, M.; Van Mierlo, J. Investigation of extruded heat sink assisted air cooling system for lithium-ion capacitor batteries. In Proceedings of the International Conference on Renewable Energy Systems and Environmental Engineering, Brussels, Belgium, 18–20 July 2020; Global Publishers: Glendale, WI, USA, 2020; pp. 1–6. [Google Scholar]
- Behi, H.; Karimi, D.; Behi, M.; Ghanbarpour, M.; Jaguemont, J.; Sokkeh, M.; Gandoman, F.; Berecibar, M.; Van Mierlo, J. A new concept of thermal management system in Li-ion battery using air cooling and heat pipe for electric vehicles. Appl. Therm. Eng. 2020, 174, 115280. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Youssef, R.; Patil, M.S.; Van Mierlo, J.; Berecibar, M. Comprehensive Passive Thermal Management Systems for Electric Vehicles. Energies 2021, 14, 3881. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Gandoman, F.; Akbarzadeh, M.; Khaleghi, S.; Kalogiannis, T.; Hosen, M.; Jaguemont, J.; Van Mierlo, J.; Berecibar, M. PCM assisted heat pipe cooling system for the thermal management of an LTO cell for high-current profiles. Case Stud. Therm. Eng. 2021, 25, 100920. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Jaguemont, J.; El Baghdadi, M.; Van Mierlo, J.; Hegazy, O. Thermal Concept Design of MOSFET Power Modules in Inverter Subsystems for Electric Vehicles. In Proceedings of the 2019 9th International Conference on Power and Energy Systems (ICPES), Perth, WA, Australia, 10–12 December 2019. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Jaguemont, J.; Berecibar, M.; Van Mierlo, J. Experimental study on cooling performance of flat heat pipe for lithium-ion battery at various inclination angels. Energy Perspect. 2020, 1, 77. [Google Scholar]
- Jaguemont, J.; Karimi, D.; Van Mierlo, J. Investigation of a Passive Thermal Management System for Lithium-Ion Capacitors. IEEE Trans. Veh. Technol. 2019, 68, 10518–10524. [Google Scholar] [CrossRef]
- Karimi, D.; Jaguemont, J.; Behi, H.; Berecibar, M.; Van Den Bossche, P.; Van Mierlo, J. Passive cooling based battery thermal management using phase change materials for electric vehicles. In Proceedings of the EVS33—33nd Electric Vehicle Symposium, Portland, OR, USA, 14–17 June 2020; pp. 1–12. [Google Scholar]
- Hosen, M.; Karimi, D.; Kalogiannis, T.; Pirooz, A.; Jaguemont, J.; Berecibar, M.; Van Mierlo, J. Electro-aging model development of nickel-manganese-cobalt lithium-ion technology validated with light and heavy-duty real-life profiles. J. Energy Storage 2020, 28, 101265. [Google Scholar] [CrossRef]
- Movassagh, K.; Raihan, A.; Balasingam, B.; Pattipati, K. A Critical Look at Coulomb Counting Approach for State of Charge Estimation in Batteries. Energies 2021, 14, 4074. [Google Scholar] [CrossRef]
- Wu, L.; Pang, H.; Geng, Y.; Liu, X.; Liu, J.; Liu, K. Low-complexity state of charge and anode potential prediction for lithium-ion batteries using a simplified electrochemical model-based observer under variable load condition. Int. J. Energy Res. 2022, 46, 11834–11848. [Google Scholar] [CrossRef]
- Lucu, M.; Martinez-Laserna, E.; Gandiaga, I.; Camblong, H. A critical review on self-adaptive Li-ion battery ageing models. J. Power Sources 2018, 401, 85–101. [Google Scholar] [CrossRef]
- Ahmed, R.; Rahimifard, S.; Habibi, S. Offline Parameter Identification and SOC Estimation for New and Aged Electric Vehicles Batteries. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019. [Google Scholar] [CrossRef]
- Mohammedi, M.; Kraa, O.; Becherif, M.; Aboubou, A.; Ayad, M.; Bahri, M. Fuzzy logic and passivity-based controller applied to electric vehicle using fuel cell and supercapacitors hybrid source. Energy Procedia 2014, 50, 619–626. [Google Scholar] [CrossRef]
- Lyu, P.; Liu, X.; Qu, J.; Zhao, J.; Huo, Y.; Qu, Z.; Rao, Z. Recent advances of thermal safety of lithium ion battery for energy storage. Energy Storage Mater. 2020, 31, 195–220. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Gandolfo, D.; Brandão, A.; Patiño, D.; Molina, M. Dynamic model of lithium polymer battery—Load resistor method for electric parameters identification. J. Energy Inst. 2015, 88, 470–479. [Google Scholar] [CrossRef]
- Tran, M.; Fowler, M. Sensor Fault Detection and Isolation for Degrading Lithium-Ion Batteries in Electric Vehicles Using Parameter Estimation with Recursive Least Squares. Batteries 2019, 6, 1. [Google Scholar] [CrossRef]
- Gao, Z.; Chin, C.; Woo, W.; Jia, J. Integrated equivalent circuit and thermal model for simulation of temperature-dependent LiFePO4 battery in actual embedded application. Energies 2017, 10, 85. [Google Scholar] [CrossRef]
- Khaleghi, S.; Karimi, D.; Beheshti, S.; Hosen, S.; Behi, H.; Berecibar, M.; Van Mierlo, J. Online health diagnosis of lithium-ion batteries based on nonlinear autoregressive neural network. Appl. Energy 2021, 282, 116159. [Google Scholar] [CrossRef]
- Omar, N.; Daowd, M.; Hegazy, O.; Al Sakka, M.; Coosemans, T.; Van Den Bossche, P.; Van Mierlo, J. Assessment of lithium-ion capacitor for using in battery electric vehicle and hybrid electric vehicle applications. Electrochim. Acta 2012, 86, 305–315. [Google Scholar] [CrossRef]
- Firouz, Y.; Omar, N.; Timmermans, J.; Van den Bossche, P.; Van Mierlo, J. Lithium-ion capacitor—Characterization and development of new electrical model. Energy 2015, 83, 597–613. [Google Scholar] [CrossRef]
- Soltani, M.; De Sutter, L.; Ronsmans, J.; van Mierlo, J. A high current electro-thermal model for lithium-ion capacitor technology in a wide temperature range. J. Energy Storage 2020, 31, 101624. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources. 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Pang, H.; Guo, L.; Wu, L.; Jin, J.; Zhang, F.; Liu, K. A novel extended Kalman filter-based battery internal and surface temperature estimation based on an improved electro-thermal model. J. Energy Storage 2021, 41, 102854. [Google Scholar] [CrossRef]
- Pang, H.; Jin, J.; Wu, L.; Zhang, F.; Liu, K. A Comprehensive Physics-Based Equivalent-Circuit Model and State of Charge Estimation for Lithium-Ion Batteries. J. Electrochem. Soc. 2021, 168, 090552. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Jaguemont, J.; Gandoman, F.; Kalogiannis, T.; Berecibar, M.; Van Mierlo, J. Novel thermal management methods to improve the performance of the Li-ion batteries in high discharge current applications. Energy 2021, 224, 120165. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Akbarzadeh, M.; Van Mierlo, J.; Berecibar, M. Holistic 1D Electro-Thermal Model Coupled to 3D Thermal Model for Hybrid Passive Cooling System Analysis in Electric Vehicles. Energies 2021, 14, 5924. [Google Scholar] [CrossRef]
- Hosen, M.; Kalogiannis, T.; Youssef, R.; Karimi, D.; Behi, H.; Jin, L.; Van Mierlo, J.; Berecibar, M. Twin-model framework development for a comprehensive battery lifetime prediction validated with a realistic driving profile. Energy Sci. Eng. 2021, 9, 2191–2201. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D. Heat transfer enhancement in an air to water heat exchanger with discontinuous helical turbulators; experimental and numerical studies. Energy 2016, 116, 341–352. [Google Scholar] [CrossRef]
- Karimi, D.; Khaleghi, S.; Behi, H.; Beheshti, H.; Hosen, M.; Akbarzadeh, M.; Van Mierlo, J.; Berecibar, M. Lithium-ion capacitor lifetime extension through an optimal thermal management system for smart grid applications. Energies 2021, 14, 2907. [Google Scholar] [CrossRef]




| Specification | Value/Unit |
|---|---|
| Number of cells | 10 |
| Capacitance | 2300 F |
| Min. cut-off voltage | 2.2 V |
| Max. cut-off voltage | 3.8 V |
| Weight | 350 g |
| Width | 150 mm |
| Height | 93 mm |
| Thickness | 15.5 mm |
| Current (A) | SOC (%) | Ro-dis(Ω) | Rp1-dis(Ω) | Rp2-dis(Ω) | τ1 (s) | τ2 (s) |
|---|---|---|---|---|---|---|
| 10 | 25 | |||||
| 10 | 50 | |||||
| 10 | 100 | |||||
| 20 | 25 | |||||
| 20 | 50 | |||||
| 20 | 100 | |||||
| 50 | 25 | |||||
| 50 | 50 | |||||
| 50 | 100 | |||||
| 70 | 25 | |||||
| 70 | 50 | |||||
| 70 | 100 | |||||
| 100 | 25 | |||||
| 100 | 50 | |||||
| 100 | 100 | |||||
| 150 | 25 | |||||
| 150 | 50 | |||||
| 150 | 100 | |||||
| 200 | 25 | |||||
| 200 | 50 | |||||
| 200 | 100 | |||||
| 300 | 25 | |||||
| 300 | 50 | |||||
| 300 | 100 | |||||
| 400 | 25 | |||||
| 400 | 50 | |||||
| 400 | 100 | |||||
| 500 | 25 | |||||
| 500 | 50 | |||||
| 500 | 100 |
| Parameter | Precision | Resolution | |
|---|---|---|---|
| Current | 0–50 (A) | ±0.03% | 100 µA |
| Voltage | 0–5 (V) | ±0.03% | 200 µV |
| Temperature | −40–200 (°C) | ±0.2% | 0.1 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimi, D.; Behi, H.; Van Mierlo, J.; Berecibar, M. Equivalent Circuit Model for High-Power Lithium-Ion Batteries under High Current Rates, Wide Temperature Range, and Various State of Charges. Batteries 2023, 9, 101. https://doi.org/10.3390/batteries9020101
Karimi D, Behi H, Van Mierlo J, Berecibar M. Equivalent Circuit Model for High-Power Lithium-Ion Batteries under High Current Rates, Wide Temperature Range, and Various State of Charges. Batteries. 2023; 9(2):101. https://doi.org/10.3390/batteries9020101
Chicago/Turabian StyleKarimi, Danial, Hamidreza Behi, Joeri Van Mierlo, and Maitane Berecibar. 2023. "Equivalent Circuit Model for High-Power Lithium-Ion Batteries under High Current Rates, Wide Temperature Range, and Various State of Charges" Batteries 9, no. 2: 101. https://doi.org/10.3390/batteries9020101
APA StyleKarimi, D., Behi, H., Van Mierlo, J., & Berecibar, M. (2023). Equivalent Circuit Model for High-Power Lithium-Ion Batteries under High Current Rates, Wide Temperature Range, and Various State of Charges. Batteries, 9(2), 101. https://doi.org/10.3390/batteries9020101










