An Enhanced Single-Particle Model Using a Physics-Informed Neural Network Considering Electrolyte Dynamics for Lithium-Ion Batteries
Abstract
:1. Introduction
- (1)
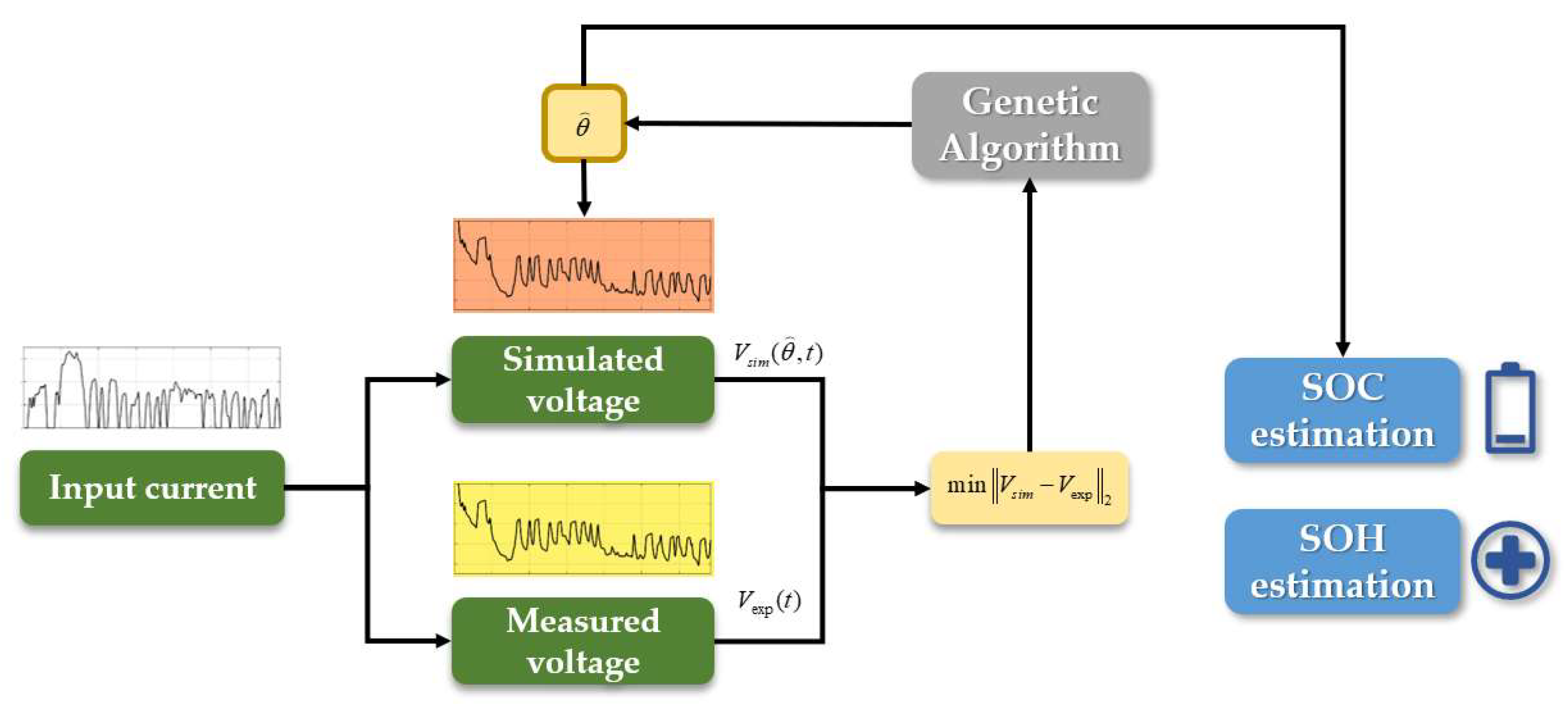
- Establishment of an SPM with electrolyte dynamics called PINN SPM. This model greatly improves the accuracy of the SPM under high C-rates. It uses a PINN to approximate the lithium-ion distribution in electrolytes and then calculates the electrolyte potential distribution so that the error of the SPM can be eliminated.
- (2)
- Creation of a physics-informed neural network called SPM-Net, which is the central part of PINN SPM. It can quickly solve the one-dimensional diffusion equation of the LIB model, which means the network can approximate the electrolyte lithium-ion concentration distribution under various applied currents with specific battery parameters.
- (3)
- Better performance of the battery electrochemical model. Using the physical constraints from PDE to design the loss function, SPM-Net can approximate the concentration results more accurately than the traditional neural network under dynamic conditions. Additionally, it is 20.8% faster than the traditional numerical method under dynamic conditions.
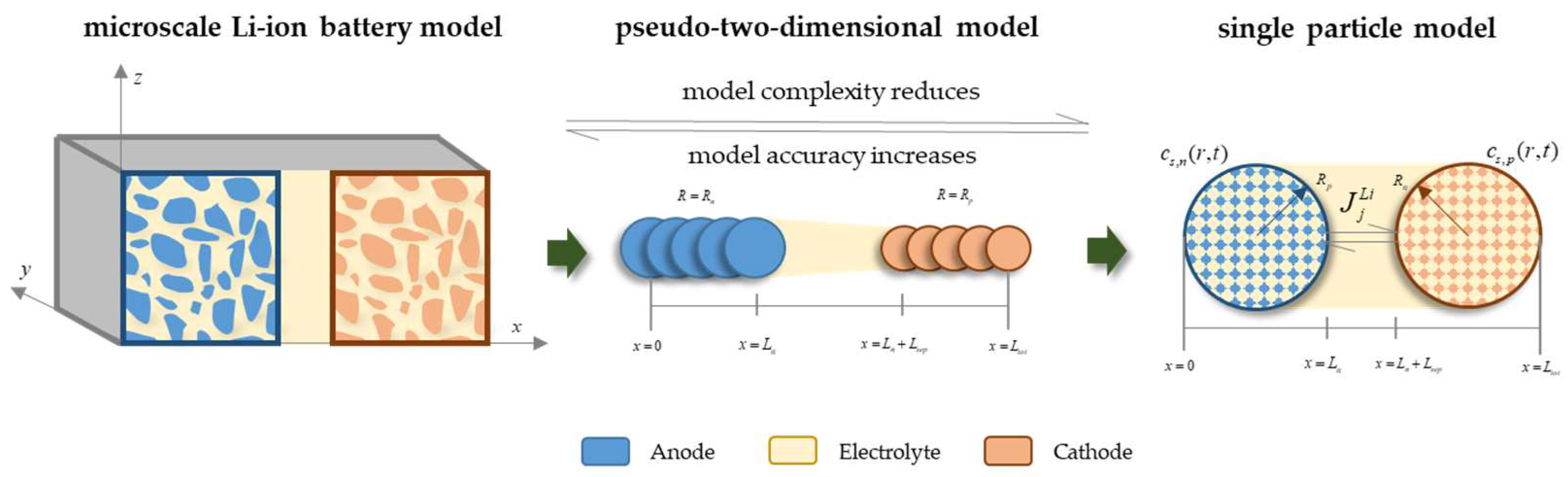
2. Modeling of the LIBs
2.1. P2D Model
2.2. Single-Particle Model
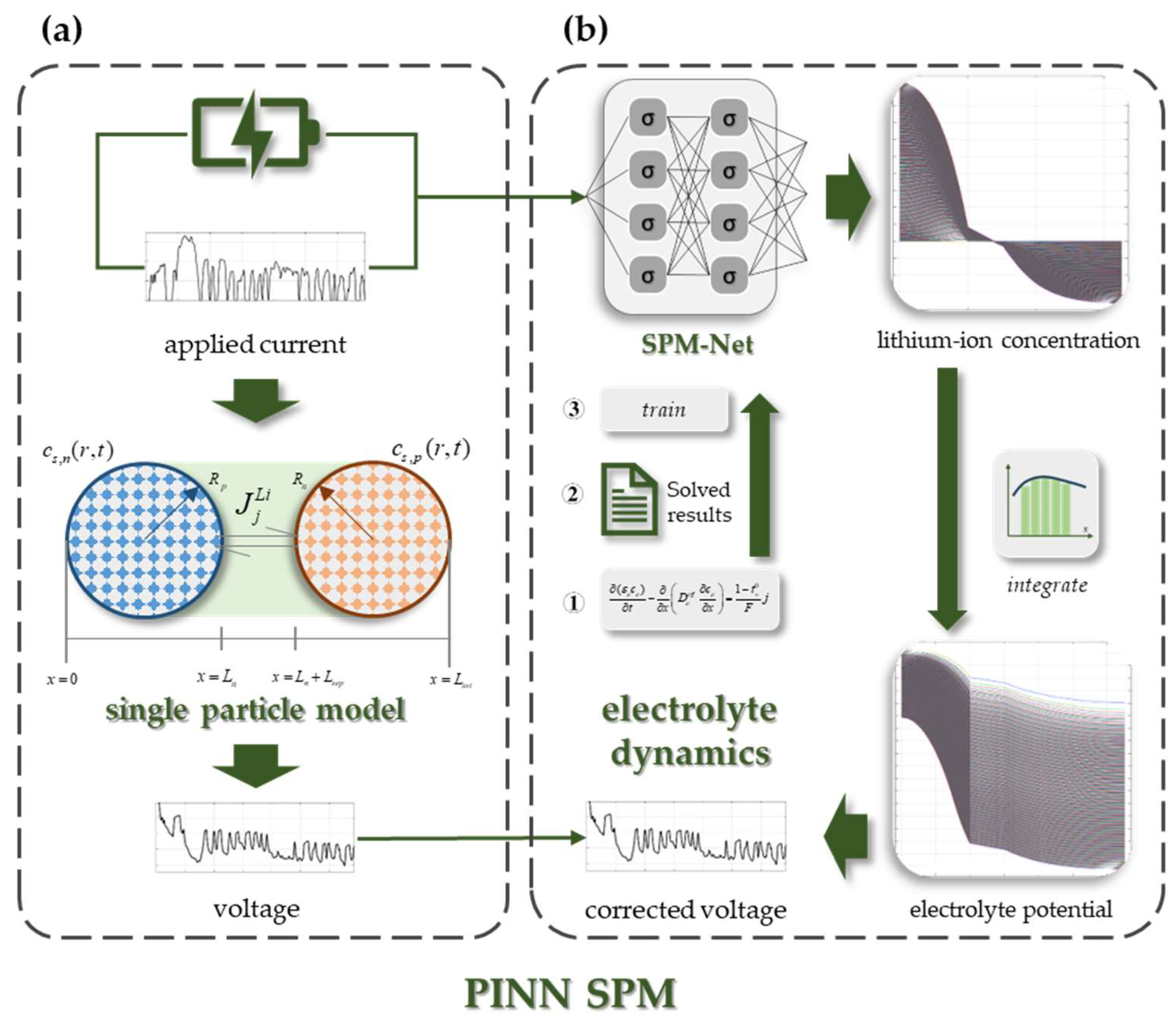
2.3. Establishment of PINN SPM
2.3.1. SPM with Electrolyte Dynamics
- (1)
- In the PINN SPM, it is assumed that the exchange current density is uniform inside the battery, so the electrolyte lithium-ion concentration distribution can be obtained by only solving the diffusion equation in Formula (2).
- (2)
- Based on the previous step, the distribution of lithium-ion concentration in the electrolyte is solved by Formula (2) under different applied currents. These solved results are divided into data set, validation set, and test set, which are utilized for SPM-Net training.
- (3)
- SPM-Net is a PDE solver and replaces numerical methods for solving the diffusion equation to accelerate the solving speed.
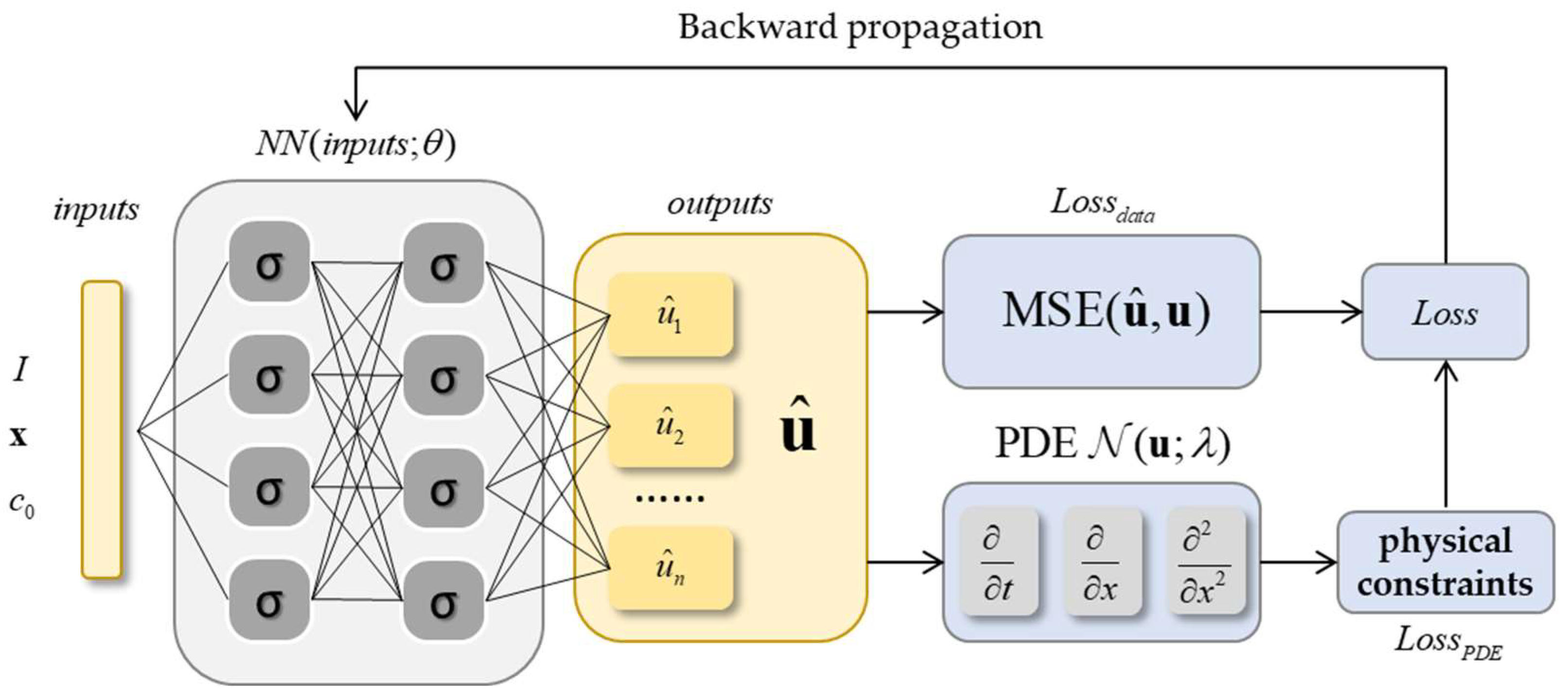
2.3.2. Physics-Informed Neural Networks
3. Method
3.1. Data Preparation
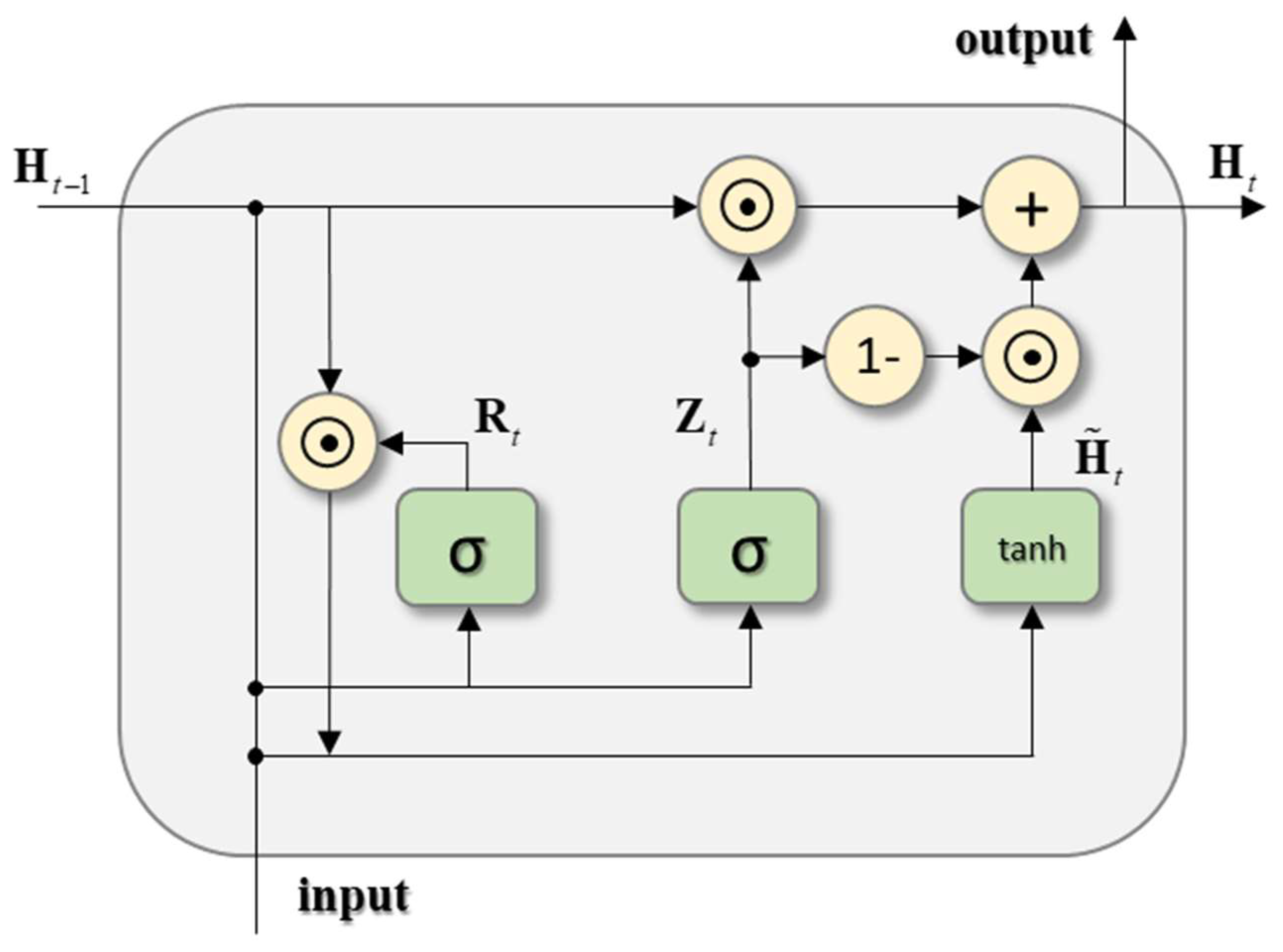
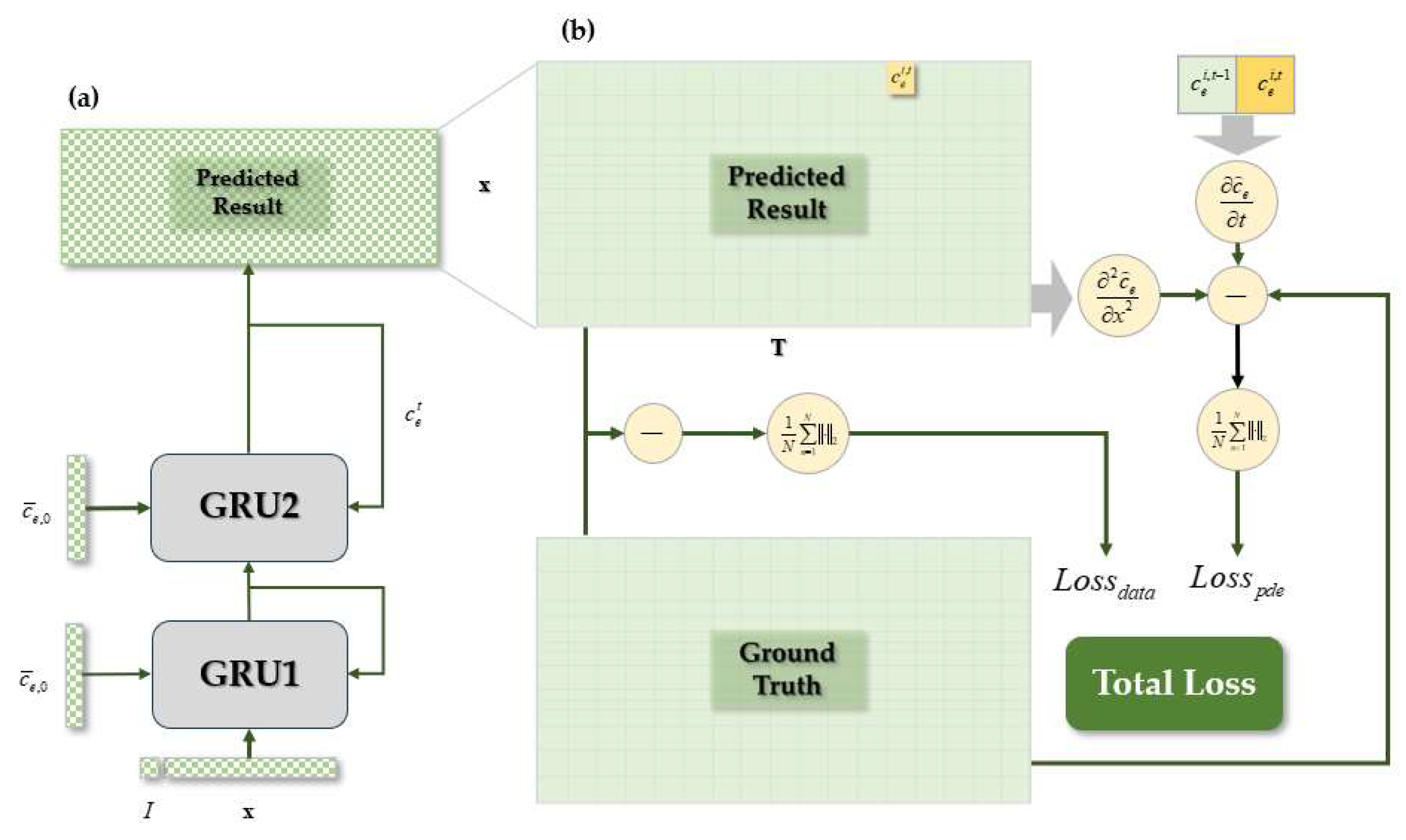
3.2. Network Architecture
3.3. Training Method
4. Simulation Results
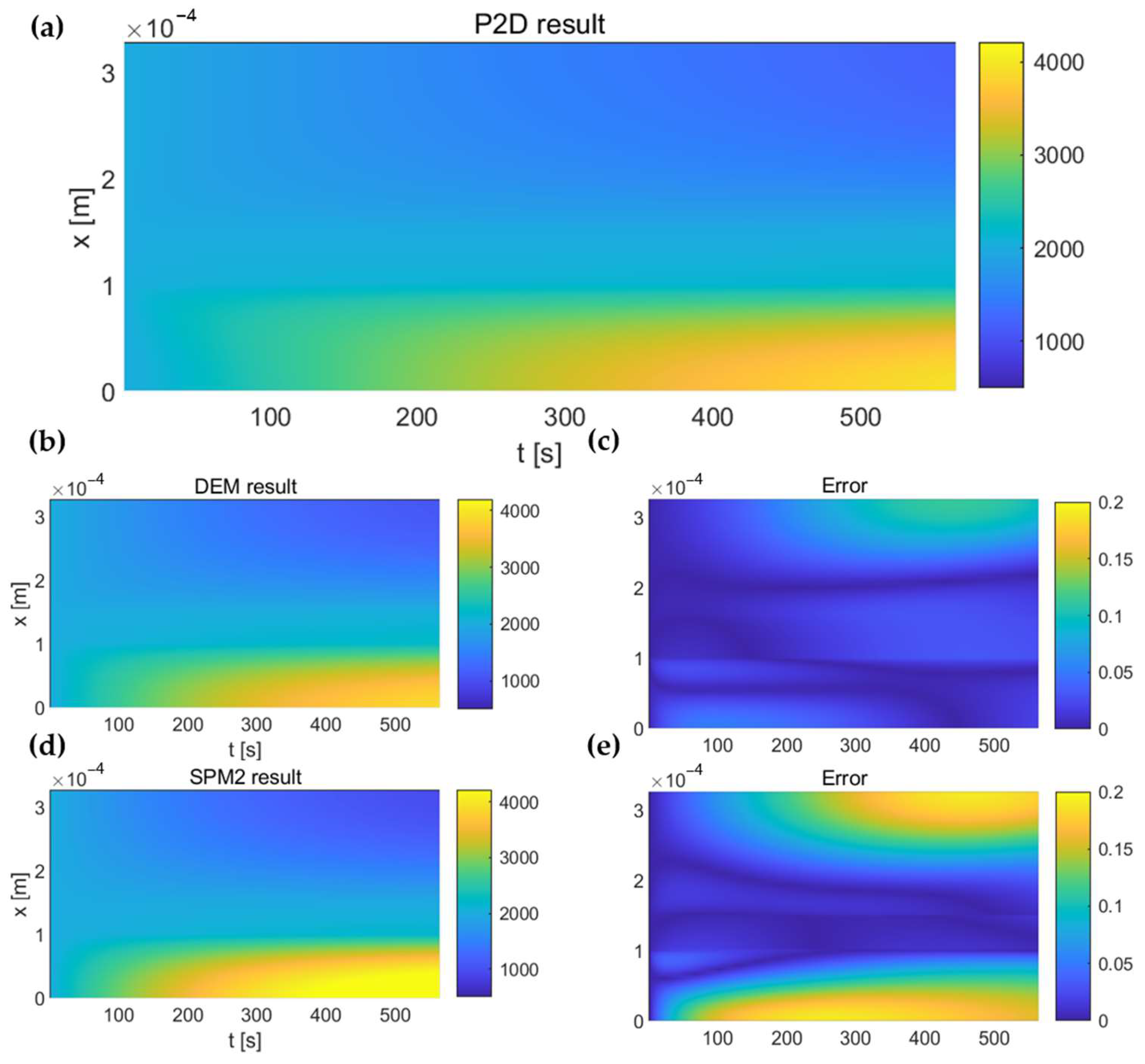
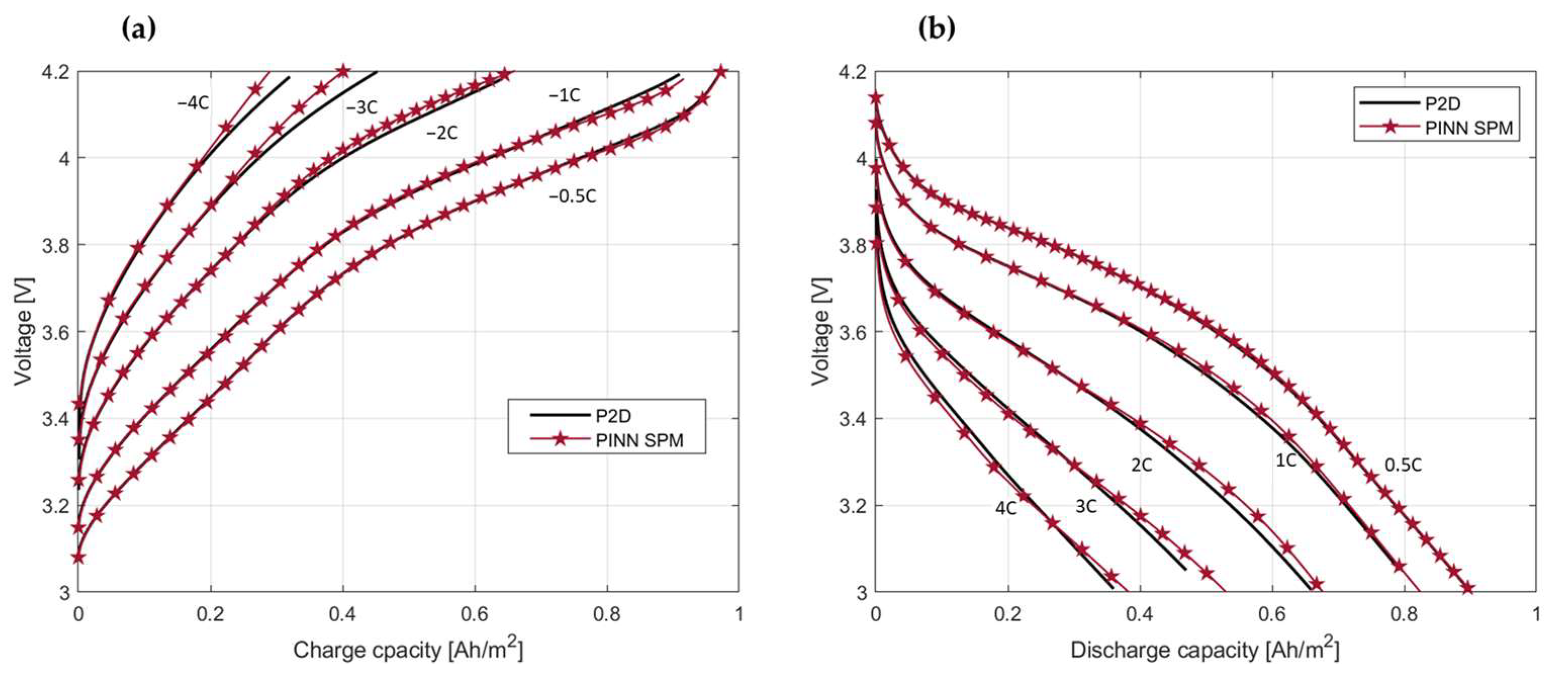
4.1. Verification of the Solving Methods for Diffusion Equation in the Electrolyte
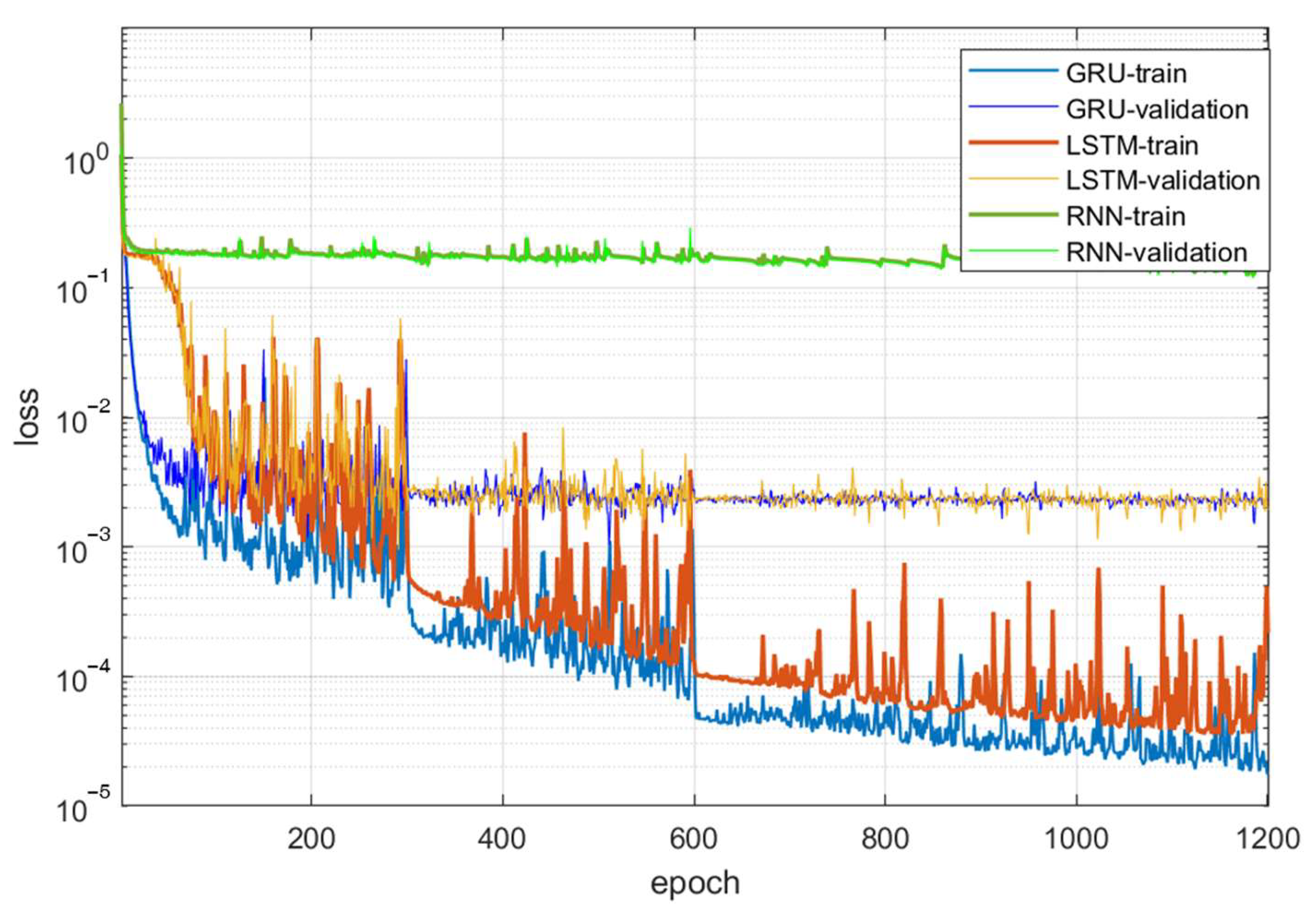
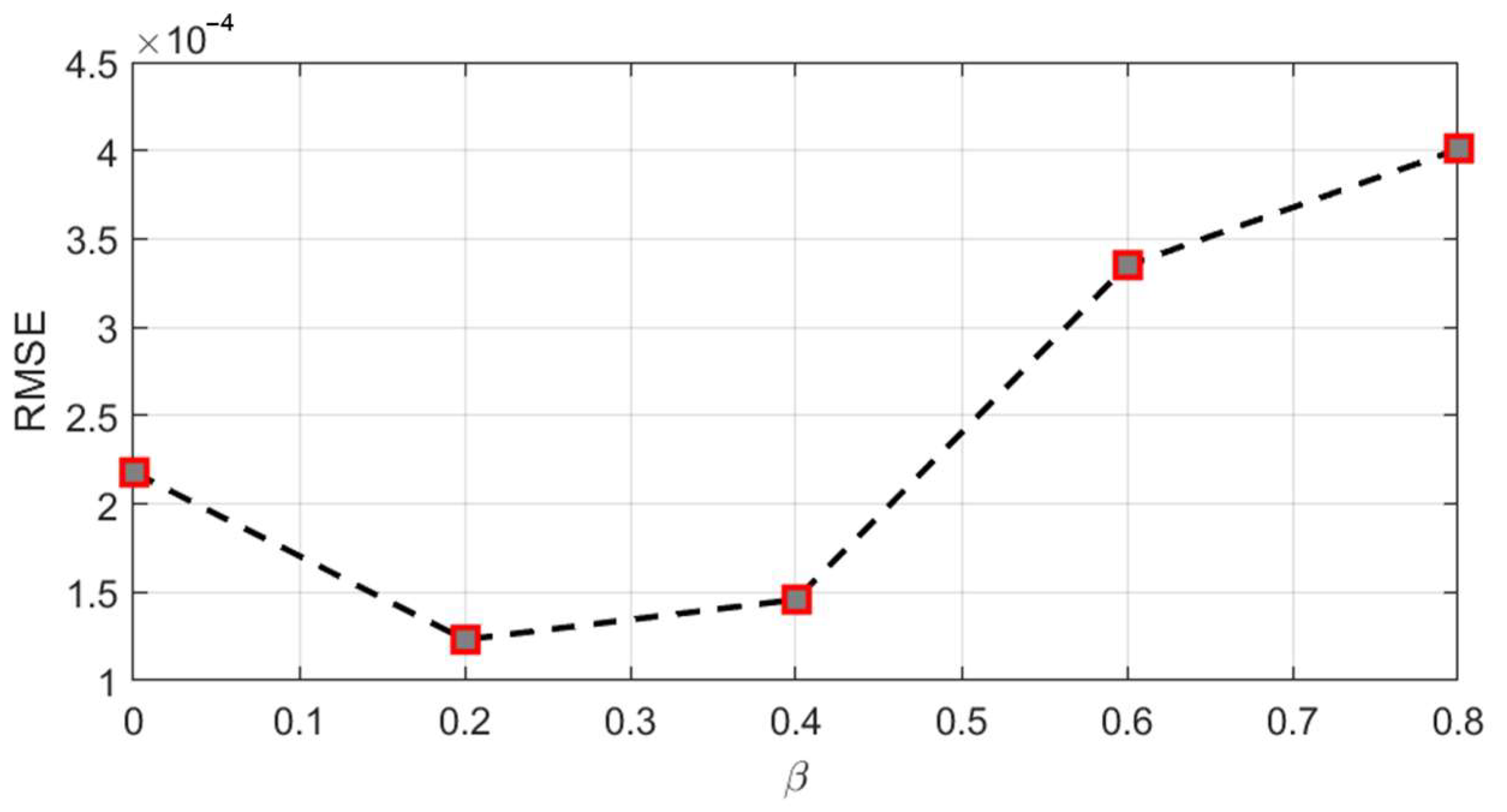
4.2. Comparison of Various Neural Networks
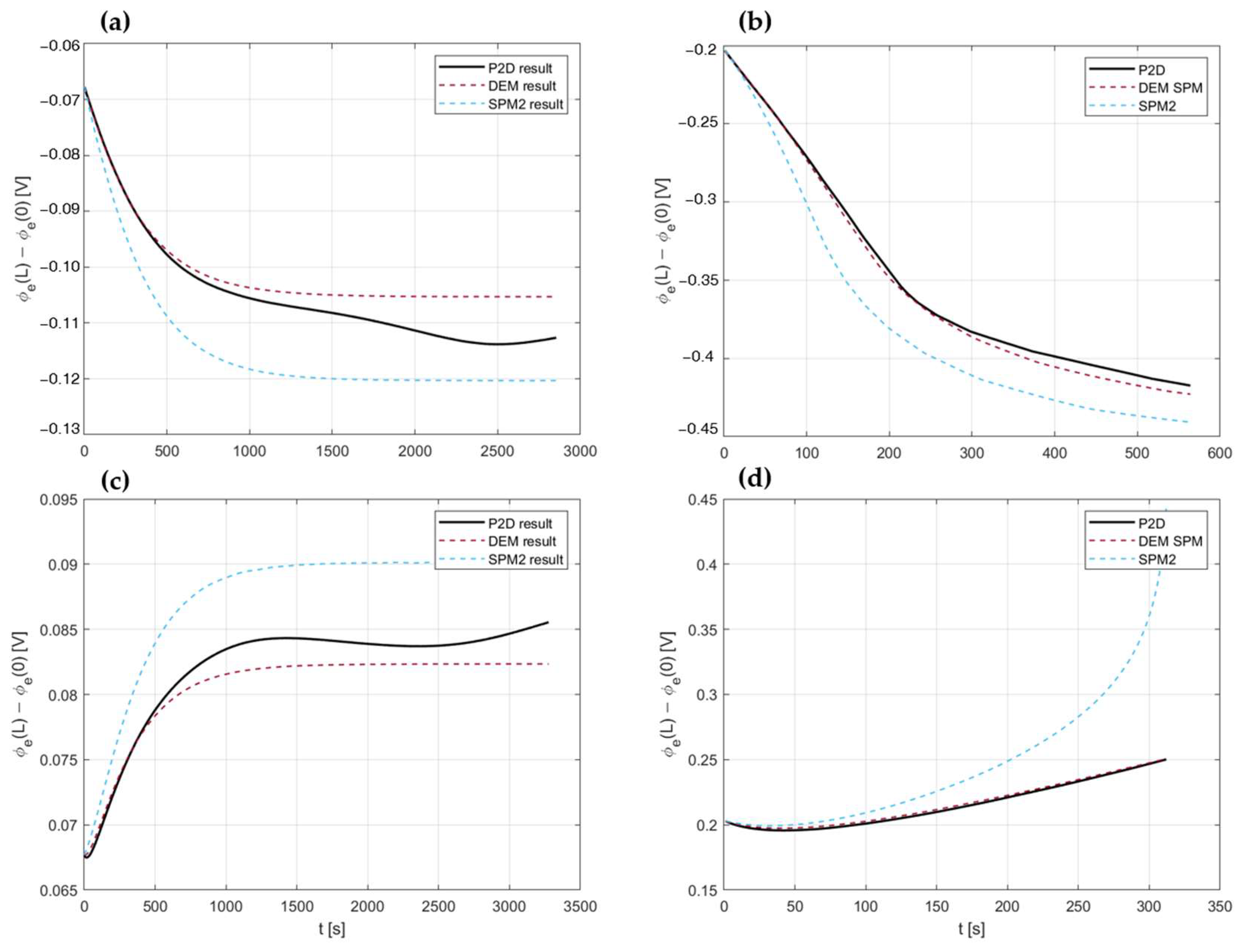
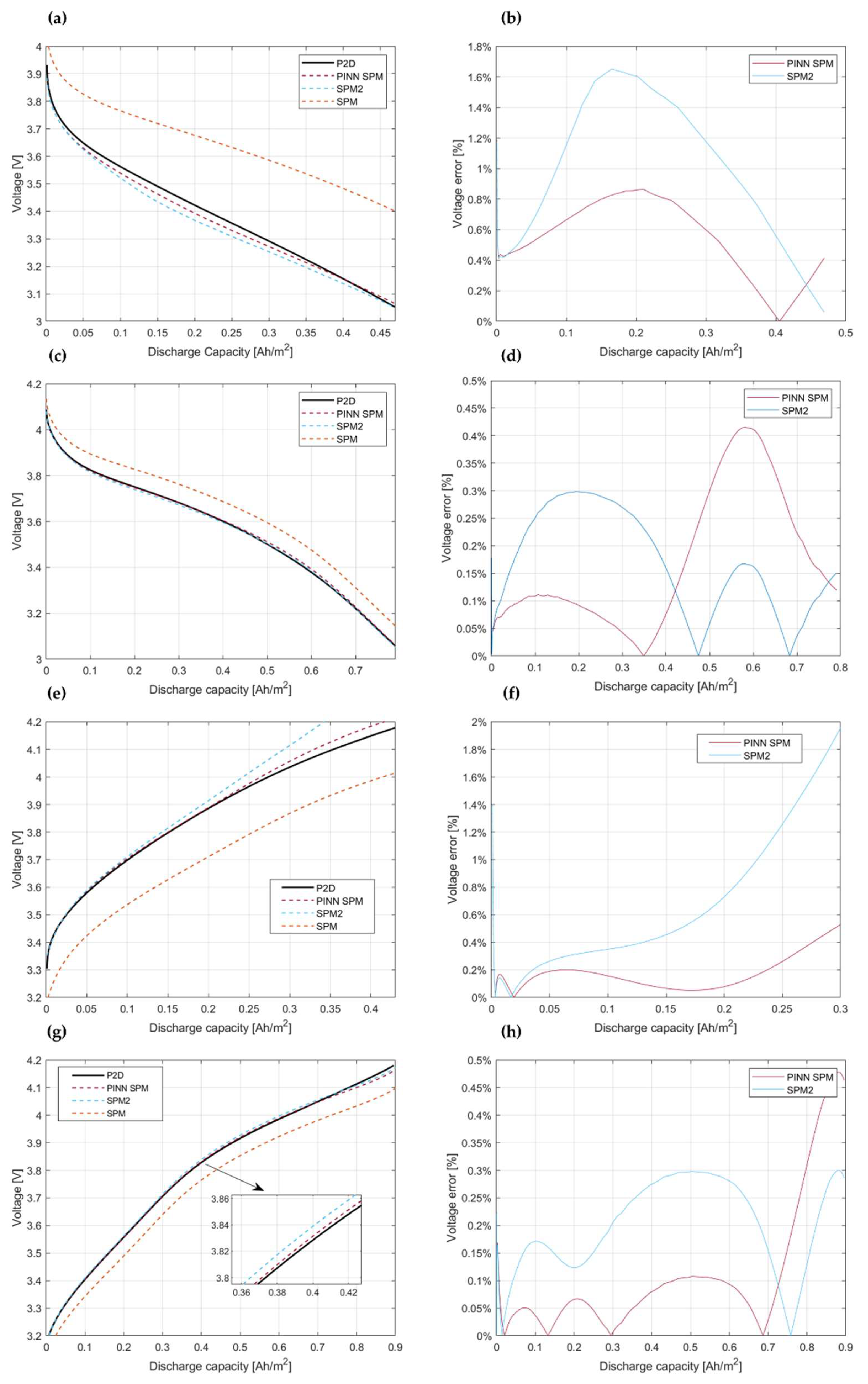
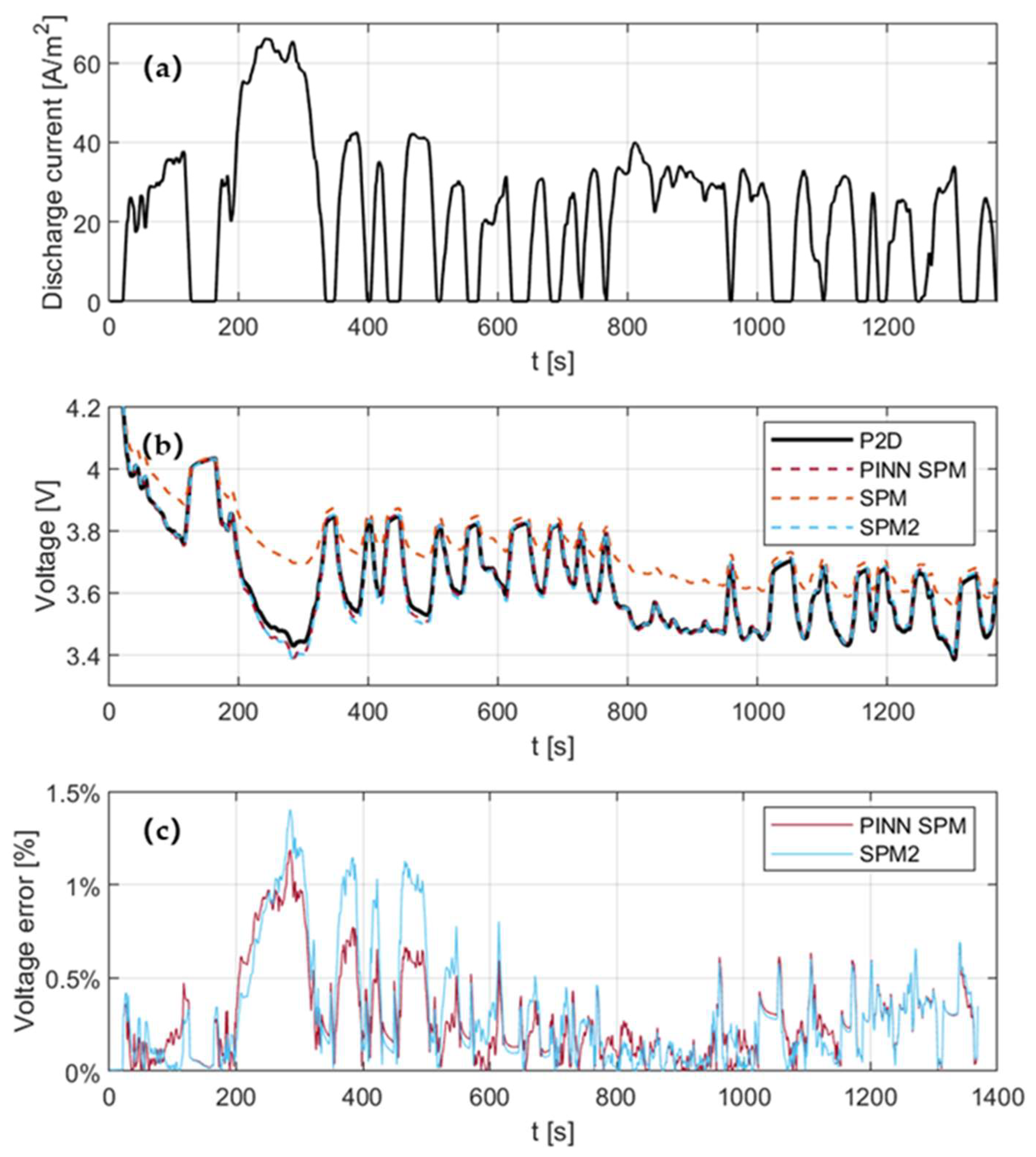
4.3. Model Assessment
5. Discussions
5.1. Limitations and Future Directions
5.2. Prospects for the Application of the PINN SPM
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, T.; Song, W.; Son, D.Y.; Ono, L.K.; Qi, Y. Lithium-ion batteries: Outlook on present, future, and hybridized technologies. J. Mater. Chem. A 2019, 7, 2942–2964. [Google Scholar] [CrossRef]
- Chen, S.; Wei, X.; Zhang, G.; Wang, X.; Zhu, J.; Feng, X.; Dai, H.; Ouyang, M. All-temperature-area battery application mechanism, performance and strategies. Innovation 2023, 4, 100465. [Google Scholar] [CrossRef]
- Horiba, T. Lithium-ion battery systems. Proc. IEEE 2014, 102, 939–950. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, J.; Yuan, S.; Yang, J.; Zhou, X. A novel method for identification of lithium-ion battery equivalent circuit model parameters considering electrochemical properties. J. Power Sources 2017, 345, 21–29. [Google Scholar] [CrossRef]
- Chen, W.; Liang, J.; Yang, Z.; Li, G. A review of lithium-ion battery for electric vehicle applications and beyond. Energy Procedia 2019, 158, 4363–4368. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, Y.; Zhu, J.; Wei, X.; Dai, H. An adaptive capacity estimation approach for lithium-ion battery using 10-min relaxation voltage within high state of charge range. Energy 2023, 263, 125802. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, X.; Chen, Z. A survey of digital twin techniques in smart manufacturing and management of energy applications. Green Energy Intell. Transp. 2022, 1, 100014. [Google Scholar] [CrossRef]
- Torchio, M.; Magni, L.; Gopaluni, R.B.; Braatz, R.D.; Raimondo, D.M. Lionsimba: A matlab framework based on a finite volume model suitable for li-ion battery design, simulation, and control. J. Electrochem. Soc. 2016, 163, A1192. [Google Scholar] [CrossRef]
- Bermejo, R.; del Sastre, P.G. An implicit-explicit Runge-Kutta-Chebyshev finite element method for the nonlinear Lithium-ion battery equations. Appl. Math. Comput. 2019, 361, 398–420. [Google Scholar] [CrossRef]
- Han, S.; Tang, Y.; Rahimian, S.K. A numerically efficient method of solving the full-order pseudo-2-dimensional (P2D) Li-ion cell model. J. Power Sources 2021, 490, 229571. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Chen, S.; Zhang, G.; Jiang, B.; Wei, X.; Dai, H. Online Detection of Lithium Plating Onset for Lithium-ion Batteries Based on Impedance Changing Trend Identification during Charging Processes. IEEE Trans. Transp. Electrif. 2022, 9, 3487–3497. [Google Scholar] [CrossRef]
- Ning, G.; Popov, B.N. Cycle life modeling of lithium-ion batteries. J. Electrochem. Soc. 2004, 151, A1584. [Google Scholar] [CrossRef]
- Li, J.; Lotfi, N.; Landers, R.G.; Park, J. A single particle model for lithium-ion batteries with electrolyte and stress-enhanced diffusion physics. J. Electrochem. Soc. 2017, 164, A874. [Google Scholar] [CrossRef]
- Liu, B.; Tang, X.; Gao, F. Joint estimation of battery state-of-charge and state-of-health based on a simplified pseudo-two-dimensional model. Electrochim. Acta 2020, 344, 136098. [Google Scholar] [CrossRef]
- Mehta, R.; Gupta, A. An improved single-particle model with electrolyte dynamics for high current applications of lithium-ion cells. Electrochim. Acta 2021, 389, 138623. [Google Scholar] [CrossRef]
- Von Srbik, M.T.; Marinescu, M.; Martinez-Botas, R.F.; Offer, G.J. A physically meaningful equivalent circuit network model of a lithium-ion battery accounting for local electrochemical and thermal behaviour, variable double layer capacitance and degradation. J. Power Sources 2016, 325, 171–184. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, M.; Farrell, T.; Tran, N.T.; Teague, J. A physics-based distributed-parameter equivalent circuit model for lithium-ion batteries. Electrochim. Acta 2019, 299, 451–469. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Zhang, T.; Offer, G.J. A fast, memory-efficient discrete-time realization algorithm for reduced-order li-ion battery models. J. Electrochem. Energy Convers. Storage 2017, 14, 011001. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef]
- Chen, M.; Lupoiu, R.; Mao, C.; Huang, D.H.; Jiang, J.; Lalanne, P.; Fan, J.A. High speed simulation and freeform optimization of nanophotonic devices with physics-augmented deep learning. ACS Photonics 2022, 9, 3110–3123. [Google Scholar]
- Misyris, G.S.; Venzke, A.; Chatzivasileiadis, S. Physics-informed neural networks for power systems. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Li, W.; Zhang, J.; Ringbeck, F.; Jöst, D.; Zhang, L.; Wei, Z.; Sauer, D.U. Physics-informed neural networks for electrode-level state estimation in lithium-ion batteries. J. Power Sources 2021, 506, 230034. [Google Scholar] [CrossRef]
- Pang, H.; Wu, L.; Liu, J.; Liu, X.; Liu, K. Physics-informed neural network approach for heat generation rate estimation of lithium-ion battery under various driving conditions. J. Energy Chem. 2023, 78, 1–12. [Google Scholar] [CrossRef]
- Nascimento, R.G.; Corbetta, M.; Kulkarni, C.S.; Viana, F.A. Hybrid physics-informed neural networks for lithium-ion battery modeling and prognosis. J. Power Sources 2021, 513, 230526. [Google Scholar] [CrossRef]
- Singh, S.; Ebongue, Y.E.; Rezaei, S.; Birke, K.P. Hybrid modeling of lithium-ion battery: Physics-informed neural network for battery state estimation. Batteries 2023, 9, 301. [Google Scholar] [CrossRef]
- Schmitt, J.; Horstkötter, I.; Bäker, B. Electrical lithium-ion battery models based on recurrent neural networks: A holistic approach. J. Energy Storage 2023, 58, 106461. [Google Scholar] [CrossRef]
- Plett, G.L. Battery Management Systems, Volume I: Battery Modeling; Artech House: London, UK, 2015. [Google Scholar]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J.M. Comparison of modeling predictions with experimental data from plastic lithium ion cells. J. Electrochem. Soc. 1996, 143, 1890. [Google Scholar] [CrossRef]
- Lotfi, N.; Li, J.; Landers, R.G.; Park, J. Li-ion battery state of health estimation based on an improved single particle model. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 86–91. [Google Scholar]
- Pang, H.; Mou, L.; Guo, L.; Zhang, F. Parameter identification and systematic validation of an enhanced single-particle model with aging degradation physics for Li-ion batteries. Electrochim. Acta 2019, 307, 474–487. [Google Scholar] [CrossRef]
- Rahimian, S.K.; Rayman, S.; White, R.E. Extension of physics-based single particle model for higher charge–discharge rates. J. Power Sources 2013, 224, 180–194. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Seo, J.H.; Plett, G.; Lu, W.; Sastry, A.M. Numerical simulation of the effect of the dissolution of LiMn2O4 particles on Li-ion battery performance. Electrochem. Solid-State Lett. 2010, 14, A14. [Google Scholar] [CrossRef]
- Zhang, D.; Park, S.; Couto, L.D.; Viswanathan, V.; Moura, S.J. Beyond battery state of charge estimation: Observer for electrode-level state and cyclable lithium with electrolyte dynamics. IEEE Trans. Transp. Electrif. 2022, 7, 3199–3204. [Google Scholar] [CrossRef]
- You, H.; Zhu, J.; Wang, X.; Jiang, B.; Sun, H.; Liu, X.; Wei, X.; Han, G.; Ding, S.; Yu, H.; et al. Nonlinear health evaluation for lithium-ion battery within full-lifespan. J. Energy Chem. 2022, 72, 333–341. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, Y.; You, M.; Xiong, R.; Zhou, X. Two-stage aging trajectory prediction of LFP lithium-ion battery based on transfer learning with the cycle life prediction. Green Energy Intell. Transp. 2022, 1, 100008. [Google Scholar] [CrossRef]
- Qiao, D.; Wei, X.; Fan, W.; Jiang, B.; Lai, X.; Zheng, Y.; Tang, X.; Dai, H. Toward safe carbon–neutral transportation: Battery internal short circuit diagnosis based on cloud data for electric vehicles. Appl. Energy 2022, 317, 119168. [Google Scholar] [CrossRef]
| Governing Equations | Boundary Conditions | ||
|---|---|---|---|
| Lithium-ion mass transport in electrolyte phase | (2) | ||
| Lithium-ion mass transport in spherical particles | (3) | ||
| Ohm’s law in electrolyte phase | (4) | ||
| Ohm’s law in electrode phase | (5) | ||
| Butler–Volmer equation | — | (6) |
| Parameter | Anode | Cathode |
|---|---|---|
| 100 × 10−6 | 174 × 10−6 | |
| 8.5 × 10−6 | 12.5 × 10−6 | |
| 0.471 | 0.276 | |
| 0.529 | 0.724 | |
| 26,390 | 22,860 | |
| Stoichiometric at 100% state of charge | 0.563 | 0.171 |
| Stoichiometric at 0% state of charge | 0.047 | 0.650 |
| 3.9 × 10−14 | 10 × 10−14 | |
| 2.2987 × 10−5 | 2.2042 × 10−5 | |
| 3.3 | ||
| 8.3145 | ||
| 298.15 | ||
| 96875 | ||
| 2000 | ||
| 7.5 × 10−11 | ||
| GRU | LSTM | RNN | |
|---|---|---|---|
| time | 3 min 5 s | 3 min 35 s | 1 min 11 s |
| Validation | Test | ||
|---|---|---|---|
| Only-data | 6.63 × 10−5 | 2.18 × 10−4 | |
| 42.21 | 1.03 × 10−2 | ||
| PINN | 6.72 × 10−5 | 1.23 × 10−4 | |
| 8.37 × 10−2 | 2.02 × 10−4 |
| Discharge Rate | DEM SPM | SPM2 | PINN SPM |
|---|---|---|---|
| 0.5C | 0.0020 | 0.0020 | 0.0020 |
| 1C | 0.0046 | 0.0050 | 0.0052 |
| 2C | 0.0099 | 0.0142 | 0.0118 |
| 3C | 0.0153 | 0.0216 | 0.0168 |
| 4C | 0.0141 | 0.0318 | 0.0207 |
| Dynamic | 0.0094 | 0.0110 | 0.0099 |
| Discharge Rate | PINN SPM | DEM SPM | SPM2 | P2D |
|---|---|---|---|---|
| 1C | 0.53 s | 0.73 s | 0.68 s | 15 s |
| 2C | 0.44 s | 0.52 s | 0.37 s | 8 s |
| 3C | 0.24 s | 0.28 s | 0.22 s | 6 s |
| 4C | 0.20 s | 0.29 s | 0.17 s | 5 s |
| Dynamic | 0.76 s | 0.96 s | 0.69 s | 36 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, C.; Jiang, B.; Zhu, J.; Wei, X.; Dai, H. An Enhanced Single-Particle Model Using a Physics-Informed Neural Network Considering Electrolyte Dynamics for Lithium-Ion Batteries. Batteries 2023, 9, 511. https://doi.org/10.3390/batteries9100511
Xue C, Jiang B, Zhu J, Wei X, Dai H. An Enhanced Single-Particle Model Using a Physics-Informed Neural Network Considering Electrolyte Dynamics for Lithium-Ion Batteries. Batteries. 2023; 9(10):511. https://doi.org/10.3390/batteries9100511
Chicago/Turabian StyleXue, Chenyu, Bo Jiang, Jiangong Zhu, Xuezhe Wei, and Haifeng Dai. 2023. "An Enhanced Single-Particle Model Using a Physics-Informed Neural Network Considering Electrolyte Dynamics for Lithium-Ion Batteries" Batteries 9, no. 10: 511. https://doi.org/10.3390/batteries9100511
APA StyleXue, C., Jiang, B., Zhu, J., Wei, X., & Dai, H. (2023). An Enhanced Single-Particle Model Using a Physics-Informed Neural Network Considering Electrolyte Dynamics for Lithium-Ion Batteries. Batteries, 9(10), 511. https://doi.org/10.3390/batteries9100511








