Unraveling the Correlation between Structure and Lithium Ionic Migration of Metal Halide Solid-State Electrolytes via Neutron Powder Diffraction

Abstract

Metal halide solid-state electrolytes (SSEs) (Li-M-X system, typically Li₃MX₆ and Li₂MX_4; M is metal or rare-earth element, X is halogen) exhibit significant potential in all solid-state batteries (ASSB) due to wide stability windows (0.36–6.71 V vs. Li/Li⁺), excellent compatibility with cathodes, and a water-mediated facile synthesis route for large-scale fabrication. Understanding the dynamics of Li⁺ transportation and the influence of the host lattice is the prerequisite for developing advanced Metal halide SSEs. Neutron powder diffraction (NPD), as the most cutting-edge technology, could essentially reflect the nuclear density map to determine the whole crystal structure. Through NPD, the Li+ distribution and occupation are clearly revealed for transport pathway analysis, and the influence of the host ion lattice on Li+ migration could be discussed. In this review, we stress NPD utilization in metal halide SSEs systems in terms of defect chemistry, phase transition, cation/anion disorder effects, dual halogen, lattice dynamics/polarizability, and in situ analysis of phase evolution. The irreplaceable role of NPD technology in designing metal halide SSEs with enhanced properties is stressed, and a perspective on future developments of NPD in metal halide SSEs is also presented.

1. Introduction

Rechargeable batteries have been widely applied in electric mobiles and vehicles in modern industrial society. However, conventional lithium-ion batteries (LIBs) still present safety risks originating from exploiting flammable liquid electrolytes and the lower energy density of graphite anodes than Li metal anodes [1]. It is therefore proposed that all solid-state batteries (ASSBs) which are assembled with a solid-state electrolyte (SSE) and a Li metal anode (or anode-less design [2]) could be an alternative solution to the above issues [3]. However, realizing the above vision relies on two key factors: that is, a promising high-Li⁺ ionic conductivity, and a wide enough electrochemical stability window. To fulfill these requirements, a wide range of SSEs have been developed [4,5,6,7,8]. One of the most famous SSEs are thiophosphates (sulfides) which often possess high ionic conductivities of >10 mS cm⁻¹ along with their ductile nature [9,10]. However, their low compatibility with typical 4 V cathode active materials (CAMs, typically LiCoO₂ and LiNi_1−x−yCo_xMn_yO₂) is problematic [11], since they would be oxidized at a low potential (2.5 V vs. Li⁺/Li) [12,13]. A coating of CAM is expected to address this problem, but searching for suitable materials with proper coating-processing to achieve a homogeneous [14] functional coating [15] is not that simple. Therefore, developing new SSEs with high-Li⁺ ionic conductivity, high stability/compatibility, and ductility is still a hot topic.

Recently developed metal halides exhibit great potential as promising SSEs [14]. Metal halides are capable of achieving wider stability windows since their anions are more electronegative than oxygen or sulfur [16,17]. In fact, metal halide SSEs were investigated decades ago, but early halides (Li₂MgCl₄, LiAlCl₄, etc.) [17,18,19,20] failed to attract wide interest due to relatively low-Li⁺ ionic conductivity. Only until recently in 2018, when Asano et al. developed a poorly crystalline Li₃YCl₆ solid electrolyte [21] that has a relatively high ionic conductivity of 0.51 mS cm⁻¹ and stable cycling in ASSBs with uncoated LiCoO₂, did halide electrolytes spur renewed interest in this system. Today, several halides have been successfully found to simultaneously possess room-temperature high-Li⁺ ionic conductivity (>10⁻³ S cm⁻¹), ideal oxidative stability (>4 V) and compatibility with CAMs. These include typical Li₃MX₆-typed halides Li₃InCl₆ [22,23], Li_3−xM_1−xZr_xCl₆ (M = Y, Er, Yb) [24,25], Li_xScCl_3+x [26], Li_2.25Zr_0.75Fe_0.25Cl₆ [27], Li_2.60Yb_0.60Hf_0.40Cl₆ [28], Li₃YBr₆ [21] and spinel-typed Li₂Sc_2/3Cl₄ [29]. Others, like Li₃YCl₆ [21], Li₂ZrCl₆ [27], also exhibit good oxidative and chemical stability but a little lower (10⁻⁴–10⁻³) ionic conductivity. Li₃Y_1−xIn_xCl₆ [30] also has a conductivity surpassing 10⁻³ S cm⁻¹ along with a high humidity tolerance. Up to now, most of these promising halides have been chlorides and bromides. Although fluorides possess the widest electrochemical window, their room-temperature ionic conductivity is considerably lower [31]. Generally, with obvious advantages of high ionic conductivity, good stability, humidity tolerance and facile synthesis routes, metal halide electrolytes have become increasingly attractive.

In searching for new metal halides as SSEs, neutron powder diffraction (NPD) [32] is a powerful technique since it determines the whole crystal structure, especially the Li⁺ sublattice, and analyzes the Li⁺ migration pathway. It offers an essential understanding of the interplay between the structure and underlying Li⁺ migration mechanism. NPD data is usually collected on a diffractometer in the national neutron beam center. It has played an increasingly indispensable role in the in-depth study of SSEs. Similar to X-ray diffraction (XRD), NPD also follows the Bragg diffraction law and diffraction geometry, and its structure-determination also follows a similar mathematical procedure: that is, firstly determining the phases of the structure factors, and secondly conducting an inversed Fourier transform to yield a 3D atomic distribution map of the rough crystal structure, followed by Rietveld refinements with least-square method to yield a final structure.

One unique advantage of NPD is that a neutron can pass through an electron cloud to directly interact with a nucleus, which is in a clear contrast to XRD, that only resonates with electron clouds. Using this capability, neutron diffraction can detect nuclei-density distribution rather than electron-cloud distribution in the crystal structure, which indicates a precise determination of true atomic positions in the structure model. Another advantage of NPD resides in its superior sensitivity to light elements H(D), Li, C, N, O, etc., while XRD is much weaker in detecting them. This is because NPD has a totally different elemental scattering length/intensity compared to XRD. In XRD, scattering intensity is proportional to the atomic number. The more electrons surround it, the stronger scattering intensity the atom contributes. Therefore, XRD is excellent in detecting heavy atoms (like metals or halogens) but very insensitive to light elements. However, NPD does not follow this rule, and its elemental scattering intensity depends on the interaction between neutron and nucleus. Since the intensity/interaction of light atoms is not much weaker than heavy atoms, the light atoms can be well-distinguished from heavy atoms, especially lithium, due to its negative neutron scattering length [32]. Last but not least, unlike XRD, neutron scattering intensity does not undergo obvious decay as the diffraction angle increases. This feature guarantees its high-angular (low d-spacing) signal to be of sufficient quality for further analysis of the local Li coordination environment and disorder. Besides all of the above, one may argue that Raman spectra also involves scattering. However, a Raman incident beam cannot trigger diffraction since its wavelength is too high (NPD and XRD wavelength is usually 0.1~3 Å corresponding to interplanar spacing), which means there is no diffraction peak at a certain angle, representing certain hkl indices. Raman spectra come from inelastic scattering, while NPD or XRD peaks come from elastic scattering, which means that Raman spectra undergo adsorption/excitation to identify components, type of bonding and functional groups via a shift in wave number. However, it is unable to locate atomic positions in a 3D crystal structure model as NPD or XRD does. In general, NPD is the only technique capable of precisely determining Li⁺ nuclei locations in the lattice, along with their surrounding chemical environments and sublattice.

In this review, we will mainly discuss application of NPD in metal halide SSEs. We will discuss (i) the crystallography of metal halide systems, a fundamental understanding in Li⁺ transport kinetics, and basic principles of NPD data processing in analyzing structure and migration behavior; (ii) details of NPD application in defects, phase transition, cation order–disorder, dual-halogen and lattice dynamics, new structure determination, and in situ analysis of phase evolution. Several representative works are chosen for a detailed discussion of how NPD refinements determine the Li⁺ ions distribution, calculate the overall energy landscape and pathways, and clarify the structural modulation mechanism for Li transport. Taken as a whole, this review will provide an insightful perspective on future developments in NPD technology applied in advanced metal halide SSEs.

2. Fundaments in Metal Halides and Neutron Powder Diffraction (NPD)

2.1. Crystallography

For a metal halide, its stacking structure is dependent on the arrangement of ions with a different radius and polarity. In halides, anions have larger ionic radii (Shannon radius [33], F⁻ 122 pm, Cl⁻ 167 pm, Br⁻ 182 pm, I⁻ 202 pm) than metal cations (88–118 pm) and Li⁺ ions (Li⁺ is 73 pm in tetrahedra, and 90 pm in octahedra). Therefore, the structural framework generally depends on an anion stacking sublattice and is modulated by the polarity and radius/volume of the cation species. According to the law of ionic packing, only when the cations and anions are in close contact (tightly stacking) can the structure be stable. Here, the radius ratio of cation to anion (r⁺/r⁻) is represented by δ. From a solid geometry deduction, when δ ranges from 0.732 to 1, the cation will adopt a MX₈ cubic polyhedron similar to that in CsCl structure. When δ is between 0.414 and 0.732, the smaller cation will coordinate with six anions to form an MX₆ octahedron. When the cation is even smaller, it will adopt an MX₄ tetrahedral structure with δ from 0.255 to 0.414, or an MX₃ triangle structure with δ from 0.155 to 0.255.

Table 1. Polarizability, Pauling radius and Shannon radius of cations and anions in metal halide SSEs. Reproduced with permission: copyright 2021, American Chemical Society [14].

Ion	Li+	In3+	Sc3+	Y3+	Er3+	La3+~Lu3+	F−	Cl−	Br−	I−
polarizability α, (Å3)	0.03	0.51	0.286	0.55	0.69	~1.14–0.606	1.04	3.66	4.77	7.10
Pauling radius (pm)	76	80	74.5	90	89	~103.2–86.1	136	181	195	216
Shannon radius a (pm)	90	94	88.5	104	103	~117.2–100.1	122	167	181	202
δM/F	0.74	0.77	0.73	0.85	0.84	~0.96–0.82
δM/Cl	0.54	0.56	0.53	0.62	0.62	~0.62–0.60
δM/Br	0.50	0.52	0.49	0.57	0.57	~0.57–0.55
δM/I	0.45	0.47	0.44	0.51	0.51	~0.51–0.50

^a the data comes from Shannon’s work [33].

summarizes the Shannon radii [33] of halide cations and anions. Fluorides generally have a δ_M/F higher than 0.732 and therefore they prefer a LiMF₄-typed structure with a coordination environment of an MF₈ cubic polyhedron. Other halides generally have a δ ranging from 0.414 to 0.732, forming a Li₃MX₆-typed structure with a coordination environment of an MX₆ octahedron.

Ternary chloride Li₃MCl₆ often adopts hexagonal close-packing (hcp) or cubic close-packing (ccp) for its Cl⁻ sublattice structures [17]. The hcp anion lattice can be further divided into a trigonal structure (space group P-3m1, marked as hcp-T), and orthorhombic structure (space group Pnma, marked as hcp-O). The difference between hcp-O and hcp-T is that, while their Cl⁻ adopts ABAB stacking, their Li⁺ and M³⁺ in octahedral sites obey orthorhombic and tetragonal symmetric arrangements, respectively. As for ccp, its anion Cl⁻ sublattice adopts an ABCABC stacking, but its cations adopt a monoclinic arrangement that makes the total structure monoclinic (marked as ccp-M). In fact, for all the above structures, it is the M metal radius that decides the lattice symmetry. When the M³⁺ Shannon radius [33] is in the range of 106.3 pm (Tb³⁺)~102 pm (Tm³⁺), the Li₃MCl₆ lattice adopts a hcp-T structure with δ_M/Cl among 0.611~0.637. When M³⁺ gets smaller, that is 102 pm~100 pm (i.e., Yb³⁺ and Lu³⁺), the Li₃MCl₆ structure will transform to the hcp-O with δ_M/Cl among 0.599~0.611. When the M³⁺ radius further reduces, the anion sublattice will transform from hcp to ccp, as illustrated by Li₃InCl₆ (δ_In/Cl = 0.563) and Li₃ScCl₆ (δ_Sc/Cl = 0.530). In contrast to the chloride-based ternary halides, bromide and iodide (Li₃MBr₆ and Li₃MI₆) all adopt the same monoclinic ccp-M structure [17].

2.2. Li⁺ Migration Kinetics

The Li⁺ ions’ transport behavior is strongly dependent on the crystal lattice. In a monoclinic ccp-M structure [16,21], Li⁺ ions migrate along shared-edge octahedral sites which are connected by tetrahedral interstitial sites that form a 3D isotropic diffusion network. In a structure with hcp anion arrangements (hcp-O and hcp-T) [16], Li⁺ ions transport in a similar way via octahedra and interstitial tetrahedra in the ab-plane, but only via octahedra along the c-axis, since neighboring octahedral sites are directly linked to form the diffusion paths. It worth mentioning that, in contrast to a long-range order crystal lattice, local order–disorder of the Li⁺ sublattice can exist as a unique feature in a halide lattice, which is often accompanied by local octahedra distortion and phase transition due to defects. Both the disorder and distortion significantly affect the Li⁺ migration behavior. In addition, Li⁺ transport kinetics can be modulated by polarity-induced lattice dynamics. The proximity of metal ions will also stimulate or block the Li⁺ hopping (blocking effects), which influences Li⁺ transport kinetics.

2.3. NPD Data Processing

Similar to XRD, NPD also follows the Bragg diffraction law and diffraction geometry. As shown in Scheme 1a,b, NPD can be performed using a constant wavelength (CW) neutron beam or time-of-flight (TOF) neutron beam. The NPD data can be proceeded by Jana [34], Fullprof [35], etc. Conventionally, as shown in Scheme 1c, NPD data-processing includes the following steps: (1) Data collection. Instrument scientists will help users to load a powder sample in the sample holder on the diffractometer. A neutron beam will penetrate the sample and trigger diffraction. Multiple detectors at different angles will simultaneously collect diffraction peaks. After data correction, the original NPD data is returned to the users. (2) Indexing. If the crystal structure is already known, then this step can be skipped. However, if the structure is new (unknown, unreported), then this step is unavoidable. One needs to identify most diffraction peaks and then run an “indexing” function to find out the lattice type, lattice parameters, and space group. Note that indexing can be pre-run in the XRD pattern. The indexed lattice must be in agreement with TEM diffraction. (3) hkl Profile matching. This is also a refinement procedure. Before solving the atomic positions, one needs firstly to refine the peak shape, peak asymmetry (if it has any), zero shift, background and lattice parameters, with correct instrument parameters. Each peak and the background line should be well-simulated, usually with a total evaluating factor χ² < 2. Since the program will later extract these simulated peak intensities of hkl indices for structure solution and structure refinements, this profile-matching step must be well-done. (4) Structure solution. If the structure model is already known, then this step is skipped. If it is new, then one must run a “solve” function. The program will try to solve the phases of structure factors and finally return a rough structure model via an inversed Fourier transform. This rough model is usually incomplete, and may have some flaws or mistakes in atom positions. (5) Rietveld refinements with structure model. By the least-square method, parameters like atom positions, occupancies and thermal displacements will be refined. As the simulated intensities (of the structure model) gradually approach the observed ones, the structure model is getting more and more close to the true crystal structure. (6) Difference Fourier calculation. This is to check the residue nuclei densities in the structure and to identify if they represent missing atoms. One needs to complement the missing atoms in the structure model and go back to step (5) to refine again, until all of the atoms are found out. (7) Completing the structure. After locating all the atoms, final rounds of refinements are needed to complete the whole structure. The structure and all parameters should be chemically reasonable, and evaluating factors should be within an acceptable range, empirically, χ² < 2, R_wp < 13%. (8) Bond-valence site energy (BVSE) calculation [36,37]. On the basis of this refined structure and hkl intensities, the BVSE will calculate the overall landscape of Li⁺ site energy and point out possible Li⁺ diffusion pathways in the structure.

For halide SSEs, NPD data can be singly used in a structure solution and subsequent Rietveld refinement to identify the Li⁺ distribution, which provides critical evidence to elucidate the mechanism of Li⁺ transport enhancement. In situ NPD as heating or charging/discharging can be used to monitor the dynamic process of continuous phase/structure evolution. Besides the above single usage, NPD and XRD/Synchrotron are often jointly refined to tackle a complicated structure or new structural phase. In this joint-refinement, NPD and XRD will be simultaneously refined. The XRD/Synchrotron data use their good advantage in detecting heavy ions (Cl⁻, Br⁻, Y³⁺, In³⁺, Zr⁴⁺, etc.) to quickly settle the whole lattice framework, while NPD data focus on locating Li⁺ ions and quantifying their chemical occupancy.

Whether singly or jointly used, the first important step is always to check the lattice type (space group) and lattice parameters, which give preliminary information on phase transition and lattice evolution. Note that lattice evolution is often associated with a distortion or tilting of Li/metal octahedra, which essentially affects Li⁺ migration behavior. The second step is to analyze the position (coordinates), occupancy, and isotropic/anisotropic thermal displacement of all ions. These three factors provide key information on the following: Li⁺ order–disorder, the existence of new Li sites, vacant interstitial sites (as intermediate states for ionic motion), blocking effects from metal ions, distortion or tilting of Li/Metal octahedra, dual-halogen mixing, etc. Particularly, Li⁺ thermal displacements are associated with migration behavior and anion lattice modulation. Last but not least is the difference Fourier procedure, which is based on the difference between simulated and observed hkl intensities to calculate residual nuclei densities in one’s structure model. Some of these residual densities may represent missing atoms. Difference Fourier procedure is significantly advantageous in discovering unexpected new Li⁺ sites which may reside in Li⁺ migration pathways and promote the migration.

The comprehensive structure model determined by neutron powder diffraction refinements enable the probable Li⁺ migration pathways to be revealed via a bond-valence site energy (BVSE) calculation [36,37]. Li⁺ site energies, E_BVSE (Li), will be calculated and presented in the form of a dense grid of points throughout the whole structure with the user-defined resolution (for instance 0.1 Å) using the Morse-type SoftBV interaction potential. An overall 3D isosurface landscape of E_BVSE (Li) will be depicted, superimposed upon the crystal structure. Regions of low BVSE can be identified as probable Li⁺ diffusion pathways. Metastable interstitial Li⁺ sites as a possible transition state for motion in the pathway can even be found. Moreover, an energy profile along certain migration pathways can be extracted from the above overall landscape to further analyze the migration barrier. The above information provides an intuitive explanation as to how structural modulation exactly affects migration behavior.

3. Application of Neutron Powder Diffraction (NPD) in Metal Halides SSEs

3.1. Defect Chemistry and Phase Transition

Defects in the solid-state structure, which are often accompanied by phase transition and local structure distortion, directly affect active Li⁺ and vacancy concentrations. Since the Li⁺ hopping process is very sensitive to these concentrations, tuning defects can be an effective strategy towards a facile Li⁺ hopping process, which in turn boosts the ionic conductivity in orders of magnitude. The ion transport via vacancies is the predominant migration behavior for many kinds of superionic conductors [39]. According to one study [39], in the close-packed lattice, the Li⁺ migration barrier through vacancies is much lower than the direct or ring exchange diffusion process. In a layered structure, the Li⁺ ion would prefer to migrate from one octahedron site to another via their adjacent tetrahedral vacancy. For layered Li₃MX₆-type halides, when the compound is stoichiometric, there are 1/3 vacancies that reside in octahedral interstitial sites. These vacancies are essential in achieving high ionic conductivity in the Li₃MX₆ structure.

An aliovalent substitution of metal ions could readily enrich the active Li⁺ and vacancy concentration to improve the ionic conductivity. The increased vacancy concentration may lead to a redistribution of Li ions, and even bring new Li⁺ sites (as new active Li⁺). It also should be noted that aliovalent substitution often triggers phase transition and distortion in the lattice. Here we discuss four published works [24,40,41,42] to show how NPD assists the above study.

The first work is about a Zr⁴⁺ substituted halide system Li_3−xM_1−xZr_xCl₆ (M = Y, Er) (x = 0–0.6) that mainly involves the finding of a new Li⁺ site after phase transition, as reported by Park et al. [24]. Zr⁴⁺ (r = 72 pm) was specifically adopted to substitute Y³⁺ (r = 90 pm) and Er³⁺ (r = 89 pm) since its ionic radius is larger than other M⁴⁺ metal ions. After substitution, the halide transits from a trigonal to an orthorhombic structure, and achieves a highest room-temperature ionic conductivity of 1.1 × 10⁻³ S cm⁻¹ at x = 0.367 for Li_3−xEr_1−xZr_xCl₆ (phase III, orthorhombic Pnma), and 1.4 × 10⁻³ S cm⁻¹ at x = 0.5 for Li_3−xY_1−xZr_xCl₆ (phase III, orthorhombic Pnma). Such ionic conductivity is among the top class of reported chloride compounds. The author also discovered that orthorhombic Li_3−xM_1−xZr_xCl₆ has excellent electrochemical oxidation stability against non-coated 4 V-class cathode materials that does not show any observable oxidative interfacial decomposition in full cells. It was concluded that the phase transition from trigonal to orthorhombic structure and additional Li⁺ sites (marked as Li3) account for the superior conductivity.

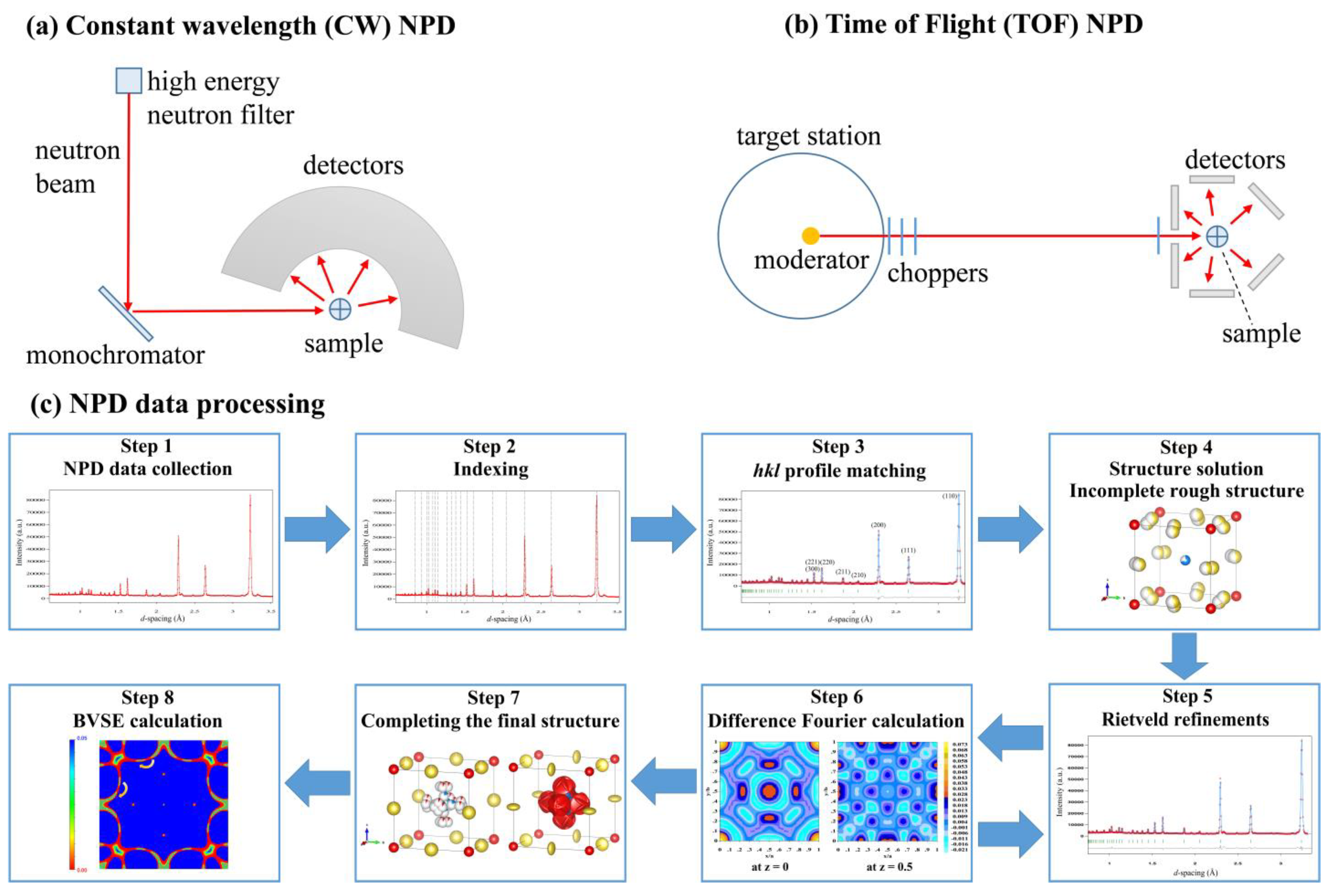
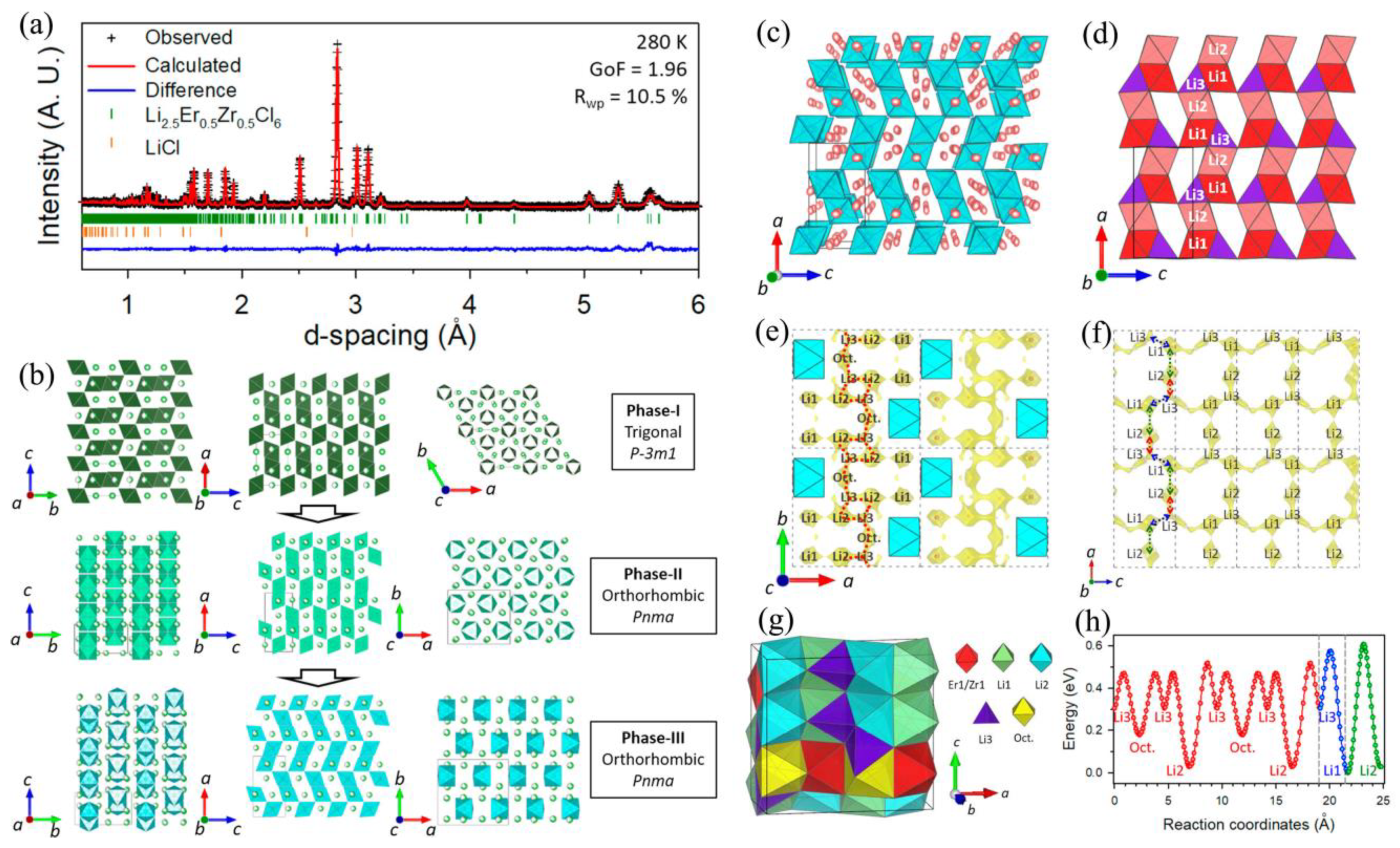
TOF NPD was performed in combination with single crystal XRD. First, they used single-crystal XRD to solve the location of heavy ions Er³⁺, Y³⁺, Zr⁴⁺, Cl⁻. Second, this model was directly used in neutron diffraction Rietveld refinements to refine the Li⁺ position (while keeping the heavy ions fixed). Third, the Er/Zr ratio was set to the single-crystal value while other parameters like occupancies and thermal displacements were freely refined. Note that a constraint on total Li occupancy was added for charge balance. The final NPD refinement plot is shown in Figure 1a, which is often presented in research papers including observed neutron data, a mathematically calculated line obtained from the final structure, index of diffraction peaks (indicating which plane the peak belongs to), and difference between observed and calculated data. Empirically, when the χ² (=GoF²) is lower than 2, along with a residual factor R_wp lower than 13%, the refinement result is acceptable.

The trigonal-to-orthorhombic phase transition as identified by NPD data is shown in Figure 1b. Pristine Li₃ErCl₆ and Li₃YCl₆ are trigonal in structure (space group P-3m1, marked as phase I). When Zr⁴⁺ is 0.2 ≤ x ≤ 0.3, the phase transition occurs and an orthorhombic Li₃LuCl₆-typed [43] structure (Pnma, phase II) appears. At higher substitution levels (0.367 ≤ x ≤ 0.600), the MCl₆ octahedra undergo further tilting that distorts the orthorhombic structure (Pnma, phase III). Tilting or distortion of octahedra often happen with phase transition.

The new tetrahedral Li3 site that is about 20% occupied was only observed in phase III, as shown in Figure 1c,d. In phase III, the Li1 and Li2 octahedra are face-shared in pairs, and the Li3 tetrahedron connects these Li1/Li2 octahedral pairs in a trigonal face-shared manner to establish Li⁺ ion diffusion chains along the a-axis. Note that all three Li⁺ sites contain a significant vacancy population between 25% and 80%. The emergence of a Li3 tetrahedral site indicates a redistribution of Li⁺ ions. As concluded by the author, these Li3 sites and vacancies are responsible for the higher Li⁺ conductivity in phase III.

Bond-valence site energy (BVSE) methods [36,37] can calculate the energy landscape of the Li⁺ diffusion pathway. In Figure 1e, the [Li3–Oct.–Li3–Li2] zigzag chain running along the [010] direction was the most desired one-dimensional pathway. This pathway along the b-axis intersects with [Li2–Li3–Li1] chains of the ac-plane (Figure 1f) to form a 3D network for Li⁺ migration. In Figure 1g, a metastable octahedral interstitial site, namely “Oct”, which is face-shared with Er/Zr octahedra, was suggested to participate in the Li⁺ migration. Moreover, the site energy profile (Figure 1h) extracted from the overall landscape reveals a lower energy barrier for orthorhombic Li_2.5Er_0.5Zr_0.5Cl₆ (phase III). The barrier for trigonal Li₃ErCl₆ (phase I) was claimed be about 1.5-fold higher than this orthorhombic one.

The second work is about Li_3−xIn_1−xZr_xCl₆ [40] that mainly involves octahedral distortion, accompanied with Li⁺ redistribution and Li⁺-metal cations disorder (disorder will be discussed further in a following section). The author concluded that local M2/Li4 octahedra distortion, along with Li⁺ redistribution and disorder, accounts for the conductivity improvement from 0.47 mS·cm⁻¹ of Li₃InCl₆ to 1.25 mS·cm⁻¹ of Li_2.6In_0.6Zr_0.4Cl₆. It should be noted that pristine Li₃InCl₆ has been reported to possess higher conductivity (~1.49 mS·cm⁻¹ [22], ~2 mS cm⁻¹ [23,44]) than in this work. However, this should be related to the synthesis method. It can be expected that after optimization on a synthesis route, Li_2.6In_0.6Zr_0.4Cl₆ would achieve higher conductivity than Li₃InCl₆ of 1.49~2 mS cm⁻¹.

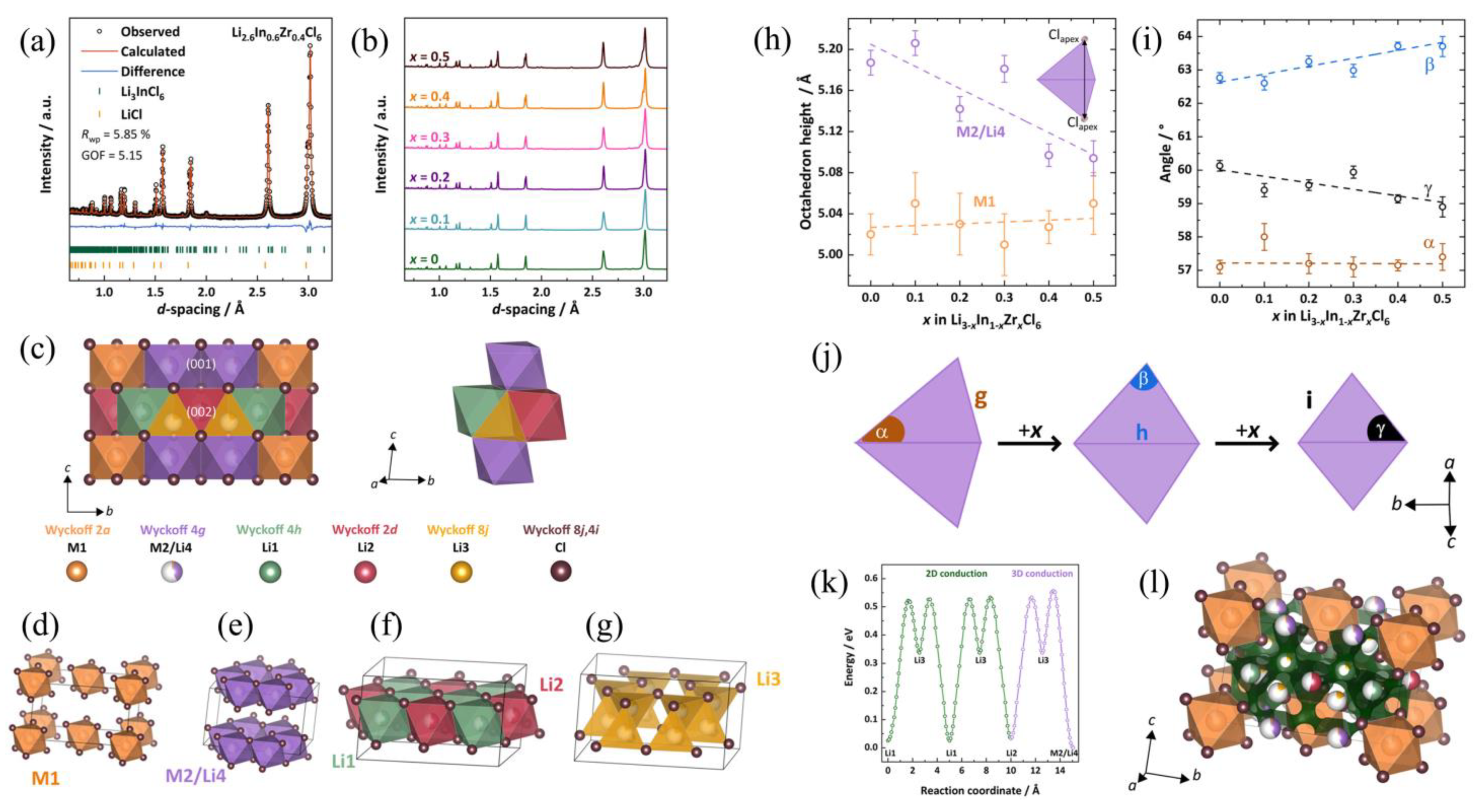
The indication of the existence of octahedral distortion is the lattice compression along the c-axis. The NPD refinements on the Li_3−xIn_1−xZr_xCl₆ series as shown in Figure 2a,b reveal that, as Zr increases, lattice parameters a and b are nearly unchanged, while c decreases, possibly due to the smaller ionic radius of Zr⁴⁺ than In³⁺ ions [33]. This represents a compression on the c direction and lattice volume asymmetric shrinkage, which would act on Li/metal octahedra to undergo asymmetric distortion.

However, to further understand this distortion from atomic scale, structure determination based on NPD is very necessary. The crystallography is shown in Figure 2c–g. The substituted Li_3−xIn_1−xZr_xCl₆ is isostructural to Li₃InCl₆. For a typical Li₃InCl₆, it adopts a monoclinic layered structure with space group C2/m. The (InCl₆)³⁻ octahedra are exclusively located within the (001) lattice plane (marked as M1 and M2/Li4 in Figure 2d,e). In this (001) plane, most In³⁺ ions occupy M1 isolated octahadral sites, while only a few of them occupy M2 honeycomb sites (occupancy 5–10%). Li⁺ ions only occupy M2 sites (occupancy ~40%) to make M2/Li4 co-occupation (Figure 2e). In the (002) plane, only (LiCl₆)⁵⁻ octahedra and (LiCl₄)³⁻ tetrahedra (occupancy ~17%) reside in this layer (marked as Li1, Li2, and Li3 in Figure 2f,g).

The most intriguing factor with structure is that, with Zr⁴⁺ substitution, In³⁺ and Zr⁴⁺ still prefer M1 positions with a few on the M2/Li4 position, while Li⁺ ions would remarkably occupy a M2/Li4 position, together with a gradually decrease of occupancy on Li1, Li2 octahedral sites, and a total loss of occupancy on Li3 tetrahedral sites. The Li3 tetrahedral site is explained to be a higher-energy intermediate site [16] that would be depopulated first when removing Li⁺ from the system. (For charge balance, Li⁺ will be removed as Zr⁴⁺ increases.) These results represent a redistribution of Li⁺ ions and a Li-In-Zr disorder on the M2/Li4 position, which may lead to a 3D diffusion pathway for facile Li⁺ migration.

Bearing the above in mind, octahedral distortion can be discussed and its correlation with the Li sublattice can be unraveled. With Zr⁴⁺ substitution, the octahedron height of the M2/Li4 site significantly decreases (Figure 2h), while the M1 octahedron height keeps almost constant. These changes are the main reason for the c-direction compression. In addition, the apex Cl⁻ approaches the center, accompanied by angle changes (Figure 2i) that alter the degree of octahedral distortion (Figure 2j). Since M2/Li4 sites are preferably occupied by Li⁺ with Zr⁴⁺ substitution, the primary driven force for this distortion should be lithium redistribution and disorder. Finally, BVSE [36,37] based on neutron data provides the 3D migration pathway (Figure 2l) with its site energy profile (Figure 2k).

The third [42] and fourth [41] works are both about rare-earth metal halides that mainly involve phase transition. It has been known that Li₃MCl₆ (M = Ln³⁺) can crystallize in a trigonal (space group P-3m1), orthorhombic (space group Pnma) and monoclinic (space group C2/m) structure. Different symmetric arrangements of cations and vacancies lead to a distinct Li⁺ migration. Conventionally, Li₃MCl₆ (M = Tb, Dy, Ho, Er, Tm) crystallizes in a trigonal P-3m1 structure. However, Liang et al. [42] modified the Li/M ratio to induce a phase transition from trigonal to orthorhombic structure and successfully achieved a series of orthorhombic Li_3−3xM_1+xCl₆ (−0.14 < x ≤ 0.5, M = Dy, Ho, Y, Er, Tm) with enhanced ionic conductivity. Taking orthorhombic Li_3−3xHo_1+xCl₆ (0.04 < x ≤ 0.2) as an instance, a tiny modification of the Li/Ho ratio (x = 0.09) could boost the room-temperature ionic conductivity from 2.9 × 10⁻⁴ S cm⁻¹ to 1.3 × 10⁻³ S cm⁻¹. NPD refinement clearly confirmed the rearrangement of the cation and anion sublattice after phase transition, and an expansion in the triangular area of face-shared octahedra/tetrahedral. It is explained that such an expansion broadens the size of the bottleneck for a facile Li⁺ diffusion along the c-lattice direction. The diffusion in the c direction via face-sharing octahedral is faster than that in the xy-plane via a face-sharing octa-tetra-octahedra path. Its activation energy is also reduced compared to that in the trigonal phase.

The above study can be seen as a typical example of isovalent self-substitution, in which its own rare-earth content was tuned to trigger Li vacancies and phase transition. Their success with orthorhombic Li_2.73Ho_1.09Cl₆ encouraged Zhou et al. [41] to perform aliovalent substitution on the Li_3−xZr_xHo_1−xCl₆ and Li_3−xZr_xLu_1−xCl₆ series. Zr substitution is also beneficial in relieving the dependence on rare-earth elements and promoting scalable production. In their work, Zr⁴⁺ substitution lifts the ionic conductivities up to ~1.8 mS cm⁻¹, and suppresses the activation energies down to ~0.34 eV. At cutoff potentials of both 4.3 and 4.6 V vs. Li⁺/Li, their ASSB, comprised of Li_2.6Zr_0.4(Ho/Lu)_0.6Cl₆ SSE paired with LiNi_0.85Co_0.1Mn_0.05O₂ (NCM85), show stable cycling. Even upon 4.8 V, their ASSB still exhibits long-term stable cycling. When assembled with an Si or Li_0.7Si anode, NCM85 ASSBs with Li_2.6Zr_0.4Lu_0.6Cl₆ as the SSE still perform long-term stable cycling at a high areal capacity of 16 mAh cm⁻².

Pure Li₃HoCl₆ has a trigonal structure. Similar to the above mentioned Li_2.73Ho_1.09Cl₆ and Li_3−xZr_x(Y/Er)_1−xCl₆ [24], the Zr⁴⁺ substituted Li_3−xZr_xHo_1−xCl₆ (0.2 < x ≤ 0.8) series transform from a trigonal to an orthorhombic-II structure (space group Pnma). Li₃LuCl₆ itself is an orthorhombic-I structure (space group Pnma), but Li_3−xZr_xLu_1−xCl₆ (0.2 ≤ x ≤ 0.8) also transform to the orthorhombic-II structure with (Lu/Zr)Cl₆ octahedra tilting. All solid solutions Li_3−xZr_x(Ho/Lu)_1−xCl₆ (0.2 ≤ x ≤ 0.6) exhibit superior conductivities (up to 1.8 mS cm⁻¹) compared to pristine Li₃HoCl₆ and Li₃LuCl₆ (~0.1 mS cm⁻¹).

NPD plays a key role in Li_3−xZr_x(Ho/Lu)_1−xCl₆ structure phase transition analysis and Li occupancy. In layers of the ab-plane, trigonal Li₃HoCl₆ and orthorhombic-I Li₃LuCl₆ both possess honeycomb-ordered shared-edge Li⁺ octahedra adjacent with their interstitial tetrahedral voids, which allow Li⁺ ions to diffuse in the ab-plane via the Oct–Tet–Oct pathway. Along the c axis, the LiCl₆ octahedra are directly linked in a face-shared manner to establish a c-direction Li⁺ pathway. Similar to the above, substituted orthorhombic-II Li_2.4Zr_0.6(Lu/Ho)_0.4Cl₆ still maintains a honeycomb ordered layer but arranged on the bc-plane. These layers have a stacking fault along the a-axis that forms a zigzag chain of faced-shared or edge-shared LiCl₆ octahedra along the a-axis, which allows Li⁺ migration along this direction. All of these Li sites in the above structures are not fully occupied, leaving abundant Li vacancies in the diffusion pathway, as confirmed by BVSE calculation [36,37] based on NPD. From NPD refinements, Li_2.4Zr_0.6(Lu/Ho)_0.4Cl₆ possesses prominently more vacancies in its Li octahedral sites in honeycomb layers and zigzag chains compared to Li₃HoCl₆ and Li₃LuCl₆. This is the explanation for its higher conductivity triggered by phase transition.

3.2. Disorder and Blocking Effect

The disorder discussed here refers to Li⁺ disorder and metal cation disorder. Both of these are accompanied with vacancies. As we know, disorder is very common in solid structures, and also in metal halide SSEs. Even within the same anion sublattice, there could there be a remarkable difference in the disorder, according to the different type of cations. Since the structure provided by neutron/XRD refinements is actually a space-and-time-averaged one, the most common instance we can find of so-called disorder is the multiple crystallographic sites for Li⁺ and cations with different partial occupancies. The common way to induce disorder is to vary the components or valence of metal cations. The induced disorder will in turn promote the Li⁺ hopping in its pathway. The blocking effect means that the M cation on its position will yield a Coulombic repulsion to Li⁺ migration. Therefore, the Li⁺ diffusion via the interstitial tetrahedral site surrounding the M cation is to some extent blocked. Tuning or decreasing the M contents to relieve the blocking effect is plausible for better ionic conductivity.

Utilizing disorder strategies, Zhou et al. [29] construct a Li⁺ and cation disordered halo-spinel chloride Li₂Sc_2/3Cl₄ with superionic conductivity as high as 1.5 mS cm⁻¹ that has far surpassed other spinel-type halides Li₂MgCl₄, Li₂ZnCl₄ (<10⁻³ mS cm⁻¹ at room temperature) [45,46], and most halides including Li₃InCl₆, Li₃YCl₆, Li₃ErCl₆, and Li_3−xM_1−xZr_xCl₆ (M = Er, Y) (0.31–1.49 mS cm⁻¹) [21,24]. Such superior ionic conductivity was ascribed to the significant Li-site disorder, which creates a redistribution of Li⁺ ions that brings about new Li sites (marked as Li2 and Li3). These new interstitial Li sites serve as intermediate sites residing on the pathway that are critical for Li⁺ ion diffusion.

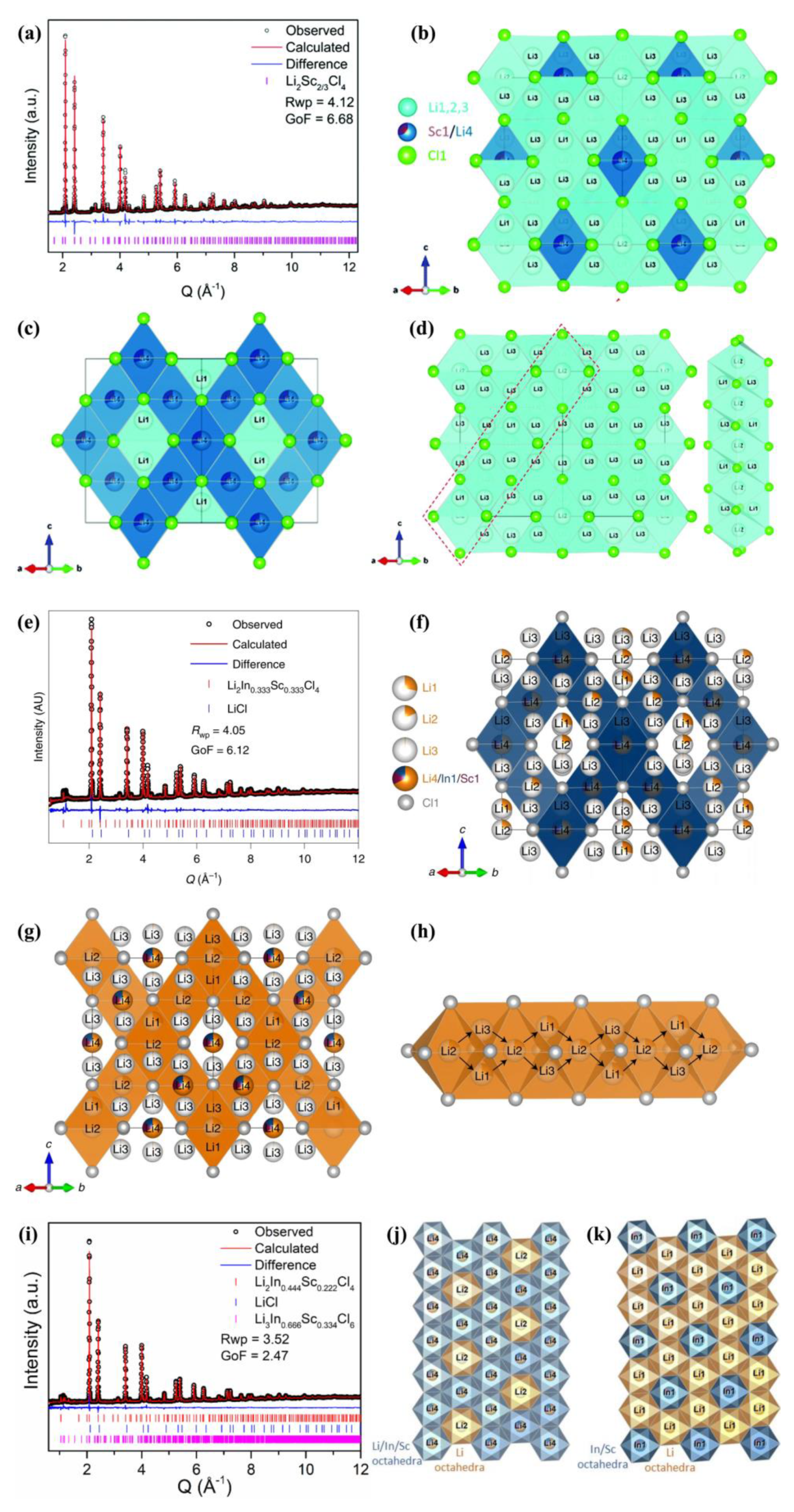
Above explanation is actually based on time-of-flight (TOF) NPD refinements that exactly determine Li⁺ distribution and occupancy on each crystallographic site. As shown in Figure 3a, the neutron pattern is well refined by the Li₂Sc_2/3Cl₄ spinel structure with cubic space group Fd-3m. The crystal structure of spinel Li₂Sc_2/3Cl₄ are shown in Figure 3b,c. The framework of Li₂Sc_2/3Cl₄ is somewhat similar to spinel Li₂MgCl₄, but the atomic occupancies are quite different. Li₂Sc_2/3Cl₄ possesses four Li sites: Li2 and Li3 are newly discovered positions while Li1 and Li4 are original positions similar to Li₂MgCl₄. The conventional spinel Li₂MgCl₄ is constituted of edge-shared Mg1 and Li2 octahedra where both Mg and Li take a half occupation, and Li1 fills the corner-sharing Li1 tetrahedra site (Li1 coordinates: 1/8, 1/8, 1/8). However, in Li₂Sc_2/3Cl₄, its edge-shared Sc1 and Li4 octahedra have a Sc:Li4 occupation ratio of 0.311:0.689, which means that more Sc ions are substituted by Li ions. While Li1 also take the same position of tetrahedra sites (similar to Li₂MgCl₄), its new Li2 fills the edge-sharing Li2 octahedra site, and its new Li3 occupy another edge-sharing tetrahedra site.

The most striking point is that the wide spread of new Li2 and Li3 over the whole lattice links the Li1 tetrahedra, Li2 octahedra, and Li3 tetrahedra all together in series in a face-shared manner that forms an infinite pathway for Li⁺ diffusion in Li₂Sc_2/3Cl₄ (Figure 3d). This new pathway plays the decisive role in the ionic conductivity enhancement. In this new pathway, the relatively low occupancies of the Li1,2,3 sites have provided abundant vacancies which would help to skip the defect formation step during Li+ ion migration. Moreover, the Li⁺ redistribution over tetrahedra and octahedra sites also indicates that the Li⁺ site energies on the sites are probably similar, that is, a flat energy landscape for facile ion diffusion [47,48].

A blocking effect may reside on the Sc1/Li4 octahedra site, as reflected by NPD refinements that the thermal displacement parameter of Li4 on this octahedral site is very low. Although Sc1/Li4 octahedra also border Li3 tetrahedra in a face-shared manner, trivalent Sc³⁺ ions still sit in this octahedra site that may block Li⁺ ion diffusion, as Mg²⁺ does in Li₂MgCl₄ [49]. Hence, Li⁺ ions on this site appear to show small thermal displacements and low mobility. Therefore, the main diffusion pathway may not involve Sc1/Li4 octahedra sites. Overall, these new possible Li1,2,3 diffusion pathways with considerable amounts of vacancies achieve a relatively low activation energy for Li⁺ hopping. In a battery test, Li₂Sc_2/3Cl₄ also shows excellent performance in a potential window up to 4.6 V due to its high oxidative stability, when assembled with uncoated LiCoO₂ (LCO), LiNi_0.6Mn_0.2Co_0.2O₂ (NCM622) and high-Ni LiNi_0.85Mn_0.1Co_0.05O₂ (NCM85) cathodes.

It would be very meaningful to induce a higher extent of disorder into Li₂Sc_2/3Cl₄ to further improve ionic conductivity, along with good stability against electrodes. Zhou et al. [50] continued their research and developed an isovalent In³⁺ substituted Li₂In_xSc_0.666−xCl₄ (0 < x < 0.666) system as a fast Li ion conducting chloride SSE, which exhibits an improved ionic conductivity up to 2.0 mS cm⁻¹ (Li₂Sc_2/3Cl₄ is 1.5 mS cm⁻¹). According to their report, incorporating only 10 wt% Li₂In_1/3Sc_1/3Cl₄ with cathode active material (CAM, typical 4V, LiCoO₂, LiNi_1−x−yCo_xMn_yO₂) [11] could form a cathode composite with a low-impedance SE/CAM interface that enables excellent electrochemical performance. All-solid-state Li batteries (ASSBs) utilizing uncoated LCO, NCM622 and NCM85 could exhibit a superior rate capability and apparently more stable long-term cycling up to 4.8 V versus Li⁺/Li, compared with most advancing ASSBs. Their high-voltage, high-loading and ultra-stable solid-state cells indeed provide inspiration for the design of advancing ASSBs.

In this Li₂In_xSc_0.666−xCl₄ series, a highly disordered Li⁺ distribution was observed. It was then concluded that such disorder brought about a lattice with metastable intermediate Li⁺ sites that enable a fast Li⁺ diffusion and rate capability. The phase of Li₂In_xSc_0.666−xCl₄ series can be varied according to In³⁺ x contents. When x is between 0~0.444, the obtained Li₂In_xSc_0.666−xCl₄ is a cubic spinel phase with little impurity, as illustrated in Figure 3e, exampled with spinel Li₂In_1/3Sc_1/3Cl₄. However, when x content goes higher, typically ≥ 0.555, the fractions of monoclinic Li₃MCl₆-typed phase and LiCl impurities begin to increase, as illustrated in Figure 3i, exampled with spinel Li₂In_0.444Sc_0.222Cl₄ and Li₃ScCl₆-typed Li₃In_2/3Sc_1/3Cl₆. The structure of Li₂In_1/3Sc_1/3Cl₄ (Figure 3f) is similar to the halo-spinel Li₂Sc_2/3Cl₄ [29] mentioned before, and also contains four Li⁺ sites (with two new sites) per unit cell, though with different occupancies. From Figure 3f,g, one can readily see the significant Li⁺ disorder as metastable intermediate Li sites that are supposed to benefit Li-ion mobility and fast rate capability. The face-shared Li2 octahedra and Li1 or Li3 tetrahedra with relatively low occupancies (~0.2–0.3) construct a 3D Li⁺ migration pathway (Figure 3g,h). Benefiting from a relatively low activation energy (0.33 eV simulated from EIS measurements) for Li⁺ diffusion, and 3D migration pathways (from BVSE calculation based on NPD Rietveld refinements) with considerable amounts of site vacancies (i.e., disorder, based on NPD Rietveld refinements), a high ionic conductivity of 2.0 mS cm⁻¹ was finally achieved. As for Li₃ScCl₆-typed monoclinic phase Li₃In_2/3Sc_1/3Cl₆ (Figure 3i), its main diffraction peaks overlapped with that of spinel Li₂In_0.444Sc_0.222Cl₄. One difference between the spinel Li₂In_0.444Sc_0.222Cl₄ and monoclinic Li₃In_2/3Sc_1/3Cl₆ is that, in spinel Li₂In_0.444Sc_0.222Cl₄ its Li4/Sc1/In1 metal sites are all shared (Figure 3j), but in monoclinic Li₃In_2/3Sc_1/3Cl₆ its Li1 sites and Sc1/In1 metal sites are all crystallographically distinct, that is, ordered (Figure 3k). In one word, this work can be seen as an intuitive illustration of how metal contents switch the cation arrangements between order and disorder.

Figure 3. (a) Time-of-flight NPD Rietveld refinement on Li₂Sc_2/3Cl₄. (b) Structure of disordered spinel Li₂Sc_2/3Cl_4. (c) Structure without showing Li2 octahedra and Li3 tetrahedra. One can see that it basically has a Li₂MgCl₄-typed structure framework but with different site occupancies. (d) Li⁺ diffusion pathway of Li₂Sc_2/3Cl₄ along the face-shared Li1, Li3 tetrahedra and Li2 octahedra; right inset is the expansion of the red dot area illustrating a potential diffusion pathway through Li2 octahedra and Li1, Li3 tetrahedra. Reproduced with permission: Copyright 2020, Royal Society of Chemistry [29]. (e) TOF NPD Rietveld refinement of Li₂In_1/3Sc_1/3Cl₄. (f) Structure of Li₂In_1/3Sc_1/3Cl₄ viewed as only Li4/In1/Sc1 octahedral framework. (g) Li⁺ diffusion pathway via face-shared Li1 tetrahedra and Li2 octahedra. (h) Enlarged Li⁺ diffusion pathway through Li2 octahedra and adjacent Li1 or Li3 tetrahedra. (i) NPD Rietveld refinements with spinel Li₂In_0.444Sc_0.222Cl₄ and monoclinic Li₃In_0.666Sc_0.334Cl₆. (j) Illustration of spinel structure in which Sc/In/Li sites are all shared. (k) Illustration of monoclinic structure in which In/Sc and Li sites are distinct. Reproduced with permission: Copyright 2022, Springer Nature [50].

Figure 3. (a) Time-of-flight NPD Rietveld refinement on Li₂Sc_2/3Cl₄. (b) Structure of disordered spinel Li₂Sc_2/3Cl_4. (c) Structure without showing Li2 octahedra and Li3 tetrahedra. One can see that it basically has a Li₂MgCl₄-typed structure framework but with different site occupancies. (d) Li⁺ diffusion pathway of Li₂Sc_2/3Cl₄ along the face-shared Li1, Li3 tetrahedra and Li2 octahedra; right inset is the expansion of the red dot area illustrating a potential diffusion pathway through Li2 octahedra and Li1, Li3 tetrahedra. Reproduced with permission: Copyright 2020, Royal Society of Chemistry [29]. (e) TOF NPD Rietveld refinement of Li₂In_1/3Sc_1/3Cl₄. (f) Structure of Li₂In_1/3Sc_1/3Cl₄ viewed as only Li4/In1/Sc1 octahedral framework. (g) Li⁺ diffusion pathway via face-shared Li1 tetrahedra and Li2 octahedra. (h) Enlarged Li⁺ diffusion pathway through Li2 octahedra and adjacent Li1 or Li3 tetrahedra. (i) NPD Rietveld refinements with spinel Li₂In_0.444Sc_0.222Cl₄ and monoclinic Li₃In_0.666Sc_0.334Cl₆. (j) Illustration of spinel structure in which Sc/In/Li sites are all shared. (k) Illustration of monoclinic structure in which In/Sc and Li sites are distinct. Reproduced with permission: Copyright 2022, Springer Nature [50].

3.3. Dual-Halogen and Lattice Dynamics

Tuning halogen anions in halides (F⁻, Cl⁻, Br⁻, I⁻) or introducing dual-halogen mixing can be an effective way to lower the Li⁺ migration barrier, and improve moisture tolerance and electrode compatibility. In fact, this strategy of anion modulation involves changes on the polarizability of anions and the lattice. The host lattice polarizability can affect the lattice vibration strength (that is, lattice dynamics) and correspondingly the Li⁺ mobility kinetics, which has been rationalized by the Arrhenius equation [51] in which the activation barrier and prefactor are modulated. According to Wakamura et al.’s [52] study, low activation energies of Li⁺ migration correspond to “low-energy” phonon frequencies (that is, low lithium vibration frequency) and a high frequency dielectric constant. From this perspective, a softer and more polarizable anion sublattice much favors a facile ionic transport. The polarizability of different metal cations and anions is shown in Table 1. It can be found that F⁻ has the lowest polarizability, and fluorides often exhibit low ionic conductivity (less than 10⁻⁵ S cm⁻¹). Bromide and iodide generally show higher polarizability than chloride, and hence higher ionic conductivity has been observed [21,53,54]. In one word, halogens with higher polarizability are expected to facilitate Li migration.

Bearing this in mind, Liu et al. [55] utilized bromide with higher polarizability to make an anion-mixed halide Li₃Y(Br₃Cl₃) via the hot-pressing method to promote conductivity, along with optimization on the grain boundary. Conventionally, Li₃Cl₆ yields the trigonal phase while Li₃YBr₆ yields the monoclinic phase. The ball-milled Li₃Y(Br₃Cl₃) was initially a mixture of Li₃YCl₆ and Li₃YBr₆. However, after hot-pressing, the Li₃Y(Br₃Cl₃) mixture transformed into a single Li₃YBr₆-type monoclinic phase and then reached a strikingly high conductivity of 7.2 mS cm⁻¹ (room-temperature). The author then ascribes this to the high occupancy of tetrahedral Li sites and the optimized contact between grain boundaries that resulted from the hot-pressing method.

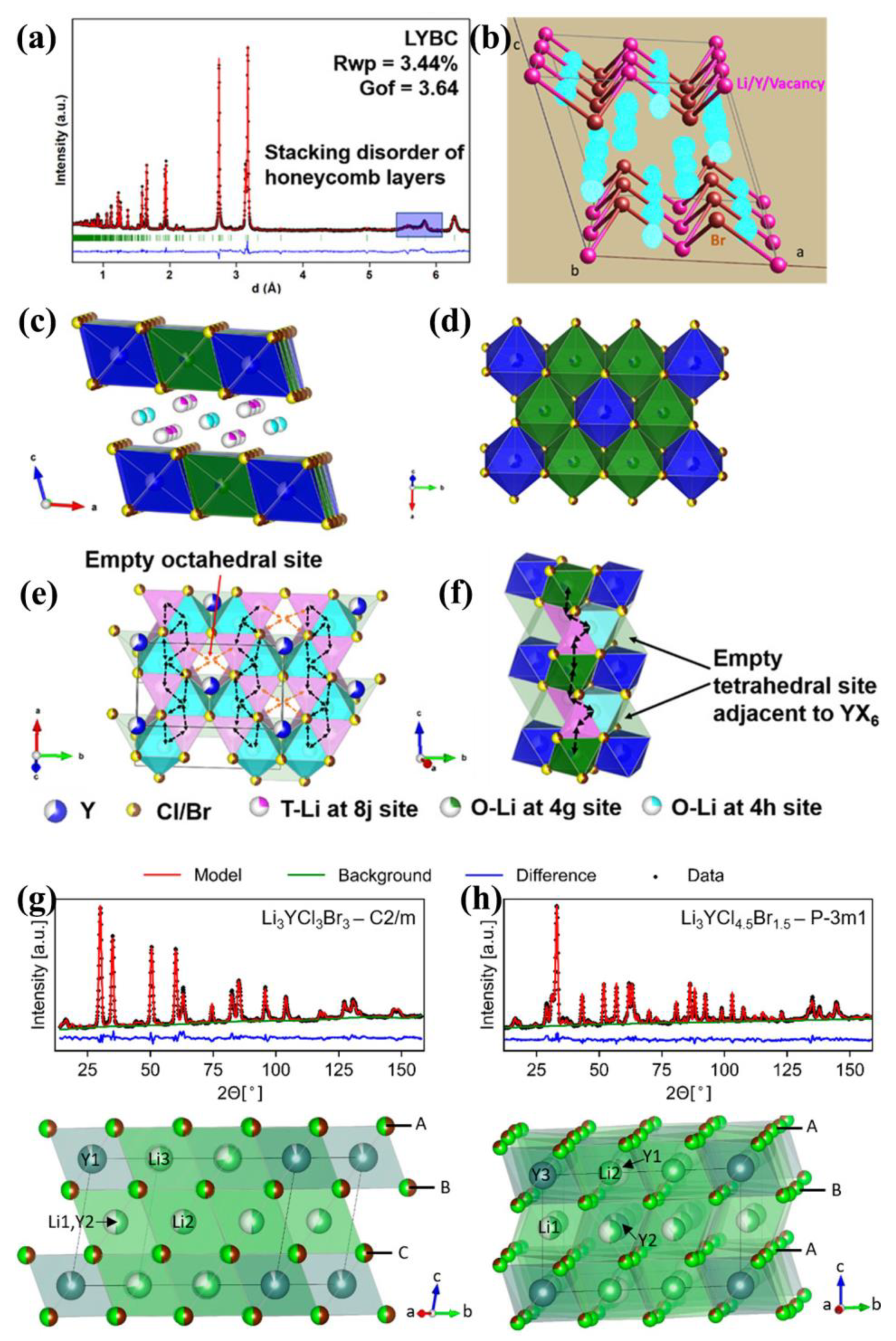
NPD refinement (Figure 4a) clearly confirmed the whole structure and the significant amounts of additional tetrahedral Li sites (cyan sphere in Figure 4b) in the lattice. The refinement was completed on the basis of the Li₃YBr₆ structure model with half of the Br replaced by Cl. The whole structure consists of a transition metal chloride layer and lithium chloride layer (Figure 4c). In the metal chloride layer, Li⁺ ions partially occupy the Y³⁺ ions’ position to form a honeycomb-type local ordering of YX₆ and LiX₆ (X = Br and Cl) octahedra (Figure 4d), along with some vacancies on both sites. This honeycomb ordering has been mentioned above [40,41], and is also similar to Li-Mn rich cathode materials [56]. Moreover, a stacking faults along the c-axis could be confirmed by NPD refinements on 5.5~6 A data, representing a long-range disorder of the honeycomb’s location along the c-axis, which is also observed in layered oxide Na(Ni_2/3Sb_1/3)O₂ [57].

The above-mentioned tetrahedral Li sites are actually located by an NPD Difference Fourier map (cyan sphere in Figure 4b). We have mentioned this Difference Fourier procedure in Section 2.3; it is very effective in locating residue density which probably represents missing Li⁺ ions. Four different tetrahedral sites (pink sphere in Figure 4c,e,f), with two sites in the lithium layer and the other two in the transition metal layer, were successfully located using this procedure. They were found to coexist with Li⁺ octahedral sites in their lithium chloride layer. However, the author mentioned that the residual densities on these sites probably result from the presence of stacking faults along the c-axis, and some of them are very likely to be empty tetrahedral sites due to repulsion from Y³⁺ ions [16,21] (Figure 4e,f). Through BVSE calculation [36,37], the author proposed that the presence of these tetrahedral Li⁺ sites (marked as “T-Li at 8j site”) depopulates the octahedral Li⁺ occupancies (that is, creates more vacancies); in which case, it brings about a more flat energy landscape for a concerted Li⁺ diffusion. Such Li⁺ distribution enables an octahedra–tetrahedra–octahedra (O-T-O) Li⁺ hopping chain along the a-direction, which is then connected by octahedral sites (2d) to form a 2D diffusion network in the ab-plane (Figure 4e). Along the c-direction, hopping along an “O-T-O-T” zigzag route nearby Y³⁺ sites is allowed, which fulfills a 3D diffusion pathway (Figure 4f). In a word, tetrahedral Li⁺ lowers the diffusion activation energy in the ab-plane and promotes O-T-O-T zigzag diffusion along the c-direction.

In addition, the low resistance grain boundaries as formed during hot-pressing are also beneficial to conductivity enhancements. Such boundaries are proposed to originate from partial melting during the hot-pressing process, and the formation of fused grain boundaries might be relevant to the eutectic melting of multiple halide components. This study indicates that these anion-mixed halides have higher than expected potential as promising SSEs. Their easy-forming fused grain boundaries are quite advantageous in large scale fabrication.

However, the incorporations Br and I would lower the oxidation stability according to thermodynamic calculation. Therefore, one needs to carefully consider the trade-off between high ionic conductivity and good stability, and try to balance these two by delicately controlling the ratio of halogens. Bearing this in mind, Maas et al. [58] delicately designed the Cl/Br ratio in a Li₃YBr_xCl_6−x system and successfully realized the above. They found that Br⁻-rich halides are more conductive (5.36 × 10⁻³ S/cm at 30 °C for Li₃YBr_4.5Cl_1.5) but less oxidative stable (∼3 V) compared to Li₃YCl₆ (~3.5 V). Thus, they introduced only a small quantity of Br⁻ in the halide, that is Li₃YBr_1.5Cl_4.5, to keep its oxidative stability unaffected but make its ionic conductivity substantially improved (2.1 × 10⁻³ S/cm at 30 °C), compared to pristine Li₃YCl₆ (0.049 × 10⁻³ S/cm at 30 °C). Neutron diffraction refinement (Figure 4g,h) revealed that as Br contents increase, a phase transition happens, from the P-3m1 trigonal phase of Li₃YBr_xCl_6−x at x = 0, 1.5 with hexagonal close-packing (hcp) lattice, to monoclinic C2/m phase of Li₃YBr_xCl_6−x at x = 3, 4.5, 6 with a cubic close-packing (ccp) lattice. In all series, Br and Cl were randomly distributed on halogen sites. This study highlights that appropriate modulation of halogen substituents in the anion framework to optimize the balance between conductivity and stability is reasonable and feasible.

Figure 4. (a) NPD Rietveld refinement of hot-pressed Li₃Y(Br₃Cl₃). Black dots are observed data, red lines are simulated data. (b) Fourier difference map based on NPD Rietveld refinements of hot-pressed Li₃Y(Br₃Cl₃). The light-blue spheres represent the tetrahedral Li sites. (c,d) Monoclinic structure of hot-pressed Li₃Y(Br₃Cl₃) shown in different directions. (e,f) Li⁺ diffusion pathways depicted by black and red arrows in ab-plane and along c-direction. Reproduced with permission: Copyright 2020, American Chemical Society [55]. (g,h) Neutron powder diffraction of monoclinic and trigonal phase. Their corresponding structure are shown below. Reproduced with permission: Copyright 2022, Royal Society of Chemistry [58].

Figure 4. (a) NPD Rietveld refinement of hot-pressed Li₃Y(Br₃Cl₃). Black dots are observed data, red lines are simulated data. (b) Fourier difference map based on NPD Rietveld refinements of hot-pressed Li₃Y(Br₃Cl₃). The light-blue spheres represent the tetrahedral Li sites. (c,d) Monoclinic structure of hot-pressed Li₃Y(Br₃Cl₃) shown in different directions. (e,f) Li⁺ diffusion pathways depicted by black and red arrows in ab-plane and along c-direction. Reproduced with permission: Copyright 2020, American Chemical Society [55]. (g,h) Neutron powder diffraction of monoclinic and trigonal phase. Their corresponding structure are shown below. Reproduced with permission: Copyright 2022, Royal Society of Chemistry [58].

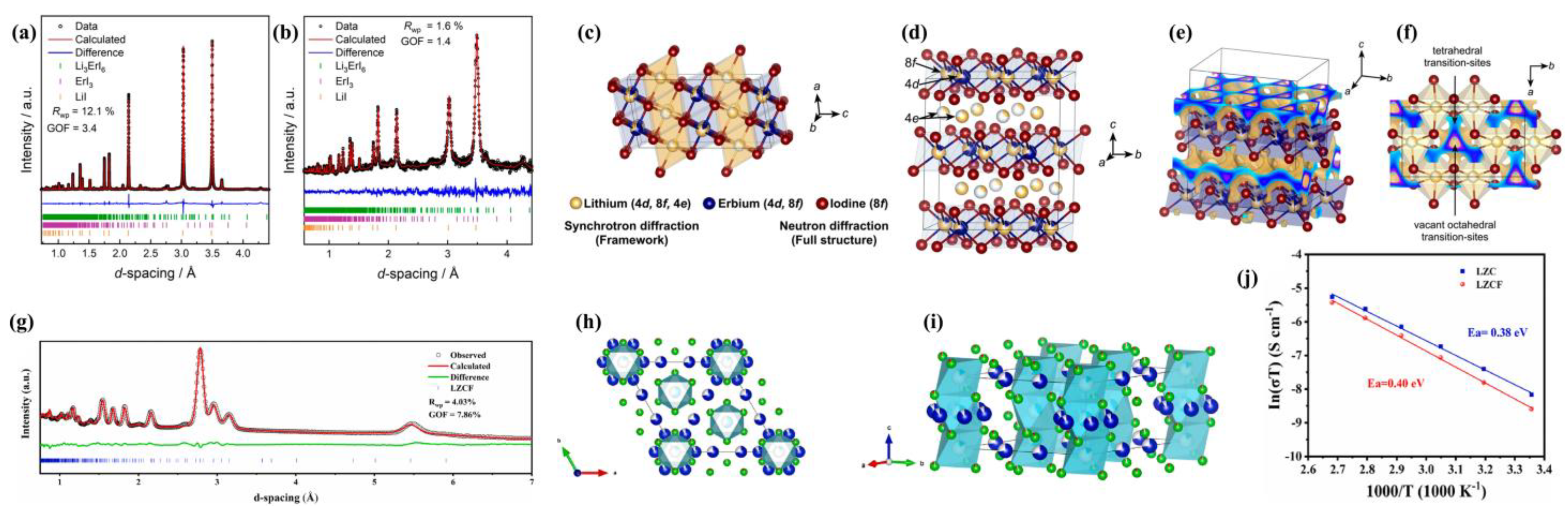
Regardless of oxidative stability, using iodine to yield the possibly largest polarizability in a halide lattice would provide a good chance for studying lattice polarizability effects. Schlem et al. [54] report the first experimentally obtained iodine-based halide superconductor Li₃ErI₆, of which the Li⁺ ionic conductivity is close to 1 mS cm⁻¹. In their work, Iodine (I) was adopted as a more-polarization anion to make a softer lattice of Li₃ErI₆ compared to Li₃ErCl₆. Using NPD, they performed a thorough investigation of the highly polarized lattice and the transport mechanism. Through their investigation of the Debye frequency of the lattice and impedance spectroscopy, they corroborated that improved ionic transport results from the iodide anion induced softer and more polarizable framework. Their results demonstrate that the idea of softer lattices also holds up in this class of materials.

Refinements on NPD and Synchrotron diffraction data are shown in Figure 5a,b. Li₃ErI₆ resembles a new monoclinic structure (space group C2/c). Synchrotron diffraction data was firstly refined to identify the lattice parameters, space group, Er³⁺, I⁻ ion positions and their thermal displacements. Later, NPD was refined to determine the coordinates and thermal displacements of Li⁺. The final structure (Figure 5c,d) consists of isolated layers of edge-shared ErI₆³⁻ octahedra, with LiI₆⁵⁻ octahedra interlayers between them. Er³⁺ partially occupies two different Wyckoff positions (8f, 4d) with remarkably different occupancies, which can be seen as a rare-earth cation disorder. Interestingly, the Li⁺ ions also occupy these partially vacant Er³⁺ sites, resulting in a Li⁺-Er³⁺ disorder within these layers. Essentially, the structure can be seen as alternating layers of Er/Li co-occupied edge-shared [Er_xLi_(1−x)I₆^(5−2x)−] octahedra (on Wyckoff 8f, 4d sites) and edge-sharing [LiI₆⁵⁻] octahedra (on Wyckoff 4e sites). In addition, through BVSE calculation [36,37] a two-dimensional Li⁺ diffusion pathway in the ab plane has been revealed (Figure 5e,f). The beige isosurface corresponds to the possible Li⁺ residence representing diffusion pathway. The blue section of this isosurface in the ab-plane is to show the interconnectivity of Li⁺ residence. Note that the interstitial tetrahedral voids and vacant octahedral sites (Figure 5f) could both serve as transition-sites for Li⁺ diffusion.

Incorporating I⁻ anion could soften the lattice and decrease the entropy of migration, which is correlated with the activation barrier as rationalized by the Arrhenius prefactor of the ionic conductivity [59]. The author conducted speed of sound measurements and found that from Li₃ErCl₆ (for comparison) to Li₃ErI₆, the longitudinal, transverse, mean speed, and calculated Debye frequencies, all decrease. Such a decline reflects the weakening in average bond strength and increase in bond length. Hence, the iodide anions indeed bring a softer anionic framework in Li₃ErI₆. Li3ErI₆ shows a lower prefactor σ₀, lower activation barriers E_a and higher room-temperature conductivity σ_RT as a function of Debye frequency.

Finally, fluorine substitution was also reported by Tang et al. [60]. They successfully fabricated a dual-halogen trigonal Li₂ZrCl_6−xF_x. Admittedly, among all halogens, fluorine has the least polarizability and strongest electronegativity, leading to inferior conductivity. However, a fluorine substitution strategy has been proposed to inhibit interfacial reaction against electrodes and moisture corrosion owing to its strong electronegativity [61,62]. Therefore, similar to the above-mentioned Cl-Br mixing [58], a trade-off between conductivity and stability has been investigated by Tang et al. [60] in their Li₂ZrCl_6−xF_x system.

Dual-halogen trigonal Li₂ZrCl_6−xF_x systems have considerable moisture stability and excellent electrode compatibility. In their optimal Li₂ZrCl_6−xF_x (x = 0.4), there are three crystallographic Cl⁻ sites, and the F⁻ occupancies on these three sites are a little different: that is 7.9%, 8.5% and 4.8% on the Cl1 (6i), Cl2 (6i) and Cl3 (6i) sites, respectively, as confirmed by NPD refinements shown in Figure 5g. The refined structure is shown in Figure 5h,i, in which Li₂ZrCl_6−xF_x (x = 0.4) adopts a trigonal hcp anion stacking, forming [LiX₆] and [ZrX₆] (X = Cl, F) octahedral with vacancies. There are two Li sites along the c-direction, one occupies about 3/4 of the Li1 layer on (001) planes, and the other one almost fully occupies the Li2 layer on (002) planes. Each ZrX₆³⁻ octahedron is surrounded and connected by six LiX₆⁵⁻ octahedra in an edge-shared manner that forms a honeycomb arrangement in the ab-plane.

However, since the F-Li bond is stronger and its bond length is shorter than Cl-Li, F substitution will cause Li⁺ octahedra distortion along with lattice contraction, which would reversibly increase the Li⁺ migration energy barrier and decrease ionic conductivity. Therefore, the fluorine contents have to be carefully controlled and the best one is Li₂ZrCl_6−xF_x (x = 0.4), which retains an ionic conductivity of 3.21 × 10⁻⁴ S cm⁻¹ that is very close to non-fluorine Li₂ZrCl₆ (Figure 5j). Moreover, Li₂ZrCl_6−xF_x can be applied to protective-layer-free ASSLBs with a lithium alloy anode and high-voltage cathode LiCoO₂. These cells were reported to have an initial coulombic efficiency as high as 95.57%, and to be able to reversibly cycle in a wide potential window from 2.52 to 4.32 V (versus Li⁺/Li). The author concluded that a self-passivating behavior of Li₂ZrCl_6−xF_x SSE occurring on its contacting surface against the Li alloy anode was found to be responsible for its interfacial stabilization. The thin solid-electrolyte interphase (SEI) layers containing LiCl and LiF as a passivating layer would prevent Li₂ZrCl_6−xF_x from decomposition by limiting its electron transfer, but it still allows facile Li⁺ transport. In addition, the stronger stability against moisture in LZCF could originate from robust Li-F and Zr-F bonds due to more electronegativity of F⁻.

Figure 5. Rietveld refinements on (a) synchrotron diffraction data and (b) NPD data with the monoclinic C2/c structure of Li₃ErI₆. (c,d) Refined crystal structure of Li₃ErI₆, showing alternating layers of [Er_xLi_(1−x)I₆^(5−2x)−] and [LiI₆⁵⁻] octahedra. (e) BVSE [36,37] calculation for possible Li⁺ migration pathway. The beige isosurface is actually an electrostatic estimation. It means the probable lithium residence and lithium diffusion pathway. The blue section in the ab-plane is to show the strongly interconnected nature of Li sites, possibly related to a fast in-plane diffusion. (f) Tetrahedral voids are adjacent to edge-shared LiI₆⁵⁻ octahedral. Both the voids and octahedral vacancies may act as transitional states for Li⁺ diffusion. Reproduced with permission: Copyright 2022, American Chemical Society [54]. (g) Rietveld refinement of the NPD data for the Li₂ZrCl_6−xF_x (x = 0.4). (h,i) The crystal structure obtained from above refinement. The blue, cyan, green and red balls represent Li, Zr, Cl and F, respectively. (j) Arrhenius plots of Li₂ZrCl_6−xF_x (x = 0.4) (LZCF) and Li₂ZrCl₆ (LZC). Reproduced with permission: Copyright 2023, Elsevier [60].

Figure 5. Rietveld refinements on (a) synchrotron diffraction data and (b) NPD data with the monoclinic C2/c structure of Li₃ErI₆. (c,d) Refined crystal structure of Li₃ErI₆, showing alternating layers of [Er_xLi_(1−x)I₆^(5−2x)−] and [LiI₆⁵⁻] octahedra. (e) BVSE [36,37] calculation for possible Li⁺ migration pathway. The beige isosurface is actually an electrostatic estimation. It means the probable lithium residence and lithium diffusion pathway. The blue section in the ab-plane is to show the strongly interconnected nature of Li sites, possibly related to a fast in-plane diffusion. (f) Tetrahedral voids are adjacent to edge-shared LiI₆⁵⁻ octahedral. Both the voids and octahedral vacancies may act as transitional states for Li⁺ diffusion. Reproduced with permission: Copyright 2022, American Chemical Society [54]. (g) Rietveld refinement of the NPD data for the Li₂ZrCl_6−xF_x (x = 0.4). (h,i) The crystal structure obtained from above refinement. The blue, cyan, green and red balls represent Li, Zr, Cl and F, respectively. (j) Arrhenius plots of Li₂ZrCl_6−xF_x (x = 0.4) (LZCF) and Li₂ZrCl₆ (LZC). Reproduced with permission: Copyright 2023, Elsevier [60].

3.4. Structure Determination in New Halide System

In search of SSEs, it would be very exhilarating to discover a novel halide system as a promising SSE to support the ASSB battery. In fact, this crystalline novel halide system strongly needs NPD to reveal its inner mechanism. Utilizing NPD data to solve its unprecedented structure with an unconventional Li sublattice is also a good reflection of NPD’s superiority. Here we take a recently reported new LaCl₃-based halide system [63] as an example to discuss NPD’s role in this study.

Yin et al. [63] have made shocking progress on a new LaCl₃-based halide system as a lithium superionic conductor, which possesses promising interfacial electrochemical compatibility with lithium metal anodes. According to their report, unlike conventional Li₃MCl₆ (M = Sc, Y, In, and Ho) [21,22,26,42], this halide system possesses a UCl₃-type LaCl₃ structure with large 1D channels that enable fast Li⁺ conduction. These 1D channels are interconnected via La vacancies induced by Ta doping, in which case a 3D Li⁺ migration network is established. In their optimized Li_0.388Ta_0.238La_0.475Cl₃, the Li⁺ ionic conductivity (at 30 °C) is as high as 3.02 mS cm⁻¹ and the activation energy is as low as 0.197 eV. It also fulfills a long-term cycling in Li symmetric cell with 1 mAh cm⁻² for more than 5000 h. The author ascribed such stability to the gradient interfacial passivation layer that helps stabilize the Li metal electrode. It is also reported that, under a cutoff voltage of 4.35 V and with the areal capacity of more than 1 mAh cm⁻², the battery with Li_0.388Ta_0.238La_0.475Cl₃ SSE assembled with a Li metal anode and uncoated LiNi_0.5Co_0.2Mn_0.3O₂ cathode can run for more than 100 cycles. Rapid Li⁺ conduction was also demonstrated in this lanthanide-based system (LnCl3; Ln = La, Ce, Nd, Sm and Gd).

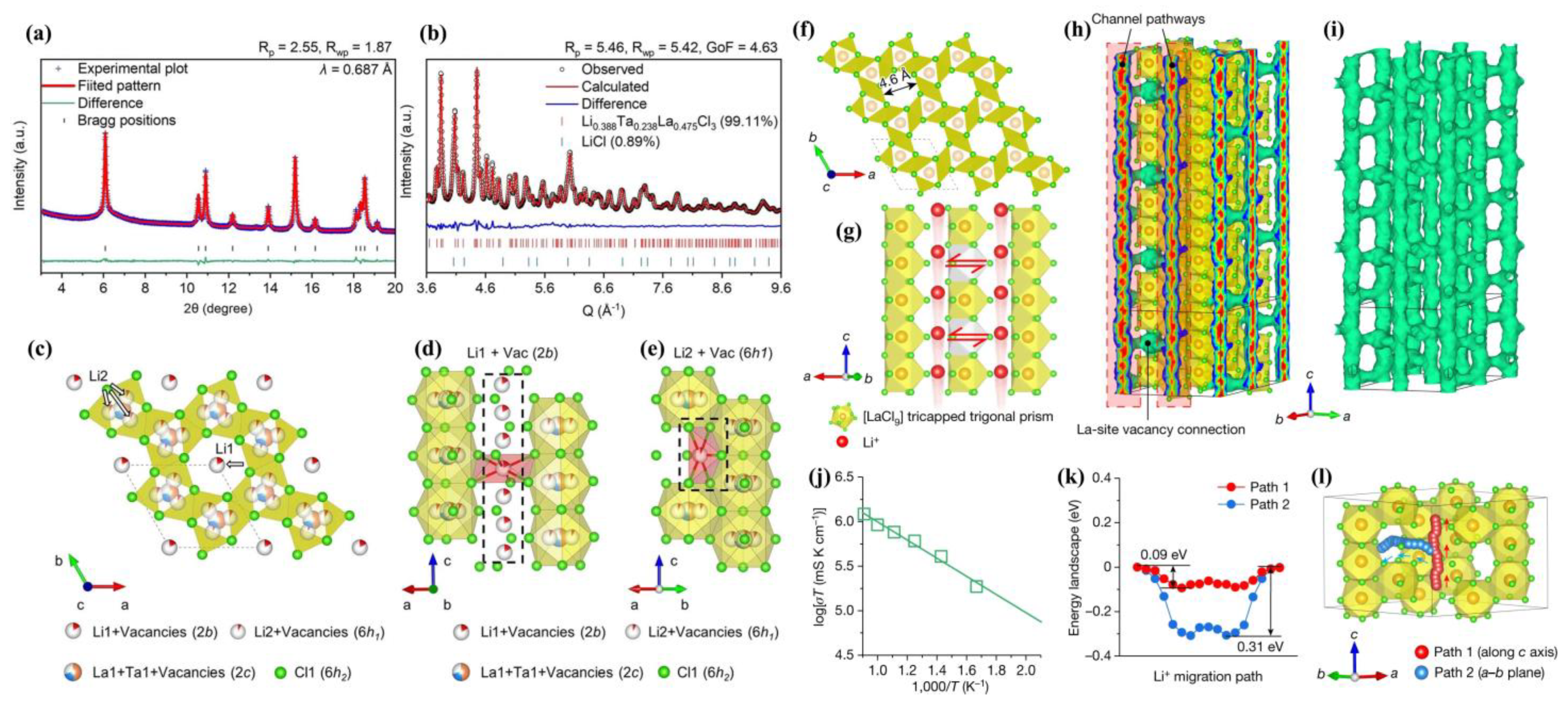
Neutron powder diffraction has played an indispensable role in this inspiring work, especially in determining the new crystal structure with explicit Li distribution/occupation, and elucidating the Li migration pathway, which provides a fundamental understanding of structural design for property enhancements. Figure 6a,b provide a joint refinement of synchrotron X-ray and Neutron diffraction. The synchrotron X-ray identifies Ta, La, Cl, especially La/Ta vacancies to confirm the whole lattice framework, while the neutron data confirm lithium distribution. We can see that neutron data ranges from approximately 0.28 Å (Q ~3.6 Å⁻¹) to 0.1 Å (Q ~9.6 Å⁻¹). Such low d-spacing data is especially beneficial in determining the local coordination environment and Li⁺ disorder.

The lattice presents a UCl₃-type structure with P6₃/m space group (Figure 6c–e), possessing a channel-typed non-close-packed anion lattice different from hcp Li₃YCl₆ and ccp Li₃InCl₆ types [21,22,26,42]. La³⁺ vacancies were clearly found after introducing Ta⁵⁺. Two Li⁺ positions were found, namely Li1 and Li2, along with their surrounding Cl⁻ constituting the compressed [Li1Cl₆] octahedra in the channels and [Li2Cl₅] rectangular pyramids near La sites. The author mentioned that 6h1 is an intermediate Li site in a metastable state that is critical in supporting the Li⁺ fast motion across adjacent channels. Figure 6f clearly shows 1D channels constructed by six columns of edge-shared [LaCl₉] tricapped trigonal prisms in the LaCl₃ lattice. Its large inner diameter around 4.6 Å offers a wide space that accommodates abundant octahedral sites for Li⁺ ionic motion. The author further proposed that 1D channels are interconnected by La vacancies to form a 3D Li-diffusion lattice, as shown in Figure 6g. The lithium not only migrates along the 1D channel but also migrates to the neighboring one via La vacancies sites. This could be supported by bond valence site energy (BVSE) analysis [36,37] on the basis of an NPD-determined structure. Finally, BVSE calculation illustrates an energetically favored 1D diffusion chain [Li1–Li2–Li1] along the c-direction, with an energy barrier of merely 0.18 eV that is much lower than that of 0.5 eV for diffusion across adjacent channels via La vacancies.

Ab initio molecular dynamics (AIMD) simulations also confirm a fast Li⁺ transport along a spread of closely spaced sites in the 1D channels (Figure 6h). The irregularly elongated Li⁺ probability density was suggested to be related to Li⁺ site disordering, which was considered to be a crucial factor to fulfill rapid Li⁺ conduction [64]. The Li⁺ could migrate between adjacent channels via La vacancies (Figure 6h). The interconnected 3D Li⁺ diffusion pathway is depicted in Figure 6i (all polyhedrons are omitted). The AIMD simulation yields a calculated ionic conductivity as high as 13.8 mS cm⁻¹ at 300 K (Figure 6j). The energy landscape in Figure 6k clearly illustrates two different Li⁺ diffusion pathways, with an energy barrier of 0.09 eV along the c-direction channels (red path in Figure 6k,l), and an energy barrier of 0.31 eV across channels in the a–b plane (blue path in Figure 6k,l). Both values are lower than the above BVSE results. These results imply that La³⁺ vacancies, which mainly originate from Ta⁵⁺ doping, are of vital importance to endow the LaCl₃ lattice with a rapid Li⁺ conduction.

These unique structure features and interconnected migration pathways allow the halide system to reach its best ionic conductivity σ of 3.02 mS cm⁻¹ (at 30 °C) in Li_0.388Ta_0.238La_0.475Cl₃. It also exhibits an excellent electrode compatibility that allows stable cycling with an areal capacity of 1.16 mAh cm⁻² in Li/Li_0.388Ta_0.238La_0.475Cl₃/NCM523 full cell. This research also manifests the superiority of the electrode compatibility of LaCl₃-based SEs. It can be expected that this work in future will inspire far more investigation of this brand new UCl₃-type SSE system of LnCl3 lattice with multiple element-doping choices.

3.5. In Situ NPD Study on Phase Evolution (Transition)

In situ NPD can directly monitor the dynamics process of phase evolution (or transition). The in situ NPD utilization discussed here mainly involves phase analysis during the dehydration process and heating process. The first work on dehydration analysis comes from an investigation on Li₃InCl₆ humidity tolerance and degradation. The second work on heating analysis come from an investigation of Li₂ZrCl₆ thermal stability.

In terms of humidity tolerance, it has been acknowledged that most SSEs will degrade when exposed to ambient air [65,66,67]; however, Li₃InCl₆ appears to possess much stronger humidity tolerance than others [30], along with high ionic conductivity and high voltage compatibility [22,23]. According to Li et al.’ s study [30], Li₃YCl₆ is unstable even in low humidity, and will decompose to simple chloride hydrates LiCl·H₂O and YCl₃·6H₂O after exposure in air for 12 h with 3−5% humidity. This decomposition cannot be recovered by reheating in an inert atmosphere. However, when introducing certain amounts of In³⁺ into Li₃YCl₆, the humidity tolerance was significantly improved. This is because Li₃Y_1−xIn_xCl₆ (with x > 0.5) [30] and also Li₃InCl₆ after humidity exposure can form Li₃Y_1−xIn_xCl₆·H₂O and Li₃InCl₆·H₂O intermediates rather than decompose to simple chloride hydrates. More importantly, the Li₃Y_1−xIn_xCl₆ SSEs could be regained after reheating at 260 °C. The above results demonstrate that high In³⁺ contents could help to retain the (Y/In)Cl₆³⁻ octahedral frameworks after humidity exposure by forming hydrated intermediates, which could then be regenerated after a careful dehydration process.

Since Li₃Y_1−xIn_xCl₆ (with x > 0.5) and Li₃InCl₆ all adopt a ccp monoclinic structure rather than hcp orthorhombic structure as in Li₃YCl₆, we deduce that the stronger humidity tolerance is possibly related to this ccp monoclinic structure that is able to accommodate water molecules in the lattice without being broken. This is also a possible explanation why Li₃InCl₆ can be synthesized via a water-mediated route followed by controlled dehydration [23].

Nevertheless, there is still some remaining further debate. For instance, how does the phase change during dehydration? Why does the conductivity of reheated Li₃Y_1−xIn_xCl₆ not fully recover after dehydration (retention: 85.37% for Li₃Y_0.2In_0.8Cl₆, 87.22% for Li₃Y_0.1In_0.9Cl₆)? Apparently, deciphering the dehydration/tolerance process in this halide system could be of much significance.

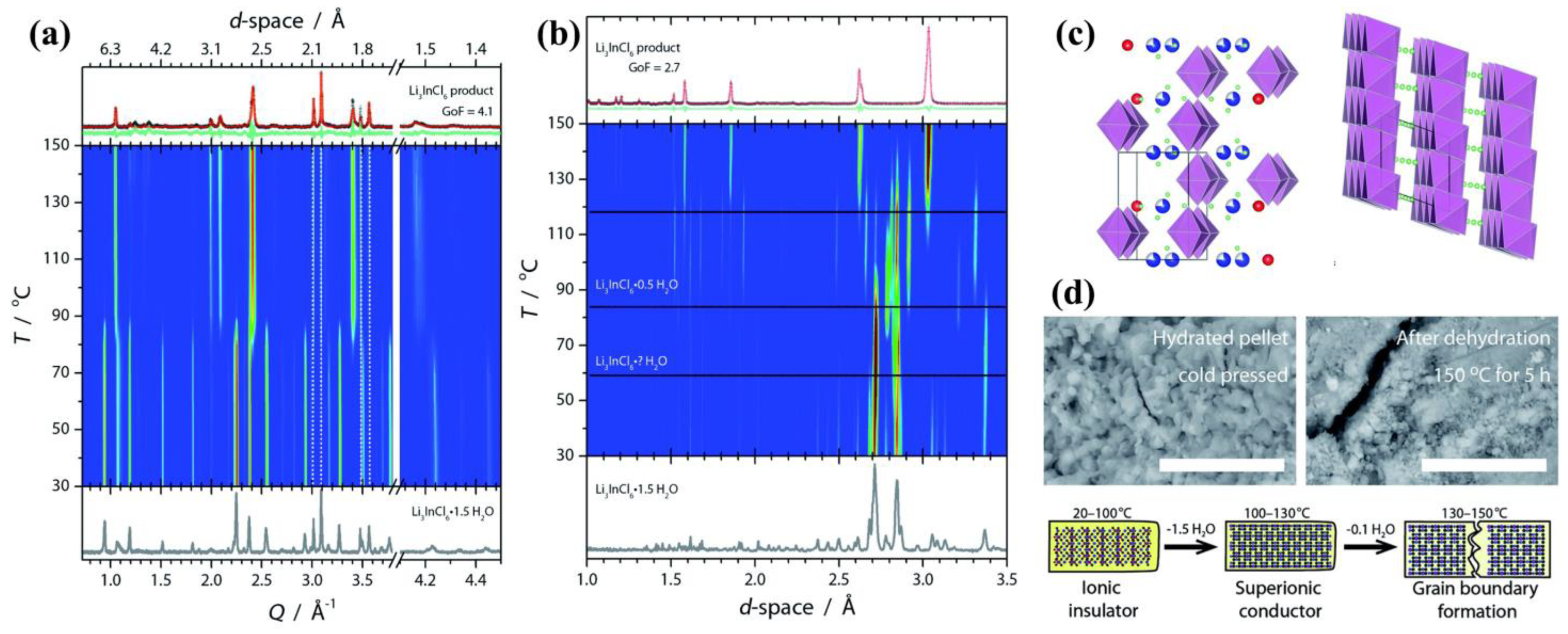
Bearing this in mind, the first work discussed here is about the in situ NPD/XRD study of the dehydration process of Li₃InCl₆ (that is from Li₃InCl₆·1.5H₂O to pure Li₃InCl₆) conducted by Sacci et al. [44]. They emphasize that careful consideration should be taken during the dehydration process and a strong vacuum is indispensable. In situ NPD revealed that the dehydration process actually involves multiple phase transitions that could significantly vary the conductivity. The lithium conductivity can be related to the amount of residual H₂O, the structural stability and ordering of the lithium sublattice.

As shown in Figure 7a,c, in situ XRD measurements detected two sets of diffraction peaks upon heating, which represents a single transition of the host framework from the fully hydrated to the anhydrous phase. The hydrate Li₃InCl₆·1.5H₂O can maintain from 30 to 80 °C, which bares a P2₁/c space group. Above 80 °C, the anhydrous phase appears with a C2/m space group, and the remaining hydrate transforms to anhydrate rapidly between 110 and 150 °C. However, under in situ neutron diffraction (Figure 7b) (deuterated water is used in sample synthesis), at least four distinct phases could be identified with overlapping on their temperature ranges. The reason for this is that XRD lacks sensitivity with light elements like Li or H, so that structural changes in the Li sublattice would not be observed. The variation of neutron data demonstrates that, as they dehydrate, the sublattices of Li⁺ and H⁺ are drastically modulated. Note that in neutron data the transition from phase 2 (Li₃InCl₆·xH₂O) to 3 (Li₃InCl₆·0.5H₂O) also occurs above 80 °C. This coincides well with the XRD transition temperature and the conductivity boost. Since not much change is observed in XRD above 90 °C, this means that the In and Cl host frameworks basically lock in above 90 °C. In other words, the In–Cl octahedra support the layered structure frameworks for H₂O and Li ions to reside within.

As the remaining H₂O is further removed, Li transport becomes more facile, and reaches its maximum when water molecules are totally removed. Subsequent cooling in the absence of water makes no observable change on the ionic conductivity, demonstrating that water molecules in the hydrate lattice are the main cause for its inferior conductivity. Dehydration is accompanied by pellet contraction, with the observation of clear grain boundary formation shown in Figure 7d. The dehydrate Li₃InCl₆ exhibits orders of magnitude higher conductivity (1.1 × 10⁻³ S cm⁻¹) than hydrate Li₃InCl₆·1.5H₂O (3.5 × 10⁻⁷ S cm⁻¹). The author concludes that the presence of H₂O molecules would probably extend the required Li⁺ or block the original facile Li⁺ transport pathway, and eventually lead to the decrease in Li mobility.

The grain boundary as formed during dehydration (Figure 7d) may be one reason that the above-mentioned reheated Li₃Y_1−xIn_xCl₆ [30] fails to fully recover its ionic conductivity. Although dehydration of the hydrate is a feasible and facile synthesis route toward Li₃InCl₆, the final removal of trace H₂O would inevitably lead to stress fractures and therefore the formation of the grain boundary. It may be possible to alleviate grain boundaries’ formation by careful control of the dehydration rate or exertion of mechanical pressure. The author finally emphasized that the control of the as-formed grain boundary implies high-through put processing during roll-to-roll fabrication of solid electrolytes.

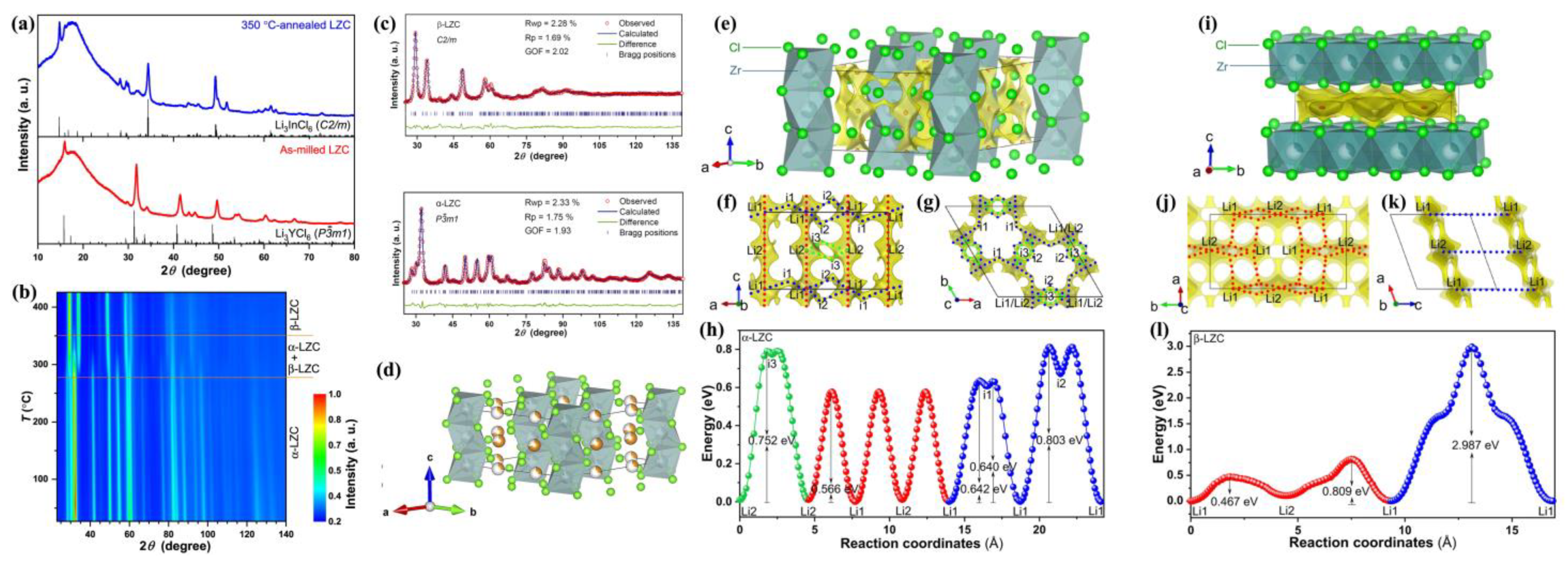
The second work is about the in situ NPD analysis of the phase transition of Li₂ZrCl₆ [68] while heating. The Li₂ZrCl₆ (LZC) system generally preserves high humidity tolerance, good deformability, excellent compatibility with 4V-class cathodes, and significantly low cost in terms of the raw materials. Unlike Li₃InCl₆, Li₂ZrCl₆ undergoes neither moisture uptake nor conductivity deterioration after being exposed to the atmosphere with 5% relative humidity. However, it undergoes phase transition during heating. As reported by Wang et al. [68], two type of Li₂ZrCl₆ (LZC) phases exist, i.e., trigonal α-LZC from ball-milling (without calcined) and monoclinic β-LZC from annealing at 350 °C. Trigonal α-LZC has higher room-temperature ionic conductivity (8.08 × 10^–4 S cm⁻¹).

Phase transition from trigonal α- to monoclinic β-LZC occurs above 277 °C, accompanied by a decrease in conductivity. After annealing at 350 °C, the ionic conductivity of LZC at 25 °C will decrease by two orders of magnitude, that is, from 8.08 × 10^–4 S cm^–1 of α-LZC, to 5.81 × 10^–6 S cm^–1 of β-LZC. The XRD and in situ NPD analysis (Figure 8a,b) reveal a α-LZC phase below 277 °C, and the coexistence of α- and β-LZC phases from 277 °C to 350 °C. Above 350 °C, only β-LZC could be observed, and above 450 °C the LZC would melt. The α-LZC is isostructural to Li₃YCl₆ (space group P-3m1, trigonal), while β-LZC is isostructural to Li₃InCl₆, (space group C2/m, monoclinic). Considering that the material annealed at 350 °C, then followed by furnace cooling, still maintains a pure β-LZC structure (Figure 8a) rather than turning into α-LZC structure, it could be deduced that α-LZC is likely a metastable phase originating from the high energy planetary mill. This is the quite distinctive to other chlorides in which planetary mill can only change the crystallinity rather than the crystal structure [21,22,30].

Through NPD refinements (Figure 8c), they found that Li+ ions in as-milled α-LZC prefer to occupy 6h sites (Figure 8d), but in contrast, in Li₃YCl₆ two Li sites (6g and 6h) are both well-occupied (occupancy > 0.50) [21]. The BVSE method [36,37] calculates the migration pathway and energy barrier (Figure 8e–l). For α-LZC, the most energetically favorable diffusion pathway is the [Li1–Li2–Li1] chain along the c-direction, as marked in red in Figure 8f–h. Beside this diffusion chain, Li⁺ is also likely to diffuse along the [Li1–i1–Li1–i2–Li1] pathway (i represents the interstitial site), or [Li2–i3–Li2] pathway, as marked in blue and green, respectively, in Figure 8f–h. These two alternative pathways could link the above [Li1–Li2–Li1] chains to establish a 3D diffusion network, of which the migration barrier is 0.803 eV (Figure 8g,h). For the β-LZC structure (Figure 8i), the relatively favorable Li⁺ pathways reside within the layers in the ab-plane, as marked in red in Figure 8j–l, with a similar barrier of 0.809 eV (Figure 8l). However, the barrier of migration between adjacent layers is significantly higher (2.987 eV), as marked in blue in Figure 8k,l.

However, the author proposed that the true reason for the higher ionic conductivity of α-LZC should be attributed to non-periodic features including defects, surface structure, amorphous phase, etc., which are induced by the high-energy intense ball milling during synthesis. This is because, first, the effective migration barriers of α-LZC (0.803 eV) and β-LZC (0.809 eV) are similar, and second, the conductivity of as-milled α-LZC will drop to 3.22 × 10^–5 S cm^–1 after being annealed at 215 °C. Yet, further investigation using advanced techniques with ultrahigh spatial resolution is still required to identify the microscopic mechanism of the fast ionic transport and make a rational optimization. In spite of this, this work can be seen as a good illustration of how an in situ NPD technique provides an in-depth understanding of the structure–property relationship of advanced SSEs. Li₂ZrCl₆ SSE is cost-effective, moisture-resistant (5% relative humidity), deformable, and cathode compatible (4 V-class). Specifically, its merits of humidity tolerance and cost-effectiveness remove two major obstacles in the way towards wide usage of SSEs.

4. Perspective

Generally, we have reviewed the utilization of neutron powder diffraction (NPD) in the metal halides family. NPD as a powerful technology provides an in-depth understanding of the interplay between their structures and Li⁺ transport behavior. With its unique advantage of nuclei detection, NPD clearly determines the nuclear density distribution of Li⁺ ions, metal cations and halogen anions, which can be further analyzed by the BVSE method [36,37] to reveal Li⁺ migration pathways and energy landscapes. Some perspectives on future directions of NPD application in metal halides systems are presented as follows:

(1) In situ or in operando NPD analysis of metal halide SSEs during battery charging/discharging process. This in situ NPD allows direct experimental observation of Li migration pathways the during charging/discharging process, which serves as the basis for more precisely understanding this migration behavior and better designing the metal halide components. In addition, the possible deterioration of the halide crystal structure under long-time cycling could be investigated via this in situ technique.

(2) In situ or in operando NPD analysis of interfacial compatibility with electrodes without disassembling the batteries. A neutron beam possesses a stronger penetrating ability to detect the interfacial heterogeneous phases during or after the running of the battery. This technique may provide direct observation of the formation and deterioration of the interface. Failure of the interface can also be analyzed in terms of chemical and structural changes.

(3) High-resolution, high-intensity and wide d-spacing-ranged NPD for the study of novel halide SSEs with a complicated structure. High-resolution and high-intensity signals indicate a precise nuclei density distribution that is very beneficial for a facile structure determination of new phases. A wide d-spacing range indicates that diffraction peaks from lattice planes with smaller interplanar spacing can be collected, which provides key information for local disorder analysis.

(4) Combination of NPD and other advanced techniques for a comprehensive investigation of microscopic structure. NPD can be jointly used with Synchrontron, PDF, EXAFS, CT imaging, etc. Synchrontron is powerful in determining heavy ions. It provides high-intensity, high-resolution X-ray diffraction peaks to confirm the metal and halogen host lattice, in which case the NPD could focus on determining the Li⁺ distribution inside. PDF (pair distribution function) and also EXAFS could be utilized in combination with NPD to analyze local structures and coordination environments, particularly in nano-crystalline SSEs. The X-ray CT imaging could reveal cracks or defects in SSEs while NPD refinement could study their origin from the perspective of residual stress in the lattice. More ways for the joint usage of NPD and other characterizations are still being explored to tackle more complicated issues in SSEs.

To date, research in SSEs for ASSBs have made a giant leap in the past decades, with a variety of different SSEs being discovered. However, a series of thorny problems still stand in the way towards advancing SSEs for next generation ASSBs, including ionic conductivity, electrochemical stability, and large-scale fabrication. Addressing the above problems robustly requires support from neutron powder diffraction to yield fundament and structural understanding for the delicate design of advanced SSEs. It can be anticipated that more powerful NPD technology will emerge in the near future to assist SSEs development, and NPD will as always play an indispensable role in this research.