Online State-of-Health Estimation for NMC Lithium-Ion Batteries Using an Observer Structure
Abstract
:1. Introduction
2. Online State-of-Health Estimator
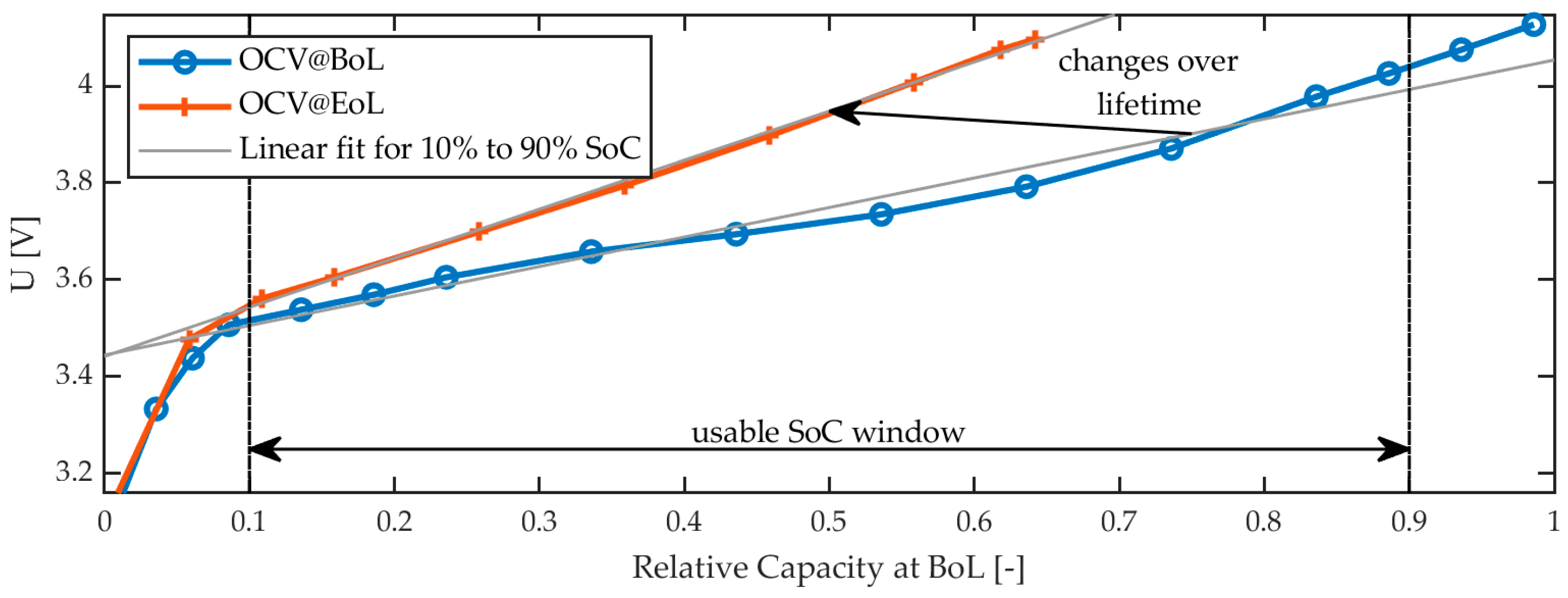
2.1. OCV Curve
2.1.1. Basics
- Due to current direction, the OCV potential can be higher or lower; therefore, a hysteresis is observed for most cell chemistries. While the hysteresis for NMC cells is only a few mV, it can be a multiple of 10 mV for lithium iron phosphate (LFP) cells. Baghdadi et al. [40] and Lavigne et al. [41] both show in their studies that the hysteresis increases at low and high SoC. In typical SoC usage windows, the effect is very small. In this investigation, the focus is on NMC. Therefore, hysteresis effects are neglected for the moment.
- Often the relaxation time also becomes larger with older cells [36].
2.1.2. Aging Characteristics
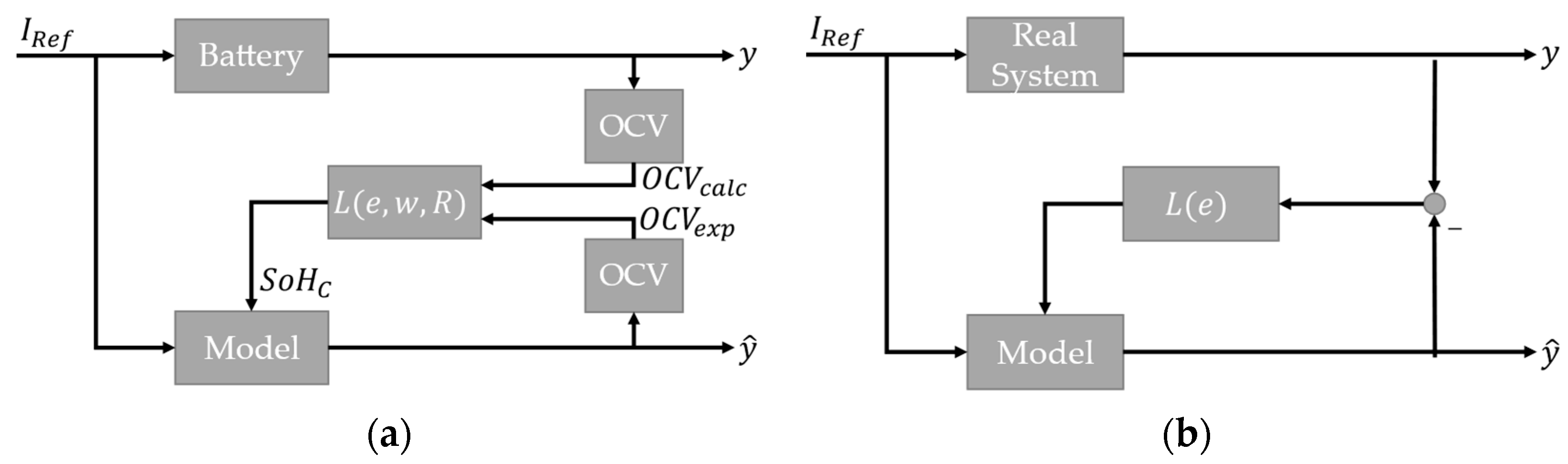
2.2. Approach
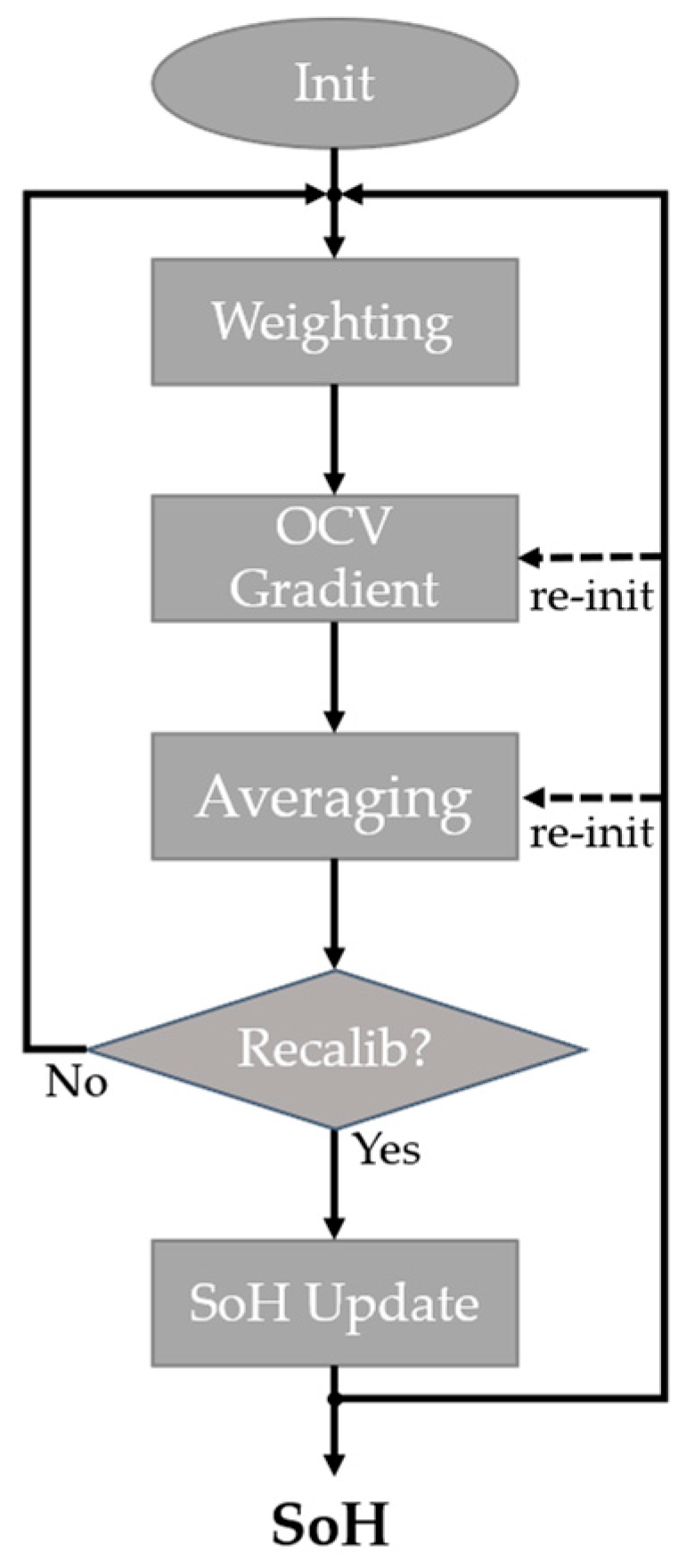
2.3. Realization
2.3.1. Weighting
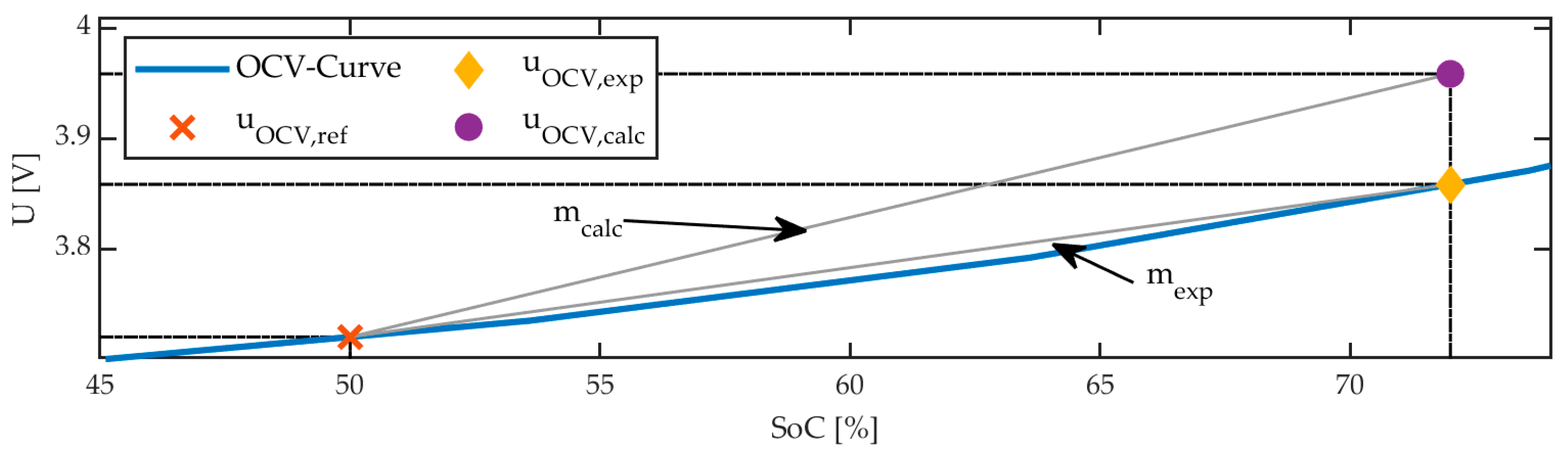
2.3.2. OCV Gradients
2.3.3. Mean Correction Factor
2.3.4. Conditional SoH Update
3. Experimental Evaluation
3.1. Battery System under Test
3.2. Real Usage Data
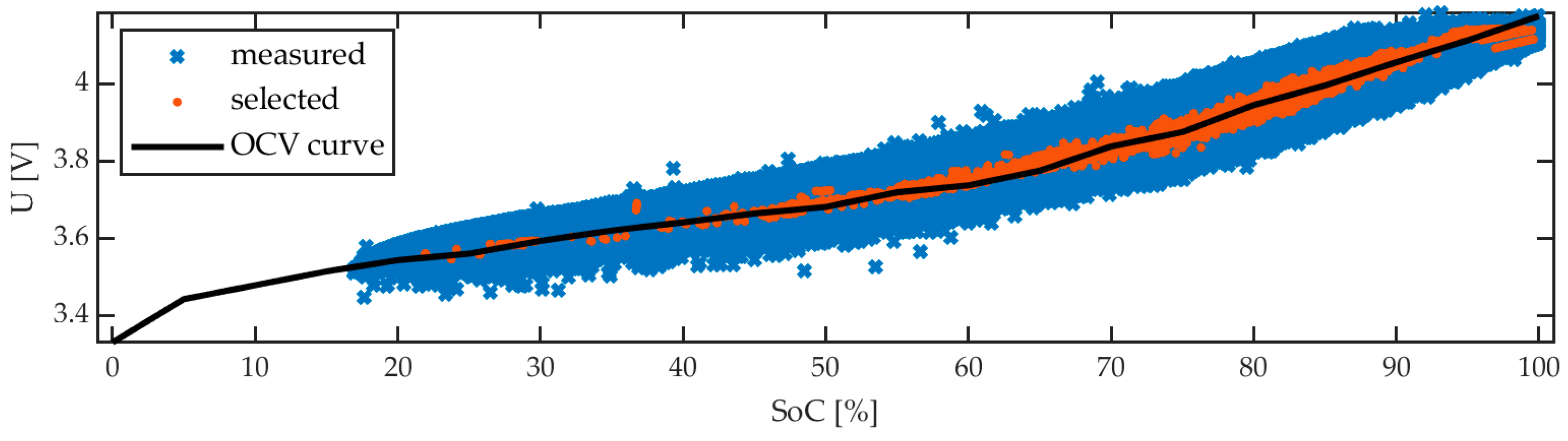
3.3. Checkup Measurements
3.4. Parametrization
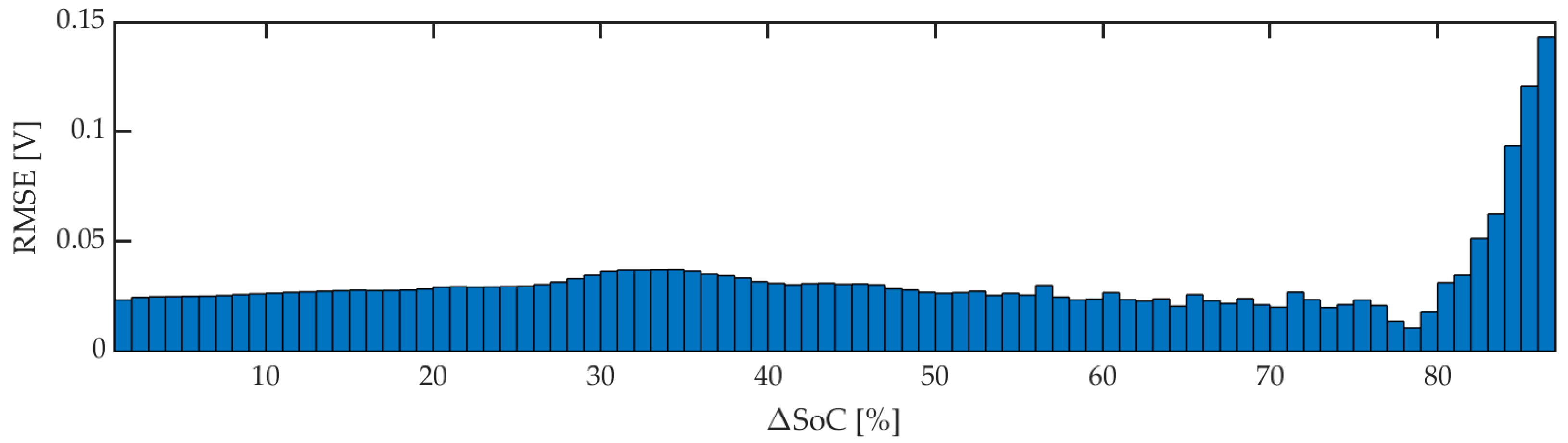
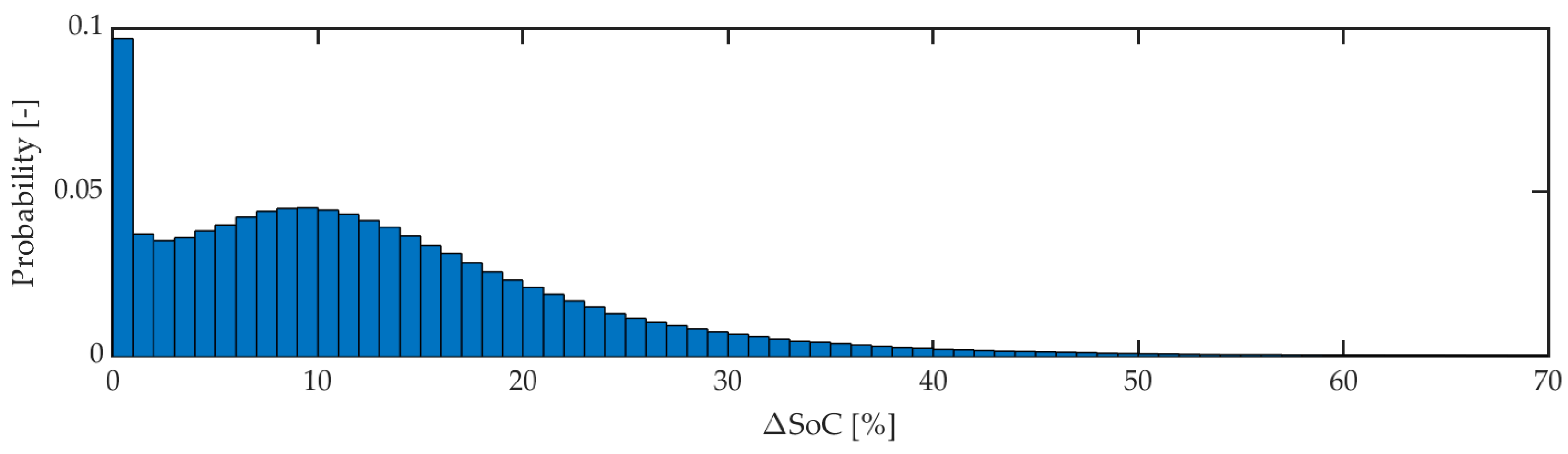
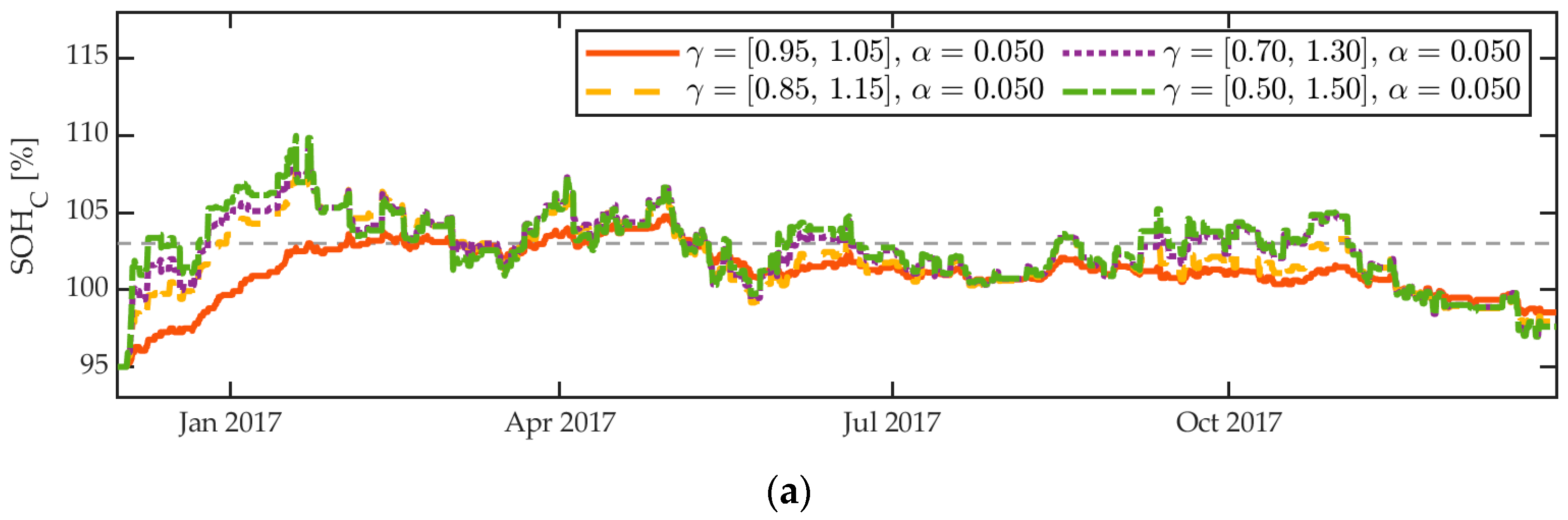
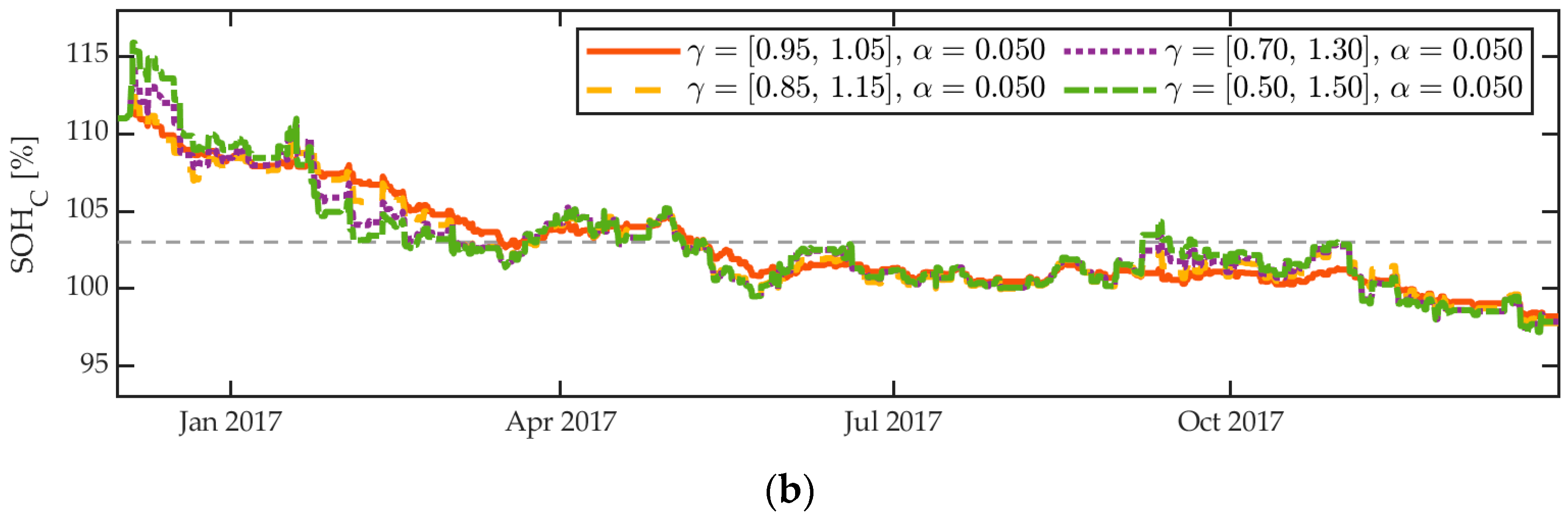
3.4.1. Weighting-Rules Parameters
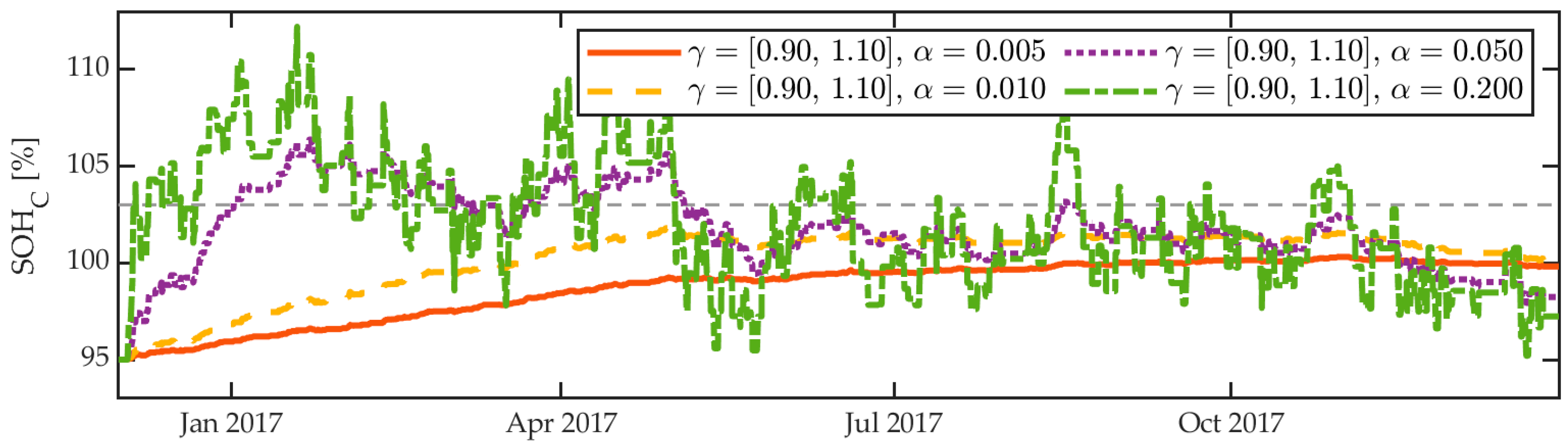
3.4.2. Dynamic Parameters
4. Result and Discussion
4.1. Result
4.2. Discussion
4.2.1. Dynamic Behavior
- The estimator is capable of compensating for initial SoH deviations. With the chosen parameters, the initial deviation of approximately 2% is compensated for in about four months. This might seem slow, but compared to the expected lifetime of the battery used it is rather a short period. The dynamic parameters were intentionally chosen to be conservative to avoid overshooting and to obtain a smooth curve. In practice, unknown initial deviations significantly larger than 2% are not to be expected.
- The recorded data used for the evaluation have a sample time of 6 s. Typically, BMS tasks have a cycle time in the range of several milliseconds. Therefore, we expect to see a different dynamic behavior when the observer runs directly on a BMS, as the observer will be acting on more dynamic data because of the higher sample rate. This will primarily affect the data being selected by the weighting rules (Equations (5a) and (5b)), which in turn results in a different calculation of the mean correction factor mmean (Equation (13)). Therefore, it is expected that it is necessary to adapt the dynamic parameters of the algorithm when the observer is run directly on a BMS.
- The accuracy and dynamic behavior of the estimator needs to be better verified. The presented results are initial validation results that give an impression of the performance and behavior of the estimator. The two available checkup measurements are not enough to evaluate the accuracy of the estimator in general. It was not possible to carry out more checkup measurements because the bus with the battery pack under consideration was in operational use most of the time and the workshop routine for carrying out the checkup measurement (see Section 3.3) is time-consuming. Therefore, the fleet operator did not agree to any further checkup measurements. But a new field study has already been started to validate the estimator, integrated in a BMS, with more frequent checkup measurements. The results will be published in future work.
- It must be noted that the observed period of about two years is short in comparison to the expected lifetime of the battery examined. Therefore, the dynamic behavior in the future cannot fully be inferred from the assessed data. It is planned to further monitor the system and to perform additional checkup measurements to obtain more confidence in the dynamic interpretation.
4.2.2. Parametrization
- The parameterization demonstrated in Section 3.4 is based on statistical analysis of the available real operating data. In cases where this is not possible, it might be an option to use synthetic data from simulations to find a suitable parameter set for the respective system. Ultimately, the option remains to set the parameters based on know-how about the system used, as the rule-based design of the estimator gives an intuitive way to understand the influence of each parameter.
4.2.3. Alternative Methods and Possible Extensions
- A common approach to SoH estimation is to use a Kalman filter (KF) [48]. The difference to the approach chosen in this work lies in the calculation of the feedback term L (see also Figure 2). In the Kalman filter, the feedback is computed recursively by a computational rule which results from minimizing the mean square estimation error while considering uncertainties in the system model as well as in the measurements. It can be proved that the KF gives the optimal minimum mean square error estimate under some specific conditions. While in practice these conditions are often violated, the KF still results in acceptable performance in most cases. Thus, the KF is widely used in practice. The “magic” to acquire an acceptable dynamic behavior lies mainly in the parameterization of the system noise covariance matrix. However, there is no universal approach to this, leaving engineers with a lengthy trial-and-error process. In contrast, our motivation was to develop feedback that could be parametrized in an intuitive way, since the meaning of each parameter is directly interpretable.
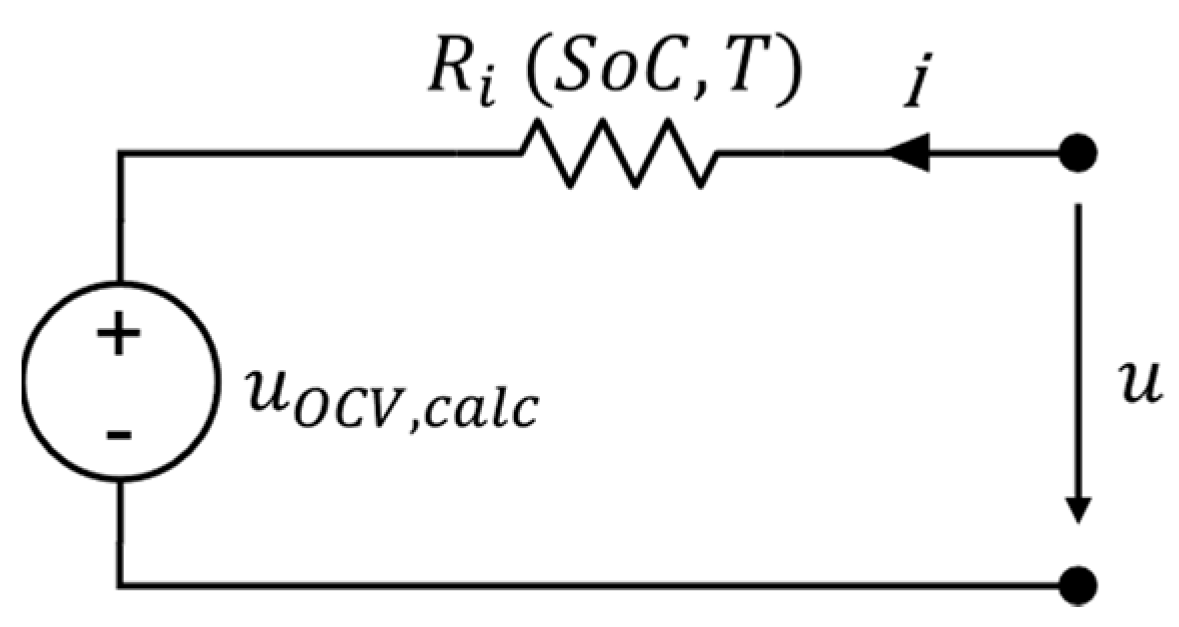
- Currently, the internal resistance Ri in Equation (9) is considered to be constant over the battery’s lifetime, which is not true, as the resistance increases significantly as the battery ages. Therefore, the estimate of SoHc unintentionally also compensates for aging effects originating from the resistance increase. The solution would be to implement a separate estimator for the aging effects in Ri and to use the estimate in Equation (9). For example, the structure shown here could also be applied to implement such an Ri estimator.
- Another possible extension to the estimator would be to add an additional model which accounts for calendric aging during long standstill phases where the estimator is not updated. However, in the commercial vehicle applications the standstill phases are significantly lower in comparison to passenger car applications, so that the estimator would be most probably able to self-correct for these deviations during the runtime after standstill phases.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L. “Green” effects of hybrid actors through carbon trading: Cases in Beijing. Glob. Transit. Proc. 2020, 1, 13–22. [Google Scholar] [CrossRef]
- Shi, H.; Wang, Y.; Chen, J.; Huisingh, D. Preventing smog crises in China and globally. J. Clean. Prod. 2016, 112, 1261–1271. [Google Scholar] [CrossRef]
- Choma, E.F.; Evans, J.S.; Hammitt, J.K.; Gómez-Ibáñez, J.A.; Spengler, J.D. Assessing the health impacts of electric vehicles through air pollution in the United States. Environ. Int. 2020, 144, 106015. [Google Scholar] [CrossRef] [PubMed]
- Rizza, V.; Torre, M.; Tratzi, P.; Fazzini, P.; Tomassetti, L.; Cozza, V.; Naso, F.; Marcozzi, D.; Petracchini, F. Effects of deployment of electric vehicles on air quality in the urban area of Turin (Italy). J. Environ. Manag. 2021, 297, 113416. [Google Scholar] [CrossRef]
- Maji, K.J.; Li, V.O.; Lam, J.C. Effects of China’s current Air Pollution Prevention and Control Action Plan on air pollution patterns, health risks and mortalities in Beijing 2014–2018. Chemosphere 2020, 260, 127572. [Google Scholar] [CrossRef]
- Li, W.; Shao, L.; Wang, W.; Li, H.; Wang, X.; Li, Y.; Li, W.; Jones, T.; Zhang, D. Air quality improvement in response to intensified control strategies in Beijing during 2013–2019. Sci. Total Environ. 2020, 744, 140776. [Google Scholar] [CrossRef]
- Özener, O.; Özkan, M. Fuel consumption and emission evaluation of a rapid bus transport system at different operating conditions. Fuel 2020, 265, 117016. [Google Scholar] [CrossRef]
- Europäisches Parlament. VERORDNUNG (EU) 2019/631 DES EUROPÄISCHEN PARLAMENTS UND DES RATES: Zur Festsetzung von CO2-Emissionsnormen für Neue Personenkraftwagen und für Neue Leichte Nutzfahrzeuge und zur Aufhebung der Verordnungen (EG) Nr. 443/2009 und (EU) Nr. 510/2011. Available online: https://eur-lex.europa.eu/legal-content/DE/TXT/HTML/?uri=CELEX:32019R0631&from=DE (accessed on 19 October 2020).
- Iwan, S.; Allesch, J.; Celebi, D.; Kijewska, K.; Hoé, M.; Klauenberg, J.; Zajicek, J. Electric mobility in European urban freight and logistics—Status and attempts of improvement. Transp. Res. Procedia 2019, 39, 112–123. [Google Scholar] [CrossRef]
- An, K. Battery electric bus infrastructure planning under demand uncertainty. Transp. Res. Part C Emerg. Technol. 2020, 111, 572–587. [Google Scholar] [CrossRef]
- Schmitt, J.; Maheshwari, A.; Heck, M.; Lux, S.; Vetter, M. Impedance change and capacity fade of lithium nickel manganese cobalt oxide-based batteries during calendar aging. J. Power Sources 2017, 353, 183–194. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Kabitz, S.; Ecker, M.; Sauer, D.U. From accelerated aging tests to a lifetime prediction model: Analyzing lithium-ion batteries. In Proceedings of the World Electric Vehicle Symposium and Exposition (EVS 27), Barcelona, Spain, 17–20 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–12, ISBN 978-1-4799-3832-2. [Google Scholar]
- Käbitz, R. Untersuchung der Alterung von Lithium-Ionen-Batterien Mittels Elektroanalytik und Elektrochemischer Impedanzspektroskopie; RWTH Aachen University: Aachen, Germany, 2016. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Fleckenstein, M. Modellbasiertes Thermomanagement für Li-Ionen-Zellen in Elektrischen Fahrzeuganwendungen; Verlag Dr. Hut: München, Germany, 2013; ISBN 978-3-8439-1166-5. [Google Scholar]
- Komsiyska, L.; Buchberger, T.; Diehl, S.; Ehrensberger, M.; Hanzl, C.; Hartmann, C.; Hölzle, M.; Kleiner, J.; Lewerenz, M.; Liebhart, B.; et al. Critical Review of Intelligent Battery Systems: Challenges, Implementation, and Potential for Electric Vehicles. Energies 2021, 14, 5989. [Google Scholar] [CrossRef]
- Pop, V.; Bergveld, H.J.; Notten, P.; Op het Veld, J.; Regtien, P. Accuracy analysis of the State-of-Charge and remaining run-time determination for lithium-ion batteries. Measurement 2009, 42, 1131–1138. [Google Scholar] [CrossRef]
- Held, M.; Schücking, M. Utilization effects on battery electric vehicle life-cycle assessment: A case-driven analysis of two commercial mobility applications. Transp. Res. Part D Transp. Environ. 2019, 75, 87–105. [Google Scholar] [CrossRef]
- Wolff, S.; Madlener, R. Driven by change: Commercial drivers’ acceptance and efficiency perceptions of light-duty electric vehicle usage in Germany. Transp. Res. Part C Emerg. Technol. 2019, 105, 262–282. [Google Scholar] [CrossRef]
- Figenbaum, E. Can battery electric light commercial vehicles work for craftsmen and service enterprises? Energy Policy 2018, 120, 58–72. [Google Scholar] [CrossRef]
- Bauer, S. AkkuWelt, 1. Auflage; Vogel Business Media: Würzburg, Germany, 2017; ISBN 978-3-8343-3409-1. [Google Scholar]
- Jossen, A.; Weydanz, W. Moderne Akkumulatoren Richtig Einsetzen, 2. Überarbeitete Auflage, Unverändert zur 2. Auflage vom Februar 2019; MatrixMedia Verlag: Göttingen, Germany, 2021; ISBN 978-3-946891-18-5. [Google Scholar]
- Yao, L.; Xu, S.; Tang, A.; Zhou, F.; Hou, J.; Xiao, Y.; Fu, Z. A Review of Lithium-Ion Battery State of Health Estimation and Prediction Methods. World Electr. Veh. J. 2021, 12, 113. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.-S.; Chen, Y.-P.; Hsieh, Y.-C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined State of Charge and State of Health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Fang, L.; Li, J.; Peng, B. Online Estimation and Error Analysis of both SOC and SOH of Lithium-ion Battery based on DEKF Method. Energy Procedia 2019, 158, 3008–3013. [Google Scholar] [CrossRef]
- Sun, T.; Wu, R.; Cui, Y.; Zheng, Y. Sequent extended Kalman filter capacity estimation method for lithium-ion batteries based on discrete battery aging model and support vector machine. J. Energy Storage 2021, 39, 102594. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Wen, J.; Chen, X.; Li, X.; Li, Y. SOH prediction of lithium battery based on IC curve feature and BP neural network. Energy 2022, 261, 125234. [Google Scholar] [CrossRef]
- Weng, C.; Sun, J.; Peng, H. A unified open-circuit-voltage model of lithium-ion batteries for state-of-charge estimation and state-of-health monitoring. J. Power Sources 2014, 258, 228–237. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; Liu, L.; Pan, C. State of health estimation of battery modules via differential voltage analysis with local data symmetry method. Electrochim. Acta 2017, 256, 81–89. [Google Scholar] [CrossRef]
- Kong, X.; Bonakdarpour, A.; Wetton, B.T.; Wilkinson, D.P.; Gopaluni, B. State of Health Estimation for Lithium-Ion Batteries. IFAC-PapersOnLine 2018, 51, 667–671. [Google Scholar] [CrossRef]
- Maher, K.; Yazami, R. A study of lithium ion batteries cycle aging by thermodynamics techniques. J. Power Sources 2014, 247, 527–533. [Google Scholar] [CrossRef]
- Lavigne, L.; Sabatier, J.; Francisco, J.M.; Guillemard, F.; Noury, A. Lithium-ion Batteries Aging Motinoring througth Open Circuit Voltage (OCV) Curve Modelling and Adjustment. In ICINCO 2016, Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics, Lisbon, Portugal, 29–31 July 2016; Gusikhin, O., Peaucelle, D., Madani, K., Eds.; SCITEPRESS—Science and Technology Publications Lda: Setúbal, Portugal, 2016; ISBN 9789897581984. [Google Scholar]
- Ungurean, L.; Cârstoiu, G.; Micea, M.V.; Groza, V. Battery state of health estimation: A structured review of models, methods and commercial devices. Int. J. Energy Res. 2017, 41, 151–181. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. A study on the dependency of the open-circuit voltage on temperature and actual aging state of lithium-ion batteries. J. Power Sources 2017, 347, 1–13. [Google Scholar] [CrossRef]
- Ma, Z.; Jiang, J.; Shi, W.; Zhang, W.; Mi, C.C. Investigation of path dependence in commercial lithium-ion cells for pure electric bus applications: Aging mechanism identification. J. Power Sources 2015, 274, 29–40. [Google Scholar] [CrossRef]
- Gering, K.L.; Sazhin, S.V.; Jamison, D.K.; Michelbacher, C.J.; Liaw, B.Y.; Dubarry, M.; Cugnet, M. Investigation of path dependence in commercial lithium-ion cells chosen for plug-in hybrid vehicle duty cycle protocols. J. Power Sources 2011, 196, 3395–3403. [Google Scholar] [CrossRef]
- Plett, G.L. Battery Management Systems: Battery Modeling; Artech House: Boston, MA, USA; London, UK, 2015; ISBN 1630810231. [Google Scholar]
- Baghdadi, I.; Briat, O.; Gyan, P.; Vinassa, J.M. State of health assessment for lithium batteries based on voltage–time relaxation measure. Electrochim. Acta 2016, 194, 461–472. [Google Scholar] [CrossRef]
- Lavigne, L.; Sabatier, J.; Francisco, J.M.; Guillemard, F.; Noury, A. Lithium-ion Open Circuit Voltage (OCV) curve modelling and its ageing adjustment. J. Power Sources 2016, 324, 694–703. [Google Scholar] [CrossRef]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 13th ed.; Global Edition; Pearson: Harlow, UK, 2017; ISBN 0-13-440762-8. [Google Scholar]
- Adamy, J. Nonlinear Systems and Controls, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2022; ISBN 978-3662656327. [Google Scholar]
- Sundararajan, D. Signals and Systems: A Practical Approach, 2nd ed.; Springer: Cham, Switzerland, 2023; ISBN 978-3-031-19377-4. [Google Scholar]
- Gustav Klein|Stromversorgungslösungen Weltweit. Bidirektionaler Programmierbarer Batterie-Tester—Gustav Klein|Stromversorgungslösungen Weltweit. Available online: https://www.gustav-klein.com/geschaeftsfelder/testen-und-simulieren/bidirektionaler-programmierbarer-batterie-tester_/ (accessed on 23 February 2023).
- Hoekstra, F.; Raijmakers, L.; Donkers, M.; Bergveld, H.J. Comparison of battery electromotive-force measurement and modelling approaches. J. Energy Storage 2022, 56, 105910. [Google Scholar] [CrossRef]
- Huynh, P.-L. Beitrag zur Bewertung des Gesundheitszustands von Traktionsbatterien in Elektrofahrzeugen; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2016; ISBN 978-3-658-16561-1. [Google Scholar]
- Plett, G. Battery Management Systems, Volume II Equivalent-Circuit Methods; Artech House: Norwood, MA, USA, 2015; ISBN 9781630810283. [Google Scholar]

| Specification | |
|---|---|
| Cell chemistry | NMC—Graphite |
| Cell design | pouch |
| Pack configuration | 90s2p |
| Nominal capacity | 92 Ah |
| Energy | 30.6 kWh |
| Nominal voltage | 333 V |
| Voltage (min) | 243 V |
| Voltage (max) | 378 V |
| Discharging power max (10 s) | 266 kW |
| Charging power max (10 s) | 153 kW |
| Continuous power (RMS) | 77 kW |
| Charge/discharge current max (10 s) | 736 A |
| Continuous current (RMS) | 230 A |
| Parameter | Value |
|---|---|
| Time period | 1 December 2016 to 22 January 2019 |
| Operational days/Overall days | 712/783 |
| Mean daily operation time in hours | 13.8 |
| Mean cell temperature in °C | 27 |
| Mean SoC in % | 83 |
| Test Device | Nominal Power | Measurement | Full Scale | Accuracy |
|---|---|---|---|---|
| Gustav Klein Type 3865 | 100 kW | Voltage | Up to 1000 V DC | 0.5% fs ± 1 Digit/12 Bit |
| Current | Up to 600 A | 0.5% fs ± 1 Digit/12 Bit |
| Parameter | Value |
|---|---|
| 12 A | |
| 15 A/30 s | |
| 3.5 h | |
| 6%/31% | |
| 23 °C/27 °C |
| Rule | Proportion in % | RMSE() |
|---|---|---|
| Current Limitation | 38.69 | 0.0211 |
| Current History | 35.27 | 0.0283 |
| Time since last update | 44.08 | 0.0227 |
| Delta SoC | 66.26 | 0.0276 |
| Temperature | 30.15 | 0.0251 |
| All | 0.78% | 0.0155 |
| Parameter | Value |
|---|---|
| 0.90/1.05 | |
| 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neunzling, J.; Winter, H.; Henriques, D.; Fleckenstein, M.; Markus, T. Online State-of-Health Estimation for NMC Lithium-Ion Batteries Using an Observer Structure. Batteries 2023, 9, 494. https://doi.org/10.3390/batteries9100494
Neunzling J, Winter H, Henriques D, Fleckenstein M, Markus T. Online State-of-Health Estimation for NMC Lithium-Ion Batteries Using an Observer Structure. Batteries. 2023; 9(10):494. https://doi.org/10.3390/batteries9100494
Chicago/Turabian StyleNeunzling, Jan, Hanno Winter, David Henriques, Matthias Fleckenstein, and Torsten Markus. 2023. "Online State-of-Health Estimation for NMC Lithium-Ion Batteries Using an Observer Structure" Batteries 9, no. 10: 494. https://doi.org/10.3390/batteries9100494
APA StyleNeunzling, J., Winter, H., Henriques, D., Fleckenstein, M., & Markus, T. (2023). Online State-of-Health Estimation for NMC Lithium-Ion Batteries Using an Observer Structure. Batteries, 9(10), 494. https://doi.org/10.3390/batteries9100494








