State-of-Health Estimation and Anomaly Detection in Li-Ion Batteries Based on a Novel Architecture with Machine Learning
Abstract
1. Introduction
2. Related Works
2.1. SOH and RUL Estimation Using DNNs
2.2. Battery State Estimation Using FFNN
2.3. DNNs from the NASA Dataset
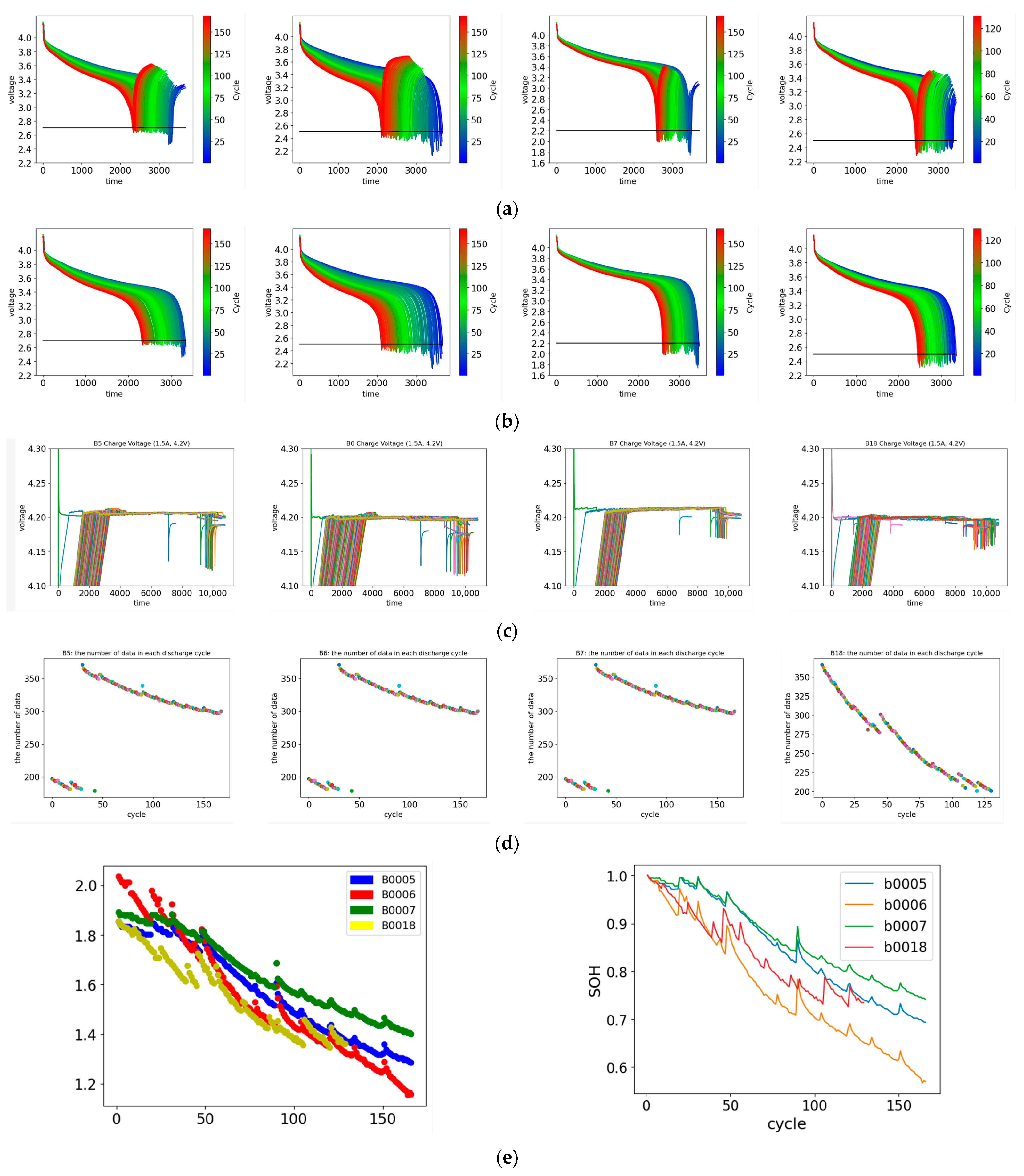
3. Data Cleansing and Feature Extraction
3.1. NASA DATASET
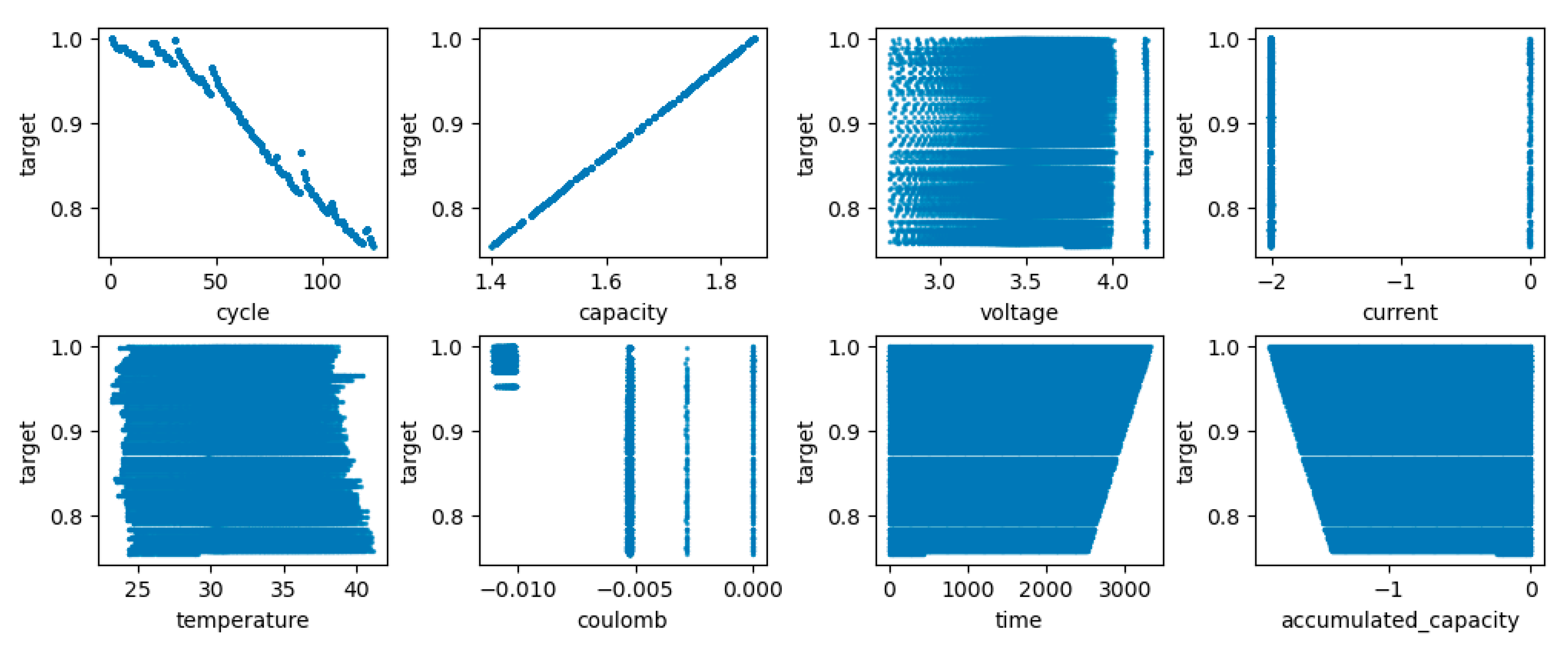
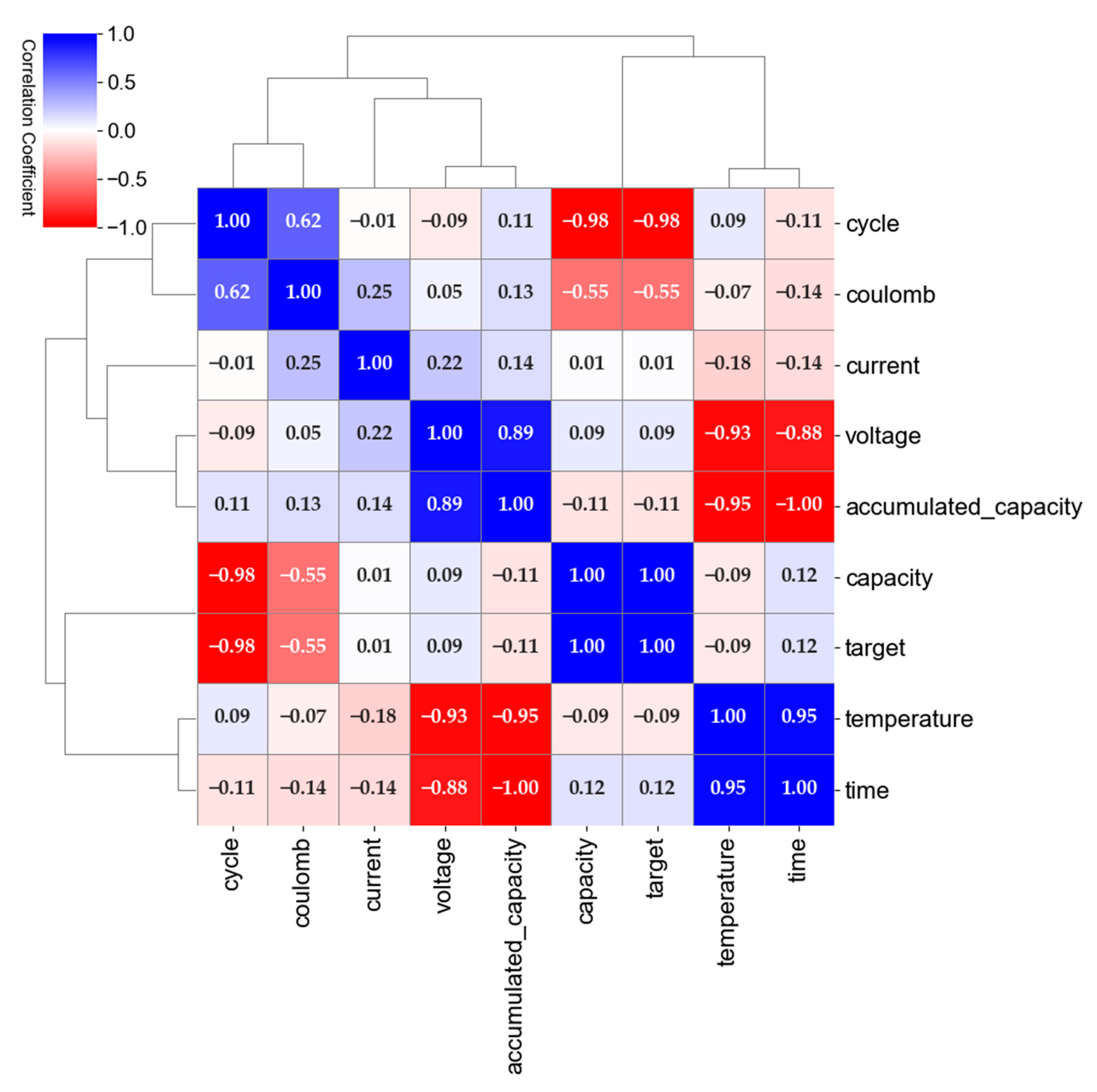
3.2. Feature Extraction
4. Experiments and Results
4.1. Training and Testing Method
4.2. The Generalized Models
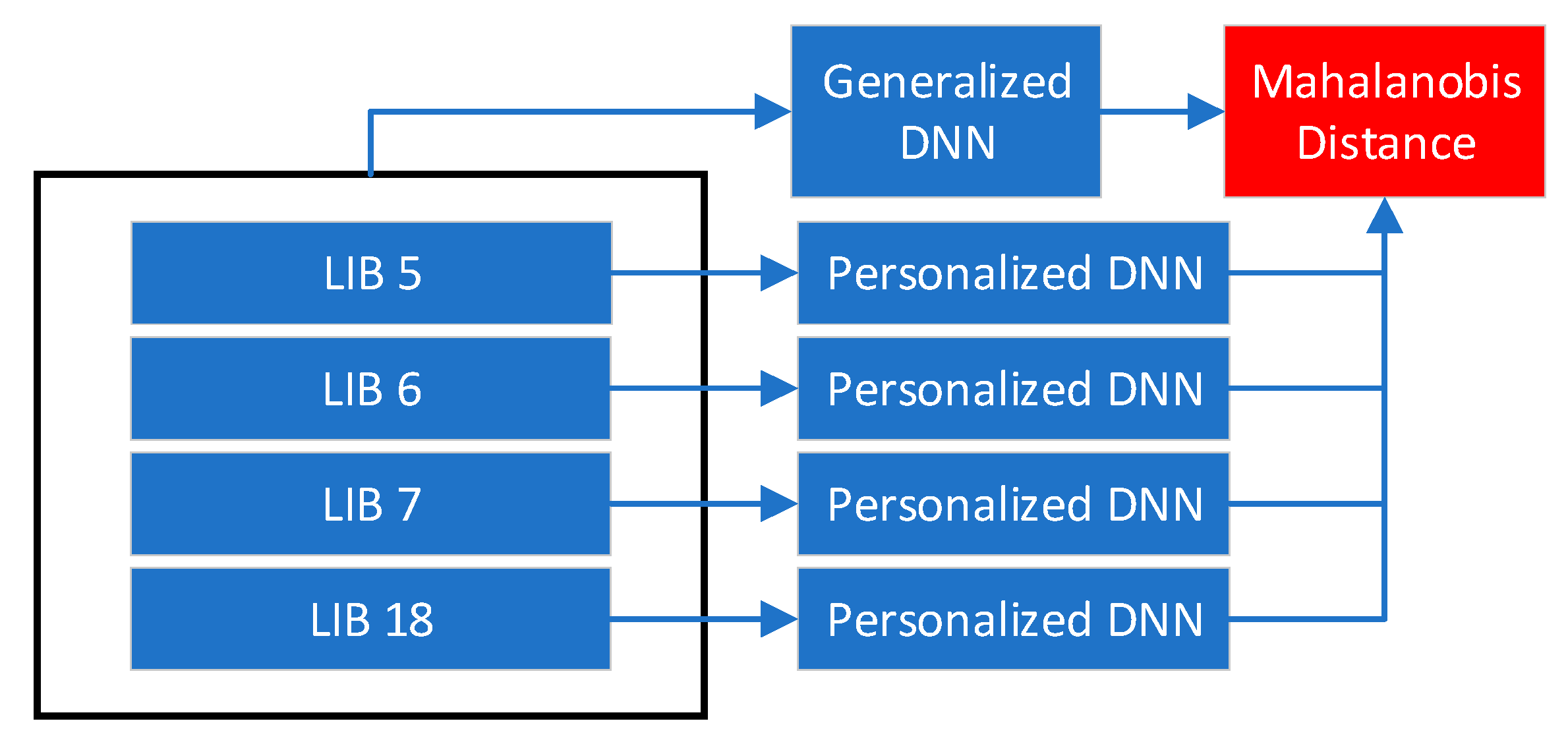
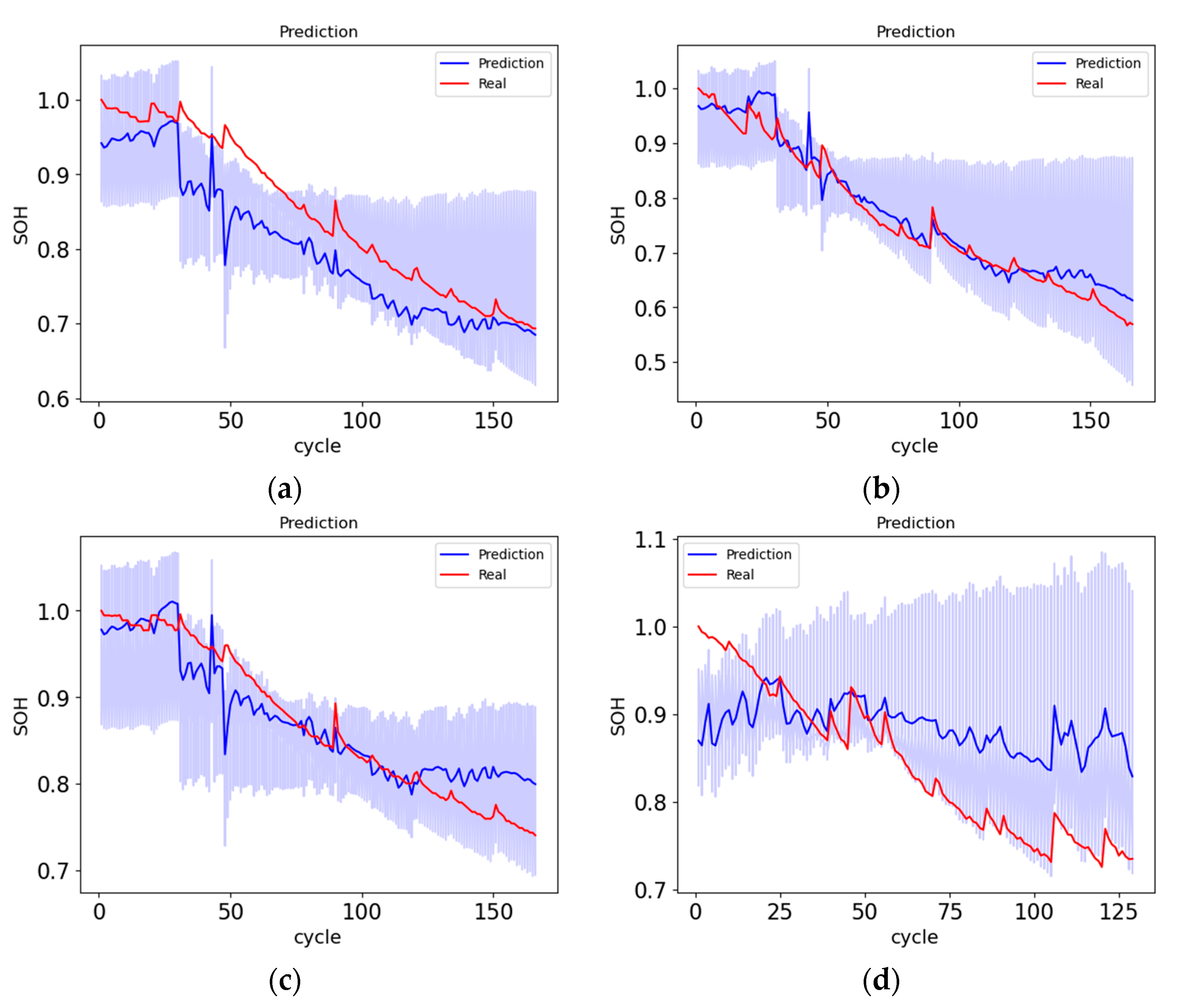
4.3. The Personalized Models
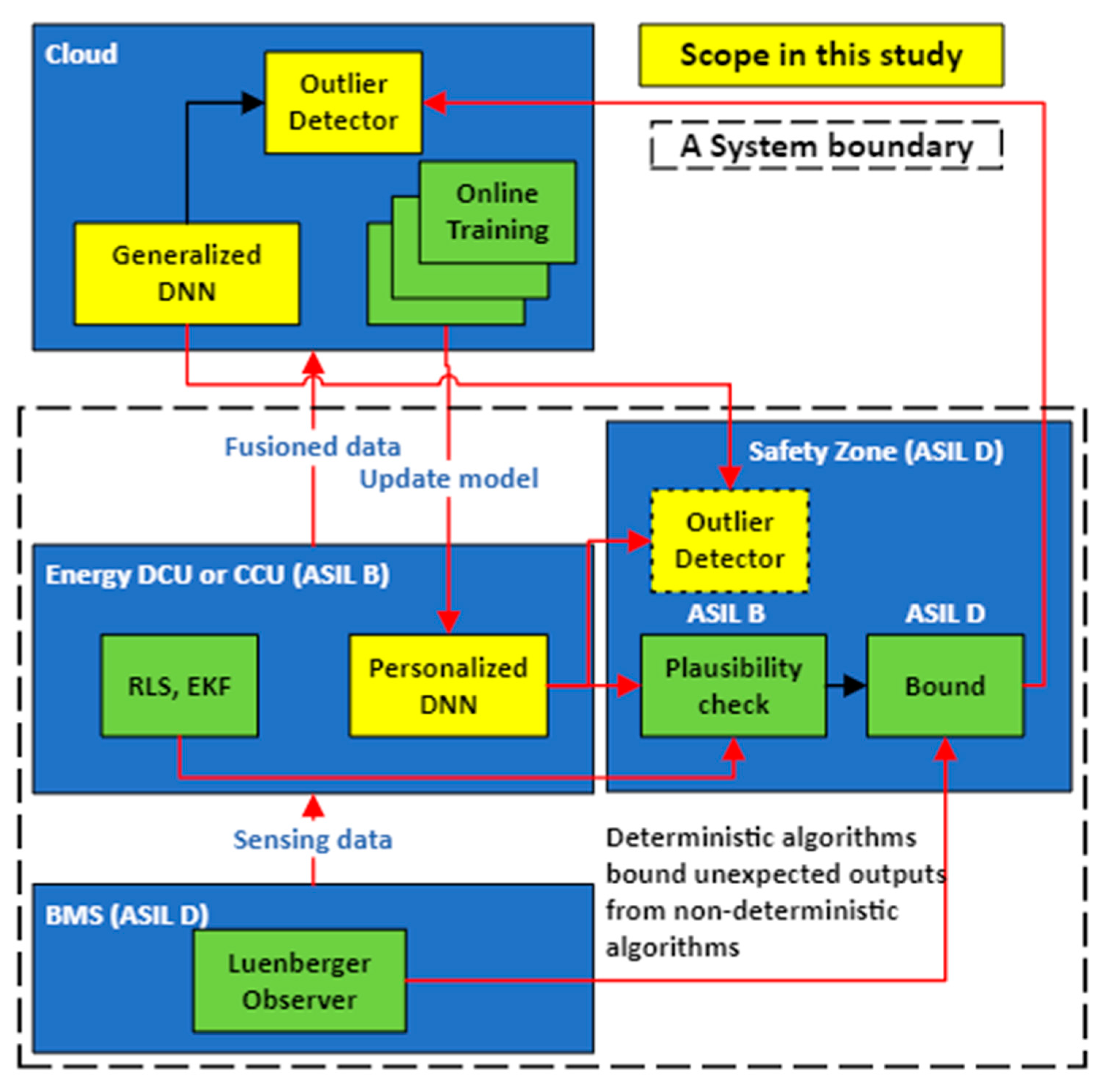
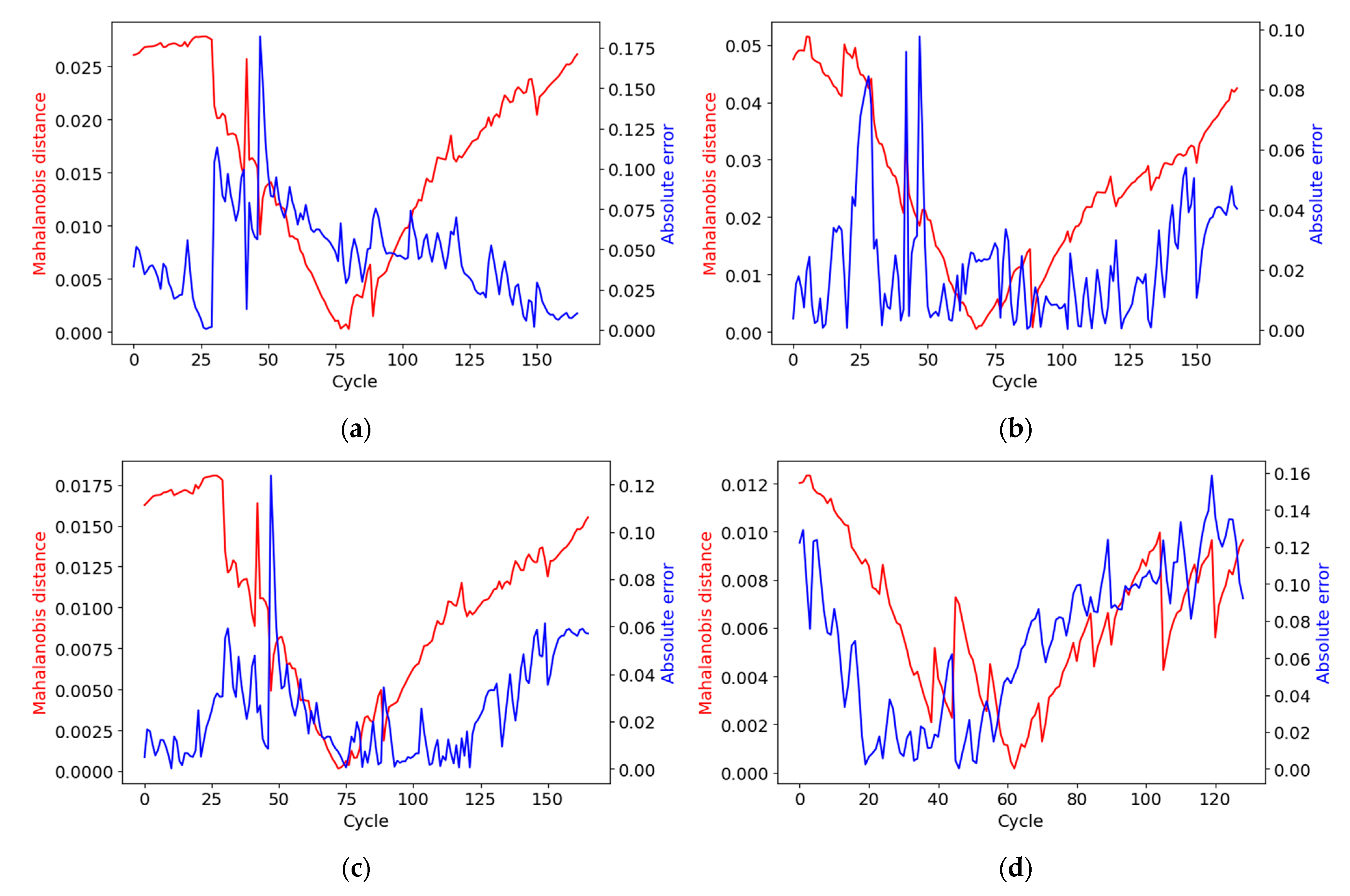
4.4. Outlier Detector
5. Hyperparameter Configuration
5.1. The Number of Hidden Layers and Nodes
5.2. Activation Functions
5.3. Loss Functions
5.4. Gradient Descent Optimizer
5.5. Batch Normalization, L2, and Dropout Regularization
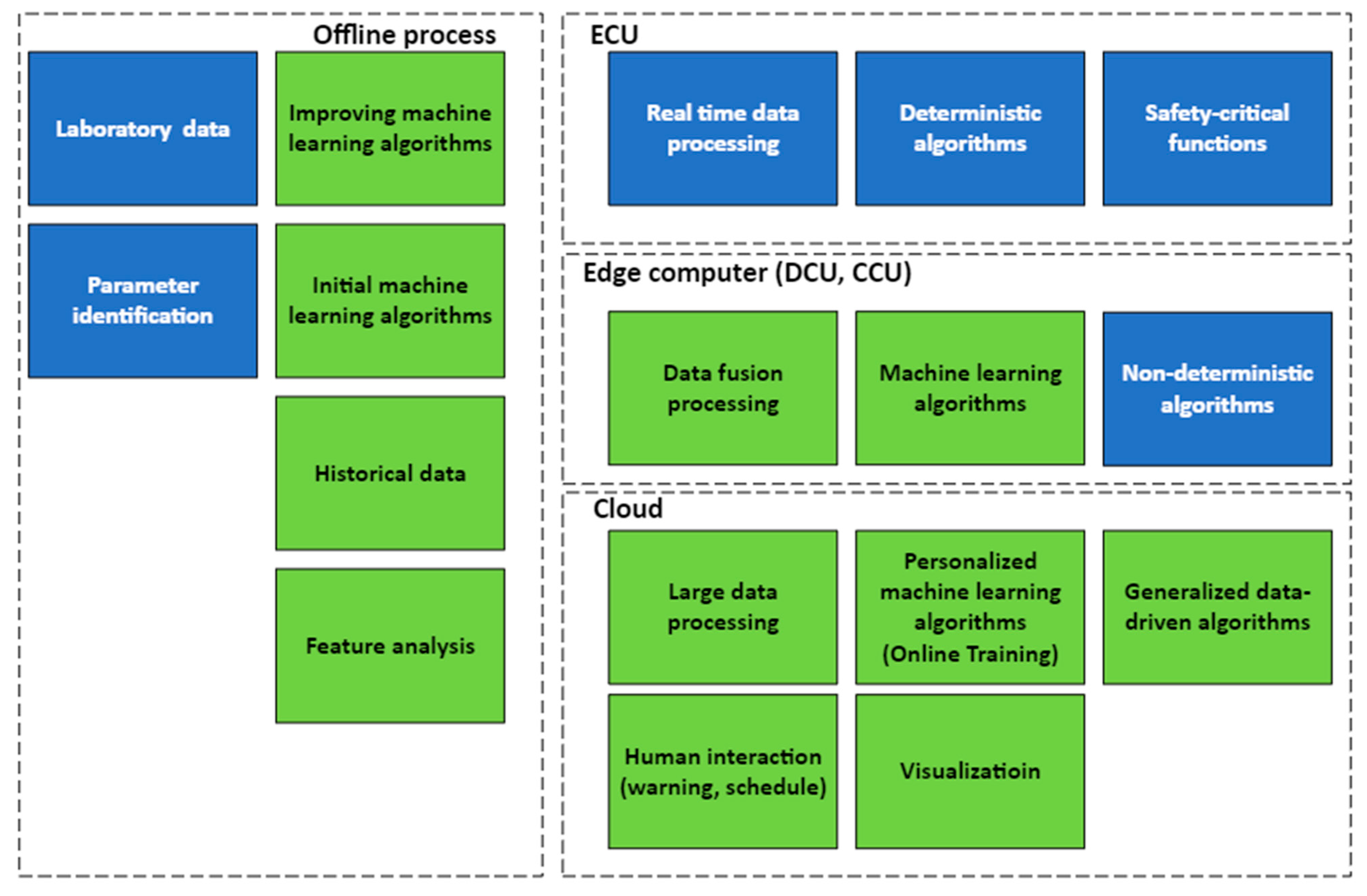
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Models | Network | Optimizer (ADAM) | Cost Function | Batch Norm | L2 | Dropout | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Layers | Node | Activation | a | b1 | b2 | Amsgrad | |||||
| 1 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | |
| 2 | 2 | 10 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | |
| 3 | 3 | 10 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | |
| 4 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | |
| 5 | 3 | 20 | ReLU | 0.01 | 0.9 | 0.999 | Y | Huber | N | 0.01 | |
| 6 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | MSE | N | 0.01 | |
| 7 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | |
| 8 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | |
| 9 | 4 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | |
| 10 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | |
| 11 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | |
| 12 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.7, 0.5 |
| 13 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.5, 0.3 |
| 14 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.3, 0.1 |
| 15 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.7, 0.5 |
| 16 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.5, 0.3 |
| 17 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.3, 0.1 |
| 18 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.7, 0.5 |
| 19 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.5, 0.3 |
| 20 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.3, 0.1 |
| 21 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.7, 0.5 |
| 22 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.5, 0.3 |
| 23 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.3, 0.1 |
| 24 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.7, 0.5 |
| 25 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.5, 0.3 |
| 26 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.3, 0.1 |
| 27 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.7, 0.5 |
| 28 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.5, 0.3 |
| 29 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.3, 0.1 |
| 30 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.7, 0.5 |
| 31 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.5, 0.3 |
| 32 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | 0.3, 0.1 |
| 33 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.7, 0.5 |
| 34 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.5, 0.3 |
| 35 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | 0.3, 0.1 |
| 36 | 2 | 20 | ReLU | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.01 | |
| 37 | 3 | 20 | ReLU | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.01 | |
| 38 | 4 | 20 | ReLU | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.01 | |
| 39 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.01 | |
| 40 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.01 | |
| 41 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.01 | |
| 42 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | |
| 43 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | |
| 44 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | |
| 45 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 0.01 | |
| 46 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 1 | |
| 47 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 1 | |
| 48 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 1 | |
| 49 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 1 | |
| 50 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 1 | |
| 51 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | Y | Huber | N | 1 | |
| 52 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | Y | 1 | |
| 53 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 1 | |
| 54 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | Y | 1 | |
| 55 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 1 | |
| 56 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | Y | 1 | |
| 57 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 1 | |
| 58 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | Y | 0.1 | |
| 59 | 2 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.1 | |
| 60 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | Y | 0.1 | |
| 61 | 3 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.1 | |
| 62 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | Y | 0.1 | |
| 63 | 4 | 20 | tanh | 0.001 | 0.9 | 0.999 | N | Huber | N | 0.1 | |
| 64 | 4 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.01 | |
| 65 | 4 | 20 | ReLU | 0.001 | 0.9 | 0.999 | Y | Huber | Y | 0.1 | |
| Models | B5 (%) | B6 (%) | B7 (%) | B18 (%) | Mean (%) | Models | B5 (%) | B6 (%) | B7 (%) | B18 (%) | Mean (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 7.98 | 3.04 | 2.75 | 6.83 | 5.15 | 34 | 5.68 | 8.69 | 2.80 | 12.06 | 7.31 |
| 2 | 8.72 | 3.29 | 3.25 | 5.90 | 5.29 | 35 | 8.26 | 5.09 | 1.93 | 13.39 | 7.17 |
| 3 | 8.76 | 3.80 | 3.15 | 5.63 | 5.33 | 36 | 8.68 | 3.16 | 3.22 | 5.80 | 5.21 |
| 4 | 7.26 | 3.60 | 2.95 | 6.98 | 5.20 | 37 | 9.44 | 3.68 | 2.92 | 5.15 | 5.30 |
| 5 | 9.13 | 3.20 | 2.95 | 6.48 | 5.44 | 38 | 7.30 | 3.56 | 3.02 | 7.65 | 5.38 |
| 6 | 8.72 | 5.99 | 3.13 | 5.31 | 5.79 | 39 | 8.70 | 2.83 | 2.58 | 5.17 | 4.82 |
| 7 | 13.50 | 8.67 | 0.36 | 15.31 | 9.46 | 40 | 7.73 | 2.59 | 2.68 | 5.77 | 4.69 |
| 8 | 13.96 | 7.54 | 0.37 | 11.20 | 8.27 | 41 | 7.34 | 2.47 | 2.86 | 6.43 | 4.77 |
| 9 | 16.48 | 10.32 | 1.17 | 19.53 | 11.87 | 42 | 5.30 | 6.58 | 4.19 | 9.68 | 6.44 |
| 10 | 16.93 | 9.02 | 1.98 | 19.69 | 11.90 | 43 | 12.71 | 5.36 | 5.56 | 19.38 | 10.75 |
| 11 | 6.41 | 2.97 | 3.09 | 6.64 | 4.78 | 44 | 5.42 | 6.53 | 4.20 | 9.55 | 6.43 |
| 12 | 6.29 | 8.93 | 5.25 | 9.16 | 7.41 | 45 | 9.03 | 2.70 | 6.04 | 8.71 | 6.62 |
| 13 | 5.56 | 8.56 | 4.69 | 9.45 | 7.06 | 46 | 14.76 | 8.10 | 0.59 | 14.78 | 9.56 |
| 14 | 5.10 | 8.56 | 4.35 | 9.69 | 6.92 | 47 | 5.68 | 6.32 | 4.19 | 9.25 | 6.36 |
| 15 | 6.48 | 5.86 | 6.22 | 9.60 | 7.04 | 48 | 11.23 | 4.06 | 3.68 | 11.52 | 7.62 |
| 16 | 4.98 | 6.12 | 3.73 | 14.82 | 7.41 | 49 | 4.54 | 6.45 | 3.94 | 9.86 | 6.20 |
| 17 | 5.43 | 3.62 | 4.84 | 11.35 | 6.31 | 50 | 5.32 | 6.64 | 4.20 | 9.62 | 6.44 |
| 18 | 7.79 | 12.04 | 4.61 | 8.97 | 8.35 | 51 | 5.52 | 6.45 | 4.20 | 9.46 | 6.41 |
| 19 | 10.84 | 11.64 | 9.53 | 8.32 | 10.08 | 52 | 11.37 | 7.00 | 10.04 | 15.23 | 10.91 |
| 20 | 7.25 | 9.91 | 5.45 | 9.67 | 8.07 | 53 | 8.07 | 2.69 | 2.66 | 5.70 | 4.78 |
| 21 | 11.61 | 9.09 | 10.19 | 11.23 | 10.53 | 54 | 12.84 | 6.11 | 0.92 | 8.11 | 6.99 |
| 22 | 6.59 | 2.67 | 6.06 | 11.61 | 6.73 | 55 | 8.37 | 2.90 | 2.68 | 5.80 | 4.94 |
| 23 | 9.97 | 4.07 | 4.43 | 9.57 | 7.01 | 56 | 13.86 | 8.62 | 2.02 | 6.28 | 7.69 |
| 24 | 5.21 | 8.84 | 4.14 | 13.50 | 7.92 | 57 | 6.78 | 2.39 | 2.84 | 6.41 | 4.61 |
| 25 | 5.71 | 8.49 | 4.77 | 9.10 | 7.02 | 58 | 16.05 | 7.31 | 0.90 | 5.89 | 7.54 |
| 26 | 5.17 | 8.02 | 4.36 | 9.44 | 6.75 | 59 | 7.66 | 2.39 | 2.82 | 5.92 | 4.70 |
| 27 | 6.49 | 6.18 | 3.71 | 12.87 | 7.31 | 60 | 12.80 | 7.04 | 0.83 | 20.50 | 10.29 |
| 28 | 4.69 | 6.33 | 3.82 | 15.39 | 7.56 | 61 | 8.42 | 3.15 | 2.59 | 5.56 | 4.93 |
| 29 | 5.93 | 6.40 | 4.98 | 8.56 | 6.47 | 62 | 13.23 | 8.03 | 1.90 | 3.50 | 6.67 |
| 30 | 7.32 | 11.88 | 4.88 | 10.29 | 8.59 | 63 | 8.27 | 3.00 | 2.70 | 5.71 | 4.92 |
| 31 | 7.59 | 10.40 | 3.71 | 11.30 | 8.25 | 64 | 11.84 | 6.11 | 0.73 | 22.94 | 10.41 |
| 32 | 7.02 | 11.13 | 3.58 | 9.20 | 7.73 | 65 | 19.62 | 11.06 | 0.29 | 15.54 | 11.63 |
| 33 | 11.29 | 12.07 | 9.92 | 8.54 | 10.45 |
References
- Alibrahim, H.; Ludwig, S.A. Hyperparameter Optimization: Comparing Genetic Algorithm against Grid Search and Bayesian Optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June 2021; pp. 1551–1559. [Google Scholar]
- Yang, L.; Shami, A. On Hyperparameter Optimization of Machine Learning Algorithms: Theory and Practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A Comprehensive Review of Battery Modeling and State Estimation Approaches for Advanced Battery Management Systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Lee, J.; Wang, L. A Method for Designing and Analyzing Automotive Software Architecture: A Case Study for an Autonomous Electric Vehicle. In Proceedings of the 2021 IEEE International Conference on Computer Engineering and Artificial Intelligence (ICCEAI), Shanghai, China, 27–29 August 2021; pp. 20–26. [Google Scholar]
- Pang, G.; Shen, C.; Cao, L.; Hengel, A.V.D. Deep Learning for Anomaly Detection: A Review. ACM Comput. Surv. 2022, 54, 1–38. [Google Scholar] [CrossRef]
- Alwosheel, A.; van Cranenburgh, S.; Chorus, C.G. Is Your Dataset Big Enough? Sample Size Requirements When Using Artificial Neural Networks for Discrete Choice Analysis. J. Choice Model. 2018, 28, 167–182. [Google Scholar] [CrossRef]
- Hasib, S.A.; Islam, S.; Chakrabortty, R.K.; Ryan, M.J.; Saha, D.K.; Ahamed, M.H.; Moyeen, S.I.; Das, S.K.; Ali, M.F.; Islam, M.R.; et al. A Comprehensive Review of Available Battery Datasets, RUL Prediction Approaches, and Advanced Battery Management. IEEE Access 2021, 9, 86166–86193. [Google Scholar] [CrossRef]
- Stojanovic, V.; Nedic, N.; Prsic, D.; Dubonjic, L. Optimal Experiment Design for Identification of ARX Models with Constrained Output in Non-Gaussian Noise. Appl. Math. Model. 2016, 40, 6676–6689. [Google Scholar] [CrossRef]
- Stojanovic, V.; Nedic, N. Robust Kalman Filtering for Nonlinear Multivariable Stochastic Systems in the Presence of Non-Gaussian Noise: Robust filtering for nonlinear stochastic systems. Int. J. Robust. Nonlinear Control 2016, 26, 445–460. [Google Scholar] [CrossRef]
- Lee, J.; Kim, M. Isolation of Shared Resources for Mixed-Criticality AUTOSAR Applications. J. Comput. Sci. Eng. 2022, 16, 129–142. [Google Scholar] [CrossRef]
- Mohammed, A.; Kora, R. A Comprehensive Review on Ensemble Deep Learning: Opportunities and Challenges. J. King Saud Univ. -Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. NASA Ames Prognostic Data Repository. Available online: https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/#battery (accessed on 6 January 2020).
- Venugopal, P.; Shankar, S.S.; Jebakumar, C.P.; Agarwal, R.; Alhelou, H.H.; Reka, S.S.; Golshan, M.E.H. Analysis of Optimal Machine Learning Approach for Battery Life Estimation of Li-Ion Cell. IEEE Access 2021, 9, 159616–159626. [Google Scholar] [CrossRef]
- Long, B.; Li, X.; Gao, X.; Liu, Z. Prognostics Comparison of Lithium-Ion Battery Based on the Shallow and Deep Neural Networks Model. Energies 2019, 12, 3271. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Xiong, R.; Chen, N.-Y.; Li, J.; Tsou, N.-T. Deep Neural Network Battery Life and Voltage Prediction by Using Data of One Cycle Only. Appl. Energy 2022, 306, 118134. [Google Scholar] [CrossRef]
- Khaleghi, S.; Hosen, M.S.; Karimi, D.; Behi, H.; Beheshti, S.H.; Van Mierlo, J.; Berecibar, M. Developing an Online Data-Driven Approach for Prognostics and Health Management of Lithium-Ion Batteries. Appl. Energy 2022, 308, 118348. [Google Scholar] [CrossRef]
- Khaleghi, S.; Karimi, D.; Beheshti, S.H.; Md Hosen, S.; Behi, H.; Berecibar, M.; Van Mierlo, J. Online Health Diagnosis of Lithium-Ion Batteries Based on Nonlinear Autoregressive Neural Network. Appl. Energy 2021, 282, 116159. [Google Scholar] [CrossRef]
- Ezemobi, E.; Silvagni, M.; Mozaffari, A.; Tonoli, A.; Khajepour, A. State of Health Estimation of Lithium-Ion Batteries in Electric Vehicles under Dynamic Load Conditions. Energies 2022, 15, 1234. [Google Scholar] [CrossRef]
- Li, A.G.; Wang, W.; West, A.C.; Preindl, M. Health and Performance Diagnostics in Li-Ion Batteries with Pulse-Injection-Aided Machine Learning. Appl. Energy 2022, 315, 119005. [Google Scholar] [CrossRef]
- Xia, Z.; Qahouq, J.A.A. Lithium-Ion Battery Ageing Behavior Pattern Characterization and State-of-Health Estimation Using Data-Driven Method. IEEE Access 2021, 9, 98287–98304. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Fahmy, Y.; Emadi, A. A Convolutional Neural Network Approach for Estimation of Li-Ion Battery State of Health from Charge Profiles. Energies 2022, 15, 1185. [Google Scholar] [CrossRef]
- Navega Vieira, R.; Mauricio Villanueva, J.M.; Sales Flores, T.K.; Tavares de Macêdo, E.C. State of Charge Estimation of Battery Based on Neural Networks and Adaptive Strategies with Correntropy. Sensors 2022, 22, 1179. [Google Scholar] [CrossRef]
- Khan, N.; Haq, I.U.; Ullah, F.U.M.; Khan, S.U.; Lee, M.Y. CL-Net: ConvLSTM-Based Hybrid Architecture for Batteries’ State of Health and Power Consumption Forecasting. Mathematics 2021, 9, 3326. [Google Scholar] [CrossRef]
- Shi, J.; Rivera, A.; Wu, D. Battery Health Management Using Physics-Informed Machine Learning: Online Degradation Modeling and Remaining Useful Life Prediction. Mech. Syst. Signal Process. 2022, 179, 109347. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, C.; Wang, Y. Lithium-Ion Battery Capacity and Remaining Useful Life Prediction Using Board Learning System and Long Short-Term Memory Neural Network. J. Energy Storage 2022, 52, 104901. [Google Scholar] [CrossRef]
- Toughzaoui, Y.; Toosi, S.B.; Chaoui, H.; Louahlia, H.; Petrone, R.; Le Masson, S.; Gualous, H. State of Health Estimation and Remaining Useful Life Assessment of Lithium-Ion Batteries: A Comparative Study. J. Energy Storage 2022, 51, 104520. [Google Scholar] [CrossRef]
- Chinomona, B.; Chung, C.; Chang, L.-K.; Su, W.-C.; Tsai, M.-C. Long Short-Term Memory Approach to Estimate Battery Remaining Useful Life Using Partial Data. IEEE Access 2020, 8, 165419–165431. [Google Scholar] [CrossRef]
- Wu, J.; Fang, L.; Dong, G.; Lin, M. State of Health Estimation of Lithium-Ion Battery with Improved Radial Basis Function Neural Network. Energy 2023, 262, 125380. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation Diagnostics for Lithium Ion Cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Ramyachitra, D.D.; Manikandan, P. Imbalanced Dataset Classification and Solutions: A Review. Int. J. Comput. Bus. Res. 2014, 5, 1–29. [Google Scholar]
- Yan, W.; Zhang, B.; Zhao, G.; Tang, S.; Niu, G.; Wang, X. A Battery Management System With a Lebesgue-Sampling-Based Extended Kalman Filter. IEEE Trans. Ind. Electron. 2019, 66, 3227–3236. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Y.; Cheng, J. A Hybrid Method for Remaining Useful Life Estimation of Lithium-Ion Battery with Regeneration Phenomena. Appl. Sci. 2019, 9, 1890. [Google Scholar] [CrossRef]
- De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D.L. The Mahalanobis Distance. Chemom. Intell. Lab. Syst. 2000, 50, 1–18. [Google Scholar] [CrossRef]
- Stathakis, D. How Many Hidden Layers and Nodes? Int. J. Remote Sens. 2009, 30, 2133–2147. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, Y.; Zhao, K.; Tian, Y. A Comprehensive Survey of Loss Functions in Machine Learning. Ann. Data Sci. 2022, 9, 187–212. [Google Scholar] [CrossRef]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of Adam and beyond. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018; 1–23; pp. 1–23. [Google Scholar]
- Zaheer, M.; Reddi, S.; Sachan, D.; Kale, S.; Kumar, S. Adaptive methods for non-convex optimization. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; 9793–9803; pp. 9793–9803. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Santurkar, S.; Tsipras, D.; Ilyas, A.; Madry, A. How Does Batch Normalization Help Optimization? In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; pp. 2483–2493. [Google Scholar]
- Wager, S.; Wang, S.; Liang, P.S. Dropout Training as Adaptive Regularization. In Proceedings of the Advances in Neural Information Processing Systems 26, Lake Tahoe, NV, USA, 5–10 December 2013; Volume 1, pp. 351–359. [Google Scholar]

| Hyperparameters | M57 | M65 | |
|---|---|---|---|
| Network | Structure | FFNN | FFNN |
| Hidden layers | 4 | 4 | |
| Nodes | 20 | 20 | |
| Activation function | tanh | ReLU | |
| Gradient Descent | Optimizer | ADAM | ADAM |
| A | 0.001 | 0.001 | |
| b1 | 0.9 | 0.9 | |
| b2 | 0.999 | 0.999 | |
| AMSgrad | N | Y | |
| Normalization | Cost function | Huber | Huber |
| Batch normalization | N | Y | |
| Regularization | L2 | N | Y |
| Dropout | N | N | |
| Hyperparameter | M57 | M40 | M59 | M41 |
|---|---|---|---|---|
| Hidden layers | 4 | 4 | 2 | 4 |
| L2 | N | 0.01 | 0.1 | 0.01 |
| Models | B5 (%) | B6 (%) | B7 (%) | B18 (%) | Mean (%) |
|---|---|---|---|---|---|
| M57 | 6.77 | 2.39 | 2.84 | 6.41 | 4.60 |
| M40 | 7.73 | 2.59 | 2.68 | 5.76 | 4.69 |
| M59 | 7.65 | 2.39 | 2.81 | 5.92 | 4.69 |
| M41 | 7.34 | 2.47 | 2.85 | 6.42 | 4.77 |
| Hyperparameters | M65 | M7 | M8 | M46 |
|---|---|---|---|---|
| Hidden layers | 4 | 2 | 3 | 2 |
| Activation function | ReLU | ReLU | ReLU | tanh |
| L2 | 0.1 | 0.01 | 0.1 | N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Sun, H.; Liu, Y.; Li, X.; Liu, Y.; Kim, M. State-of-Health Estimation and Anomaly Detection in Li-Ion Batteries Based on a Novel Architecture with Machine Learning. Batteries 2023, 9, 264. https://doi.org/10.3390/batteries9050264
Lee J, Sun H, Liu Y, Li X, Liu Y, Kim M. State-of-Health Estimation and Anomaly Detection in Li-Ion Batteries Based on a Novel Architecture with Machine Learning. Batteries. 2023; 9(5):264. https://doi.org/10.3390/batteries9050264
Chicago/Turabian StyleLee, Junghwan, Huanli Sun, Yuxia Liu, Xue Li, Yixin Liu, and Myungjun Kim. 2023. "State-of-Health Estimation and Anomaly Detection in Li-Ion Batteries Based on a Novel Architecture with Machine Learning" Batteries 9, no. 5: 264. https://doi.org/10.3390/batteries9050264
APA StyleLee, J., Sun, H., Liu, Y., Li, X., Liu, Y., & Kim, M. (2023). State-of-Health Estimation and Anomaly Detection in Li-Ion Batteries Based on a Novel Architecture with Machine Learning. Batteries, 9(5), 264. https://doi.org/10.3390/batteries9050264








