Abstract
In order to meet the increasing demands of the battery in terms of range, safety and performance, it is necessary to ensure optimal operation conditions of a lithium-ion cell. In this thesis, the influence of mechanical boundary conditions on the cell is investigated theoretically and experimentally. First, fundamental equations are derived that lead to coupled models that can be parameterized based on specific cell measurements and predict the pressure evolution due to capacity aging and vice versa. The model is used to derive optimal operating points of the cell, which can be considered in the module design.
1. Introduction
1.1. Motivation and Background
The demands on a battery in terms of charging time, range, safety and lifetime are becoming increasingly more stringent. These requirements are often competing with each other, so it is increasingly necessary to quantify all relevant influencing variables and to optimize these variables globally. The quest for long ranges and high energy densities has led to the use of staked pouch and prismatic cells in a modular frame structure. The cells are pressed into a defined installation space. The module frame is subject to different mechanical loads, both external loads such as oscillations or vibrations [1,2,3] and as well as internal loads due to the expansion of the lithium ion cells [4,5,6,7]. The expansion can be divided into reversible and irreversible processes. The reversible expansion is caused by the thermal expansion and by the volumetric change due to the intercalation/deintercalation of the ions into the anode/cathode and has already been investigated in numerous studies [8,9,10,11,12,13,14]. Irreversible cell growth is a result of various aging phenomena that are strongly influenced by cell operation, module design and lifetime. The main reason for the irreversible cell growth or swelling is the cycling and calendrical SEI formation [2,3,10,11,15,16,17,18] at the anode. In particular, due to the cyclic operation of the cell (reversible expansion), the SEI top layer is broken up by the intercalation processes, resulting in the formation of new SEI in the new surface. The deposition of metallic lithium on the surface of the anode [9,19,20,21] also causes irreversible swelling. The irreversible swelling is always related to the pressure [6,10,22,23,24,25].
The reversible and irreversible cell swelling over capacity aging is investigated by Mohat et al. [8] under variation of temperature, charging rate, depth of discharge and pressure. The pressure is kept constant by a special apparatus and varies in the range of 35 to 172 kPa. It can be seen that as the pressure increases, the capacity degradation and (especially the irreversible) cell swelling decrease over the course of the operation. It can also be seen that with increasing pressure and aging, the reversible expansion behavior decreases. The reason for this is that the increased pressure leads on the one hand to an increased compression of the cell and, in addition, the aging causes that the available lithium is decreased and is therefore no longer involved in the intercalation process. Thus, the capacity or capacity loss is directly correlated to the reversible. and irreversible cell swelling. Since under real conditions in the module, the pressure increases as a result of cell swelling and is not constant, it is not clear whether the findings are transferable to the behavior in the cell stack. The influence of module stiffness and initial preload force on aging was investigated by Deich et al. [6]. The cells were cyclized under a constant stiffness and previously strained with an initial pressure. The optimum in terms of pressure development, capacity and internal resistance degradation resulted in a high initial preload (>70 kPa) and a tendency towards low module stiffness (<2 MPa/mm). The low module stiffness means that the resulting pressure change due to cell growth is low and, as a result, the pressure and the stress on is constant. The Studies by Daubinger et al. [4] and Cannarella et al. [7] evaluated the cell growth and aging of strained and unstrained cells. Based on post-mortem analyses, the unstrained cell showed ripple formation on the cathode and equally extensive lithium plating on the anode was found.
Whereas the strained cell has particle cracks at the cathode, which arise from the combination of cyclic expansion and contraction. In addition, the strained cell has a smaller decrease in capacity over the number of cycles. Cannarella et al. [7] reported on the influence of high pressures in the range of 2–3 MPa, showing that chemical degradation at the anode and a more abrupt capacity degradation can also be observed at high pressure loads.
As analysed by Attia et al. [26], mechanically induced sudden death behavior in lithium-ion batteries has also been described, in addition to excessively high pressures, inhomogeneous pressure distributions lead to local lithium plating [12,26,27,28] and thus also to an abrupt buckling behavior. The review points out the complexity of the mechanically induced buckling behavior, since an electrochemical coupling is always accompanied. In addition to the electrical and thermal boundary conditions, cell growth also depends on the tensioning conditions and the pressure present.
1.2. Contribution and Organization
The prior studies shows a variety of investigations regarding the characterization and explanation of cell expansion in dependence of the state of charge SOC and state of health SOH. Numerous studies prove the causality and interaction between the pressure and aging of lithium-ion cells. In addition, a large number of measurements procedures have been developed, which can be divided into two groups:
- (1)
- explicit characterization methods that apply the pressure to the cell. The pressure is adjusted independently or almost independently of the aging and charge state of the cell from the external.
- (2)
- implicit characterization methods are characterized by the fact that the pressure arises as a result of cell expansion.
Within the scope of this work, both characterization methods are applied and compared with each other. A special evaluation methodology developed, which enables a transfer of both characterization methods into each other. In addition, a novel electro-chemo-mechanical and pressure-coupled aging model is derived and presented. The models based on semi-analytical differential equations. The mechanical model predicts the pressure development as a result of cell growth, taking into account the mechanical boundary conditions. In order to derive the model, first the basic theoretical equations required for modeling and derivation of the hypotheses are discussed. Subsequently, the model parameters are determined by means of experiments and validated by further independent measurements. As part of the investigations, a pouch cell from the automotive sector with the following dimensions of 322 mm · 101 mm (32,522 mm²) is used. The cell consists of 34 stacked anode sheets and 33 cathode sheets and has an initial cell thickness (in the pouched state) of 11.68 mm at a state of charge and a pressure of 10 kPa. The pouch cell consists of a graphite anode and an NMC622 cathode, which a nominal capacity of 61 Ah. According to the cell manufacturer, the cells can be operated between 2.8 and 4.21 V.
2. Theoretical Modeling
In this chapter, theoretical considerations are presented, which for the analysis techniques and modeling. First it is assumed, that the expansion and pressure load of the cell is homogeneous on the entire cell surface (see Figure 1). Thus, the displacement field can be described one-dimensionally in the thickness direction of the cell. The resulting equations will thus be independent of the location of the cell.
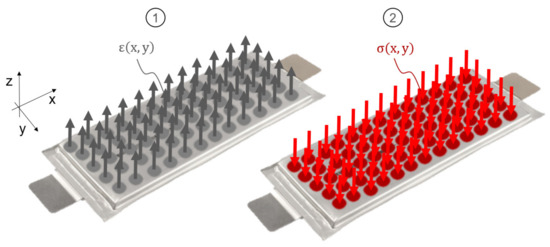
Figure 1.
The schematic representation of the homogeneous displacement and pressure field, which is assumed for the modelling in order to neglect the location dependence for the time being.
In addition, this work deals only with the expansion due to irreversible growth via aging. However, the expansion due to the intercalation can be taken into account by simple adjustments. To exclude the influence of the thermal expansion, all tests are operated with active cooling and identical current profile.
2.1. Modeling of Irreveribeles Cell Swelling
First, the (technical) compressive stress is defined as dividing the homogeneous compressive force and by the (orthogonal to the force) active material surface of the cell
Furthermore, the technical strain is defined by the division of the length change and the initial length
The initial length or cell thickness is defined at a pressure 10 kPa at the fully charged ( = 100%), Begin of Life” (BOL) state ( = 100%). The BOL state is the initial electrical measurement of the capacitance in the installed state.
In order to describe the mechanism of cell swelling as a result of aging, the total differential is used to couple capacity degradation and pressure development.
The first term describes the explicit dependence of the pressure development to the under constant boundary conditions.
This dependence does not exist, since the compressive stress arises as a result of cell growth, so this term is negligible
In the studies [12,29], mechanical stresses that did not arise as a result of cell growth were investigated. The studies show that external mechanical loads such as shocks, vibrations and deformations lead to local damage and delamination of the active material when mechanical limits are exceeded. The local damage has a direct influence on the electrical performance of the cell. The influence is not examined in the context of this work.
The second term describes the product of the pressure change due to cell growth and the cell growth due to aging. The first part of the product is the mechanical stiffness, thus corresponding to a modulus of elasticity
The second part presents the irreversible increase thickness. This term is referred to as the growth rate in the following work. In addition the and the cell swelling it influenced by the of temperature , current profile , time , the number of equivalent full cycles , the state of charge and depth of discharge . For better clarity, the non-mechanical load quantities are vectorial combined in an auxiliary vector
Under these assumptions, there is no explicit dependence of an external pressure on the aging of the cell and the resulting cell swelling exists, but an implicit dependency. In real operating conditions, force loads due to assembly, vibration and mechanical shocks are conceivable. However, consideration would be possible with model theory.
Under these assumptions, the following correlation arises for the full-surface force development as a result of capacity loss
The definition of capacity degradation is defined
as the quotient of the current and the nominal capacity .
2.2. Consideration of Ealstomachnics
The previous equation only describes the electro-chemo-mechanical pressure development of the cell as a result of aging. To take elastic deformations into account, elasto-mechanical properties (Hook’s law) are included in the equation leading to
The basic idea of the model approach is to consider cell growth analogously to a thermally induced strain. For better illustration and readability, the growth rate
and the integral of the growth rate
will be used in the following. The negative sign from Equation (9) results from the clamping situation of the cell, since the resulting compressive force acts against the growth . In summary, the relationship is as follows:
The strain cell is given by the following equations
2.3. Characterization Method
As already introduced, there are two pressure-induced characterization methods can exist, mechanically, three basic scenarios can be defined, which are shown in Figure 2. The cell is simplified as a line, as the expansion of the cell is independent of location and only spreads in the thickness direction. Scenario (A) describes the constant force state, where cell expansion is possible because the degree of free-heating is open, but cell expansion is always subject to a constant force. Scenario (B) describes the constant gap state, where cell expansion is not possible and is limited by a fixed restraint, but the fixed restraint causes the force to steadily increase as the cell expands. Scenario (C) describes a constant stiffness state. In the schematic illustration in Figure 2C, a linear spring with constant stiffness is connected. Movement or expansion of the cell is therefore possible, but subject to the resistance of the spring. All three scenarios are theoretically investigated using the model derived previously.
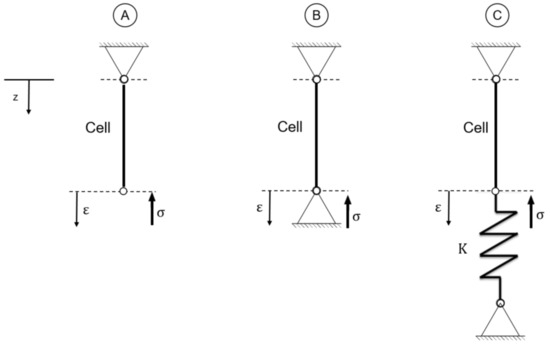
Figure 2.
Basic mechanical scenarios of a homogeneous cell swelling. Scenario (A) describes the constant force state; (B) describes the constant gap state; and (C) describes a constant stiffness state. All three scenarios are theoretically investigated using the model derived previously.
2.3.1. Constant Force Scenario
If an external and constant pressure u is applied to the cell, there is no interaction with the expanding cell [7,8,26,30]. Using this case, the following basic equation results from Equation (12):
Due to the constant pressure condition the differential simplifies to
With the help of Schwarz’s theorem, the differentiation of the modulus of elasticity via aging can be simplified to
since the pressure over aging is constant.
Under this simplification a characteristic equation of constant force measurement.
The characteristic equation states that the measurable strain change over aging corresponds to the irreversible cell swelling. It should be noted that in the variation in Equation (15) the state of charge is constant. In operation, in addition to the irreversible growth also the reversible growth measured over the charging, nevertheless the displacement measurement is independent of the modulus of elasticity and elastic compression. Thus, the constant force test is suitable for measuring the irreversible growth behaviour and makes discretization based on pressure possible. With the help of the constant force test, it is thus possible to parameterize the growth rates from the mechanical model. However, the basic hypothesis that emerges is whether the aging behavior of the different types of characterization is equivalent.
2.3.2. Constant Gap Scenario
The constant gap case is treated in the course of the work for completeness, but is a (rather) theoretical limit case, since the cell is strained in an infinitely fixed clamping (. The constant gap corresponds to an implicit characterization method, but is rarely used for characterization, since the feasibility is associated with considerable effort. Based on Equation (12) the following characteristic equation for the constant gap case
In the constant gap case, it can be seen that the balance of compression and expansion must cancel each other out and three model parameters are present in equation. This also means that the constant gap proves to be disadvantageous here, since neither the (irreversible) growth can still be decidedly characterized by the modulus of elasticity.
2.3.3. Constant Stiffness Scenario
The constant stiffness case describes, in addition to the limit cases described above, real conditions of the cell in a module [10], but it is that also to some extent an idealized assumption, since in module structures, often in- and compressible materials (including cells) are stacked that exhibit highly non-linear behavior. Nevertheless, the constant stiffness test represents a generalization of the constant gap tests and thus also corresponds to an explicit characterization procedure. The stiffness of the cell is mapped via a linear-elastic plate tension, which is compliant according to a stiffness and geometrically described over a surface and plate thickness . Under this clamping, according to Hook’s law, the following system stiffness results
From this, applying the model, follows the following characteristic equation under a constant stiffness condition
It can be seen that in the limit case of an infinite stiffness the characteristic equation of the constant gap condition (see Equation (18)) follows.
2.4. Aging Model
In the previous Section 2.2, the electro-chemo-mechanical equation for homogenous pressure development taking into account cell expansion due to aging was derived. The pressure-induced characterization methods were shown that were consistent with mechanical model. However, the basic hypothesis is that the aging behaviour over the lifetime is invariant of the characterization process. To model the pressure-dependent aging, a semi-analytical aging model of the following form is used
For better readability of the equation, a damage rate is introduced
The damage rate thus describes the degradation of the capacitance at an applied pressure and fixed boundary conditions depending on the equivalent of the cycles .
2.5. Solution of Model Equations
The introduced model Equations (12) and (21) are semi-analytical, copeled (via pressure), nonlinear differential equations which can generally be solved by numerical integration.
It can be seen (cf. Figure 3) that Equation (12) for describing the aging-specific pressure development can be integrated independently if the initial values and boundary conditions are defined. On the other hand, the Equation (12) depends on the pressure development and can only solved by coupling with the Equation (21). For the concrete solution of the equations, it is first necessary to take into account the initial values and the mechanical boundary conditions, because after all, the pressure development is only possible if there is resistance to cell growth.
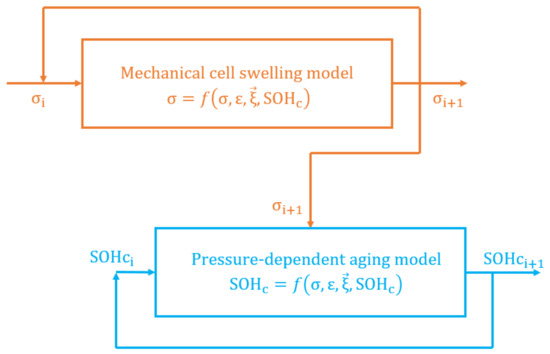
Figure 3.
Schematic representation of the model equations and the coupling. The upper loop represents the mechanical model, which is independent of the ageing model. The lower loop represents the ageing model, which depends on the mechanical model and is therefore coupled.
In the Section 4.3, the electro-chemo-mechanical Equation (12) is solved using the Ritz method. However, for the equations to be valid, it must first be fulfilled that the cell aging is identical and independent of the type of pressure. Conversely, this means that the degradation is invariant from the force applied. This must be checked by measurements. For this purpose, definitions and a description of the measurement setup are given in the following.
3. Test Setup
To investigate the pressure dependence of aging as a result of cell growth, aging measurements are conducted under defined mechanical boundary conditions. In order to investigate the terms, it is necessary to satisfy the constraints of the introduced basic Equation (3). These require stationarity for the clamping conditions, temperature and electrical operation. Therefore, the test procedure, structure and test matrix are described below.
3.1. Test Procedure
The aim of the test procedure is to measure and determine the relevant variables under stationary conditions. For this purpose, a reference parameter test (RPT) is carried out after a defined number of cycles in order to record the intrinsic capacity via a C/10 measurement.
3.2. Measurement Setup
To ensure measurement of cell expansion, a special cell press was designed to keep the pressure conditions within the cell over the entire duration of the experiment constant. In the course of these investigations, a mechanical jig setup was used, which has inherent properties that do not have a significant (and active) influence on the cell (see Figure 4).
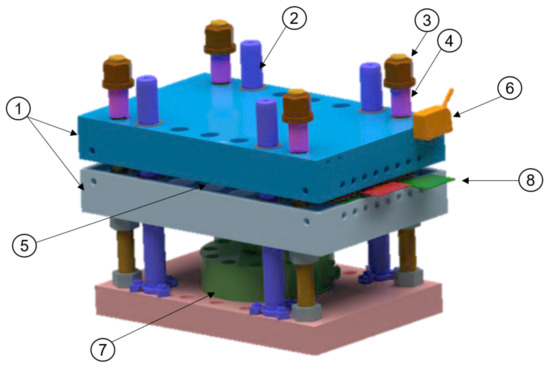
Figure 4.
Representation of the jig setup. The cell (5) is inserted into two large aluminium plates (1) which are supported by compression springs (4), threaded rods (3) and guide columns (2). The force is measured by a force box (7), which is mounted under the intermediate plate and measures a force via the vertical displacement of the plates. The design criteria for the plates are to minimise deformation and to ensure a homogeneous pressure distribution across the cell. The thickness is increased by measuring the distance between the plates. This is done using a laser sensor (6). To measure the distance from the outside, an insert plate (8) is placed under the cell.
The cell (5) is fed into two large aluminum plates (1) braced via compression springs (4), threaded rods (3) and through guide columns (2). The measurement of the force is possible via a force measuring box (7) from HDM (Hottinger Baldwin Messtechnik GmbH, Germany) of the type C10 which is mounted under the intermediate plate and measures a force via the vertical displacement of the plates. The criterion of the plate design is, that the deformation is as low as possible and conversely a homogeneous pressure distribution on the cell is guaranteed. The thickness increase takes place via a distance measurement of the plates. This includes a laser sensor (6) from Mirco-Epsilon (MICRO-EPSILON Optronic GmbH, Germany) of the type ILD-1420-10. To measure the distance from the outside, an insert plate (8) is placed under the cell. The setup is then operated in a climatic chamber at constant temperatures. If the temperature control via the climatic chamber is not sufficient, it is possible to use an integrated cooling circuit in the cover and intermediate plate.
3.3. Test Matrix and Cycling
In order to investigate the influence of pressure on aging and cell swelling, a single-factor design (see Table 1) is chosen, which is listed in the table.

Table 1.
Single-factor constant force testplan.
The cycle is a synthetic profile to maximally stimulate SEI growth or the aging mechanism. The operating window of the cell is maintained throughout the test. The choice of high temperature is to stimulate SEI growth as quickly as possible [6,7,8,9,10]. If the temperature is too high, there is a risk of electrolyte decomposition due to gas formation and inhomogeneous aging [31,32,33,34].
It should be noted that the basic Equation (7) describe the pressure development due to cell growth and aging. Conversely, the present pressure is caused by the aging and cell thickness growth and influences the aging in turn. In experimental setups, the pressure is applied (explicitly) via springs. This initially results in the basic hypothesis as to whether pressure dependence in both scenarios (implicitly and explicitly) has an identical effect on aging. For this purpose, three validation measurements (cf. Table 2) are carried out. There are no springs in the structure and the plates are tightly clamped with the help of nuts. The structure is thus converted into a so-called constant stiffness structure. The constant rigidity of the structure in the vertical direction is achieved via the threaded rods, compression of the plates and the stiffness of the load cell. Using an ideal FE simulation, the complex jig stiffness of 90 kN/mm in the vertical direction was quantified. The cell is clamped with an initial pressure by tightening the threaded rods and then operated with the identical test profile analogous to the constant force measurements.

Table 2.
Validation measurement Constant stiffness testplan.
4. Evaluation, Modeling and Parameterization
In the following, the aging measurements are presented in relation to the mechanical preload conditions. In order to distinguish the type of test, the constant force measurements are abbreviated as CF tests and the constant stiffness measurements are abbreviated as CS tests. The evaluations are also shown separately. In Figure 5 the results of the constant force tests and from D to F the results of the constant stiffness measurement are shown in Figure 5A–C. Figure 5A,D shows capacitance degradation over the equivalent full cycle. Figure 5B,E shows irreversible cell growth using strain over capacitance degradation and Figure 5C,F shows pressure evolution over capacitance degradation.
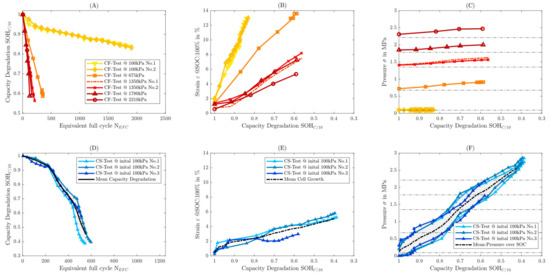
Figure 5.
Overview of the result variables on constant force measurements (A–C) and constant stiffness measurements (D–F). (A,D) shows the capacity degradation, (B,E) show the cell growth (at = 100%) over the . In (C,F) is the Pressure evolution over the shown.
From Figure 5A,D it can be seen that increasing pressure results in accelerated aging for both in the constant force measurement and in the CS test. Figure 5A shows that there is a significant reduction in life at pressures above 675 kPa. It can also be seen that the slope of the capacity reduction is constant and dependent on pressure. In Figure 5D it can be seen that the scatter appears to be relatively small and that two clearly identifiable buckling points (for a = 90% and for = 70%) can be seen in the capacitance curve. After reaching the buckling points, the degradation rate changes significantly in all three CS measurements.
In Figure 5B, according to the characteristic Equation (17), the measured expansion is identical to the irreversible cell growth. The influence of the pressure on the irreversible cell growth is clearly visible, where it can be seen that as the pressure increases, the cell growth is lower and the capacity degradation is proportionally greater.
The rate of the swelling over the capacity degradation (cf. Figure 5B) are constant and dependent on the pressure. Figure 5C,F shows the pressure evolution via capacitance degradation. It can be seen from Figure 5C hat the CF measurements show an increase in pressure due to the springs and cell swelling which is always less than 10% of the initial pressure and therefore negligible. Figure 5F shows the pressure evolution of the CS. The minimum ( = 0%) and maximum ( = 100%) pressures per RPT measurement have been plotted. As the capacity ages, the stroke or reversible cell growth across the state of charge decreases. This is because, on the one hand, the pressure increases and the compression of the cells becomes greater. On the other hand, the thickness is mainly caused by the intercalation of lithium ions in the anode. Ageing causes a loss of lithium, which in turn reduces the amount of lithium that can be intercalated [8].
As already mentioned, it is generally evident that the capacity ageing and cell swelling curves for the constant force measurements show a largely linear decrease (capacity) or increase (cell swelling) and are correlated with pressure. In order to analyse the influence of pressure on ageing, the slope rate is determined and analysed below. In the case of ageing quantities, this is referred to as the damage rate and irreversible cell swelling is referred to as the growth rate. In Figure 5A,B it can be seen that the gradients are divided into two ranges. The gradients can be divided into an initial ( > 90%) and a stationary area ( < 90%). Throughout this paper, the damage and growth rates will always refer to the static area. This analysis technique allows the constant force measurement of discrete parameters to be correlated with the associated pressure. To analyse the buckling points and the influence of pressure in the CS tests, the damage and growth rates are also determined, but numerical differentiation is required because the pressure is variable and influences ageing and cell swelling. Thus, the damage and growth rates from the constant stiffness measurements are continuous functions over pressure.
4.1. Aging Model Parameterization via Constant Force Measurements
Figure 6 below shows the damage rate over the mean applied pressure. The CF measurements result in discrete points, since the damage rates and the pressure per test are constant, whereas the CS tests show continuous trajectories because the pressure increases and the slope changes constantly.
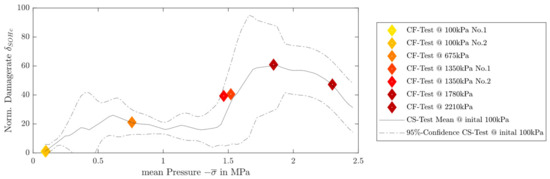
Figure 6.
The normalized damage rate pressure diagram shows the pressure influence on capacity aging. The diagram shows the damage rates resulting from the constant force measurement via the red diamonds and the damage rate progression from the CS measurement as a continuous measurement.
It should be noted that the damage rates are normalized to the damage rate of the measurement @100 kPa for better illustration. In addition, the 95% confidence interval of the CS measurements was evaluated alongside the mean damage rate curve. The course of the damage rates shows that the relationship over pressure has a nonlinear relationship for both CF and CS measurement. The maximum damage is, contrary to expectations, not at the maximal pressure, but at a pressure of 1.78 MPa. The damage rate at this pressure is 50 times higher than at 100 kPa. The CS test has an average 60-fold higher damage in relation to the damage rate than at 100 kPa. The agreement between CF and CS thus seems to be given by the developed analysis technique, therefore the basic hypothesis that the capacitance degradation is invariant of the way of the applied force can also be confirmed statistically, since all constant force measurements are within the confidence range. Looking at the entire damage rate curve of the CS measurement, one recognizes a local maximum at 0.6 MPa in addition to the global maximum at 1.78 MPa. The two pressures from these extremes correlate with the buckling points during ageing (see Figure 6).
This developed analysis technique thus also shows the average pressure is decisive for pressure-induced aging and thus relevant for aging modeling. As a result, Equation (21) is now adjusted by the mean pressure:
The mean pressure is defined as follows
The integration via the state of charge corresponds approximately for the present cell chemistry and the cycle of the compressive stress at a state of charge of 50%
For other cell chemistries or cathode materials with a high nickel content, the average pressure does not have to be to correspond to the pressure at = 50% due to the expansion behavior over the charging stroke [13]. For mechanical components, the maximum pressure development is decisive. The course from the CS tests shows the complex course of the damage function and has an abrupt, but cyclical course. The damage rate reaches local maxima at certain pressures, as soon as these are reached, there is a recovery that falls to a comparable level.
In the course of this investigation, 4 different types of models are used for interpolation in the ageing model. The following modelling approaches are examined:
- Piecewise linear interpolation
- Smoothing spline
- Nearest-neighbor interpolation.
In the study the CS curve itself is used as a fourth interpolation method. Figure 7 shows the different interpolation methods with the damage rates from the CF measurements. It is evident that the piecewise linear interpolation and smoothing splines interpolation method largely overestimate the constitutive damage rate function. The nearest-neighbor interpolation method approach is intermediate.
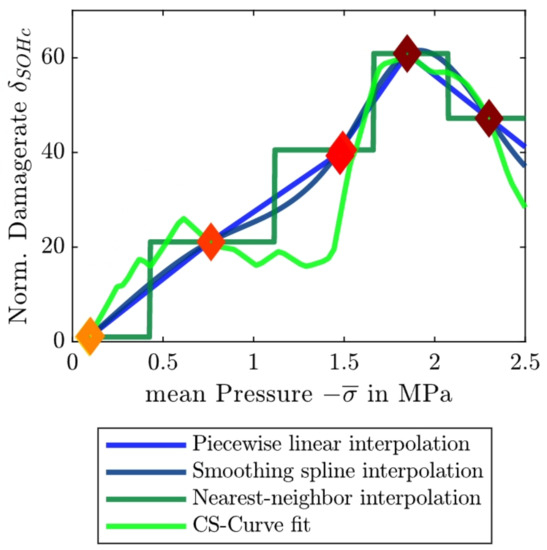
Figure 7.
Comparison of the four different interpolation methods that are investigated in the study. The diamonds correspond to the damage rates based on the CF tests.
4.2. Mechanical Model Parameterization of Irreversible Cell Growth
According to the modeling and derivation of the characteristic Equation (17), it is known that the growth rate is identical to the irreversible cell growth is. In Figure 8, these were determined for both the CF tests and the CS tests and applied over the applied pressure.
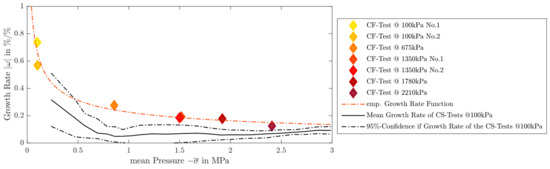
Figure 8.
The normalized growth rate pressure diagram shows the growth behavior, related to the aging of the cell as a function of the applied pressure normalized growth rate pressure diagram. The diagram contains the growth rates resulting from the constant force measurement via the red diamonds and the damage rate progression from the CS measurement as a continuous measurement.
It can be seen that the constant force measurements represent a limit case and form an enveloping function, compared to the CS measurement. This can also be described by the characteristic equations, as compression-independent growth (irreversible cell swelling) can only be measured in the constant force case. The constant stiffness and constant gap case, according to the Equations (19) and (22), is influenced by cell compression itself. The discrete growth rates from the CF tests can be achieved on average with a power function of the form
The function consists of a normalised scaling parameter , which describing the growth behavior at 1 MPa and a power coefficient , which describing the pressure decay behavior of the cell. It should be noted that in the plot the cell thickness and pressure have been evaluated at a of 100%. In Figure 8, the power function is shown dashed in red via a regression. The influence of the state of charge on the emp. Growth rate function has been studied and shows no significant influence of the , so it is not discussed here.
4.3. Mechanical Model Parameterization of Cell Stiffness
The stiffness of a cell is an extremely complex quantity consisting of the mechanical system of the cell. The cell stiffness is a combination of the visco-elastic behavior of the electrolyte and highly non-linear material properties, for example due to porous structures. The cell stiffness can be characterised by different methods. Most of the methods are based on explicit characterization methods. As described by Kessel et al. [35], cell stiffness is described by mechanical impedance spectroscopy and rheological material models in different frequency ranges. In the work of Deich et al. [30], the cell stiffness was characterized by a quasi-static pressure test. The main difference is that cell stiffness strongly depends on time scales or frequency. The cell stiffness from a quasi-static pressure test is more appropriate for modelling pressure development over ageing, as cell growth develops over long periods of time. In addition to the well-known pressure dependence in stiffness, the stiffness of the cell changes due to the changes in the internal structures in the cell as a result of aging and SEI formation [3].
In the course of this work, the cell stiffness is divided into a mechanical and electrochemical cell stiffness, both are described below.
As reported by Sauerteig et al. [36], the cell stiffness in the cell network is given by the following equation
where describes the elastomechanical modulus of elasticity and describes the electro-chemical modulus of elasticity resulting from SEI surface layer formation [37].
4.3.1. Elastomechanical Cell Stiffness
First, cell stiffness is required via a quasi-static pressure test to describe the elasto-mechanical properties of the cell in the BOL state. In Figure 9, the modulus of elasticity is shown over the applied pressure and statistically evaluated for 5 different cells at a of 100% (see Figure 9A) and a of 50% (see Figure 9B).
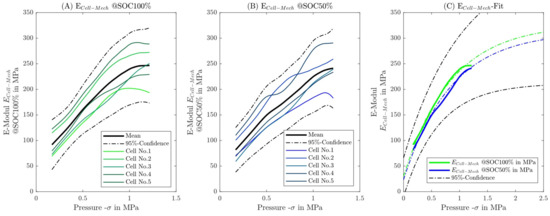
Figure 9.
Representation of elastomechanical E−Modu via pressure. In (A), the measurements are shown at a SOC of 100% and in (B) at a SOC of 50%. In addition, the mean value and 95% confidence range were evaluated. In (C) the empirical regression for the mean courses at SOC 100% and 50% and with the 95% confidence interval is shown.
Reducing the state of charge (from 100 to 50%) leads to a decrease in the elastic modulus of elasticity, as demonstrated in [35]. The dispersion of elastic module cell stiffness amounts to 15% in both cases. Figure 9A,B show that the elastomechanical modulus of elasticity of the cell can be described empirically in the following context:
Figure 9C shows the empirical relationship via a regression with the measurement. The minimal influence of the state of charge can be seen. The scaling parameter describes the limit value to be achieved and the parameter describes the limit value in the unpressurized state. The eigenvalue and gives information about the slope of the modulus of elasticity with respect to the opposing force Table 3 below lists the parameters of mechanical cell stiffness. It can be seen that the state of charge essentially only influences the limit values and . The eigenvalue or slope parameter is invariant of the . Using a statistical test, the influence is not significant under “statistical” conditions.

Table 3.
Empirical description of elasto-mechanical cell stiffness.
4.3.2. Electrochemical Cell Stiffness
In order to take into account the structural property changes of the cell as a result of cell expansion, the relationship of growth rates is used
First, the growth rate is integrated over aging
this results in the irreversible growth due to aging. In order to determine the stiffness, secondly the growth is differentiated according to the stress (pressure)
By applying the reciprocal value, an empirical relationship of the modulus of elasticity as a result of the cell expansion of the cell, as a function of the aging state and the pressure results.
It can be seen that the aging is indirect proportional and the pressure proportional on the electrochemical modulus of elasticity. The greater the aging, the more the modulus of elasticity decreases; conversely, the higher the modulus of elasticity results in higher compressive stress. It can be seen that the theory for the borderline case = 100% has a singularity. The significance of this singularity only becomes apparent when considering electrochemical and elastomechanical cell stiffness as a whole.
4.3.3. Total Cell Stiffness
Since both elastomechanical and electrochemical stiffness are subject to identical pressure, the total cell stiffness can be determined mechanically, using Hook’s law, as follows:
Here, the described singularity of the electrochemical stiffness can be analyzed by a limit value analysis
As a result, it becomes clear that electrochemical stiffness only becomes effective as a result of existing aging and contributes to overall cell stiffness. BOL has only the elastomechanical stiffness. A limit value analysis for the pressure less state shows the convergence to the parameter
This limit value analysis also includes the BOL case ( = 100%). Therefore, the theory seems consistent in the border areas that exist in reality.
4.4. Modeling for Linear Full Cell Element
In order to describe the clamping conditions of the cell in the experimental setup, the Ritz method, a well-known FE method based on the extremal principle from the variation calculation, is used. As in Section 2 already described, it is assumed that the increase in cell thickness is flat and homogeneous and thus can only be described in the first approach about the cell thickness. First, the displacement function at cell thickness (cf. Figure 1) is generally used with the following test function,
as a polynomial function of degree of .
The test function must meet all geometrical boundary conditions. The strain corresponds to the differentiation
The local displacement function is divided into the coefficients and in the displacement. The displacement is determined by the boundary conditions and the coefficients are determined by means of the calculus of variations. However, this first requires the determination of the deformation energy (internal work):
The external work or load at the discretization points
The principle of variation calculation now states that the elastic potential
extremal for all chosen coefficients of the test function, if the following necessary condition (Euler-Lagrangian equation) is satisfied
for i = 1, 2, …, n.
In our approach, the cell is simply discretized in two points ( = 2) and the displacement is discretized with a simple test function of the form
described.
The test function states that the displacement over the cell thickness is linear. Using the geometric boundary conditions
results in the following approach function
and the associated strain
The coefficients and are determined using the Euler-Lagrange Equation (41).
The calculation of the internal energy is given below:
Through integration and transformation, the following relationship for the inner work results
The calculation of the external work is based on the product sum of the applied forces on the displacement nodes, or on the free values given
Applying the necessary condition (see. Equation (41)) results in the following system of equations
The system of equations can now be simplified into the well-known basic equation of the finite element method with the addition of the swelling vector
This results in the element stiffness matrix
The stress vector of the external forces
and the swelling vector, which takes irreversible cell swelling taken into account
The advantage of this method is the possibility to use any discretization of the cell or any sequence of cells or other materials with different properties. For a quadratic test function n = 2 and a simple discretization m = 1, the following element stiffness matrix is obtained
and following swelling vector
For a discretization of the whole cell by two cell elements ( = 2) with linear test functions ( = 1) and with half cell thickness per element, the following global stiffness matrix for the full cell
and the following swelling vector results
4.5. Consideration of the Boundary Conditions from the Measurement Setup
For a discretion of the full cell by a cell element with linear test function, the following global stiffness matrix for the full cell results. Figure 10 shows this schematically, both the cell (indicated as a rod element) and the jig (indicated as a spring element) experience the identical force.
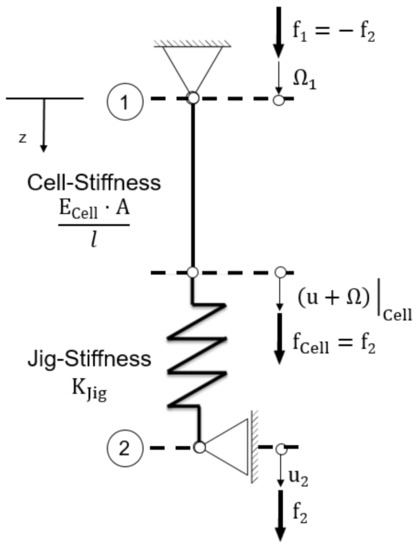
Figure 10.
Mechanical equivalent circuit diagram for clamping conditions of the cell in the structure.
Since that the upper plate is fixed, so the local displacement is also zero:
The lower plate, on the other hand, is movable in the vertical direction and the movement is the result of the total system stiffness of the cell and the jig. The total system stiffness results from the following relationship
describes the structural stiffness of the jig, which was determined by means of an FE simulation. Since both FE modeling to determine the jig stiffness and 1-dimensional modeling require many assumptions and idealizations that are not given in reality, a correction factor can has to be integrated.
Below are some ideal assumptions that influence the build-up stiffness of the jig:
- Optimal central placement of the cell
- Homogeneous cell surface
- Optimal homogeneous cell aging and cell expansion
- Homogeneous pressure application and distribution by threaded rods.
Based on the replacement stiffness in the Equation (51), the following equation results
and is used to describe cell expansion in the jig setup. By applying a linear approach function, the relationship to a scalar equation is simplified.
When choosing a polynomial function of nth order or with m further discretization’s of the cell, corresponding () equations result that have to be solved. The solution becomes more complex, systems of equations have to be solved with nonlinear material behavior. In the following, a numeric, recursive algorithm is presented in Algorithm 1, to solve the equations.
| Algorithm 1: Recursive numerical solution algorithms |
| Initialization ) |
| Force-Prediction-Step: |
| Displacement-Correction-Step: |
The algorithm according in Algorithm 1, is structured in an initialization step and in a recursive iteration loop. The initialization step creates the deformation state after attachment of the initial load vector. The iteration loop, on the other hand, first determines the resulting force due to the cell expansion and finally the displacements due to the increase in force, with constant aging.
5. Simulation and Validation
In the following chapter, the simulation is compared with the validation measurements already used in Section 4.1. In addition, an additional validation measurement with increased preload condition of 675 kPa at = 30% was carried out and compared with the simulation. The validation measurements are summarized below in Table 4.

Table 4.
Test matrix for validation measurement.
5.1. Comparison of the Simulation with the Validation Measurement I
In the Figure 11A the pressure evolution and in Figure 11B the resulting strain are compared according to the simulation with the average of the CS measurements at = 100% and = 50% (corresponding to the mean pressure).
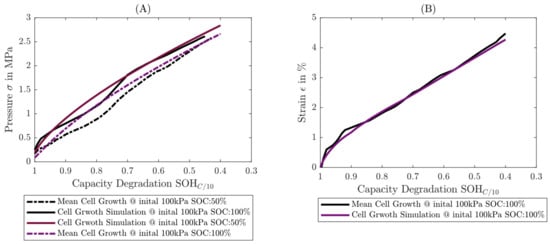
Figure 11.
Comparison of mechanical simulation with measurement. In (A), the measured pressure development over aging is compared with the simulation at a SOC = 100 and 50%. In (B) is the measured irreversible growth compared to the simulation.
In Figure 12, the four coupled lifetime predictions are compared with the measurements in a subplot. As the scatter behavior in the aging curves is large, in addition to the mean ageing behavior (black dashed line), the actual measurement curves and the confidence interval (95%) are shown.
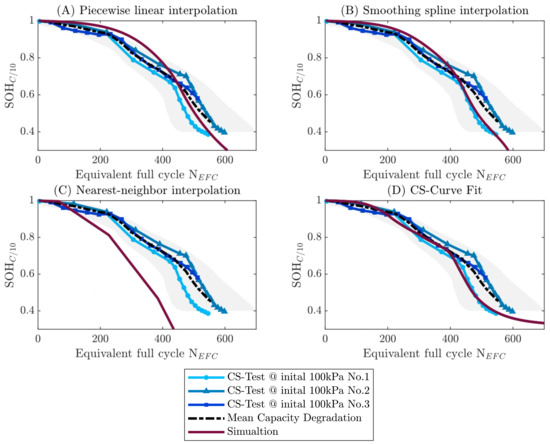
Figure 12.
Complete comparison measurements with the aging simulation. The subplots are divided according to the four interpolation methods used for the simulation. In the plots, the individual measurements are shown in blue, the mean is shown in black dashed lines, the 95% confidence interval of the measurements is shown in grey as a grey corridor, and the ageing simulation is shown in purple. The two interpolation methods (A,B) lead to very comparable results, whereas methods (C,D) are very different: (C) shows the largest deviation, which occurs first and then remains. In (D) the smallest deviation can be seen, as here only the deviation from the mechanical forecast has an effect.
It can be seen that in the range of = 80 to 90% there is a large deviation in the development simulation to the mean value of the measurement data, both at = 100% and at = 50%.
The reason for this is that in the pressure range from 0.1 to 1.5 MPa (according Figure 5C) only 1 constant force measurements are available at 0.675 MPa @ = 30%. The course of the empirical growth rate function shows the greatest sensitivity to pressure due to the equation and the regression. This results in a direct influence on the growth rates and the electrochemical modulus of elasticity and, in addition, a direct error propagation on the pressure development and on the coupled lifetime simulation. In Figure 11B shows the strain of the cell at = 100% of the mean strain from the CS measurement. It can be seen that the deviations in the print are not present here. Figure 12 shows the lifetime simulations based on the different interpolation variants (see Section 4.1). The direct influence of the interpolation variant of the CS measurement can be seen. The interpolation methods in Figure 12A,B are only slightly different, but this is also evident from the evaluation in Figure 7. The “Nearst-neigbor approach” differs significantly, as it has the largest deviation and is the most conservative approach. The large deviation is due to the fact that, the damage rate is increased abruptly after 0.5 MPa (cf. Figure 7) is exceeded, resulting in a high damage being applied earlier than in the other interpolation methods. Using CS-Curve Fit as the interpolation method shows the smallest deviation, which is to be expected as it only includes the deviation from the pressure prediction model. In addition, the error propagation from the pressure development simulation is significant on the aging simulation. This results to the largest deviation in the range = 80 to 90%. In order to quantify the quality of the simulation and the interpolation methods, error measures are determined in relation to the number of cycles The mean deviation or residual
is the difference between the simulated number of cycles and the average number of cycles from the three validation measurements. The mean square deviation is defined as follows over aging, is given by the following relation
Taking into account the variation from the validation measurements, the mean square deviation can be related depending on the confidence ranges. It is assumed that the residual is normally distributed. Table 5 shows the mean square deviation for the different simulation or interpolation methods and compares the standard deviation and the 95 and 99% confidence levels (CL).

Table 5.
Overview of mean square deviations.
It can be seen that, as expected, the CS curve fit results in the smallest deviation and lies within the standard deviation. When applying the CS-Curve fit interpolation approach, only the deviation from the print development simulation and the description quality of the 1D modeling are evaluated. In the case of the other interpolation methods, the deviations of the interpolation are also added, so these are greater. It can be seen that the nearest-neighbor approach is significant outside the trust ranges and has the largest deviation.
5.2. Comparison of the Simulation with the Validation Measurement II
For further validation of the model, a second independent validation measurement was performed. The initial pressure was increased to 675 kPa at a of 30%. The aim is to investigate how well the change preload force can be mapped with the model. The next higher pressure level (cf. Figure 5) selected from the present constant force measurements. Figure 13A shows the measured pressure evolution at = 100% and at the average = 50% compared to the simulation. It can be seen that there is a very high overlap between simulation and measurement. The biggest deviation is initial. The reason for this is that the growth rates only describe the stationary growth area and not the initial usually nonlinear growth. On the other hand, the change in the state of charge also influences the modulus of elasticity as well as the growth rates. In the model, only the measurements at a of 100 and 50% are available.
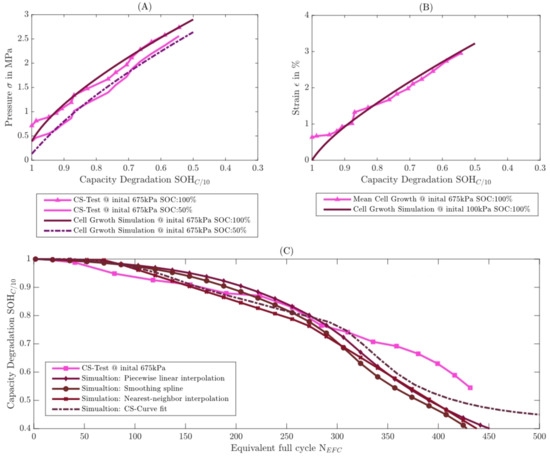
Figure 13.
Complete simulation and measurement comparison with validation measurements II. In (A), the measured pressure development over aging is compared with the simulation at a SOC = 10 and 50%. In (B) is the measured irreversible growth compared to the simulation. In (C) the comparison between the measured capacitance aging with four different simulations is shown.
Figure 13B shows the strain of the cell over aging at a of 100%. Here, too, the high level of agreement in the stationary area is clearly visible. In Figure 13C, the capacitance degradation measurement is compared with the different aging simulations. It can be seen that all simulation approaches are more conservative than the measurement. Moreover, as expected, Nearst-neigbor interpolation approach is the most conservative. The initial deviation in the pressure development is clearly visible in the capacitance degradation measurement. The simulation underestimates the initial pressure increase over the charge state, as a result of which the aging simulation is initially above the measured capacity degradation. In the further course of capacity degradation, there is a high overlap up to = 60%. From 60% there is a significant difference between the measurement and the simulation, but this is not due to the pressure or cell thickness growth.
6. Discussion and Conclusions
There are a large number of studies and investigations that experimentally demonstrate the causality and interaction between pressure and aging of lithium-ion cells. The methods used in the literature can be classified into two categories: (1) explicit characterization methods, where a specified pressure is applied to the cell; (2) implicit characterization methods, where the pressure arises as a result of the cell expansion.
The purpose of this paper is to confirm or disprove the following hypothesis: Does the chosen characterization method (1) or (2) have an influence on cell expansion and conversely, on aging depend on the type of load. Using the developed mechanical model, the different characterization methods were investigated analytically. The hypothesis was experimentally and statistically verified using specially developed evaluation techniques, such as damage-pressure diagrams, and the non-linearity of pressure with ageing was demonstrated.
In addition, the characteristic equations for three basic mechanical scenarios were derived for the first time using the basic boundary conditions: Constant Force, Constant Gap and Constant Stiffness. The derived mechanical model was solved using the Ritz method and reformulated to the basic equations of FEM with the extension of a swelling vector for a homogeneous load and cell expansion via aging. With the help of the method, further local discretization or nonlinear test functions can be selected. The model can describe both, several cells in the stacked in a module or individual layers within a cell. The big advantage to the models that correspond to the state of the art is that different material properties can be taken into account. The pressure-based aging model is also applicable to local discretization. To validate the models, two independent test series were carried out using constant stiffness tests. For both tests, studies to evaluate different interpolation methods of nonlinear pressure dependence were conducted. It has been shown that the pressure-based aging prognosis is very sensitive, and small deviations accumulate. Thus, the use of a CS-Curve Fit proved to be the most accurate interpolation among the tested interpolation methods. The accuracy is about 20% smaller than the standard deviation of the aging measurement itself. Future work will include extensions of the model to describe swelling based on intercalaction and deintercalation (SoC) and application at the module level. In addition, the derivation of analytical equations and parameters allows comparison and transferability to other cell chemistries. Chemical system-specific properties, such as reversible or irreversible swelling or the influence of pressure on capacity aging, can be quantified.
In many cases they is no information or possibility to measure the pressure development in the module. Using the model offers the opportunity to develop methods that use observer models or data-based approaches to teach the parameters during operation as in [38,39]. The advantage would be that expensive measurement technology would not be required and customer usage and aging forecasts would be ensured during operation.
Author Contributions
A.A.: Conceptualization, Methodology, Software, Investigation, Writing—orginal draft, Resources. A.F.: Visualization, Investigation, Writing—review & edting. K.P.B.: Supervision, Writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable. No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Brand, M.J.; Schuster, S.F.; Bach, T.; Fleder, E.; Stelz, M.; Gläser, S.; Müller, J.; Sextl, G.; Jossen, A. Effects of vibrations and shocks on lithium-ion cells. J. Power Sources 2015, 288, 62–69. [Google Scholar] [CrossRef]
- Pistorio, F.; Clerici, D.; Mocera, F. Review on the Experimental Characterization of Fracture in Active Material for Lithium-Ion Batteries. Energies 2022, 15, 9168. [Google Scholar] [CrossRef]
- Jones, E.M.C.; Çapraz, Ö.Ö.; White, S.R.; Sottos, N.R. Reversible and Irreversible Deformation Mechanisms of Composite Graphite Electrodes in Lithium-Ion Bateries. J. Electrochem. Soc. 2016, 163, A1965. [Google Scholar] [CrossRef]
- Daubinger, P.; Schelter, M.; Petersohn, R.; Nagler, F.; Hartmann, S.; Herrmann, M.; Giffin, G.A. Impact of Bracing on Large Format Prismatic Lithium-Ion Battery Cells during Aging. Adv. Energy Mater. 2022, 12, 2102448. [Google Scholar] [CrossRef]
- Mussa, A.S.; Klett, M.; Lindbergh, G.; Lindström, R.W. Effects of external pressure on the performance and ageing of single-layer lithium-ion pouch cells. J. Power Sources 2018, 385, 18–26. [Google Scholar] [CrossRef]
- Deich, T.; Storch, M.; Steiner, K.; Bund, A. Effects of module stiffness and initial compression on lithium-ion cell aging. J. Power Sources 2021, 506, 230163. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Stress evolution and capacity fade in constrained lithium-ion pouch cells. J. Power Sources 2014, 245, 745–751. [Google Scholar] [CrossRef]
- Mohtat, P.; Lee, S.; Siegel, J.B.; Stefanopoulou, A.G. Reversible and Irreversible Expansion of Lithium-Ion Batteries under a Wide Range of Stress Factors. J. Electrochem. Soc. 2021, 168, 100520. [Google Scholar] [CrossRef]
- Grimsmann, F.; Brauchle, F.; Gerbert, T.; Gruhle, A.; Parisi, J.; Knipper, M. Impact of different aging mechanisms on the thickness change and the quick-charge capability of lithium-ion cells. J. Energy Storage 2017, 14, 158–162. [Google Scholar] [CrossRef]
- Hahn, S.; Theil, S.; Kroggel, J.; Birke, K.P. Pressure Prediction Modeling and Validation for Lithium-Ion Pouch Cells in Buffered Module Assemblies. J. Energy Storage 2021, 40, 102517. [Google Scholar] [CrossRef]
- Louli, A.J.; Li, J.; Trussler, S.; Fell, C.R.; Dahn, J.R. Volume, pressure and thickness evolution of li-ion pouch cells with silicon-composite negative electrodes. J. Electrochem. Soc. 2017, 164, A2689. [Google Scholar] [CrossRef]
- Pegel, H.; von Kessel, O.; Heugel, P.; Deich, T.; Tübke, J.; Birke, K.P.; Sauer, D.U. Volume and thickness change of NMC811|SiOx-graphite large-format lithium-ion cells: From pouch cell to active material level. J. Power Sources 2022, 537, 231443. [Google Scholar] [CrossRef]
- Spingler, F.B.; Kücher, S.; Phillips, R.; Moyassari, E.; Jossen, A. Electrochemically Stable In Situ Dilatometry of NMC, NCA and Graphite Electrodes for Lithium-Ion Cells Compared to XRD Measurements. J. Electrochem. Soc. 2021, 168, 040515. [Google Scholar] [CrossRef]
- Aufschläger, A.; Kücher, S.; Kraft, L.; Spingler, F.; Niehoff, P.; Jossen, A. High precision measurement of reversible swelling and electrochemical performance of flexibly compressed 5Ah NMC622/graphite lithium-ion pouch cells. J. Energy Storage 2023, 59, 106483. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. State of health and charge measurements in lithium-ion batteries using mechanical stress. J. Power Sources 2014, 269, 7–14. [Google Scholar] [CrossRef]
- Sauerteig, D.; Ivanov, S.; Reinshagen, H.; Bund, A. Reversible and irreversible dilation of lithium-ion battery electrodes investigated by in-situ dilatometry. J. Power Sources 2017, 342, 939–946. [Google Scholar] [CrossRef]
- Ivanov, S.; Sauerteig, D.; Dimitrova, A.; Krischok, S.; Bund, A. Irreversible dilation of graphite composite anodes influenced by vinylene carbonate. J. Power Sources 2020, 457, 228020. [Google Scholar] [CrossRef]
- Louli, A.J.; Ellis, L.D.; Dahn, J.R. Operando Pressure Measurements Reveal Solid Electrolyte Interphase Growth to Rank Li-Ion Cell Performance. Joule 2018, 3, 745–761. [Google Scholar] [CrossRef]
- Bitzer, B.; Gruhle, A. A new method for detecting lihium plating by measuring the cell thickness. J. Power Sources 2014, 262, 297–302. [Google Scholar] [CrossRef]
- Adam, A.; Wandt, J.; Knobbe, E.; Bauer, G.; Kwade, A. Fast-Charging of Automotive Lithium-Ion Cells: In-Situ Lithium-Plating Detection and Comparison of Different Cell Designs. J. Electrochem. Soc. 2020, 167, 130503. [Google Scholar] [CrossRef]
- Zhao, Y.; Spingler, F.B.; Patel, Y.; Offer, G.J.; Jossen, A. Localized Swelling Inhomogeneity Detection in Lithium Ion Cells Using Multi-Dimensional Laser Scanning. J. Electrochem. Soc. 2019, 166, A27–A34. [Google Scholar] [CrossRef]
- Li, J.; Dozier, A.K.; Li, Y.; Yang, F.; Cheng, Y.-T. Crack Pattern Formation in Thin Film Lithium-Ion Battery Electrodes. J. Electrochem. Soc. 2011, 158, A689–A694. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Li, T.; Yuan, X.-Z.; Zhang, L.; Song, D.; Shi, K.; Bock, C. Degradation Mechanisms and Mitigation Strategies of Nickel-Rich NMC-Based Lithium-Ion Batteries. Electrochem. Energy Rev. 2020, 3, 43–80. [Google Scholar] [CrossRef]
- Lin, N.; Jia, Z.; Wang, Z.; Zhao, H.; Ai, G.; Song, X.; Bai, Y.; Battaglia, V.; Sun, C.; Qiao, J.; et al. Understanding the crack formation of graphite particles in cycled commercial lithium-ion batteries by focused ion beam–scanning electron microscopy. J. Power Sources 2017, 365, 235–239. [Google Scholar] [CrossRef]
- Leonard, A.; Planden, B.; Lukow, K.; Morrey, D. Investigation of constant stack pressure on lithium-ion battery performance. J. Energy Storage 2023, 72, 108422. [Google Scholar] [CrossRef]
- Attia, P.M.; Bills, A.; Planella, F.B.; Dechent, P.; Dos Reis, G.; Dubarry, M.; Gasper, P.; Gilchrist, R.; Greenbank, S.; Howey, D.; et al. Review—“Knees” in Lithium-Ion Battery Aging Trajectories. J. Electrochem. Soc. 2022, 169, 060517. [Google Scholar] [CrossRef]
- Bach, T.C.; Schuster, S.F.; Fleder, E.; Müller, J.; Brand, M.J.; Lorrmann, H.; Jossen, A.; Sextl, G. Nonlinear aging of cylindrical lithium-ion cells linked to heterogeneous compression. J. Energy Storage 2016, 5, 212. [Google Scholar] [CrossRef]
- Müller, V.; Scurtu, R.-G.; Memm, M.; Danzer, M.A.; Wohlfahrt-Mehrens, M. Study of the influence of mechanical pressure on the performance and aging of Lithium-ion battery cells. J. Power Sources 2019, 440, 227148. [Google Scholar] [CrossRef]
- Deich, T.; Hahn, S.L.; Both, S.; Birke, K.P.; Bund, A. Validation of an actively-controlled pneumatic press to simulate automotive module stiffness for mechanically representative lithium-ion cell aging. J. Energy Storage 2020, 28, 101192. [Google Scholar] [CrossRef]
- Jeong, J.; Kwak, E.; Kim, J.-H.; Oh, K.-Y. Novel active management of compressive pressure on a lithium-ion battery using a phase transition actuator. Energy Rep. 2022, 8, 10762–10775. [Google Scholar] [CrossRef]
- Rieger, B.; Schlueter, S.; Erhard, S.V.; Schmalz, J.; Reinhart, G.; Jossen, A. Multi-scale investigation of thickness changes in a commercial pouch type lithium-ion battery. J. Energy Storage 2016, 6, 213–221. [Google Scholar] [CrossRef]
- Ebert, F.; Spielbauer, M.; Bruckmoser, M.; Lienkamp, M. Simulation of spatial strain inhomogeneities in lithium-ion-cells due to electrode dilation dependent on internal and external cell structures. J. Energy Storage 2022, 49, 104143. [Google Scholar] [CrossRef]
- Daubinger, P.; Göttlinger, M.; Hartmann, S.; Giffin, G.A. Consequences of Different Pressures and Electrolytes on the Irreversible Expansion of Lithium Metal Half Cells. Batter. Supercaps 2023, 6, e202200452. [Google Scholar] [CrossRef]
- von Kessel, O.; Deich, T.; Hahn, S.; Brauchle, F.; Vrankovic, D.; Soczka-Guth, T.; Birke, K.P. Mechanical impedance as a tool for electromechanical investigation and equivalent modeling of lithium-ion batteries. J. Power Sources 2021, 508, 230337. [Google Scholar] [CrossRef]
- Sauerteig, D.; Hanselmann, N.; Arzberger, A.; Reinshagen, H.; Ivanov, S.; Bund, A. Electrochemical-mechanical coupled modeling and parameterization of swelling and ionic transport in lithium-ion batteries. J. Power Sources 2018, 378, 235–247, ISSN 0378-7753. [Google Scholar] [CrossRef]
- Feiler, S.; Daubinger, P.; Gold, L.; Hartmann, S.; Giffin, G.A. Interplay between Elastic and Electrochemical Properties during Active Material Transitions and Aging of a Lithium-Ion Battery. Batter. Supercaps 2023, 6, e202200518. [Google Scholar] [CrossRef]
- Fill, A.; Avdyli, A.; Birke, K.P. Online Data-based Cell State Estimation of a Lithium-Ion Battery. In Proceedings of the 2020 2nd IEEE International Conference on Industrial Electronics for Sustainable Energy Systems (IESES), Cagliari, Italy, 1–3 September 2020; pp. 351–356. [Google Scholar]
- Avdyli, A.; Fill, A.; Birke, K.P. Statistical approach for continuous internal resistance estimation of lithium ion cells under dynamic loads. In Proceedings of the 2022 IEEE 21st Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 14–16 June 2022; pp. 189–194. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).