IBM Quantum Platforms: A Quantum Battery Perspective
Abstract
:1. Introduction
2. Model
3. Calibration
4. Results
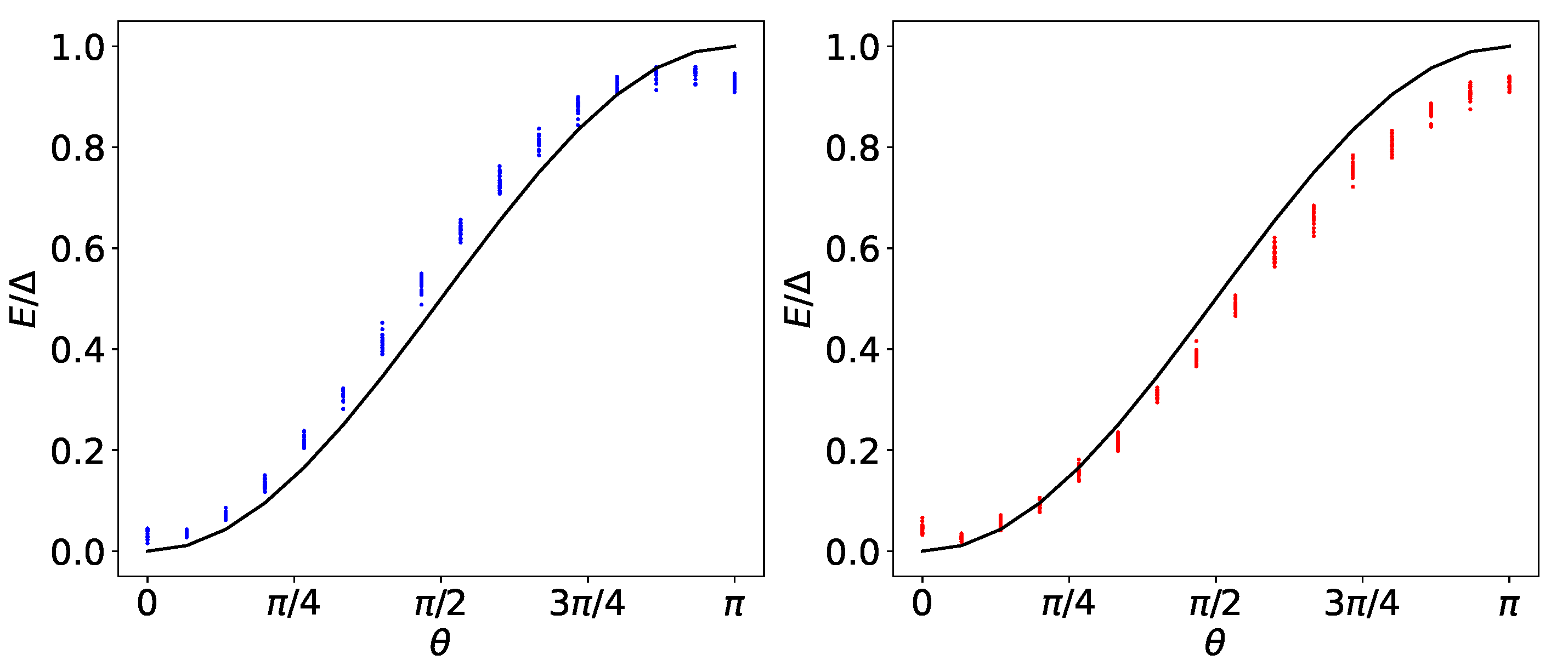
4.1. Universal Charging Behavior and Technical Constraints on the Pulses
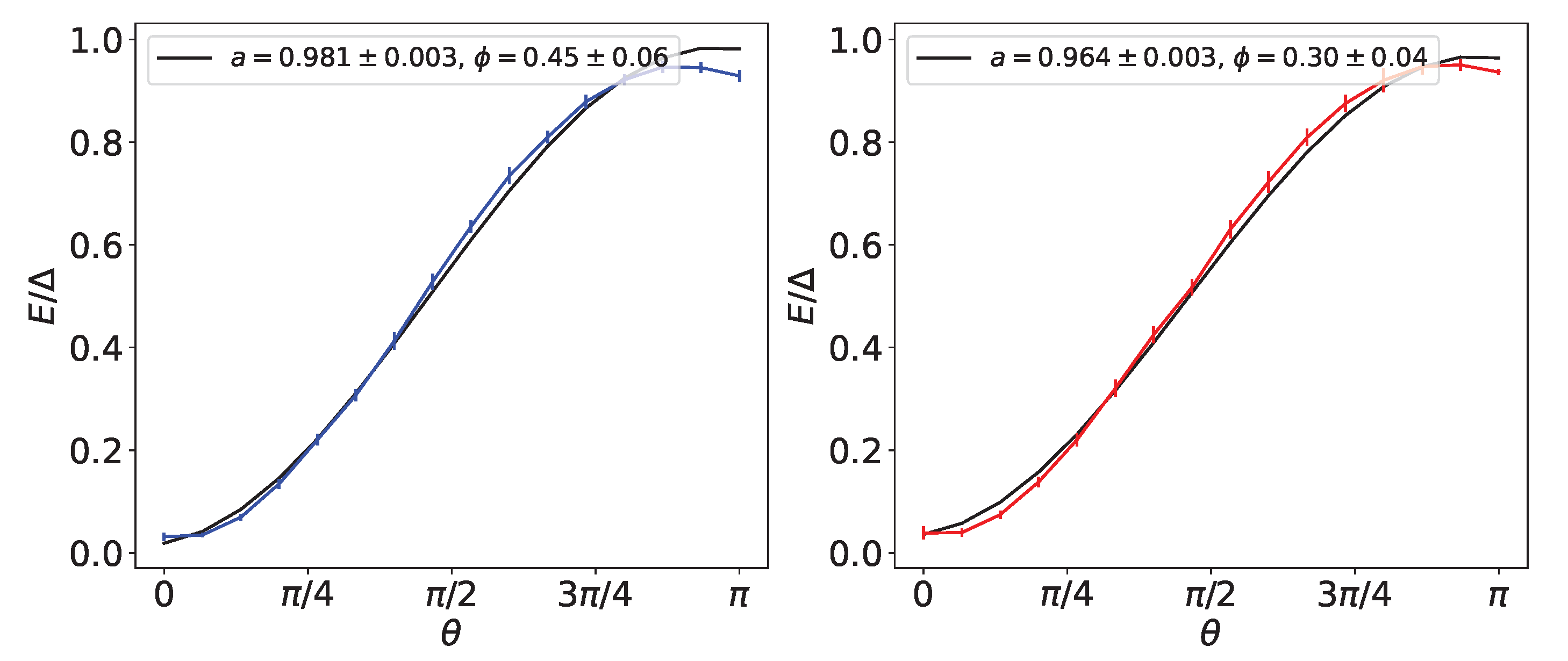
4.2. Best Fit of the Data and Characterization of the QB Performances
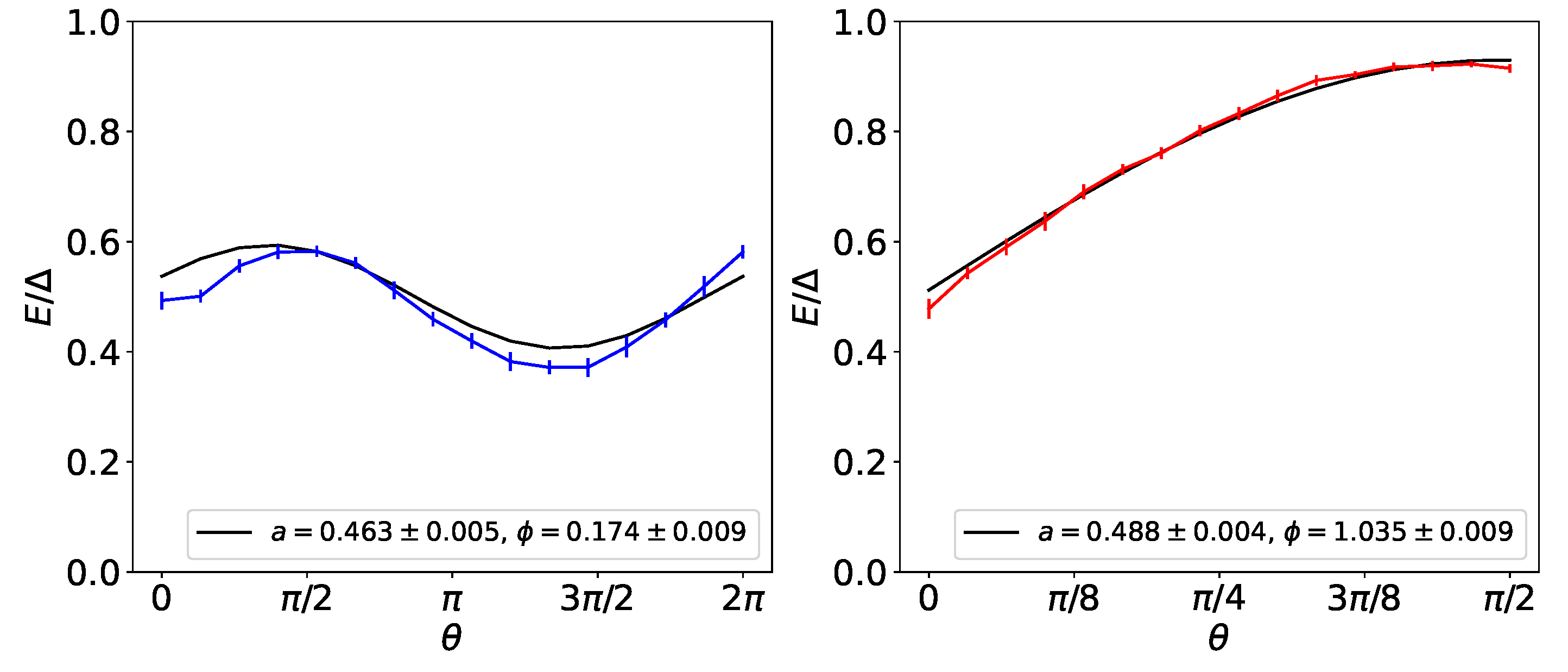
4.3. More General Initial Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| QB | Quantum Battery |
Nomenclature
| Level spacing of the qubit | |
| g | Qubit–radiation coupling |
| Envelop of the applied pulse | |
| Frequency of the modulating cosine | |
| Effective integral of the pulse | |
| Measurement time | |
| a | Ground-state probability at |
| Relative phase at |
References
- Bhattacharjee, S.; Dutta, A. Quantum thermal machines and batteries. Eur. Phys. J. B 2021, 94, 239. [Google Scholar] [CrossRef]
- Vincent, C.A.; Scrosati, B. Modern Batteries; Butterworth-Heinemann: Oxford, UK, 1997. [Google Scholar]
- Dell, R.M.; Rand, D.A.J. Understanding Batteries; The Royal Society of Chemistry: Cambridge, UK, 2001. [Google Scholar]
- Campaioli, F.; Pollock, F.A.; Vinjanampathy, S. Thermodynamics in the Quantum Regime; Springer: Berlin, Germany, 2018. [Google Scholar]
- Alicki, R.; Fannes, M. Entanglement boost for extractable work from ensembles of quantum batteries. Phys. Rev. E 2013, 87, 042123. [Google Scholar] [CrossRef] [Green Version]
- Binder, F.C.; Vinjanampathy, S.; Modi, K.; Goold, J. Quantacell: Powerful charging of quantum batteries. New J. Phys. 2015, 17, 075015. [Google Scholar] [CrossRef] [Green Version]
- Campaioli, F.; Pollock, F.A.; Binder, F.C.; Céleri, L.; Goold, J.; Vinjanampathy, S.; Modi, K. Enhancing the Charging Power of Quantum Batteries. Phys. Rev. Lett. 2017, 118, 150601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Julià-Farré, S.; Salamon, T.; Riera, A.; Bera, M.N.; Lewenstein, M. Bounds on the capacity and power of quantum batteries. Phys. Rev. Res. 2020, 2, 023113. [Google Scholar] [CrossRef]
- Gyhm, J.-Y.; Safránek, D.; Rosa, D. Quantum Charging Advantage Cannot Be Extensive without Global Operations. Phys. Rev. Lett. 2022, 128, 140501. [Google Scholar] [CrossRef]
- Le, T.P.; Levinsen, J.; Modi, K.; Parish, M.M.; Pollock, F.A. Spin-chain model of a many-body quantum battery. Phys. Rev. A 2018, 97, 022106. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Segal, D.; Hanna, G. A loss-free excitonic quantum battery. J. Phys. Chem. C 2019, 123, 18303. [Google Scholar] [CrossRef]
- Rossini, D.; Andolina, G.M.; Rosa, D.; Carrega, M.; Polini, M. Quantum Advantage in the Charging Process of Sachdev-Ye-Kitaev Batteries. Phys. Rev. Lett. 2020, 125, 236402. [Google Scholar] [CrossRef]
- Rosa, D.; Rossini, D.; Andolina, G.M.; Polini, M.; Carrega, M. Ultra-stable charging of fast-scrambling SYK quantum batteries. J. High Energy Phys. 2020, 67, 2020. [Google Scholar] [CrossRef]
- Crescente, A.; Carrega, M.; Sassetti, M.; Ferraro, D. Charging and energy fluctuations of a driven quantum battery. New J. Phys. 2020, 22, 063057. [Google Scholar] [CrossRef]
- Santos, A.C. Quantum advantage of a two-level batteries in self-discharging process. Phys. Rev. E 2021, 103, 042118. [Google Scholar] [CrossRef] [PubMed]
- Peng, L.; He, W.-B.; Chesi, S.; Lin, H.-Q.; Guan, X.-W. Lower and upper bounds of quantum battery power in multiple central spin systems. Phys. Rev. A 2021, 103, 052220. [Google Scholar] [CrossRef]
- Dou, F.-Q.; Lu, Y.-Q.; Wang, Y.-J.; Sun, J.-A. Extended Dicke quantum battery with interatomic interactions and driving field. Phys. Rev. B 2022, 105, 115405. [Google Scholar] [CrossRef]
- Shaghaghi, V.; Singh, V.; Benenti, G.; Rosa, D. Micromasers as Quantum Batteries. arXiv 2022, arXiv:2204.09995. [Google Scholar]
- Ferraro, D.; Andolina, G.M.; Campisi, M.; Pellegrini, V.; Polini, M. Quantum supercapacitors. Phys. Rev. B 2019, 100, 075433. [Google Scholar] [CrossRef] [Green Version]
- Quach, J.Q.; McGhee, K.E.; Ganzer, L.; Rouse, D.M.; Lovett, B.W.; Gauger, E.M.; Keeling, J.; Cerullo, G.; Lidzey, D.G.; Virgili, T. Superabsorption in an organic microcavity: Toward a quantum battery. Sci. Adv. 2022, 8, eabk3160. [Google Scholar] [CrossRef]
- Hu, C.-K.; Qiu, J.; Souza, P.J.P.; Yuan, J.; Zhou, Y.; Zhang, L.; Chu, J.; Pan, X.; Hu, L.; Li, J.; et al. Optimal charging of a superconducting quantum battery. arXiv 2021, arXiv:2108.04298. [Google Scholar]
- De Buy Wenniger, I.M.; Thomas, S.E.; Maffei, M.; Wein, S.C.; Pont, M.; Harouri, A.; Lemaitre, A.; Sagnes, I.; Somaschi, N.; Auffèves, A.; et al. Coherence-powered work exchanges between a solid-state qubit and light fields. arXiv 2022, arXiv:2202.01109. [Google Scholar]
- Andolina, G.M.; Farina, D.; Mari, A.; Pellegrini, V.; Giovannetti, V.; Polini, M. Charger-mediated energy transfer in exactly solvable models for quantum batteries. Phys. Rev. B 2018, 98, 205423. [Google Scholar] [CrossRef] [Green Version]
- Qi, S.-F.; Jing, J. Magnon-mediated quantum battery under systematic errors. Phys. Rev. A 2021, 104, 032606. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Yang, T.-R.; Fu, L.; Wang, X. Powerful harmonic charging in a quantum battery. Phys. Rev. E 2019, 99, 052106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Zhan, L.; Shao, L.; Zhang, X.; Zhang, Y.-Y.; Wang, X. Charging Quantum Batteries with a General Harmonic Driving Field. Ann. Phys. 2020, 532, 1900487. [Google Scholar] [CrossRef]
- Córcoles, A.D.; Kandala, A.; Javadi-Abhari, A.; McClure, D.T.; Cross, A.W.; Temme, K.; Nation, P.D.; Steffen, M.; Gambetta, J.M. Challenges and Opportunities of Near-Term Quantum Computing Systems. Proc. IEEE 2020, 108, 1338. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.D.; et al. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 19. [Google Scholar] [CrossRef] [Green Version]
- Guimaraes, J.D.; Tavares, C.; Soares, L.; Vasilevskiy, M.I. Simulation of Nonradiative Energy Transfer in Photosynthetic Systems Using a Quantum Computer. Complexity 2020, 2020, 3510676. [Google Scholar] [CrossRef]
- Chiesa, A.; Tacchino, F.; Grossi, M.; Santini, P.; Tavernelli, I.; Gerace, D.; Carretta, S. Quantum hardware simulating four-dimensional inelastic neutron scattering. Nat. Phys. 2019, 15, 5. [Google Scholar] [CrossRef]
- Fillion-Gourdeau, F.; MacLean, S.; Laflamme, R. Algorithm for the solution of the Dirac equation on digital quantum computers. Phys. Rev. A 2017, 95, 4. [Google Scholar] [CrossRef] [Green Version]
- Klco, N.; Savage, M.J.; Stryker, J.R. SU(2) non-Abelian gauge field theory in one dimension on digital quantum computers. Phys. Rev. D 2020, 101, 7. [Google Scholar] [CrossRef] [Green Version]
- Nachman, B.; Provasoli, D.; de Jong, W.A.; Bauer, C.W. Quantum Algorithm for High Energy Physics Simulations. Phys. Rev. Lett. 2021, 126, 6. [Google Scholar] [CrossRef]
- Agliardi, G.; Grossi, M.; Pellen, M.; Prati, E. Quantum integration of elementary particle processes. arXiv 2022, arXiv:2201.01547. [Google Scholar]
- Cervia, J.C.; Balantekin, A.B.; Coppersmith, S.N.; Johnson, C.W.; Love, P.J.; Poole, C.; Robbins, K.; Saffman, M. Exactly solvable model as a testbed for quantum-enhanced dark matter detection. arXiv 2020, arXiv:2201.01547. [Google Scholar]
- Herman, D.; Googin, C.; Liu, X.; Galda, A.; Safro, I.; Sun, Y.; Pistoia, M.; Alexeev, Y. A Survey of Quantum Computing for Finance. arXiv 2022, arXiv:2201.02773. [Google Scholar]
- Gao, Q.; Jones, G.O.; Motta, M.; Sugawara, M.; Watanabe, H.C.; Kobayashi, T.; Watanabe, E.; Ohnishi, Y.; Nakamura, H.; Yamamoto, N. Applications of quantum computing for investigations of electronic transitions in phenylsulfonyl-carbazole TADF emitters. NPJ Comput. Mater. 2021, 7, 70. [Google Scholar] [CrossRef]
- Moll, N.; Barkoutsos, P.; Bishop, L.S.; Chow, J.M.; Cross, A.; Egger, D.J.; Filipp, S.; Fuhrer, A.; Gambetta, J.M.; Ganzhorn, M.; et al. Quantum optimization using variational algorithms on near-term quantum devices. Quantum Sci. Technol. 2018, 3, 030503. [Google Scholar] [CrossRef]
- Alexander, T.; Kanazawa, N.; Egger, D.J.; Capelluto, L.; Wood, C.J.; Javadi-Abhari, A.; McKay, D.C. Qiskit pulse: Programming quantum computers through the cloud with pulses. Quantum Sci. Technol. 2020, 5, 044006. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Koch, J.; Yu, T.M.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 2007, 76, 042319. [Google Scholar] [CrossRef] [Green Version]
- Schleich, W.P. Quantum Optics in Phase Space; Wiley VCH: Berlin, Germany, 2021. [Google Scholar]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A Quantum Engineer’s Guide to Superconducting Qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Jeffrey, E.; Sank, D.; Mutus, J.Y.; White, T.C.; Kelly, J.; Barends, R.; Chen, Y.; Chen, Z.; Chiaro, B.; Dunsworth, A.; et al. Fast Accurate State Measurement with Superconducting Qubits. Phys. Rev. Lett. 2014, 112, 190504. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gemme, G.; Grossi, M.; Ferraro, D.; Vallecorsa, S.; Sassetti, M. IBM Quantum Platforms: A Quantum Battery Perspective. Batteries 2022, 8, 43. https://doi.org/10.3390/batteries8050043
Gemme G, Grossi M, Ferraro D, Vallecorsa S, Sassetti M. IBM Quantum Platforms: A Quantum Battery Perspective. Batteries. 2022; 8(5):43. https://doi.org/10.3390/batteries8050043
Chicago/Turabian StyleGemme, Giulia, Michele Grossi, Dario Ferraro, Sofia Vallecorsa, and Maura Sassetti. 2022. "IBM Quantum Platforms: A Quantum Battery Perspective" Batteries 8, no. 5: 43. https://doi.org/10.3390/batteries8050043
APA StyleGemme, G., Grossi, M., Ferraro, D., Vallecorsa, S., & Sassetti, M. (2022). IBM Quantum Platforms: A Quantum Battery Perspective. Batteries, 8(5), 43. https://doi.org/10.3390/batteries8050043






