A Method for Detecting the Existence of an Over-Discharged Cell in a Lithium-Ion Battery Pack via Measuring Total Harmonic Distortion
Abstract
:1. Introduction
1.1. Definition of Key Terms
1.1.1. Definition of SoC
1.1.2. Definition of SoH
2. Simulation and Measurement
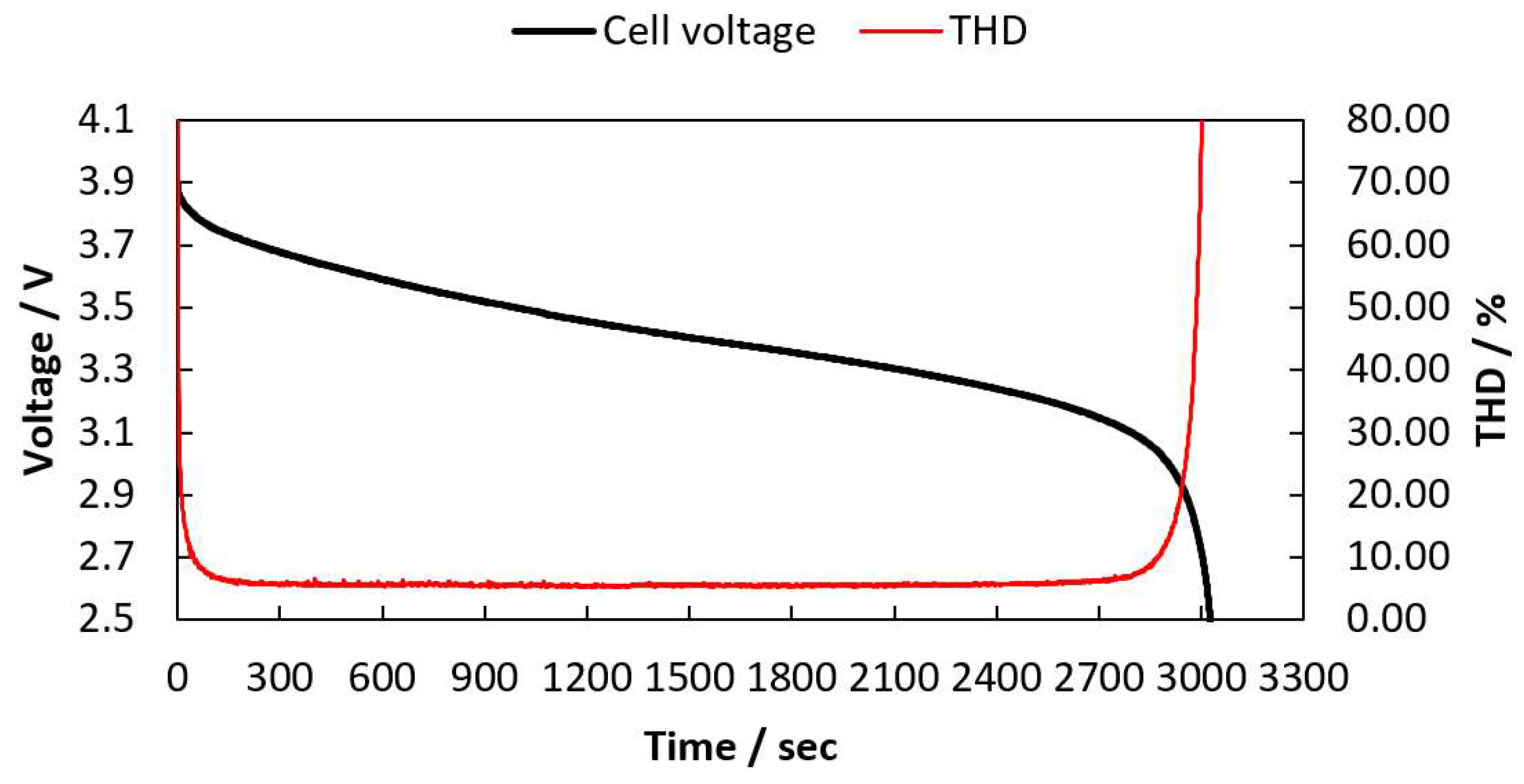
2.1. THD Simulation of a LIB Cell Being Discharged
2.2. THD Measurement of a LIB Cell Being Discharged
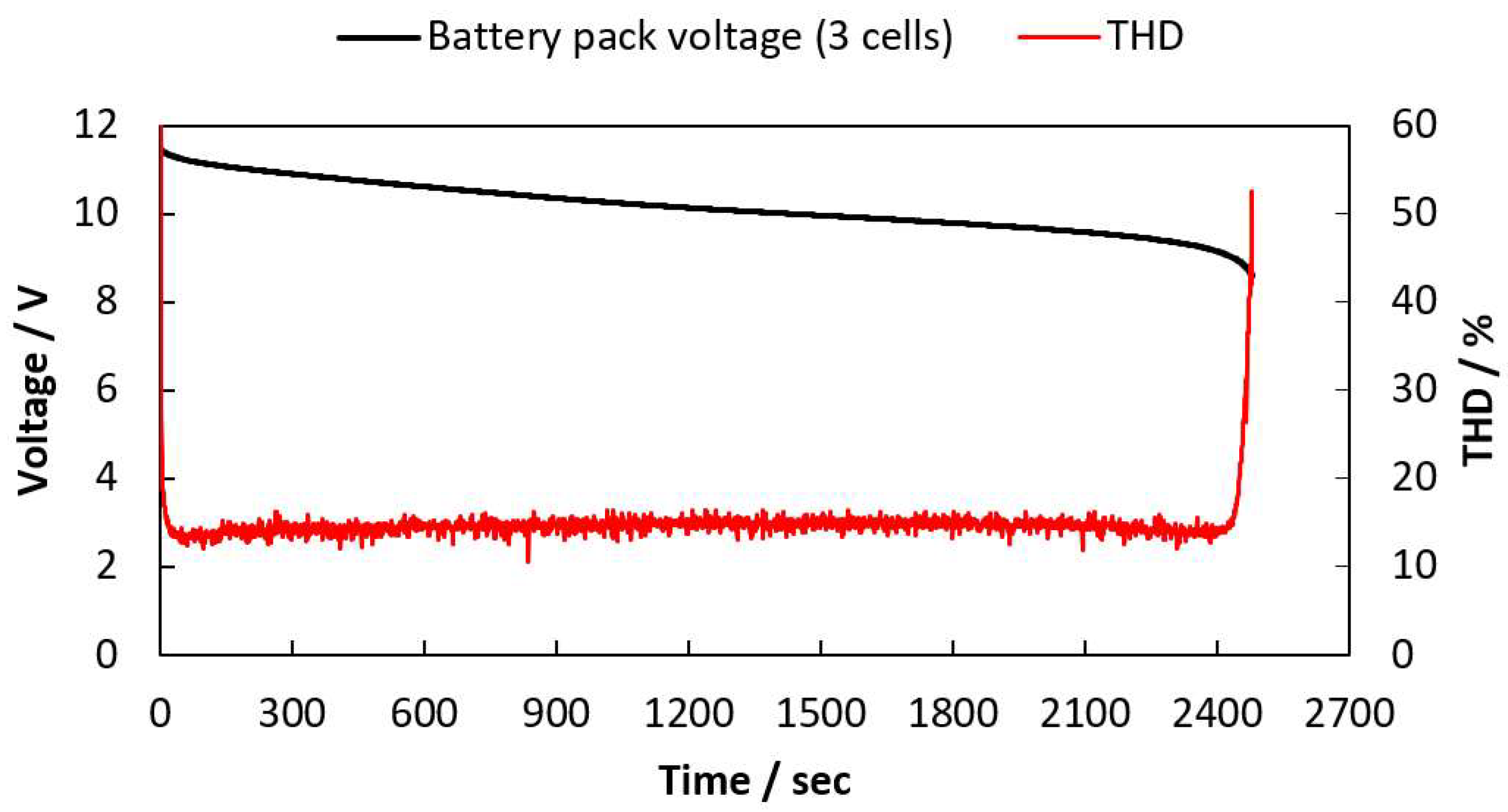
2.3. THD Measurement of a LIB Pack Being Discharged
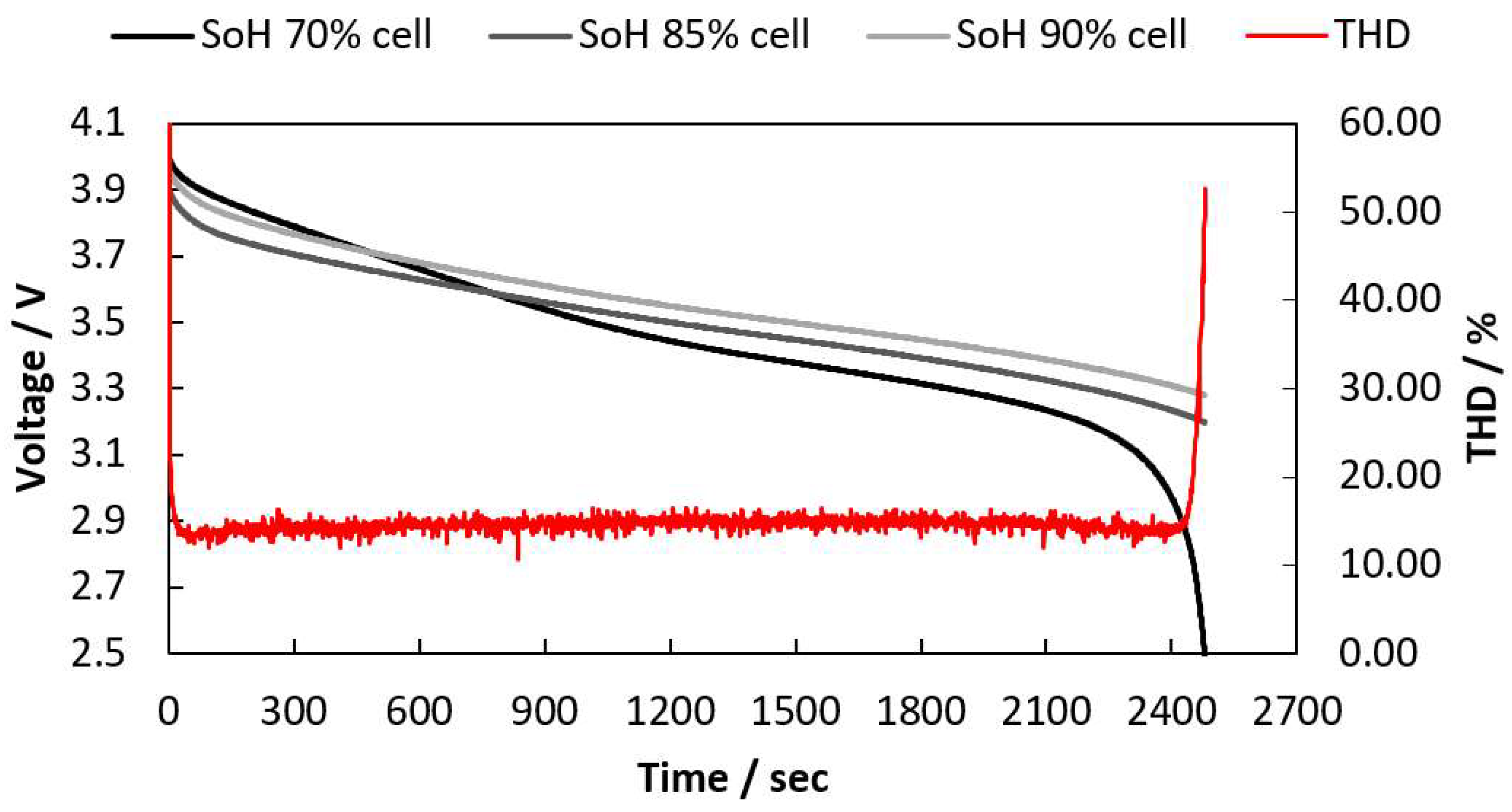
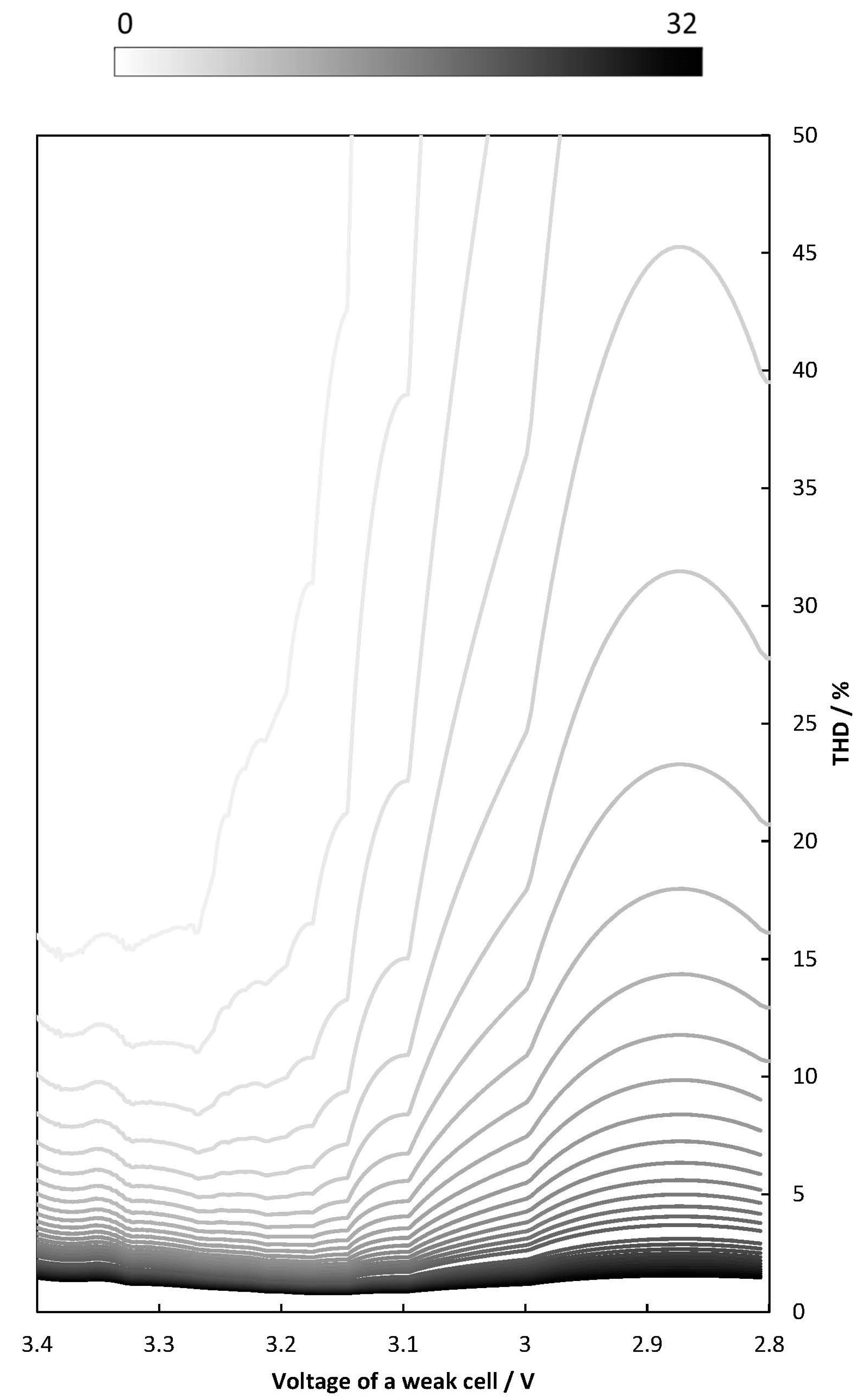
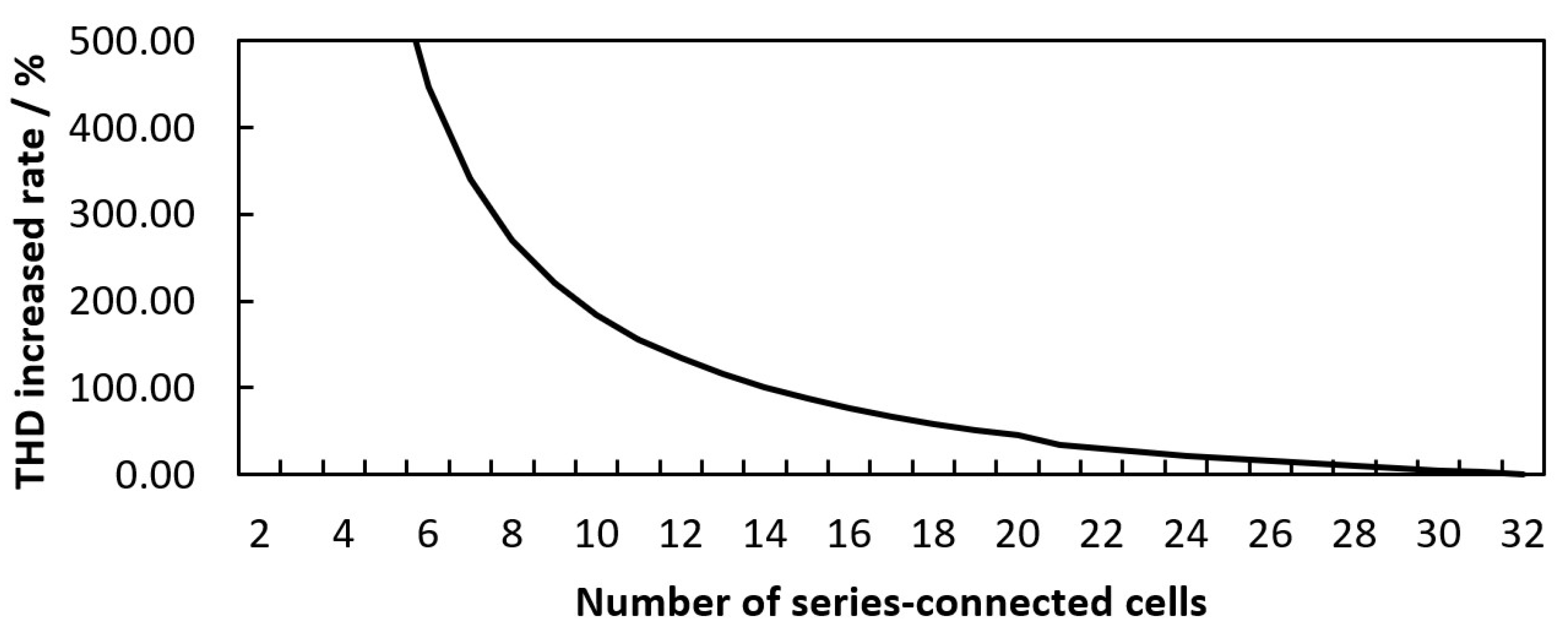
2.4. THD Simulation of LIB Packs with Different Numbers of Cells Are Connected
3. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goodenough, J.B.; Kim, Y. Challenges for rechargeable batteries. J. Power Sources 2011, 196, 6688–6694. [Google Scholar] [CrossRef]
- Mousavi, G.S.M. An autonomous hybrid energy system of wind/tidal/microturbine/battery storage. Int. J. Electr. Power Energy Syst. 2012, 43, 1144–1154. [Google Scholar] [CrossRef]
- Zhou, Z.; Benbouzid, M.; Frédéric Charpentier, J.; Scuiller, F.; Tang, T. A review of energy storage technologies for marine current energy systems. Renew. Sustain. Energy Rev. 2013, 18, 390–400. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A review of lithium-ion battery safety concerns: The issues, strategies, and testing standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; Liaw, B.Y. Cell-balancing currents in parallel strings of a battery system. J. Power Sources 2016, 321, 36–46. [Google Scholar] [CrossRef] [Green Version]
- Qi, G.; Li, X.; Yang, D. A Control Strategy for Dynamic Balancing of Lithium Iron Phosphate Battery Based on the Performance of Cell Voltage. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5, ISBN 978-1-4799-4239-8. [Google Scholar]
- Bruen, T.; Marco, J.; Gama, M. Model Based Design of Balancing Systems for Electric Vehicle Battery Packs. IFAC-PapersOnLine 2015, 48, 395–402. [Google Scholar] [CrossRef]
- Lin, J.-C. Development of a New Battery Management System with an Independent Balance Module for Electrical Motorcycles. Energies 2017, 10, 1289. [Google Scholar] [CrossRef] [Green Version]
- Yusof, M.S.; Toha, S.F.; Kamisan, N.; Hashim, N.; Abdullah, M.A. Battery Cell Balancing Optimisation for Battery Management System. IOP Conf. Ser. Mater. Sci. Eng. 2017, 184, 12021. [Google Scholar] [CrossRef]
- Gallardo-Lozano, J.; Romero-Cadaval, E.; Milanes-Montero, M.I.; Guerrero-Martinez, M.A. Battery equalization active methods. J. Power Sources 2014, 246, 934–949. [Google Scholar] [CrossRef]
- Gallardo-Lozano, J.; Romero-Cadaval, E.; Milanes-Montero, M.I.; Guerrero-Martinez, M.A. A novel active battery equalization control with on-line unhealthy cell detection and cell change decision. J. Power Sources 2015, 299, 356–370. [Google Scholar] [CrossRef]
- Bouchhima, N.; Schnierle, M.; Schulte, S.; Birke, K.P. Active model-based balancing strategy for self-reconfigurable batteries. J. Power Sources 2016, 322, 129–137. [Google Scholar] [CrossRef]
- Williard, N.; He, W.; Hendricks, C.; Pecht, M. Lessons Learned from the 787 Dreamliner Issue on Lithium-Ion Battery Reliability. Energies 2013, 6, 4682–4695. [Google Scholar] [CrossRef] [Green Version]
- Orcioni, S.; Ricci, A.; Buccolini, L.; Scavongelli, C.; Conti, M. Effects of variability of the characteristics of single cell on the performance of a lithium-ion battery pack. In Proceedings of the 2017 13th Workshop on Intelligent Solutions in Embedded Systems (WISES), Hamburg, Germany, 12–13 June 2017; pp. 15–21, ISBN 978-1-5386-1157-9. [Google Scholar]
- Hoque, M.M.; Hannan, M.A.; Mohamed, A. Voltage equalization control algorithm for monitoring and balancing of series connected lithium-ion battery. J. Renew. Sustain. Energy 2016, 8, 25703. [Google Scholar] [CrossRef]
- Han, W.; Zhang, L. Mathematical analysis and coordinated current allocation control in battery power module systems. J. Power Sources 2017, 372, 166–179. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D.U. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Gao, F.; Tang, Z. Kinetic behavior of LiFePO4/C cathode material for lithium-ion batteries. Electrochim. Acta 2008, 53, 5071–5075. [Google Scholar] [CrossRef]
- Hung, M.-H.; Lin, C.-H.; Lee, L.-C.; Wang, C.-M. State-of-charge and state-of-health estimation for lithium-ion batteries based on dynamic impedance technique. J. Power Sources 2014, 268, 861–873. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Momma, T.; Matsunaga, M.; Mukoyama, D.; Osaka, T. Ac impedance analysis of lithium ion battery under temperature control. J. Power Sources 2012, 216, 304–307. [Google Scholar] [CrossRef]
- Tröltzsch, U.; Kanoun, O.; Tränkler, H.-R. Characterizing aging effects of lithium ion batteries by impedance spectroscopy. Electrochim. Acta 2006, 51, 1664–1672. [Google Scholar] [CrossRef]
- Buller, S.; Thele, M.; Karden, E.; de Doncker, R.W. Impedance-based non-linear dynamic battery modeling for automotive applications. J. Power Sources 2003, 113, 422–430. [Google Scholar] [CrossRef]
- Osaka, T.; Mukoyama, D.; Nara, H. Review—Development of Diagnostic Process for Commercially Available Batteries, Especially Lithium Ion Battery, by Electrochemical Impedance Spectroscopy. J. Electrochem. Soc. 2015, 162, A2529–A2537. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, C.; Wen, G. Equivalent circuit model analysis on electrochemical impedance spectroscopy of lithium metal batteries. J. Power Sources 2015, 294, 67–74. [Google Scholar] [CrossRef]
- Mingant, R.; Bernard, J.; Sauvant Moynot, V.; Delaille, A.; Mailley, S.; Hognon, J.-L.; Huet, F. EIS Measurements for Determining the SoC and SoH of Li-Ion Batteries. ECS Trans. 2011, 33, 41–53. [Google Scholar] [CrossRef]
- Howey, D.A.; Yufit, V.; Mitcheson, P.D.; Offer, G.J.; Brandon, N.P. Impedance measurement for advanced battery management systems. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; pp. 1–7, ISBN 978-1-4799-3832-2. [Google Scholar]
- Kim, J.; Krüger, L.; Kowal, J. On-line state-of-health estimation of Lithium-ion battery cells using frequency excitation. J. Energy Storage 2020, 32, 101841. [Google Scholar] [CrossRef]
- Kim, J.; Kowal, J. Development of a Matlab/Simulink Model for Monitoring Cell State-of-Health and State-of-Charge via Impedance of Lithium-Ion Battery Cells. Batteries 2022, 8, 8. [Google Scholar] [CrossRef]
- Abu Qahouq, J.A. Online battery impedance spectrum measurement method. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 3611–3615, ISBN 978-1-4673-8393-6. [Google Scholar]
- Waag, W.; Fleischer, C.; Sauer, D.U. On-line estimation of lithium-ion battery impedance parameters using a novel varied-parameters approach. J. Power Sources 2013, 237, 260–269. [Google Scholar] [CrossRef]
- Huang, W.; Qahouq, J.A. An Online Battery Impedance Measurement Method Using DC–DC Power Converter Control. IEEE Trans. Ind. Electron. 2014, 61, 5987–5995. [Google Scholar] [CrossRef]
- Howey, D.A.; Mitcheson, P.D.; Yufit, V.; Offer, G.J.; Brandon, N.P. Online Measurement of Battery Impedance Using Motor Controller Excitation. IEEE Trans. Veh. Technol. 2014, 63, 2557–2566. [Google Scholar] [CrossRef]
- Mog, G.E.; Ribeiro, E.P. Total harmonic distortion calculation by filtering for power quality monitoring. In Proceedings of the 2004 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America (IEEE Cat. No. 04EX956), Sao Paulo, Brazil, 8–11 November 2004; pp. 629–632, ISBN 0-7803-8775-9. [Google Scholar]
- Giner-Sanz, J.J.; Ortega, E.M.; Pérez-Herranz, V. Total harmonic distortion based method for linearity assessment in electrochemical systems in the context of EIS. Electrochim. Acta 2015, 186, 598–612. [Google Scholar] [CrossRef] [Green Version]
- Kiel, M.; Bohlen, O.; Sauer, D.U. Harmonic analysis for identification of nonlinearities in impedance spectroscopy. Electrochim. Acta 2008, 53, 7367–7374. [Google Scholar] [CrossRef]
- Mao, Q.; Krewer, U. Total harmonic distortion analysis of oxygen reduction reaction in proton exchange membrane fuel cells. Electrochim. Acta 2013, 103, 188–198. [Google Scholar] [CrossRef]
- Ramschak, E.; Peinecke, V.; Prenninger, P.; Schaffer, T.; Baumgartner, W.; Hacker, V. Online stack monitoring tool for dynamically and stationary operated fuel cell systems. Fuel Cells Bull. 2006, 2006, 12–15. [Google Scholar] [CrossRef]
- Kadyk, T.; Hanke-Rauschenbach, R.; Sundmacher, K. Nonlinear frequency response analysis of PEM fuel cells for diagnosis of dehydration, flooding and CO-poisoning. J. Electroanal. Chem. 2009, 630, 19–27. [Google Scholar] [CrossRef]
- Wong, D.K.Y.; MacFarlane, D.R. Harmonic impedance spectroscopy. Theory and experimental results for reversible and quasi-reversible redox systems. J. Phys. Chem. 1995, 99, 2134–2142. [Google Scholar] [CrossRef]
- Mao, Q.; Krewer, U. Sensing methanol concentration in direct methanol fuel cell with total harmonic distortion: Theory and application. Electrochim. Acta 2012, 68, 60–68. [Google Scholar] [CrossRef]
- Mao, Q.; Krewer, U.; Hanke-Rauschenbach, R. Total harmonic distortion analysis for direct methanol fuel cell anode. Electrochem. Commun. 2010, 12, 1517–1519. [Google Scholar] [CrossRef]
- Okazaki, S.; Higuchi, S.; Takahashi, S. Second-Order Harmonic in the Current Response to Sinusoidal Perturbation Voltage for Lead-Acid Battery: An Application to a State-of-Charge Indicator. J. Electrochem. Soc. 1985, 132, 1516–1520. [Google Scholar] [CrossRef]
- Harting, N.; Wolff, N.; Röder, F.; Krewer, U. Nonlinear Frequency Response Analysis (NFRA) of Lithium-Ion Batteries. Electrochim. Acta 2017, 248, 133–139. [Google Scholar] [CrossRef]
- Bagotsky, V.S. Fundamentals of Electrochemistry, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-471-70058-6. [Google Scholar]
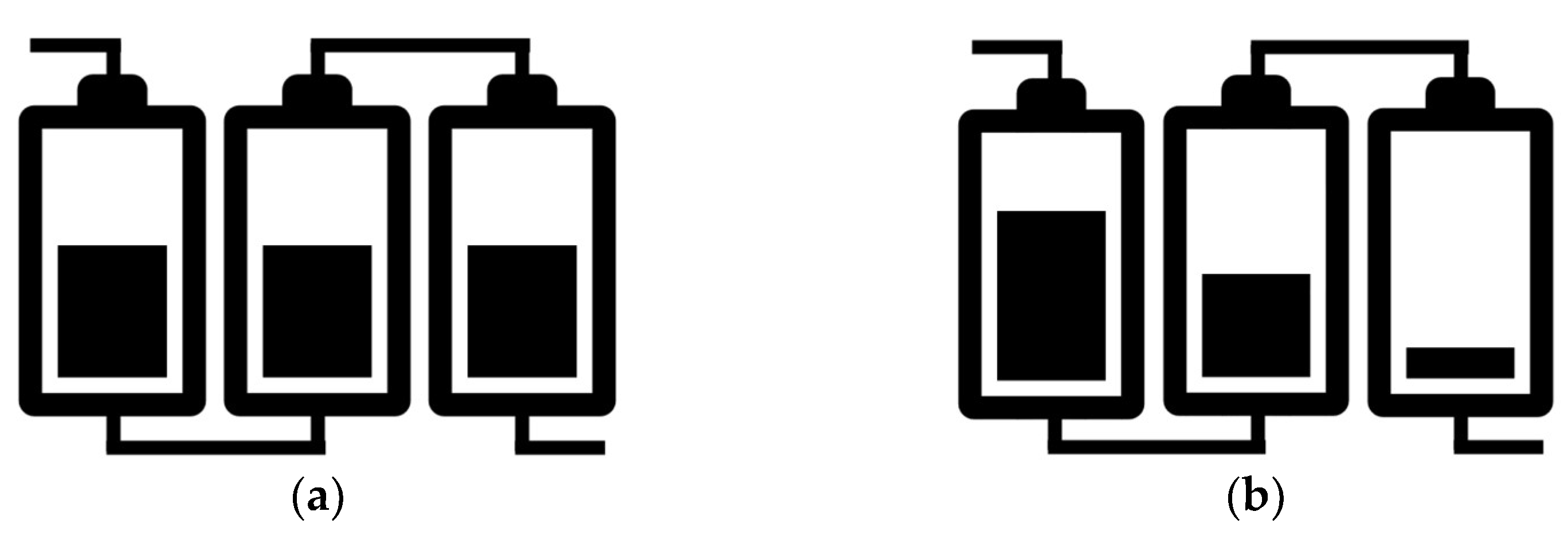
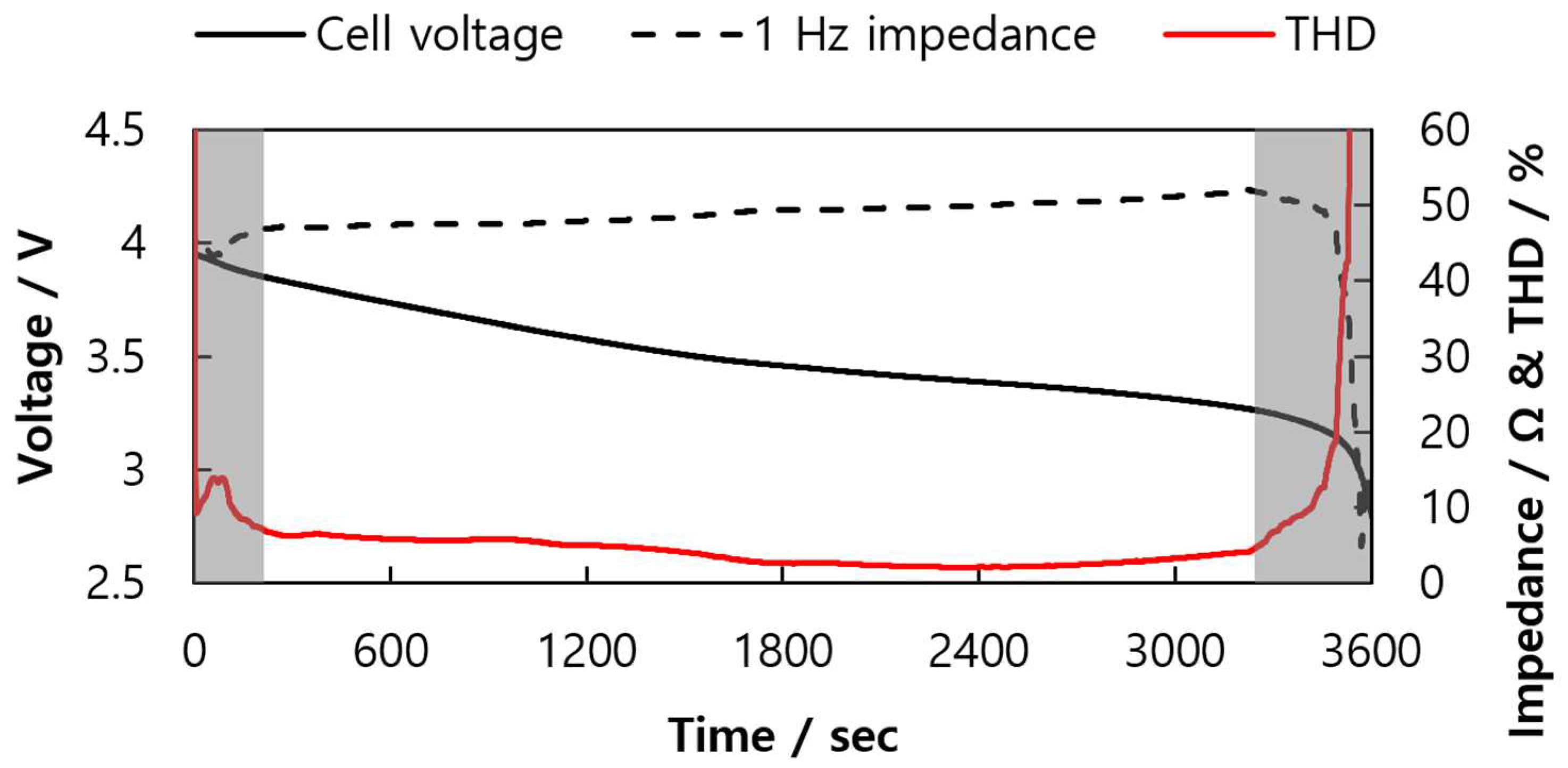
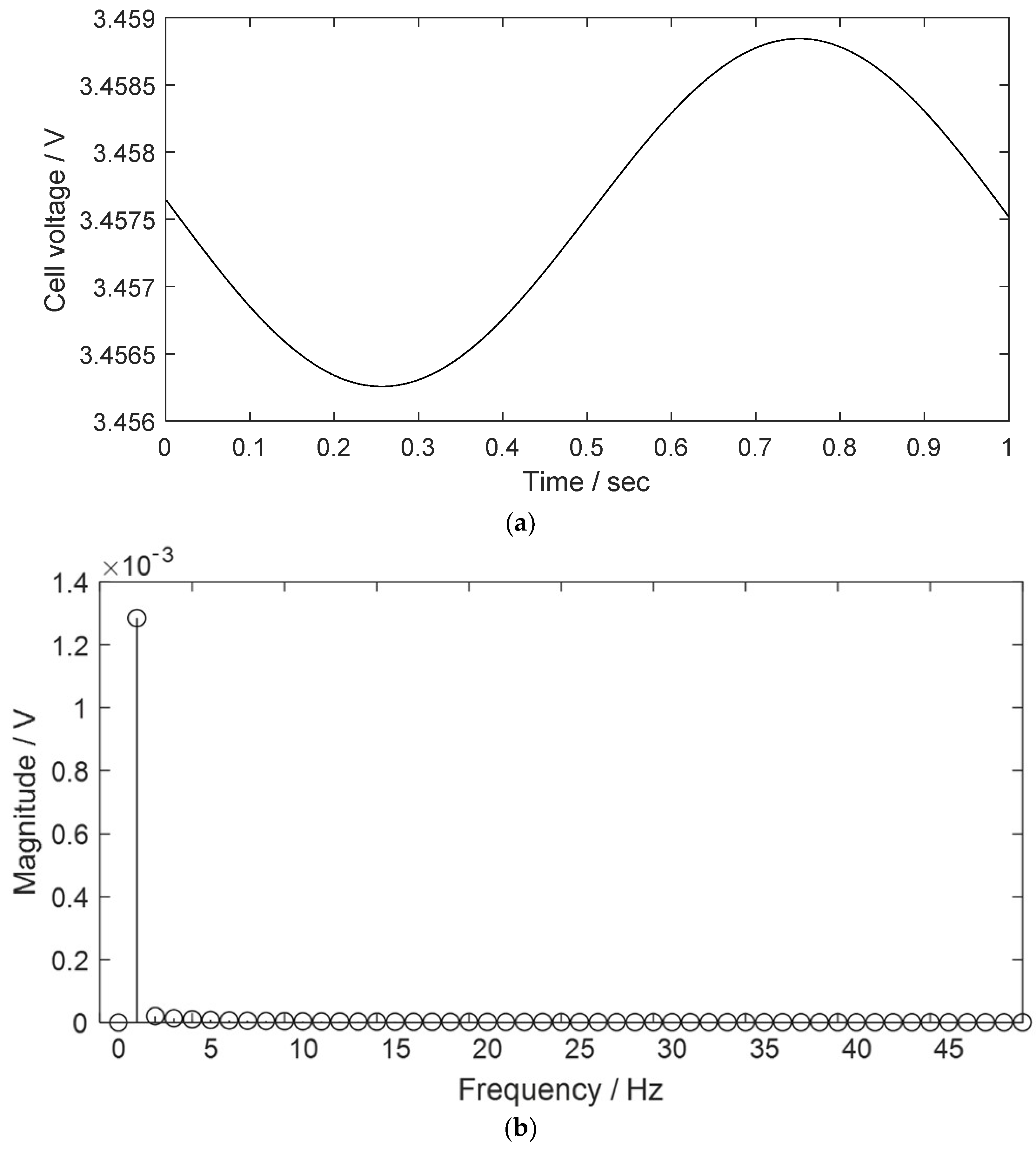
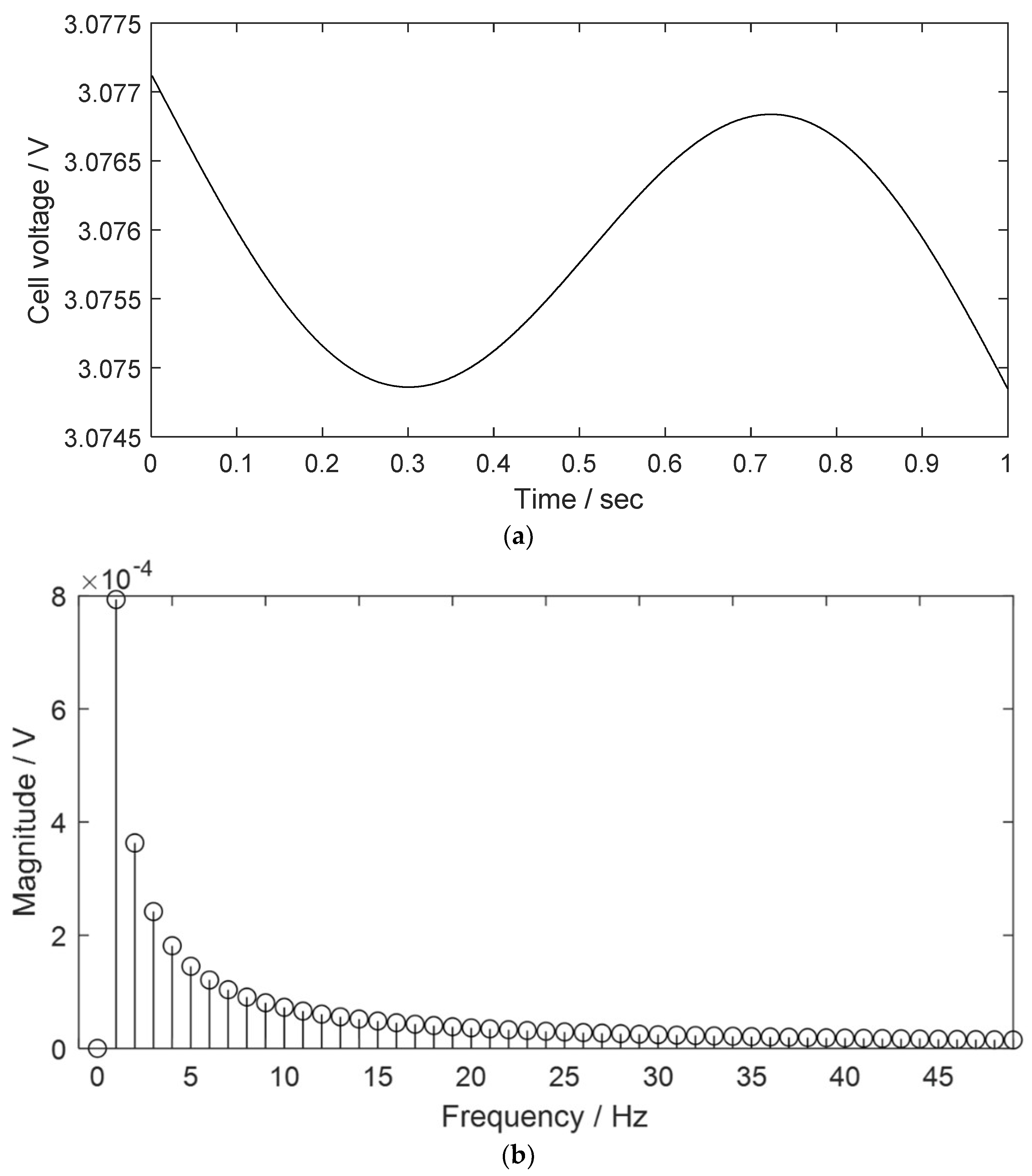


| Parameter | Description |
|---|---|
| Test frequency | 1 Hz |
| Initial SoC | 100% |
| Cell state of health (SoH) | 100% |
| DC bias | 2.6 A (1 C) |
| Sampling rate | 1024 Hz |
| Amplitude | 26 mA |
| Lower cut-off voltage | 2.8 V |
| Cell Voltage (V) | THD (%) |
|---|---|
| 3.0 | 13.29 |
| 2.9 | 25.50 |
| 2.8 | 46.31 |
| 2.7 | 86.87 |
| 2.6 | 311.74 |
| 2.5 | 538.78 |
| Voltage of the Cell with 70% SoH (V) | THD (%) |
|---|---|
| 3.0 | 14.37 |
| 2.9 | 14.70 |
| 2.8 | 18.57 |
| 2.7 | 27.14 |
| 2.6 | 36.62 |
| 2.5 | 49.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kowal, J. A Method for Detecting the Existence of an Over-Discharged Cell in a Lithium-Ion Battery Pack via Measuring Total Harmonic Distortion. Batteries 2022, 8, 26. https://doi.org/10.3390/batteries8030026
Kim J, Kowal J. A Method for Detecting the Existence of an Over-Discharged Cell in a Lithium-Ion Battery Pack via Measuring Total Harmonic Distortion. Batteries. 2022; 8(3):26. https://doi.org/10.3390/batteries8030026
Chicago/Turabian StyleKim, Jonghyeon, and Julia Kowal. 2022. "A Method for Detecting the Existence of an Over-Discharged Cell in a Lithium-Ion Battery Pack via Measuring Total Harmonic Distortion" Batteries 8, no. 3: 26. https://doi.org/10.3390/batteries8030026
APA StyleKim, J., & Kowal, J. (2022). A Method for Detecting the Existence of an Over-Discharged Cell in a Lithium-Ion Battery Pack via Measuring Total Harmonic Distortion. Batteries, 8(3), 26. https://doi.org/10.3390/batteries8030026







