Optimization of LIB Electrolyte and Exploration of Novel Compounds via the Molecular Dynamics Method
Abstract
:1. Introduction
2. Computational Details and Models
2.1. Computational Procedure
2.2. Estimation of Electric Conductivity and Diffusivity of Ions
3. Results and Discussion
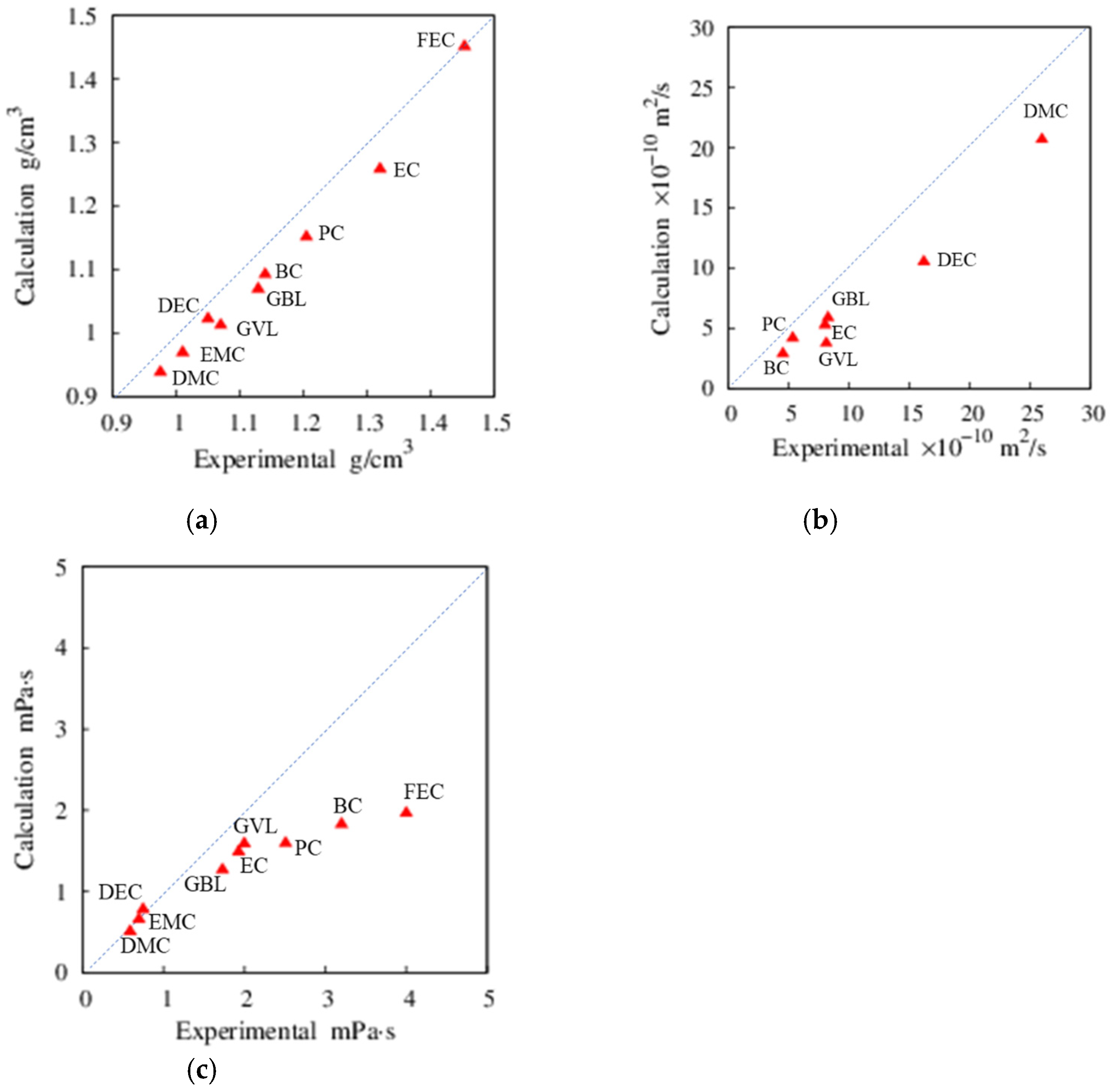
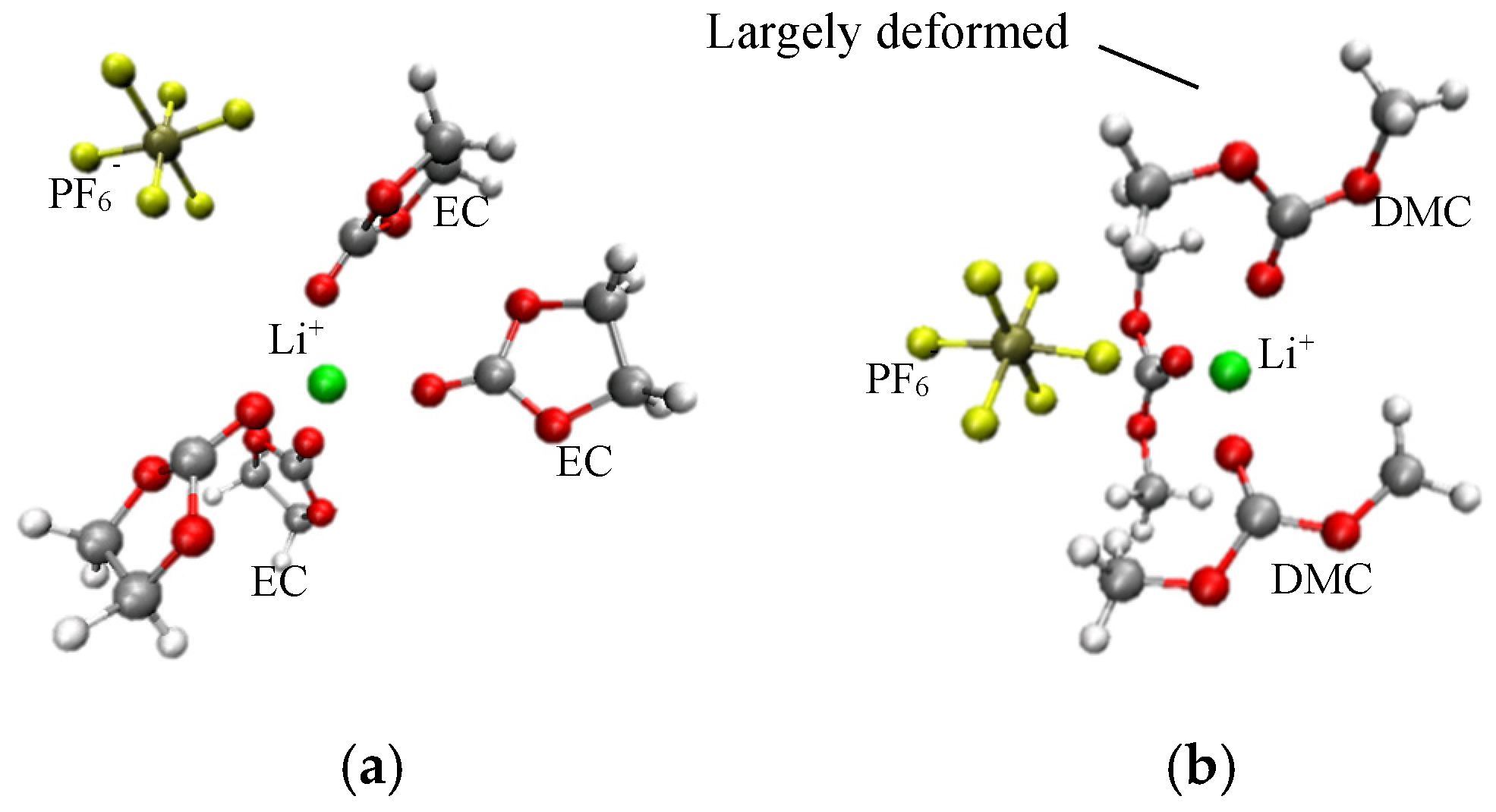
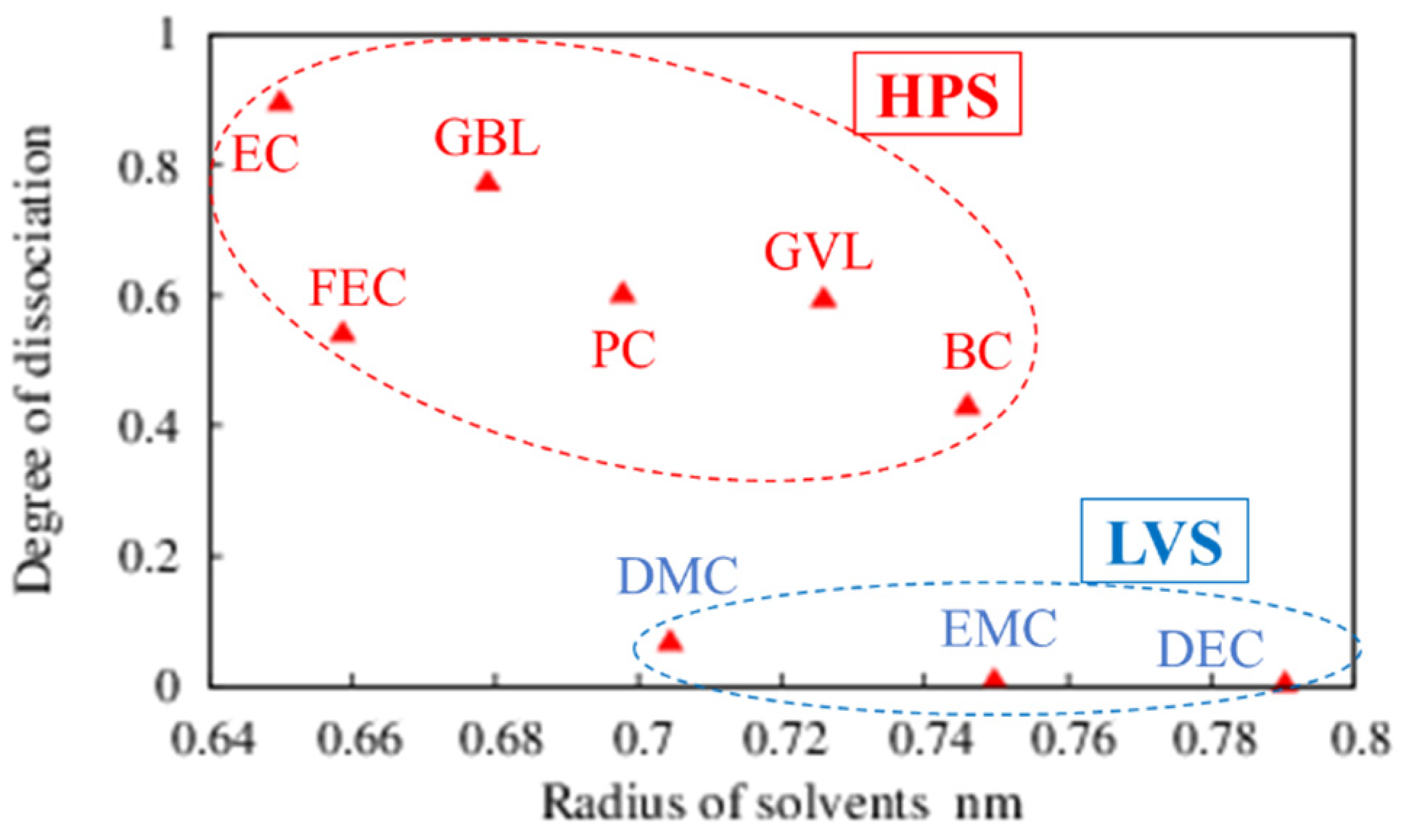
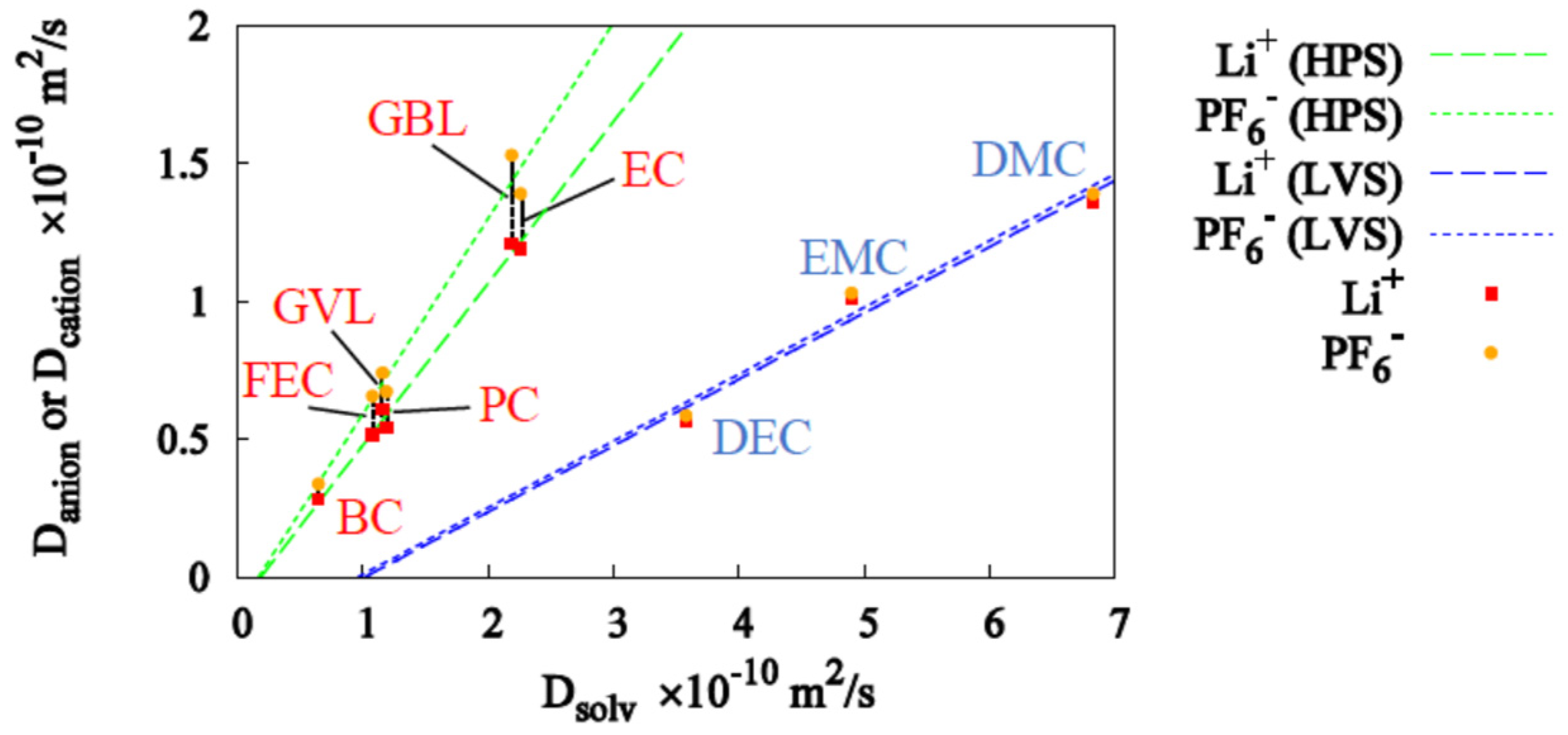
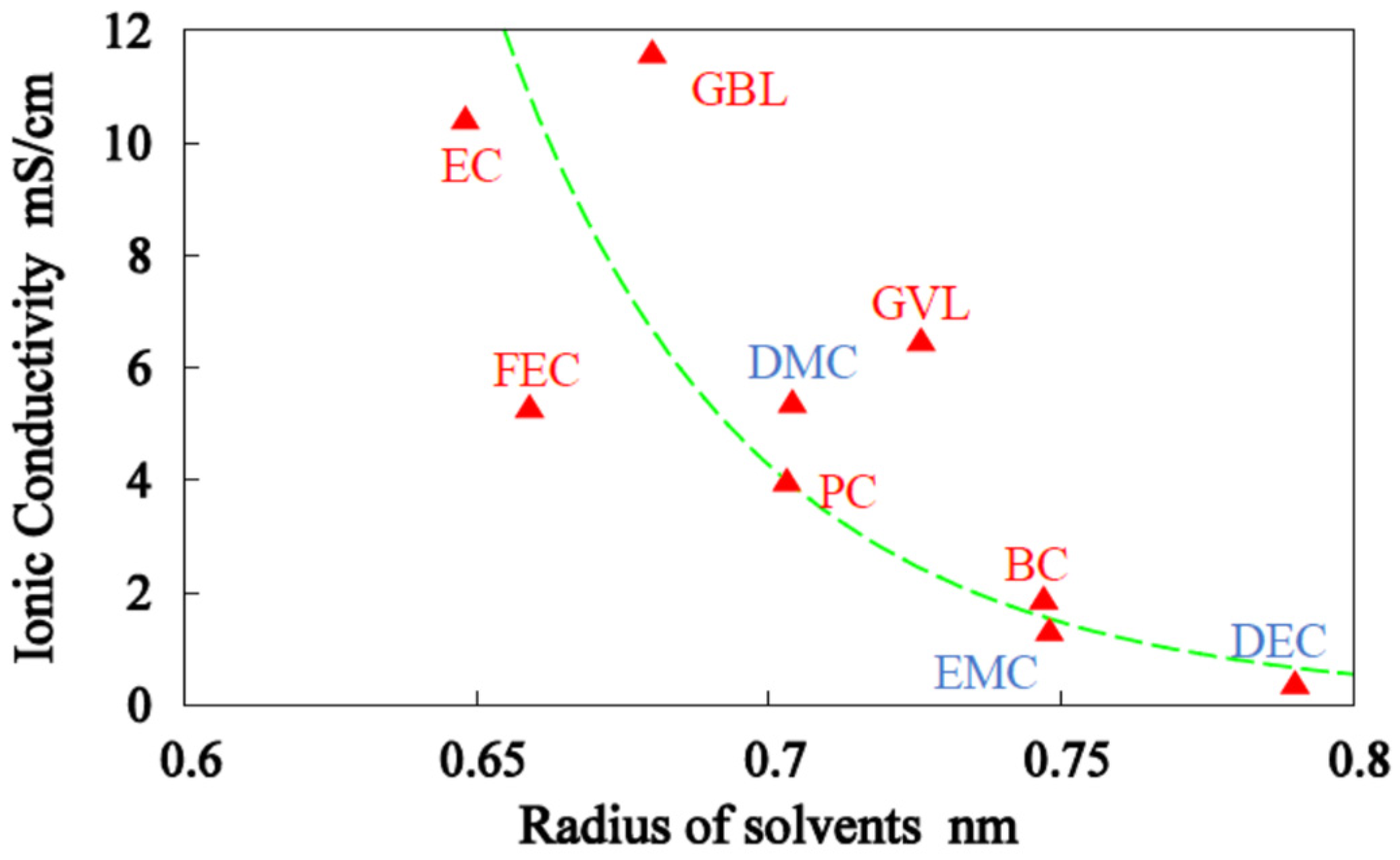
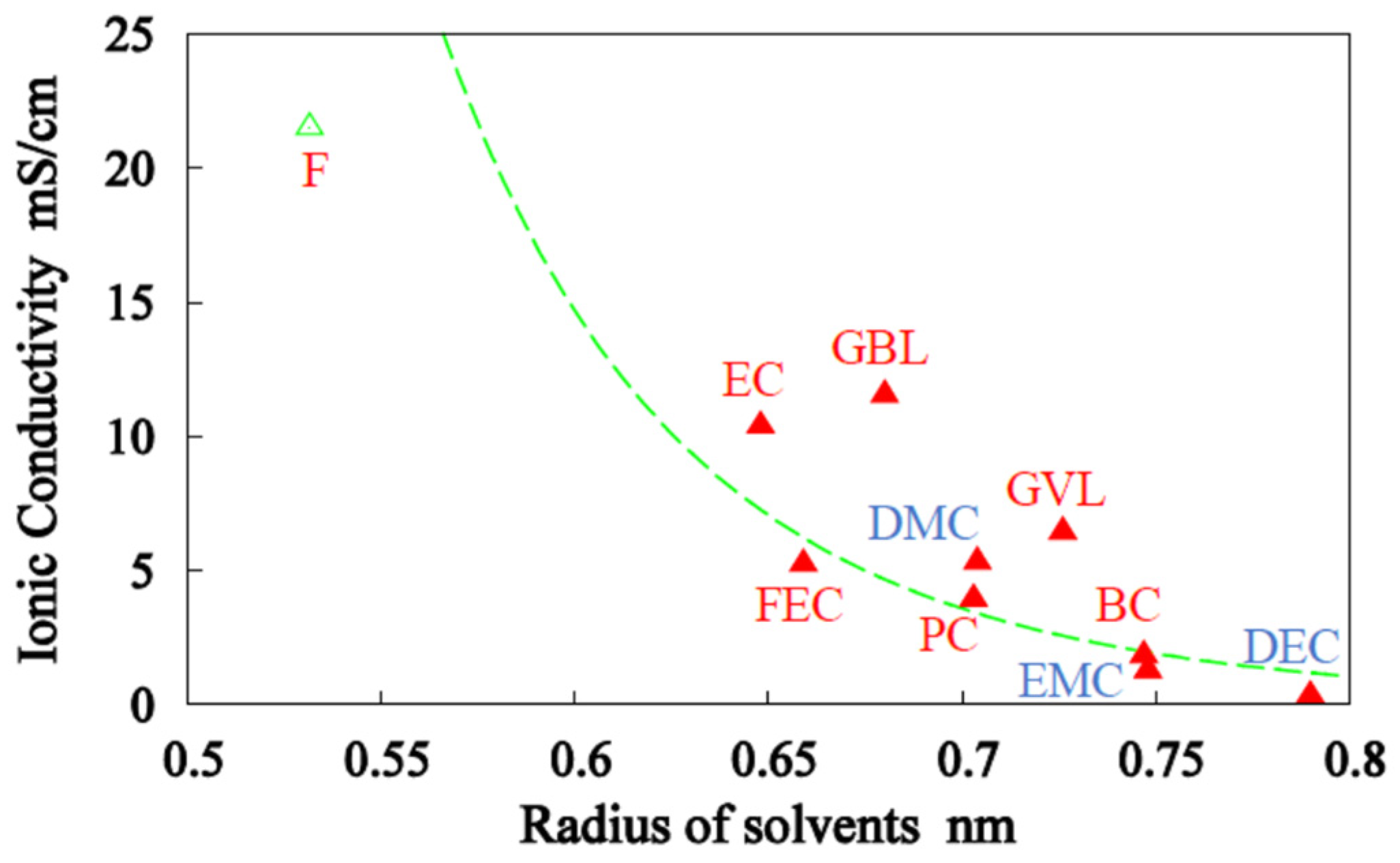
3.1. Single-Solvent + 1M-LiPF6 Electrolyte Solutions
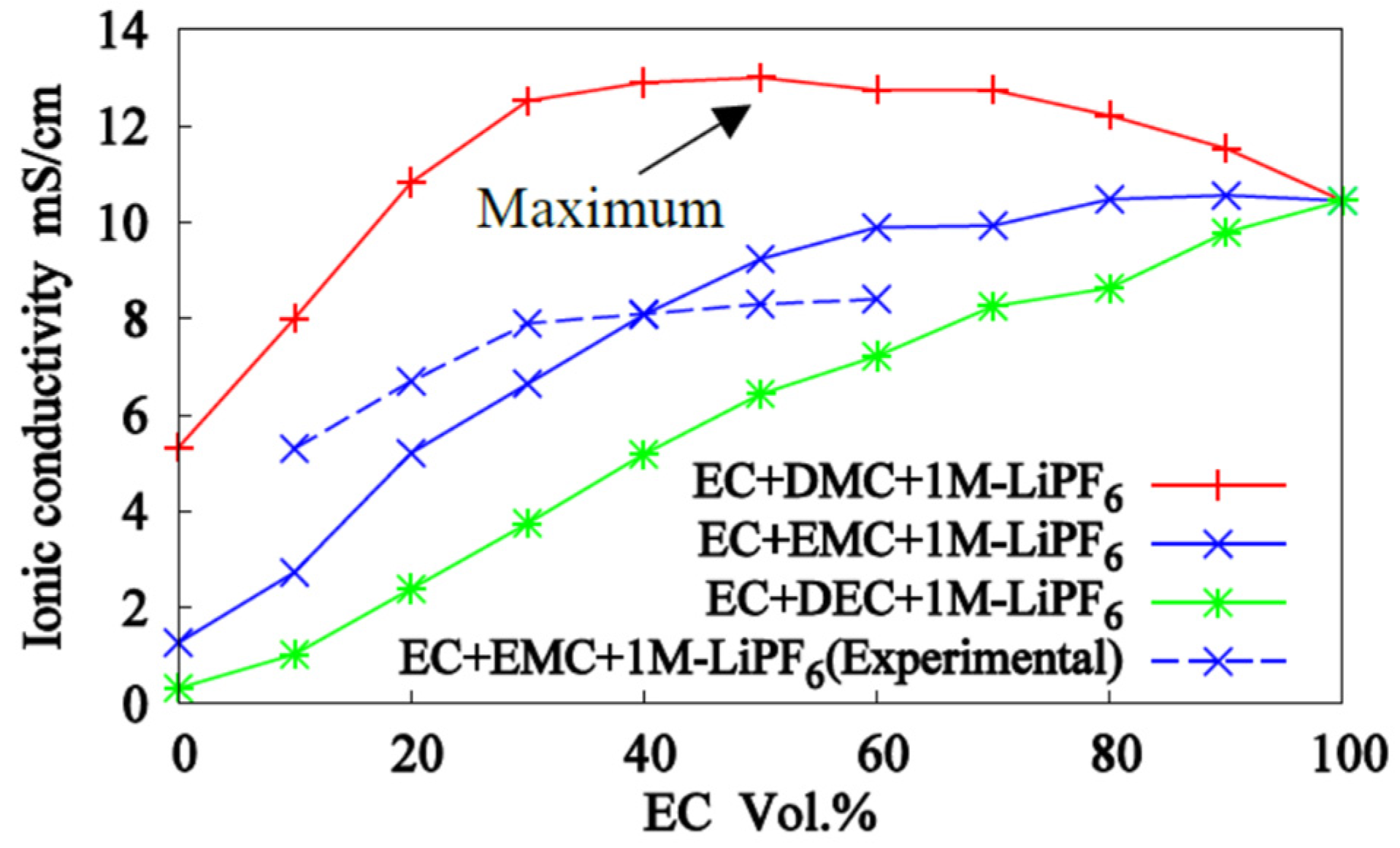
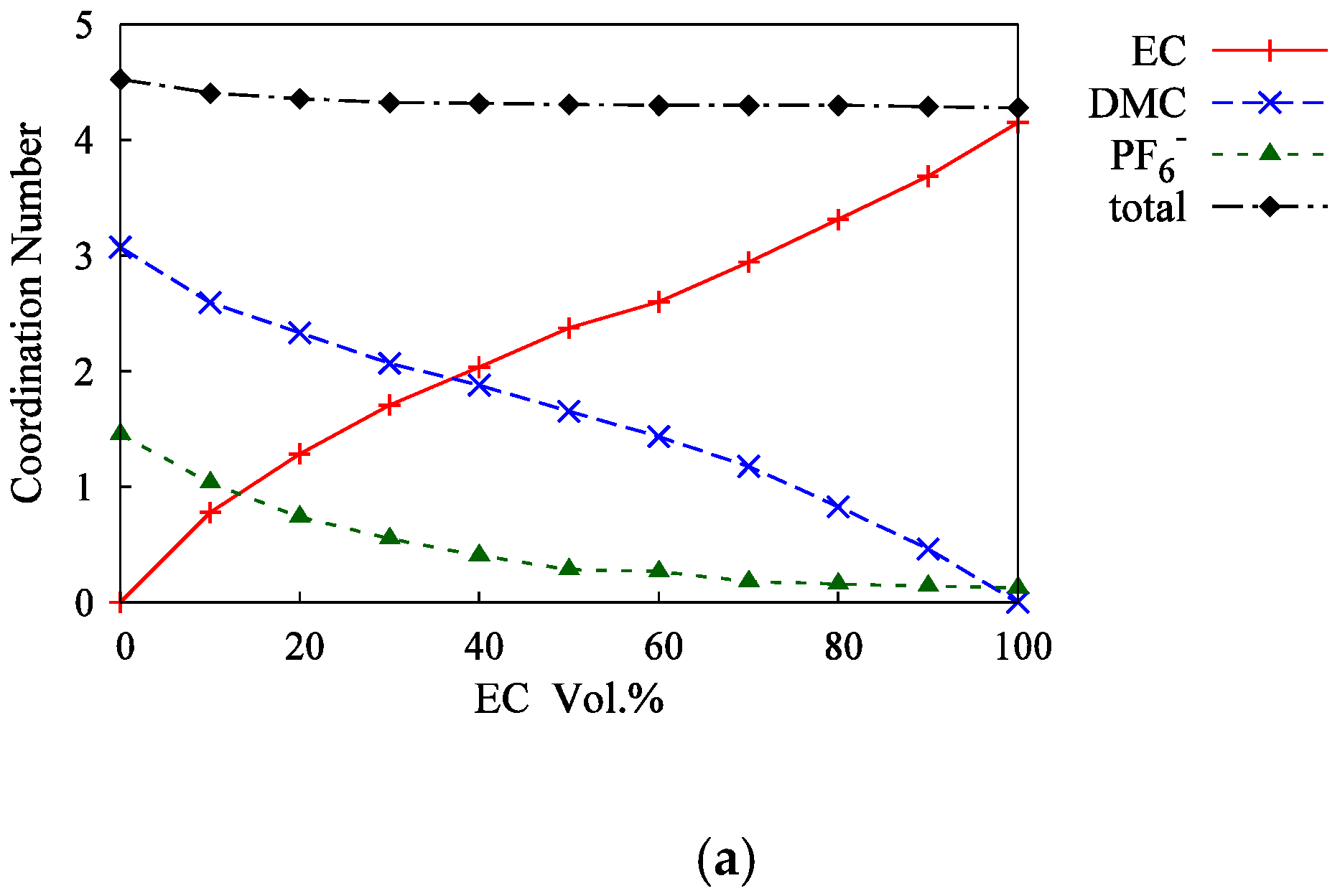
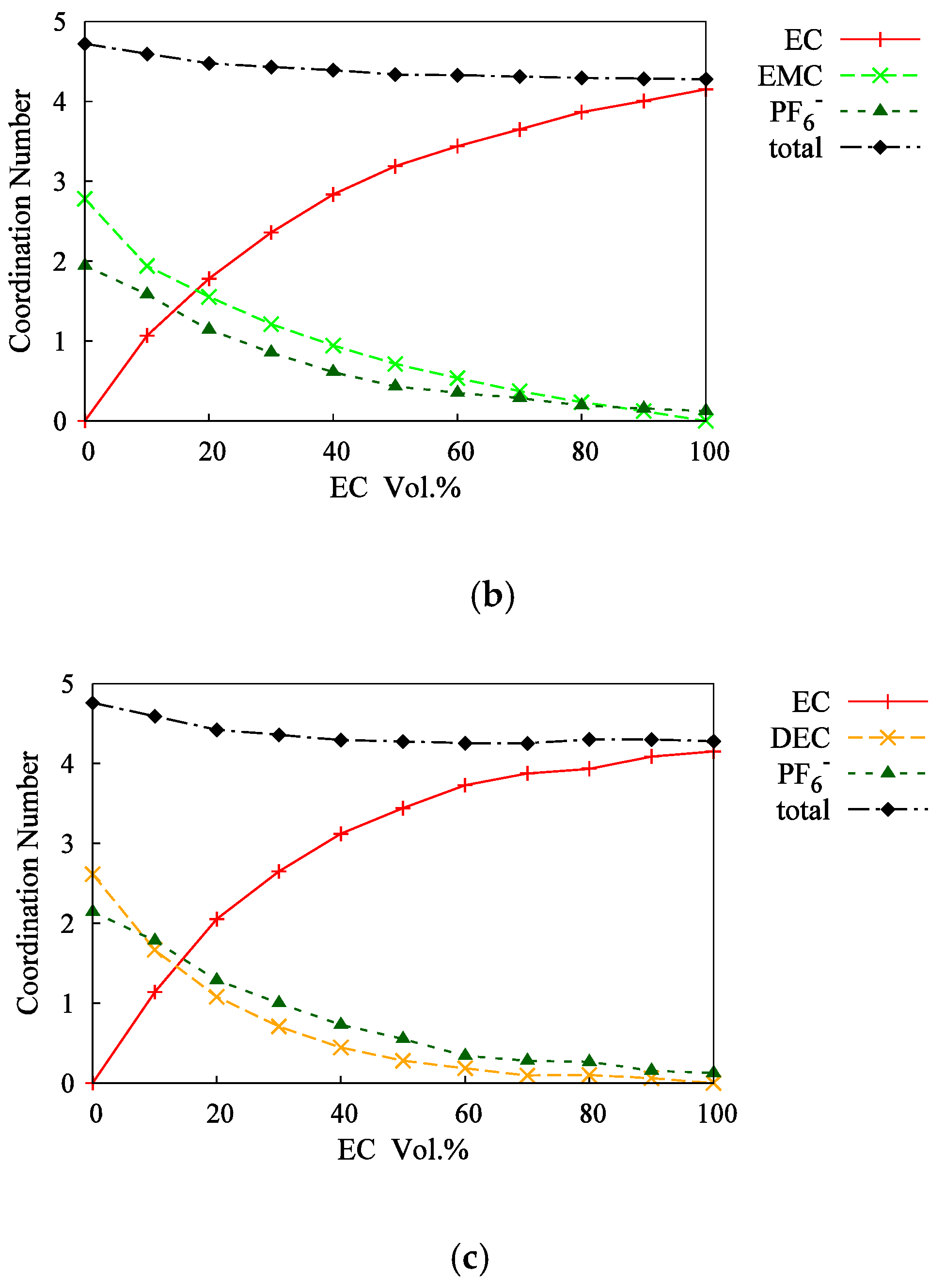
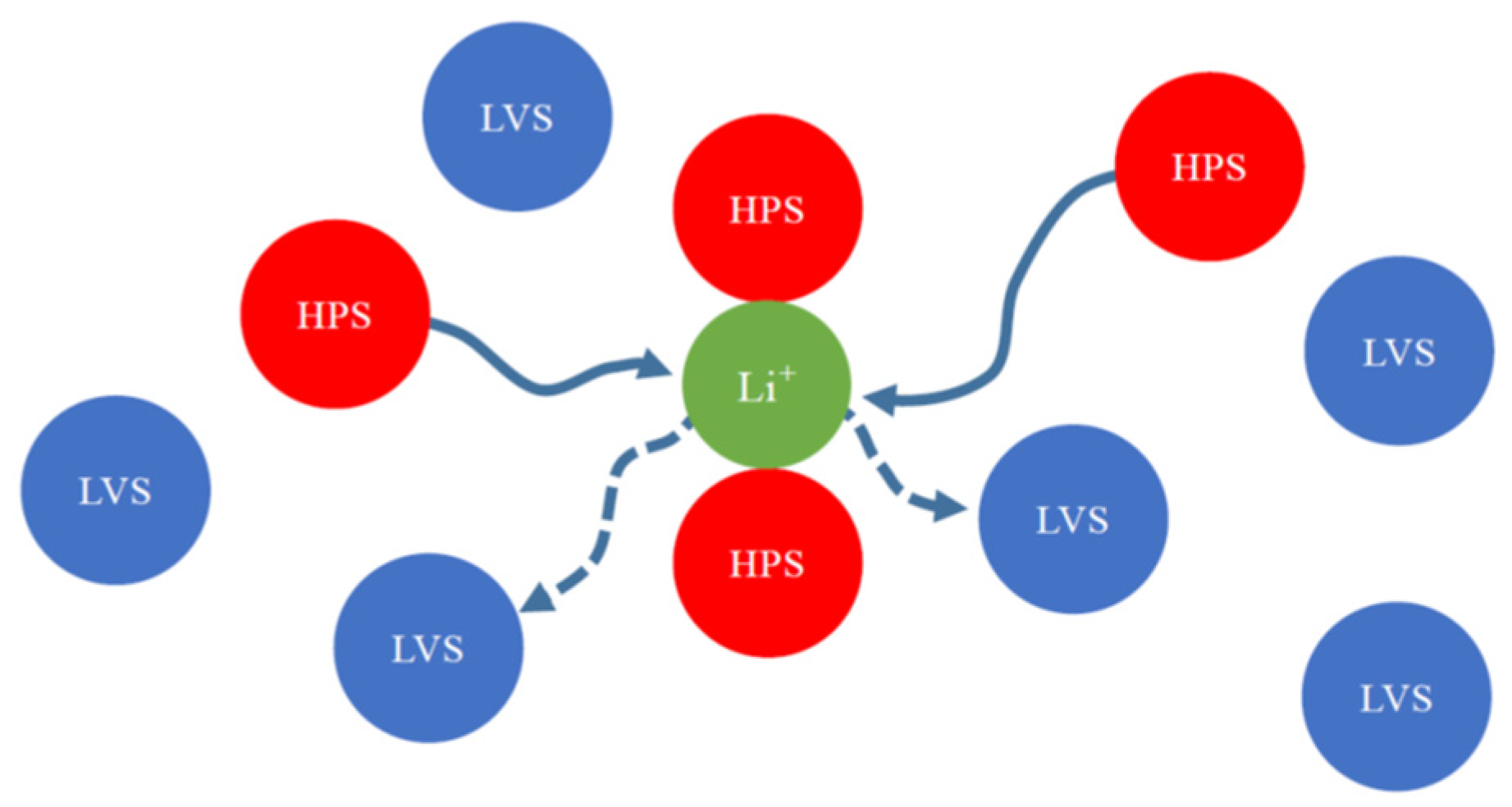
3.2. Mixed Solvents + 1M-LiPF6 Electrolyte Solutions
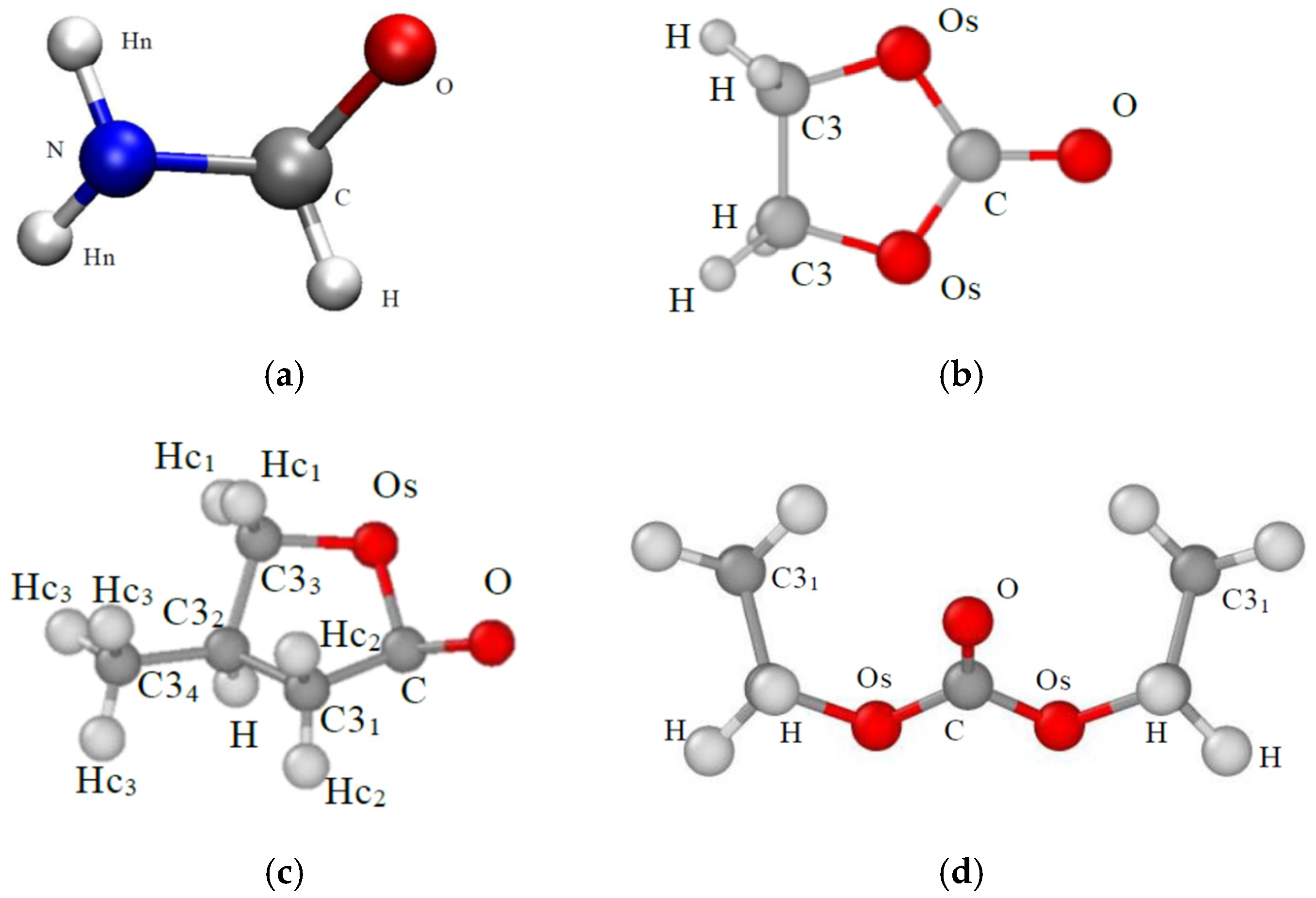
3.3. Using Formamide for the Electrolyte Solution
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Girishkumar, G.; McCloskey, B.; Luntz, A.C.; Swanson, S.; Wilcke, W. Lithium–air battery: Promise and challenges. J. Phys. Chem. Lett. 2010, 1, 2193–2203. [Google Scholar] [CrossRef]
- Mikhaylik, Y.V.; Akridge, J.R. Polysulfide shuttle study in the Li/S battery system. J. Electrochem. Soc. 2004, 151, A1969. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, R.; Wang, J.; Wang, Y. Current and future lithium-ion battery manufacturing. iScience 2021, 24, 102332. [Google Scholar] [CrossRef] [PubMed]
- De Luna, Y.; Abdullah, M.; Dimassi, S.N.; Bensalah, N. All-solid lithium-sulfur batteries: Present situation and future progress. Ionics 2021, 27, 4937–4960. [Google Scholar] [CrossRef]
- Wang, J.; Yamada, Y.; Sodeyama, K.; Chiang, C.H.; Tateyama, Y.; Yamada, A. Superconcentrated electrolytes for a high-voltage lithium-ion battery. Nat. Commun. 2016, 7, 12032. [Google Scholar] [CrossRef]
- Peled, E. The electrochemical behavior of alkali and alkaline earth metals in nonaqueous battery systems—The solid electrolyte interphase model. J. Electrochem. Soc. 1979, 126, 2047–2051. [Google Scholar] [CrossRef]
- Aurbach, D. Review of selected electrode–solution interactions which determine the performance of Li and Li ion batteries. J. Power Sources 2000, 89, 206–218. [Google Scholar] [CrossRef]
- Yazami, R.; Reynier, Y.F. Mechanism of self-discharge in graphite–lithium anode. Electrochem. Acta 2002, 47, 1217–1223. [Google Scholar] [CrossRef]
- Broussely, M.; Herreyre, S.; Biensan, P.; Kasztejna, P.; Nechev, K.; Staniewicz, R.J. Aging mechanism in Li ion cells and calendar life predictions. J. Power Sources 2001, 97–98, 13–21. [Google Scholar] [CrossRef]
- Smart, M.C.; Ratnakumar, B.V.; Ryan-Mowrey, V.S.; Surampudi, S.; Prakash, G.K.S.; Hu, J.; Cheung, I. Improved performance of lithium-ion cells with the use of fluorinated carbonate-based electrolytes. J. Power Sources 2003, 119–121, 359–367. [Google Scholar] [CrossRef]
- McBrayer, J.D.; Apblett, C.A.; Harrison, K.L.; Fenton, K.R.; Minteer, S.D. Mechanical studies of the solid electrolyte interphase on anodes in lithium and lithium ion batteries. Nanotechnology 2021, 32, 502005. [Google Scholar] [CrossRef]
- Ding, M.S.; Xu, K.; Zhang, S.S.; Amine, K.; Henriksen, G.L.; Jow, T.R. Change of conductivity with salt content, solvent composition, and temperature for electrolytes of LiPF6 in ethylene carbonate-ethyl methyl carbonate. J. Electrochem. Soc. 2001, 148, A1196–A1204. [Google Scholar] [CrossRef]
- Shkerin, S.N.; Profatilova, I.A.; Roh, S. Effect of ethylene carbonate concentration on the conductivity of carbonate-based electrolytes with LiPF6 for Li-ion batteries. Ionics 2009, 15, 761–764. [Google Scholar] [CrossRef]
- Lia, Q.; Chenb, J.; Fanb, L.; Kong, X.; Lua, Y. Progress in electrolytes for rechargeable Li-based batteries and beyond. Green Energy Environ. 2016, 1, 18–42. [Google Scholar] [CrossRef] [Green Version]
- Niu, H.; Wang, L.; Guan, P.; Zhang, N.; Yan, C.; Ding, M.; Guo, X.; Huang, T.; Hu, X. Recent advances in application of ionic liquids in electrolyte of lithium ion batteries. J. Energy Storage 2021, 40, 102659. [Google Scholar] [CrossRef]
- Aihara, Y.; Sugimoto, K.; Price, W.S.; Hayamizu, K. Ionic conduction and self-diffusion near infinitesimal concentration in lithium salt-organic solvent electrolytes. J. Chem. Phys. 2000, 113, 1981–1991. [Google Scholar] [CrossRef]
- Saito, Y.; Morimura, W.; Kuratani, R.; Nishikawa, S. Factors controlling the ionic mobility of lithium electrolyte solutions in separator membranes. J. Phys. Chem. C 2016, 120, 3619–3624. [Google Scholar] [CrossRef]
- Hayamizu, K. Direct relations between ion diffusion constants and ionic conductivity for lithium electrolyte solutions. Electrochim. Acta 2017, 254, 101–111. [Google Scholar] [CrossRef]
- Barthel, J.; Buchner, R.; Wismeth, E. FTIR spectroscopy of ion solvation of LiClO4 and LiSCN in acetonitrile, benzonitrile, and propylene carbonate. J. Solut. Chem. 2000, 29, 937–954. [Google Scholar] [CrossRef]
- Fulfer, K.D.; Kuroda, D.G. A comparison of the solvation structure and dynamics of the lithium ion in linear organic carbonates with different alkyl chain lengths. Phys. Chem. Chem. Phys. 2017, 19, 25140–25150. [Google Scholar] [CrossRef]
- Cazzanelli, E.; Mustarelli, P.; Benevelli, F.; Appetecchi, G.B.; Croce, F. Raman and NMR Analysis of LiClO4 concentrated solutions in ethylene carbonate–propylene carbonate. Solid State Ion. 1996, 86–88, 379–384. [Google Scholar] [CrossRef]
- Yang, L.; Xiao, A.; Lucht, B.L. Investigation of solvation in lithium ion battery electrolytes by NMR spectroscopy. J. Mol. Liq. 2010, 154, 131–133. [Google Scholar] [CrossRef]
- Miyamoto, K.; Yamakawa, S.; Hyodo, S.; Asahi, R. Annual Meeting of Japan Society for Molecular Science 2010 Abstract. 2010, 2B20. Available online: http://molsci.center.ims.ac.jp/area/2010/bk2010/papers/2B20_w.pdf (accessed on 25 February 2022). (In Japanese).
- Ong, M.T.; Verners, O.; Draeger, E.W.; Duin, A.C.T.V.; Lordi, V.; Pask, J.E. Lithium ion solvation and diffusion in bulk organic electrolytes from first-principles and classical reactive molecular dynamics. J. Phys. Chem. B 2015, 119, 1535–1545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skarmoutsos, I.; Ponnuchamy, V.; Vetere, V.; Mossa, S. Li+ solvation in pure, binary, and ternary mixtures of organic carbonate electrolytes. J. Phys. Chem. C 2015, 119, 4502–4515. [Google Scholar] [CrossRef] [Green Version]
- Masia, M.; Probst, M.; Rey, R. Ethylene carbonate–Li+: A theoretical study of structural and vibrational properties in gas and liquid phases. J. Phys. Chem. B 2004, 108, 2016–2027. [Google Scholar] [CrossRef]
- Borodin, O.; Smith, G.D.; Fan, P. Molecular dynamics simulations of lithium alkyl carbonates. J. Phys. Chem. B 2006, 110, 22773–22779. [Google Scholar] [CrossRef]
- Borodin, O.; Smith, G.D. Quantum chemistry and molecular dynamics simulation study of dimethyl carbonate: Ethylene carbonate electrolytes doped with LiPF6. J. Phys. Chem. B 2009, 113, 1763–1776. [Google Scholar] [CrossRef]
- Starovoytov, O.N. Development of a polarizable force field for molecular dynamics simulations of lithium-ion battery electrolytes: Sulfone-based solvents and lithium salts. J. Phys. Chem. B 2021, 125, 11242–11255. [Google Scholar] [CrossRef]
- Lytle, T.K.; Muralidharan, A.; Yethiraj, A. Why lithium ions stick to some anions and not others. J. Phys. Chem. B 2021, 125, 4447–4455. [Google Scholar] [CrossRef]
- Karatrantosa, A.V.; Ohba, T.; Cai, Q. Diffusion of ions and solvent in propylene carbonate solutions for lithium-ion battery applications. J. Mol. Liq. 2020, 320, 114351. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Pall, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Case, D.A.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; Greene, D.; Homeyer, N.; et al. AMBER 2017 Reference Manual; University of California: San Francisco, CA, USA, 2017. [Google Scholar]
- Xu, K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 2004, 104, 4303–4417. [Google Scholar] [CrossRef] [PubMed]
- Martinez, L.; Andrade, R.; Birgin, E.G.; Martinez, J.M. Packing optimization for automated generation of complex system’s initial configurations for molecular dynamics and docking. J. Comput. Chem. 2003, 24, 819–825. [Google Scholar] [CrossRef] [PubMed]
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Crystal structure and pair potentials: A molecular-dynamics study. Phys. Rev. Lett. 1980, 45, 1196–1199. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Aksimentiev, A.; Schulten, K. Imaging α-hemolysin with molecular dynamics: Ionic conductance, osmotic permeability, and the electrostatic potential map. Biophys. J. 2005, 88, 3745–3761. [Google Scholar] [CrossRef] [Green Version]
- Calero, C.; Faraudo, J.; Aguilella-Arzo, M. Molecular dynamics simulations of concentrated aqueous electrolyte solutions. Mol. Simul. 2011, 37, 123–134. [Google Scholar] [CrossRef] [Green Version]
- Palmer, B.J. Transverse-current autocorrelation-function calculations of the shear viscosity for molecular liquids. Phys. Rev. E 1994, 49, 359–366. [Google Scholar] [CrossRef]
- Takai, Y.; Terai, Y.; Saitoh, K.; Takuma, M.; Takahashi, Y.; Sato, T. Molecular dynamics simulation of Li-ion coordination structure and transport properties in LIB electrolytes: Influence of molecular size. Sci. Tech. Rep. Kansai Univ. 2019, 61, 1–10. [Google Scholar]
- National Center for Biotechnology Information. PubChem Compound Database. Available online: https://pubchem.ncbi.nlm.nih.gov (accessed on 25 February 2022).
- Chemicalbook. Available online: https://www.chemicalbook.com/ (accessed on 13 March 2022).
- Hayamizu, K. Ion and Solvent Self-Diffusion Coefficients for Lithium Battery Electrolytes (Part 1): Organic Solution Electrolytes. JEOL Application Note. 2012, pp. 1–77. Available online: http://j-resonance.com/corporate/images/application/nmr/nm131015.pdf (accessed on 25 February 2022). (In Japanese).
- Hayamizu, K.; Aihara, Y.; Arai, S.; Martinez, C.G. Pulse-gradient spin-echo 1H, 7Li, and 19F NMR diffusion and ionic conductivity measurements of 14 organic electrolytes containing LiN(SO2CF3)2. J. Phys. Chem. B 1999, 103, 519–524. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, K.; Nemoto, Y.; Tobishima, S.; Yamaki, J. Electrolyte composition dependence on lithium secondary cell performance. Key Eng. Mater. 1999, 157–158, 273–280. [Google Scholar] [CrossRef]
- Sekhar, B.C.; Hachicha, R.; Maffre, M.; Bodin, C.; Le Vot, S.; Favier, F.; Fontaine, O. Evaluation of the properties of an electrolyte based on formamide and LiTFSI for electrochemical capacitors. J. Electrochem. Soc. 2020, 167, 110508. [Google Scholar] [CrossRef]
- You, L.; Duan, K.; Zhang, G.; Song, W.; Yang, T.; Song, X.; Wang, S.; Liu, J. N,N-dimethylformamide electrolyte additive via a blocking strategy enables high-performance lithium-ion battery under high temperature. J. Phys. Chem. C 2019, 123, 5942–5950. [Google Scholar] [CrossRef]
- Leung, K.; Budzien, J.L. Ab initio molecular dynamics simulations of the initial stages of solid–electrolyte interphase formation on lithium ion battery graphitic anodes. Phys. Chem. Chem. Phys. 2010, 12, 6583–6586. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Park, S.-S. Dielectric properties of organic solvents from non-polarizable molecular dynamics simulation with electronic continuum model and density functional theory. J. Phys. Chem. B 2011, 115, 12571–12576. [Google Scholar] [CrossRef]
- Leung, K.; Rempe, S.B.; Foster, M.E.; Ma, Y.; Martinez del la Hoz, J.M.; Sai, N.; Balbuena, P.B. Modeling electrochemical decomposition of fluoroethylene carbonate on silicon anode surfaces in lithium ion batteries. J. Electrochem. Soc. 2014, 161, A213–A221. [Google Scholar] [CrossRef]
- Takenaka, N.; Sakai, H.; Suzuki, Y.; Uppula, P.; Nagaoka, M. A computational chemical insight into microscopic additive effect on solid electrolyte interphase film formation in sodium-ion batteries: Suppression of unstable film growth by intact fluoroethylene carbonate. J. Phys. Chem. C. 2015, 119, 18046–18055. [Google Scholar] [CrossRef]
- Alzate-Vargas, L.; Blau, S.M.; Spotte-Smith, E.W.C.; Allu, S.; Persson, K.A.; Fattebert, J.-L. Insight into SEI growth in Li-ion batteries using molecular dynamics and accelerated chemical reactions. J. Phys. Chem. C 2021, 125, 18588–18596. [Google Scholar] [CrossRef]
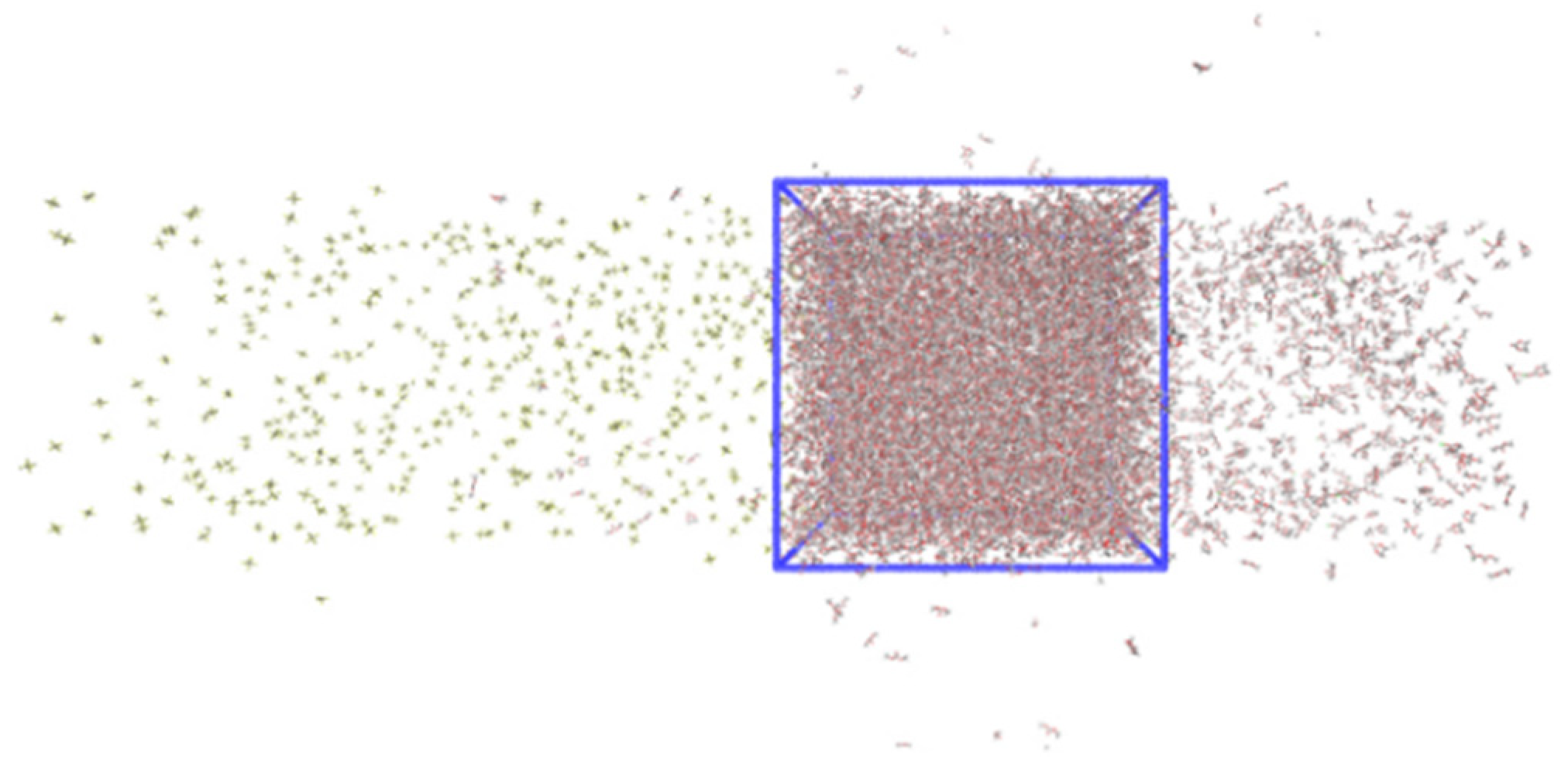



| (a) | ||||
|---|---|---|---|---|
| Molecule | The Number of Molecules | |||
| EC | 7184 | |||
| FEC | 6664 | |||
| PC | 5572 | |||
| BC | 4639 | |||
| GBL | 6191 | |||
| GVL | 4951 | |||
| DMC | 5607 | |||
| EMC | 4580 | |||
| DEC | 3896 | |||
| (b) | ||||
| Model * | The Number of Molecules | |||
| HPS | LVS | |||
| EC | DMC | EMC | DEC | |
| 1EC9LVS | 718 | 5047 | 4122 | 3507 |
| 2EC8LVS | 1437 | 4486 | 3664 | 3117 |
| 3EC7LVS | 2155 | 3925 | 3206 | 2727 |
| 4EC6LVS | 2873 | 3365 | 2748 | 2338 |
| 5EC5LVS | 3592 | 2804 | 2290 | 1948 |
| 6EC4LVS | 4310 | 2243 | 1832 | 1559 |
| 7EC3LVS | 5028 | 1682 | 1374 | 1169 |
| 8EC2LVS | 5747 | 1121 | 916 | 799 |
| 9EC1LVS | 6465 | 561 | 458 | 390 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saitoh, K.-i.; Takai, Y.; Sato, T.; Takuma, M.; Takahashi, Y. Optimization of LIB Electrolyte and Exploration of Novel Compounds via the Molecular Dynamics Method. Batteries 2022, 8, 27. https://doi.org/10.3390/batteries8030027
Saitoh K-i, Takai Y, Sato T, Takuma M, Takahashi Y. Optimization of LIB Electrolyte and Exploration of Novel Compounds via the Molecular Dynamics Method. Batteries. 2022; 8(3):27. https://doi.org/10.3390/batteries8030027
Chicago/Turabian StyleSaitoh, Ken-ichi, Yoshihiro Takai, Tomohiro Sato, Masanori Takuma, and Yoshimasa Takahashi. 2022. "Optimization of LIB Electrolyte and Exploration of Novel Compounds via the Molecular Dynamics Method" Batteries 8, no. 3: 27. https://doi.org/10.3390/batteries8030027
APA StyleSaitoh, K.-i., Takai, Y., Sato, T., Takuma, M., & Takahashi, Y. (2022). Optimization of LIB Electrolyte and Exploration of Novel Compounds via the Molecular Dynamics Method. Batteries, 8(3), 27. https://doi.org/10.3390/batteries8030027






