Experimental Benchmarking of Redox Flow Cells
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
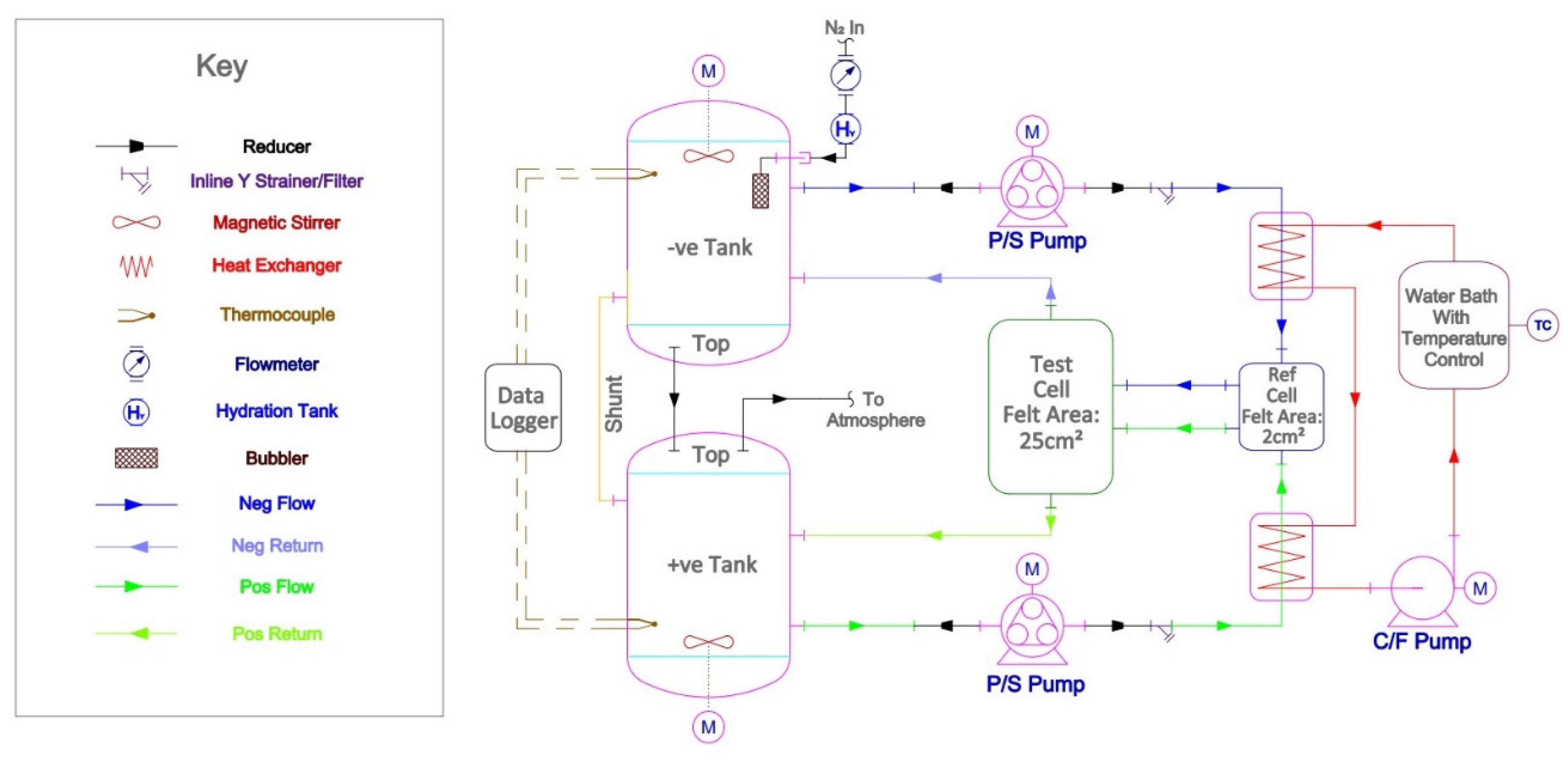
2.2. Measurement Set-Up
3. Results and Discussion
3.1. Resistivity, ρ, and Voltage Efficiency, ηV
3.1.1. General Considerations
- current density is constant over the whole surface of the membrane in the test cell;
- current density through the membrane is equal to current density through the electrodes.
3.1.2. Flow Rate Dependence
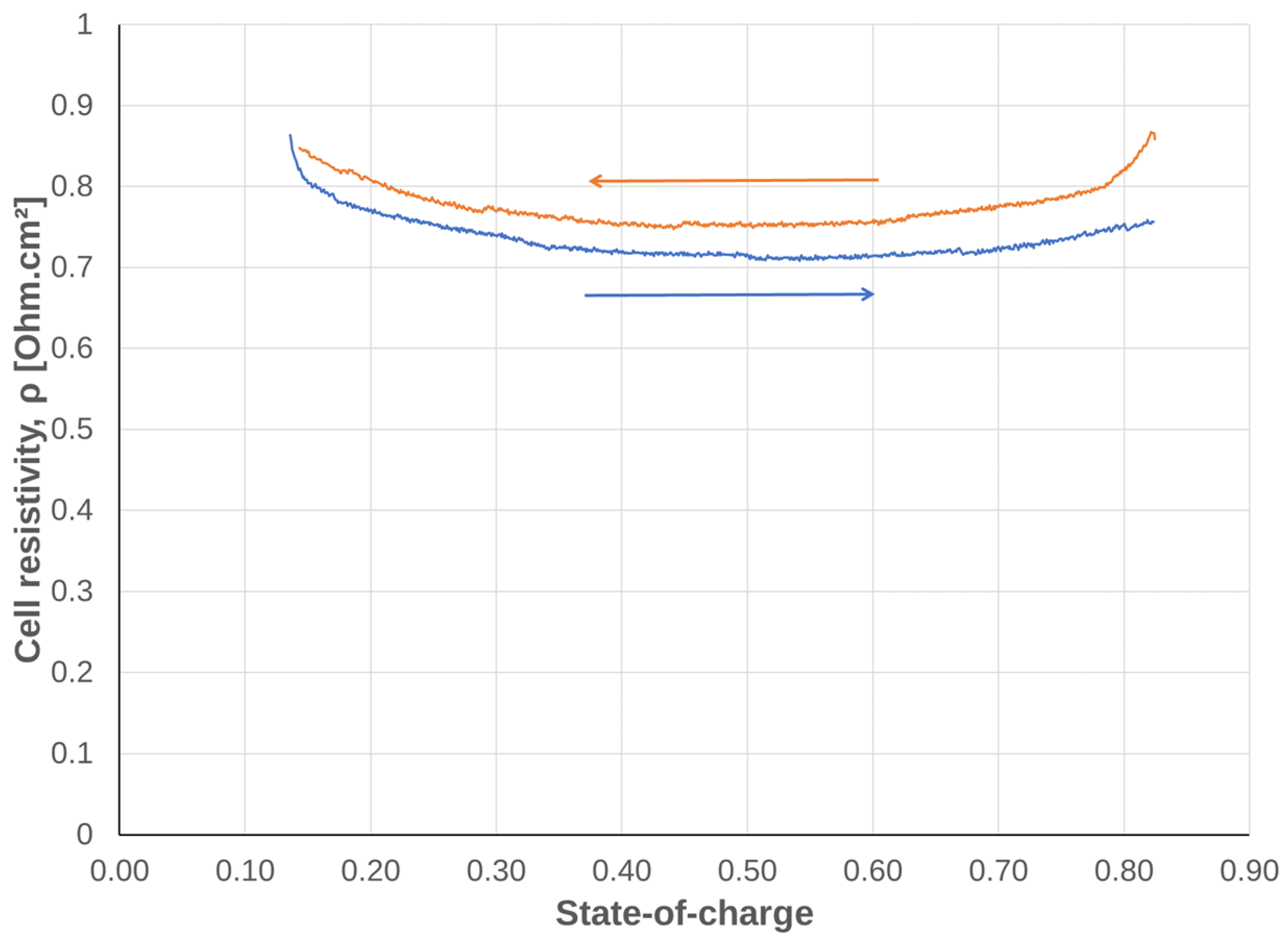
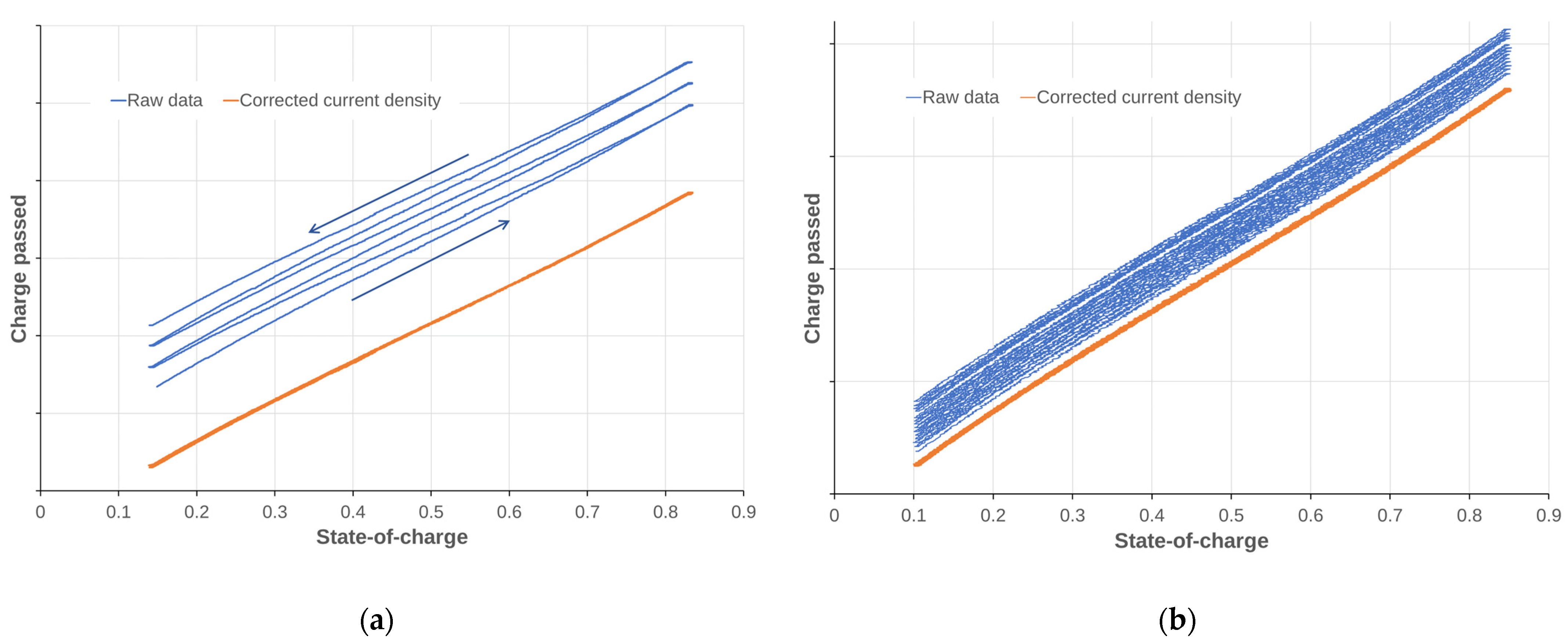
3.1.3. Dependency on SOC
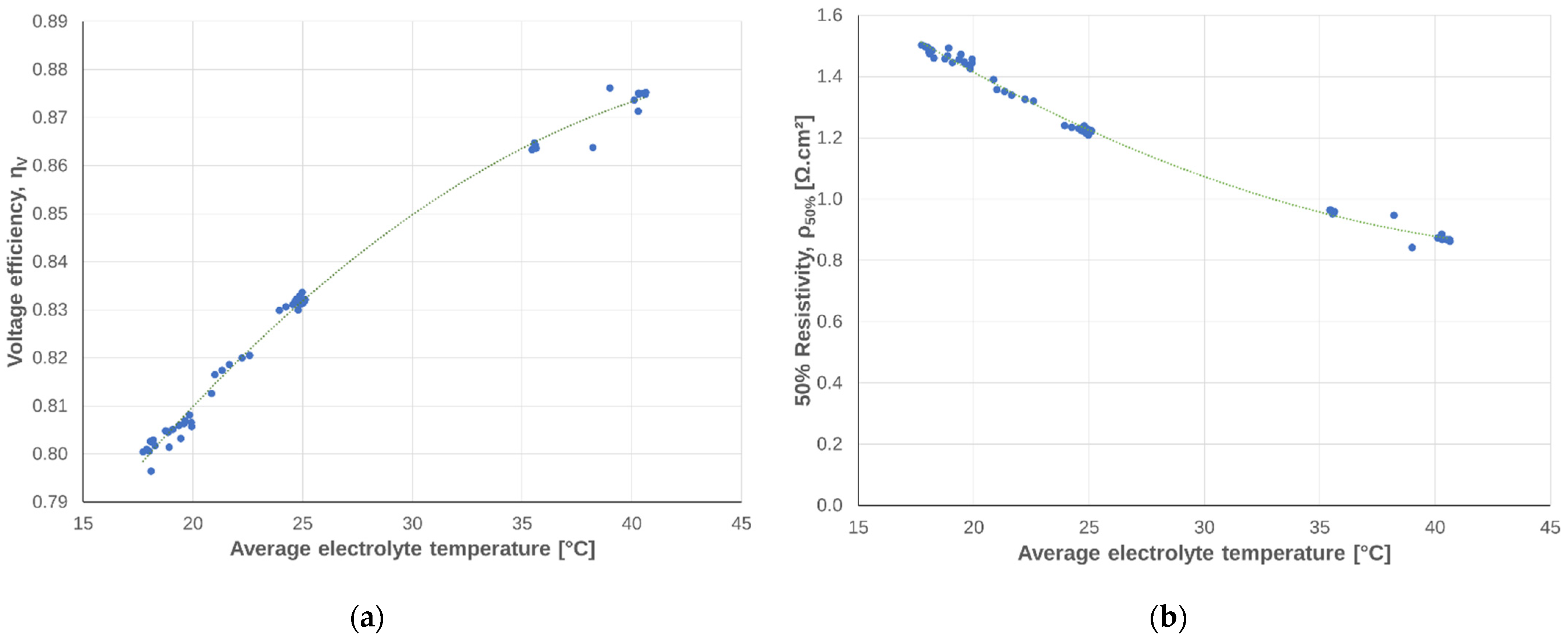
3.1.4. Dependency on Temperature
3.1.5. Dependency on Current Density
3.2. Self-Discharge Current Density, jsd, and Coulombic Efficiency, ηQ
3.2.1. General Considerations
3.2.2. Dependency on SOC
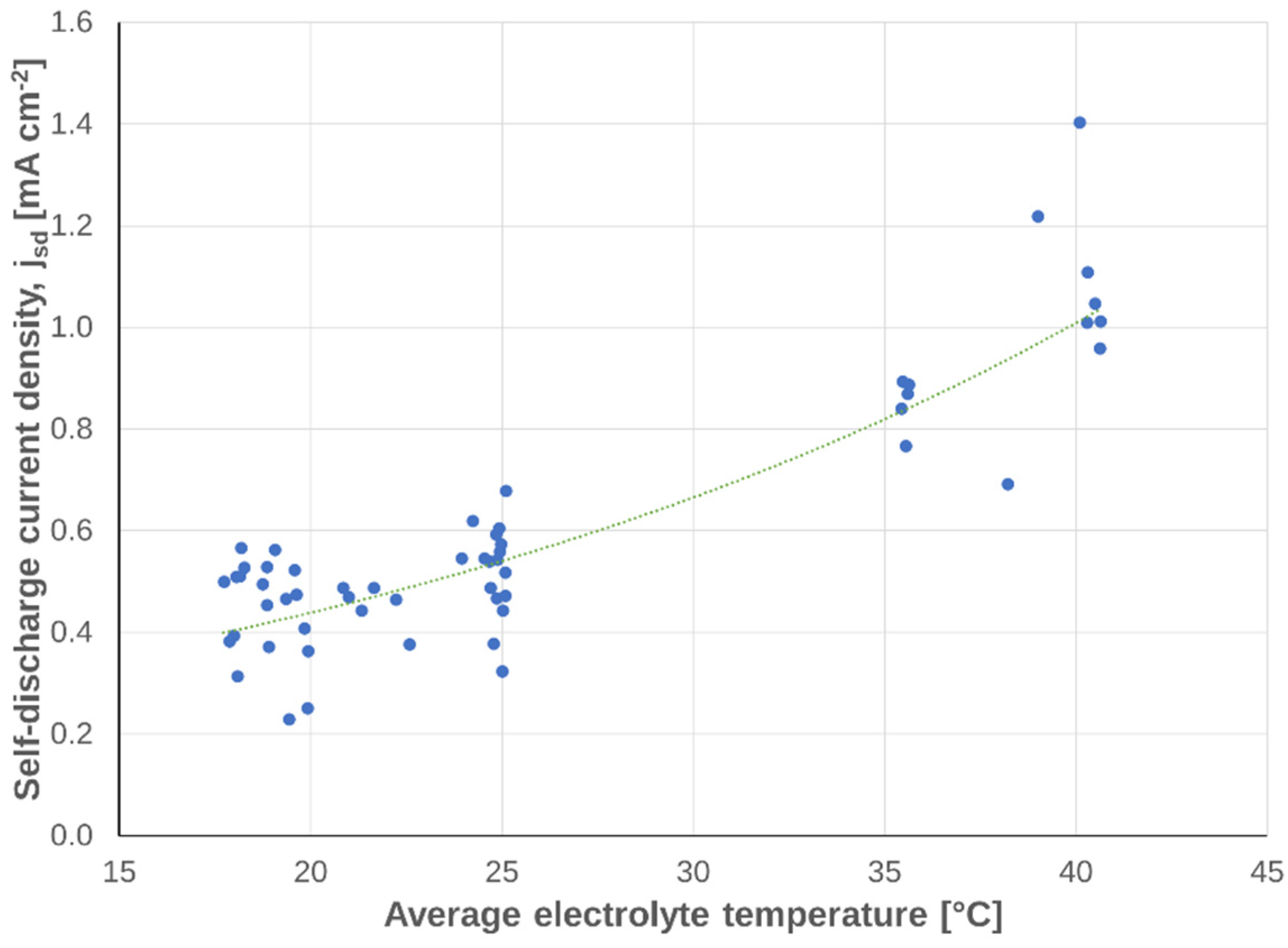
3.2.3. Dependency on Temperature
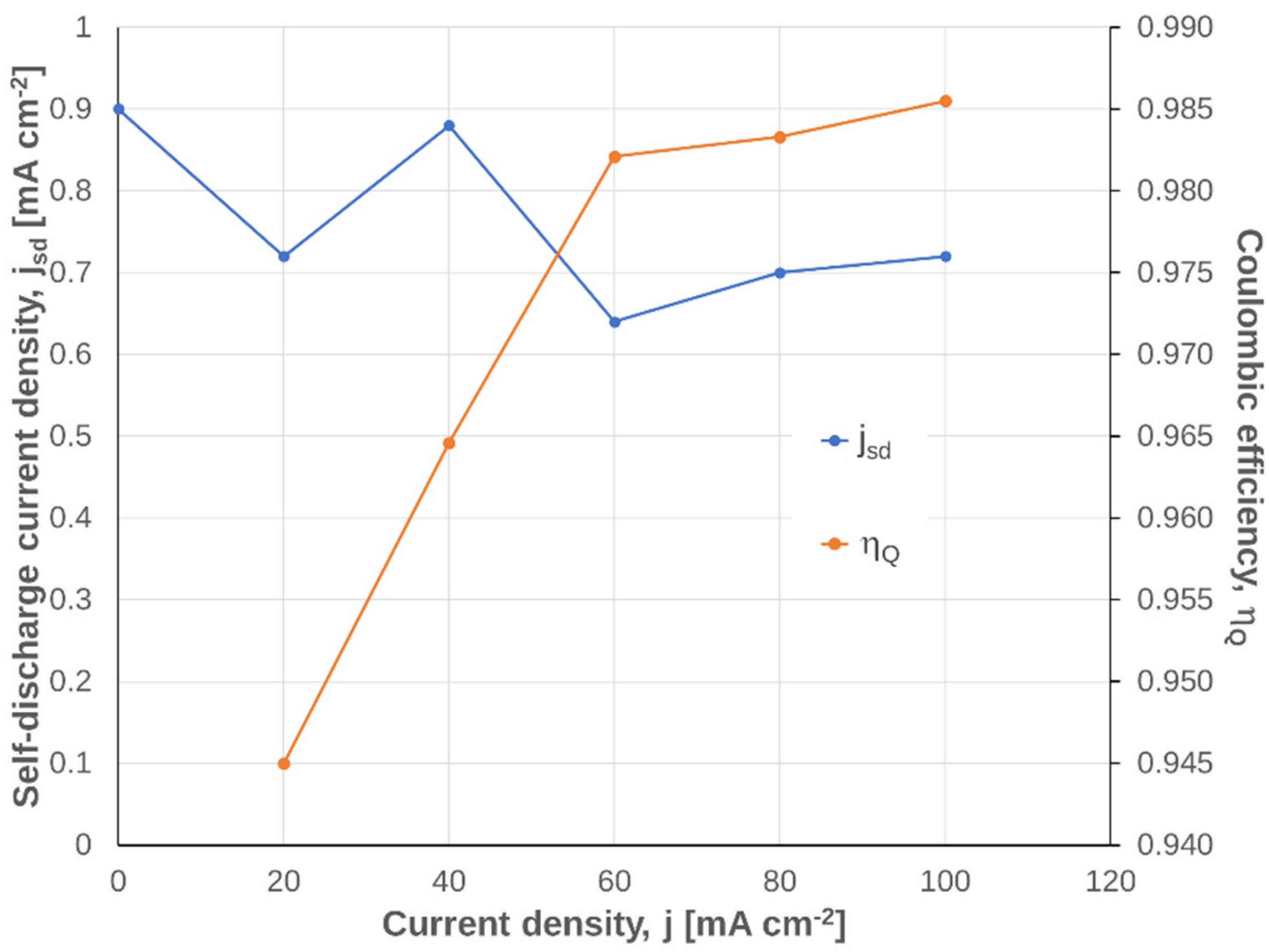
3.2.4. Dependency on Current Density
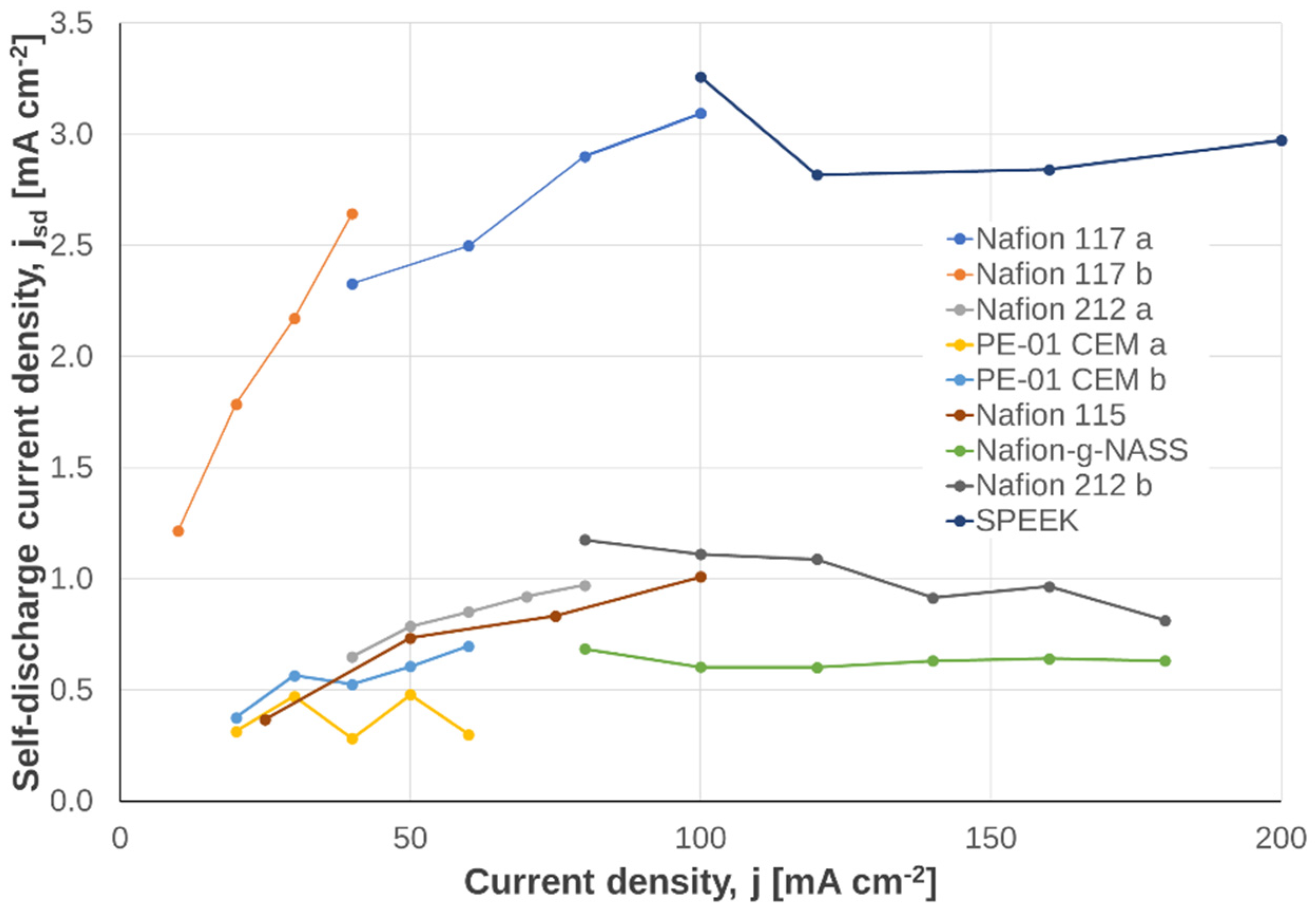
3.2.5. Additional Information
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Li, X.; Zhang, J. Redox Flow Batteries Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2018; p. 432. [Google Scholar]
- Perry, M.L.; Weber, A.Z. Advanced redox-flow batteries: A perspective. J. Electrochem. Soc. 2016, 163, A5064–A5067. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Kazacos, G.; Poon, G.; Verseema, H. Recent advances with UNSW vanadium-based redox flow batteries. Int. J. Energy Res. 2010, 34, 182–189. [Google Scholar] [CrossRef]
- Díaz-Ramírez, M.C.; Ferreira, V.J.; García-Armingol, T.; López-Sabirón, A.M.; Ferreira, G. Environmental Assessment of Electrochemical Energy Storage Device Manufacturing to Identify Drivers for Attaining Goals of Sustainable Materials 4.0. Sustainability 2020, 12, 342. [Google Scholar] [CrossRef]
- Bielitz, C. Life-Cycle Assessment of Battery Technologies for Electricity Storage. Master’s Thesis, ETH Zürich, PSI, Zürich, Switzerland, 2016. [Google Scholar]
- Jones, C.; Gilbert, P.; Stamford, L. Assessing the Climate Change Mitigation Potential of Stationary Energy Storage for Electricity Grid Services. Environ. Sci. Technol. 2020, 54, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Türker, B. Modeling and Utilzing a Vanadium Redox Flow Battery for Easier Grid and Market Integration of Wind Power. Master’s Thesis, Universität Bremen, Bremen, Germany, 2014. [Google Scholar]
- Zhang, X.; Li, Y.; Skyllas-Kazacos, M.; Bao, J. Optimal Sizing of Vanadium Redox Flow Battery Systems for Residential Applications Based on Battery Electrochemical Characteristics. Energies 2016, 9, 857. [Google Scholar] [CrossRef]
- Butler, P.C.; Robinson, C.E. Flowing electrolyte batteries. Test methods and results. J. Power Sources 1986, 17, 127–134. [Google Scholar] [CrossRef]
- Haddadi-Asl, V. Conductive Carbon-Polymer Composite Electrode. Ph.D. Thesis, UNSW, Sydney, Australia, 1995. [Google Scholar]
- Sun, C.; Chen, J.; Zhang, H.; Han, X.; Luo, Q. Investigations on transfer of water and vanadium ions across Nafion membrane in an operating vanadium redox flow battery. J. Power Sources 2010, 195, 890–897. [Google Scholar] [CrossRef]
- Whitehead, A.H. Benchmarking flow cell performance. In Proceedings of the International Flow Battery Forum (IFBF), Brussels, Belgium, 28–29 June 2022; pp. 84–86. [Google Scholar]
- Skyllas-Kazacos, M. G1 and G2 Vanadium Redox Batteries for Renewable Energy Storage. In Proceedings of the IRES 2006, Gelskirchen, Germany, 30–31 October 2006. [Google Scholar]
- Tam, N.D. Development of a Halide-Free, Stabilised Vanadium Redox Flow Battery Electrolyte. Ph.D. Thesis, Nanyang Technical University, Singapore, 2017. [Google Scholar]
- Bhattarai, A.; Ghimire, P.C.; Whitehead, A.; Schweiss, R.; Scherer, G.G.; Wai, N.; Hng, H.H. Novel Approaches for Solving the Capacity Fade Problem during Operation of a Vanadium Redox Flow Battery. Batteries 2018, 4, 48. [Google Scholar] [CrossRef]
- Liufeng, M.; Mianyan, H.; Klassen, A.P.; Harper, M.A.M. Redox Flow Battery and Method for Enabling Battery to Operate Continuously for Long Time. CN Patent CN 102055000, 29 October 2009. [Google Scholar]
- Qiu, G.; Dennison, C.R.; Knehr, K.W.; Kumbur, E.C.; Sun, Y. Pore-scale analysis of effects of electrode morphology and electrolyte flow conditions on performance of vanadium redox flow batteries. J. Power Sources 2012, 219, 223–234. [Google Scholar] [CrossRef]
- Chen, C.L.; Yeoh, H.K.; Chakrabarti, M.H. An enhancement to Vynnycky’s model for the all-vanadium redox flow battery. Electrochim. Acta 2014, 120, 167–179. [Google Scholar] [CrossRef]
- Goulet, M.-A.; Eikerling, M.; Kjeang, E. Direct measurement of electrochemical reaction kinetics in flow-through porous electrodes. Electrochem. Commun. 2015, 57, 14–17. [Google Scholar] [CrossRef]
- Roznyatovskaya, N.; Noack, J.; Pinkwart, K.; Tübke, J. Aspects of electron transfer processes in vanadium redox-flow batteries. Curr. Opin. Electrochem. 2020, 19, 42–48. [Google Scholar] [CrossRef]
- Banerjee, R.; Bevilacqua, N.; Eifert, L.; Zeis, R. Characterization of carbon felt electrodes for vanadium redox flow batteries—A pore network modeling approach. J. Energy Storage 2019, 21, 163–171. [Google Scholar] [CrossRef]
- Becker, M.; Bredemeyer, N.; Tenhumberg, N.; Turek, T. Polarization curve measurements combined with potential probe sensing for determining current density distribution in vanadium redox-flow batteries. J. Power Sources 2016, 307, 826–833. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.A.-Z.A.-Y. Modelling and Simulation of All-Vanadium Redox Flow Batteries. Ph.D. Thesis, University of Southampton, Southampton, UK, 2010. [Google Scholar]
- Bhattarai, A.; Whitehead, A.; Schweiss, R.; Scherer, G.G.; Wai, N.; Nguyen, T.D.; Ghimire, P.C.; Hng, H.H. “Power Drop Effect (PDE)” in operation of a vanadium redox flow battery. In Proceedings of the IFBF, Lausanne, Switzerland, 10–12 July 2018. [Google Scholar]
- Nguyen, T.D.; Whitehead, A.; Wai, N.; Ong, S.J.H.; Scherer, G.G.; Xu, Z.J. Equilibrium and Dynamic Absorption of Electrolyte Species in Cation/Anion Exchange Membranes of Vanadium Redox Flow Battery. ChemSusChem 2019, 12, 1076–1083. [Google Scholar] [CrossRef] [PubMed]
- Roznyatovskaya, N.V.; Fühl, M.; Roznyatovsky, V.A.; Noack, J.; Fischer, P.; Pinkwart, K.; Tübke, J. The influence of free acid in VRFB electrolyte on “power drop” effect and thermally-induced degradation. Energy Technol. 2020, 8, 2000445. [Google Scholar] [CrossRef]
- Mazur, P.; Mrlik, J.; Charvat, J.; Pocedic, J.; Vrana, J.; Dundalek, J.; Kosek, J. A complex four-point method for the evaluation of ohmic and faradaic losses within a redox flow battery single-cell. MethodsX 2019, 6, 534–539. [Google Scholar] [CrossRef]
- Menictas, C. The Preparation and Feasibilty Study of Vanadium Electrolytes Prepared from Intermediate Vanadium Compounds and the Investigation of the Kinetics for the Dissolution of V2O5 in Vanadium Solution. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 1993. [Google Scholar]
- Lallo, E.; Khataee, A.; Lindström, R.W. Vanadium Redox Flow Battery Using Aemion™ Anion Exchange Membranes. Processes 2022, 10, 270. [Google Scholar] [CrossRef]
- Chieng, S.C.; Kazacos, M.; Skyllas-Kazacos, M. Preparation and evaluation of composite membrane for vanadium redox battrey applications. J. Power Sources 1992, 39, 11–19. [Google Scholar] [CrossRef]
- Jiang, H.R.; Shyy, W.; Ren, Y.X.; Zhang, R.H.; Zhao, T.S. A room-temperature activated graphite felt as the cost-effective, highly active and stable electrode for vanadium redox flow batteries. Appl. Energy 2019, 233–234, 544–553. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Dynamic modelling of the effects of ion diffusion and side reactions on the capacity loss for vanadium redox flow battery. J. Power Sources 2011, 196, 10737–10747. [Google Scholar] [CrossRef]
- Lutz, C.; Hampel, S.; Ke, X.; Beuermann, S.; Turek, T.; Kunz, U.; Buzanich, A.G.; Radtke, M.; Fittschen, U.E.A. Evidence for redox reactions during vanadium crossover inside the nanoscopic water-body of Nafion 117 using X-ray absorption near edge structure spectroscopy. J. Power Sources 2021, 483, 229176. [Google Scholar] [CrossRef]
- Elgammal, R.A.; Tang, Z.; Sun, C.N.; Lawton, J.; Zawodzinski, T.A. Species Uptake and Mass Transport in Membranes for Vanadium Redox Flow Batteries. Electrochim. Acta 2017, 237, 1–11. [Google Scholar] [CrossRef]
- Wei, L.; Zhao, T.S.; Zeng, L.; Zhou, X.L.; Zeng, Y.K. Copper nanoparticle-deposited graphite felt electrodes for all vanadium redox flow batteries. Appl. Energy 2016, 180, 386–391. [Google Scholar] [CrossRef]
- Agar, E. Species Transport Mechanisms Governing Crossover and Capacity Loss in Vanadium Redox Flow Batteries. Ph.D. Thesis, Drexel University, Philadelphia, PA, USA, 2014. [Google Scholar]
- Chen, D.; Hickner, M.A.; Agar, E.; Kumbur, E.C. Selective anion exchange membranes for high coulombic efficiency vanadium redox flow batteries. Electrochem. Commun. 2013, 26, 37–40. [Google Scholar]
- Zhao, N.; Riley, H.; Song, C.; Jiang, Z.; Tsay, K.-C.; Neagu, R.; Shi, Z. Ex-Situ Evaluation of Commercial Polymer Membranes for Vanadium Redox Flow Batteries (VRFBs). Polymers 2021, 13, 926. [Google Scholar] [CrossRef]
- Benjamin, A.; Agar, E.; Dennison, C.R.; Kumbu, E.C. On the quantification of coulombic efficiency for vanadium redox flow batteries: Cutoff voltages vs. state-of-charge limits. Electrochem. Commun. 2013, 35, 42–44. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Y.; Liu, L.; Xi, J.; Wu, Z.; Qiu, X. Broad temperature adaptability of vanadium redox flow battery-Part 3: The effects of total vanadium concentration and sulfuric acid concentration. Electrochim. Acta 2018, 259, 11–19. [Google Scholar] [CrossRef]
- Xi, J.; Jiang, B.; Yu, L.; Liu, L. Membrane evaluation for vanadium flow batteries in a temperature range of −20–50 °C. J. Membrane Sci. 2017, 522, 45–55. [Google Scholar] [CrossRef]
- Gandomi, Y.A.; Aaron, D.S.; Mench, M.M. Coupled Membrane Transport Parameters for Ionic Species in All-Vanadium Redox Flow Batteries. Electrochim. Acta 2016, 218, 174–190. [Google Scholar] [CrossRef]
- Kim, J.; Lee, Y.; Jeon, J.D.; Kwak, S.Y. Ion-exchange composite membranes pore-filled with sulfonated poly(ether ether ketone) and Engelhard titanosilicate-10 for improved performance of vanadium redox flow batteries. J. Power Sources 2018, 383, 1–9. [Google Scholar] [CrossRef]
- Sha’rani, S.S.; Jusoh, N.W.C.; Abouzari-Lotf, E.; Ahmad, A.; Ali, R.R. Evaluation of Perfluorinated Sulfonic Acid Membranes for Vanadium Redox. IOCP Conf. Ser. Mater. Sci. Eng. 2020, 808, 012026. [Google Scholar] [CrossRef]
- Qian, P.; Zhang, H.; Chen, J.; Wen, Y.; Luo, Q.; Liu, Z.; You, D.; Yi, B. A novel electrode-bipolar plate assembly for vanadium redox flow battery applications. J. Power Sources 2008, 175, 613–620. [Google Scholar] [CrossRef]
- Yue, L.; Li, W.; Sun, F.; Zhao, L.; Xing, L. Highly hydroxylated carbon fibres as electrode materials of all-vanadium redox flow battery. Carbon 2010, 48, 3079–3090. [Google Scholar] [CrossRef]
- Wu, X.; Xu, H.; Xu, P.; Shen, Y.; Lu, L.; Shi, J.; Fu, J.; Zhao, H. Microwave-treated graphite felt as the positive electrode for all-vanadium redox flow battery. J. Power Sources 2014, 263, 104–109. [Google Scholar] [CrossRef]
- Su, A.-Q.; Wang, N.-F.; Liu, S.-Q.; Wu, T.; Peng, S. Modification of carbon paper via hydrothermal oxidation for vanadium redox battery. Acta Phys. Chim. Sin. 2012, 28, 1387–1392. [Google Scholar]
- Wu, T.; Huang, K.; Liu, S.; Zhuang, S.; Fang, D.; Li, S.; Lu, D.; Su, A. Hydrothermal ammoniated treatment of PAN-graphite felt for vanadium redox flow battery. J. Solid State Electrochem. 2012, 16, 579–585. [Google Scholar] [CrossRef]
- Bellani, S.; Najafi, L.; Prato, M.; Oropesa-Nunñez, R.; Martín-García, B.; Gagliani, L.; Mantero, E.; Marasco, L.; Bianca, G.; Zappia, M.I.; et al. Graphene-Based Electrodes in a Vanadium Redox Flow Battery Produced by Rapid Low-Pressure Combined Gas Plasma Treatments. Chem. Mater. 2021, 33, 4106–4121. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-H.; Yang, M.-C.; Wei, H.-J. Method of Fabricating Separating Membrane of Flow Battery for Achieving Low Impedance and Low Permeability. TW Patent TW 201933654, 18 January 2018. [Google Scholar]
- Zhao, L.; Xiao, W.; Liu, J.; Yan, C. Preparation of All-Vanadium Flow Battery with Low-Cost Composite Proton Exchange Membrane. CN Patent CN 106972185, 14 January 2016. [Google Scholar]
- Lawton, J.S.; Jones, A.; Zawodzinski, T. Concentration dependence of VO2+ crossover of Nafion for vanadium redox flow batteries. J. Electrochem. Soc. 2013, 160, A697–A702. [Google Scholar] [CrossRef]
- Hagedorn, N.; Hoberecht, M.A.; Thaller, L.H. NASA Redox Cell Stack Shunt Current, Pumping Power, and Cell Performance Tradeoffs; DOE/NASA/12726-11 NASA TM-82686; National Aeronautics and Space Administration, Lewis Research Centre: Cleveland, OH, USA, February 1982. [Google Scholar]
| Metric | Sensitivity | ||
|---|---|---|---|
| Cycle Limits (SOC Limits) | Current Density | Electrolyte Temperature | |
| Voltage efficiency, ηV | Some | Strong | Strong |
| 50% Resistivity, ρ50% | None | Almost none | Strong |
| Coulombic efficiency, ηQ | Strong | Strong | Strong |
| Self-discharge current density, jsd | Almost none | Almost none to strong | Strong |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Whitehead, A.H.; Robertson, A.; Martin, B.; Martin, E.; Wilson, E. Experimental Benchmarking of Redox Flow Cells. Batteries 2022, 8, 207. https://doi.org/10.3390/batteries8110207
Whitehead AH, Robertson A, Martin B, Martin E, Wilson E. Experimental Benchmarking of Redox Flow Cells. Batteries. 2022; 8(11):207. https://doi.org/10.3390/batteries8110207
Chicago/Turabian StyleWhitehead, Adam H., Alasdair Robertson, Benjamin Martin, Elisha Martin, and Emma Wilson. 2022. "Experimental Benchmarking of Redox Flow Cells" Batteries 8, no. 11: 207. https://doi.org/10.3390/batteries8110207
APA StyleWhitehead, A. H., Robertson, A., Martin, B., Martin, E., & Wilson, E. (2022). Experimental Benchmarking of Redox Flow Cells. Batteries, 8(11), 207. https://doi.org/10.3390/batteries8110207









