Development of a Data-Driven Method for Online Battery Remaining-Useful-Life Prediction
Abstract
1. Introduction
- A specific indirect HI is extracted from the charge monitoring data. A correlation analysis is used to show that these indirect HIs accurately reflect the capacity. Therefore, complicated measurements or elaborate calculations are no longer needed.
- The combination of soft-sensing and GRU NN with sliding window produces a model capable of both accurate state-of-health estimation and reliable long-term RUL prediction using historical data sets.
- Dropout and early stopping methods were also used to prevent overfitting.
- The effectiveness of the method is validated and verified by the real-world NASA data set.
2. Gated Recurrent Unit Neural Network
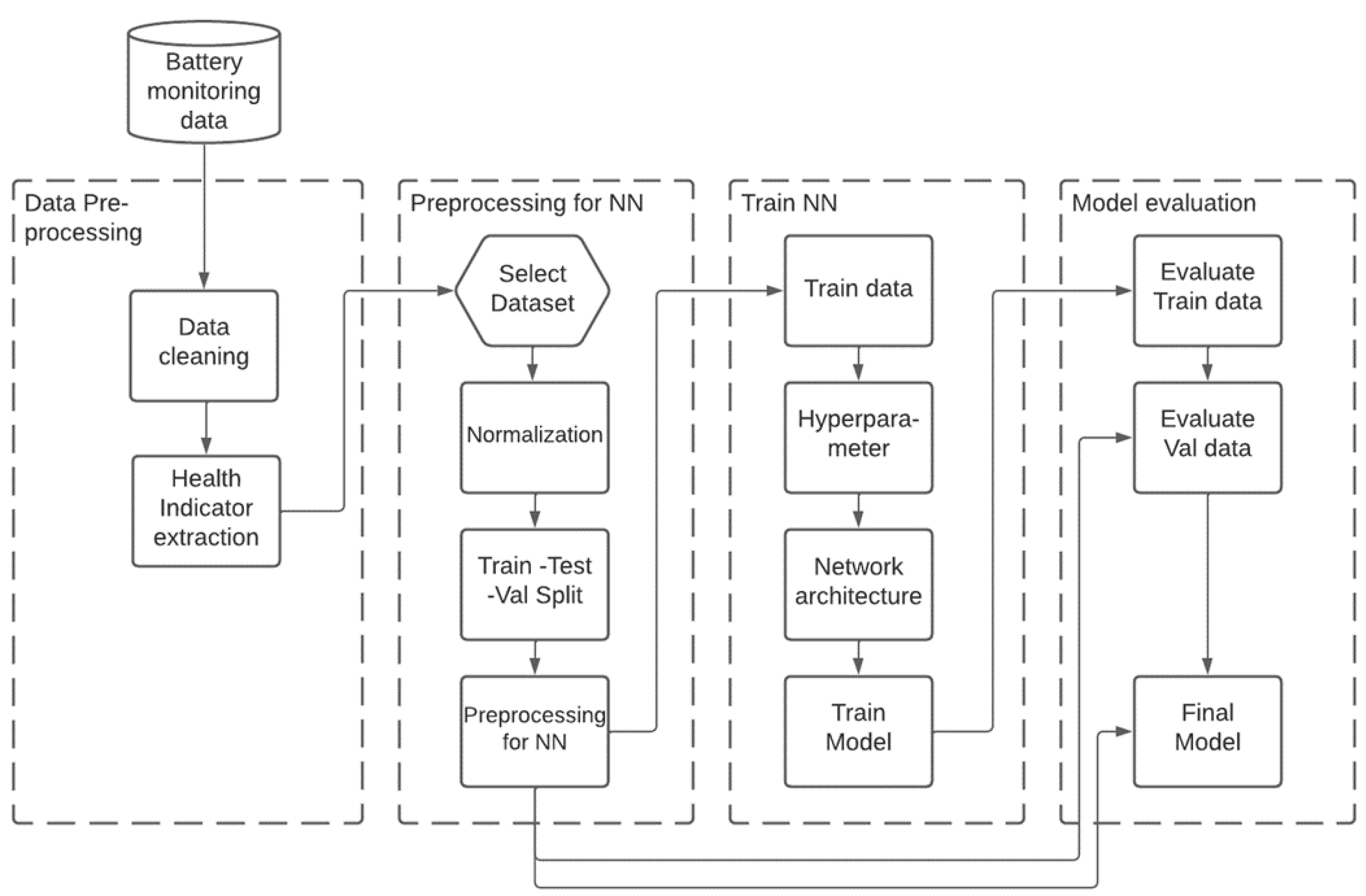
3. Data Preparation
3.1. Test Data
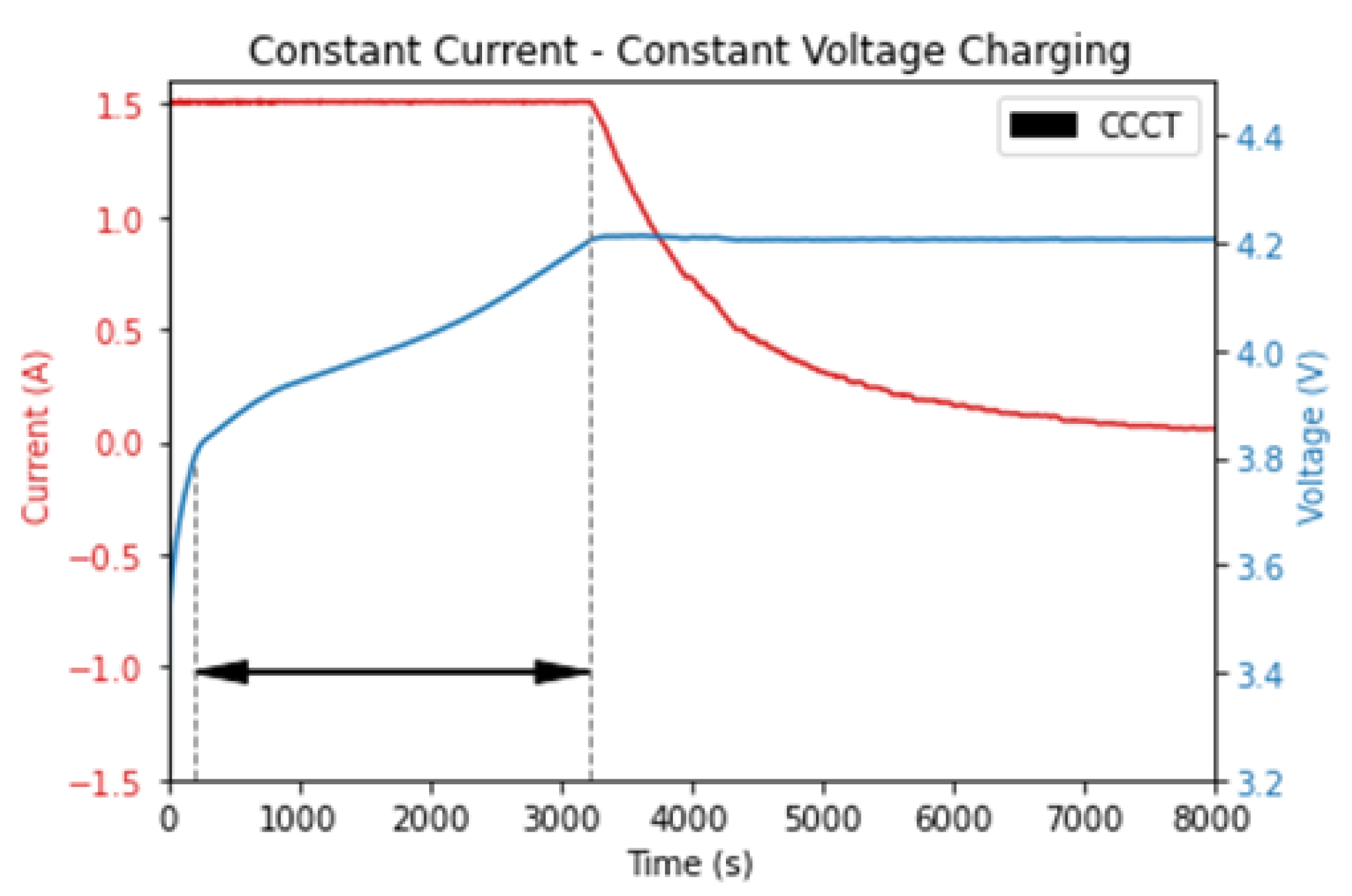
3.2. Health Indicator Extraction
3.3. Correlation Analysis
4. Algorithm and Approach
4.1. General Algorithm
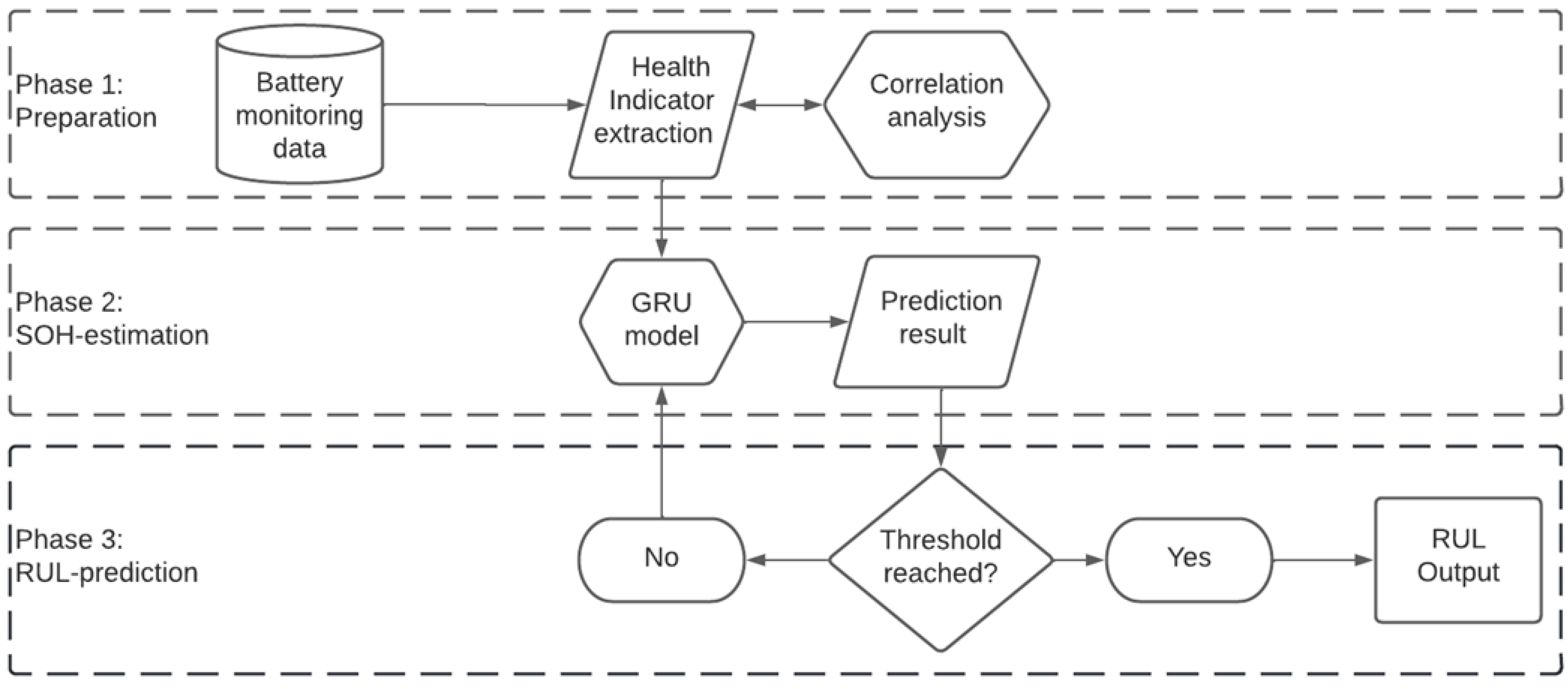
4.2. SOH Estimation Framework
4.3. Approach
4.3.1. Data Set Selection
4.3.2. Hyperparameter Optimization
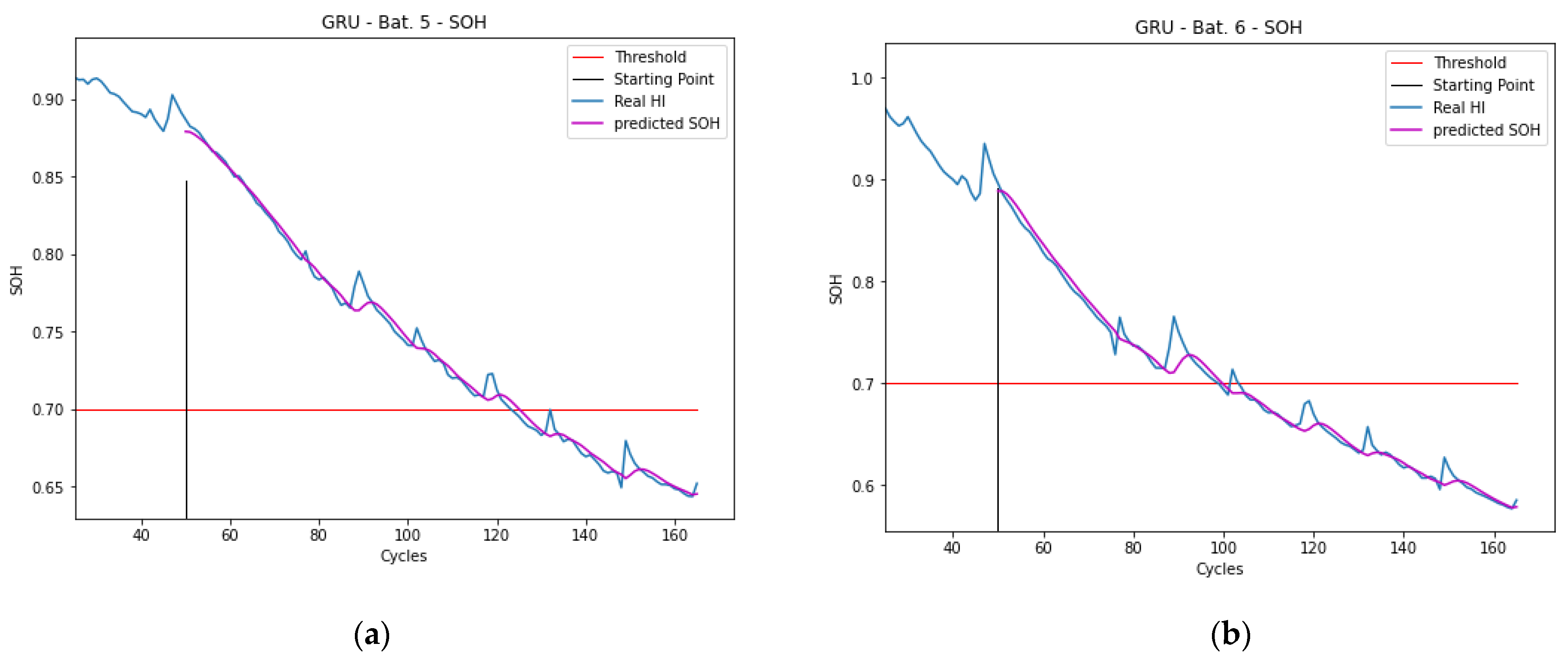
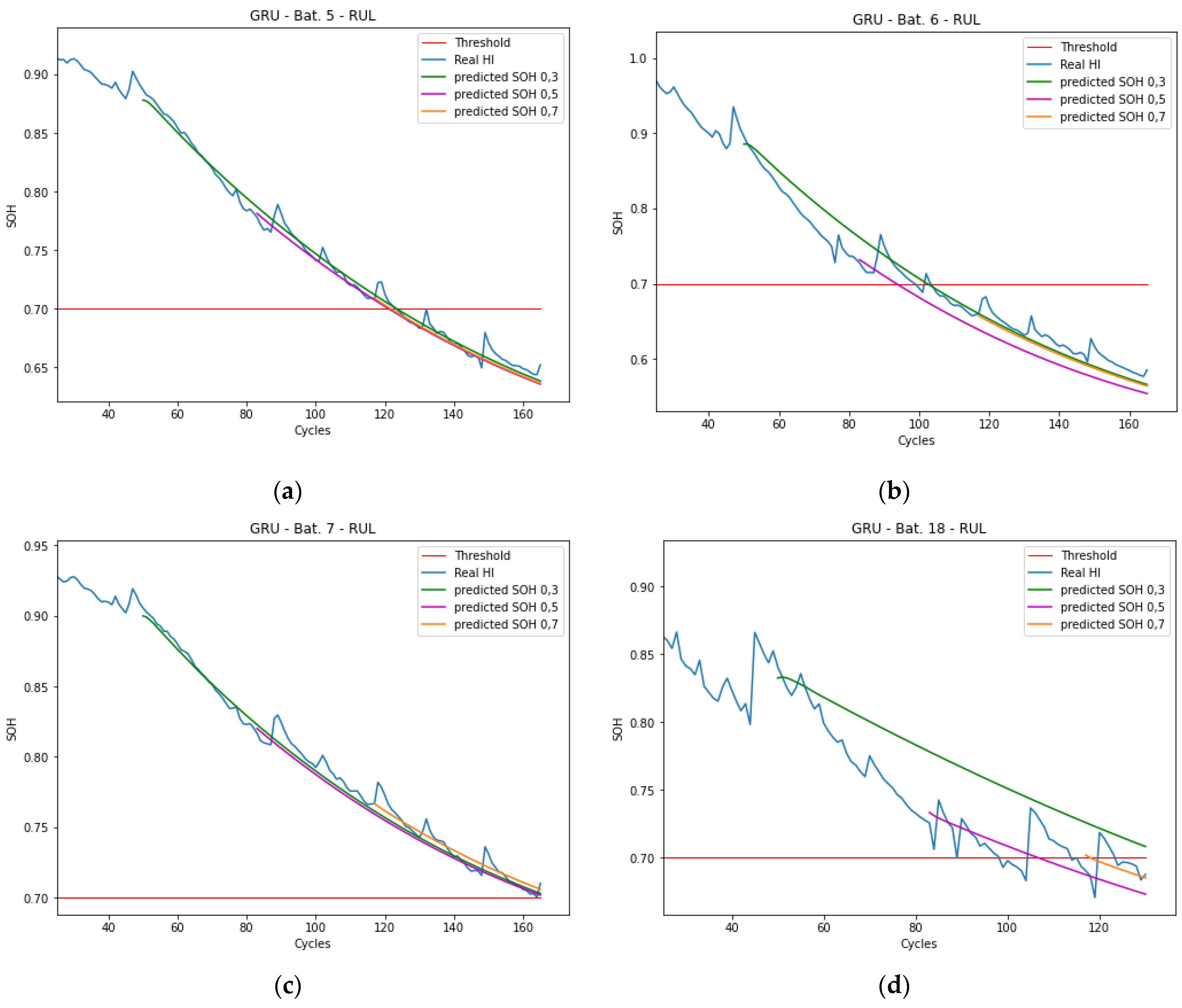
5. Results and Discussion
5.1. Evaluation Parameters
5.2. SOH Results Analysis
5.3. RUL Results Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Korthauer, R. Handbuch Lithium-Ionen-Batterien; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bundes-Ministerium für Wirtschaft und Klimaschutz, “bmwk.de”. Available online: https://www.bmwk.de/Redaktion/DE/Dossier/elektromobilitaet.html (accessed on 15 July 2022).
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Sources 2013, 239, 253–264. [Google Scholar] [CrossRef]
- Hao, J.; Jing, L.; Ke, H.-L.; Wang, Y.; Gao, Q.; Wang, X.-X.; Sun, Q.; Xu, Z.-J. Determination of cut-off time of accelerated aging test under temperature stress for LED lamps. Front. Inf. Technol. Electron. Eng. 2017, 18, 1197–1204. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q.; Widanage, W.D. A Data-Driven Approach With Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-ion Battery. IEEE Trans. Ind. Electron. 2021, 68, 3170–3180. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Qu, J.; Liu, F.; Ma, Y.; Fan, J. A Neural-Network-Based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 2019, 7, 87178–87191. [Google Scholar] [CrossRef]
- Jin, S.; Sui, X.; Huang, X.; Wang, S.; Teodorescu, R.; Stroe, D.-I. Overview of Machine Learning Methods for Lithium-Ion Battery Remaining Useful Lifetime Prediction. Electronics 2021, 10, 3126. [Google Scholar] [CrossRef]
- Lui, Y.H.; Li, M.; Downey, A.; Shen, S.; Nemani, V.P.; Ye, H.; VanElzen, C.; Jain, G.; Hu, S.; Laflamme, S.; et al. Physics-based prognostics of implantable-grade lithium-ion battery for remaining useful life prediction. J. Power Sources 2021, 485, 229327. [Google Scholar] [CrossRef]
- Wang, S.; Jin, S.; Deng, D.; Fernandez, C. A Critical Review of Online Battery Remaining Useful Lifetime Prediction Methods. Front. Mech. Eng. 2021, 7, 719718. [Google Scholar] [CrossRef]
- Wu, Y.; Li, W.; Wang, Y.; Zhang, K. Remaining Useful Life Prediction of Lithium-Ion Batteries Using Neural Network and Bat-Based Particle Filter. IEEE Access 2019, 7, 54843–54854. [Google Scholar] [CrossRef]
- She, C.; Wang, Z.; Sun, F.; Liu, P.; Zhang, L. Battery Aging Assessment for Real-World Electric Buses Based on Incremental Capacity Analysis and Radial Basis Function Neural Network. IEEE Trans. Ind. Inform. 2019, 16, 3345–3354. [Google Scholar] [CrossRef]
- Zhou, D.; Li, Z.; Zhu, J.; Zhang, H.; Hou, L. State of Health Monitoring and Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Temporal Convolutional Network. IEEE Access 2020, 8, 53307–53320. [Google Scholar] [CrossRef]
- Zhao, Q.; Qin, X.; Zhao, H.; Feng, W. A novel prediction method based on the support vector regression for the remaining useful life of lithium-ion batteries. Microelectron. Reliab. 2018, 85, 99–108. [Google Scholar] [CrossRef]
- Wang, F.-K.; Mamo, T. A hybrid model based on support vector regression and differential evolution for remaining useful lifetime prediction of lithium-ion batteries. J. Power Sources 2018, 401, 49–54. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining Useful Life Prediction and State of Health Diagnosis for Lithium-Ion Batteries Using Particle Filter and Support Vector Regression. IEEE Trans. Ind. Electron. 2018, 65, 5634–5643. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Park, K.; Choi, Y.; Choi, W.J.; Ryu, H.-Y.; Kim, H. LSTM-Based Battery Remaining Useful Life Prediction With Multi-Channel Charging Profiles. IEEE Access 2020, 8, 20786–20798. [Google Scholar] [CrossRef]
- Lee, C.-J.; Kim, B.-K.; Kwon, M.-K.; Nam, K.; Kang, S.-W. Real-Time Prediction of Capacity Fade and Remaining Useful Life of Lithium-Ion Batte-ries Based on Charge/Discharge Characteristics. Electronics 2021, 10, 846. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Wang, H.; Wang, Y.; An, J.; Yang, R.; Pan, H. Remaining Useful Life Prediction of Battery Using a Novel Indicator and Framework With Fractional Grey Model and Unscented Particle Filter. IEEE Trans. Power Electron. 2020, 35, 5850–5859. [Google Scholar] [CrossRef]
- Abdulwahab, S. Deep Learning Models for Paraphrases Identification. Master’s Thesis, Universitat Rovira I Virgili, Tarragona, Spain, 2017. [Google Scholar]
- Saha, B.; Goebel, K. NASA Ames Prognostics Data Repository. 2007. Available online: https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/ (accessed on 28 April 2022).
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]


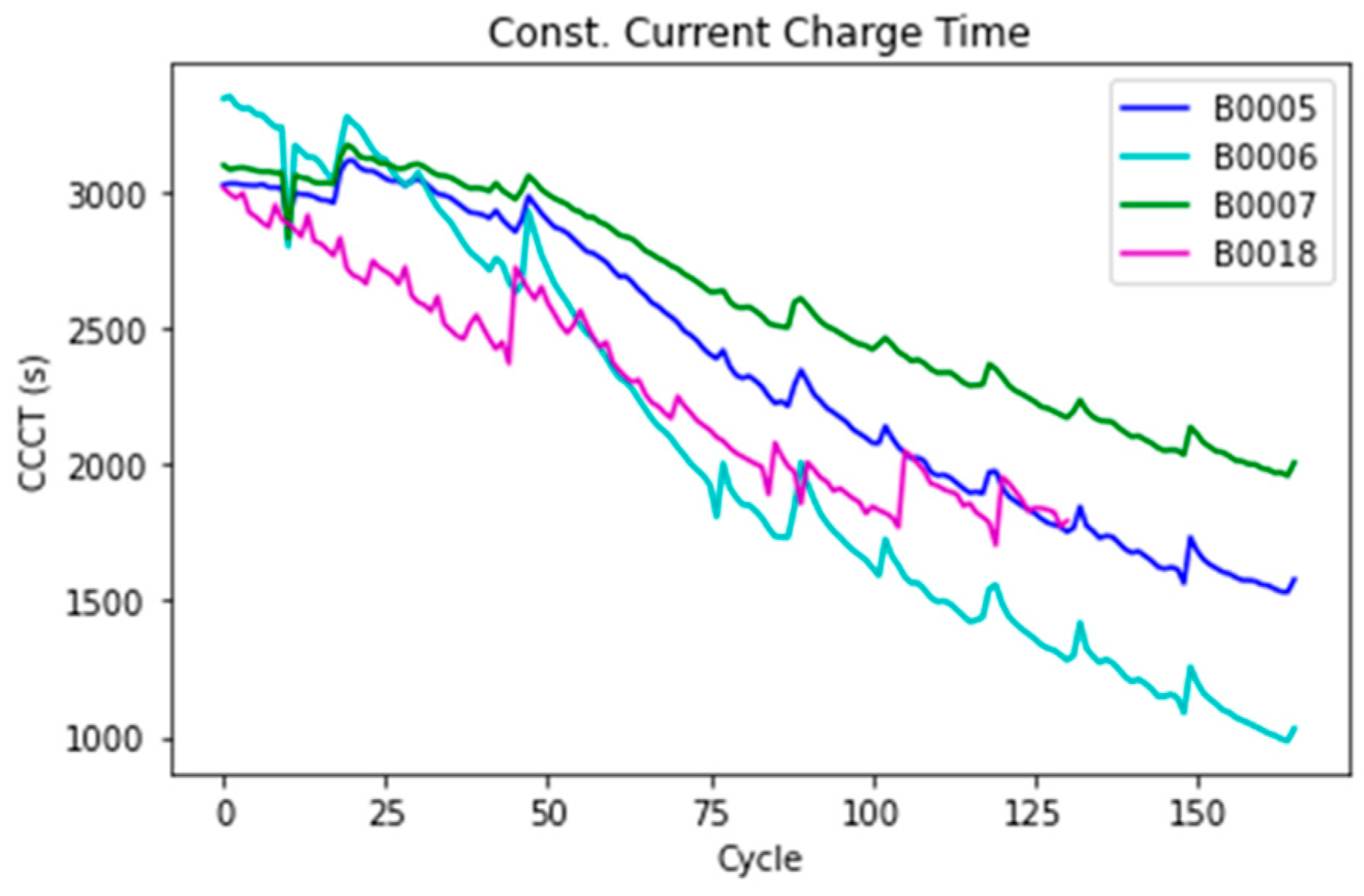

| Correlation between CCCT and Capacity | Bat. 5 | Bat. 6 | Bat. 7 | Bat. 18 |
|---|---|---|---|---|
| Spearman: | 0.993 | 0.996 | 0.992 | 0.975 |
| Pearson: | 0.997 | 0.993 | 0.990 | 0.986 |
| Test | Train | Val |
|---|---|---|
| Bat. 5 | Bat. 7 and 18 | Bat. 6 |
| Bat. 6 | Bat. 5 and 18 | Bat. 7 |
| Bat. 7 | Bat. 6 and 18 | Bat. 5 |
| Bat. 18 | Bat. 6 and 7 | Bat. 5 |
| Description | Parameter |
|---|---|
| Sequence length | 10 |
| Learning rate | 9 × 10−4 |
| Number of Epochs | 100 |
| Batch size | 16 |
| Optimizer | Adam |
| Loss | Mean Square Error |
| Battery | RMSE | MAE | R2 |
|---|---|---|---|
| Bat. 5 | 0.0060 | 0.0041 | 0.993 |
| Bat. 6 | 0.0103 | 0.0065 | 0.984 |
| Bat. 7 | 0.0056 | 0.0037 | 0.991 |
| Bat. 18 | 0.0121 | 0.0089 | 0.925 |
| Battery | Starting Point | Real RUL | Pred. RUL | AE RUL |
|---|---|---|---|---|
| Bat. 5 | 0.3 | 75 | 75 | 0 |
| 0.5 | 42 | 40 | −2 | |
| 0.7 | 8 | 6 | −2 | |
| Bat. 6 | 0.3 | 50 | 54 | 4 |
| 0.5 0.7 | 17 - | 12 - | −5 - | |
| Bat. 7 | 0.3 | 115 | 120 | 5 |
| 0.5 | 82 | 85 | 3 | |
| 0.7 | 48 | 56 | 8 | |
| Bat.18 | 0.3 | 47 | - | - |
| 0.5 0.7 | 14 - | 25 - | 11 - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hell, S.M.; Kim, C.D. Development of a Data-Driven Method for Online Battery Remaining-Useful-Life Prediction. Batteries 2022, 8, 192. https://doi.org/10.3390/batteries8100192
Hell SM, Kim CD. Development of a Data-Driven Method for Online Battery Remaining-Useful-Life Prediction. Batteries. 2022; 8(10):192. https://doi.org/10.3390/batteries8100192
Chicago/Turabian StyleHell, Sebastian Matthias, and Chong Dae Kim. 2022. "Development of a Data-Driven Method for Online Battery Remaining-Useful-Life Prediction" Batteries 8, no. 10: 192. https://doi.org/10.3390/batteries8100192
APA StyleHell, S. M., & Kim, C. D. (2022). Development of a Data-Driven Method for Online Battery Remaining-Useful-Life Prediction. Batteries, 8(10), 192. https://doi.org/10.3390/batteries8100192





