A Perspective on Li/S Battery Design: Modeling and Development Approaches
Abstract
:1. Introduction
2. Modeling Methodologies
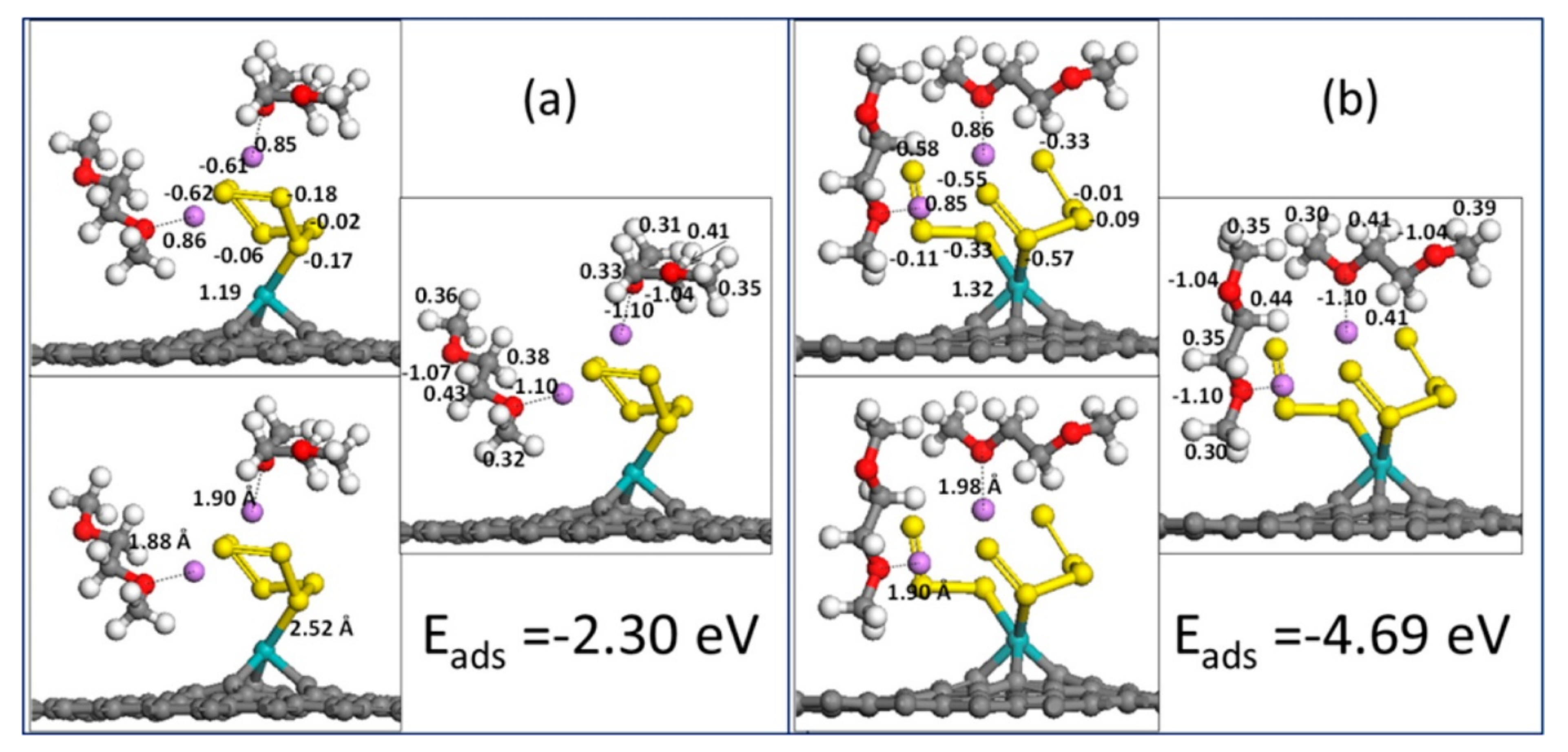
2.1. Density Functional Theory
2.1.1. Application
2.1.2. Challenges
2.1.3. Perspective
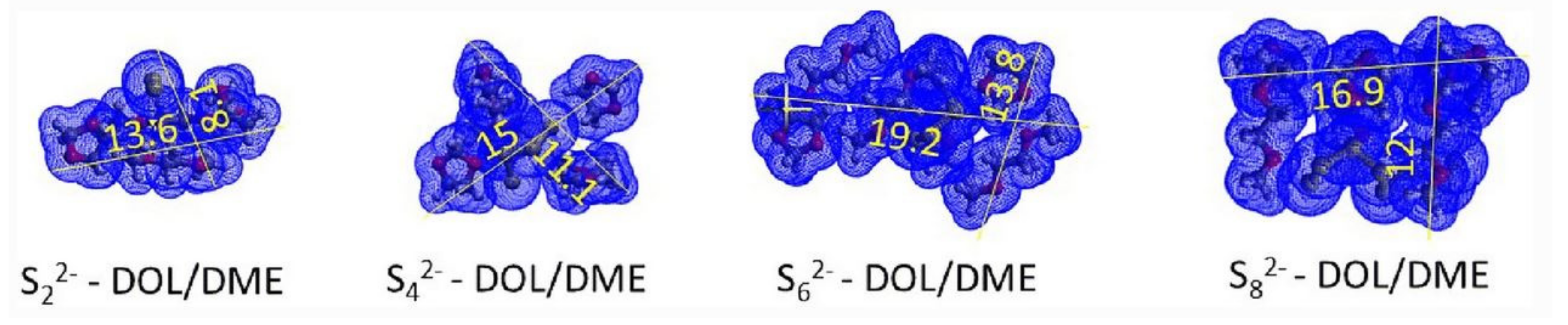
2.2. Molecular Dynamics
2.2.1. Application
2.2.2. Challenges
2.2.3. Perspective
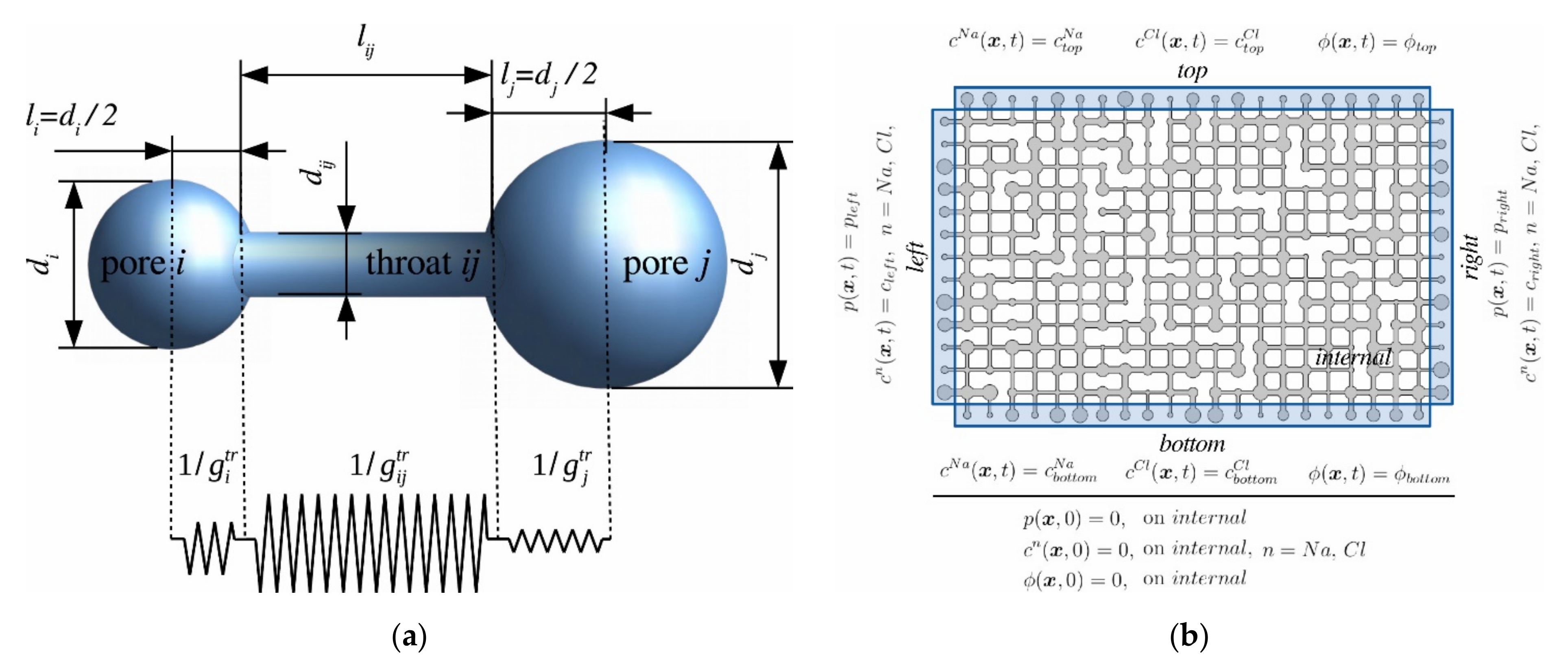
2.3. Continuum Models
2.3.1. Application
2.3.2. Challenges
2.3.3. Perspective
2.4. Modeling and Manufacturing
3. Challenges in the Design and Development of Li/S Cell Components
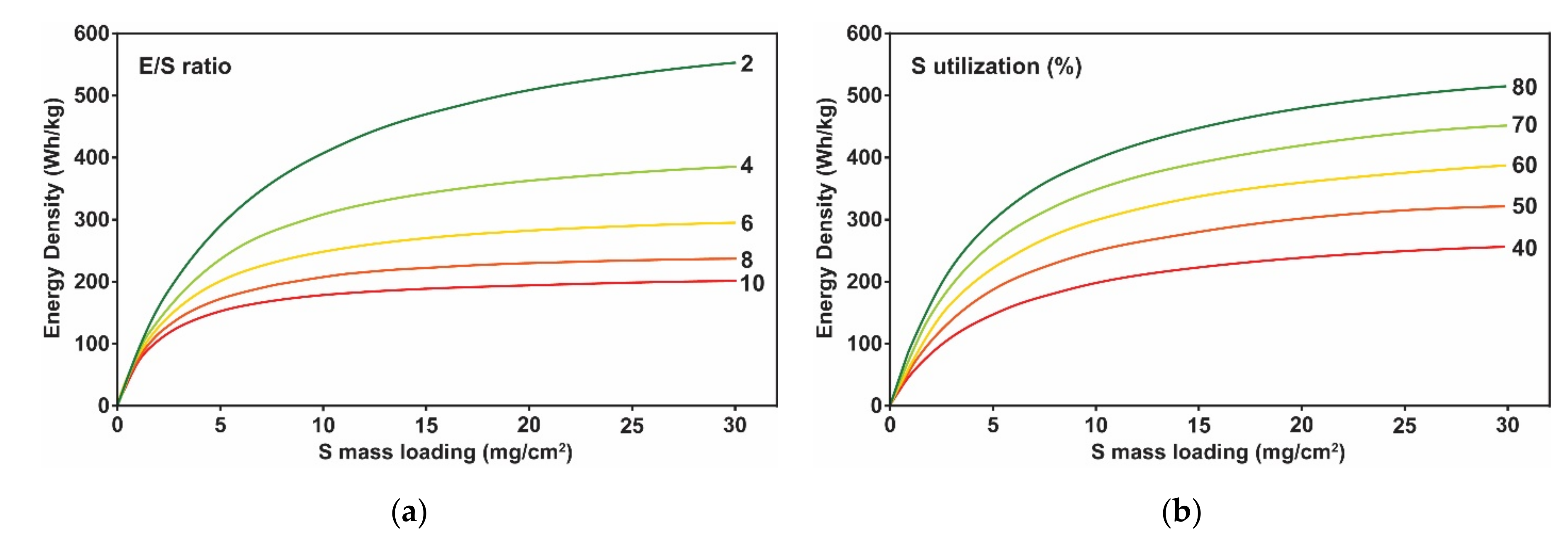
3.1. Sulfur Electrode Design Challenges
3.2. Challenges in Lithium Metal Electrode
3.3. Electrolyte Design Challenges
3.4. Separator Design Challenges
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- The Paris Agreement|UNFCCC. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 23 August 2021).
- Coronese, M.; Lamperti, F.; Keller, K.; Chiaromonte, F.; Roventini, A. Evidence for sharp increase in the economic damages of extreme natural disasters. Proc. Natl. Acad. Sci. USA 2019, 116, 21450–21455. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.V.; Perry, S.; Klemeš, J.J.; Lee, C.T. A review on air emissions assessment: Transportation. J. Clean. Prod. 2018, 194, 673–684. [Google Scholar] [CrossRef]
- Reddy, M.V.; Mauger, A.; Julien, C.M.; Paolella, A.; Zaghib, K. Brief History of Early Lithium-Battery Development. Materials 2020, 13, 1884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, S.; Wang, G. Advanced Lithium-Ion Batteries for Practical Applications: Technology, Development, and Future Perspectives. Adv. Mater. Technol. 2018, 3, 1700376. [Google Scholar] [CrossRef]
- Vernardou, D. Progress and Challenges in Industrially Promising Chemical Vapour Deposition Processes for the Synthesis of Large-Area Metal Oxide Electrode Materials Designed for Aqueous Battery Systems. Materials 2021, 14, 4177. [Google Scholar] [CrossRef] [PubMed]
- Thackeray, M.M.; Wolverton, C.; Isaacs, E.D. Electrical energy storage for transportation—Approaching the limits of, and going beyond, lithium-ion batteries. Energy Environ. Sci. 2012, 5, 7854–7863. [Google Scholar] [CrossRef]
- Frey, H.C.; Kuo, P.-Y. Assessment of Potential Reduction in Greenhouse Gas (GHG) Emissions in Freight Transportation; Emission Inventory Conference: Raleigh, NC, USA, 2007; pp. 15–17. [Google Scholar]
- Masias, A.; Marcicki, J.; Paxton, W.A. Opportunities and Challenges of Lithium Ion Batteries in Automotive Applications. ACS Energy Lett. 2021, 6, 621–630. [Google Scholar] [CrossRef]
- Sripad, S.; Viswanathan, V. Performance Metrics Required of Next-Generation Batteries to Make a Practical Electric Semi Truck. ACS Energy Lett. 2017, 2, 1669–1673. [Google Scholar] [CrossRef] [Green Version]
- Hasa, I.; Adelhelm, P.; Cao, G.; Mai, L. Batteries & Supercaps: Beyond Lithium-Ion Batteries. Batter. Supercaps 2021, 4, 1036–1038. [Google Scholar]
- Robinson, J.; Xi, K.; Kumar, R.V.; Ferrari, A.C.; Au, H.; Titirici, M.-M.; Puerto, A.P.; Kucernak, A.; Fitch, S.D.S.; Garcia-Araez, N.; et al. 2021 Roadmap on Lithium Sulfur Batteries. J. Phys. Energy 2021, 3, 031501. [Google Scholar] [CrossRef]
- Thompson, S.C.; Paredis, C.J.J. An Introduction to Rational Design Theory; American Society of Mechanical Engineers Digital Collection: Montreal, QC, Canada, 2011; pp. 59–72. [Google Scholar]
- Fang, R.; Zhao, S.; Sun, Z.; Wang, D.-W.; Cheng, H.-M.; Li, F. More Reliable Lithium-Sulfur Batteries: Status, Solutions and Prospects. Adv. Mater. 2017, 29, 1606823. [Google Scholar] [CrossRef]
- Bruce, P.G.; Freunberger, S.A.; Hardwick, L.J.; Tarascon, J.-M. Li-O2 and Li-S batteries with high energy storage. Nat. Mater. 2012, 11, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Fotouhi, A.; Auger, D.J.; O’Neill, L.; Cleaver, T.; Walus, S. Lithium-Sulfur Battery Technology Readiness and Applications—A Review. Energies 2017, 10, 1937. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.-J.; Huang, J.-Q.; Cheng, X.-B.; Zhang, Q. Review on High-Loading and High-Energy Lithium–Sulfur Batteries. Adv. Energy Mater. 2017, 7, 1700260. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Otaegui, L.; Singh, G.; Armand, M.; Rodriguez-Martinez, L.M. Estimation of energy density of Li-S batteries with liquid and solid electrolytes. J. Power Sources 2016, 326, 1–5. [Google Scholar] [CrossRef]
- Durmus, Y.E.; Zhang, H.; Baakes, F.; Desmaizieres, G.; Hayun, H.; Yang, L.; Kolek, M.; Küpers, V.; Janek, J.; Mandler, D.; et al. Side by Side Battery Technologies with Lithium-Ion Based Batteries. Adv. Energy Mater. 2020, 10, 2000089. [Google Scholar] [CrossRef]
- Huang, X.; Xue, J.; Xiao, M.; Wang, S.; Li, Y.; Zhang, S.; Meng, Y. Comprehensive evaluation of safety performance and failure mechanism analysis for lithium sulfur pouch cells. Energy Storage Mater. 2020, 30, 87–97. [Google Scholar] [CrossRef]
- Manthiram, A.; Fu, Y.; Chung, S.-H.; Zu, C.; Su, Y.-S. Rechargeable Lithium–Sulfur Batteries. Chem. Rev. 2014, 114, 11751–11787. [Google Scholar] [CrossRef]
- Yang, C.; Li, P.; Yu, J.; Zhao, L.-D.; Kong, L. Approaching energy-dense and cost-effective lithium–sulfur batteries: From materials chemistry and price considerations. Energy 2020, 201, 117718. [Google Scholar] [CrossRef]
- Rappold, T.A.; Lackner, K.S. Large scale disposal of waste sulfur: From sulfide fuels to sulfate sequestration. Energy 2010, 35, 1368–1380. [Google Scholar] [CrossRef]
- Hagen, M.; Hanselmann, D.; Ahlbrecht, K.; Maça, R.; Gerber, D.; Tübke, J. Lithium–Sulfur Cells: The Gap between the State-of-the-Art and the Requirements for High Energy Battery Cells. Adv. Energy Mater. 2015, 5, 1401986. [Google Scholar] [CrossRef]
- Song, M.-K.; Cairns, E.J.; Zhang, Y. Lithium/sulfur batteries with high specific energy: Old challenges and new opportunities. Nanoscale 2013, 5, 2186. [Google Scholar] [CrossRef] [PubMed]
- Moon, S.; Jung, Y.H.; Jung, W.K.; Jung, D.S.; Choi, J.W.; Kim, D.K. Encapsulated Monoclinic Sulfur for Stable Cycling of Li–S Rechargeable Batteries. Adv. Mater. 2013, 25, 6547–6553. [Google Scholar] [CrossRef]
- Fang, R.; Zhao, S.; Pei, S.; Qian, X.; Hou, P.-X.; Cheng, H.-M.; Liu, C.; Li, F. Toward More Reliable Lithium–Sulfur Batteries: An All-Graphene Cathode Structure. ACS Nano 2016, 10, 8676–8682. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.-X.; Xin, S.; Guo, Y.-G.; Wan, L.-J. Lithium–Sulfur Batteries: Electrochemistry, Materials, and Prospects. Angew. Chem. Int. Ed. 2013, 52, 13186–13200. [Google Scholar] [CrossRef]
- Ji, X.; Lee, K.T.; Nazar, L.F. A highly ordered nanostructured carbon–sulphur cathode for lithium–sulphur batteries. Nat. Mater. 2009, 8, 500–506. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Peng, H.-J.; Hou, T.-Z.; Huang, J.-Q.; Chen, C.-M.; Wang, D.-W.; Cheng, X.-B.; Wei, F.; Zhang, Q. Powering Lithium–Sulfur Battery Performance by Propelling Polysulfide Redox at Sulfiphilic Hosts. Nano Lett. 2016, 16, 519–527. [Google Scholar] [CrossRef]
- Zhao, M.-Q.; Zhang, Q.; Huang, J.-Q.; Tian, G.-L.; Nie, J.-Q.; Peng, H.-J.; Wei, F. Unstacked double-layer templated graphene for high-rate lithium–sulphur batteries. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.T.; Chen, Y.M.; Li, J.; Lou, X.W. (David) Pie-like electrode design for high-energy density lithium–sulfur batteries. Nat. Commun. 2015, 6, 8850. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Xia, X.; Deng, S.; Zhan, J.; Fang, R.; Xia, Y.; Wang, X.; Zhang, Q.; Tu, J. Popcorn Inspired Porous Macrocellular Carbon: Rapid Puffing Fabrication from Rice and Its Applications in Lithium–Sulfur Batteries. Adv. Energy Mater. 2018, 8, 1701110. [Google Scholar] [CrossRef]
- Zhou, G.; Paek, E.; Hwang, G.S.; Manthiram, A. Long-life Li/polysulphide batteries with high sulphur loading enabled by lightweight three-dimensional nitrogen/sulphur-codoped graphene sponge. Nat. Commun. 2015, 6, 7760. [Google Scholar] [CrossRef]
- Wei Seh, Z.; Li, W.; Cha, J.J.; Zheng, G.; Yang, Y.; McDowell, M.T.; Hsu, P.-C.; Cui, Y. Sulphur–TiO 2 yolk–shell nanoarchitecture with internal void space for long-cycle lithium–sulphur batteries. Nat. Commun. 2013, 4, 1331. [Google Scholar] [CrossRef] [Green Version]
- Gu, P.-Y.; Zhao, Y.; Xie, J.; Binte Ali, N.; Nie, L.; Xu, Z.J.; Zhang, Q. Improving the Performance of Lithium–Sulfur Batteries by Employing Polyimide Particles as Hosting Matrixes. ACS Appl. Mater. Interfaces 2016, 8, 7464–7470. [Google Scholar] [CrossRef]
- Zeng, F.; Wang, W.; Wang, A.; Yuan, K.; Jin, Z.; Yang, Y. Multidimensional Polycation β-Cyclodextrin Polymer as an Effective Aqueous Binder for High Sulfur Loading Cathode in Lithium–Sulfur Batteries. ACS Appl. Mater. Interfaces 2015, 7, 26257–26265. [Google Scholar] [CrossRef]
- Bao, W.; Zhang, Z.; Gan, Y.; Wang, X.; Lia, J. Enhanced cyclability of sulfur cathodes in lithium-sulfur batteries with Na-alginate as a binder. J. Energy Chem. 2013, 22, 790–794. [Google Scholar] [CrossRef]
- Wang, H.; Ling, M.; Bai, Y.; Chen, S.; Yuan, Y.; Liu, G.; Wu, C.; Wu, F. Cationic polymer binder inhibit shuttle effects through electrostatic confinement in lithium sulfur batteries. J. Mater. Chem. A 2018, 6, 6959–6966. [Google Scholar] [CrossRef]
- Li, G.; Cai, W.; Liu, B.; Li, Z. A multi functional binder with lithium ion conductive polymer and polysulfide absorbents to improve cycleability of lithium–sulfur batteries. J. Power Sources 2015, 294, 187–192. [Google Scholar] [CrossRef]
- Qie, L.; Zu, C.; Manthiram, A. A High Energy Lithium-Sulfur Battery with Ultrahigh-Loading Lithium Polysulfide Cathode and its Failure Mechanism. Adv. Energy Mater. 2016, 6, 1502459. [Google Scholar] [CrossRef]
- Zhang, S.S.; Tran, D.T. Pyrite FeS2 as an efficient adsorbent of lithium polysulphide for improved lithium–sulphur batteries. J. Mater. Chem. A 2016, 4, 4371–4374. [Google Scholar] [CrossRef]
- Moy, D.; Manivannan, A.; Narayanan, S.R. Direct Measurement of Polysulfide Shuttle Current: A Window into Understanding the Performance of Lithium-Sulfur Cells. J. Electrochem. Soc. 2014, 162, A1. [Google Scholar] [CrossRef]
- Mikhaylik, Y.V.; Akridge, J.R. Polysulfide Shuttle Study in the Li/S Battery System. J. Electrochem. Soc. 2004, 151, A1969. [Google Scholar] [CrossRef]
- Cheon, S.-E.; Ko, K.-S.; Cho, J.-H.; Kim, S.-W.; Chin, E.-Y.; Kim, H.-T. Rechargeable Lithium Sulfur Battery: I. Structural Change of Sulfur Cathode During Discharge and Charge. J. Electrochem. Soc. 2003, 150, A796. [Google Scholar] [CrossRef]
- Hofmann, A.F.; Fronczek, D.N.; Bessler, W.G. Mechanistic modeling of polysulfide shuttle and capacity loss in lithium–sulfur batteries. J. Power Sources 2014, 259, 300–310. [Google Scholar] [CrossRef] [Green Version]
- Fuller, T.F.; Harb, J.N. Electrochemical Engineering, 1st ed.; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 2018; Volume 1, ISBN 978-1-119-44658-3. [Google Scholar]
- Ryu, H.S.; Ahn, H.J.; Kim, K.W.; Ahn, J.H.; Cho, K.K.; Nam, T.H. Self-discharge characteristics of lithium/sulfur batteries using TEGDME liquid electrolyte. Electrochim. Acta 2006, 52, 1563–1566. [Google Scholar] [CrossRef]
- Li, S.-Y.; Wang, W.-P.; Duan, H.; Guo, Y.-G. Recent progress on confinement of polysulfides through physical and chemical methods. J. Energy Chem. 2018, 27, 1555–1565. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.-Q.; Zhuang, T.-Z.; Zhang, Q.; Peng, H.-J.; Chen, C.-M.; Wei, F. Permselective Graphene Oxide Membrane for Highly Stable and Anti-Self-Discharge Lithium–Sulfur Batteries. ACS Nano 2015, 9, 3002–3011. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Ward, A.L.; Doris, S.E.; Pascal, T.A.; Prendergast, D.; Helms, B.A. Polysulfide-Blocking Microporous Polymer Membrane Tailored for Hybrid Li-Sulfur Flow Batteries. Nano Lett. 2015, 15, 5724–5729. [Google Scholar] [CrossRef]
- Liang, X.; Hart, C.; Pang, Q.; Garsuch, A.; Weiss, T.; Nazar, L.F. A highly efficient polysulfide mediator for lithium–sulfur batteries. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Hwa, Y.; Cairns, E.J. Nanostructured Sulfur and Sulfides for Advanced Lithium/Sulfur Cells. ChemElectroChem 2020, 7, 3927–3942. [Google Scholar] [CrossRef]
- Zhao, H.; Deng, N.; Yan, J.; Kang, W.; Ju, J.; Ruan, Y.; Wang, X.; Zhuang, X.; Li, Q.; Cheng, B. A review on anode for lithium-sulfur batteries: Progress and prospects. Chem. Eng. J. 2018, 347, 343–365. [Google Scholar] [CrossRef]
- Ma, L.; Hendrickson, K.E.; Wei, S.; Archer, L.A. Nanomaterials: Science and applications in the lithium–sulfur battery. Nano Today 2015, 10, 315–338. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Manthiram, A. A review on the status and challenges of electrocatalysts in lithium-sulfur batteries. Energy Storage Mater. 2019, 20, 55–70. [Google Scholar] [CrossRef]
- Fan, X.; Sun, W.; Meng, F.; Xing, A.; Liu, J. Advanced chemical strategies for lithium–sulfur batteries: A review. Green Energy Environ. 2018, 3, 2–19. [Google Scholar] [CrossRef]
- Kim, S.; Kim, K.; Park, J.; Sung, Y. Role and Potential of Metal Sulfide Catalysts in Lithium-Sulfur Battery Applications. ChemCatChem 2019, 11, 2373–2387. [Google Scholar] [CrossRef]
- Burke, K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef]
- Grotendorst, J. Modern Methods and Algorithms of Quantum Chemistry: Winterschool, 21–25 February 2000, Forschungszentrum Jülich, Germany. Proceedings; Grotendorst, J., Ed.; NIC Series; NIC-Directors: Jülich, Germany, 2000; Volume 1, ISBN 978-3-00-005618-5. [Google Scholar]
- Liu, Z.; Bertolini, S.; Balbuena, P.B.; Mukherjee, P.P. Li2S Film Formation on Lithium Anode Surface of Li–S batteries. ACS Appl. Mater. Interfaces 2016, 8, 4700–4708. [Google Scholar] [CrossRef]
- Du, G.-Y.; Liu, C.-Y.; Li, E.Y. A DFT Investigation on the Origins of Solvent-Dependent Polysulfide Reduction Mechanism in Rechargeable Li-S Batteries. Catalysts 2020, 10, 911. [Google Scholar] [CrossRef]
- Arneson, C.; Wawrzyniakowski, Z.D.; Postlewaite, J.T.; Ma, Y. Lithiation and Delithiation Processes in Lithium–Sulfur Batteries from Ab Initio Molecular Dynamics Simulations. J. Phys. Chem. C 2018, 122, 8769–8779. [Google Scholar] [CrossRef]
- Kamphaus, E.P.; Balbuena, P.B. First-Principles Investigation of Lithium Polysulfide Structure and Behavior in Solution. J. Phys. Chem. C 2017, 121, 21105–21117. [Google Scholar] [CrossRef]
- Hou, T.-Z.; Chen, X.; Peng, H.-J.; Huang, J.-Q.; Li, B.-Q.; Zhang, Q.; Li, B. Design Principles for Heteroatom-Doped Nanocarbon to Achieve Strong Anchoring of Polysulfides for Lithium–Sulfur Batteries. Small 2016, 12, 3283–3291. [Google Scholar] [CrossRef] [PubMed]
- Kamphaus, E.P.; Balbuena, P.B. Long-Chain Polysulfide Retention at the Cathode of Li–S Batteries. J. Phys. Chem. C 2016, 120, 4296–4305. [Google Scholar] [CrossRef]
- Liang, P.; Zhang, L.; Wang, D.; Man, X.; Shu, H.; Wang, L.; Wan, H.; Du, X.; Wang, H. First-principles explorations of Li2S@V2CT hybrid structure as cathode material for lithium-sulfur battery. Appl. Surf. Sci. 2019, 489, 677–683. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, J.; Yin, L.; Hu, G.; Fang, R.; Cheng, H.-M.; Li, F. Conductive porous vanadium nitride/graphene composite as chemical anchor of polysulfides for lithium-sulfur batteries. Nat. Commun. 2017, 8, 14627. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, R.; Pang, Y.; Chen, X.; Lang, J.; Xu, J.; Xiao, C.; Li, H.; Xi, K.; Ding, S. Carbon@titanium nitride dual shell nanospheres as multi-functional hosts for lithium sulfur batteries. Energy Storage Mater. 2019, 16, 228–235. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, Q.; Hu, L.; Pan, H.; Shi, X. BC2N monolayers as promising anchoring materials for lithium-sulfur batteries: First-principles insights. Carbon 2019, 149, 530–537. [Google Scholar] [CrossRef]
- Park, H.; Siegel, D.J. Tuning the Adsorption of Polysulfides in Lithium–Sulfur Batteries with Metal–Organic Frameworks. Chem. Mater. 2017, 29, 4932–4939. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Seh, Z.W.; Fu, Z.; Zhang, R.; Cui, Y. Understanding the Anchoring Effect of Two-Dimensional Layered Materials for Lithium–Sulfur Batteries. Nano Lett. 2015, 15, 3780–3786. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, R.; Chen, J.; Wu, H.; Lu, S.; Wang, K.; Li, H.; Harris, C.J.; Xi, K.; Kumar, R.V.; et al. Enhancing Catalytic Activity of Titanium Oxide in Lithium–Sulfur Batteries by Band Engineering. Adv. Energy Mater. 2019, 9, 1900953. [Google Scholar] [CrossRef]
- Tao, X.; Wang, J.; Liu, C.; Wang, H.; Yao, H.; Zheng, G.; Seh, Z.W.; Cai, Q.; Li, W.; Zhou, G.; et al. Balancing surface adsorption and diffusion of lithium-polysulfides on nonconductive oxides for lithium–sulfur battery design. Nat. Commun. 2016, 7, 11203. [Google Scholar] [CrossRef]
- Yang, X.; Gao, X.; Sun, Q.; Jand, S.P.; Yu, Y.; Zhao, Y.; Li, X.; Adair, K.; Kuo, L.-Y.; Rohrer, J.; et al. Promoting the Transformation of Li2S2 to Li2S: Significantly Increasing Utilization of Active Materials for High-Sulfur-Loading Li–S Batteries. Adv. Mater. 2019, 31, 1901220. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zhang, X.; Li, M.; Liu, J.; Wu, Y. Sulfur-deficient MoS2-x promoted lithium polysulfides conversion in lithium-sulfur battery: A first-principles study. Appl. Surf. Sci. 2019, 487, 452–463. [Google Scholar] [CrossRef]
- Zhou, G.; Zhao, S.; Wang, T.; Yang, S.-Z.; Johannessen, B.; Chen, H.; Liu, C.; Ye, Y.; Wu, Y.; Peng, Y.; et al. Theoretical Calculation Guided Design of Single-Atom Catalysts toward Fast Kinetic and Long-Life Li–S Batteries. Nano Lett. 2020, 20, 1252–1261. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Fan, L.; Wu, X.; Qiu, Y.; Guan, B.; Wang, Y.; Zhang, N.; Sun, K. Metallic NiSe2 nanoarrays towards ultralong life and fast Li2S oxidation kinetics of Li–S batteries. J. Mater. Chem. A 2019, 7, 15302–15308. [Google Scholar] [CrossRef]
- Wild, M.; O’Neill, L.; Zhang, T.; Purkayastha, R.; Minton, G.; Marinescu, M.; Offer, G.J. Lithium sulfur batteries, a mechanistic review. Energy Environ. Sci. 2015, 8, 3477–3494. [Google Scholar] [CrossRef]
- Barchasz, C.; Molton, F.; Duboc, C.; Leprêtre, J.-C.; Patoux, S.; Alloin, F. Lithium/Sulfur Cell Discharge Mechanism: An Original Approach for Intermediate Species Identification. Anal. Chem. 2012, 84, 3973–3980. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, S.; Wang, H.; He, J.; Huang, Q.; Chang, S. Machine learning method for tight-binding Hamiltonian parameterization from ab-initio band structure. NPJ Comput. Mater. 2021, 7, 1–10. [Google Scholar] [CrossRef]
- McDonagh, J.L.; Shkurti, A.; Bray, D.J.; Anderson, R.L.; Pyzer-Knapp, E.O. Utilizing Machine Learning for Efficient Parameterization of Coarse Grained Molecular Force Fields. J. Chem. Inf. Model. 2019, 59, 4278–4288. [Google Scholar] [CrossRef]
- Murillo, M.S.; Marciante, M.; Stanton, L.G. Machine Learning Discovery of Computational Model Efficacy Boundaries. Phys. Rev. Lett. 2020, 125, 085503. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.; Benavides-Riveros, C.L.; Marques, M.A.L. Machine Learning the Physical Nonlocal Exchange–Correlation Functional of Density-Functional Theory. J. Phys. Chem. Lett. 2019, 10, 6425–6431. [Google Scholar] [CrossRef] [Green Version]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambrige, UK, 2004; ISBN 978-1-139-45176-5. [Google Scholar]
- Park, C.; Kanduč, M.; Chudoba, R.; Ronneburg, A.; Risse, S.; Ballauff, M.; Dzubiella, J. Molecular simulations of electrolyte structure and dynamics in lithium–sulfur battery solvents. J. Power Sources 2018, 373, 70–78. [Google Scholar] [CrossRef] [Green Version]
- Han, S. Structure and dynamics in the lithium solvation shell of nonaqueous electrolytes. Sci. Rep. 2019, 9, 5555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, K.S.; Chen, J.; Cao, R.; Rajput, N.N.; Murugesan, V.; Shi, L.; Pan, H.; Zhang, J.-G.; Liu, J.; Persson, K.A.; et al. Effects of Anion Mobility on Electrochemical Behaviors of Lithium–Sulfur Batteries. Chem. Mater. 2017, 29, 9023–9029. [Google Scholar] [CrossRef]
- Babar, S.; Lekakou, C. Molecular modeling of electrolyte and polysulfide ions for lithium-sulfur batteries. Ionics 2021, 27, 635–642. [Google Scholar] [CrossRef]
- Li, Y.; Romero, N.A.; Lau, K.C. Structure–Property of Lithium–Sulfur Nanoparticles via Molecular Dynamics Simulation. ACS Appl. Mater. Interfaces 2018, 10, 37575–37585. [Google Scholar] [CrossRef]
- Scheers, J.; Fantini, S.; Johansson, P. A review of electrolytes for lithium–sulphur batteries. J. Power Sources 2014, 255, 204–218. [Google Scholar] [CrossRef]
- Glueckauf, E. The influence of ionic hydration on activity coefficients in concentrated electrolyte solutions. Trans. Faraday Soc. 1955, 51, 1235–1244. [Google Scholar] [CrossRef]
- Zhang, L.; Qian, T.; Zhu, X.; Hu, Z.; Wang, M.; Zhang, L.; Jiang, T.; Tian, J.-H.; Yan, C. In situ optical spectroscopy characterization for optimal design of lithium–sulfur batteries. Chem. Soc. Rev. 2019, 48, 5432–5453. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Y.; Brusseau, M.L.; Ouni, A.E.; Araujo, J.B.; Su, X. The Gas-Absorption/Chemical-Reaction Method for Measuring Air-Water Interfacial Area in Natural Porous Media. Water Resour. Res. 2017, 53, 9519–9527. [Google Scholar] [CrossRef]
- Komini Babu, S.; Mohamed, A.I.; Whitacre, J.F.; Litster, S. Multiple imaging mode X-ray computed tomography for distinguishing active and inactive phases in lithium-ion battery cathodes. J. Power Sources 2015, 283, 314–319. [Google Scholar] [CrossRef]
- He, X.; Ren, J.; Wang, L.; Pu, W.; Jiang, C.; Wan, C. Expansion and shrinkage of the sulfur composite electrode in rechargeable lithium batteries. J. Power Sources 2009, 190, 154–156. [Google Scholar] [CrossRef]
- Wu, H.-L.; Huff, L.A.; Gewirth, A.A. In Situ Raman Spectroscopy of Sulfur Speciation in Lithium–Sulfur Batteries. ACS Appl. Mater. Interfaces 2015, 7, 1709–1719. [Google Scholar] [CrossRef]
- Tian, J.-H.; Jiang, T.; Wang, M.; Hu, Z.; Zhu, X.; Zhang, L.; Qian, T.; Yan, C. In Situ/Operando Spectroscopic Characterizations Guide the Compositional and Structural Design of Lithium–Sulfur Batteries. Small Methods 2020, 4, 1900467. [Google Scholar] [CrossRef]
- Yan, Y.; Cheng, C.; Zhang, L.; Li, Y.; Lu, J. Deciphering the Reaction Mechanism of Lithium–Sulfur Batteries by In Situ/Operando Synchrotron-Based Characterization Techniques. Adv. Energy Mater. 2019, 9, 1900148. [Google Scholar] [CrossRef]
- Pattnaik, P.; Raghunathan, S.; Kalluri, T.; Bhimalapuram, P.; Jawahar, C.V.; Priyakumar, U.D. Machine Learning for Accurate Force Calculations in Molecular Dynamics Simulations. J. Phys. Chem. A 2020, 124, 6954–6967. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lamim Ribeiro, J.M.; Tiwary, P. Machine learning approaches for analyzing and enhancing molecular dynamics simulations. Curr. Opin. Struct. Biol. 2020, 61, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Bertei, A.; Finegan, D.P.; Tan, C.; Daemi, S.R.; Weaving, J.S.; O’Regan, K.B.; Heenan, T.M.M.; Hinds, G.; Kendrick, E.; et al. 3D microstructure design of lithium-ion battery electrodes assisted by X-ray nano-computed tomography and modelling. Nat. Commun. 2020, 11, 2079. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Doolen, G.D. Lattice boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Jia, X.; Li, Y.; Amador, C.; Ding, Y. CFD-DNS simulation of irregular-shaped particle dissolution. Particuology 2020, 50, 144–155. [Google Scholar] [CrossRef]
- Kumaresan, K.; Mikhaylik, Y.; White, R.E. A Mathematical Model for a Lithium–Sulfur Cell. J. Electrochem. Soc. 2008, 155, A576. [Google Scholar] [CrossRef]
- Zhang, T.; Marinescu, M.; O’Neill, L.; Wild, M.; Offer, G. Modeling the voltage loss mechanisms in lithium–sulfur cells: The importance of electrolyte resistance and precipitation kinetics. Phys. Chem. Chem. Phys. 2015, 17, 22581–22586. [Google Scholar] [CrossRef] [Green Version]
- Marinescu, M.; Zhang, T.; Offer, G.J. A zero dimensional model of lithium–sulfur batteries during charge and discharge. Phys. Chem. Chem. Phys. 2016, 18, 584–593. [Google Scholar] [CrossRef] [Green Version]
- Marinescu, M.; O’Neill, L.; Zhang, T.; Walus, S.; Wilson, T.E.; Offer, G.J. Irreversible vs Reversible Capacity Fade of Lithium-Sulfur Batteries during Cycling: The Effects of Precipitation and Shuttle. J. Electrochem. Soc. 2017, 165, A6107. [Google Scholar] [CrossRef]
- Hua, X.; Zhang, T.; Offer, G.J.; Marinescu, M. Towards online tracking of the shuttle effect in lithium sulfur batteries using differential thermal voltammetry. J. Energy Storage 2019, 21, 765–772. [Google Scholar] [CrossRef]
- Ghaznavi, M.; Chen, P. Analysis of a Mathematical Model of Lithium-Sulfur Cells Part III: Electrochemical Reaction Kinetics, Transport Properties and Charging. Electrochim. Acta 2014, 137, 575–585. [Google Scholar] [CrossRef]
- Danner, T.; Zhu, G.; Hofmann, A.F.; Latz, A. Modeling of nano-structured cathodes for improved lithium-sulfur batteries. Electrochim. Acta 2015, 184, 124–133. [Google Scholar] [CrossRef] [Green Version]
- Thangavel, V.; Xue, K.-H.; Mammeri, Y.; Quiroga, M.; Mastouri, A.; Guéry, C.; Johansson, P.; Morcrette, M.; Franco, A.A. A Microstructurally Resolved Model for Li-S Batteries Assessing the Impact of the Cathode Design on the Discharge Performance. J. Electrochem. Soc. 2016, 163, A2817. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.X.; Zhao, T.S.; Liu, M.; Tan, P.; Zeng, Y.K. Modeling of lithium-sulfur batteries incorporating the effect of Li2S precipitation. J. Power Sources 2016, 336, 115–125. [Google Scholar] [CrossRef]
- Wen, G.; Rehman, S.; Tranter, T.G.; Ghosh, D.; Chen, Z.; Gostick, J.T.; Pope, M.A. Insights into Multiphase Reactions during Self-Discharge of Li-S Batteries. Chem. Mater. 2020, 32, 4518–4526. [Google Scholar] [CrossRef]
- Price, C.W. Use of Kolmogorov-Johnson-Mehl-Avrami kinetics in recrystallization of metals and crystallization of metallic glasses. Acta Metall. Mater. 1990, 38, 727–738. [Google Scholar] [CrossRef]
- Andrei, P.; Shen, C.; Zheng, J.P. Theoretical and experimental analysis of precipitation and solubility effects in lithium-sulfur batteries. Electrochim. Acta 2018, 284, 469–484. [Google Scholar] [CrossRef]
- Yoreo, J.J.D.; Vekilov, P.G. Principles of Crystal Nucleation and Growth. Rev. Mineral. Geochem. 2003, 54, 57–93. [Google Scholar] [CrossRef] [Green Version]
- Danner, T.; Latz, A. On the influence of nucleation and growth of S8 and Li2S in lithium-sulfur batteries. Electrochim. Acta 2019, 322, 134719. [Google Scholar] [CrossRef]
- Xiong, C.; Zhao, T.S.; Ren, Y.X.; Jiang, H.R.; Zhou, X.L. Mathematical modeling of the charging process of Li-S batteries by incorporating the size-dependent Li2S dissolution. Electrochim. Acta 2019, 296, 954–963. [Google Scholar] [CrossRef]
- Tan, C.; Kok, M.D.R.; Daemi, S.R.; Brett, D.J.L.; Shearing, P.R. Three-dimensional image based modelling of transport parameters in lithium–sulfur batteries. Phys. Chem. Chem. Phys. 2019, 21, 4145–4154. [Google Scholar] [CrossRef] [Green Version]
- Tan, C.; Heenan, T.M.M.; Ziesche, R.F.; Daemi, S.R.; Hack, J.; Maier, M.; Marathe, S.; Rau, C.; Brett, D.J.L.; Shearing, P.R. Four-Dimensional Studies of Morphology Evolution in Lithium–Sulfur Batteries. ACS Appl. Energy Mater. 2018, 1, 5090–5100. [Google Scholar] [CrossRef] [Green Version]
- Thangavel, V.; Guerrero, O.X.; Quiroga, M.; Mikala, A.M.; Rucci, A.; Franco, A.A. A three dimensional kinetic Monte Carlo model for simulating the carbon/sulfur mesostructural evolutions of discharging lithium sulfur batteries. Energy Storage Mater. 2020, 24, 472–485. [Google Scholar] [CrossRef]
- Mistry, A.; Mukherjee, P.P. Precipitation–Microstructure Interactions in the Li-Sulfur Battery Electrode. J. Phys. Chem. C 2017, 121, 26256–26264. [Google Scholar] [CrossRef]
- Agnaou, M.; Sadeghi, M.A.; Tranter, T.G.; Gostick, J.T. Modeling transport of charged species in pore networks: Solution of the Nernst–Planck equations coupled with fluid flow and charge conservation equations. Comput. Geosci. 2020, 140, 104505. [Google Scholar] [CrossRef]
- DuBeshter, T.; Sinha, P.K.; Sakars, A.; Fly, G.W.; Jorne, J. Measurement of Tortuosity and Porosity of Porous Battery Electrodes. J. Electrochem. Soc. 2014, 161, A599–A605. [Google Scholar] [CrossRef]
- Liu, B.; Fang, R.; Xie, D.; Zhang, W.; Huang, H.; Xia, Y.; Wang, X.; Xia, X.; Tu, J. Revisiting Scientific Issues for Industrial Applications of Lithium–Sulfur Batteries. Energy Environ. Mater. 2018, 1, 196–208. [Google Scholar] [CrossRef] [Green Version]
- Miller, E.C.; Toney, M.F. X-Ray Studies of Energy Materials. In Synchrotron Light Sources and Free-Electron Lasers: Accelerator Physics, Instrumentation and Science Applications; Jaeschke, E.J., Khan, S., Schneider, J.R., Hastings, J.B., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 1803–1824. ISBN 978-3-030-23201-6. [Google Scholar]
- Safari, M.; Kwok, C.Y.; Nazar, L.F. Transport Properties of Polysulfide Species in Lithium–Sulfur Battery Electrolytes: Coupling of Experiment and Theory. ACS Cent. Sci. 2016, 2, 560–568. [Google Scholar] [CrossRef] [PubMed]
- Shah, K.; Subramaniam, A.; Mishra, L.; Jang, T.; Bazant, M.Z.; Braatz, R.D.; Subramanian, V.R. Editors’ Choice—Perspective—Challenges in Moving to Multiscale Battery Models: Where Electrochemistry Meets and Demands More from Math. J. Electrochem. Soc. 2020, 167, 133501. [Google Scholar] [CrossRef]
- Franco, A.A.; Rucci, A.; Brandell, D.; Frayret, C.; Gaberscek, M.; Jankowski, P.; Johansson, P. Boosting Rechargeable Batteries R&D by Multiscale Modeling: Myth or Reality? Chem. Rev. 2019, 119, 4569–4627. [Google Scholar]
- Mistry, A.; Franco, A.A.; Cooper, S.J.; Roberts, S.A.; Viswanathan, V. How Machine Learning Will Revolutionize Electrochemical Sciences. ACS Energy Lett. 2021, 6, 1422–1431. [Google Scholar] [CrossRef] [PubMed]
- Kolodziejczyk, F.; Mortazavi, B.; Rabczuk, T.; Zhuang, X. Machine learning assisted multiscale modeling of composite phase change materials for Li-ion batteries’ thermal management. Int. J. Heat Mass Transf. 2021, 172, 121199. [Google Scholar] [CrossRef]
- Kilic, A.; Odabaşı, Ç.; Yildirim, R.; Eroglu, D. Assessment of critical materials and cell design factors for high performance lithium-sulfur batteries using machine learning. Chem. Eng. J. 2020, 390, 124117. [Google Scholar] [CrossRef]
- Barrett, D.H.; Haruna, A. Artificial intelligence and machine learning for targeted energy storage solutions. Curr. Opin. Electrochem. 2020, 21, 160–166. [Google Scholar] [CrossRef]
- Evers, S.; Nazar, L.F. New Approaches for High Energy Density Lithium–Sulfur Battery Cathodes. Acc. Chem. Res. 2013, 46, 1135–1143. [Google Scholar] [CrossRef]
- Liu, M.; Jiang, H.R.; Ren, Y.X.; Zhou, D.; Kang, F.Y.; Zhao, T.S. In-situ Fabrication of a Freestanding Acrylate-based Hierarchical Electrolyte for Lithium-sulfur Batteries. Electrochim. Acta 2016, 213, 871–878. [Google Scholar] [CrossRef]
- Feng, L.; Ji, Y.; Zhu, Z.; Yu, P.; Fu, X.; Yang, M.; Wang, Y.; Yang, W. Rational design and superfast production of biomimetic, calendering-compatible, catalytic, sulfur-rich secondary particles for advanced lithium-sulfur batteries. Energy Storage Mater. 2021, 40, 415–425. [Google Scholar] [CrossRef]
- Thomitzek, M.; Schmidt, O.; Röder, F.; Krewer, U.; Herrmann, C.; Thiede, S. Simulating Process-Product Interdependencies in Battery Production Systems. Procedia CIRP 2018, 72, 346–351. [Google Scholar] [CrossRef]
- Schmidt, O.; Thomitzek, M.; Röder, F.; Thiede, S.; Herrmann, C.; Krewer, U. Modeling the Impact of Manufacturing Uncertainties on Lithium-Ion Batteries. J. Electrochem. Soc. 2020, 167, 060501. [Google Scholar] [CrossRef]
- Ngandjong, A.C.; Lombardo, T.; Primo, E.N.; Chouchane, M.; Shodiev, A.; Arcelus, O.; Franco, A.A. Investigating electrode calendering and its impact on electrochemical performance by means of a new discrete element method model: Towards a digital twin of Li-Ion battery manufacturing. J. Power Sources 2021, 485, 229320. [Google Scholar] [CrossRef]
- Fan, F.Y.; Woodford, W.H.; Li, Z.; Baram, N.; Smith, K.C.; Helal, A.; McKinley, G.H.; Carter, W.C.; Chiang, Y.-M. Polysulfide Flow Batteries Enabled by Percolating Nanoscale Conductor Networks. Nano Lett. 2014, 14, 2210–2218. [Google Scholar] [CrossRef]
- Liang, J.; Sun, Z.-H.; Li, F.; Cheng, H.-M. Carbon materials for Li–S batteries: Functional evolution and performance improvement. Energy Storage Mater. 2016, 2, 76–106. [Google Scholar] [CrossRef]
- Eftekhari, A.; Kim, D.-W. Cathode materials for lithium–sulfur batteries: A practical perspective. J. Mater. Chem. A 2017, 5, 17734–17776. [Google Scholar] [CrossRef]
- Huang, L.; Li, J.; Liu, B.; Li, Y.; Shen, S.; Deng, S.; Lu, C.; Zhang, W.; Xia, Y.; Pan, G.; et al. Electrode Design for Lithium–Sulfur Batteries: Problems and Solutions. Adv. Funct. Mater. 2020, 30, 1910375. [Google Scholar] [CrossRef]
- Hagen, M.; Fanz, P.; Tübke, J. Cell energy density and electrolyte/sulfur ratio in Li–S cells. J. Power Sources 2014, 264, 30–34. [Google Scholar] [CrossRef]
- Mikhaylik, Y.V.; Kovalev, I.; Schock, R.; Kumaresan, K.; Xu, J.; Affinito, J. High Energy Rechargeable Li-S Cells for EV Application: Status, Remaining Problems and Solutions. ECS Trans. 2010, 25, 23. [Google Scholar] [CrossRef]
- Dörfler, S.; Althues, H.; Härtel, P.; Abendroth, T.; Schumm, B.; Kaskel, S. Challenges and Key Parameters of Lithium-Sulfur Batteries on Pouch Cell Level. Joule 2020, 4, 539–554. [Google Scholar] [CrossRef] [Green Version]
- Bhargav, A.; He, J.; Gupta, A.; Manthiram, A. Lithium-Sulfur Batteries: Attaining the Critical Metrics. Joule 2020, 4, 285–291. [Google Scholar] [CrossRef]
- Hwa, Y.; Kim, H.W.; Shen, H.; Parkinson, D.Y.; McCloskey, B.D.; Cairns, E.J. A sustainable sulfur–carbonaceous composite electrode toward high specific energy rechargeable cells. Mater. Horiz. 2020, 7, 524–529. [Google Scholar] [CrossRef]
- Lv, D.; Zheng, J.; Li, Q.; Xie, X.; Ferrara, S.; Nie, Z.; Mehdi, L.B.; Browning, N.D.; Zhang, J.-G.; Graff, G.L.; et al. High Energy Density Lithium–Sulfur Batteries: Challenges of Thick Sulfur Cathodes. Adv. Energy Mater. 2015, 5, 1402290. [Google Scholar] [CrossRef]
- Chung, S.-H.; Manthiram, A. Designing Lithium-Sulfur Cells with Practically Necessary Parameters. Joule 2018, 2, 710–724. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zhang, Y.; Bai, Z.; Liu, W.W.; Liu, T.; Gim, J.; Jiang, G.; Yuan, Y.; Luo, D.; Feng, K.; et al. A Lithium–Sulfur Battery using a 2D Current Collector Architecture with a Large-Sized Sulfur Host Operated under High Areal Loading and Low E/S Ratio. Adv. Mater. 2018, 30, 1804271. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Li, Y.; Cui, Y. Lithium Metal Anode Materials Design: Interphase and Host. Electrochem. Energy Rev. 2019, 2, 509–517. [Google Scholar] [CrossRef] [Green Version]
- Aurbach, D.; Zinigrad, E.; Cohen, Y.; Teller, H. A short review of failure mechanisms of lithium metal and lithiated graphite anodes in liquid electrolyte solutions. Solid State Ion. 2002, 148, 405–416. [Google Scholar] [CrossRef]
- Chen, X.; Hou, T.; Persson, K.A.; Zhang, Q. Combining theory and experiment in lithium–sulfur batteries: Current progress and future perspectives. Mater. Today 2019, 22, 142–158. [Google Scholar] [CrossRef]
- Park, M.S.; Ma, S.B.; Lee, D.J.; Im, D.; Doo, S.-G.; Yamamoto, O. A Highly Reversible Lithium Metal Anode. Sci. Rep. 2014, 4, 3815. [Google Scholar] [CrossRef] [PubMed]
- Schmuch, R.; Wagner, R.; Hörpel, G.; Placke, T.; Winter, M. Performance and cost of materials for lithium-based rechargeable automotive batteries. Nat. Energy 2018, 3, 267–278. [Google Scholar] [CrossRef]
- Ye, Y.; Song, M.-K.; Xu, Y.; Nie, K.; Liu, Y.; Feng, J.; Sun, X.; Cairns, E.J.; Zhang, Y.; Guo, J. Lithium nitrate: A double-edged sword in the rechargeable lithium-sulfur cell. Energy Storage Mater. 2019, 16, 498–504. [Google Scholar] [CrossRef] [Green Version]
- Qu, C.; Chen, Y.; Yang, X.; Zhang, H.; Li, X.; Zhang, H. LiNO3-free electrolyte for Li-S battery: A solvent of choice with low Ksp of polysulfide and low dendrite of lithium. Nano Energy 2017, 39, 262–272. [Google Scholar] [CrossRef]
- Suo, L.; Hu, Y.-S.; Li, H.; Armand, M.; Chen, L. A new class of Solvent-in-Salt electrolyte for high-energy rechargeable metallic lithium batteries. Nat. Commun. 2013, 4, 1481. [Google Scholar] [CrossRef]
- Weber, R.; Genovese, M.; Louli, A.J.; Hames, S.; Martin, C.; Hill, I.G.; Dahn, J.R. Long cycle life and dendrite-free lithium morphology in anode-free lithium pouch cells enabled by a dual-salt liquid electrolyte. Nat. Energy 2019, 4, 683–689. [Google Scholar] [CrossRef]
- Yue, J.; Yan, M.; Yin, Y.-X.; Guo, Y.-G. Progress of the Interface Design in All-Solid-State Li–S Batteries. Adv. Funct. Mater. 2018, 28, 1707533. [Google Scholar] [CrossRef]
- Lei, D.; Shi, K.; Ye, H.; Wan, Z.; Wang, Y.; Shen, L.; Li, B.; Yang, Q.-H.; Kang, F.; He, Y.-B. Solid-State Electrolytes: Progress and Perspective of Solid-State Lithium–Sulfur Batteries (Adv. Funct. Mater. 38/2018). Adv. Funct. Mater. 2018, 28, 1870272. [Google Scholar] [CrossRef] [Green Version]
- Umeshbabu, E.; Zheng, B.; Yang, Y. Recent Progress in All-Solid-State Lithium–Sulfur Batteries Using High Li-Ion Conductive Solid Electrolytes. Electrochem. Energy Rev. 2019, 2, 199–230. [Google Scholar] [CrossRef]
- Deimede, D.; Elmasides, C. Separators for Lithium-Ion Batteries: A Review on the Production Processes and Recent Developments. Energy Technol. 2015, 3, 453–468. [Google Scholar] [CrossRef]
- Xiang, Y.; Li, J.; Lei, J.; Liu, D.; Xie, Z.; Qu, D.; Li, K.; Deng, T.; Tang, H. Advanced Separators for Lithium-Ion and Lithium–Sulfur Batteries: A Review of Recent Progress. ChemSusChem 2016, 9, 1–18. [Google Scholar] [CrossRef]
- Deng, N.; Kang, W.; Liu, Y.; Ju, J.; Wu, D.; Lia, L.; Hassan, B.S.; Cheng, B. A review on separators for lithium–sulfur battery: Progress and prospects. J. Power Sources 2016, 331, 132–155. [Google Scholar] [CrossRef]
- Wood, D.L.; Li, J.; Daniel, C. Prospects for reducing the processing cost of lithium ion batteries. J. Power Sources 2015, 275, 234–242. [Google Scholar] [CrossRef] [Green Version]

| Component | Weight | |
|---|---|---|
| Current collectors | Aluminum foil for sulfur electrode | 4.05 mg cm−2 |
| Copper foil for lithium electrode | 8.96 mg cm−2 | |
| Lithium Metal | 1.5 × theoretical relative to S loading | |
| Separator (porosity 55%) | 1.035 mg cm−2 | |
| Pouch materials | Tab-negative electrode | 221.9 mg |
| Tab-positive electrode | 76.4 mg | |
| Pouch laminate | 75.6 mg cm−2 | |
| Unit electrode area | 20 cm2 | |
| The number of lithium electrodes (or sulfur electrodes) | 10 | |
| Electrolyte density | 1 | |
| Li/S cell operating voltage | 2.15 V | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCreary, C.; An, Y.; Kim, S.U.; Hwa, Y. A Perspective on Li/S Battery Design: Modeling and Development Approaches. Batteries 2021, 7, 82. https://doi.org/10.3390/batteries7040082
McCreary C, An Y, Kim SU, Hwa Y. A Perspective on Li/S Battery Design: Modeling and Development Approaches. Batteries. 2021; 7(4):82. https://doi.org/10.3390/batteries7040082
Chicago/Turabian StyleMcCreary, Chase, Yuhui An, Sun Ung Kim, and Yoon Hwa. 2021. "A Perspective on Li/S Battery Design: Modeling and Development Approaches" Batteries 7, no. 4: 82. https://doi.org/10.3390/batteries7040082
APA StyleMcCreary, C., An, Y., Kim, S. U., & Hwa, Y. (2021). A Perspective on Li/S Battery Design: Modeling and Development Approaches. Batteries, 7(4), 82. https://doi.org/10.3390/batteries7040082






