Evaluation of Computational Chemistry Methods for Predicting Redox Potentials of Quinone-Based Cathodes for Li-Ion Batteries
Abstract
:1. Introduction
2. Methods
2.1. Choice of Descriptors
2.2. Experimental Data for Validation
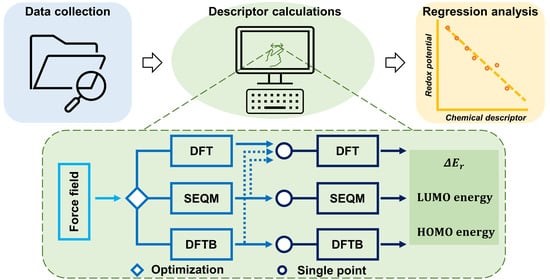
2.3. Computational Scheme
- (1)
- The three-dimensional (3D) molecular geometries were initially created by using the Maestro editor in the Schrödinger Materials Science Suite (version 2019-3) [31].
- (2)
- A search for the lowest energy conformer was performed for all the compounds using the OPLS3e [32] force field.
- (3)
- The lowest energy conformers were further optimized in the gas phase with various SEQM, DFTB, and DFT methods that are described below. As an additional step, single point energy (SPE) calculations using two representative DFT methods were performed on frozen atom coordinates obtained from the SEQM or DFTB optimizations. Altogether, these optimizations yielded descriptor data that were obtained at three levels of approximation: SEQM or DFTB, DFT, and a hybrid of the two.
- (4)
- To explore the possible contributions of solvation effects (as explored in previous studies [18,33]), SPE calculations were performed again in an implicit solvation environment within the standard Poisson–Boltzmann Formalism (PBF) [34], in which the parameters for the solvent phase were set according to the experimental conditions from each dataset.
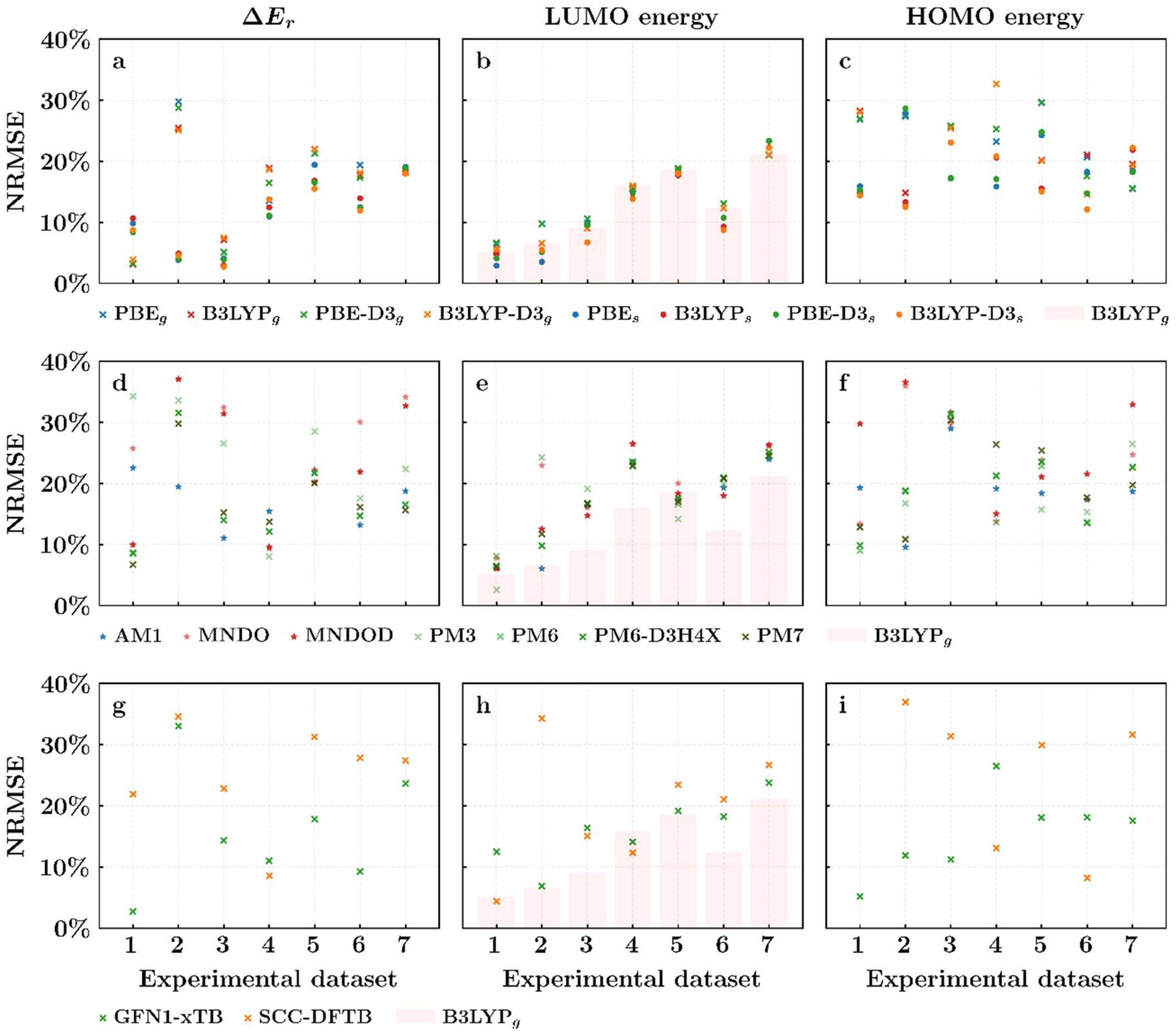
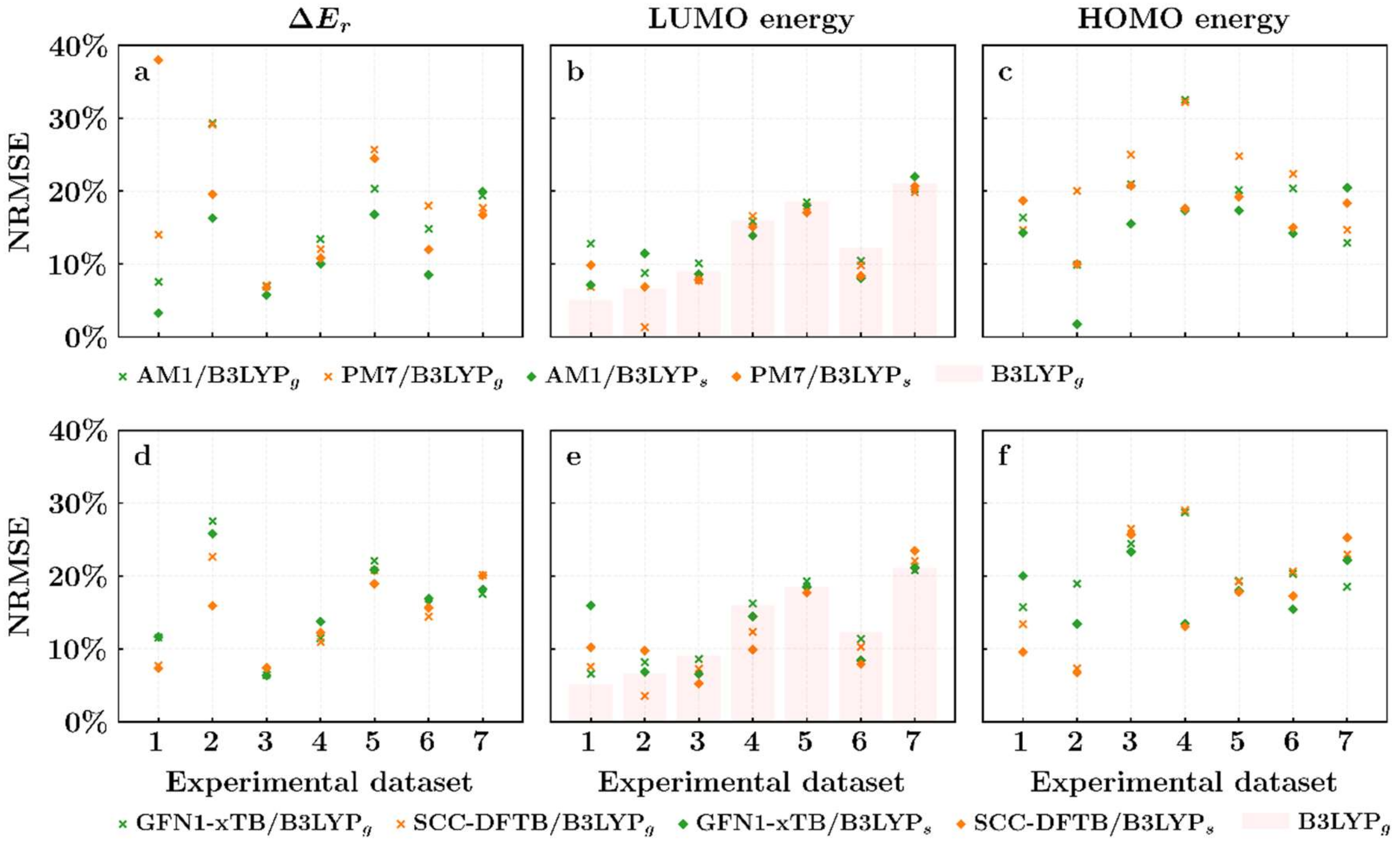
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thackeray, M.M.; Wolverton, C.; Isaacs, E.D. Electrical energy storage for transportation-approaching the limits of, and going beyond, lithium-ion batteries. Energy Environ. Sci. 2012, 5, 7854–7863. [Google Scholar] [CrossRef]
- Lee, S.; Kwon, G.; Ku, K.; Yoon, K.; Jung, S.K.; Lim, H.D.; Kang, K. Recent progress in organic electrodes for Li and Na rechargeable batteries. Adv. Mater. 2018, 30, 1704682. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.Y.; Liang, M.X.; Qi, S.; Sun, W.W.; Lv, L.P.; Du, F.H.; Wang, B.F.; Chen, S.Q.; Wang, Y.; Yu, Y. The progress and prospect of tunable organic molecules for organic lithium-ion batteries. ACS Nano 2021, 15, 47–80. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.M.; Ding, G.C.; Xie, L.L.; Cao, X.Y.; Liu, J.P.; Lei, X.F.; Ma, J.X. Conjugated carbonyl compounds as high-performance cathode materials for rechargeable batteries. Chem. Mater. 2019, 31, 8582–8612. [Google Scholar] [CrossRef]
- Lyu, H.L.; Sun, X.G.; Dai, S. Organic cathode materials for lithium-Ion batteries: Past, present, and future. Adv. Energy Sustain. Res. 2021, 2, 2000044. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, Q.; Li, L.; Niu, Z.Q.; Chen, J. Design strategies toward enhancing the performance of organic electrode materials in metal-ion batteries. Chem 2018, 4, 2786–2813. [Google Scholar] [CrossRef] [Green Version]
- Han, C.P.; Li, H.F.; Shi, R.Y.; Zhang, T.F.; Tong, J.; Li, J.Q.; Li, B.H. Organic quinones towards advanced electrochemical energy storage: Recent advances and challenges. J. Mater. Chem. A 2019, 7, 23378–23415. [Google Scholar] [CrossRef]
- Yokoji, T.; Matsubara, H.; Satoh, M. Rechargeable organic lithium-ion batteries using electron-deficient benzoquinones as positive-electrode materials with high discharge voltages. J. Mater. Chem. A 2014, 2, 19347–19354. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.L.; Zhang, P.; Chen, J. Function-oriented design of conjugated carbonyl compound electrodes for high energy lithium batteries. Chem. Sci. 2013, 4, 1330–1337. [Google Scholar] [CrossRef]
- Liang, Y.L.; Zhang, P.; Yang, S.Q.; Tao, Z.L.; Chen, J. Fused heteroaromatic organic compounds for high-power electrodes of rechargeable lithium batteries. Adv. Energy Mater. 2013, 3, 600–605. [Google Scholar] [CrossRef]
- Nagamura, N.; Taniki, R.; Kitada, Y.; Masuda, A.; Kobayashi, H.; Oka, N.; Honma, I. Electronic states of quinones for organic energy devices: The effect of molecular structure on electrochemical characteristics. ACS Appl. Energy Mater. 2018, 1, 3084–3092. [Google Scholar] [CrossRef]
- Cheng, L.; Assary, R.S.; Qu, X.H.; Jain, A.; Ong, S.P.; Rajput, N.N.; Persson, K.; Curtiss, L.A. Accelerating electrolyte discovery for energy storage with high-throughput screening. J. Phys. Chem. Lett. 2015, 6, 283–291. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Khetan, A.; Er, S. Comparison of computational chemistry methods for the discovery of quinone-based electroactive compounds for energy storage. Sci. Rep. 2020, 10, 22149. [Google Scholar] [CrossRef]
- Zhang, Q.; Khetan, A.; Er, S. A quantitative evaluation of computational methods to accelerate the study of alloxazine-derived electroactive compounds for energy storage. Sci. Rep. 2021, 11, 4089. [Google Scholar] [CrossRef]
- Tezsevin, I.; van de Sanden, M.C.M.; Er, S. High-throughput computational screening of cubic perovskites for solid oxide fuel cell cathodes. J. Phys. Chem. Lett. 2021, 12, 4160–4165. [Google Scholar] [CrossRef]
- Sorkun, M.C.; Astruc, S.; Koelman, J.M.V.A.; Er, S. An artificial intelligence-aided virtual screening recipe for two-dimensional materials discovery. NPJ Comput. Mater. 2020, 6, 106. [Google Scholar] [CrossRef]
- Sorkun, E.; Zhang, Q.; Khetan, A.; Sorkun, M.C.; Er, S. RedDB, A computational database of electroactive molecules for aqueous redox flow batteries. ChemRxiv 2021. [Google Scholar] [CrossRef]
- Pineda Flores, S.D.; Martin-Noble, G.C.; Phillips, R.L.; Schrier, J. Bio-inspired electroactive organic molecules for aqueous redox flow batteries. 1. Thiophenoquinones. J. Phys. Chem. C 2015, 119, 21800–21809. [Google Scholar] [CrossRef]
- Liu, C.F.; Neale, Z.G.; Cao, G.Z. Understanding electrochemical potentials of cathode materials in rechargeable batteries. Mater. Today 2016, 19, 109–123. [Google Scholar] [CrossRef]
- Manzhos, S. Organic electrode materials for lithium and post-lithium batteries: An ab initio perspective on design. Curr. Opin. Green Sustain. Chem. 2019, 17, 8–14. [Google Scholar] [CrossRef]
- Yokoji, T.; Kameyama, Y.; Maruyama, N.; Matsubara, H. High-capacity organic cathode active materials of 2,2′-bis-p-benzoquinone derivatives for rechargeable batteries. J. Mater. Chem. A 2016, 4, 5457–5466. [Google Scholar]
- Hernández-Burgos, K.; Burkhardt, S.E.; Rodríguez-Calero, G.G.; Hennig, R.G.; Abruña, H.D. Theoretical studies of carbonyl-based organic molecules for energy storage applications: The heteroatom and substituent effect. J. Phys. Chem. C 2014, 118, 6046–6051. [Google Scholar] [CrossRef]
- Kim, K.C.; Liu, T.Y.; Jung, K.H.; Lee, S.W.; Jang, S.S. Unveiled correlations between electron affinity and solvation in redox potential of quinone-based sodium-ion batteries. Energy Storage Mater. 2019, 19, 242–250. [Google Scholar] [CrossRef]
- Botchkarev, A. Performance metrics (error measures) in machine learning regression, forecasting and prognostics: Properties and typology. arXiv 2018. arXiv:1809.03006. [Google Scholar]
- Yao, M.; Senoh, H.; Yamazaki, S.I.; Siroma, Z.; Sakai, T.; Yasuda, K. High-capacity organic positive-electrode material based on a benzoquinone derivative for use in rechargeable lithium batteries. J. Power Sources 2010, 195, 8336–8340. [Google Scholar] [CrossRef]
- Shimizu, A.; Kuramoto, H.; Tsujii, Y.; Nokami, T.; Inatomi, Y.; Hojo, N.; Suzuki, H.; Yoshida, J.I. Introduction of two lithiooxycarbonyl groups enhances cyclability of lithium batteries with organic cathode materials. J. Power Sources 2014, 260, 211–217. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.C.; Liu, T.Y.; Lee, S.W.; Jang, S.S. First-principles density functional theory modeling of Li binding: Thermodynamics and redox properties of quinone derivatives for lithium-ion batteries. J. Am. Chem. Soc. 2016, 138, 2374–2382. [Google Scholar] [CrossRef] [PubMed]
- Barrès, A.L.; Geng, J.; Bonnard, G.; Renault, S.; Gottis, S.; Mentré, O.; Frayret, C.; Dolhem, F.; Poizot, P. High-potential reversible Li deintercalation in a substituted tetrahydroxy-p-benzoquinone dilithium salt: An experimental and theoretical study. Chem.-A Eur. J. 2012, 18, 8800–8812. [Google Scholar] [CrossRef] [PubMed]
- Wodrich, M.D.; Corminboeuf, C.; Schreiner, P.R.; Fokin, A.A.; Schleyer, P.V.R. How accurate are DFT treatments of organic energies? Org. Lett. 2007, 9, 1851–1854. [Google Scholar] [CrossRef]
- Tang, M.; Zhu, S.L.; Liu, Z.T.; Jiang, C.; Wu, Y.C.; Li, H.Y.; Wang, B.; Wang, E.J.; Ma, J.; Wang, C.L. Tailoring π-conjugated systems: From π-π stacking to high-rate-performance organic cathodes. Chem 2018, 4, 2600–2614. [Google Scholar] [CrossRef] [Green Version]
- User Manual. Schrödinger: New York, NY, USA, 2019. Available online: https://www.schrodinger.com/ (accessed on 27 October 2021).
- Roos, K.; Wu, C.J.; Damm, W.; Reboul, M.; Stevenson, J.M.; Lu, C.; Dahlgren, M.K.; Mondal, S.; Chen, W.; Wang, L.; et al. OPLS3e: Extending force field coverage for drug-like small molecules. J. Chem. Theory Comput. 2019, 15, 1863–1874. [Google Scholar] [CrossRef]
- Niu, Z.H.; Wu, H.X.; Lu, Y.H.; Xiong, S.Y.; Zhu, X.; Zhao, Y.; Zhang, X.H. Orbital-dependent redox potential regulation of quinone derivatives for electrical energy storage. RSC Adv. 2019, 9, 5164–5173. [Google Scholar] [CrossRef] [Green Version]
- Marten, B.; Kim, K.; Cortis, C.; Friesner, R.A.; Murphy, R.B.; Ringnalda, M.N.; Sitkoff, D.; Honig, B. New model for calculation of solvation free energies: Correction of self-consistent reaction field continuum dielectric theory for short-range hydrogen-bonding effects. J. Phys. Chem. 1996, 100, 11775–11788. [Google Scholar] [CrossRef]
- Mohamadi, F.; Richards, N.G.J.; Guida, W.C.; Liskamp, R.; Lipton, M.; Caufield, C.; Chang, G.; Hendrickson, T.; Still, W.C. MacroModel-An integrated software system for modeling organic and bioorganic molecules using molecular mechanics. J. Comput. Chem. 1990, 11, 440–467. [Google Scholar] [CrossRef]
- Stewart, J.J.P. MOPAC: A semiempirical molecular orbital program. J. Comput. Aided. Mol. Des. 1990, 4, 1–105. [Google Scholar] [CrossRef]
- Bachrach, S.M. Jaguar 5.5. Schrödinger, Inc. J. Am. Chem. Soc. 2004, 126, 5018. [Google Scholar] [CrossRef]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A robust and accurate tight-binding quantum chemical method for structures, vibrational frequencies, and noncovalent interactions of large molecular systems parametrized for all spd-block elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Oliveira, A.F.; Philipsen, P.; Heine, T. DFTB parameters for the periodic table, part 2: Energies and energy gradients from hydrogen to calcium. J. Chem. Theory Comput. 2015, 11, 5209–5218. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitale. J. Chem. Phys. 1985, 82, 299–310. [Google Scholar] [CrossRef]
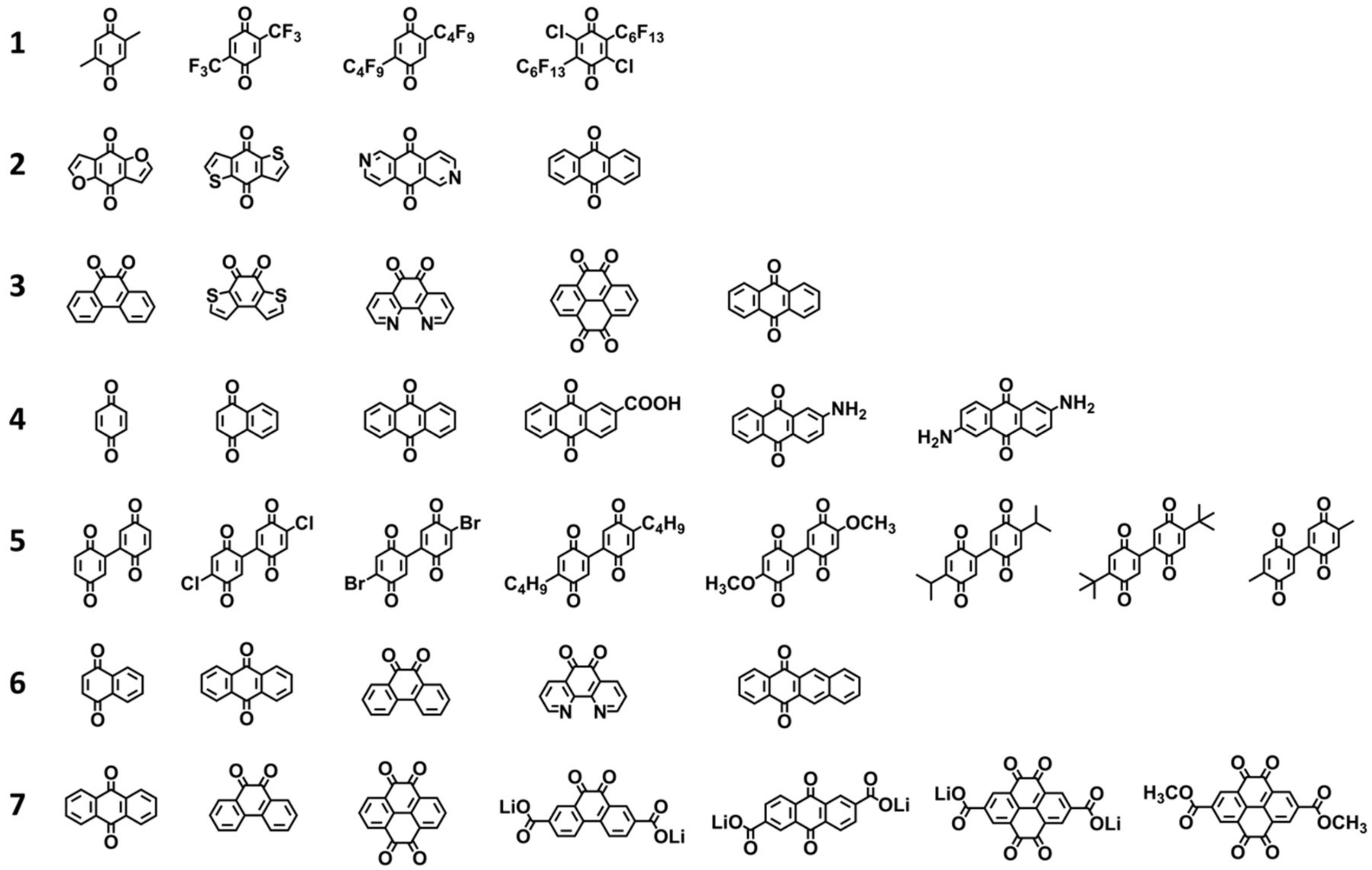
| Dataset | Electrolyte | Number of Molecules | Discharge Condition | Range of Redox Potential (vs. Li/Li+) | Data Source * |
|---|---|---|---|---|---|
| 1 | 1 M LiPF6-EC + DEC (v/v = 3:7) | 4 | 0.1 mA | 0.60 V | Table |
| 2 | 1 M LiPF6-EC + DMC (w/w = 1:1) | 4 | 1 Li per 5 h | 0.44 V | Text |
| 3 | 1 M LiPF6-EC + DMC (w/w = 1:1) | 5 | 1 Li per 5 h | 0.66 V | Table |
| 4 | 1 M LiPF6-EC + DMC (v/v = 3:7) | 6 | 1 mV/s | 1.55 V | Text |
| 5 | 2.75 M LiTFSI-Tetraglyme | 8 | 40 mA/g | 0.30 V | Table |
| 6 | 1 M LiTFSI-Tetraglyme | 5 | 40 mA/g | 1.00 V | Table |
| 7 | 1 M LiPF6-PC | 7 | 1 Li per 10 h | 0.82 V | Text |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Khetan, A.; Er, S. Evaluation of Computational Chemistry Methods for Predicting Redox Potentials of Quinone-Based Cathodes for Li-Ion Batteries. Batteries 2021, 7, 71. https://doi.org/10.3390/batteries7040071
Zhou X, Khetan A, Er S. Evaluation of Computational Chemistry Methods for Predicting Redox Potentials of Quinone-Based Cathodes for Li-Ion Batteries. Batteries. 2021; 7(4):71. https://doi.org/10.3390/batteries7040071
Chicago/Turabian StyleZhou, Xuan, Abhishek Khetan, and Süleyman Er. 2021. "Evaluation of Computational Chemistry Methods for Predicting Redox Potentials of Quinone-Based Cathodes for Li-Ion Batteries" Batteries 7, no. 4: 71. https://doi.org/10.3390/batteries7040071
APA StyleZhou, X., Khetan, A., & Er, S. (2021). Evaluation of Computational Chemistry Methods for Predicting Redox Potentials of Quinone-Based Cathodes for Li-Ion Batteries. Batteries, 7(4), 71. https://doi.org/10.3390/batteries7040071