Effect of Ball Milling on the Electrochemical Performance of Activated Carbon with a Very High Specific Surface Area
Abstract
1. Introduction
2. Materials and Methods
2.1. Ball Milling and Materials Characterization
2.2. Electrochemical Characterization
3. Results and Discussion
3.1. Material Properties of the Milled ACs
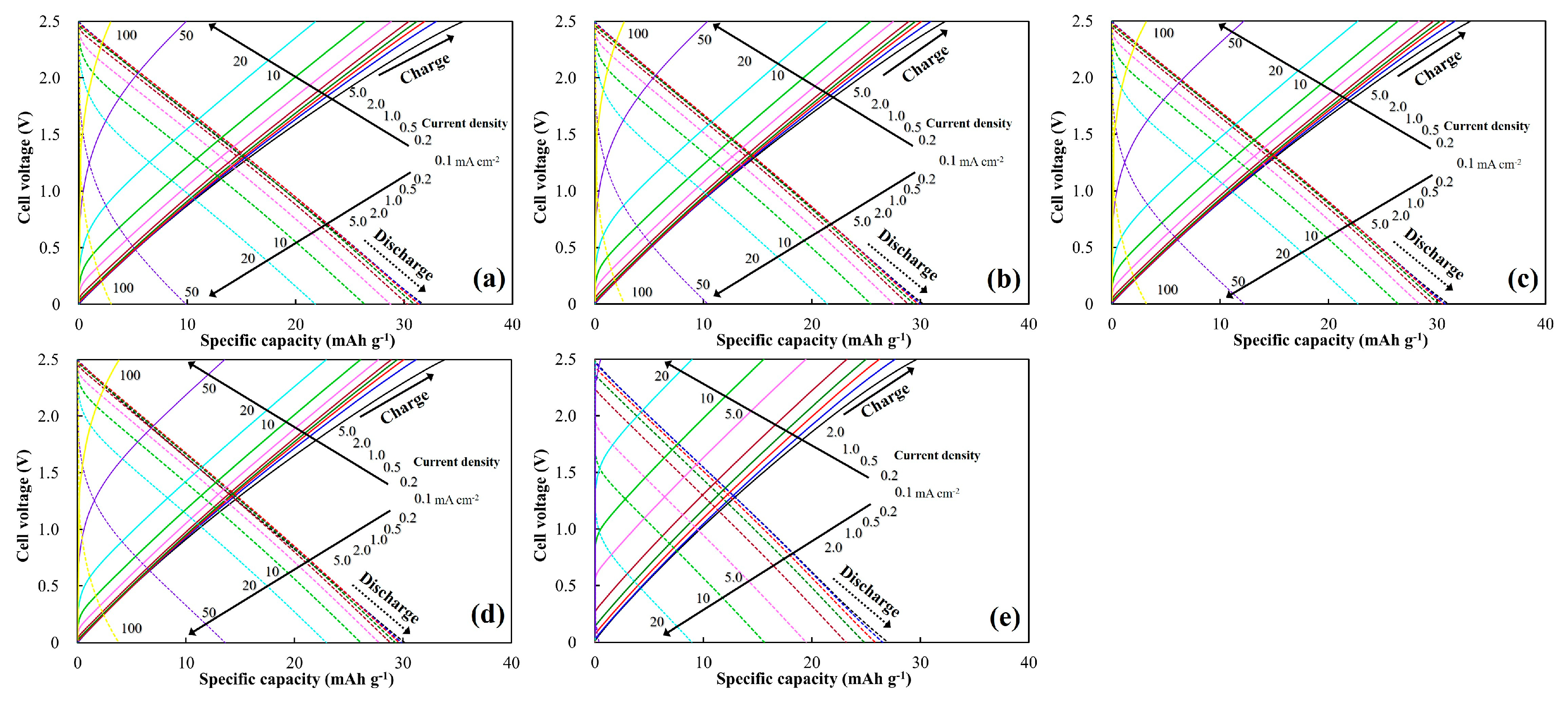
3.2. Electrochemical Properties of the Milled ACs
3.3. Material and Electrochemical Properties of the ACs with Different Particle Sizes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Sakka, M.A.; Gualous, H.; Mierlo, J.V.; Culcu, H. Thermal modeling and heat management of supercapacitor modules for vehicle applications. J. Power Sources 2009, 194, 581–587. [Google Scholar] [CrossRef]
- Kurzweil, P.; Shamonin, M. State-of-charge monitoring by impedance spectroscopy during long-term self-discharge of supercapacitors and lithium-ion batteries. Batteries 2018, 4, 35. [Google Scholar] [CrossRef]
- Liu, C.F.; Liu, Y.C.; Yi, T.Y.; Hu, C.C. Carbon materials for high-voltage supercapacitors. Carbon 2019, 145, 529–548. [Google Scholar] [CrossRef]
- Mori, T.; Iwamura, S.; Ogino, I.; Mukai, S.R. Cost-effective synthesis of activated carbons with high surface areas for electrodes of non-aqueous electric double layer capacitors. Sep. Purif. Technol. 2019, 214, 174–180. [Google Scholar] [CrossRef]
- Huang, G.; Wang, Y.; Zhang, T.; Wu, X.; Cai, J. High-performance hierarchical N-doped porous carbons from hydrothermally carbonized bamboo shoot shells for symmetric supercapacitors. J. Taiwan Inst. Chem. Eng. 2019, 96, 672–680. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, M.; Zhang, Y.; Zhao, W.; Wang, C. A biomass-derived nitrogen-doped porous carbon for high-energy supercapacitor. Carbon 2018, 140, 404–412. [Google Scholar] [CrossRef]
- Sevilla, M.; Ferrero, G.A.; Diez, N.; Fuertes, A.B. One-step synthesis of ultra-high surface area nanoporous carbons and their application for electrochemical energy storage. Carbon 2018, 131, 193–200. [Google Scholar] [CrossRef]
- Gopiraman, M.; Deng, D.; Kim, B.S.; Chung, I.M.; Kim, I.S. Three-dimensional cheese-like carbon nanoarchitecture with tremendous surface area and pore construction derived from corn as superior electrode materials for supercapacitors. Appl. Surf. Sci. 2017, 409, 52–59. [Google Scholar] [CrossRef]
- Peng, L.; Liang, Y.; Dong, H.; Hu, H.; Zhao, X.; Cai, Y.; Xiao, Y.; Liu, Y.; Zheng, M. Super-hierarchical porous carbons derived from mixed biomass wastes by a stepwise removal strategy for high-performance supercapacitors. J. Power Sources 2018, 377, 151–160. [Google Scholar] [CrossRef]
- Pontiroli, D.; Scaravonati, S.; Magnani, G.; Fornasini, L.; Bersani, D.; Bertoni, G.; Milanese, C.; Girella, A.; Ridi, F.; Verucchi, R.; et al. Super-activated biochar from poultry litter for high-performance supercapacitors. Microporous Mesoporous Mater. 2019, 285, 161–169. [Google Scholar] [CrossRef]
- Zou, Z.; Liu, T.; Jiang, C. Highly mesoporous carbon flakes derived from a tubular biomass for high power electrochemical energy storage in organic electrolyte. Mater. Chem. Phys. 2019, 223, 16–23. [Google Scholar] [CrossRef]
- Gao, Y.; Li, L.; Jin, Y.; Wang, Y.; Yuan, C.; Wei, Y.; Chen, G.; Ge, J.; Lu, H. Porous carbon made from rice husk as electrode material for electrochemical double layer capacitor. Appl. Energy 2015, 153, 41–47. [Google Scholar] [CrossRef]
- Raymundo-Pinero, E.; Kierzek, K.; Machnikowski, J.; Béguin, F. Relationship between the nanoporous texture of activated carbons and their capacitance properties in different electrolytes. Carbon 2006, 44, 2498–2507. [Google Scholar] [CrossRef]
- Yang, I.; Kim, S.G.; Kwon, S.H.; Kim, M.S.; Jung, J.C. Relationships between pore size and charge transfer resistance of carbon aerogels for organic electric double-layer capacitor electrodes. Electrochim. Acta 2017, 223, 21–30. [Google Scholar] [CrossRef]
- Dong, X.L.; Lu, A.H.; Li, W.C. Highly microporous carbons derived from a complex of glutamic acid and zinc chloride for use in supercapacitors. J. Power Sources 2016, 327, 535–542. [Google Scholar] [CrossRef]
- Chmiola, J.; Yushin, G.; Gogotsi, Y.; Portet, C.; Simon, P.; Taberna, P.L. Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer. Science 2006, 313, 1760–1763. [Google Scholar] [CrossRef] [PubMed]
- Simon, P.; Burke, A. Nanostructured carbons: Double-layer capacitance and more. Electrochem. Soc. Interface 2008, 17, 38–43. [Google Scholar]
- Yoshida, A.; Nonaka, S.; Aoki, I.; Nishino, A. Electric double-layer capacitors with sheet-type polarizable electrodes and application of the capacitors. J. Power Sources 1996, 60, 213–218. [Google Scholar] [CrossRef]
- Pandolfo, A.G.; Wilison, G.J.; Huynh, T.D.; Hollenkamp, A.F. The influence of conductive additives and inter-particle voids in carbon EDLC electrodes. Fuel Cells 2010, 5, 856–864. [Google Scholar] [CrossRef]
- Rennine, A.J.R.; Martins, V.L.; Smith, R.M.; Hall, P.J. Influence of particle size distribution on the performance of ionic liquid-based electrochemical double layer capacitors. Sci. Rep. 2016, 6, 22062. [Google Scholar] [CrossRef] [PubMed]
- Dyatkin, B.; Gogotsi, O.; Malinovskiy, B.; Zozulya, Y.; Simon, P.; Gogotsi, Y. High capacitance of coarse-grained carbide derived carbon electrodes. J. Power Sources 2016, 306, 32–41. [Google Scholar] [CrossRef]
- Kado, Y.; Imoto, K.; Soneda, Y.; Yoshizawa, N. Correlation between the pore structure and electrode density of MgO-templated carbons for electric double layer capacitor applications. J. Power Sources 2016, 305, 128–133. [Google Scholar] [CrossRef]
- Azaïs, P. Manufacturing of Industrial Supercapacitor. Supercapacitor Materials, Systems, and Applications; Béguin, F., Frackowiak, E., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; p. 320. [Google Scholar]
- Kado, Y.; Soneda, Y. Void-bearing electrodes with microporous activated carbon for electric double-layer capacitors. J. Electroanal. Chem. 2019, 833, 33–38. [Google Scholar] [CrossRef]
- Tanaka, S.; Nakao, H.; Mukai, T.; Katayama, Y.; Miyake, Y. An experimental investigation of the ion storage/transfer behavior in an electrical double-layer capacitor by using monodisperse carbon spheres with microporous structure. J. Phys. Chem. C 2012, 116, 26791–26799. [Google Scholar] [CrossRef]
- Nandhini, R.; Mini, P.A.; Avinash, B.; Nair, S.V.; Subramanian, K.R.V. Supercapacitor electrodes using nanoscale activated carbon from graphite by ball milling. Mater. Lett. 2012, 87, 165–168. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, R.; Wang, J.; Ge, S.; Zhou, H.; Liu, Y.; Chen, P. Effective control of the microstructure of carbide-derived carbon by ball-milling the carbide precursor. Carbon 2013, 52, 499–508. [Google Scholar] [CrossRef]
- Welham, N.J.; Berbenni, V.; Chapman, P.G. Increased chemisorption onto activated carbon after ball-milling. Carbon 2002, 40, 2307–2315. [Google Scholar] [CrossRef]
- Choi, W.S.; Shim, W.G.; Ryu, D.W.; Hwang, M.J.; Moon, H. Effect of ball milling on electrochemical characteristics of walnut shell-based carbon electrodes for EDLCs. Microporous Mesoporous Mater. 2012, 155, 274–280. [Google Scholar] [CrossRef]
- Müller, B.R. Effect of particle size and surface area on the adsorption of albumin-bonded bilirubin on activated carbon. Carbon 2010, 48, 3607–3615. [Google Scholar] [CrossRef]
- Ong, T.S.; Yang, H. Effect of atmosphere on the mechanical milling of natural graphite. Carbon 2000, 38, 2077–2085. [Google Scholar] [CrossRef]
- Partlan, E.; Davis, K.; Ren, Y.; Aqul, O.G.; Mefford, O.T.; Karanfil, T.; Ladner, D.A. Effect of bead milling on chemical and physical characteristics of activated carbons pulverized to superfine sizes. Water Res. 2016, 89, 161–170. [Google Scholar] [CrossRef] [PubMed]
- Macías-García, A.; Torrejón-Martín, D.; Díaz-Díez, M.Á.; Carrasco-Amador, J.P. Study of the influence of particle size of activate carbon for the manufacture of electrodes for supercapacitors. J. Energy Storage 2019, 25, 100829. [Google Scholar] [CrossRef]
- Portet, C.; Yushin, G.; Gogotsi, Y. Effect of carbon particle size on electrochemical performance of EDLC. J. Electrochem. Soc. 2008, 155, 531–536. [Google Scholar] [CrossRef]
- Otowa, T.; Tanibata, R.; Itoh, M. Production and adsorption characteristics of MAXSORB: High-surface-area active carbon. Gas. Sep. Purif. 1993, 7, 241–245. [Google Scholar] [CrossRef]
- Katagiri, G.; Ishida, H.; Ishitani, A. Raman spectra of graphite edge planes. Carbon 1988, 26, 565–571. [Google Scholar] [CrossRef]
- Eckmann, A.; Felten, A.; Mishchenko, A.; Britnell, L.; Krupke, R.; Novoselov, K.S.; Casiraghi, C. Probing the nature of defects in graphene by Raman spectroscopy. Nano Lett. 2012, 12, 3925–3930. [Google Scholar] [CrossRef]
- Guizani, C.; Haddad, K.; Limousy, L.; Jeguirim, M. New insights on the structural evolution of biomass char upon pyrolysis as revealed by the Raman spectroscopy and elemental analysis. Carbon 2017, 119, 519–521. [Google Scholar] [CrossRef]
- Neimark, A.V.; Lin, Y.; Ravikovitch, P.I.; Thommes, M. Quenched solid density functional theory and pore size analysis of micro-mesoporous carbons. Carbon 2009, 47, 1617–1628. [Google Scholar] [CrossRef]
- Gor, G.Y.; Thommes, M.; Cychosz, K.A.; Neimark, A.V. Quenched solid density functional theory method for characterization of mesoporous carbons by nitrogen adsorption. Carbon 2012, 50, 1583–1590. [Google Scholar] [CrossRef]
- Piedboeuf, M.L.C.; Léonard, A.F.; Traina, K.; Job, N. Influence of the textural parameters of resorcinol–formaldehyde dry polymers and carbon xerogels on particle sizes upon mechanical milling. Colloids Surf. A Phys. Eng. Asp. 2015, 471, 124–132. [Google Scholar] [CrossRef]
- Li, Z.Q.; Lu, C.J.; Xia, Z.P.; Zhou, Y.; Luo, Z. X-ray diffraction patterns of graphite and turbostratic carbon. Carbon 2007, 45, 1686–1695. [Google Scholar] [CrossRef]
- Sathyaseelan, B.; Manikandan, E.; Baskaran, I.; Senthilnathan, K.; Sivakumar, K.; Moodley, M.K.; Ladchumananandasivam, R.; Maaza, M. Studies on structural and optical properties of ZrO2 nanopowder for opto-electronic applications. J. Alloys Compd. 2017, 694, 556–559. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC technical report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Jing, X.; Zhao, W.; Lan, L. The effect of particle size on electric conducting percolation threshold in polymer/conducting particle composites. J. Mater. Sci. Lett. 2000, 19, 377–379. [Google Scholar] [CrossRef]
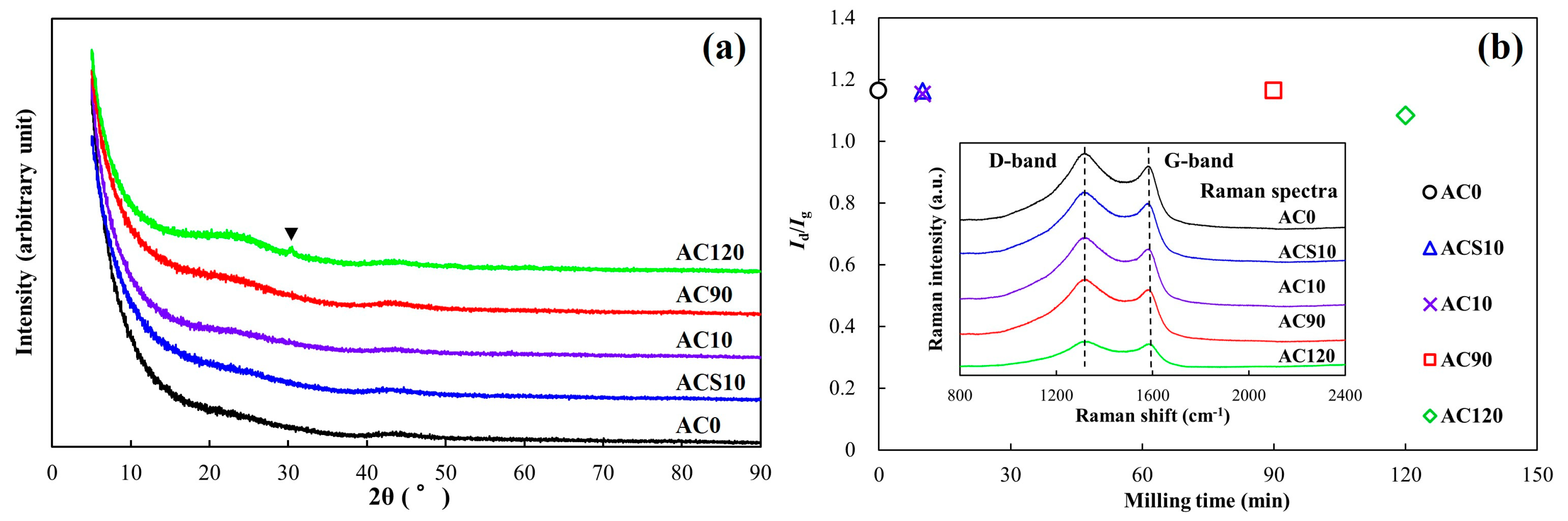
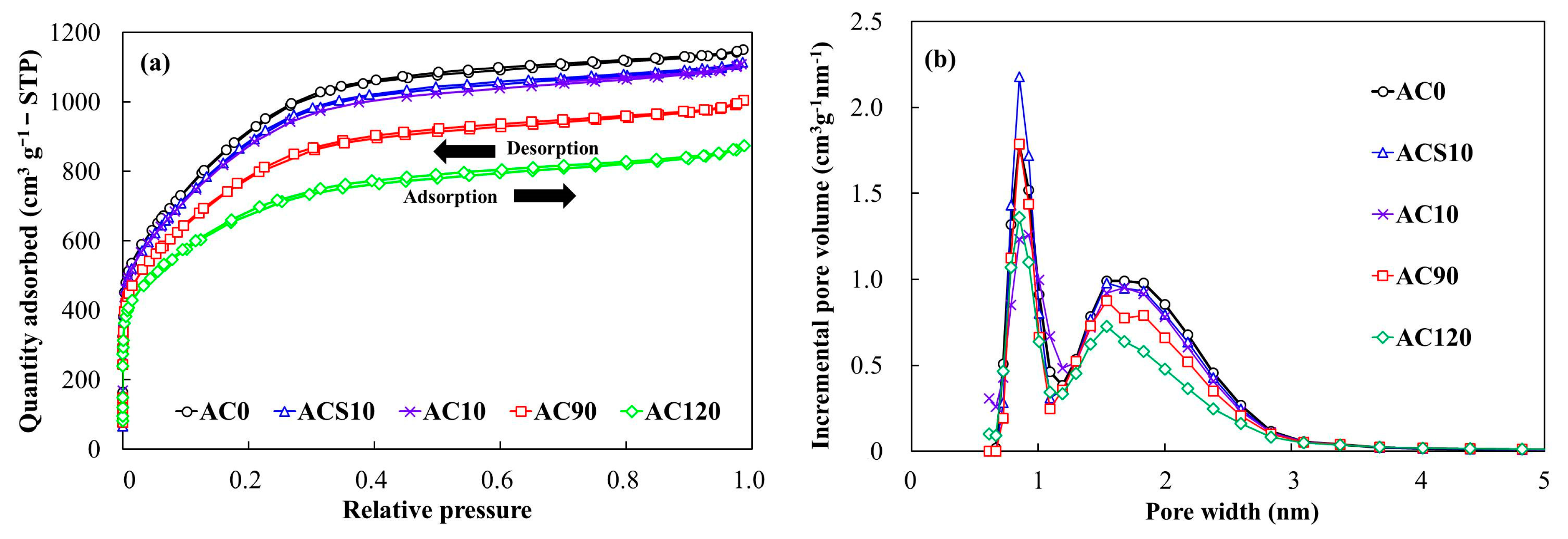
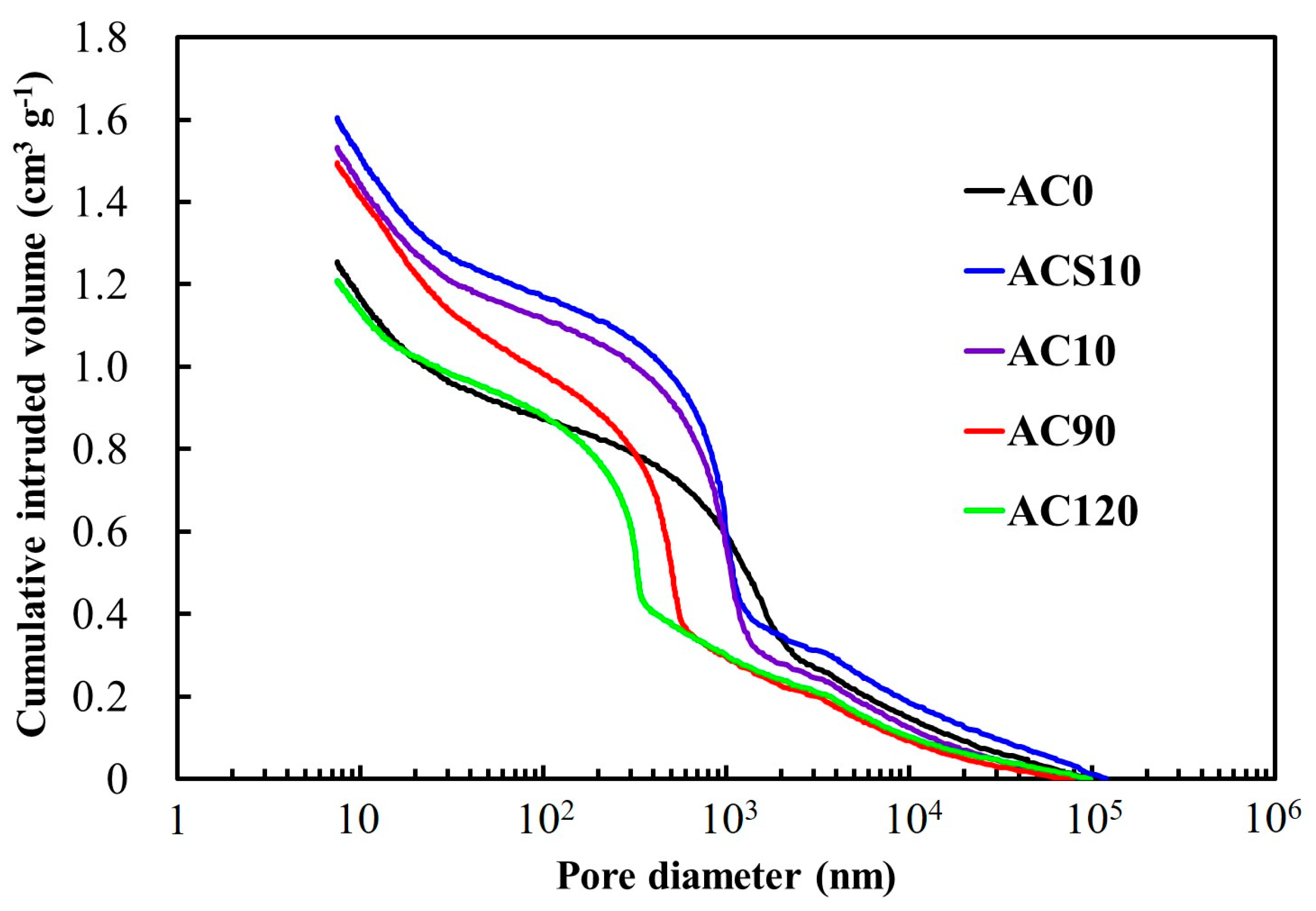



| Sequence | Current Density 1 (mA cm−2) | Number of Cycles | Cycle Selected for the Performance Evaluation |
|---|---|---|---|
| 1 | 0.1 | 2 | Second |
| 2 | 0.2 | 2 | Second |
| 3 | 0.5 | 2 | Second |
| 4 | 1.0 | 5 | Third |
| 5 | 2.0 | 5 | Third |
| 6 | 5.0 | 5 | Third |
| 7 | 10 | 11 | Sixth |
| 8 | 20 | 11 | Sixth |
| 9 | 50 | 11 | Sixth |
| 10 | 100 | 25 | Thirteenth |
| Sample Name | SBET (m2 g−1) | Vtotal (cm3 g−1) | Vmicro (cm3 g−1) | Vmeso (cm3 g−1) |
|---|---|---|---|---|
| AC0 | 3198 | 1.78 | 1.27 | 0.38 |
| ACS10 | 3073 | 1.73 | 1.23 | 0.37 |
| AC10 | 3041 | 1.72 | 1.22 | 0.37 |
| AC90 | 2755 | 1.56 | 1.09 | 0.34 |
| AC120 | 2448 | 1.36 | 0.96 | 0.28 |
| Sample Name | Dave (µm) | D25 (µm) | D50 (µm) | D75 (µm) |
|---|---|---|---|---|
| AC0 | 74.9 | 42.5 | 70.7 | 135.1 |
| ACS10 | 20.0 | 10.6 | 26.1 | 37.5 |
| AC10 | 11.6 | 6.8 | 11.7 | 19.7 |
| AC90 | 3.0 | 1.9 | 2.8 | 4.2 |
| AC120 | 2.2 | 1.6 | 2.4 | 3.3 |
| Used AC | Mass of AC in the Electrode (mg) | Thickness of the Electrode (mm) | AC Bulk Density in the Electrode (g cm−3) |
|---|---|---|---|
| AC0 | 11.7 | 0.32 | 0.32 |
| ACS10 | 10.8 | 0.30 | 0.32 |
| AC10 | 10.6 | 0.30 | 0.31 |
| AC90 | 12.1 | 0.31 | 0.34 |
| AC120 | 12.9 | 0.29 | 0.39 |
| Current Density (mA cm−2) | AC0 | ACS10 | AC10 | AC90 | AC120 |
|---|---|---|---|---|---|
| 0.1 | 46.4 | 47.8 | 46.1 | 46.7 | 141.7 |
| 1 | 19.1 | 15.3 | 19.6 | 15.2 | 108.0 |
| 5 | 16.4 | 16.2 | 16.8 | 12.7 | 96.8 |
| 10 | 13.8 | 14.3 | 14.1 | 11.9 | 73.9 |
| 50 | 13.3 | 14.0 | 13.7 | 12.5 | NM 1 |
| 100 | 12.5 | 13.8 | 13.5 | 12.6 | NM 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eguchi, T.; Kanamoto, Y.; Tomioka, M.; Tashima, D.; Kumagai, S. Effect of Ball Milling on the Electrochemical Performance of Activated Carbon with a Very High Specific Surface Area. Batteries 2020, 6, 22. https://doi.org/10.3390/batteries6020022
Eguchi T, Kanamoto Y, Tomioka M, Tashima D, Kumagai S. Effect of Ball Milling on the Electrochemical Performance of Activated Carbon with a Very High Specific Surface Area. Batteries. 2020; 6(2):22. https://doi.org/10.3390/batteries6020022
Chicago/Turabian StyleEguchi, Takuya, Yugo Kanamoto, Masahiro Tomioka, Daisuke Tashima, and Seiji Kumagai. 2020. "Effect of Ball Milling on the Electrochemical Performance of Activated Carbon with a Very High Specific Surface Area" Batteries 6, no. 2: 22. https://doi.org/10.3390/batteries6020022
APA StyleEguchi, T., Kanamoto, Y., Tomioka, M., Tashima, D., & Kumagai, S. (2020). Effect of Ball Milling on the Electrochemical Performance of Activated Carbon with a Very High Specific Surface Area. Batteries, 6(2), 22. https://doi.org/10.3390/batteries6020022







