In Situ Measurement of Orthotropic Thermal Conductivity on Commercial Pouch Lithium-Ion Batteries with Thermoelectric Device
Abstract
1. Introduction
2. Equipment Description
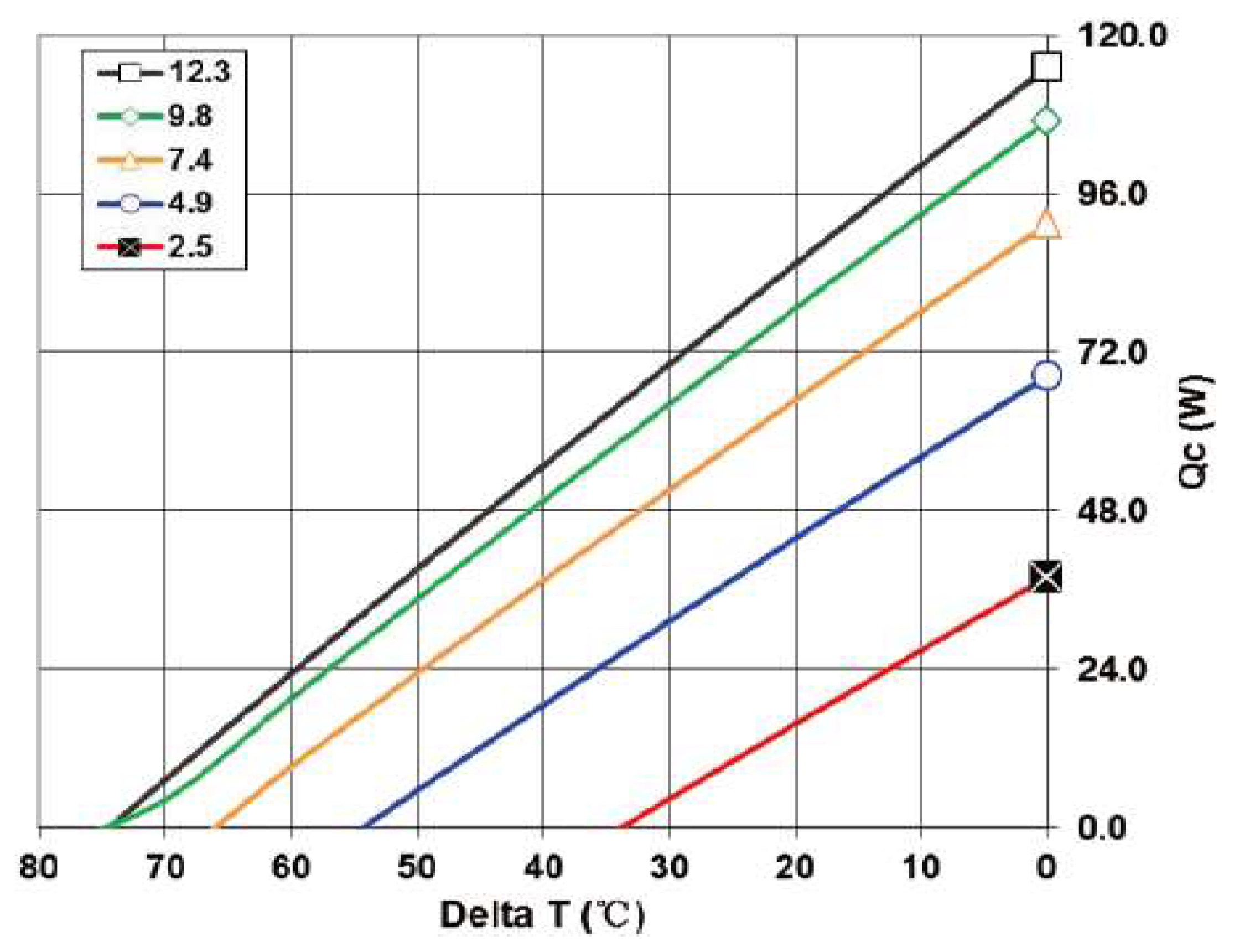
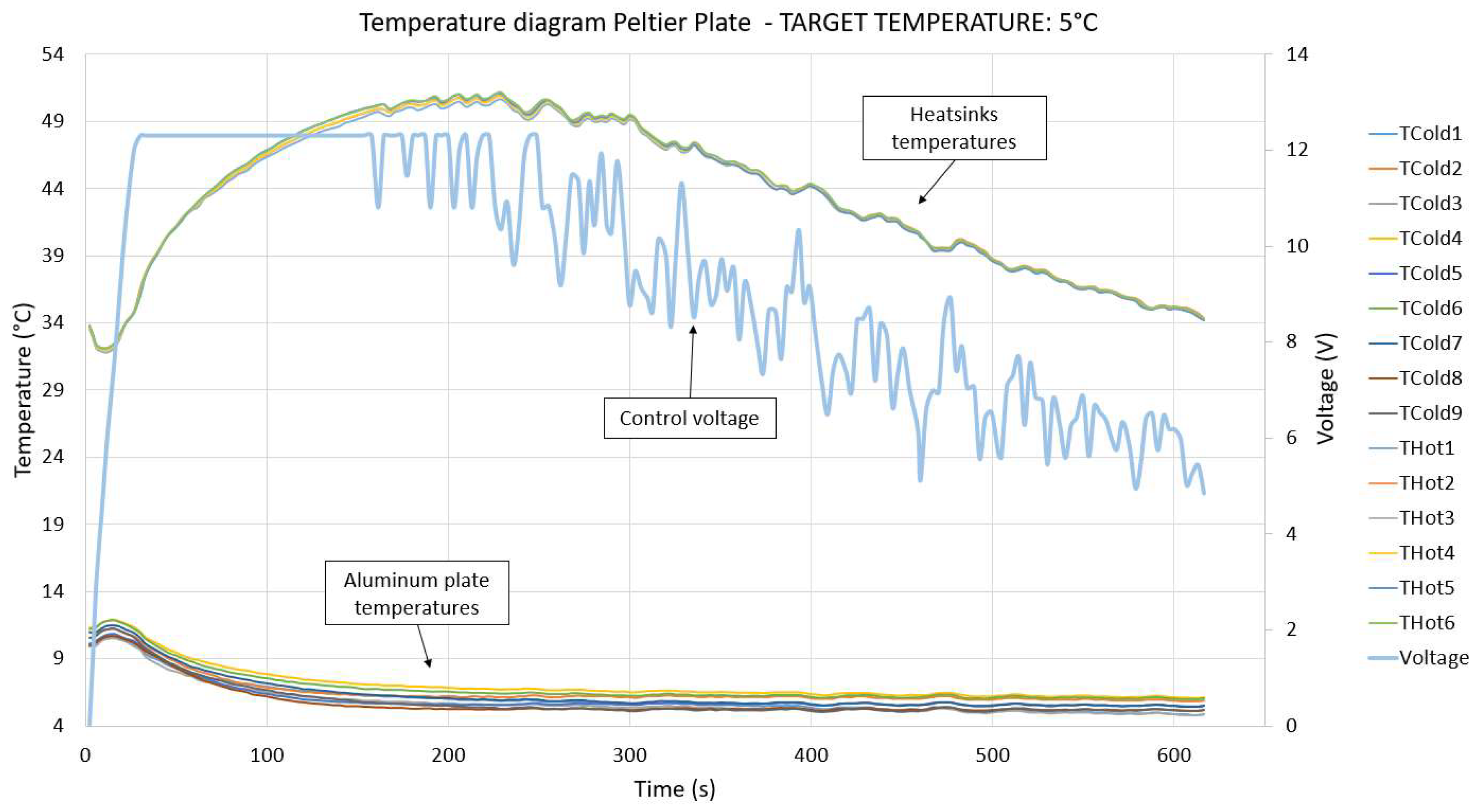
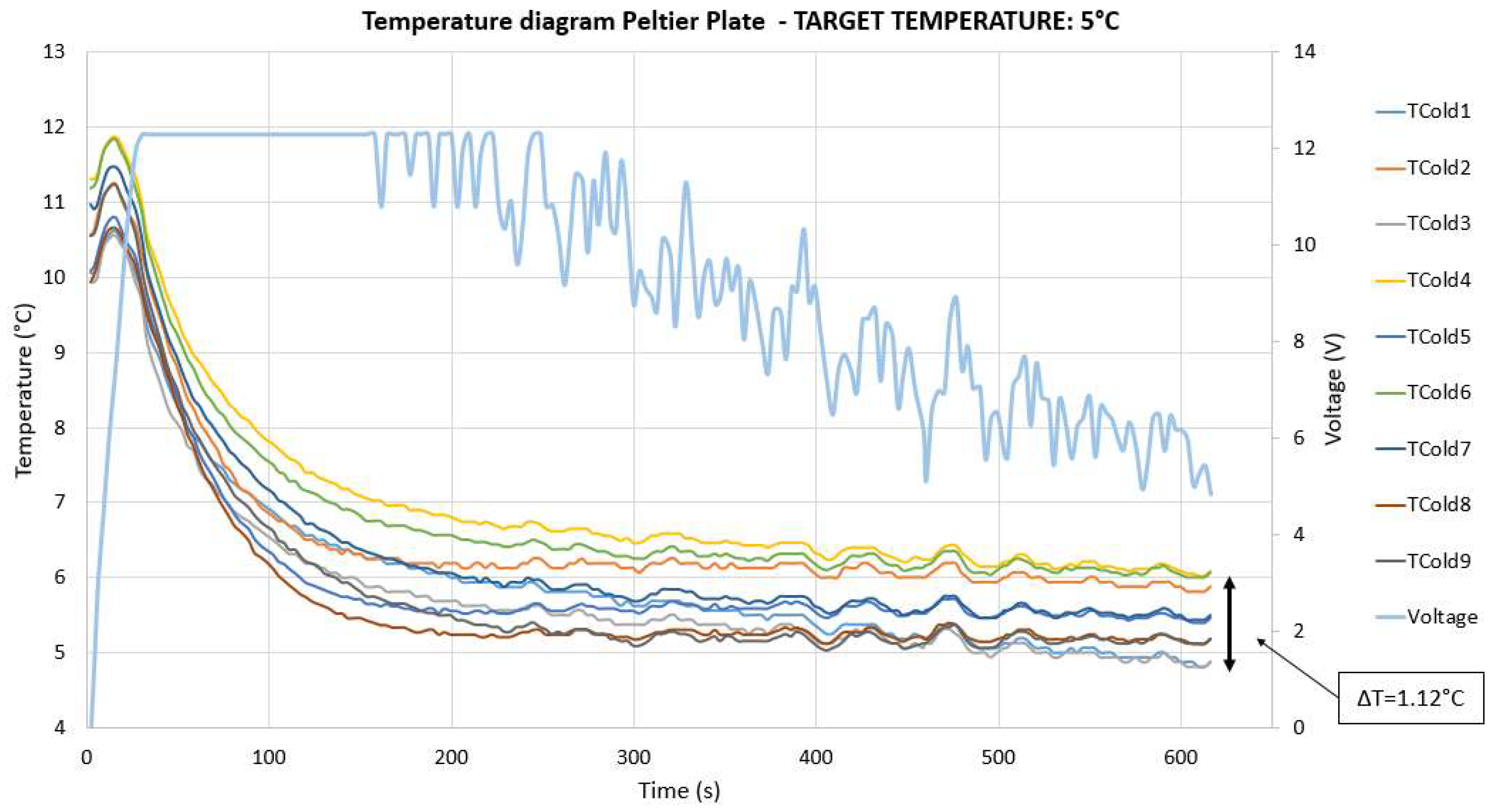
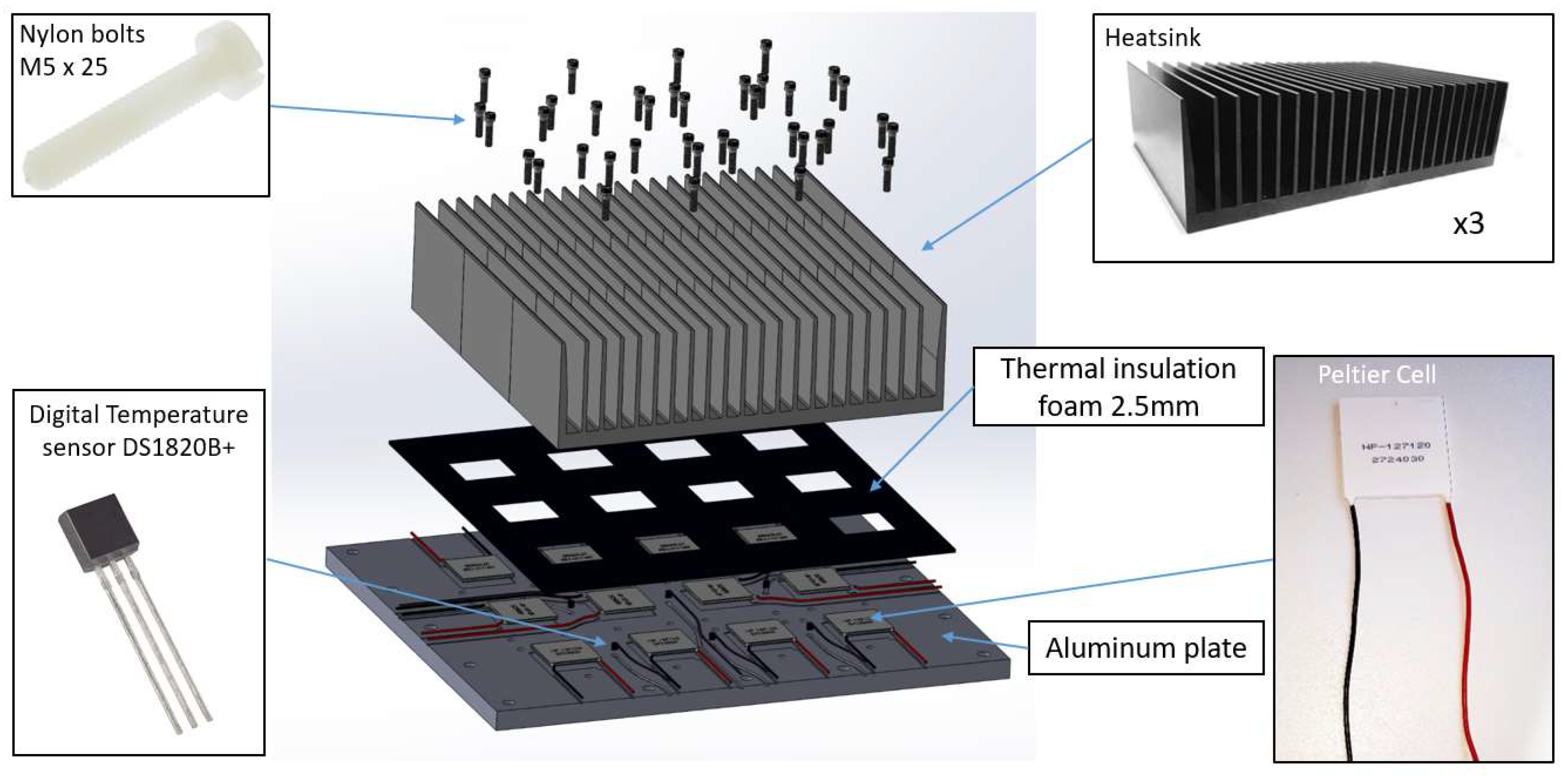
2.1. Thermoelectric Device
2.2. Flat Heat Flux Sensors
- Calibration uncertainty ±5%;
- Sensitivity range (4 to 8) × 10−6 V/(W/m2);
- Sensitivity nominal 5.5 × 10−6 V/(W/m2);
- Expected voltage output (−80 to +80) mV;
- Sensor thermal conductivity 0.29 W/(mK);
- Temperature sensor Type T incorporated;
- Accuracy ±1.0 °C or ±0.4% (whichever is greater).
2.3. Battery Sample Used for Tests
3. Method
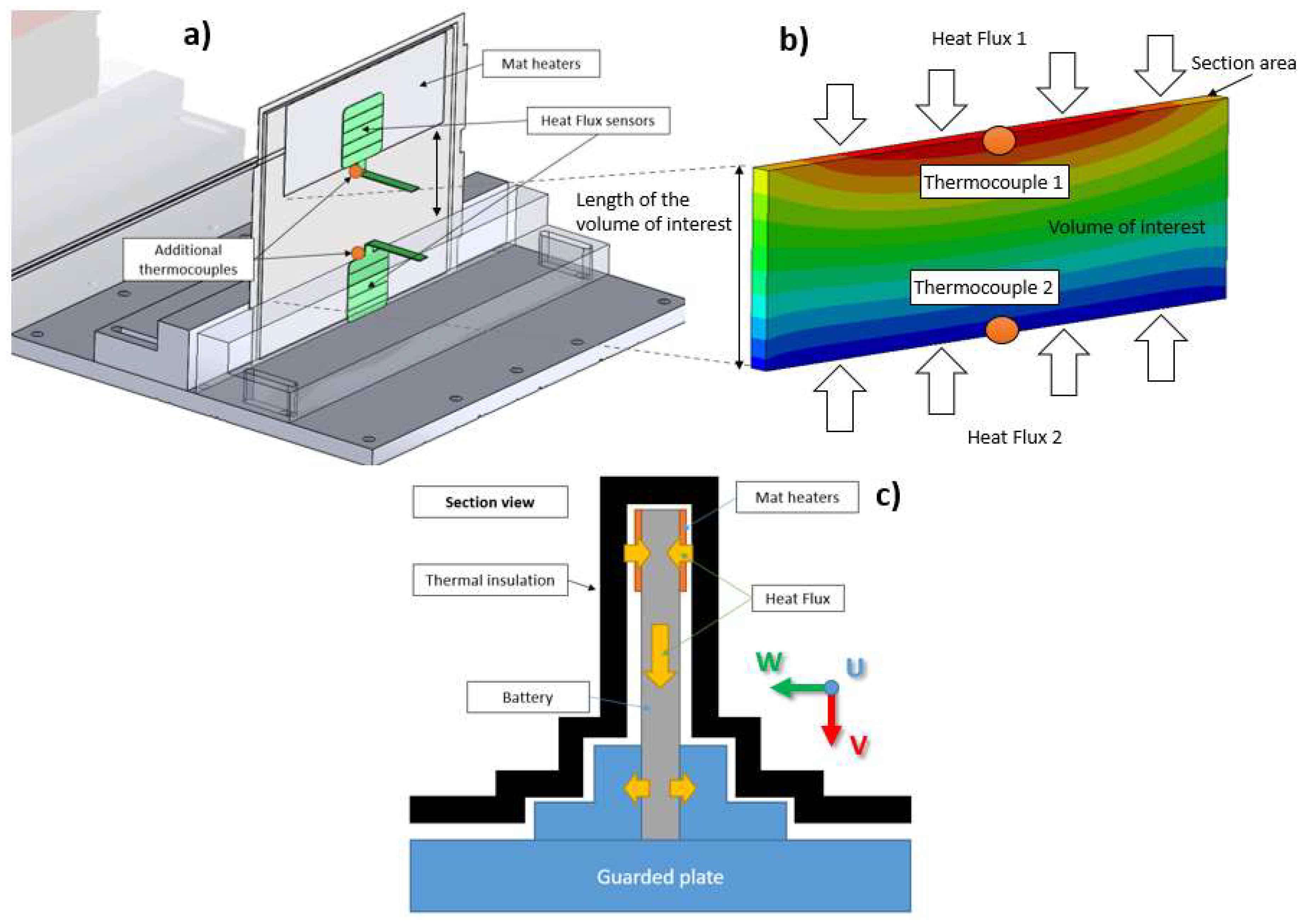
3.1. Measurement along the “w” Direction
3.2. Measurement along the “u” and “v” Directions
3.3. Measurement Uncertainty Propagation
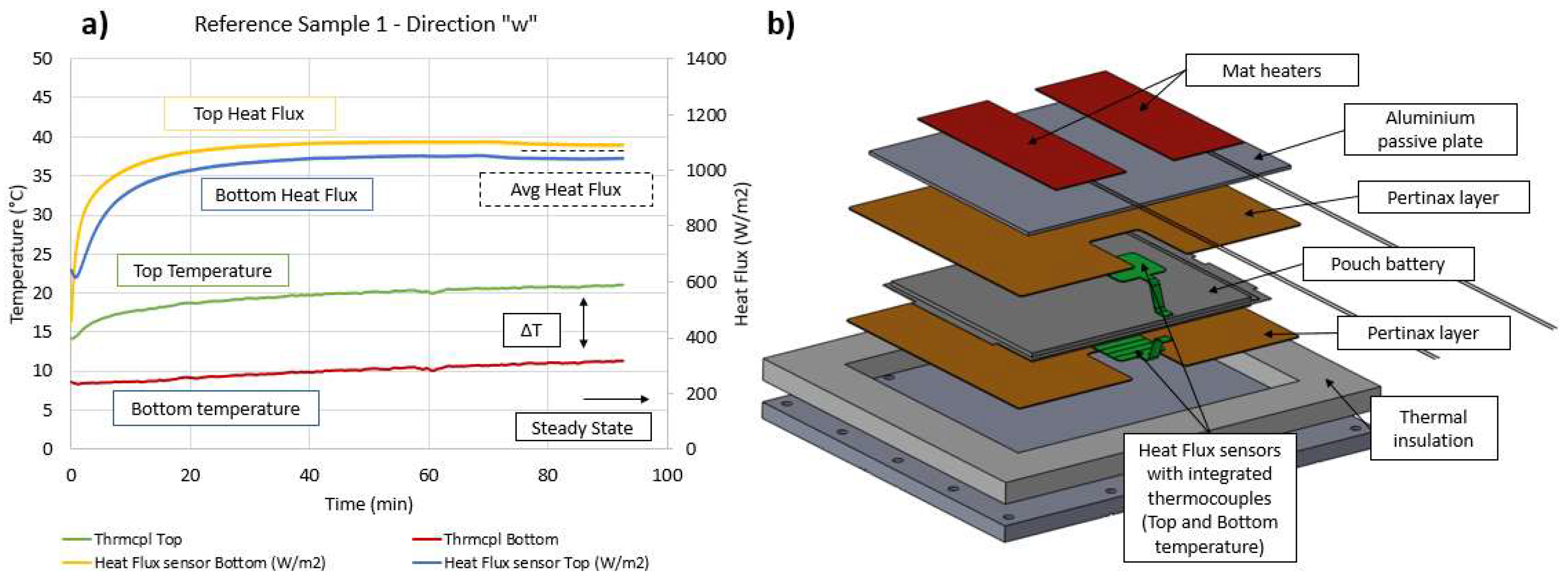
3.4. Reference Test
4. Results
4.1. Preparation and Inspection of Samples
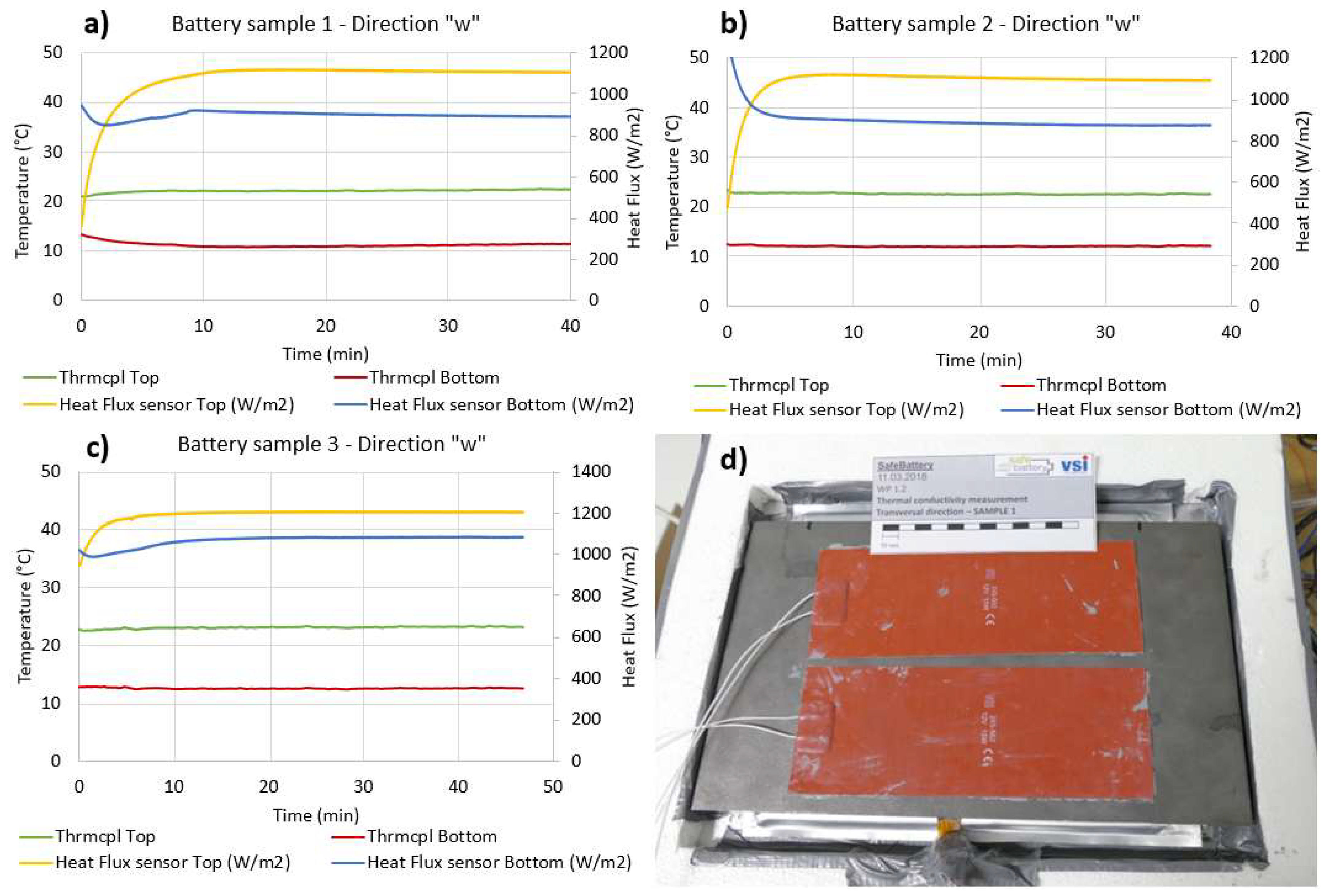
4.2. Thermal Conductivity along the “w” Direction
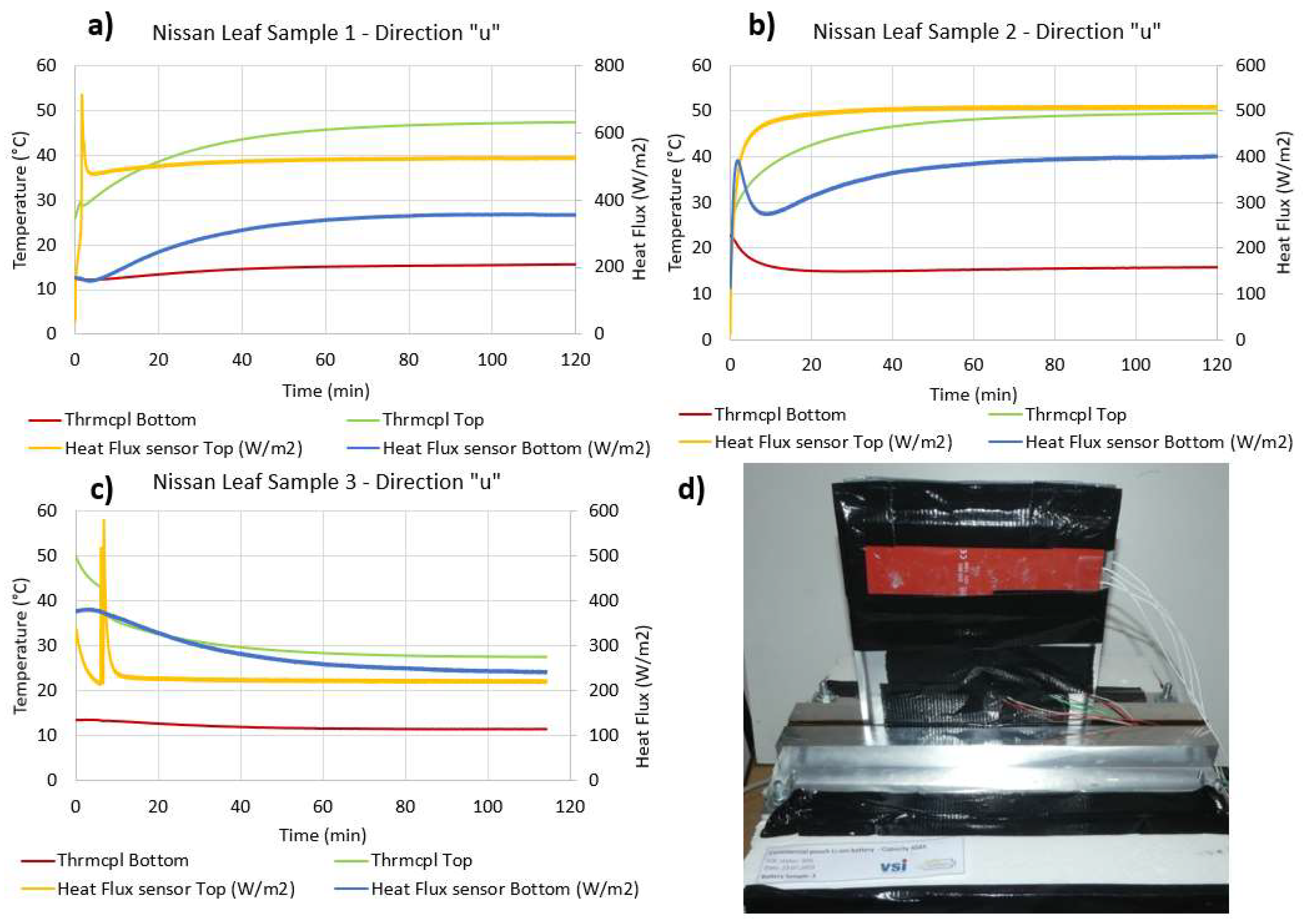
4.3. Thermal Conductivity along the “u” Direction
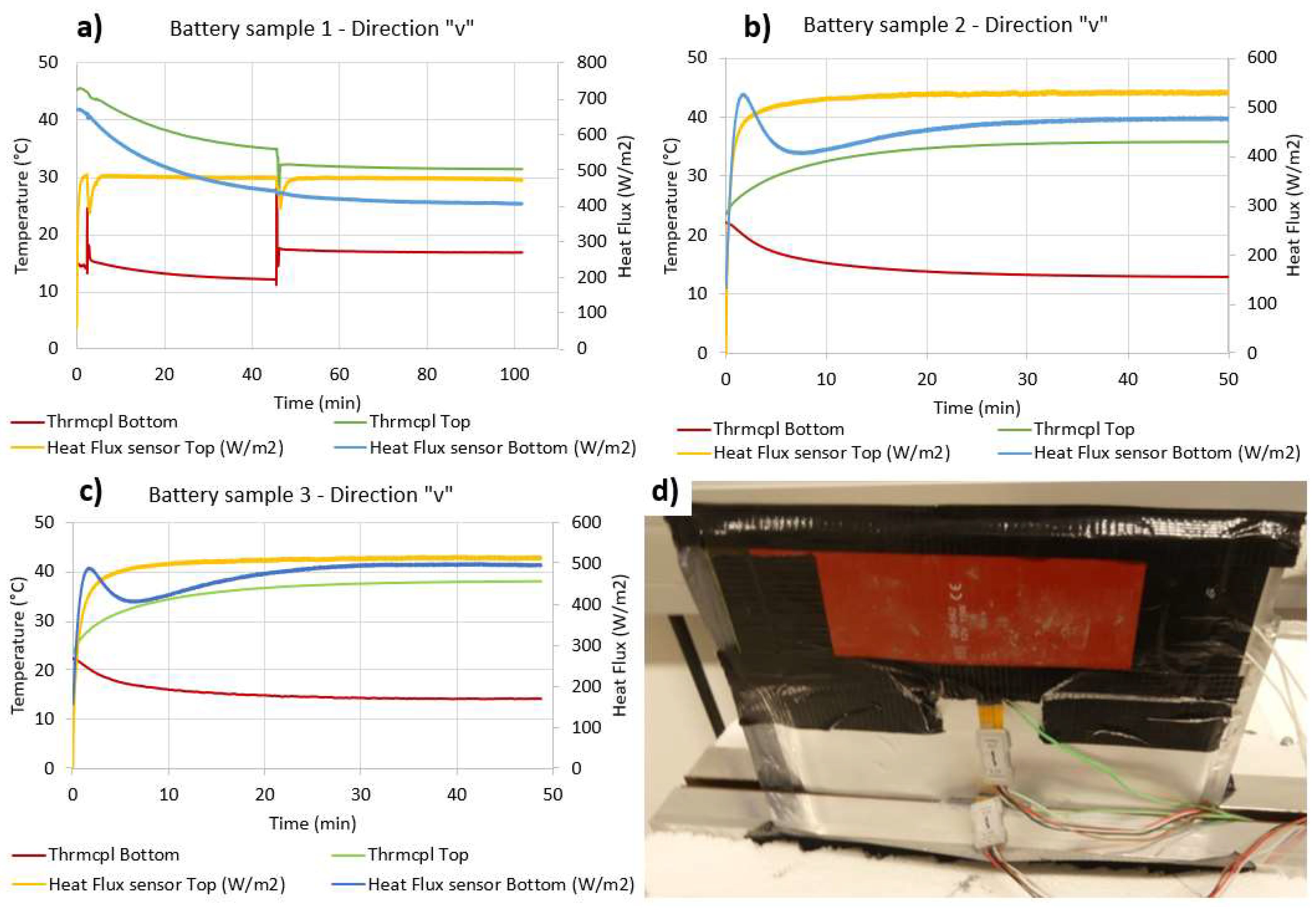
4.4. Thermal Conductivity along the “v” Direction
5. Results Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bazinski, S.J.; Wang, X. Experimental study on the influence of temperature and state-of-charge on the thermophysical properties of an lfp pouch cell. J. Power Sources 2015, 293, 283–291. [Google Scholar] [CrossRef]
- Lidbeck, A.; Syed, K.R. Experimental Characterization of Li-ion Battery Cells for Thermal Management in Heavy Duty Hybrid Applications. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2017. [Google Scholar]
- Arzberger, A.; Sauer, U.D. The change of thermal conductivity of lithium-ion pouch cells with operating point and what this means for battery thermal management. In Proceedings of the AABC—Advanced Automotive Battery Conference, AABTAM Symposium—Advanced Automotive Battery Technology, Application and Market, Atlanta, GA, USA, 2–7 February 2014. [Google Scholar]
- Song, L.; Evans, J.W. Measurements of the Thermal Conductivity of Lithium Polymer Battery Composite Cathodes. J. Electrochem. Soc. 1999, 146, 869. [Google Scholar] [CrossRef]
- Maleki, H. Thermal properties of lithium-ion battery and components. J. Electrochem. Soc. 1999, 146, 947. [Google Scholar] [CrossRef]
- Murashko, K.A.; Mityakov, A.V.; Pyrhönen, J.; Mityakov, V.Y.; Sapozhnikov, S.S. Thermal parameters determination of battery cells by local heat flux measurements. J. Power Sources 2014, 271, 48–54. [Google Scholar] [CrossRef]
- Richter, F.; Vie, P.J.; Kjelstrup, S.; Burheim, O.S. Measurements of ageing and thermal conductivity in a secondary nmc-hard carbon li-ion battery and the impact on internal temperature profiles. Electrochim. Acta 2017, 250, 228–237. [Google Scholar] [CrossRef]
- Werner, D.; Loges, A.; Becker, D.J.; Wetzel, T. Thermal conductivity of Li-ion batteries and their electrode configurations–A novel combination of modelling and experimental approach. J. Power Sources 2017, 364, 72–83. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, B.; Li, Z.; Huang, J. Simultaneous estimation of thermal parameters for large-format laminated lithium-ion batteries. J. Power Sources 2014, 259, 106–116. [Google Scholar] [CrossRef]
- Zhang, Y.; Jahns, T.M. Power electronics loss measurement using new heat flux sensor based on thermoelectric device with active control. IEEE Trans. Ind. Appl. 2014, 50, 4098–4106. [Google Scholar] [CrossRef]
- Kovachev, G.; Schröttner, H.; Gstrein, G.; Aiello, L.; Hanzu, I.; Wilkening, H.M.R.; Foitzik, A.; Wellm, M.; Sinz; Ellersdorfer, C.; et al. Analytical Dissection of an Automotive Li-Ion Pouch Cell. Batteries 2019, 5, 67. [Google Scholar] [CrossRef]
- Taylor, J.R. The Study of Uncertainties in Physical Measurements, Introduction to error analysis 2nd ed.; Chapter 3—Propagation of Uncertainties; University Science Books: Sausalito, CA, USA, 1997; pp. 45–79. [Google Scholar]
- Tokunaga, T.; Tranchant, L.; Takama, N.; Volz, S.; Kim, B. Experimental Study of Heat Transfer in Micro Glass Tubes Mediated by Surface Phonon Polaritons. J. Physics: Conf. Ser. 2012, 395, 012108. [Google Scholar] [CrossRef]
- Lago, N.; Garcia-Calvo, O.; Lopez del Amo, J.M.; Rojo, T.; Armand, M. All-Solid-State Lithium-Ion Batteries with Grafted Ceramic Nanoparticles Dispersed in Solid Polymer Electrolytes. ChemSusChem 2015, 8, 3039–3043. [Google Scholar] [CrossRef] [PubMed]
- Barpanda, P.; Chotard, J.-N.; Delacourt, C.; Reynaud, M.; Filinchuk, Y.; Armand, M.; Deschamps, M.; Tarascon, J.-M. LiZnSO4F made in an ionic liquid: A ceramic electrolyte composite for solid-state lithium batteries. Angew. Chem. Int. Ed. 2011, 50, 2526–2531. [Google Scholar] [CrossRef] [PubMed]

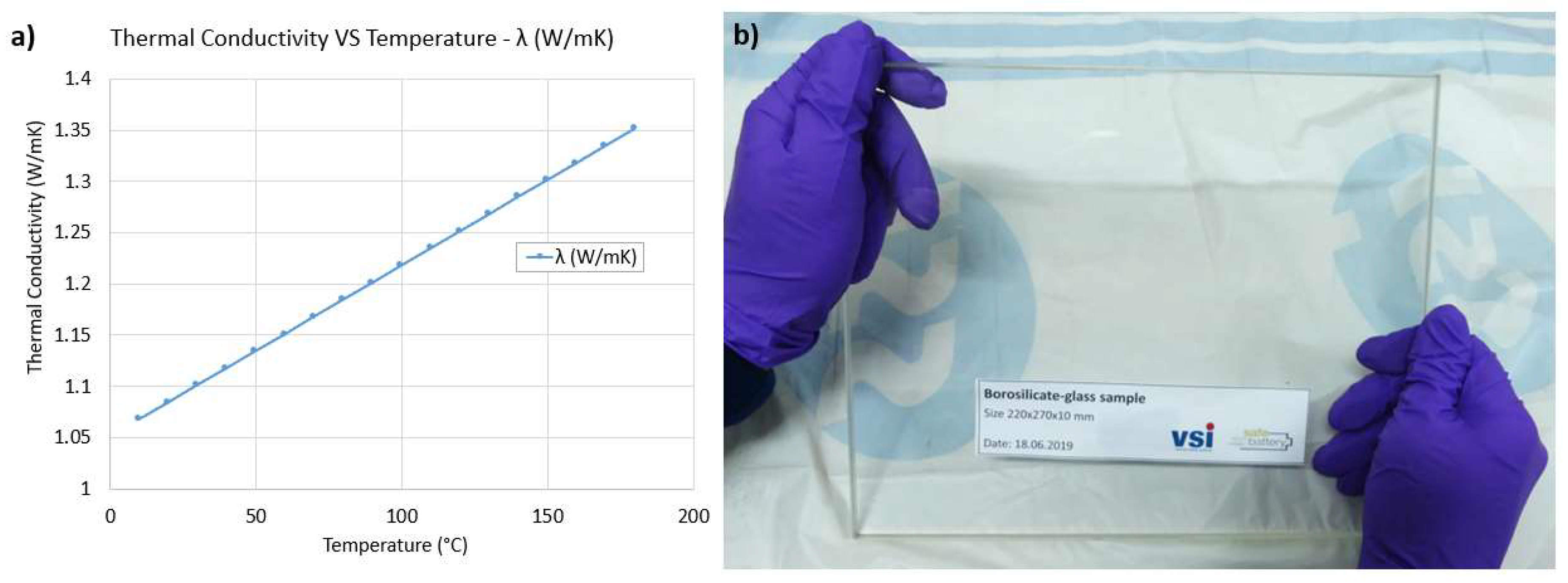

| Chemical Composition | |||
|---|---|---|---|
| SiO2 | B2O3 | Na2O+K2O | Al2O3 |
| 81% | 13% | 4% | 2% |
| Measurement direction “w”—Borosilicate Glass Sample | |||
|---|---|---|---|
| Top Heat Flux (W/m2) | Bottom Heat Flux (W/m2) | ∆Temperature (°C) | Sample Thickness (m) |
| 1042.91 | 1093.44 | 9.73 | 0.01 |
| Computed thermal conductivity (W/mK) | Datasheet value (W/mK) | Deviation (%) | |
| 1.097 | 1.08 at 15°C | 1.63 | |
| Measurement direction “v”—Borosilicate Glass Sample | ||||
|---|---|---|---|---|
| Abs. Top HF (W) | Abs. Bottom HF (W) | ∆Temp (°C) | LenVol.Int (m) | Sample Section (m2) |
| 1.31 | 0.28 | 22.59 | 0.09 | 0.0027 |
| Computed thermal conductivity (W/mK) | Datasheet value (W/mK) | Deviation (%) | ||
| 1.17 | 1.08 at 15°C | 7.69 | ||
| Measurement direction “w”—Commercial pouch Lithium ions battery/Sample 1 | |||
| Top Heat Flux (W/m2) | Bottom Heat Flux (W/m2) | ∆Temp. (°C) | Sample Thickness (m) |
| 889.56 | 1105.70 | 11.03 | 0.008 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | |
| 0.72 | 0.167 | 23.13 | |
| Measurement direction “w”—Commercial pouch Lithium ions battery/Sample 2 | |||
| Top Heat Flux (W/m2) | Bottom Heat Flux (W/m2) | ∆Temp. (°C) | Sample Thickness (m) |
| 876.49 | 1093.86 | 10.37 | 0.008 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | |
| 0.76 | 0.184 | 24.28 | |
| Measurement direction “w”—Commercial pouch Lithium ions battery/Sample 3 | |||
| Top Heat Flux (W/m2) | Bottom Heat Flux (W/m2) | ∆Temp. (°C) | Sample Thickness (m) |
| 1041.26 | 1084.30 | 9.52 | 0.0077 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | |
| 0.84 | 0.2 | 23.97 | |
| Measurement direction “u”—Commercial pouch Lithium ions battery/Sample 1 | ||||
| Abs. Top HF (W) | Abs. Bottom HF (W) | ∆Temp (°C) | LenVol.Int (m) | Sample Section (m2) |
| 15.76 | 7.12 | 31.81 | 0.115 | 0.0016 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | ||
| 25.84 | 2.92 | 11.29 | ||
| Measurement direction “u”—Commercial pouch Lithium ions battery/Sample 2 | ||||
| Abs. Top HF (W) | Abs. Bottom HF (W) | ∆Temp (°C) | LenVol.Int (m) | Sample Section (m2) |
| 15.27 | 8.03 | 33.75 | 0.115 | 0.0016 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | ||
| 24.80 | 2.71 | 10.93 | ||
| Measurement direction “u”—Commercial pouch Lithium ions battery/Sample 3 | ||||
| Abs. Top HF (W) | Abs. Bottom HF (W) | ∆Temp (°C) | LenVol.Int (m) | Sample Section (m2) |
| 6.61 | 4.83 | 16.06 | 0.115 | 0.00154 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | ||
| 26.58 | 4.64 | 17.45 | ||
| Measurement direction “v”—Commercial pouch Lithium ions battery/Sample 1 | ||||
| Abs. Top HF (W) | Abs. Bottom HF (W) | ∆Temp (°C) | LenVol.Int (m) | Sample Section (m2) |
| 14.19 | 9.12 | 20.54 | 0.085 | 0.00192 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | ||
| 25.18 | 3.71 | 14.74 | ||
| Measurement direction “v”—Commercial pouch Lithium ions battery/Sample 2 | ||||
| Abs. Top HF (W) | Abs. Bottom HF (W) | ∆Temp (°C) | LenVol.Int (m) | Sample Section (m2) |
| 15.85 | 10.77 | 22.87 | 0.085 | 0.00192 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | ||
| 25.77 | 3.54 | 13.75 | ||
| Measurement direction “v”—Commercial pouch Lithium ions battery/Sample 3 | ||||
| Abs. Top HF (W) | Abs. Bottom HF (W) | ∆Temp (°C) | LenVol.Int (m) | Sample Section (m2) |
| 15.38 | 11.20 | 23.80 | 0.085 | 0.001848 |
| Computed thermal conductivity (W/mK) | Abs. uncertainty | Uncertainty (%) | ||
| 25.69 | 3.44 | 13.40 | ||
| Measurement Direction | Sample n. | Th. Cond. (W m−1K−1) | Avg. Th. Cond. (W m−1K−1) |
|---|---|---|---|
| “w” | 1 | 0.72 | 0.77 |
| 2 | 0.76 | ||
| 3 | 0.84 | ||
| “u” | 1 | 25.84 | 25.74 |
| 2 | 24.80 | ||
| 3 | 26.58 | ||
| “v” | 1 | 25.18 | 25.55 |
| 2 | 25.77 | ||
| 3 | 25.69 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aiello, L.; Kovachev, G.; Brunnsteiner, B.; Schwab, M.; Gstrein, G.; Sinz, W.; Ellersdorfer, C. In Situ Measurement of Orthotropic Thermal Conductivity on Commercial Pouch Lithium-Ion Batteries with Thermoelectric Device. Batteries 2020, 6, 10. https://doi.org/10.3390/batteries6010010
Aiello L, Kovachev G, Brunnsteiner B, Schwab M, Gstrein G, Sinz W, Ellersdorfer C. In Situ Measurement of Orthotropic Thermal Conductivity on Commercial Pouch Lithium-Ion Batteries with Thermoelectric Device. Batteries. 2020; 6(1):10. https://doi.org/10.3390/batteries6010010
Chicago/Turabian StyleAiello, Luigi, Georgi Kovachev, Bernhard Brunnsteiner, Martin Schwab, Gregor Gstrein, Wolfgang Sinz, and Christian Ellersdorfer. 2020. "In Situ Measurement of Orthotropic Thermal Conductivity on Commercial Pouch Lithium-Ion Batteries with Thermoelectric Device" Batteries 6, no. 1: 10. https://doi.org/10.3390/batteries6010010
APA StyleAiello, L., Kovachev, G., Brunnsteiner, B., Schwab, M., Gstrein, G., Sinz, W., & Ellersdorfer, C. (2020). In Situ Measurement of Orthotropic Thermal Conductivity on Commercial Pouch Lithium-Ion Batteries with Thermoelectric Device. Batteries, 6(1), 10. https://doi.org/10.3390/batteries6010010







