Real-Time State-of-Charge Estimation via Particle Swarm Optimization on a Lithium-Ion Electrochemical Cell Model

Abstract

With the ever-increasing usage of lithium-ion batteries, especially in transportation applications, accurate estimation of battery state of charge (SOC) is of paramount importance. A majority of the current SOC estimation methods rely on data collected and calibrated offline, which could lead to inaccuracies in SOC estimation under different operating conditions or when the battery ages. This paper presents a novel real-time SOC estimation of a lithium-ion battery by applying the particle swarm optimization (PSO) method to a detailed electrochemical model of a single cell. This work also optimizes both the single-cell model and PSO algorithm so that the developed algorithm can run on an embedded hardware with reasonable utilization of central processing unit (CPU) and memory resources while estimating the SOC with reasonable accuracy. A modular single-cell electrochemical model, as well as the proposed constrained PSO-based SOC estimation algorithm, was developed in Simulink©, and its performance was theoretically verified in simulation. Experimental data were collected for healthy and aged Li-ion battery cells in order to validate the proposed algorithm. Both simulation and experimental results demonstrate that the developed algorithm is able to accurately estimate the battery SOC for 1C charge and 1C discharge operations for both healthy and aged cells.

1. Introduction

Human-generated greenhouse gases are believed to be the primary contributor to the climate change observed in the mid 20th century [1]. The United States (US) Environmental Protection Agency (EPA) estimated that electricity generation and transportation contributed to 56% of greenhouse gases in 2014. The EPA recommends several means of reducing these emissions, one of them being fuel switching. The use of public transport fueled by compressed natural gas (CNG), and the increased use of hybrid and electric vehicles are some of the examples of fuel switching. With this directive, one can expect a dramatic increase in the usage of portable energy sources, such as high-energy-density traction batteries, in the field of transportation. Batteries have become an integral part of our daily lives. They are used in a wide variety of products, ranging from consumer electronic devices, such as cell phones, laptops, etc., to safety critical applications in the field of medicine. The effective utilization and management of battery energy is of paramount importance to improving the efficiency of such energy storage devices.

Battery state of charge (SOC) is one of the most important parameters that must be estimated by the battery management system (BMS). It is comparable to the fuel gauge in an internal combustion-engine-powered car. SOC indicates the amount of usable energy left in the battery at a given time. Accurate knowledge of SOC offers the following benefits, to name a few:

• Effective battery operation and management;
• Reliable diagnostics;
• Safety in operation.

Unfortunately, SOC cannot be measured directly in real time and must be estimated using the data of other measurable variables such as voltage, current, battery temperature, etc. A wide range of methods were researched to estimate SOC depending on the application [2]. A number of online estimation techniques were proposed for the estimation of SOC. The Kalman filter method and its variants were one of the important methods used in literature. A series of articles by Plett [3,4,5] proposed the extended Kalman filter method to estimate battery states including SOC, power fade, capacity fade, and instantaneous available power. Kurzweil and Shamonin investigated SOC monitoring using impedance spectroscopy during long-term self-discharge of supercapacitors and lithium-ion batteries [6]. The main focus of this paper was to study the self-discharge behavior of Li-ion batteries and supercapacitors in the frequency domain. Panchal et al. [7,8] developed a mathematical model to predict the transient temperature distributions of a large-sized LiFePO₄ prismatic battery (20 Ah) at different C-rates. Their study showed that the increased C-rates resulted in increased temperatures on the principle surface of the battery.

In this paper, the particle swarm optimization (PSO) method was leveraged as an estimation technique to explore SOC estimation under varying operating conditions of the battery. Another important objective of this work was to demonstrate that the developed battery and estimator models can run on a real-time embedded device with good performance.

2. Battery Model

A wide variety of battery models were proposed in the literature. The appropriateness of a battery model depends on the application and its performance requirements. One of the most popular battery models used is the equivalent circuit model. Here, the battery is modeled using a set of resistors (R), capacitors (C), and other circuit elements to emulate the battery behavior. The accuracy of the model depends on the order of the model reflected by the number of RC elements in the circuit. The higher the order of the model, the greater is the ability of the model to account for different physicochemical processes in the battery operation [9].

Another battery modeling technique is called empirical modeling, which is purely mathematical. Here, the experimentally obtained historical data are used to realize a model where mathematical relationships such as exponentials, polynomials, etc. are developed using the different battery parameters and variables. These models claim to be computationally efficient. However, they must be re-tuned to capture different operating conditions, which means that the data for such scenarios must be available.

Fuzzy logic and neural network techniques were also used to model battery behavior [10,11,12]. These techniques involve a learning process where the models are trained using experimental data to learn the relationship between the different battery parameters and variables. These models are then used to predict various battery states, such as voltages, SOC, etc. Again, the limitation of such models includes the lack of adaptability as the battery behavior changes over time (aging).

Electrochemical or physics-based models incorporate both the chemical and the electrical behaviors to accurately model a battery. There are a number of such models available with varying degree of complexities. The single-particle model (SPM) models the battery as constituent particles of the active material within the electrodes. An electrochemical battery model considering the diffusion phenomenon of such particles and intercalation within the particle was developed by Zhang et al. [13]. Doyle et al. [14] developed a more comprehensive model based on concentrated solution theory. This model, also known as the pseudo two-dimensional (P2D) model, aims to represent the behavior of a wide range of lithium-ion batteries with different combinations of electrolytes, separators, anodes, and cathodes.

2.1. Battery Chemistry

Lithium (Li)-ion-based chemistry has an unique combination of being lightweight (Li atomic weight of 6.94 g) and high capacity (3.86 Ah/g) making Li-ion chemistry one of the most popular chemistries used, especially in the transportation industry [15]. Lithium cobalt oxide (LCO) chemistry was chosen in this work for its high-energy-density properties. The overall electrochemical reaction in an LCO cell is shown as follows:

C + LiCoO₂ ↔ LiC₆ + Li_0.5CoO₂;

(1)

At the cathode:

LiCoO₂ − Li⁺ − e⁻ ↔ Li_0.5CoO₂ ⇒ 143 mAh/g;

(2)

At the anode:

6C + Li⁺ + e⁻ ↔ LiC₆ ⇒ 372 mAh/g.

(3)

The principal objective of this research was to develop a PSO-based SOC estimation algorithm for Li-ion batteries which would efficiently and seamlessly work under different operating conditions while being computationally efficient enough to run on an embedded device in real time. While the equivalent circuit model can be computationally efficient, it requires re-tuning for numerous operating conditions. The data-driven models (e.g., empirical, fuzzy logic, neural network, etc.) need a lot of experimental data which may not be practical in many cases. The electrochemical models, on the other hand, capture the battery physics well to give a more accurate estimation of the states and the parameters. However, some of these models, such as the one developed by Doyle et al. [14], are not suitable for running in real time due to their complex set of partial differential equations. Other such examples include the model developed by Subramanian et al. [16], derived from first principles as an isothermal pseudo two-dimensional model. A control-oriented one-dimensional (1D) electrochemical model was developed by Smith et al. [17], which is of particular interest due to its real-time computational adaptability. Based on this 1D model, Sourav and Anwar [18] developed and validated a discretized model using the finite difference method (FDM). This model demonstrates both the details of battery physics and the computational efficiency to run in real time. This model was chosen to be used in this research work.

2.2. Constituent Equations

The governing equations of the battery model in [19] were adopted here and are as shown below. This model has six states which are as follows:

• Electrolyte lithium concentration c_e(x, t)
• Electrode lithium concentration c_s(x, r, t) of both anode and cathode
• Electrolyte potential φ_e(x, t)
• Electrode potential φ_s(x, t) of both anode and cathode
• Electrolyte ionic current i_e(x, t)
• Molar ionic flux j_n(x, t)

The constituent equations are given by the following equations [14,15,16,17,18,19,20]:

$$\frac{\partial }{\partial t}{\overline{c}}_s{}^{\pm }(x,t)=-\frac{3}{R_p{}^{\pm }}{j}_n{}^{\pm }(x,t);$$

(4)

$${\epsilon }_e\frac{\partial c_e(x,t)}{\partial t}=\frac{\partial }{\partial x}({\epsilon }_e{D}_e\frac{\partial c_e(x,t)}{\partial x}+\frac{1-{t_c}^0}{F}{i}_e(x,t));$$

(5)

$$\frac{\partial c_{s,i}(x,r,t)}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}(D_{s,i}{r}^2\frac{\partial c_{s,i}(x,r,t)}{\partial r}).$$

(6)

These are further simplified as follows:

$$\frac{\partial }{\partial t}{\overline{c}}_s{}^{\pm }(t)=-\frac{3}{R_p{}^{\pm }}{j}_n{}^{\pm }(t);$$

(7)

$$\frac{\partial {\varphi }_e(x,t)}{\partial x}=-\frac{i_e(x,t)}{\kappa }+\frac{2RT}{F}(1-{t_c}^0)(1+\frac{d\ln f_{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$a$}\right.}}{d\ln c_e(x,t)})\frac{\partial c_e(x,t)}{\partial x};$$

(8)

$$\frac{\partial {\varphi }_s(x,t)}{\partial x}=\frac{i_e(x,t)-I(t)}{\sigma };$$

(9)

$$\frac{\partial i_e(x,t)}{\partial x}=\frac{3{\epsilon }_s}{R_p}F{j}_n(x,t);$$

(10)

$$j_n(x,t)=\frac{i_0(x,t)}{F}(e^{\frac{{\alpha }_{a}F\eta (x,t)}{RT}}-e^{\frac{-{\alpha }_{C}F\eta (x,t)}{RT}}).$$

(11)

In the last equation above, the exchange current density i₀(x,t) and the over-potential η(x,t) for the main reaction are modeled as follows:

$$i_0(x,t)=r_{eff}{c}_e{(x,t)}^{{\alpha }_a}{({c_s}^{\max }-c_{ss}(x,t))}^{{\alpha }_c}{c}_{ss}{(x,t)}^{{\alpha }_C};$$

(12)

$$\eta (x,t)={\varphi }_s(x,t)-{\varphi }_e(x,t)-U(c_{ss}(x,t))-F{R}_f{j}_n(x,t);$$

(13)

where c_ss(x,t) $\approx$ c_s(x,R_p,t), U(c_ss(x,t)) is the open-circuit potential of the active materials, and $c_s^{max}$ is the maximum concentration in the active material of each electrode. The internal temperature of the battery is described by

$${\rho }^{avg}{c}_p\frac{dT(t)}{dt}=h_{cell}(T_{amb}-T(t))+I(t)V(t)-{\displaystyle \underset{0^{-}}{\overset{0^{+}}{\int }}\frac{3{\epsilon }_s}{R_p}F{j}_n(x,t)\mathrm{\Delta }U(x,t)dx},$$

(14)

where

$$\mathrm{\Delta }U(x,t)\stackrel{\mathrm{\Delta }}{=}U({\overline{c}}_s(x,t))-T(t)\frac{\partial U({\overline{c}}_s(x,t))}{\partial T},$$

where T_amb is the ambient temperature, and $\overline{c_s}\left(x,t\right)$ is the volume-averaged concentration of a particle in the solid phase which is defined as

$${\overline{c}}_s(x,t)\stackrel{\mathrm{\Delta }}{=}\frac{3}{{R_p}^3}{\displaystyle \underset{0}{\overset{R_{p,i}}{\int }}{r}^2{c}_s(x,r,t)dr}.$$

(15)

The initial conditions of the battery model are given by

$$c_s{}^{\pm }(x,r,0)={\overline{c}}_{s,0}{}^{\pm }(x,r),c_e{}^{\pm }(x,0)={\overline{c}}_{e,0}{}^{\pm }(x),\mathrm{and}T(0)=T_0,$$

(16)

and the boundary conditions are given by the following equations:

$$\frac{\partial c_e(0^{-},t)}{\partial x}=\frac{\partial c_e(0^{+},t)}{\partial x}=0;$$

(17)

$$c_e(L^{-},t)=c_e(0^{sep},t);c_e(L^{sep},t)=c_e(L^{+},t);$$

(18)

$${\epsilon }_e^{-}{D}_e\frac{\partial c_e(L^{-},t)}{\partial x}={\epsilon }_e^{sep}{D}_e\frac{\partial c_e(0^{sep},t)}{\partial x};$$

(19)

$${\epsilon }_e^{sep}{D}_e\frac{\partial c_e(L^{sep},t)}{\partial x}=-{\epsilon }_e^{+}{D}_e\frac{\partial c_e(L^{+},t)}{\partial x};$$

(20)

$$\frac{\partial c_s(x,0,t)}{\partial r}=0;\frac{\partial c_s(x,R_p,t)}{\partial r}=-\frac{j_n(x,t)}{D_s};$$

(21)

$${\varphi }_e(L^{-},t)={\varphi }_e(0^{sep},t);{\varphi }_e(L^{sep},t)={\varphi }_e(L^{+},t);{\varphi }_e(0^{+},t)=0;$$

(22)

$$i_e(0^{-},t)=i_e(0^{+},t)=0;i_e(x^{sep},t)=-I(t);$$

(23)

$$i_e(L^{-},t)=-i_e(L^{+},t)=-I(t);$$

(24)

where x^sep $\in$ [0^sep, L^sep] represents the entire separator domain of the battery.

In the above equations ε_e, ε_s, σ, R, R_p, F, α_a, α_c, ρ_avg, c_p, h_cell, and $t_c^0$ are model parameters and are constant in each region of the cell. κ, fc/a, and D_e are known functions of the electrolyte concentration.

The terminal voltage is given by

$$V(t)={\varphi }_s(0^{+},t)-{\varphi }_s(0^{-},t).$$

(25)

This battery has a nominal capacity of 3.5 Ah. The SOC is directly calculated from the lithium-ion concentration as shown below.

$$SOC=\frac{\overline{C_s}}{C_{smax}},$$

(26)

where

$$\overline{C_s}=\frac{{{\displaystyle \sum }}_{i=1}^N{C}_s\left(i,t\right)}{N},$$

(27)

where N is the number of nodes in the electrode.

The lithium-ion concentration of the negative electrode was used to estimate the SOC. It was observed that the lithium-ion concentration in the negative electrode demonstrated the range and direction of the actual SOC, meaning that the SOC increases with charge and decreases with discharge. The lithium-ion concentration of the positive electrode lacks the range and exhibits reverse directional characteristics.

2.3. Reformulation of Battery Model

The two main goals of this work were the following:

-

Application of PSO in SOC estimation for improved accuracy under different operating conditions;

-

Ability to run the developed estimation algorithm in real time on an embedded target.

To achieve the above goals, the model needed to be re-formulated. Such a reformulation and the requirement for each of the above goals are discussed here.

A search-based optimization algorithm, such as PSO, evaluates the objective function by varying a set of tunable parameters to arrive at the optimal solution. This process could be repeated at every time step in a discrete time implementation. In the case of a battery model, it would have to be run with a set number values for a given state, evaluating the fitness function for each of these values and comparing to the given optimization criteria. This requirement demands the battery model to be modular, where it can be run repeatedly within a given time step.

The equations for the positive and negative electrodes, i.e., Equations (7), (9), and (11)–(13), are similar. Hence, all these equations can grouped together into a function. Similarly, the equations for the electrolyte and battery temperature can be grouped into their respective functions. Also, to run the battery model on an embedded target, it is preferred to be written in a high-level language, such as C or C++, where the code can be compiled into real-time executables.

Matlab©/Simulink© offers a platform where the modular model can not only be developed, but also simulated along with analysis of the results. Additionally, it offers rapid prototyping on an embedded hardware, such as Raspberry Pi. Once the modular battery model and PSO algorithm are developed and validated in Simulink©, its auto code generator can produce the real-time code that is capable of running on a target-embedded device.

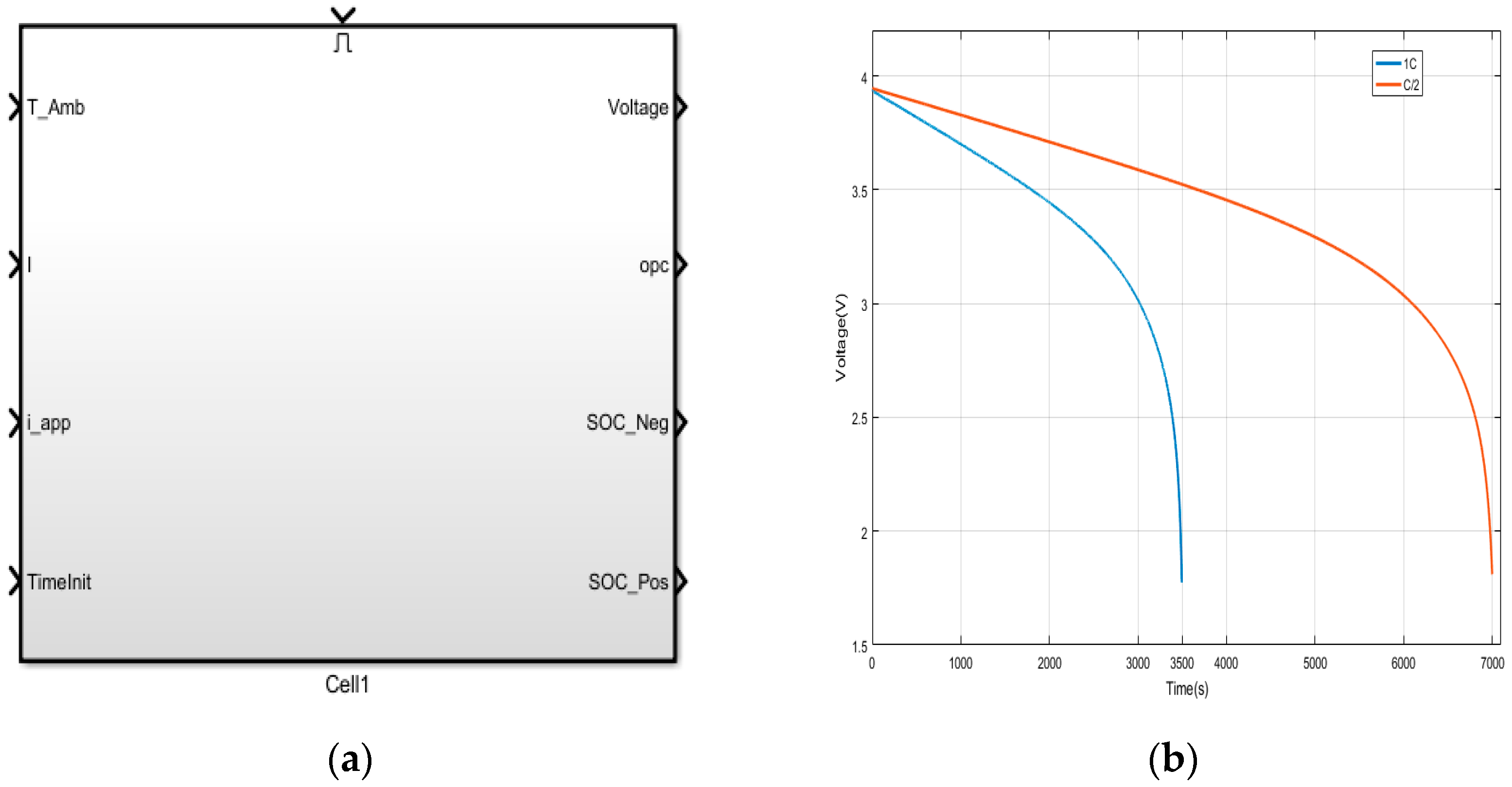
The top-level modular Simulink implementation of a single-cell model is shown in Figure 1a. which is based on Equations (4) through (27) with the suggested grouping as stated above. It takes the ambient temperature (T_Amb) and the measured current (I) as inputs. Terminal voltage, open-circuit voltage (OCV), state of charge at the negative electrode (SOC_Neg), and state of charge of positive electrode (SOC_Pos) are the model outputs. The states are calculated and updated internally. This modular approach makes the Model efficient for prototyping and analysis.

2.4. Theoretical Simulation Validation

Charge and discharge rates are often expressed in C-rate, defined as the charge or discharge current divided by the battery’s capacity to store an electrical charge. For example, for a battery with a capacity of 1000 mAh, a discharge rate of 1500 mA corresponds to a C-rate of 1.5 (per hour). This model was subjected to standard discharge rates of 1C (30 A/m²) and 0.5C (15 A/m²) in order to verify the standard battery operation via simulation. The battery parameters used in this work are listed in the

Table 1. Battery parameters [16].

Parameter	Units	Negative Electrode	Separator	Positive Electrode
$L$	m	88 × 10−6	35 × 10−6	80 × 10−6
$N$	-	88	35	80
$R_i$	m	2 × 10−6	-	2 × 10−6
$E_s$	-	0.4824	-	0.5
$E_e$	-	0.485	0.724	0.385
$\sigma$	${\Omega }^{-1}{\mathrm{m}}^{-1}$	100	-	100
$t_{+}^0$	-	0.363	0.363	0.363
$C_{s_{max,i}}$	${\mathrm{mol}\mathrm{m}}^{-3}$	30,555	-	51,554
$c_{e,i}$	${\mathrm{mol}\mathrm{m}}^{-3}$	1000	1000	1000
${\alpha }_a,{\alpha }_c$	-	0.5, 0.5	-	0.5, 0.5
$R$	${\mathrm{jmol}}^{-1}{\mathrm{K}}^{-1}$	8.314	8.314	8.314
$F$	$\mathrm{C}{\mathrm{mol}}^{-1}$	96,487	96,487	96,487
$A$	${\mathrm{m}}^2$	30	-	30

. The output voltage response shown in Figure 1b indicates that, at 1C, the battery discharges completely in 3500 s, while, at 0.5C, it takes 7000 s to completely discharge. This is in tune with the expected response of a battery with a nominal capacity of 3.5 Ah.

3. Particle Swarm Optimization

The particle swarm optimization (PSO) is a population-based stochastic optimization technique. It was invented by Dr. Kennedy and Dr. Eberhart in 1995. Similar to the movement of a flock of birds, the algorithm mimics the flock’s flight pattern for the optimal path to locate food. PSO has several advantages over genetic algorithm (GA), such as needing fewer parameters to tune, being computationally efficient, and having a higher degree of convergence.

PSO is used in a variety of industries for a wide range of applications, such as robot control optimization [21], optimization of global solar radiation estimation for regions where they cannot be measured [22], detection of ovarian cancer [23], and optimization of machine loads [24]. In the automotive applications, one of the most popular uses of PSO is in battery applications with respect to identifying battery parameters [25,26,27]. Another popular application is in optimal energy management for hybrid electric powertrains [28,29,30].

Ismail [31] presented a PSO-based SOC estimation of Li-ion batteries utilizing an equivalent-circuit-type battery model to estimate SOC of a LiFePO₄ battery. This paper focuses on PSO-based SOC estimation using the electrochemical model of a single cell of a battery with lithium cobalt oxide (LCO) cathode chemistry.

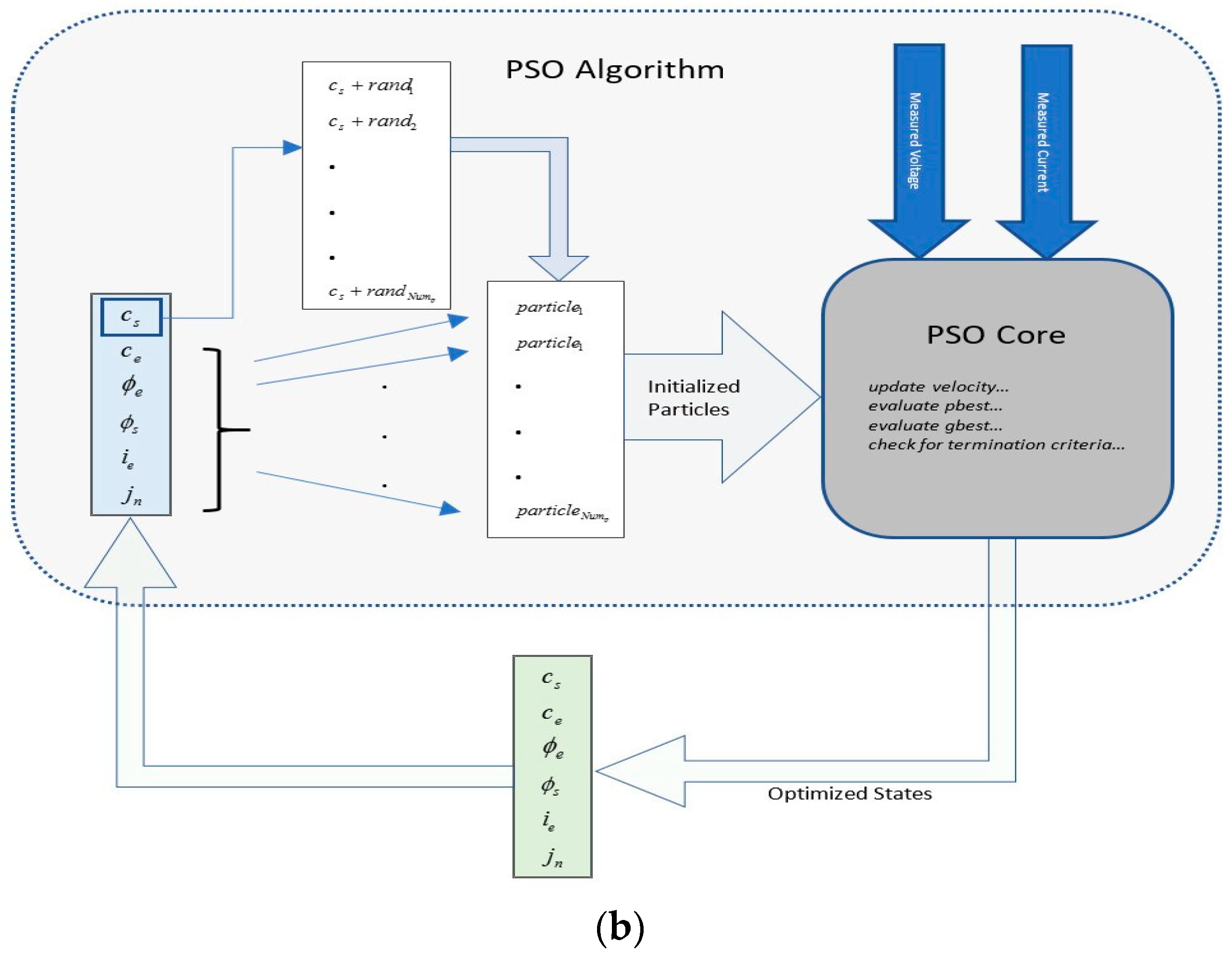
4. PSO Algorithm

In a global PSO algorithm, which is used in this work, a swarm of solutions, called particles, are initialized randomly in the solution space. These particles are then flown through the solution space based on the optimality conditions. The particles keep track of their coordinates with respect to the best solution in the problem space. This is termed as pbest which is a particle’s best position in solution space. Similarly, a global best, termed as gbest, is tracked, which is the best location or solution obtained by any particle so far. At every time step, the velocities of the particles are updated toward the pbest and the gbest values until the required optimization criteria are met or the algorithm termination condition is reached.

An outline of the PSO algorithm is presented below.

Step 1: Initialize the particles

Initialize the position array with random numbers having uniform distribution.

X = Urand (r_lowerlim, r_upperlim).

(28)

Assign this initial position to best known position array.

P = X.

(29)

Initialize particle velocity.

V = X.

(30)

If the number of particles is Num_p then, X is a Num_p-size array of particle position; similarly, P is a Num_p-size array of pbest positions, and V is a Num_p-size array of particle velocities.

Step 2: Evaluate the optimization fitness function.

Ex = F(X) and Ep = F(P) and eg = f (gbest),

(31)

where Ex and Ep are the fitness evaluation array for X and P, respectively, and eg is the function evaluation at gbest.

Step 3: Update pbest value for each particle of the population.

if Ex(i) < Ep(i) then P(i) = X(i),

(32)

where i = 1, 2,…Nump.

Step 4: Update gbest value for the entire population.

if Ep(i) < eg then gbest = P(i).

(33)

Step 5: Update the velocity and position of the particles.

$$V\left(i+1\right)=wV\left(i\right)+c_1{u}_{rand}\left(0,1\right)\left(P\left(i\right)-X\left(i\right)\right)+c_2{u}_{rand}\left(0,1\right)\left(gbest-X\left(i\right)\right),$$

(34)

$$X\left(i+1\right)=X\left(i\right)+V\left(i+1\right),$$

(35)

where w is the inertial weight, c₁ is the cognitive parameter, and c₂ is the social parameter.

Step 6: If criteria are met, then exit; otherwise, loop to Step 2. Exit criteria are usually a fitness threshold or maximum number of iterations completed.

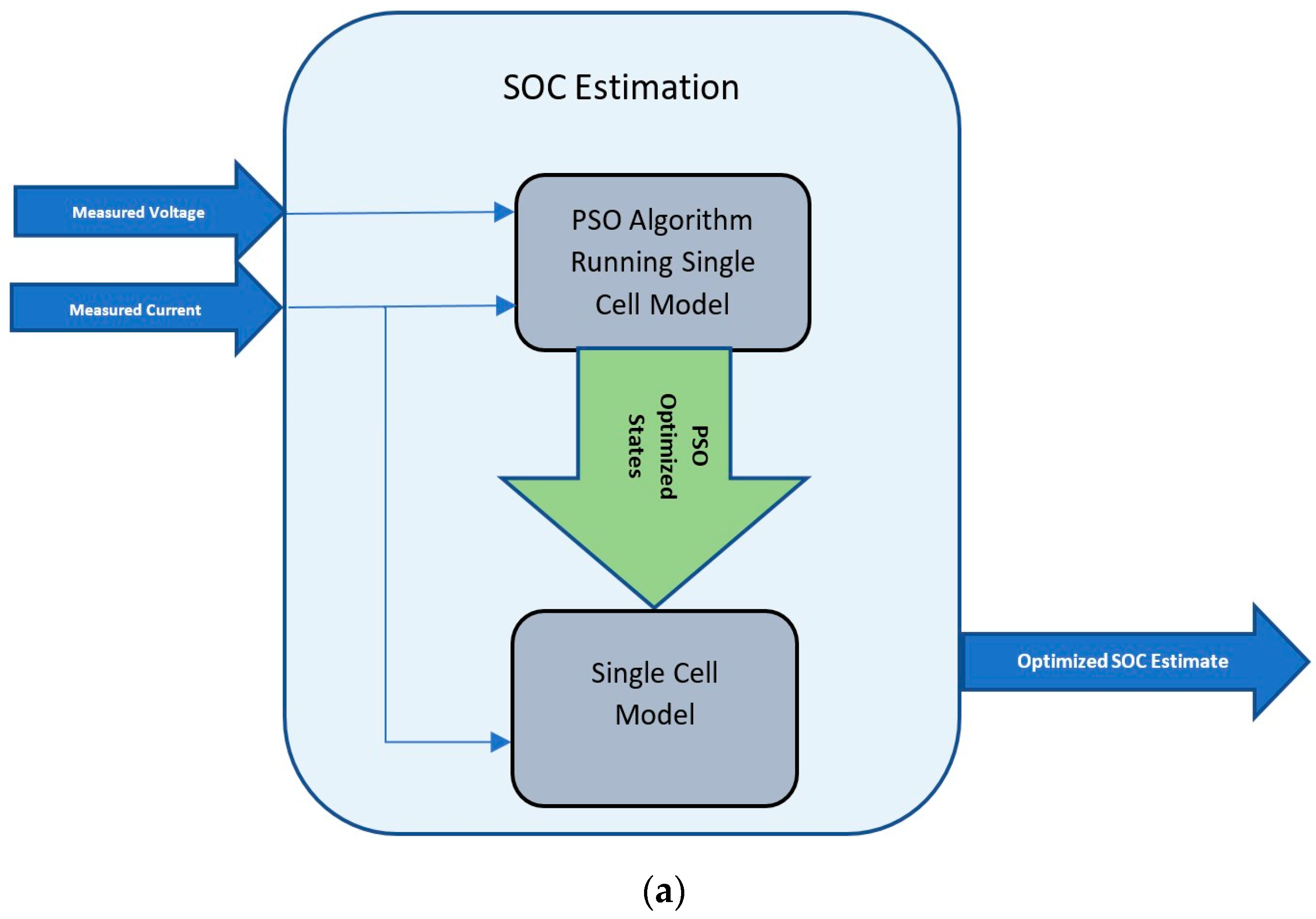
5. SOC Estimation Approach

An overview of the approach of SOC estimation using PSO is show in Figure 2. The proposed algorithm takes measured voltage and current as inputs, and outputs the estimated SOC. The approach is to optimize the states with the goal of minimizing the error between the measured voltage and estimated voltage. Once the optimized states are obtained, these states are used again in the single-cell model to estimate the SOC. Although the battery model has six states, the scope of this work is limited to optimizing one state, which is C_s(x, r, t), the lithium-ion concentration in the negative electrode. This is done to keep the algorithm simple and efficient. The rationale behind choosing C_s is that the lithium-ion concentration in the electrode intuitively represents the SOC of the cell, which is also directly proportional to the open-circuit voltage. This means that the C_s shall be used as the particles of the PSO algorithm which are initialized to uniformly random values around the previous C_s, and the terminal voltage is estimated and optimized based on these states for the measured current value. A pictorial view of this process is shown in Figure 2. According to the PSO algorithm, the initial value of the particles can be randomly initialized; however, for faster convergence, it is proposed that the best known value that would represent the current battery condition be used. A linear interpolation function is applied where the measured voltage and current are inputs, and the stoichiometric value of the concentration is the output. This value is then used in the calculation of C_s as shown below. This is done only once at the beginning of the algorithm. For subsequent time steps, the optimized states, including C_s, from the previous step are fed back as shown in Equation (36).

C_s = stoichiometric value × C_smax, i.

(36)

O Algorithm Parameters

From Equation (34), it is clear that the PSO algorithm uses only three parameters, c₁ and c₂, which are learning coefficients of the stochastic acceleration terms, and w, which is the inertial coefficient.

The values of the PSO parameters w, c₁, and c₂, as well as the number of particles and maximum iterations, chosen for this work are shown in the

Table 2. Particle swarm optimization (PSO) parameters.

Parameter	Value
w	(0.5 + urand/2)
c1	1.494
c2	1.494
Number of particles	8
Maximum number of iterations	20

. A constriction factor introduced by Clerc [32] was used to determine c₁ and c₂. Additionally, a method proposed by Eberhart and Shi [33] for application in dynamic systems was adopted to determine the inertial weight w.

6. Algorithm Validation and Results

6.1. Experimental Set-Up

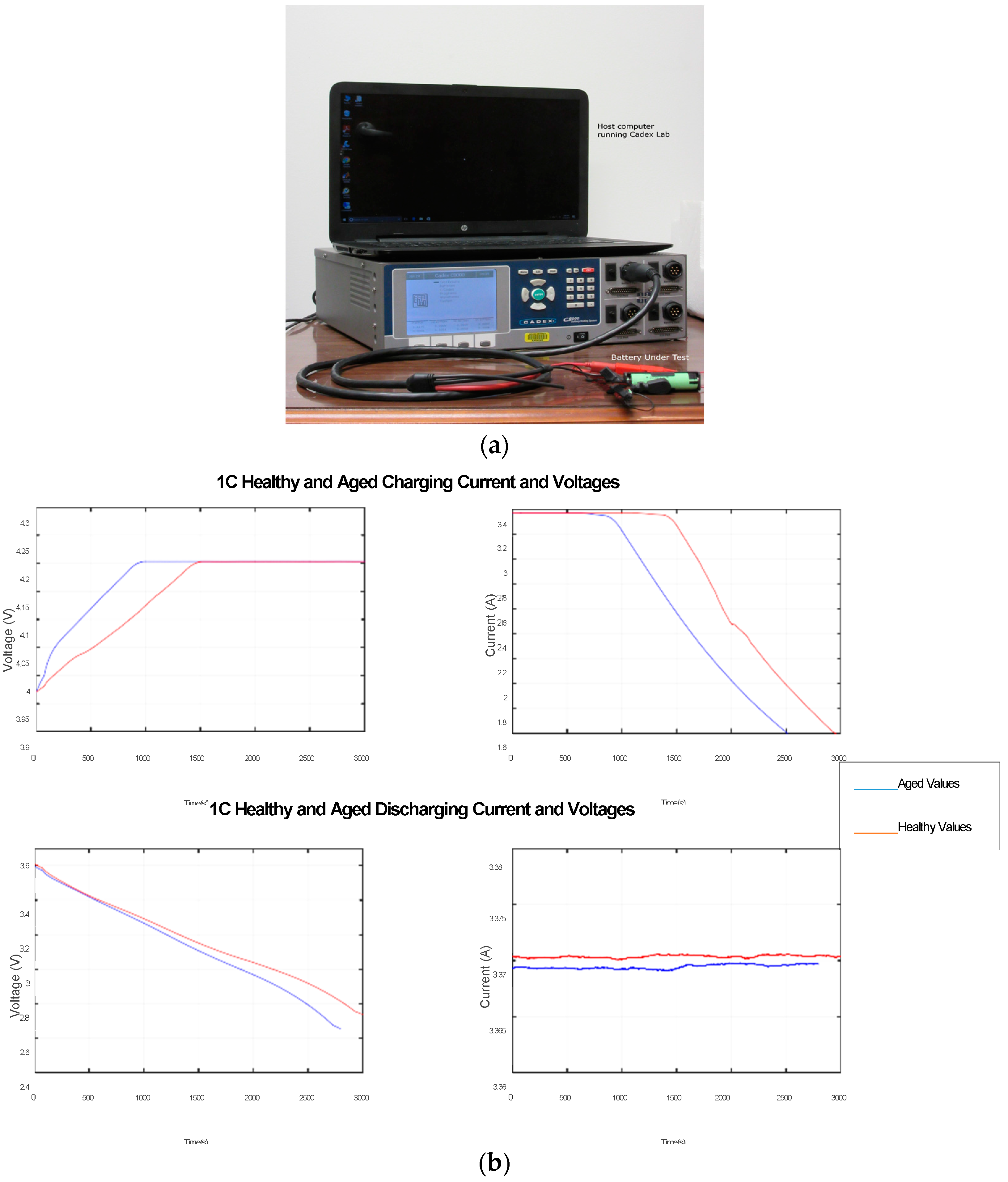
The battery used was a Panasonic NCR 18650B with LiCoO₂ (LCO) cathode chemistry. The details of the battery are as follows: rated capacity, 3200 mAh (at nominal voltage); nominal voltage, 3.6 V. Experimental data were collected by subjecting this LCO battery to various test cycles. Cadex C8000 was the test equipment used for this experiment. The set-up is shown in Figure 3a. The battery was subjected to constant current charging and discharging at 1C. This cycle was repeated for both new and aged batteries. A scheme of 100-cycle aging was used to age the new battery. A built-in profile of NCR18650B in the CADEX software was used for both charging and discharging profiles. The discharging was done at a constant current of 3.3 A. The data were logged at 1-Hz sampling rate.

Figure 3b shows the charging and discharging voltage and current of both healthy and aged batteries. These graphs clearly show the degradation of battery performance with aging.

6.2. Simulation Validation

In order to validate the proposed algorithm, the experimental data were run on the Simulink model. The model was set up with a discrete solver with a step time of 200 ms. The model was set to “normal mode” in order to verify the algorithm in simulation. Root-mean-square error (RMS) as per Equation (37) was used to measure the performance of the proposed algorithm, where xi is the difference between the measured and PSO estimated states. The simulation data for 1C charging and discharging for both healthy and aged batteries are presented in this section.

$$RMS=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^M{\left|x_i\right|}^2}{M}}.$$

(37)

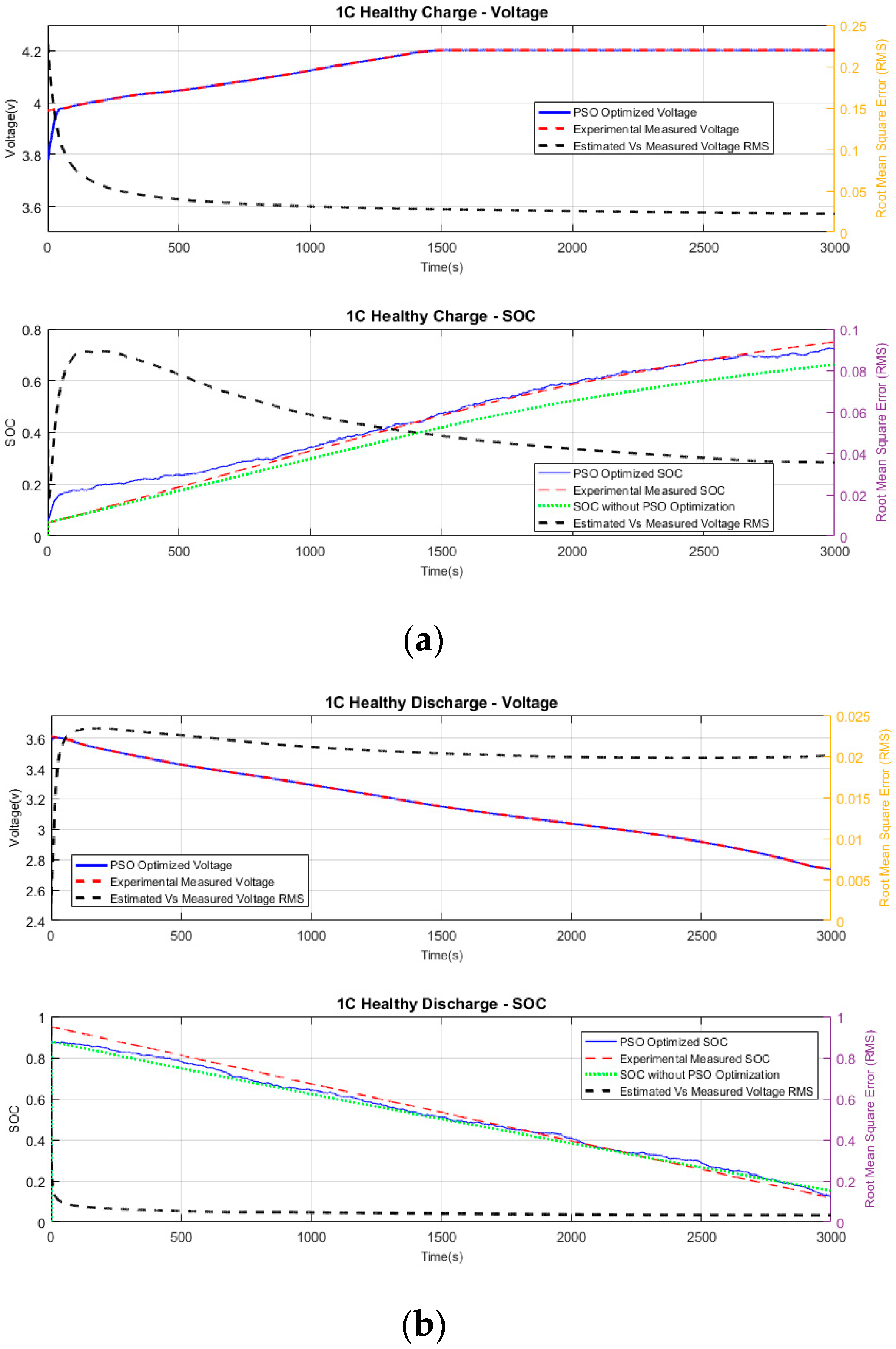
6.2.1. Healthy Charging

Figure 4a shows the measured terminal voltage against the PSO-estimated voltage in 1C charging. Although the measured and the estimated voltages start with different values, the PSO algorithm quickly converges to the measured voltage in less than 45 s. The average RMS error between the estimated and measured voltages is 0.0221. The graph of running RMS of PSO voltage and measured voltage is shown in Figure 4a (top plot).

Figure 4a (bottom plot) compares the experimental SOC with the PSO-estimated SOC. The experimental SOC value is directly obtained from the CADEX battery tester. The SOC values directly computed from the single-cell battery model (without PSO) are also plotted to provide a reference for analysis purposes. The estimated SOC converges within 2% of the experimental SOC in the first 800 s, and then continues to follow the experimental SOC with a running RMS of 0.0355, as shown in Figure 4a. It is clear from the graph that the computed SOC without PSO diverges from the experimental SOC.

6.2.2. Healthy Discharging

Figure 4b shows the measured voltage against the PSO-estimated voltage for discharging. The measured and the estimated voltages start with different values, but the PSO algorithm quickly converges to the experimental voltage in less than 15 s. The short convergence time can be attributed to the initial value of PSO voltage being close to measured voltage, with a 0.025-V voltage difference. The average RMS error between the estimated and measured voltages is 0.0200. The running RMS of PSO-estimated and measured voltages is shown in Figure 4b (top plot).

Figure 4b (bottom plot) shows the experimental SOC against the PSO-estimated SOC. The computed SOC from the single-cell battery model (without optimization) is also plotted to provide a reference for analysis purposes. The estimated SOC converges within 2% of the experimental SOC within the first 1160 s, and then continues to follow the experimental SOC with a running RMS of 0.03186, as shown in Figure 4b. The computed SOC of the single cell, the estimated SOC with PSO, and the experimental SOC converge to within 3% absolute difference in 1500 s.

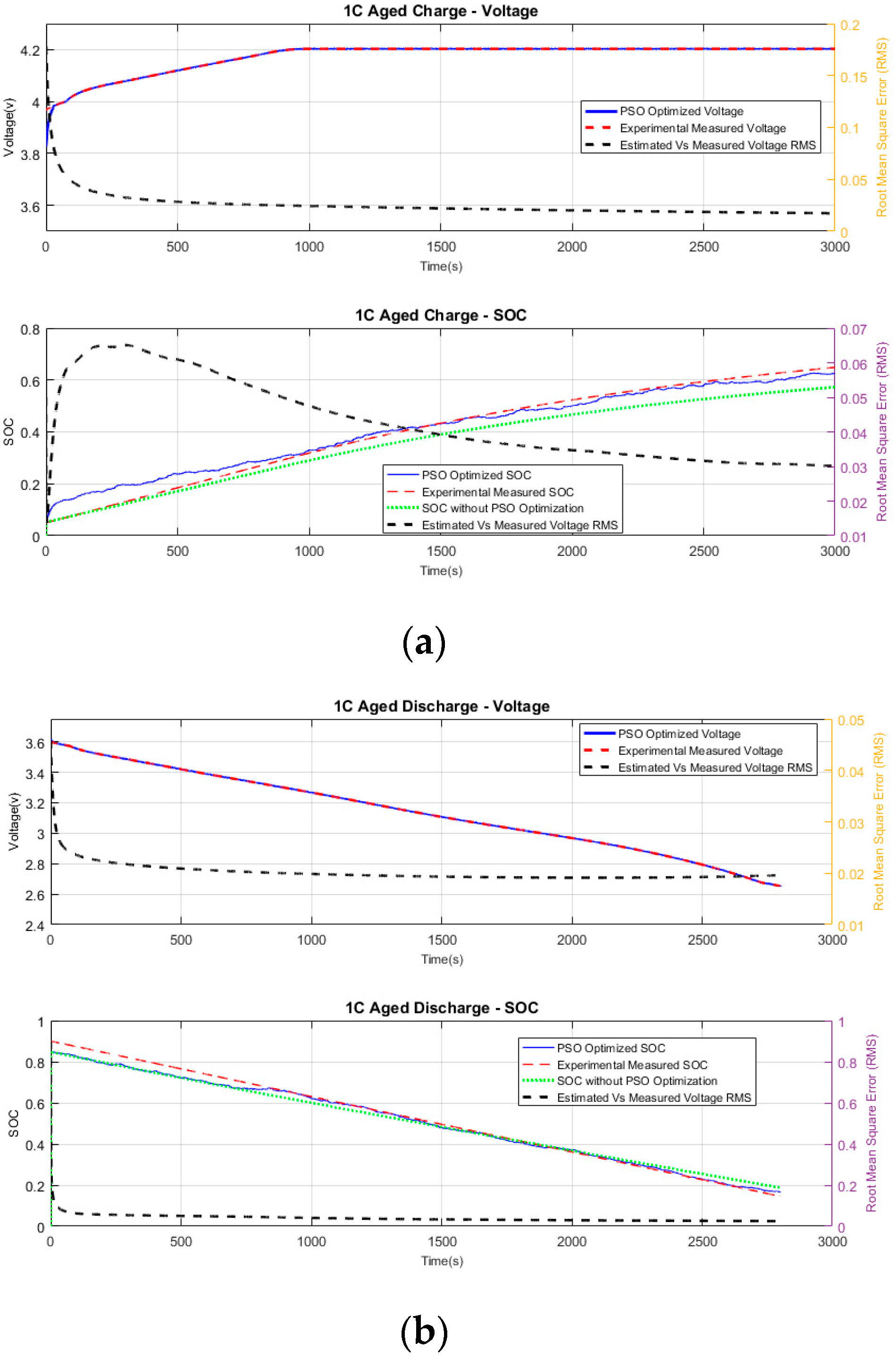
6.2.3. Aged Charging

Figure 5a illustrates the measured voltage against the PSO-estimated voltage for charging. Although the measured and the estimated voltages start with different values, the PSO algorithm converges to the measured voltage in less than 30 s. The average RMS error between the estimated and measured voltages is 0.01729. The running RMS of PSO-estimated voltage and measured voltage is shown in Figure 5a (top plot).

Figure 5a (bottom plot) illustrates the experimental SOC against the PSO-estimated SOC. The computed SOC from the single-cell battery model (without optimization) is also plotted to provide a reference for analysis purposes. Similar to the healthy charging, the estimated SOC converges within an absolute difference of less than 2% within the first 800 s, and then continues to follow the experimental SOC with a running RMS of 0.03016, as shown in Figure 5a. As in the case of the healthy battery, it is clear from the graph that the computed SOC without PSO diverges from the experimental SOC.

6.2.4. Aged Discharging

Figure 5b shows the measured voltage against the PSO-estimated voltage for discharging. The measured and the estimated voltages start with different values, but the PSO algorithm converges to the measured voltage in less than 12 s. The short convergence time is due to the initial value of the PSO voltage being closer to measured voltage, with an absolute difference of 0.0212 V for the given conditions. The average RMS error between the estimated and measured voltages is 0.0196. The running RMS of PSO voltage and measured voltage is shown in Figure 5b (top plot).

Figure 5b (bottom plot) compares the experimental SOC against the PSO-estimated SOC. The computed SOC from the single-cell battery model (without optimization) is also plotted to provide a reference for analysis purposes. The estimated SOC converges within an absolute difference of less than 1% within the first 830 s, and then continues to follow the experimental SOC with a running RMS of 0.02515 as shown in Figure 5b. The computed SOC of the single-cell model without optimization, the estimated SOC with PSO, and the experimental SOC converge to within 3% absolute difference within 1500 s. However, it is clear that the PSO-estimated SOC closely follows the experimentally calculated SOC.

The following observations were made:

• The SOC estimation accuracy for charging of a healthy battery was within 0.0355 or 3.55%;
• The SOC estimation accuracy for discharging of a healthy battery was within 0.03186 or 3.19%;
• The SOC estimation accuracy for charging of an aged battery was within 0.03016 or 3.02%;
• The SOC estimation accuracy for discharging of an aged battery was within 0.0251 or 2.51%.

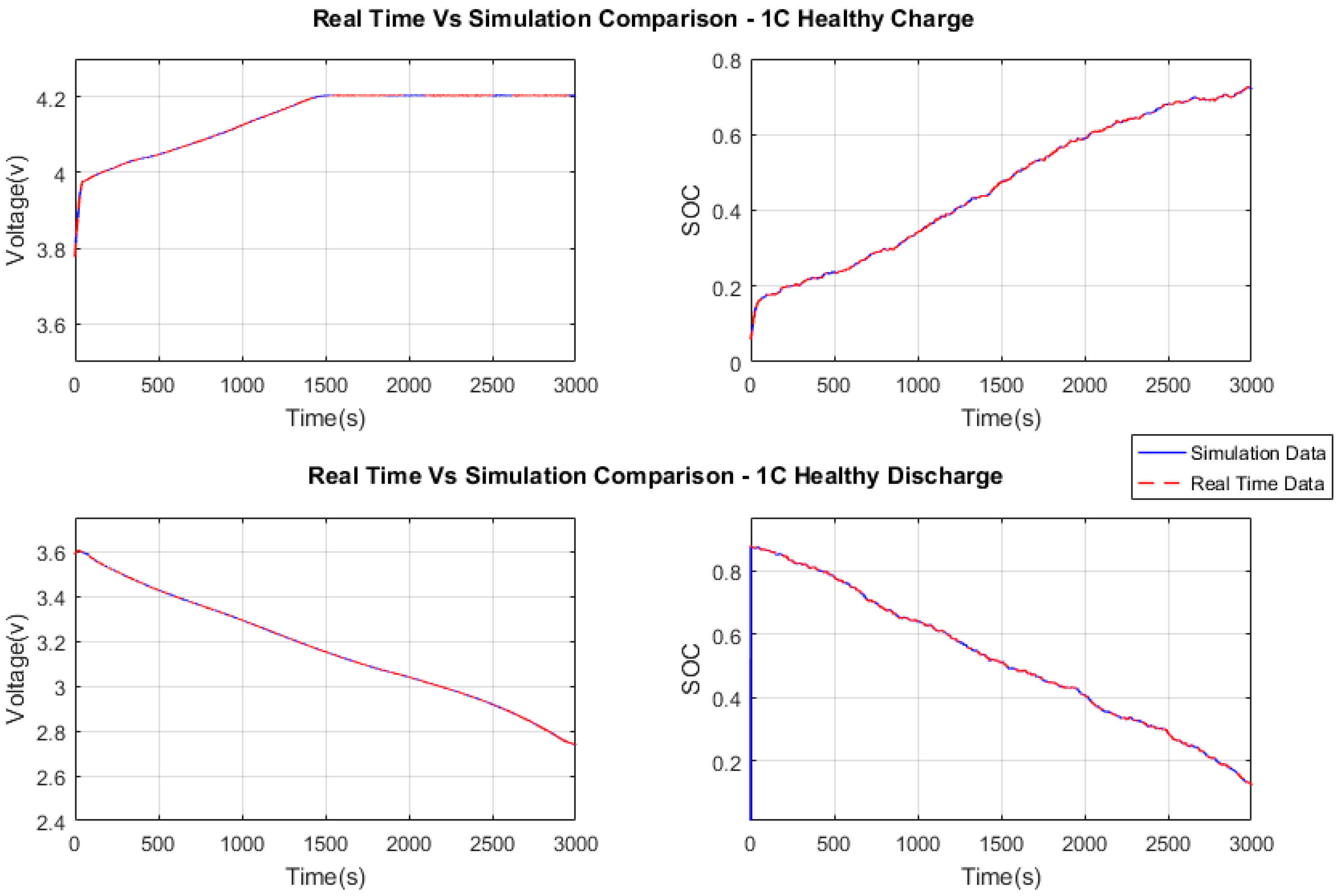
6.3. Real-Time Validation

A real-time version of the PSO estimator was run on a Raspberry Pi 3 embedded hardware using the external mode in Simulink. Raspberry Pi 3 is a single-board computer with a 64-bit quad core processor and 1 GB internal random-access memory (RAM). Being a low-cost device, it is ideal for prototyping computationally intensive algorithms like the PSO estimator presented in this work. Simulink provides a seamless interface to Raspberry Pi hardware. Once the models are validated in pure simulation mode, the same models can be run on Raspberry Pi by changing the simulation mode to “external mode” in the model. Figure 6 shows a picture of the Raspberry Pi 3 set-up.

Figure 7 and Figure 8 show the comparisons of voltage and SOC obtained from simulation and from the real-time processor (Raspberry Pi 3) for charging and discharging, respectively. The results from simulation and real-time hardware match completely, which shows that the PSO estimator is efficient on the real-time processor, offering the exact same results. The central processing unit (CPU) utilization time of Raspberry Pi was collected to evaluate the performance. A maximum of 26% CPU utilization was observed at PSO estimator initialization. During convergence, it ran at 3% average utilization for the rest of the execution.

7. Conclusions

The main goal of this work was to develop a PSO algorithm based on an electrochemical battery model to accurately estimate the SOC, which would also be capable of running in real time. It was demonstrated that the proposed particle swarm optimization (PSO)-based estimation algorithm developed in the work was able to accurately estimate of state of charge (SOC) based on an electrochemical battery model of a lithium-ion cell. The results show a close agreement between the PSO-estimated and experimental SOC values for both healthy and aged battery cells under charging and discharging conditions. It was demonstrated that the proposed real-time implementation of the PSO estimation algorithm is capable of effectively running on Raspberry Pi 3 embedded hardware in real time with good performance. It is to be noted that initial conditions need to be closer to the actual value while starting the estimation to ensure faster convergence. Also, the single-cell battery models were not optimized against the experimental data.