Lifetime Prediction of Lithium-Ion Capacitors Based on Accelerated Aging Tests
Abstract
1. Introduction
2. Experimental Setup
3. Comparison of Frequency and Time Domain Measurements
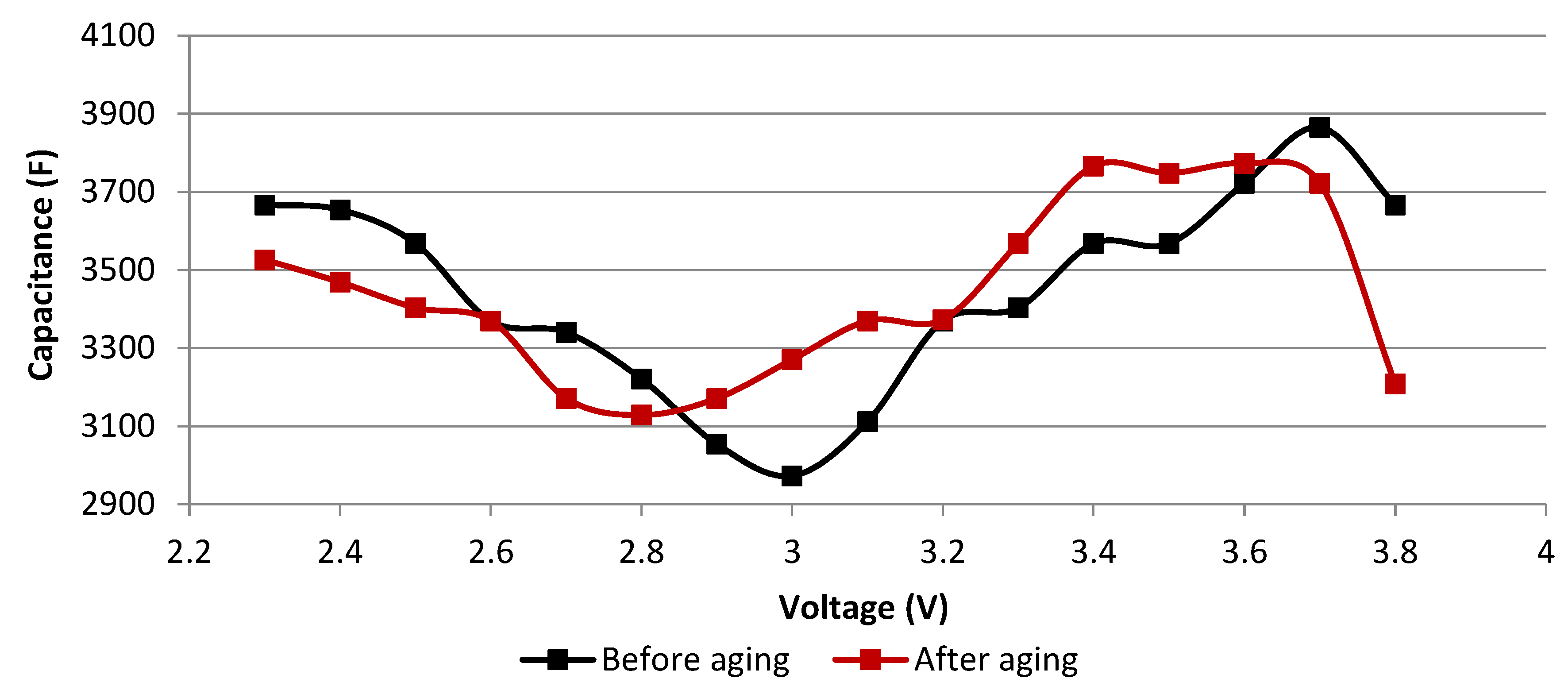
3.1. Frequency Domain Measurements
3.2. Time Domain Measurements
4. Interpretation of Calendar Aging
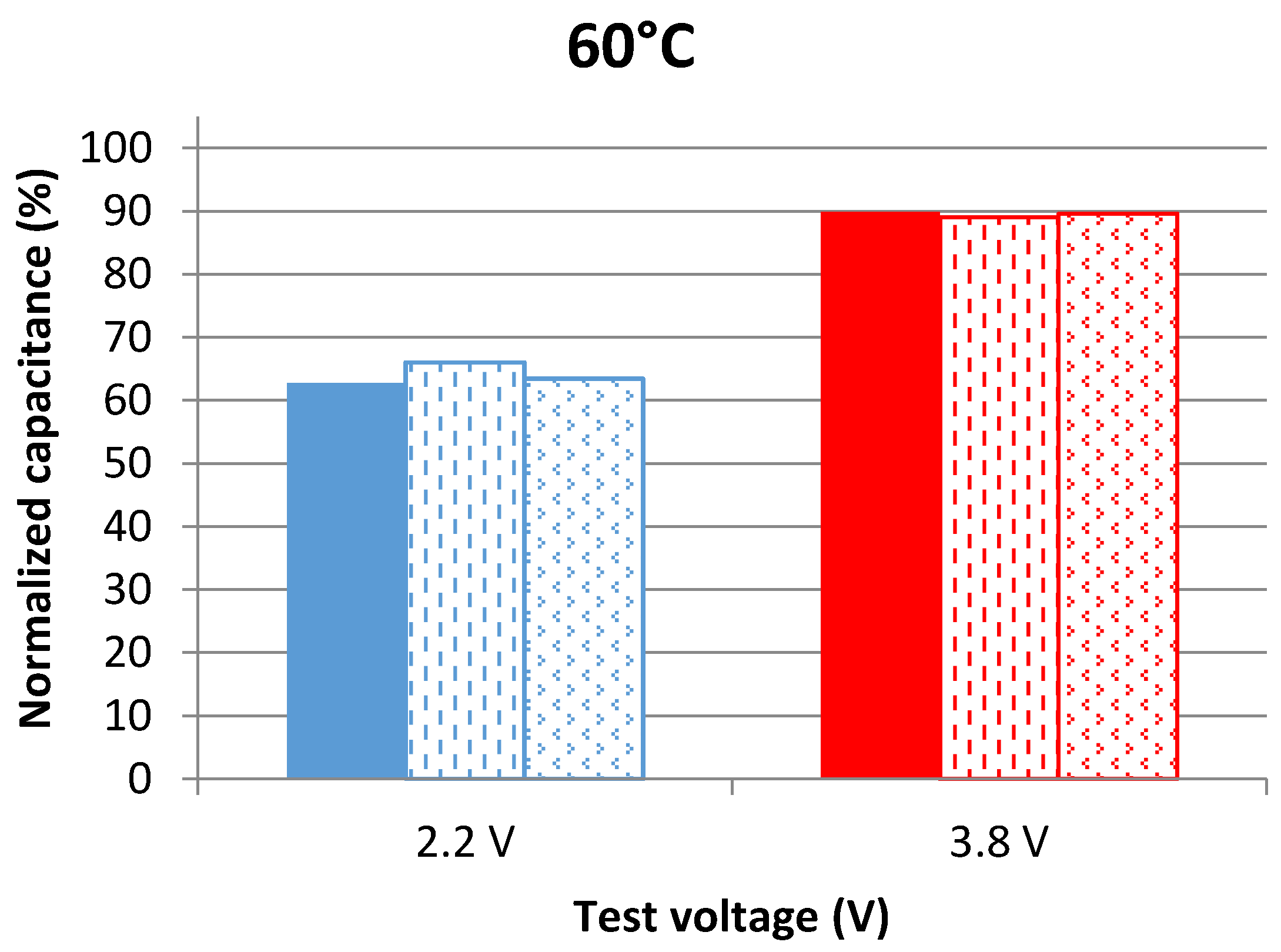
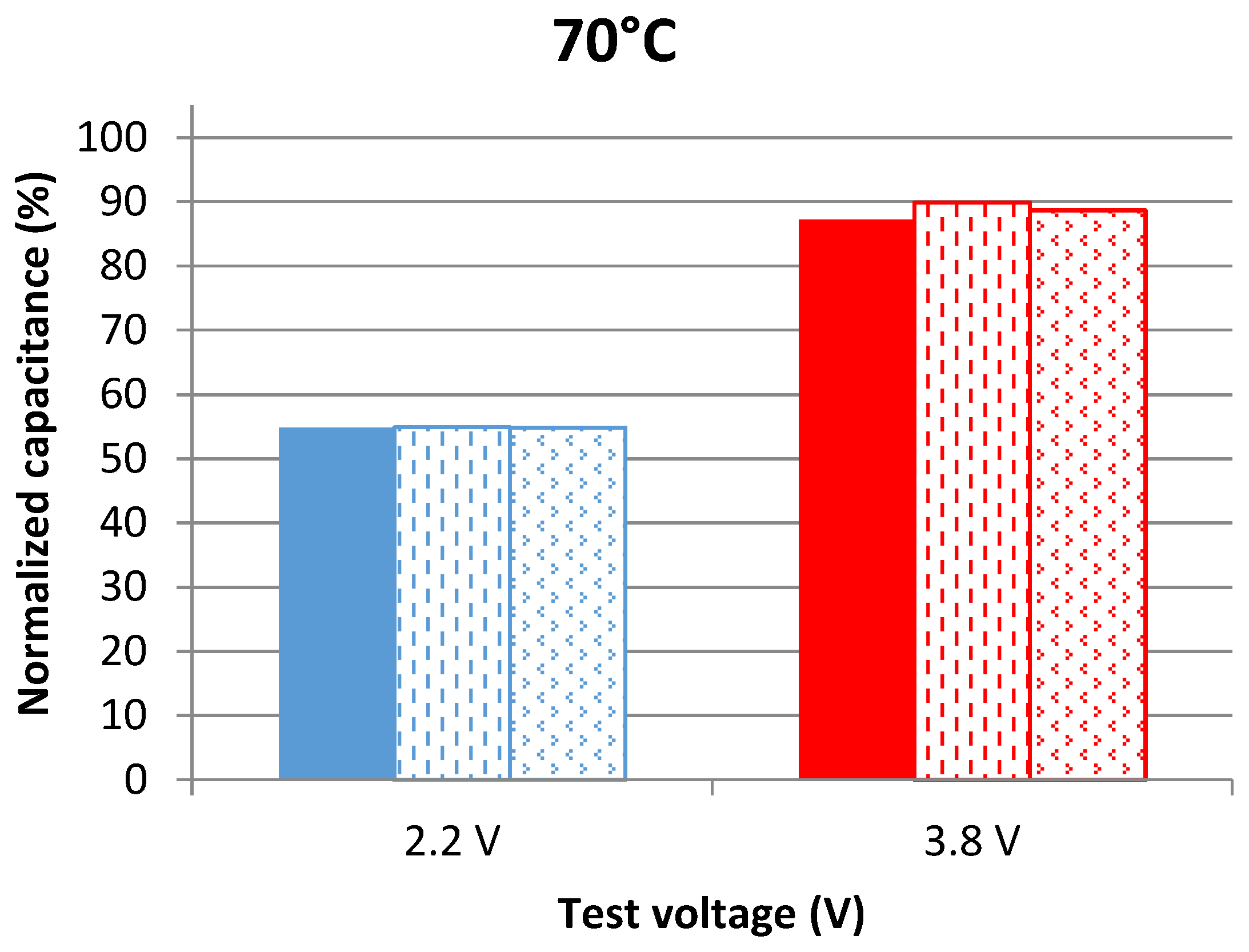
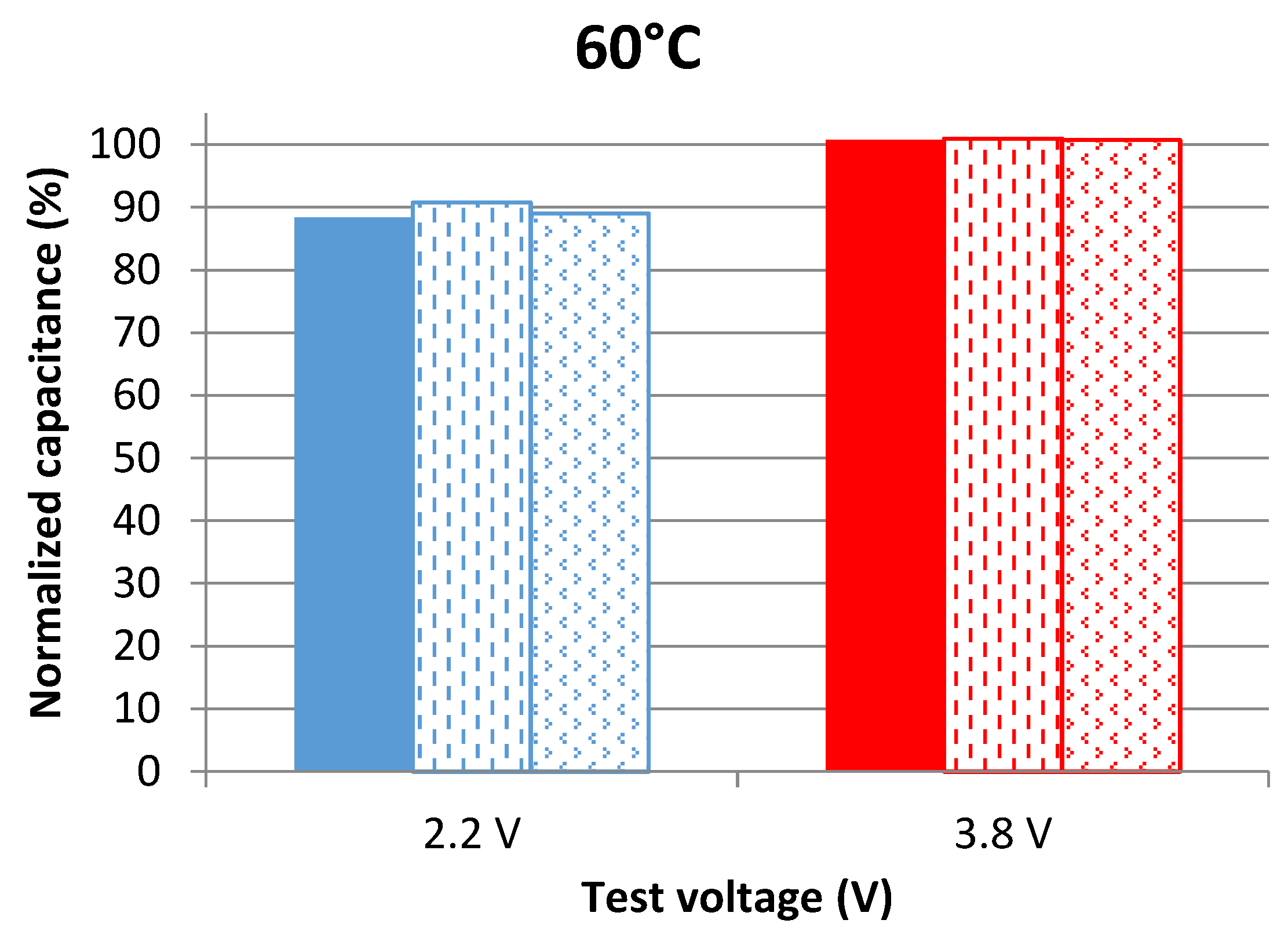
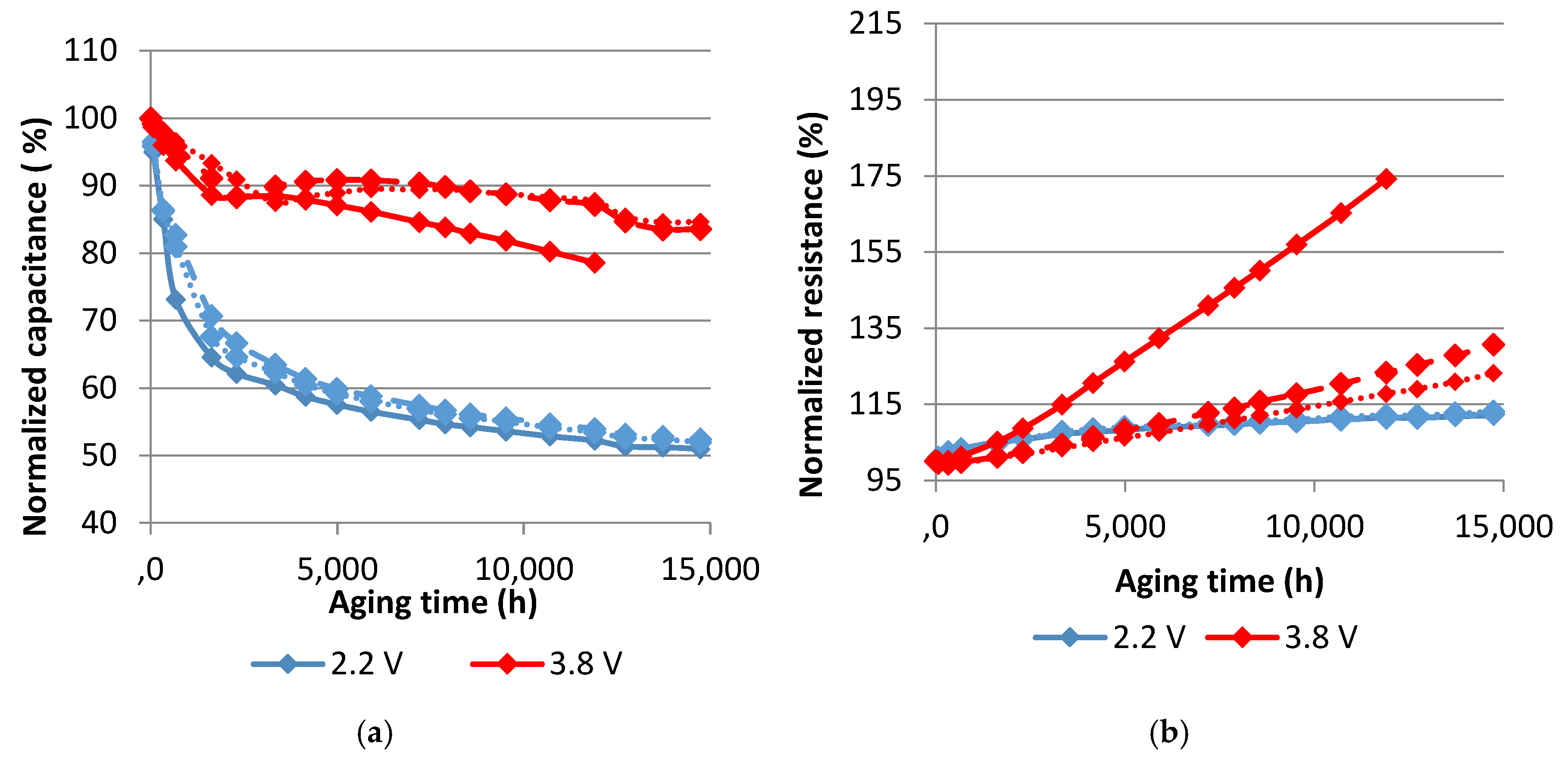
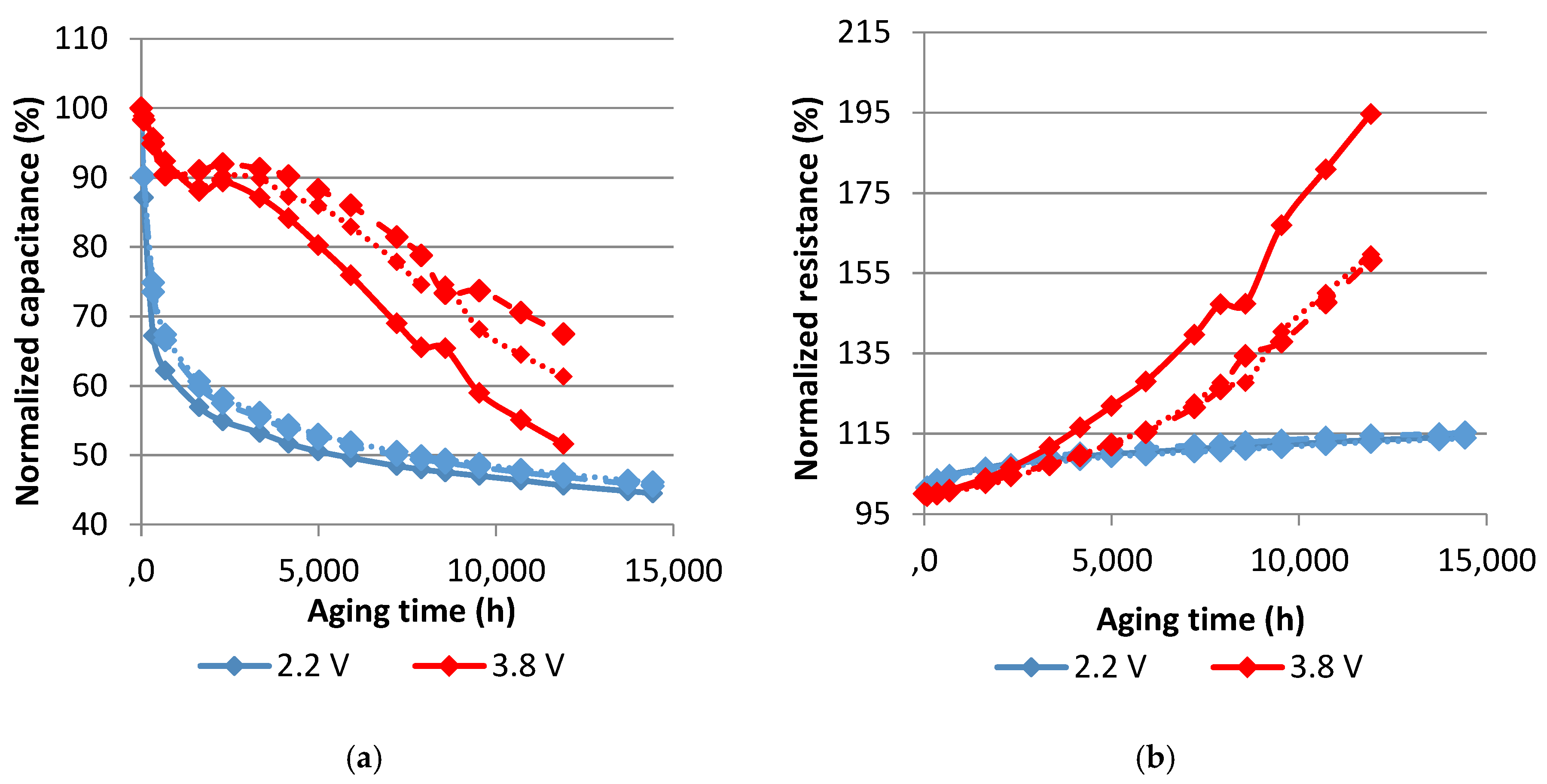
4.1. Results of Periodic Frequency Domain Measurements
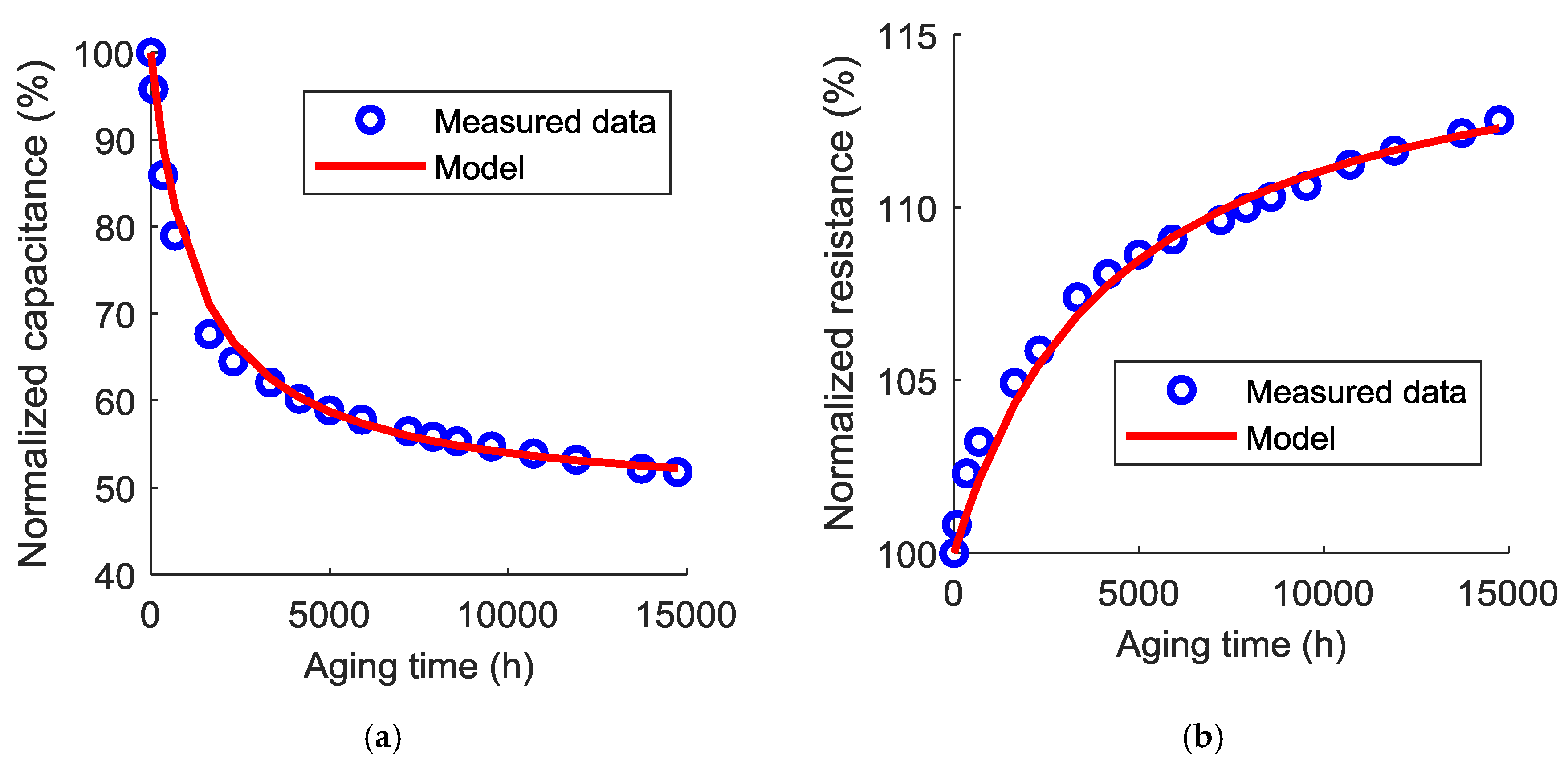
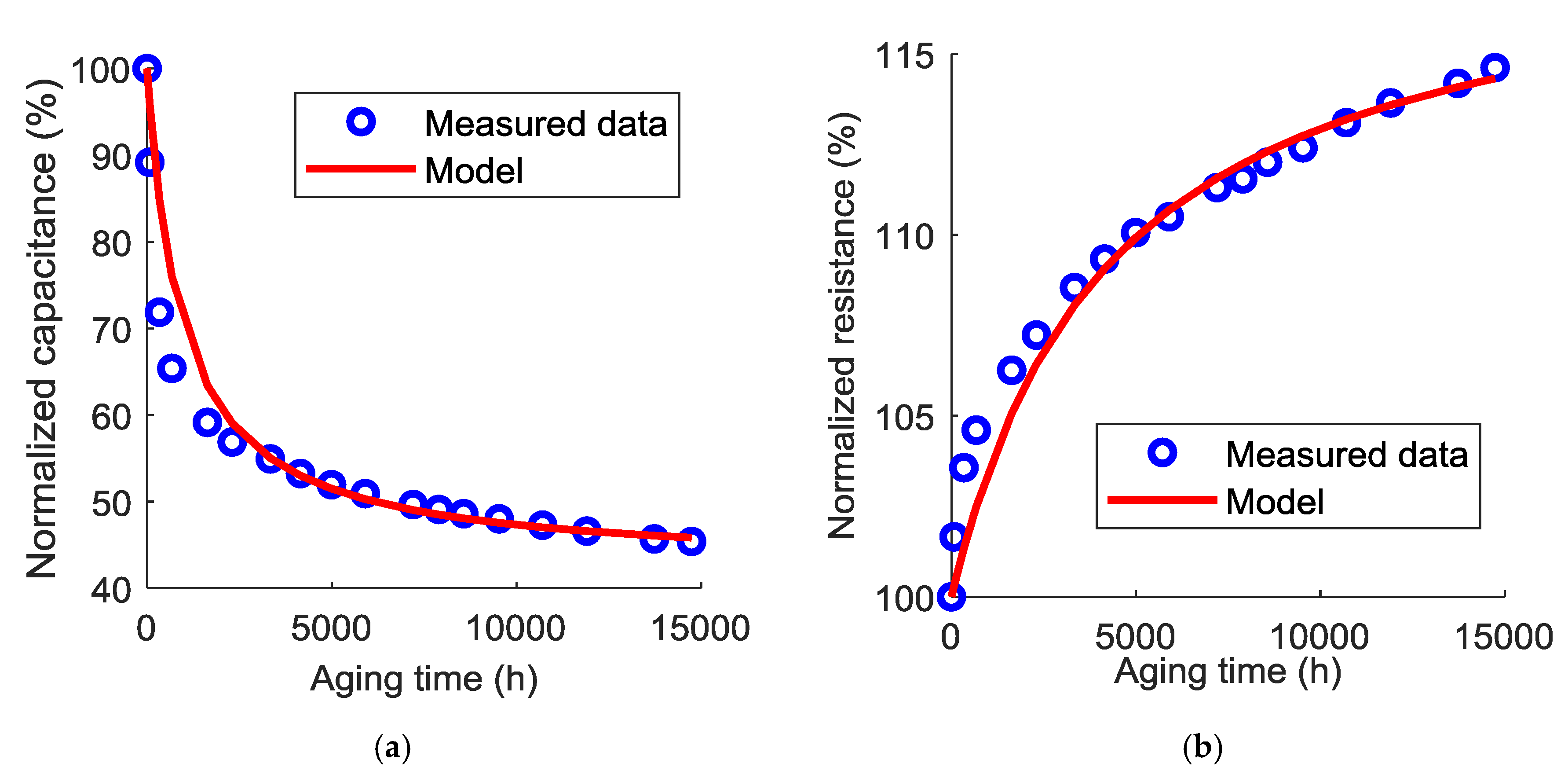
4.2. Aging Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Uddin, K.; Perera, S.; Widanage, W.D.; Somerville, L.; Marco, J. Characterising Lithium-Ion Battery Degradation through the Identification and Tracking of Electrochemical Battery Model Parameters. Batteries 2016, 2, 13. [Google Scholar] [CrossRef]
- Stroe, D.-I.; Swierczynski, M.; Stroe, A.-I.; Knudsen Kær, S. Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries 2016, 2, 37. [Google Scholar] [CrossRef]
- Kandasamy, N.K.; Badrinarayanan, R.; Kanamarlapudi, V.R.K.; Tseng, K.J.; Soong, B.-H. Performance Analysis of Machine-Learning Approaches for Modeling the Charging/Discharging Profiles of Stationary Battery Systems with Non-Uniform Cell Aging. Batteries 2017, 3, 18. [Google Scholar] [CrossRef]
- Ossai, C.I. Prognosis and Remaining Useful Life Estimation of Lithium-Ion Battery with Optimal Multi-Level Particle Filter and Genetic Algorithm. Batteries 2018, 4, 15. [Google Scholar] [CrossRef]
- German, R.; Venet, P.; Sari, A.; Briat, O.; Vinassa, J.M. Improved Supercapacitor Floating Ageing Interpretation Through Multipore Impedance Model Parameters Evolution. IEEE Trans. Power Electron. 2014, 29, 3669–3678. [Google Scholar] [CrossRef]
- German, R.; Sari, A.; Briat, O.; Vinassa, J.M.; Venet, P. Impact of Voltage Resets on Supercapacitors Aging. IEEE Trans. Ind. Electron. 2016, 63, 7703–7711. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Eyring acceleration model for predicting calendar ageing of lithium-ion batteries. J. Energy Storage 2017, 13, 176–183. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Global Model for Self-discharge and Capacity Fade in Lithium-ion Batteries Based on the Generalized Eyring Relationship. IEEE Trans. Veh. Technol. 2018. [Google Scholar] [CrossRef]
- Savoye, F.; Venet, P.; Millet, M.; Groot, J. Impact of Periodic Current Pulses on Li-Ion Battery Performance. IEEE Trans. Ind. Electron. 2012, 59, 3481–3488. [Google Scholar] [CrossRef]
- Ronsmans, J.; Lalande, B. Combining energy with power: Lithium-ion capacitors. In Proceedings of the 2015 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles (ESARS), Aachen, Germany, 3–5 March 2015; pp. 1–4. [Google Scholar]
- Zuo, W.; Li, R.; Zhou, C.; Li, Y.; Xia, J.; Liu, J. Battery-Supercapacitor Hybrid Devices: Recent Progress and Future Prospects. Adv. Sci. 2017, 4, 1600539. [Google Scholar] [CrossRef] [PubMed]
- Adelowo, E.; Baboukani, A.R.; Chen, C.; Wang, C. Electrostatically Sprayed Reduced Graphene Oxide-Carbon Nanotubes Electrodes for Lithium-Ion Capacitors. C 2018, 4, 31. [Google Scholar] [CrossRef]
- Holtstiege, F.; Bärmann, P.; Nölle, R.; Winter, M.; Placke, T. Pre-Lithiation Strategies for Rechargeable Energy Storage Technologies: Concepts, Promises and Challenges. Batteries 2018, 4, 4. [Google Scholar] [CrossRef]
- Cao, W.J.; Luo, J.F.; Yan, J.; Chen, X.J.; Brandt, W.; Warfield, M.; Lewis, D.; Yturriaga, S.R.; Moye, D.G.; Zheng, J.P. High Performance Li-Ion Capacitor Laminate Cells Based on Hard Carbon/Lithium Stripes Negative Electrodes. J. Electrochem. Soc. 2017, 164, A93–A98. [Google Scholar] [CrossRef]
- Ghossein, N.E.; Sari, A.; Venet, P. Nonlinear Capacitance Evolution of Lithium-Ion Capacitors Based on Frequency- and Time-Domain Measurements. IEEE Trans. Power Electron. 2018, 33, 5909–5916. [Google Scholar] [CrossRef]
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar Aging of Lithium-Ion Batteries I. Impact of the Graphite Anode on Capacity Fade. J. Electrochem. Soc. 2016, 163, A1872–A1880. [Google Scholar] [CrossRef]
- Savoye, F. Impact des impulsions périodiques de courant sur la performance et la durée de vie des accumulateurs lithium-ion et conséquences de leur mise en oeuvre dans une application transport. Ph.D. Thesis, Université Claude Bernard Lyon 1, Lyon, France, 2012. [Google Scholar]
- Sun, X.; Zhang, X.; Liu, W.; Wang, K.; Li, C.; Li, Z.; Ma, Y. Electrochemical performances and capacity fading behaviors of activated carbon/hard carbon lithium ion capacitor. Electrochim. Acta 2017, 235, 158–166. [Google Scholar] [CrossRef]
- Aida, T.; Murayama, I.; Yamada, K.; Morita, M. Analyses of Capacity Loss and Improvement of Cycle Performance for a High-Voltage Hybrid Electrochemical Capacitor. J. Electrochem. Soc. 2007, 154, A798–A804. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. Cycle Life Evaluation Based on Accelerated Aging Testing for Lithium-Ion Capacitors as Alternative to Rechargeable Batteries. IEEE Trans. Ind. Electron. 2016, 63, 1607–1617. [Google Scholar] [CrossRef]
- Ghossein, N.E.; Sari, A.; Venet, P. Effects of the Hybrid Composition of Commercial Lithium-Ion Capacitors on their Floating Aging. IEEE Trans. Power Electron. 2018. [Google Scholar] [CrossRef]
- Ghossein, N.E.; Sari, A.; Venet, P. Interpretation of the Particularities of Lithium-Ion Capacitors and Development of a Simple Circuit Model. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; pp. 1–5. [Google Scholar]
- Sivakkumar, S.R.; Pandolfo, A.G. Evaluation of lithium-ion capacitors assembled with pre-lithiated graphite anode and activated carbon cathode. Electrochim. Acta 2012, 65, 280–287. [Google Scholar] [CrossRef]
- Shellikeri, A.; Hung, I.; Gan, Z.; Zheng, J. In Situ NMR Tracks Real-Time Li Ion Movement in Hybrid Supercapacitor–Battery Device. J. Phys. Chem. C 2016, 120, 6314–6323. [Google Scholar] [CrossRef]
- Azaïs, P.; Duclaux, L.; Florian, P.; Massiot, D.; Lillo-Rodenas, M.-A.; Linares-Solano, A.; Peres, J.-P.; Jehoulet, C.; Béguin, F. Causes of supercapacitors ageing in organic electrolyte. J. Power Sources 2007, 171, 1046–1053. [Google Scholar] [CrossRef]
- German, R.; Sari, A.; Venet, P.; Zitouni, Y.; Briat, O.; Vinassa, J.M. Ageing law for supercapacitors floating ageing. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1773–1777. [Google Scholar]
- Chaari, R. Evaluation et Modélisation du Vieillissement des Supercondensateurs pour des Applications Véhicules Hybrides. Ph.D. Thesis, Université Bordeaux 1, Bordeaux, France, 2013. [Google Scholar]
- Zhang, T.; Fuchs, B.; Secchiaroli, M.; Wohlfahrt-Mehrens, M.; Dsoke, S. Electrochemical behavior and stability of a commercial activated carbon in various organic electrolyte combinations containing Li-salts. Electrochim. Acta 2016, 218, 163–173. [Google Scholar] [CrossRef]

| Temperature (°C) | ||||||
|---|---|---|---|---|---|---|
| 60 | 1.2 | 0.001 | 0.7 | 3.5 × 10−5 | 3.2 × 10−4 | 0.3 |
| 70 | 1.9 | 0.0014 | 3 | 4.1 × 10−5 | 3.1 × 10−4 | 0.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Ghossein, N.; Sari, A.; Venet, P. Lifetime Prediction of Lithium-Ion Capacitors Based on Accelerated Aging Tests. Batteries 2019, 5, 28. https://doi.org/10.3390/batteries5010028
El Ghossein N, Sari A, Venet P. Lifetime Prediction of Lithium-Ion Capacitors Based on Accelerated Aging Tests. Batteries. 2019; 5(1):28. https://doi.org/10.3390/batteries5010028
Chicago/Turabian StyleEl Ghossein, Nagham, Ali Sari, and Pascal Venet. 2019. "Lifetime Prediction of Lithium-Ion Capacitors Based on Accelerated Aging Tests" Batteries 5, no. 1: 28. https://doi.org/10.3390/batteries5010028
APA StyleEl Ghossein, N., Sari, A., & Venet, P. (2019). Lifetime Prediction of Lithium-Ion Capacitors Based on Accelerated Aging Tests. Batteries, 5(1), 28. https://doi.org/10.3390/batteries5010028






