The Electrochemical Sodiation of Sb Investigated by Operando X-ray Absorption and 121Sb Mössbauer Spectroscopy: What Does One Really Learn?
Abstract
:1. Introduction
2. Experimental
2.1. Materials
2.2. Methods
2.3. Theoretical Calculations
3. Results
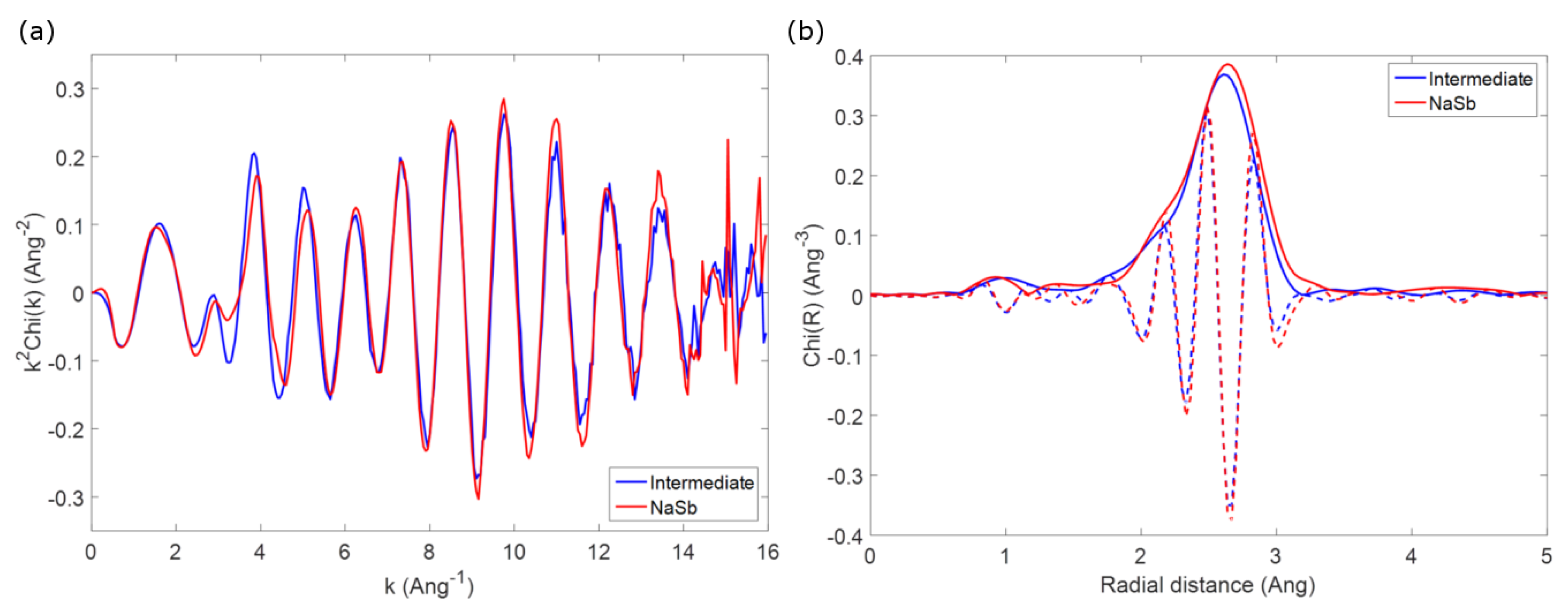
3.1. Pure Sb and Na-Sb Intermetallics
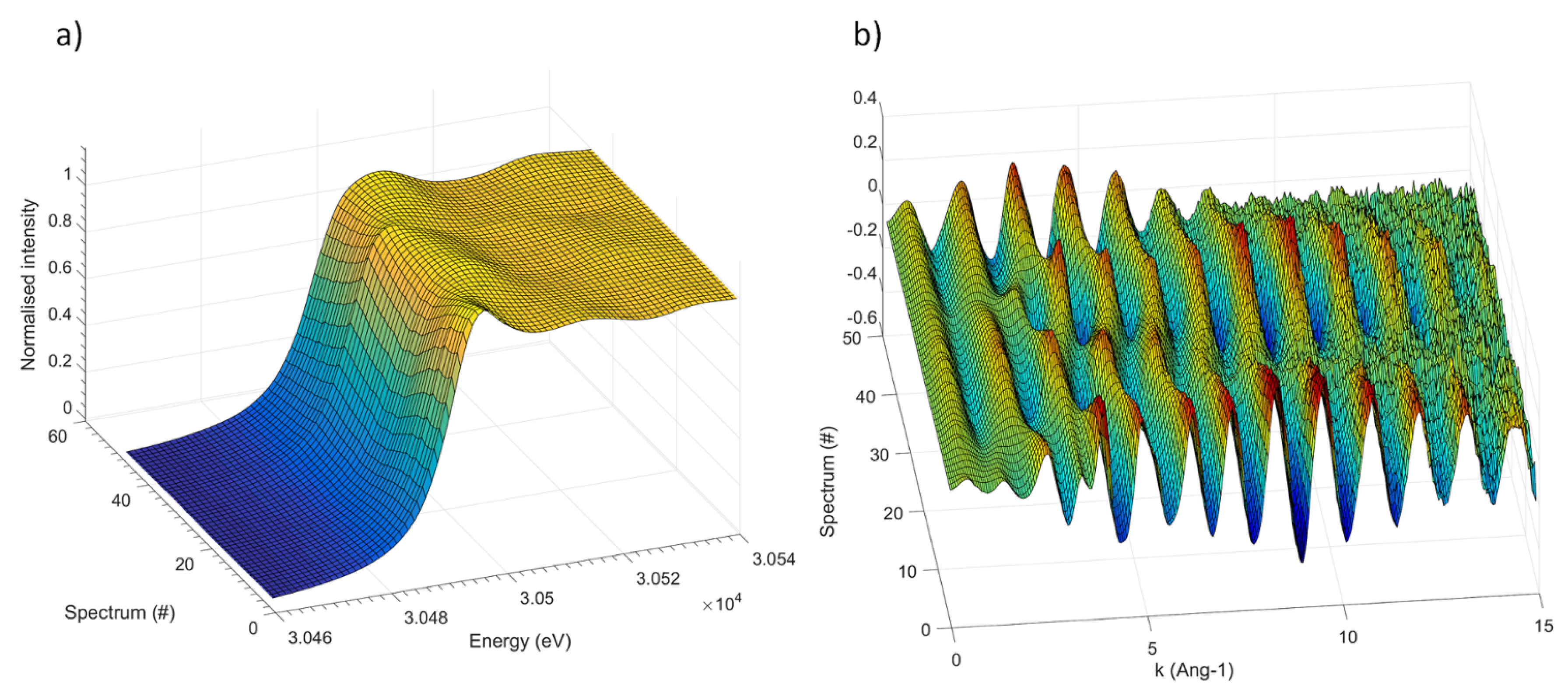
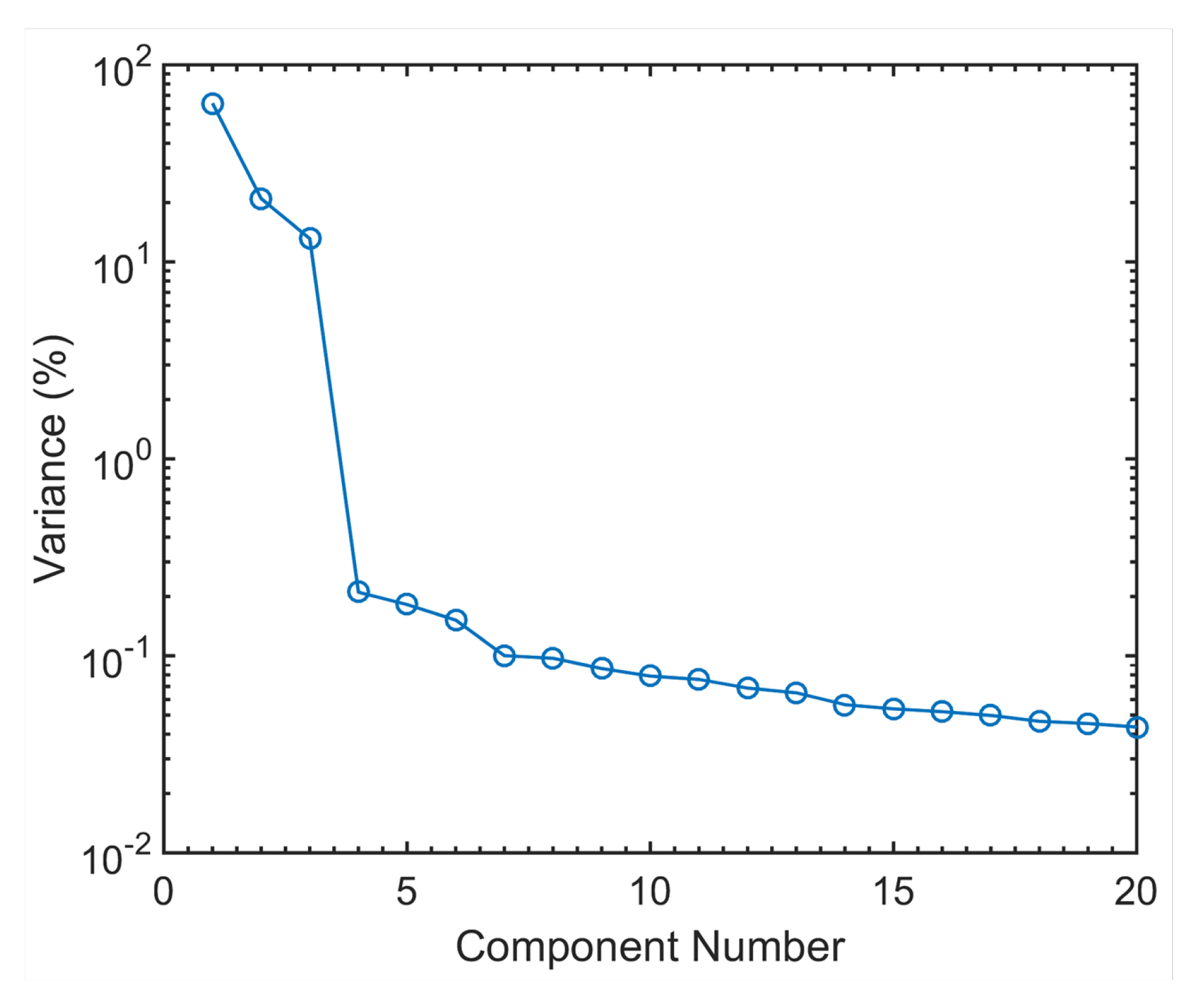
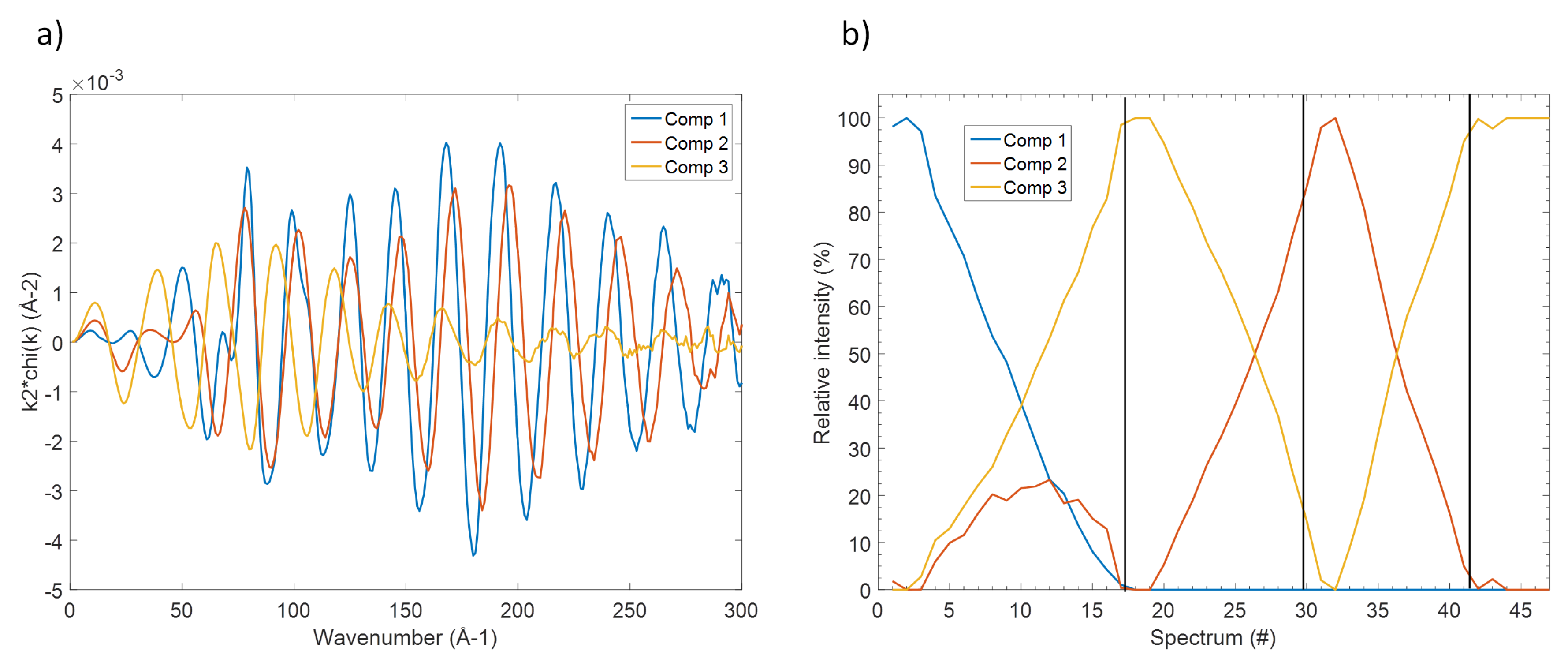
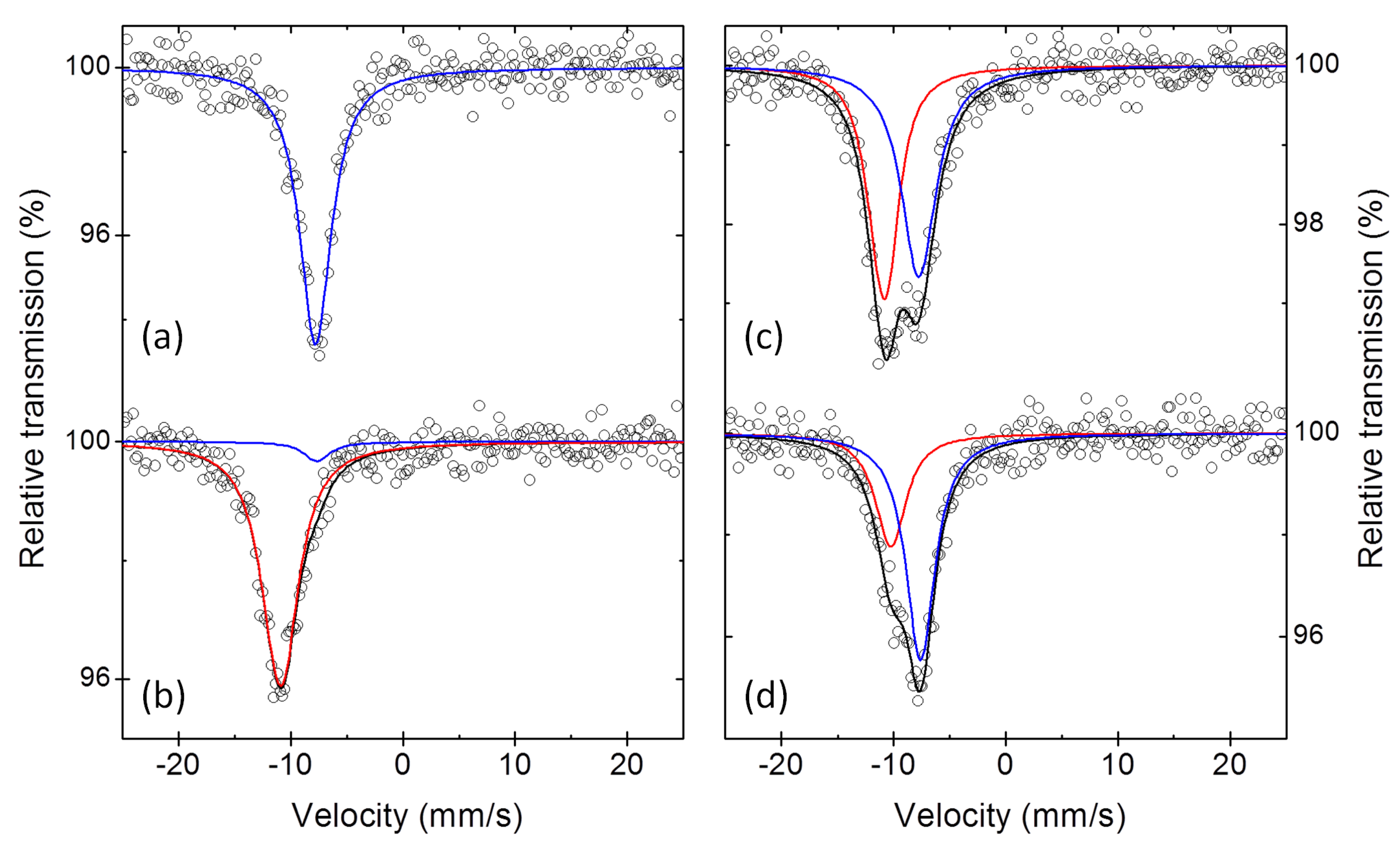
3.2. The Electrochemical Reaction of Sb with Na: Spectroscopic Results
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| XAS | X-ray Absorption spectroscopy |
| EXAFS | Extended X-ray Absorption Fine Structure |
| XANES | X-ray Absorption Near-Edge Structure |
| XRD | X-ray Diffraction |
| Pair Distribution Function | |
| PCA | Principal Component Analysis |
| MCR-ALS | Multivariate Curve Resolution-Alternating Least Squares |
| DFT | Density Functional Theory |
| NMR | Nuclear Magnetic Resonance |
References
- Tarascon, J.M. Is lithium the new gold? Nat. Chem. 2010, 2, 510. [Google Scholar] [CrossRef] [PubMed]
- Kawamoto, H.; Tamaki, W. Trends in Supply of Lithium Resources and Demand of the Resources for Automobiles. Sci. Technol. Trends Quart. Rev. 2011, 369, 51–64. [Google Scholar]
- Fang, Y.; Chen, Z.; Xiao, L.; Ai, X.; Cao, Y.; Yang, H. Recent Progress in Iron-Based Electrode Materials for Grid-Scale Sodium-Ion Batteries. Small 2018, 14, 1703116. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Wei, Y.; Zhai, T.; Li, H. Antimony-based materials as promising anodes for rechargeable lithium-ion and sodium- ion batteries. Mater. Chem. Front. 2018, 2, 437–455. [Google Scholar] [CrossRef]
- Darwiche, A.; Marino, C.; Sougrati, M.T.; Fraisse, B.; Stievano, L.; Monconduit, L. Better cycling performances of bulk Sb in Na-ion batteries compared to Li-ion systems: An unexpected electrochemical mechanism. J. Am. Chem. Soc. 2012, 134, 20805–20811. [Google Scholar] [CrossRef] [PubMed]
- Saubanère, M.; Ben Yahia, M.; Lemoigno, F.; Doublet, M.L. Influence of polymorphism on the electrochemical behavior of MxSb negative electrodes in Li/Na batteries. J. Power Sources 2015, 208, 695–702. [Google Scholar] [CrossRef]
- Allan, P.K.; Griffin, J.M.; Darwiche, A.; Borkiewicz, O.J.; Wiaderek, K.M.; Chapman, K.W.; Morris, A.J.; Chupas, P.J.; Monconduit, L.; Grey, C.P. Tracking Sodium-Antimonide Phase Transformations in Sodium-Ion Anodes: Insights from Operando Pair Distribution Function Analysis and Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 2016, 138, 2352–2365. [Google Scholar] [CrossRef] [PubMed]
- Baggetto, L.; Hah, H.Y.; Jumas, J.C.; Johnson, C.E.; Johnson, J.A.; Keum, J.K.; Bridges, C.A.; Veith, G.M. The reaction mechanism of SnSb and Sb thin film anodes for Na-ion batteries studied by X-ray diffraction, 119Sn and 121Sb Mössbauer spectroscopies. J. Power Sources 2014, 267, 329–336. [Google Scholar] [CrossRef]
- Baggetto, L.; Ganesh, P.; Sun, C.N.; Meisner, R.A.; Zawodzinski, T.A.; Veith, G.M. Intrinsic thermodynamic and kinetic properties of Sb electrodes for Li-ion and Na-ion batteries: Experiment and theory. J. Mater. Chem. A 2013, 1, 7985. [Google Scholar] [CrossRef]
- Cromer, D.T. The crystal structure of NaSb. Acta Crystallogr. 1959, 12, 41–45. [Google Scholar] [CrossRef]
- Brauer, G. Handbook of Preparative Inorganic Chemistry V1; Academic Press: New York, NY, USA, 1963; p. 1031. [Google Scholar]
- Frontera, C.; Rodríguez-Carvajal, J. FullProf as a new tool for flipping ratio analysis. Phys. B Condens. Matter 2003, 335, 219–222. [Google Scholar] [CrossRef]
- Grosse, G. PC-Mos II, Version 1.0 Manual and Program Documentation; Technische Universität München: Munich, Germany, 1993. [Google Scholar]
- Leriche, J.B.; Hamelet, S.; Shu, J.; Morcrette, M.; Masquelier, C.; Ouvrard, G.; Zerrouki, M.; Soudan, P.; Belin, S.; Elkaïm, E.; et al. An electrochemical cell for operando study of lithium batteries using synchrotron radiation. J. Electrochem. Soc. 2010, 157, A606–A610. [Google Scholar] [CrossRef]
- Ravel, B.; Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: Data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 2005, 12, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Ankudinov, A.; Rehr, J. Relativistic calculations of spin-dependent x-ray-absorption spectra. Phys. Rev. B Condens. Matter Mater. Phys. 1997, 56, R1712–R1716. [Google Scholar] [CrossRef]
- Massart, D.; Vandeginste, B.; Buydens, L.; De Jong, S.; Lewi, P.; Smeyers-Verbecke, J. Handbook of Chemometrics and Qualimetrics: Part A, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Jaumot, J.; Gargallo, R.; De Juan, A.; Tauler, R. A graphical user-friendly interface for MCR-ALS: A new tool for multivariate curve resolution in MATLAB. Chemom. Intell. Lab. Syst. 2005, 76, 101–110. [Google Scholar] [CrossRef]
- Jaumot, J.; de Juan, A.; Tauler, R. MCR-ALS GUI 2.0: New features and applications. Chemom. Intell. Lab. Syst. 2015, 140, 1–12. [Google Scholar] [CrossRef]
- Dovesi, R.; Orlando, R.; Erba, A.; Zicovich-Wilson, C.M.; Civalleri, B.; Casassa, S.; Maschio, L.; Ferrabone, M.; La Pierre, M.D.; D’Arco, P.; et al. CRYSTAL14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 2014, 1287–1317. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL 2014 User’s Manual; University of Torino: Torino, Italy, 2014. [Google Scholar]
- Becke, A. Density—Functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Lippens, P.E. Mössbauer isomer shifts of crystalline antimony compounds. Solid State Commun. 2000, 113, 399–403. [Google Scholar] [CrossRef]
- Svane, A. Calculations of hyperfine parameters in antimony compounds. Phys. Rev. B 2003, 68, 064422. [Google Scholar] [CrossRef]
- Casassa, S.; Ferrari, N.M. Calibration of 57Fe Mössbauer constants by first principles. Phys. Chem. Chem. Phys. 2016, 18, 10201–10206. [Google Scholar] [CrossRef] [PubMed]
- Brauer, G.Z.E. Konstitution von Phosphiden, Arseniden, Antimoniden und Wismutiden des Lithiums, Natriums und Kaliums. Z. Phys. Chem. 1937, 37, 323–352. [Google Scholar] [CrossRef]
- Songster, J.; Pelton, A.D. The Na-Sb (sodium-antimony) system. J. Phase Equilib. 1993, 14, 250–255. [Google Scholar] [CrossRef]
- Leonova, M.E.; Bdikin, I.K.; Kulinich, S.A.; Gulish, O.K.; Sevast’yanova, L.G.; Burdina, K.P. High-pressure phase transition of hexagonal alkali pnictides. Inorg. Mater. 2003, 39, 266–270. [Google Scholar] [CrossRef]
- Krebs, H.; Steffen, R. Neubestimmung der Nahordnung im glasigen Selen, im explosiven Antimon und im beta- und gamma-Arsen. Z. Anorg. Allg. Chem. 1964, 327, 224–237. [Google Scholar] [CrossRef]
- Sergueev, I.; Wille, H.C.; Hermann, R.P.; Bessas, D.; Shvyd’ko, Y.V.; Zając, M.; Rüffer, R. Milli-electronvolt monochromatization of hard X-rays with a sapphire backscattering monochromator. J. Synchrotron Radiat. 2011, 18, 802–810. [Google Scholar] [CrossRef] [PubMed]
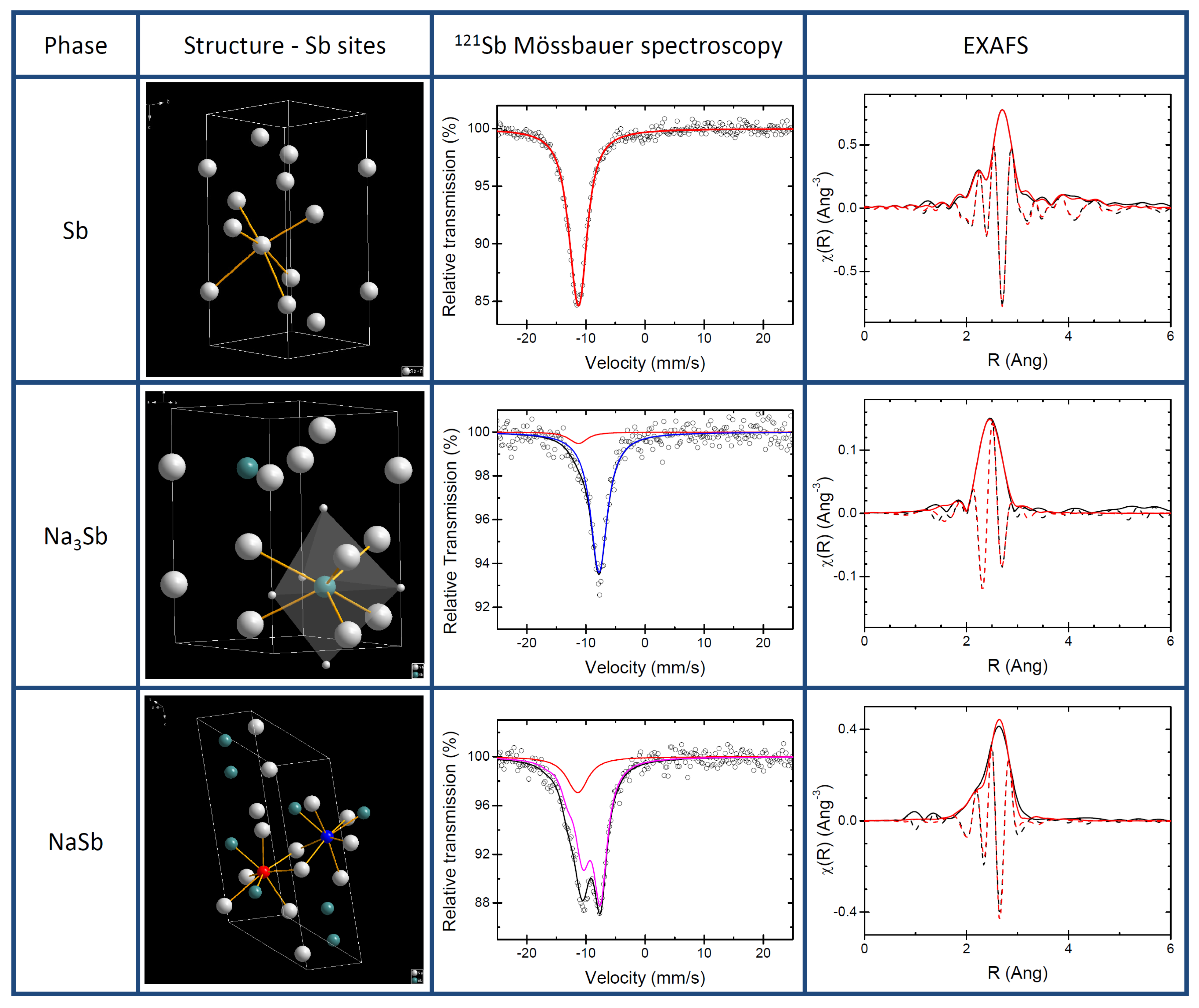
| Compound | * [mm s] | Δ [mm s] | [mm s] | Area [%] | |
|---|---|---|---|---|---|
| Sb | −11.42(2) | 4.3(8) | 0 ** | 3.33(1) | 100 |
| NaSb | −7.74(4) | 0 ** | 0 ** | 2.85(1) | 90(2) |
| Sb (impurity) | −11.42 ** | 4.3 ** | 0 ** | 3.33 ** | 10(2) |
| NaSb | −9.24(6) | −17.5(4) | 0.39(8) | 2.81(8) | 85(3) |
| Sb (impurity) | −11.42 ** | 4.3 ** | 0 ** | 3.33 ** | 15(3) |
| Compound | [mm s] | Δ [mm s] | |
|---|---|---|---|
| Sb | −11.48 | 5.6 | −1.50 |
| NaSb | −8.99 | 17.7 | 0.60 |
| −9.36 | 17.6 | 0.60 | |
| NaSb-hex | −7.39 | −1.2 | 0 |
| NaSb-cub | −7.56 | 0 | 0 |
| Sample | Shell | N | R [Å] | R [Å] | [Å] | S * |
|---|---|---|---|---|---|---|
| Sb | Sb-Sb | 3 | 2.908 | 2.905(2) | 0.0055(3) | 0.98 |
| Sb-Sb | 3 | 3.355 | 3.351(2) | 0.017(1) | 0.98 | |
| Sb-Sb | 6 | 4.308 | 4.305(2) | 0.017(1) | 0.98 | |
| Sb-Sb | 6 | 4.507 | 4.503(2) | 0.017(1) | 0.98 | |
| NaSb | Sb-Sb | 2 | 2.888 | 2.852(6) | 0.0058(2) | 0.98 |
| Sb-Na | 2 | 3.206 | 3.261(7) | 0.023(5) | 0.98 | |
| Sb-Na | 1 | 3.267 | 3.332(7) | 0.023(5) | 0.98 | |
| Sb-Na | 2 | 3.322 | 3.377 | 0.023(5) | 0.98 | |
| NaSb (Sb) | Sb-Na | 3 | 3.053 | 3.04(2) | 0.017(2) | 0.81(2) |
| Sb-Na | 2 | 3.149 | 3.13(2) | 0.017(2) | 0.81(2) | |
| Sb-Na | 6 | 3.428 | 3.41(2) | 0.04(1) | 0.81(2) | |
| Sb-Sb | 3 | 2.908 | 2.817(8) | 0.017(2) | 0.17(2) |
| Component | Shell | N | R [Å] | R [Å] | [Å] | S * |
|---|---|---|---|---|---|---|
| 1 | Sb-Sb | 3 | 2.908 | 2.905(2) | 0.0055(3) | 0.98 |
| Sb-Sb | 3 | 3.355 | 3.351(2) | 0.017(1) | 0.98 | |
| Sb-Sb | 6 | 4.308 | 4.305(2) | 0.017(1) | 0.98 | |
| Sb-Sb | 6 | 4.507 | 4.503(2) | 0.017(1) | 0.98 | |
| 2 | Sb-Sb | 3 | 2.908 | 2.850(2) | 0.0061(3) | 0.98 |
| Sb-Sb | 3 | 2.908 | 2.885(9) | 0.09(4) | 0.09(4) | |
| 3 | Sb-Na | 3 | 3.053 | 3.052(8) | 0.016(1) | 0.89(4) |
| Sb-Na | 2 | 3.149 | 3.122(8) | 0.016(1) | 0.89(4) |
| Sample | * [mm s] | Δ [mm s] | [mm s] | Area [%] | |
|---|---|---|---|---|---|
| EOD 1st cycle | −7.68(4) | 0 | 0 ** | 2.8(1) | 100 |
| EOC 1st cycle | −10.96(8) | 4.5(6) | 0 ** | 3.5(5) | 94(3) |
| −7.68 ** | 0 ** | 0 ** | 2.8 ** | 6(3) | |
| 1st disch. 1.5 Na reacted | −10.91(8) | 4.7(8) | 0 ** | 2.8(3) | 52(2) |
| 7.81(1) | 0 ** | 0 ** | 3.6(6) | 48(5) | |
| 1st disch. 2 Na reacted | −10.4(2) | 4.7(8) | 0 ** | 2.6(5) | 30(6) |
| −7.65(8) | 0 ** | 0 ** | 3.2(6) | 70(6) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darwiche, A.; Fehse, M.; Mahmoud, A.; La Fontaine, C.; Fraisse, B.; Hermann, R.P.; Doublet, M.-L.; Monconduit, L.; Sougrati, M.T.; Ben Yahia, M.; et al. The Electrochemical Sodiation of Sb Investigated by Operando X-ray Absorption and 121Sb Mössbauer Spectroscopy: What Does One Really Learn? Batteries 2018, 4, 25. https://doi.org/10.3390/batteries4020025
Darwiche A, Fehse M, Mahmoud A, La Fontaine C, Fraisse B, Hermann RP, Doublet M-L, Monconduit L, Sougrati MT, Ben Yahia M, et al. The Electrochemical Sodiation of Sb Investigated by Operando X-ray Absorption and 121Sb Mössbauer Spectroscopy: What Does One Really Learn? Batteries. 2018; 4(2):25. https://doi.org/10.3390/batteries4020025
Chicago/Turabian StyleDarwiche, Ali, Marcus Fehse, Abdelfattah Mahmoud, Camille La Fontaine, Bernard Fraisse, Raphael P. Hermann, Marie-Liesse Doublet, Laure Monconduit, Moulay T. Sougrati, Mouna Ben Yahia, and et al. 2018. "The Electrochemical Sodiation of Sb Investigated by Operando X-ray Absorption and 121Sb Mössbauer Spectroscopy: What Does One Really Learn?" Batteries 4, no. 2: 25. https://doi.org/10.3390/batteries4020025
APA StyleDarwiche, A., Fehse, M., Mahmoud, A., La Fontaine, C., Fraisse, B., Hermann, R. P., Doublet, M.-L., Monconduit, L., Sougrati, M. T., Ben Yahia, M., & Stievano, L. (2018). The Electrochemical Sodiation of Sb Investigated by Operando X-ray Absorption and 121Sb Mössbauer Spectroscopy: What Does One Really Learn? Batteries, 4(2), 25. https://doi.org/10.3390/batteries4020025







