Abstract
Due to variations among the cells, large lithium ion batteries (LIB) such as those in battery energy storage stations (BESS) and electric vehicles (EVs) must have an equalizer (EQU) circuit to balance the cell voltages. In spite of their significant losses and other limitations, passive equalizers (PEQ) are used in most applications because they are relatively simple and low cost. Active equalizers (AEQ) reduce these PEQ problems, but are not as widely used due to their much higher cost and complexity. A new hybrid circuit called the Bilevel EQU (BEQ) combines the PEQ and AEQ to provide much higher performance than a pure PEQ but at a much lower cost than a pure AEQ.
1. Introduction
Large lithium ion batteries (LIB) are now used in a wide variety of applications including electric vehicles, aerospace, and battery energy storage stations (BESS) for electric utilities. For safety and maximum performance, all of these large packs of series connected cells require a battery management system (BMS) that must provide several functions [1]. The most basic of these is to measure the voltage of each cell and to provide an equalizer (EQU) to balance the cell voltages.
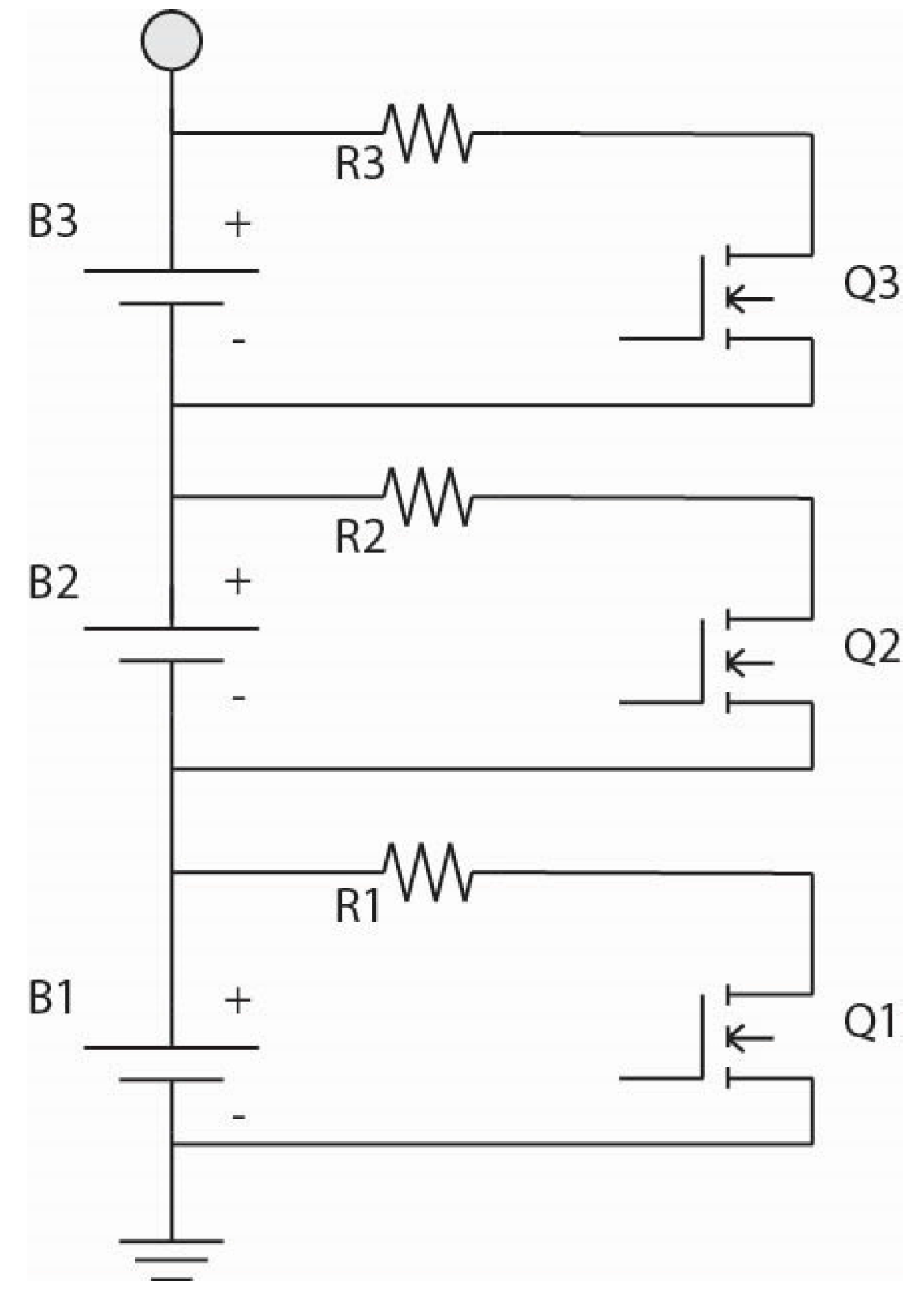
There are two basic types of EQUs: Passive (PEQ) as in Figure 1, where resistors are connected in parallel with the cells until all are discharged to the lowest cell voltage in the pack and active (AEQ) where charge is transferred between the cells.
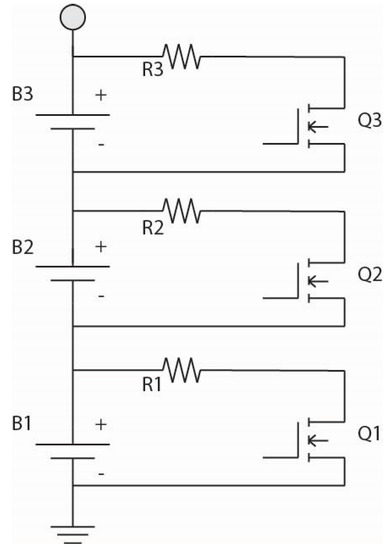
Figure 1.
Passive equalizer (PEQ) for 3 cells.
Figure 1 shows a PEQ for a three cell pack. It is simple and relatively cheap, but it can dissipate a significant amount of heat and energy loss.
PEQs have another serious limitation since they cannot add charge to lower capacity cells, which is necessary to maximize the discharge capacity of the battery. This is quite important, especially as the pack ages and cell capacities begin to decrease, usually in a non-uniform manner. Since a PEQ cannot boost weaker cells, the resulting discharge capacity is only equal to the weakest cell in the pack. In practice, the probability of one particularly weak cell may be small for small packs of four to six series cells, but it becomes much greater for large packs such as those with 100–200 cells.
By balancing the cell voltages, the PEQ also balances the state of charge (SoC) of the cells, but it does not equalize the charge in the cells or the capacity of the cells. As a battery ages and its capacity decreases, it may be difficult to determine if this is primarily due to one or two weak cells or if all cells have degraded in a uniform manner since the PEQ will mask the weak cell(s) by holding all cell voltages at the same value. Thus it may appear that the cells have uniform capacities when in fact they do not, and that a PEQ is perfectly adequate when it really isn’t.
A wide variety of AEQs [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] have been developed to reduce these PEQ problems, but PEQs still dominate most markets due to their simplicity and much lower cost. This cost difference is even greater when higher equalization currents are needed since this requires higher power AEQ components.
For new cells with fairly uniform capacities, minor imbalances are caused by temperature variations and self-discharge current, and balancing can be achieved with low current EQUs. This reduces cost, but as the cells age much larger capacity variations are likely to develop, and larger EQUs are required to achieve balance and maximize battery capacity. The merits of PEQs vs. AEQs obviously apply in both cases, but this research is focused on larger EQUs that are needed to compensate for capacity variations.
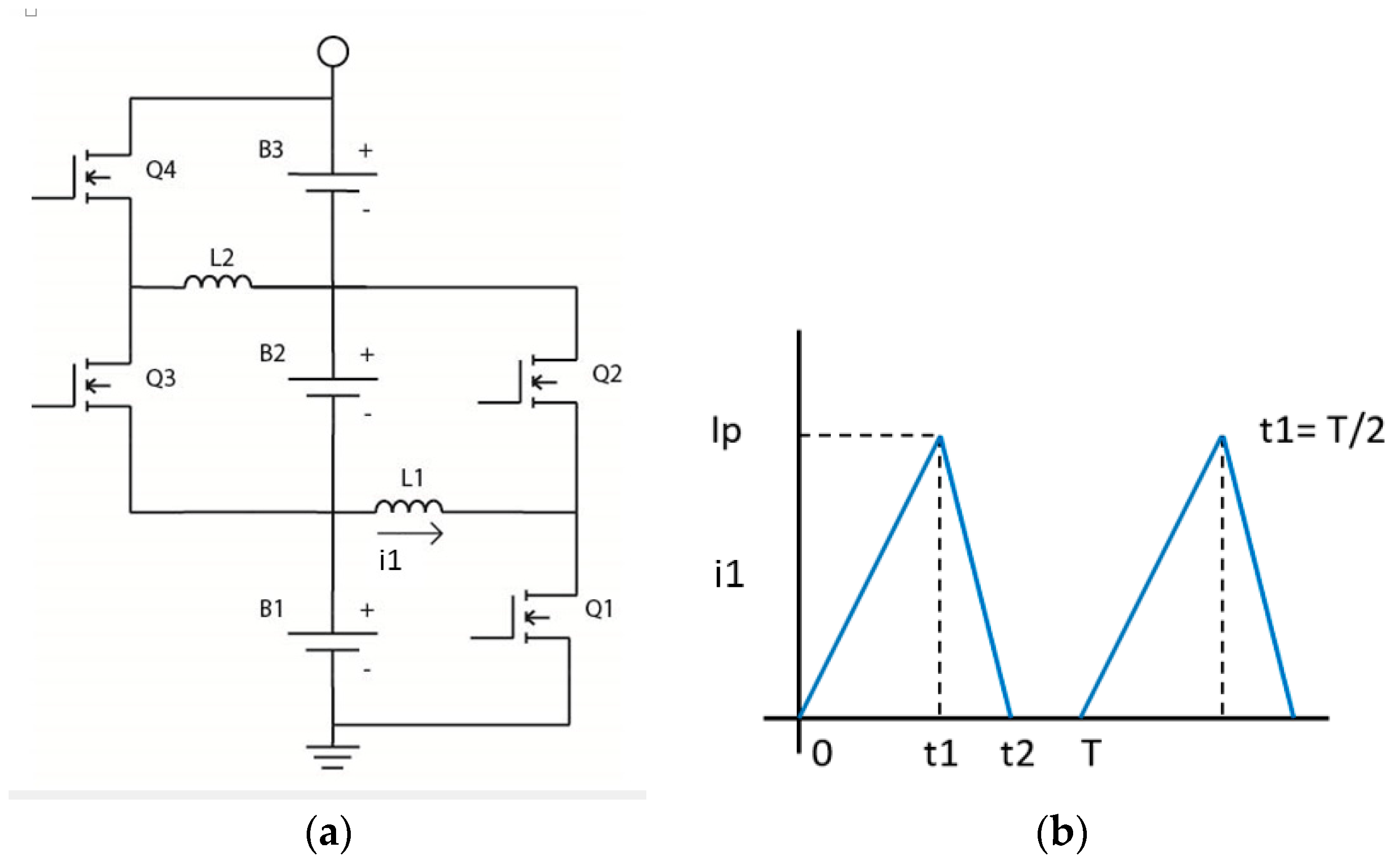
One of the simplest of these AEQ circuits is shown in Figure 2 [10], where B1–B3 may be individual cells or sections of series connected cells. Components Q1, Q2, and L1 constitute one AEQ unit, so this circuit has two units. To reduce the size of the inductors, the FETs typically switch in the range of several kHz.
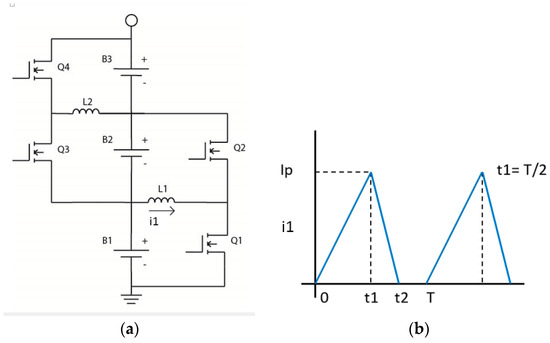
Figure 2.
Active equalizer (AEQ) (a) Schematic; (b) Current in L1.
If Q1 in Figure 2a is turned on, i1 flows from B1 into the inductor, L1, and reaches the peak, Ip, in Figure 2b. On the second half cycle Q1 turns off, and i1 flows through the body diode of Q2 and into B2. Alternately, if Q2 is the only active FET, charge is transferred from B2 to B1. Note that the interval t2−t1 is less than t1, and thus the average current from B1 is less than that into B2. This is because of conduction losses, core loss in L1 and switching losses in Q1 and Q2. This is related to the i1 peak/average ratio >2 which is higher than that for typical DC-DC converters.
A series of tests also were performed to show how the power transfer efficiency of this AEQ varies if each cell is replaced by sections of cells in series containing from 1–12 cells per section: 1 cell = 43%, 4 cells = 76%, 6 cells = 80%, and 12 cells = 87%. The efficiency increases with the number of cells because the losses become a lower percentage as the output power increases, and these results also indicate this AEQ actually is not a very good choice for single cells. Synchronous rectification also can be used to reduce the conduction loss of the FET body diodes, but tests indicated this provides only a minor improvement. For larger numbers of cells, these results are comparable to [29] which indicates an efficiency range of about 80–87.9%.
If two target cells are not adjacent, the charge is transferred via the cells between the two target cells. For example, if Q2 and Q4 are the only active FETs, charge is transferred from B3 via B2 to B1. This balancing strategy can be based on the two target cells with the greatest voltage difference, or adjacent cell balancing also can be used. In summary, the designer presently has a stark choice between a low cost, low performance PEQ or a high cost, higher performance AEQ. Neither is really satisfactory for applications that need to be cost effective over a long lifetime, thus the motivation for the hybrid BEQ which is described below.
2. BEQ Analysis
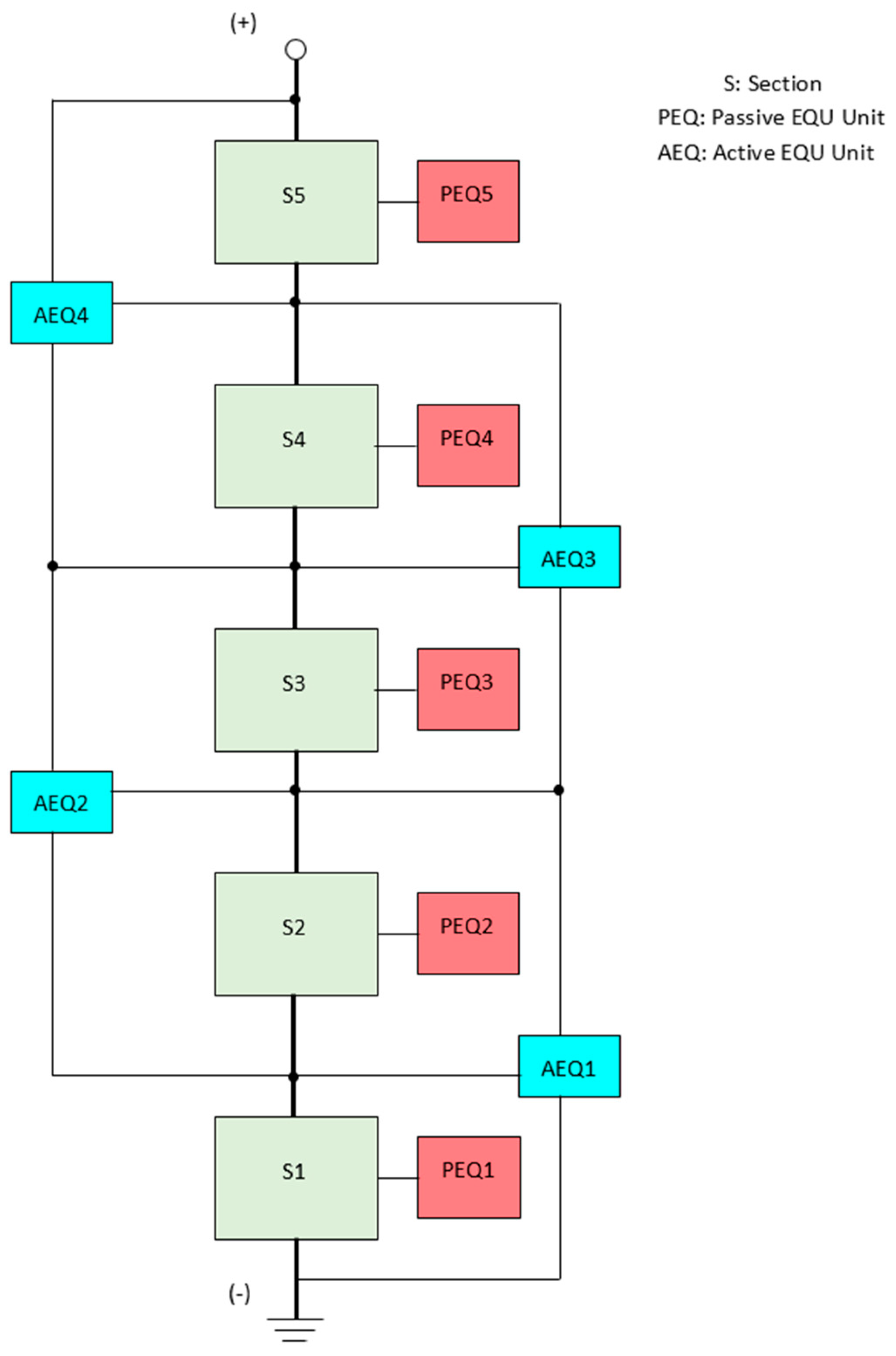
To avoid the problems with PEQs and AEQs, a new PEQ/AEQ hybrid called the Bilevel EQU (BEQ) [30] has been developed to provide much higher performance than a PEQ but at a much lower cost than an AEQ. This circuit is called the Bilevel because it provides equalization at two different voltage levels. An example block diagram where the cells are divided into five sections is shown in Figure 3.
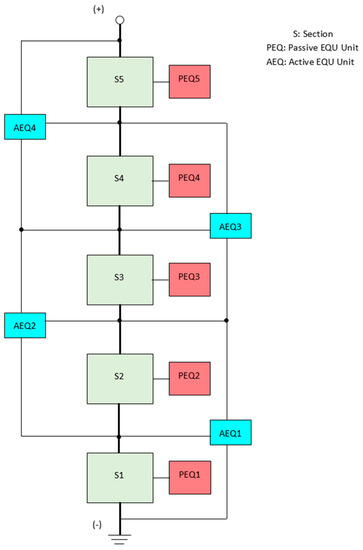
Figure 3.
Bilevel equalizer (BEQ) for a battery pack with 5 sections.
There can be any number of cells per section, but a range of four to eight allows the use of 60–100 V FETs. However, a higher number such as 12 or 14 also can be used with higher voltage switches. Each section has its own PEQ that balances only the cells within that section, i.e., PEQ1–PEQ5 equalize the cells within each section, and AEQ1–AEQ4 equalize the sections. Converting a PEQ to a BEQ is relatively simple since it basically adds an AEQ from Figure 2 to the conventional PEQ in Figure 1.
The BEQ can be designed from scratch, or an existing PEQ system can be converted to a BEQ by adding AEQ units. The additional AEQ would be controlled using the same cell voltage measurements as those for the original PEQ, and the PEQ software would be revised to equalize the cells within each section instead of the entire stack.
As a cell ages, its charge capacity (amp hours, Ah) decreases and its series resistance increases. Experience also shows that not all cells age at the same rate, so eventually capacity variations develop. With a pure PEQ, the discharge capacity of the pack is determined by the weakest cell, and this also determines the usable lifetime of the pack. Many applications now strive for lifetimes of at least 10 years and some even longer.
For example, for a 96 cell battery with a single weak cell, a PEQ will need to drag down the other 95 until they all reach the weak cell voltage. If a BEQ with 24 sections and four cells/section were used, it would only drag down the other three cells in the weak cell section. Simultaneously, charge would be transferred to the weak section from the other 23 until all the cell voltages were equal.
AEQs such as [27,28] transfer charge between each cell and a section of cells within the pack either by using a bi-directional DC-DC converter for each cell or a single bi-directional converter coupled to a matrix of switches connected to the cells. This is much more expensive than a simple PEQ for each cell, and thus PEQs presently dominate the market. The BEQ also costs more than a PEQ, but it is much cheaper than a traditional AEQ because it uses a reduced number of AEQ units that service cell sections instead of individual cells. For example, a BEQ for a 192 cell battery with 16 sections of 12 cells each would only contain 15 AEQ units (number of sections-1) instead of 192 units for a pure AEQ such as [27]. Although the AEQs in the BEQ operate at a higher voltage, the AEQ currents would be the same, and the dramatic reduction in the parts count and absence of transformers indicate a much lower cost.
As the number of cells increases for a PEQ system, the stack becomes subject to the “tyranny of large numbers”, meaning the probability of a weak cell spoiling the pack can increase dramatically. Consider the same 96 cell example with only a PEQ, where after a very large number of cycles there might be a 2% probability that any given cell will have a significant decrease in discharge capacity. Of course this also means the probability that the cell is still good is 98%. Therefore the probability that all cells will still be good is (0.98)96 × 100% = 14.4%, which means an 85.6% probability that there will be at least one weak cell to drag down the other 95.
For the same 96 cell stack with a BEQ with four cells/section, the probability that all four cells in a section will still be good is (0.98)4 × 100% = 92.2%, or a 7.8% probability that there will be at least one weak cell which will drag down the other three. However, the resulting weak section will not spoil the pack since the BEQ can transfer charge to this section to boost the weak cell.
Weaker cells will charge and discharge faster than other cells since their lower capacity and higher resistance will cause them to reach their voltage limits sooner, e.g., 4.2 V max and 2.8 V min. Therefore the EQU needs to remove charge from the weaker cells during charging to allow more time for the other cells to fully charge. PEQs, AEQs and BEQs all can do this. During discharge the EQU needs to do the opposite, i.e., charge needs to be transferred to the weak cells to allow more time for the other cells to fully discharge. However, only AEQs and BEQs have this capability. PEQs can assist the battery pack so it will fully charge, but they cannot assist it to fully discharge.
The difference in capacity between a battery with a PEQ and one with a BEQ can be dramatic, and this can be shown using the five section BEQ in Figure 3. The degree of imbalance and location of any weak sections is random and therefore impossible to predict, but we can derive a simple model that can be used for designing the AEQ units. The following analysis is only an estimate, but at least it provides a frame of reference for comparison purposes.
The capacity of a section is considered to be the capacity of the weakest cell in the section. For a section containing at least one weak cell, the worst case is when it is at one end of the stack since it only receives charge directly from one adjacent cell. We assume that S1 is the section with the weak cell and all other cells have rated capacity. The relevant variables are,
- Ahi = rated Ah discharge capacity of section i (2 to 5), ampere-hours.
- Ahw = Ah1 = discharge capacity of the weak section, ampere-hours.
- Id = discharge current, amperes.
- Ipi = average PEQ current for all cells in section I, amperes.
- t = discharge time, hours.
- Ik = average AEQ current flowing from one section to another (k = 1 to 4), amperes.
- n = efficiency of each AEQ unit, 0 to 1.0.
As the battery discharges, the weak cell in S1 will attempt to discharge faster than the other cells, but the BEQ will be designed so that S2–S5 will simultaneously transfer charge toward S1 in such a manner that S1–S5 all will reach full discharge at the same time, t. Equations (1)–(5) show the total discharge Ah for S1–S5. In Equation (2) for example, I1 flows out of 2 towards 1; n × I2 flows into 2 from 3; and Id is the discharge current for the battery.
(Id + Ip1 − n × I1)t = Ah1 = Ahw
(Id + Ip2 + I1 − n × I2)t = Ah2
(Id + Ip3 + I2 − n × I3)t = Ah3
(Id + Ip4 + I3 − n × I4)t = Ah4
(Id + Ip5 + I4)t = Ah5
During discharge, Ah1 to Ah5 actually refer to the capacity of the weakest cell in each section, but during discharge no PEQ current is drawn from these weak cells. Therefore for discharge we can assume Ip1 to Ip5 = 0. Define Ah = Ah2 to Ah5.
If we also define P = 1/t, then in matrix form we have,
Assume Ah = 64, Id = 16, Ahw = 0.8 × 64 = 51.2 (20% low), and n = 0.757. n is based on the measured efficiency for an AEQ unit transferring charge between two 4 cell sections.
Solving Equation (6) yields the following result,
I1 = 3.06 A., I2 = 2.58 A., I3 = 1.94 A., I4 = 1.11 A., t = 3.741 h.
To achieve this result, the AEQ units must be able to provide an average current of 3.06 A., about 19% of the 16 A discharge current.
Actual discharge capacity = 3.741 × 16 = 59.86 Ah (93.5% of rated). For a PEQ equalizer the capacity would only be 80% of rated. Even though the AEQ only had an efficiency of 75.7%, it increases the discharge capacity by 8.66 Ah which is 16.9% above the 51.2 Ah with only a PEQ. If the AEQ was ideal with an efficiency of 100%, the capacity would be equal to the average capacity of the sections, i.e., 96% of rated.
The above example provides a possible design criterion, but the same type of analysis can be used to find T and the Ik’s for any number of sections and values of Id and n. Likewise different values can be used for each of the Ahi’s, i.e., there can be any number of weak sections placed anywhere in the stack.
Therefore, when there are large capacity variations such as those that occur after extensive use, to achieve a battery discharge capacity close to the average of the cells, the EQU must meet two conditions:
- It must be an active or a hybrid such as an AEQ or the BEQ.
- To compensate for a large capacity imbalance, it must use an EQU current that is fairly high. In this example, the 20% imbalance required an EQU current equal to 19% of Id.
Of course if the EQU current is too small, the improvement in discharge capacity will be less, but it will still be greater than that for a PEQ.
3. Experimental Results
A BMS with a prototype BEQ was designed and tested for a battery pack with 24 randomly selected GAIA HE-602050 lithium ion cells with an original rating of 50 Ah based on a 2.8–4.2 Vdc cell voltage range. These cells were about 9 years old and had some limited cycling, although the exact amount of usage was unknown. Age and usage had reduced the cells’ discharge capacity considerably, but older cells were considered to be preferable for this testing since the BEQ benefits become more pronounced as cell imbalance increases. These experiments used a slightly smaller voltage range of 2.8–4.0 Vdc, which further reduced the capacity.
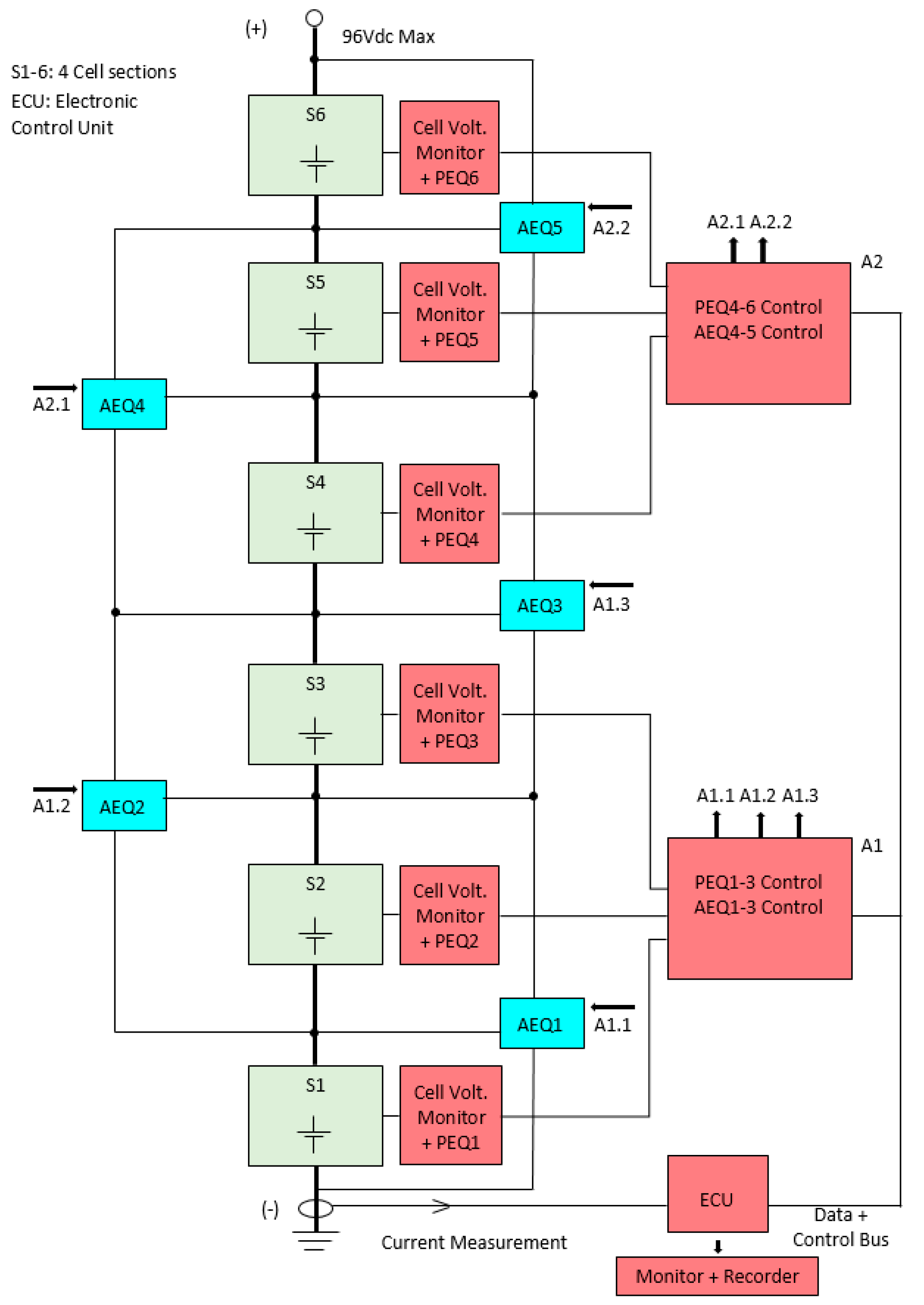
The pack was divided into 6 sections of 4 cells each, and Figure 4 shows the system block diagram. The 5 AEQ blocks shown in blue represent the additional power electronics circuitry required to convert a PEQ to a BEQ. The A1 and A2 blocks also contain some additional AEQ control circuits. All of the PEQ/AEQ circuits draw their housekeeping power from the battery, but these currents are very small in comparison to the battery load current and EQU currents in the cells.
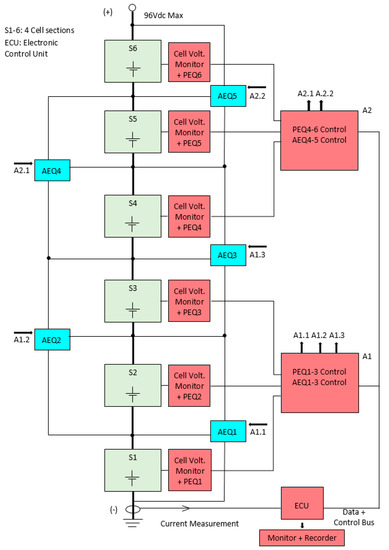
Figure 4.
Block diagram for a 24 cell BEQ.
The system can be operated as a BEQ with 6 sections of 4 cells each, or as a PEQ with 24 cells. These two modes were used to compare BEQ vs. PEQ performance using the same battery and measurement and PEQ control circuitry. The 24 cell GAIA battery pack is shown in Figure 5.

Figure 5.
24 cell GAIA battery pack.
The Cell Voltage Monitors and PEQ Controls were implemented using a Linear Technology LTC6804 cell monitor [31], which measures the cell voltages, drives the PEQs, and transfers data to and from the Electronic Control Unit (ECU). The 6804 also has 5 general I/O ports that are used along with additional circuitry for controlling the AEQ units, thus avoiding the need for an additional microcontroller in A1 and A2. After receiving the cell voltage data, the ECU determines which PEQ and AEQ switches should be activated and sends this data back to the A1 and A2 modules. The LTC6804 in each module provides the drive signals for its PEQ and AEQ units. When operating in the BEQ mode, the PEQs only equalize the 4 cells within each of the 6 sections, but in the PEQ mode all 24 cells are equalized together. The PEQ and AEQ units are similar to the circuits in Figure 1 and Figure 2, respectively. The ECU also measures the battery current to calculate the charge and discharge Ahrs, which is sent to the Monitor/Recorder along with other data.
As indicated above, this system can be operated as a BEQ or as a pure PEQ, in which case the AEQ units are disabled. In either mode, the PEQ is only used during the charging cycle since it cannot add charge to a cell, and therefore it is of no benefit during discharge. Figure 6 shows one of the PEQ control boards, including the LTC6804 and the PEQ cell discharge resistors. Figure 7 shows one of the AEQ control boards, each of which includes 3 AEQ units.

Figure 6.
PEQ control board including LTC6804 controller and 12 PEQ cell discharge resistors.

Figure 7.
AEQ control board with 3 AEQ units.
The BEQ and PEQ systems were tested by performing several battery charge/discharge cycles with each system. Charge current was set at 12.5 Adc using a constant current charger. Discharge current was initially set at about 12 Adc with a resistive load, but this gradually decreased as the battery discharged. For each test cycle, the battery was initially charged until the highest cell voltage in the pack reached 4.0 Vdc and then discharged until the lowest cell reached 2.8 Vdc. As with all PEQs, power losses and heating were a concern, so the PEQ current was limited to about 0.625 Adc for a cell voltage close to 3.7 Vdc, and the PEQ unit dissipation was about 2.3 W at this point. Naturally, this changed slightly with cell voltage.
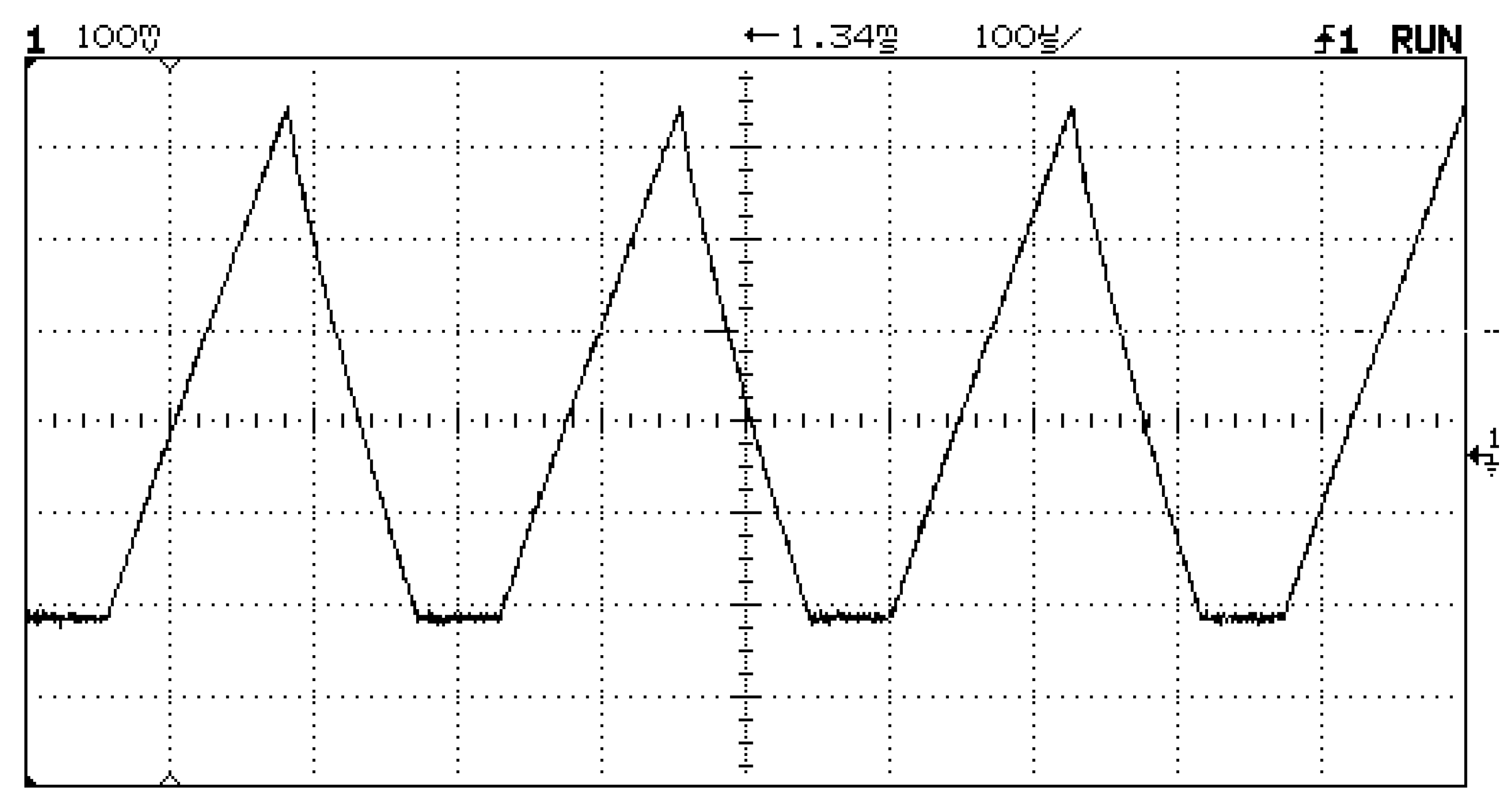
To minimize switching losses in the prototype, the AEQ used a rather low switching frequency of 3.64 kHz, but a higher frequency could be used to reduce the size and cost of the inductors. Measurements and EQU settings were performed every 4 s. At section voltages close to 14.8 Vdc, the DC equalization current flowing from a section was about 2.54 Adc, and the current into the adjacent section was about 1.94 Adc, indicating an efficiency of about 76%. These DC currents were determined from the triangular waveform of the inductor current. This current is not continuous but is switched on or off by the AEQ Controller as required for balancing. Improved circuit design and layout might be able to increase the efficiency, and this is currently under study. One possibility might be to replace the molypermalloy cores in the inductors with a lower loss material. A series of charge/discharge cycles were performed as follows. In each set, the battery was first charged and then discharged using the BEQ, and this procedure was then repeated using the PEQ. Figure 8 shows the inductor current waveform for one of the AEQ units.
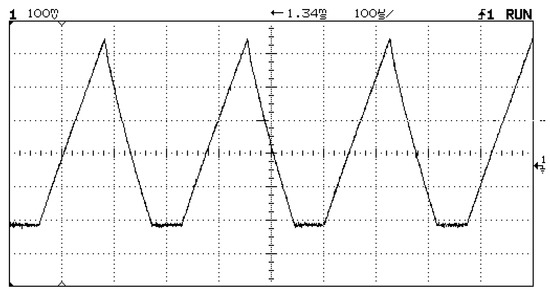
Figure 8.
Inductor current for one of the AEQ units. Vertical: 2 Amps/div, Horizontal: 100 us/div.
Results for a typical test cycle for the PEQ and the BEQ using 24 GAIA cells are shown in Table 1.

Table 1.
Discharge data with 24 GAIA cells.
These results indicate the BEQ increased the capacity by 12%, indicating the pack had a moderate level of cell capacity imbalance. Although it only provides an approximate analysis, it is interesting to compare the calculations from Equation (6) with the results of this test. Table 1 indicates the capacity for the PEQ test was 19.25 Ah, which is also assumed to be that of the weakest cell in the pack. The BEQ test produced 21.57 Ah which is approximately the average of the weak cell capacity of each section. The previous example for 5 sections shows that the discharge Ah is just slightly less the average capacity for all the sections. Therefore, if Cavg is the average capacity the 5 best sections, we have the following approximation using the results for the BEQ test,
(5 × Cavg + 19.25)/6 = 21.57, and Cavg = 22.03 Ah.
Measured average efficiency, n = 0.76; average discharge current, Id = 11.3 Adc. Using this data in Equation (6),
| required maximum Ieq = I1 = 1.37 Adc, |
| discharge time = 1.876 h., |
| discharge capacity = 21.2 Ah. |
This calculated capacity compares quite well with the measured value of 21.57 Ah. In this case, the measured maximum Ieq of 2.54 Adc is large enough so that it can modulate on and off to provide the required average current for each cell, such as 1.37 Adc for I1.
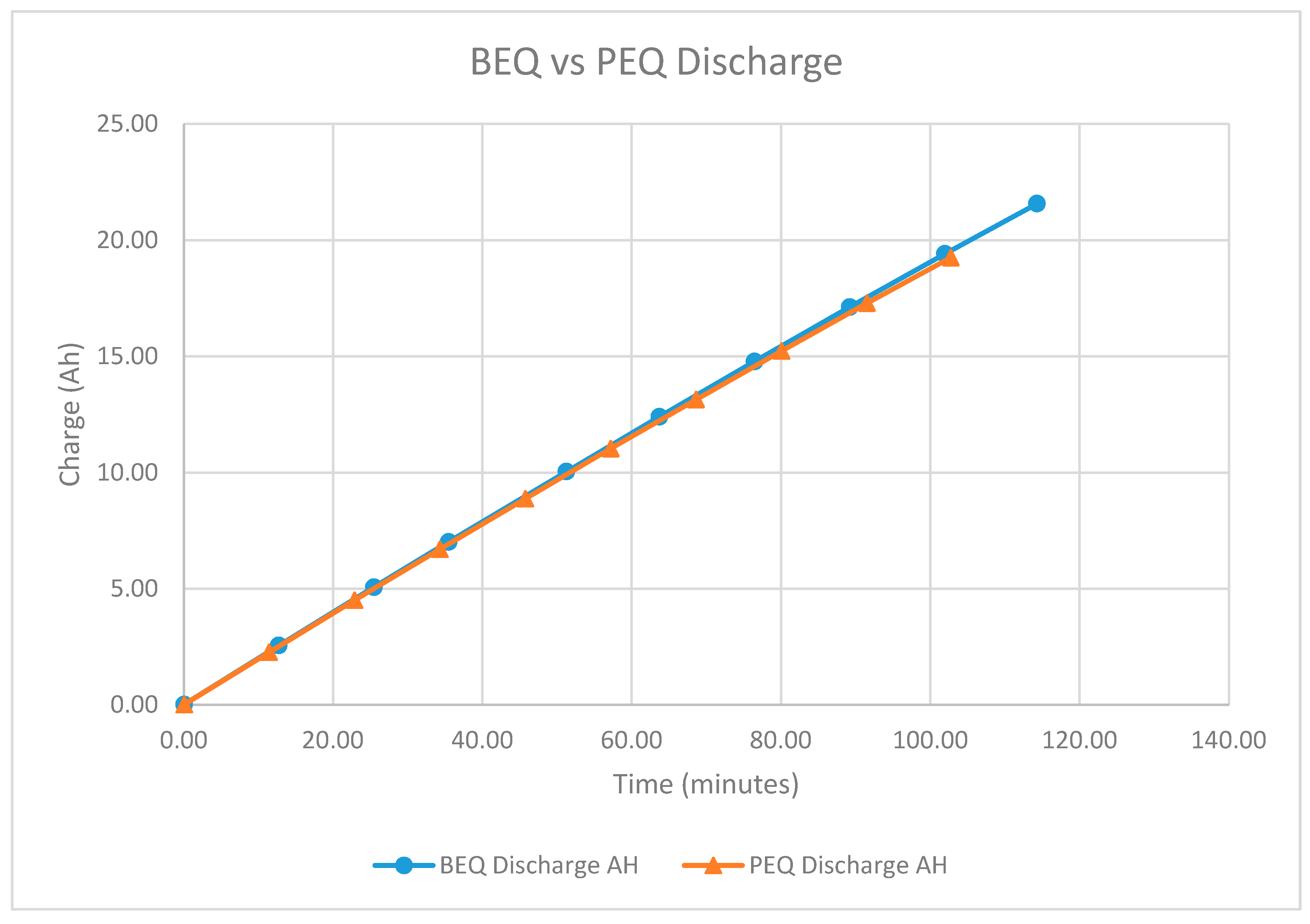
Figure 9 shows a plot of Ah vs. time for this set of PEQ and BEQ discharge cycles. As expected, the two plots are almost identical until the weak cell reaches the 2.8 Vdc limit for the PEQ test.
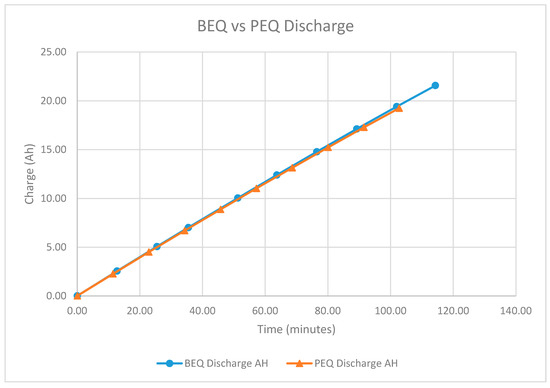
Figure 9.
Discharging Ah vs. Time for the BEQ and PEQ with 24 GAIA cells.
To simulate the effect of one dominant weak cell, GAIA cell #7 was replaced by a module of 8 Boston Power Swing 4400 cells connected in parallel. This module had an original rating of 8 × 4.4 = 35.2 Ah based on the same voltage range as the GAIA. This module had undergone several thousand charge/discharge cycles, but the exact number of cycles and its age were unknown. As with the GAIAs, the capacity of this module had decreased to a value that was much smaller than the original rating.
More cycles were performed for this case, and test results for three sets of data are shown in Table 2. These tests show that for this severe capacity imbalance caused by a dominant weak cell, the pack capacity was much smaller, but the BEQ still provided an average increase in discharge capacity of 31% over the PEQ. Using the results from tests PEQ #2 and BEQ #2, as before, it can be assumed that the PEQ capacity is the same as that of the weak cell, i.e., 7.99 Ah. If Equation (6) is used for this case, Ah1 = 7.99, and the other input data remains the same as the previous calculation. Solving Equation (6),
| required maximum Ieq = I1 = 8.22 Adc, |
| discharge time = 1.58 h., |
| discharge capacity = 17.86 Ah. |

Table 2.
Discharge data with 23 GAIA cells and 1 Boston Power cell.
This Ieq of 8.22 Adc is impractical for a battery of this size, and since it is much larger than the available 2.54 Adc, the BEQ cannot come close to the ideal capacity of 17.86 Ah, but it still provides a 31% average increase over the PEQ.
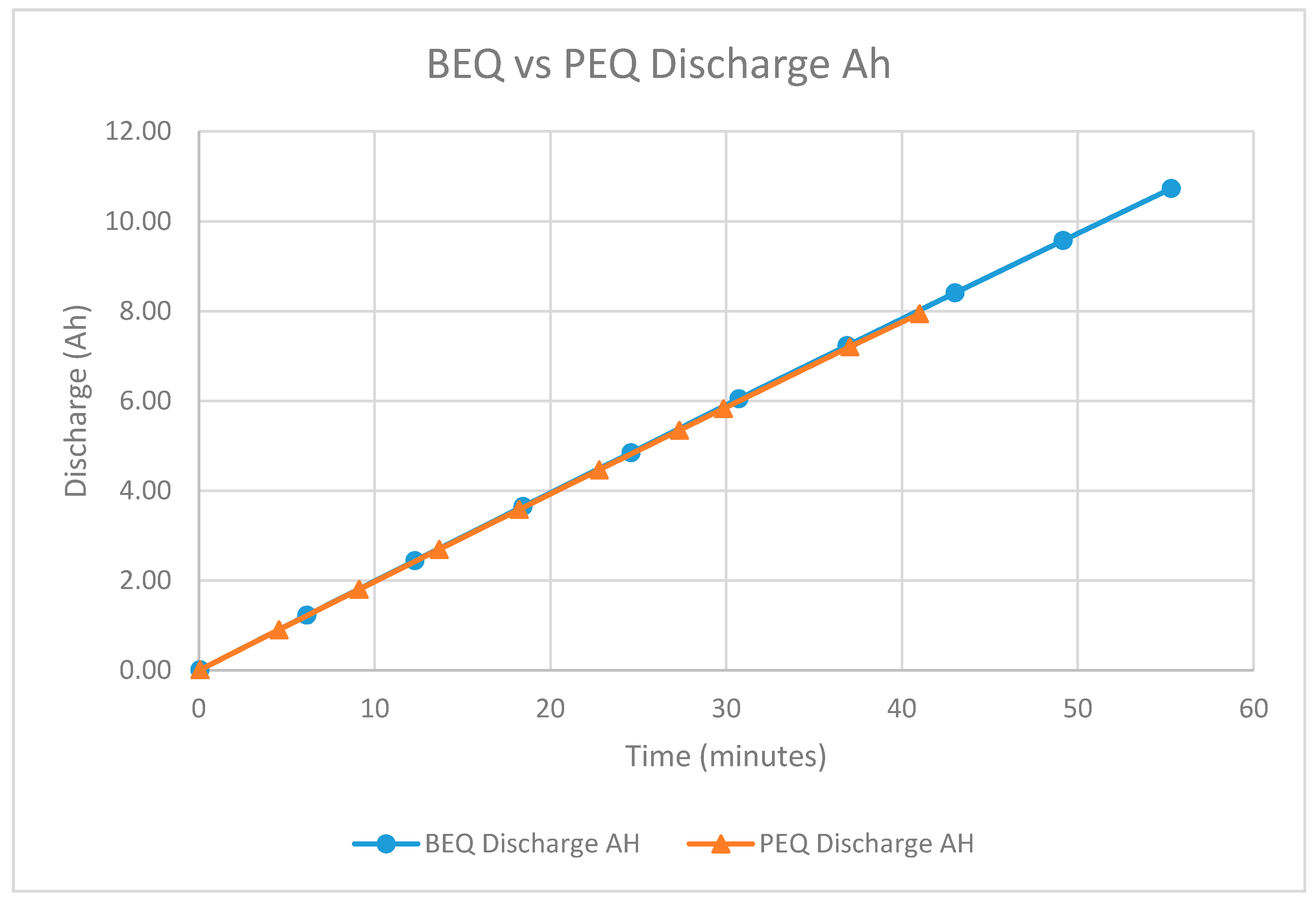
Figure 10 shows the Ah vs. time plots for two typical discharge cycles, PEQ #2 and BEQ #2. As expected, the two plots are almost identical until the weak cell reaches the 2.8 Vdc limit for the PEQ test.
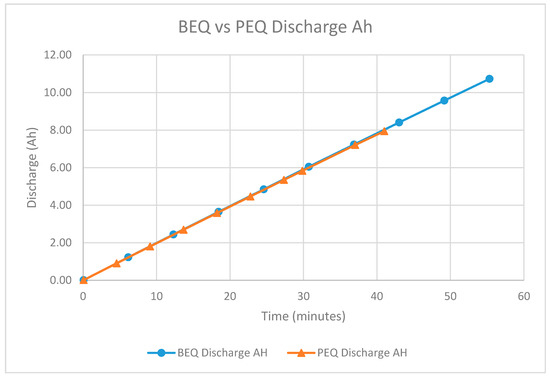
Figure 10.
Discharging Ah vs. Time for the BEQ and PEQ with 23 GAIA cells and 1 Boston Power cell.
4. Conclusions
PEQs have serious limitations which can be alleviated with AEQs, but at a cost that is usually considered excessive. The BEQ provides a good alternative since it provides much better performance than a PEQ with a relatively simple circuit and only a modest cost increase. There is no means to predict how the weak cells will be distributed in a battery pack, but a set of simple equations for a system with a single weak cell can be used to calculate the required equalization (EQU) current for a given set of specifications and provide design criteria. Similar equations also can be used to calculate the required EQU currents for any cell imbalance pattern. Experimental results on a test battery of 24 randomly selected GAIA cells indicated the discharge capacity with a BEQ had about a 12% increase above that with a PEQ. When one of the GAIA cells was replaced with a Boston Power cell with a much capacity, the BEQ still provided a 31% capacity increase above the PEQ.
Acknowledgments
This research was sponsored by grants from the Ohio I-Corps Program Grant #60050257 and the Ohio Third Frontier Technology Validation and Start-up Fund Grant TEC20160471.
Author Contributions
N. Mubenga and T. Stuart conceived and designed the experiments; N. Mubenga, Z. Linkous and T. Stuart performed the experiments; N. Mubenga and T. Stuart analyzed the data; N. Mubenga, Z. Linkous and T. Stuart designed and built the test equipment and analysis tools; N. Mubenga and T. Stuart wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Glossary
| A | Amperes |
| Ah | Ampere-hour |
| BEQ | Bilevel Equalizer |
| BMS | Battery Management System |
| ECU | Electronic Control Unit |
| EQU | Equalizer |
| FET | Field Effect Transistor |
| h | Hour |
| I | Current |
| LIB | Lithium Ion Battery |
| MCU | Microcontroller Unit |
| PEQ | Passive Equalizer |
| AEQ | Active Equalizer |
| SoC | State of Charge |
| t | Time |
| Vdc | DC Voltage |
References
- Andreas, D. Battery Management Systems for Large Lithium-Ion Battery Packs; Artech House: Boston, MA, USA, 2010; pp. 35–87. [Google Scholar]
- Lee, K.M.; Lee, S.W.; Choi, Y.G.; Kang, B. Active Balancing of Li-Ion Battery Cells Using Transformer as Energy Carrier. IEEE Trans. Ind. Electron. 2017, 64, 1251–1257. [Google Scholar] [CrossRef]
- Zhang, D.H.; Zhu, G.R.; He, S.J.; Qiu, S.; Ma, Y.; Wu, Q.M.; Chen, W. Balancing Control Strategy for Li-Ion Batteries String Based on Dynamic Balanced Point. Energies 2015, 8, 1830–1847. [Google Scholar] [CrossRef]
- Lee, K.M.; Chung, Y.C.; Sung, C.H.; Kang, B. Active Cell Balancing of Li-Ion Batteries Using LC Series Resonant Circuit. IEEE Trans. Ind. Electron. 2015, 62, 5491–5501. [Google Scholar] [CrossRef]
- Shang, Y.; Xia, B.; Lu, F.; Zhang, C.; Cui, N.; Mi, C.C. A Switched-Coupling-Capacitor Equalizer for Series-Connected Battery Strings. IEEE Trans. Power Electron. 2017, 32, 7694–7706. [Google Scholar] [CrossRef]
- Baronti, F.; Fantechi, G.; Roncella, R.; Saletti, R. High-Efficiency Digitally Controlled Charge Equalizer for Series-Connected Cells Based on Switching Converter and Super-Capacitor. IEEE Trans. Ind. Inform. 2013, 9, 1139–1147. [Google Scholar] [CrossRef]
- Cadar, D.; Petreus, D.; Patarau, T.; Palaghita, N. Active Balancing Method for Battery Cell Equalization. Acta Tech. Napoc. Electron. Telecommun. 2010. Available online: http://users.utcluj.ro/~ATN/papers/ATN_2_2010_1.pdf (accessed on 2 July 2017).
- Lee, Y.; Jeon, S.; Lee, H.; Bae, S. Comparison on Cell Balancing Methods for Energy Storage applications. Indian J. Sci. Technol. 2016, 9, 2–7. [Google Scholar] [CrossRef]
- Einhorn, M.; Roessler, W.; Fleig, J. Improved performance of serially connected Li-ion batteries with active cell balancing in electric vehicles. IEEE Trans. Veh. Technol. 2011, 60, 2448–2457. [Google Scholar] [CrossRef]
- Brainard, G.I. Non-Dissipative Battery Charger Equalizer. U.S. Patent 5,479,083, 26 December 1995. [Google Scholar]
- Kutkut, N.H.; Divan, D.M.; Novotny, D.W. Charge equalization for series connected battery strings. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 562–568. [Google Scholar] [CrossRef]
- Kutkut, N.; Wiegman, H.; Divan, D.; Novotny, D. Design considerations for charge equalization of an electric vehicle battery system. In Proceedings of the IEEE 1995 Applied Power Electronics Conference, Dallas, TX, USA, 5–9 March 1995; pp. 96–103. [Google Scholar]
- Gottwald, T.; Ye, Z.; Stuart, T. Equalization of EV and HEV batteries with a ramp converter. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 307–312. [Google Scholar] [CrossRef]
- Pascual, C.; Krein, P.T. Switched capacitor system for automatic series battery equalization. In Proceedings of the IEEE 1997 Applied Power Electronics Conference and Exposition, Atlanta, GA, USA, 27 February 1997; pp. 848–854. [Google Scholar]
- Tang, M.; Stuart, T. A selective buck-boost equalizer for series battery packs. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 201–211. [Google Scholar] [CrossRef]
- Stuart, T.; Wang, X.; Fang, F.; Pina, J.; Handle, A. A Modular Battery Management System for HEVs; U.S. Department of Energy Report NREL/SR-540-30244; Department of Energy: Washington DC, USA, 2001.
- Hart, L. TMSI Battery Balancer. 2001. Available online: http://www.geocities.com/sorefeets/balancerland/ (accessed on 3 July 2017).
- Stuart, T.; Fang, F.; Wang, X.; Ashtiani, L.; Pesaran, A. A modular battery management system for HEVs. In Proceedings of the SAE 2002 Future Car Congress, Arlington, VA, USA, 15–17 July 2002. Paper No. 07FCC-422. [Google Scholar]
- Chatzakis, J.; Kalaitzakis, K.; Voulgaris, N.C.; Manias, S.N. Designing a new generalized battery management system. IEEE Trans. Ind. Electron. 2003, 50, 990–999. [Google Scholar] [CrossRef]
- Lee, Y.; Cheng, M. Intelligent control battery equalization for series connected lithium-ion battery strings. IEEE Trans. Ind. Electron. 2005, 52, 1297–1307. [Google Scholar] [CrossRef]
- Lee, Y.; Cheng, G. Quasi-resonant zero-current switching bidirectional converter for battery equalization applications. IEEE Trans. Power Electron. 2006, 21, 1213–1224. [Google Scholar] [CrossRef]
- Arai, Y.; Yamamoto, K. Method and Apparatus for Equalizing Secondary Cells. U.S. Patent 2006/0214636A1, 28 September 2006. [Google Scholar]
- Landrum, G.; Stuart, T.; Zhu, W. Fast Equalization for Large Lithium Ion Batteries. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 27–31. [Google Scholar]
- Baughman, A.C.; Ferdowsi, M. Double-Tiered Switched-Capacitor Battery Charge Equalization Technique. IEEE Trans. Ind. Electron. 2008, 55, 2277–2285. [Google Scholar] [CrossRef]
- Cassani, P.A.; Williamson, S.S. Feasibility Analysis of a Novel Cell Equalizer Topology for Plug-In Hybrid Electric Vehicle Energy Storage-Systems. IEEE Trans. Veh. Technol. 2009, 58, 3938–3946. [Google Scholar] [CrossRef]
- Gallardo-Lozano, J.; Romero-Cadaval, E.; Milanes-Montero, M.; Guerrero-Martinez, M. Battery Equalization Active Methods. J. Power Sources 2014, 246, 934–949. Available online: www.elsevier.com/locate/powsour (accessed on 21 September 2013). [CrossRef]
- LINEAR Technology. LTC3300-1 High Efficiency Bidirectional Multicell Battery Balancer; Linear Technology Corporation: Milipitas, CA, USA, 2013. [Google Scholar]
- EM1401EVM User’s Guide; Texas Instruments: Dallas, TX, USA, 2014.
- EM1401 Rev A2 Test Report: Revision: 1.1; Texas Instruments: Dallas, TX, USA, 2014.
- Stuart, T.A. A Bilevel Equalizer for Battery Cell Charge Management. U.S. Provisional Patent Application # 62/287,575, 27 January 2016. [Google Scholar]
- LINEAR Technology. LTC6804-1/LTC6804-2 Multicell Battery Monitors; Linear Technology Corporation: Milipitas, CA, USA, 2013. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).