Study on Factors for Accurate Open Circuit Voltage Characterizations in Mn-Type Li-Ion Batteries
Abstract
:1. Introduction
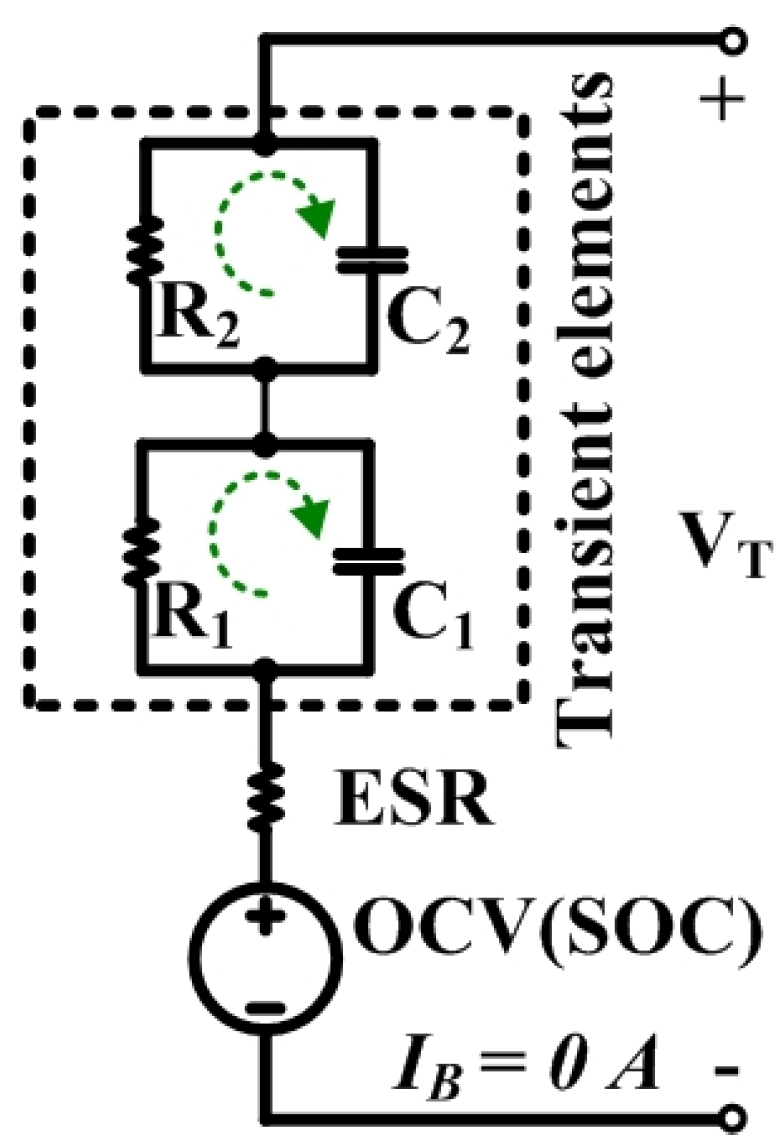
2. Open Circuit Voltage Determination for Li-Ion Battery
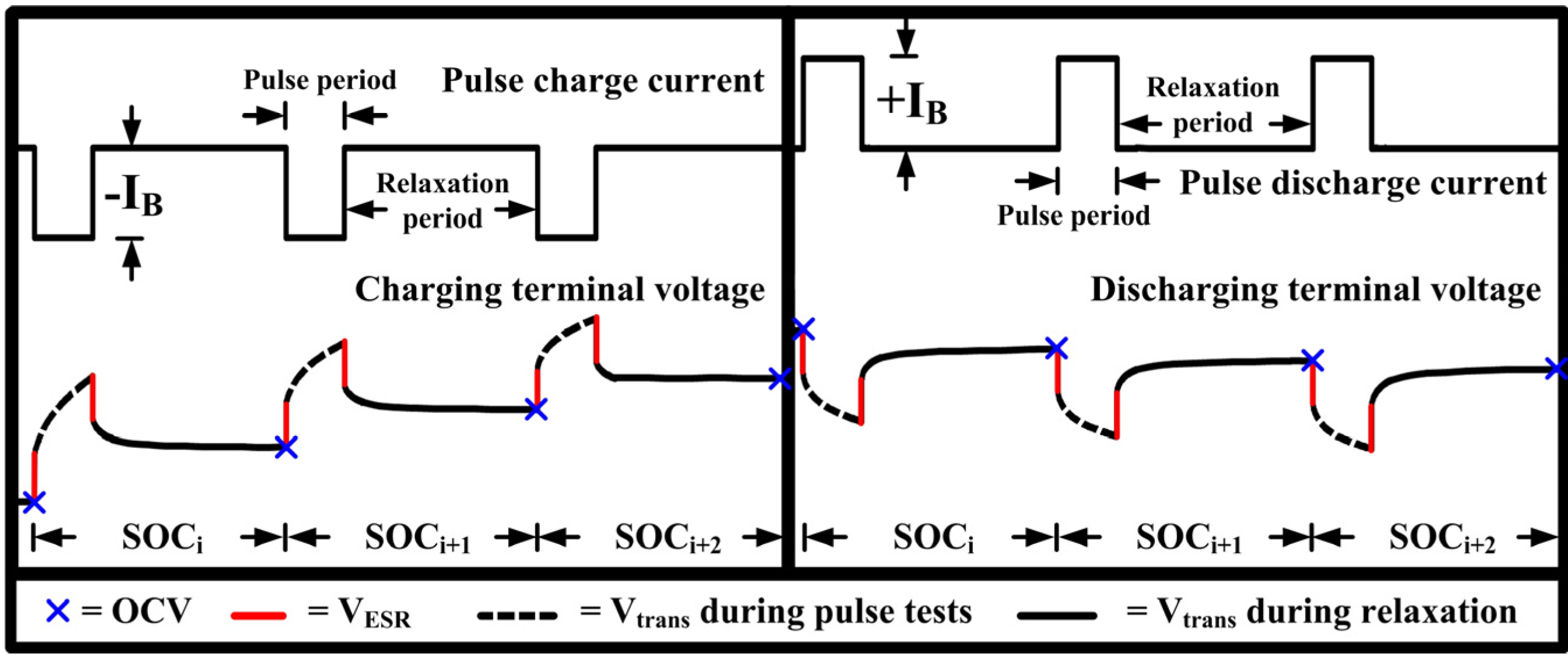
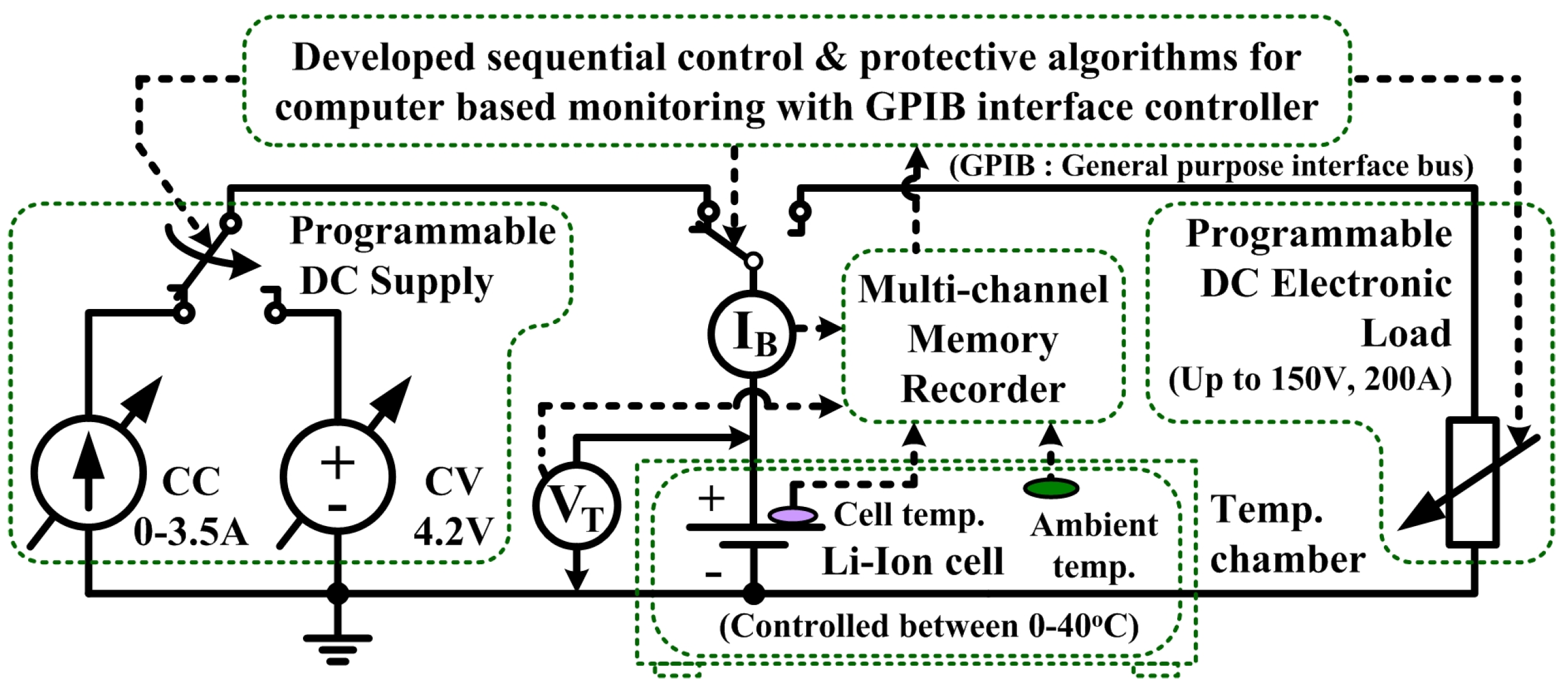
3. Open Circuit Voltage Characterization System
4. Discussion on the Factors for Accurate Open Circuit Voltage Determination
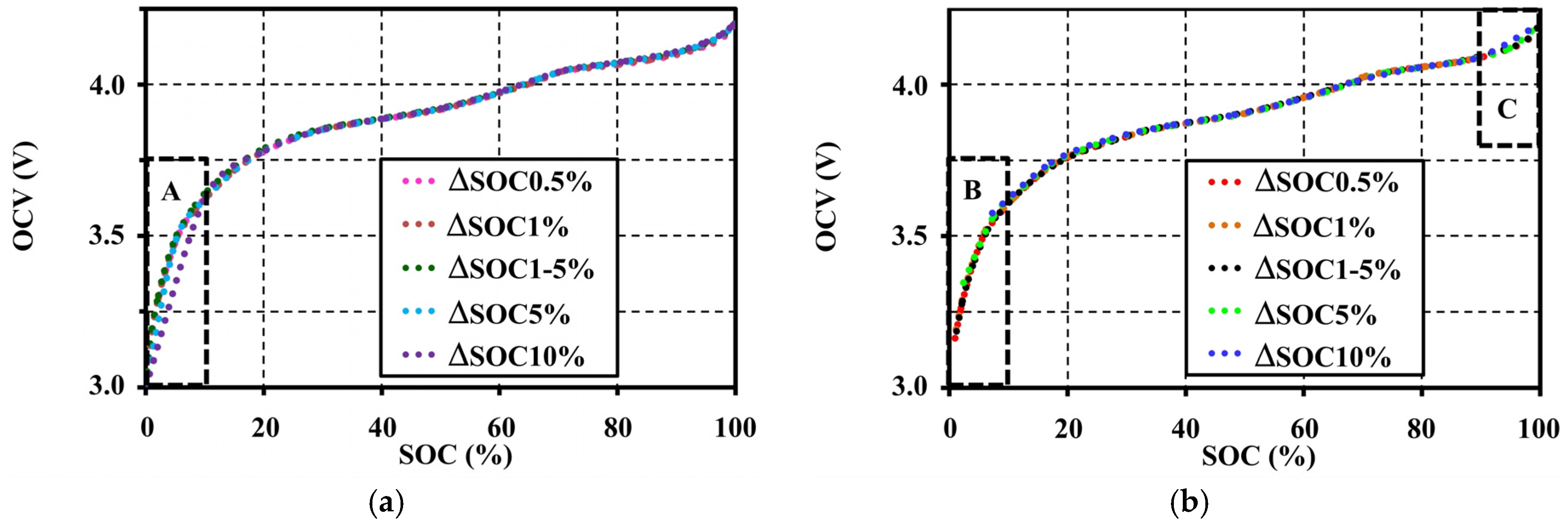
4.1. Effects of Step-Sizes during Pulse Tests on the Open Circuit Voltage Characteristic
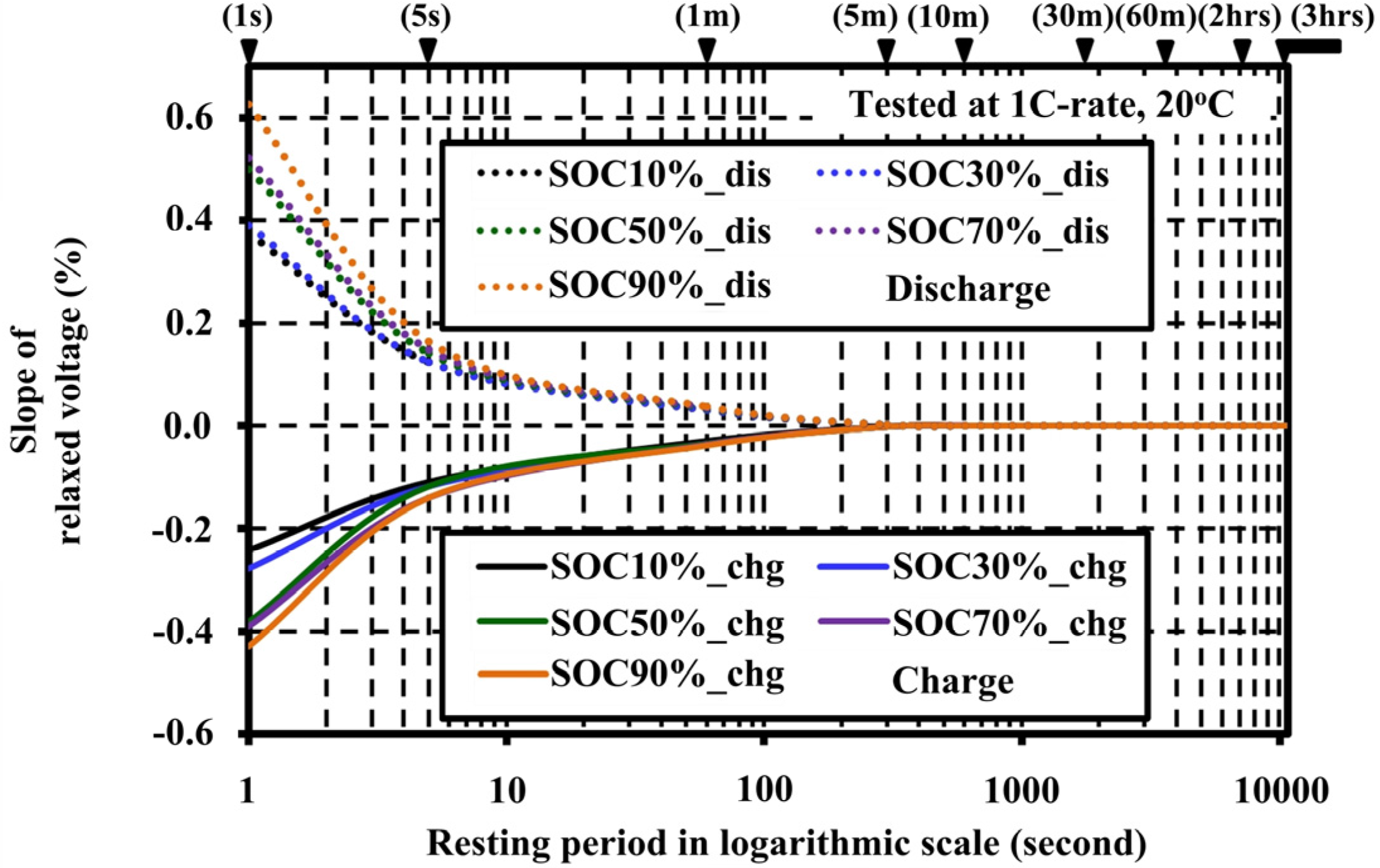
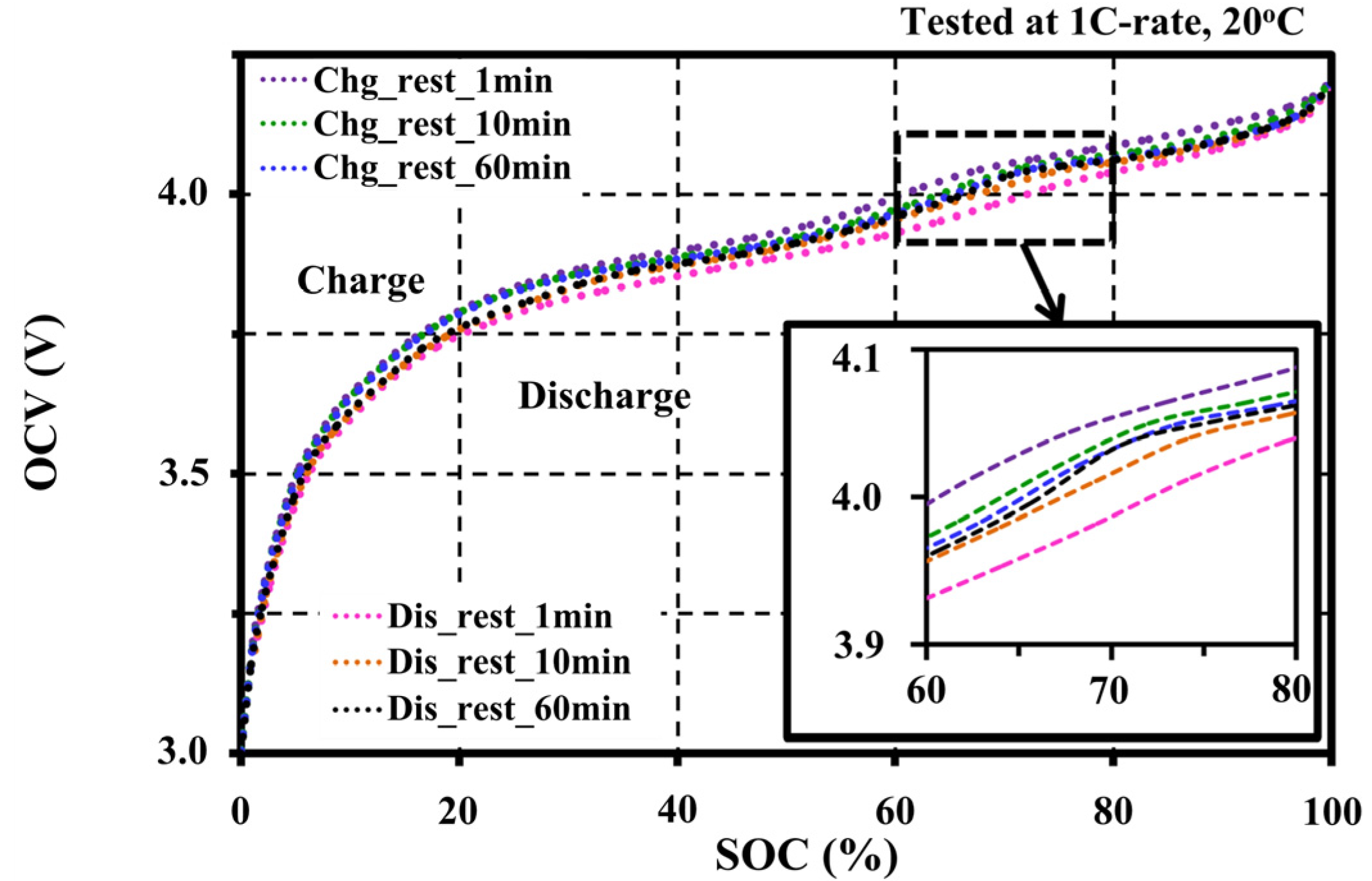
4.2. Effects of Resting Periods during Pulse Tests on the Open Circuit Voltage Characteristic
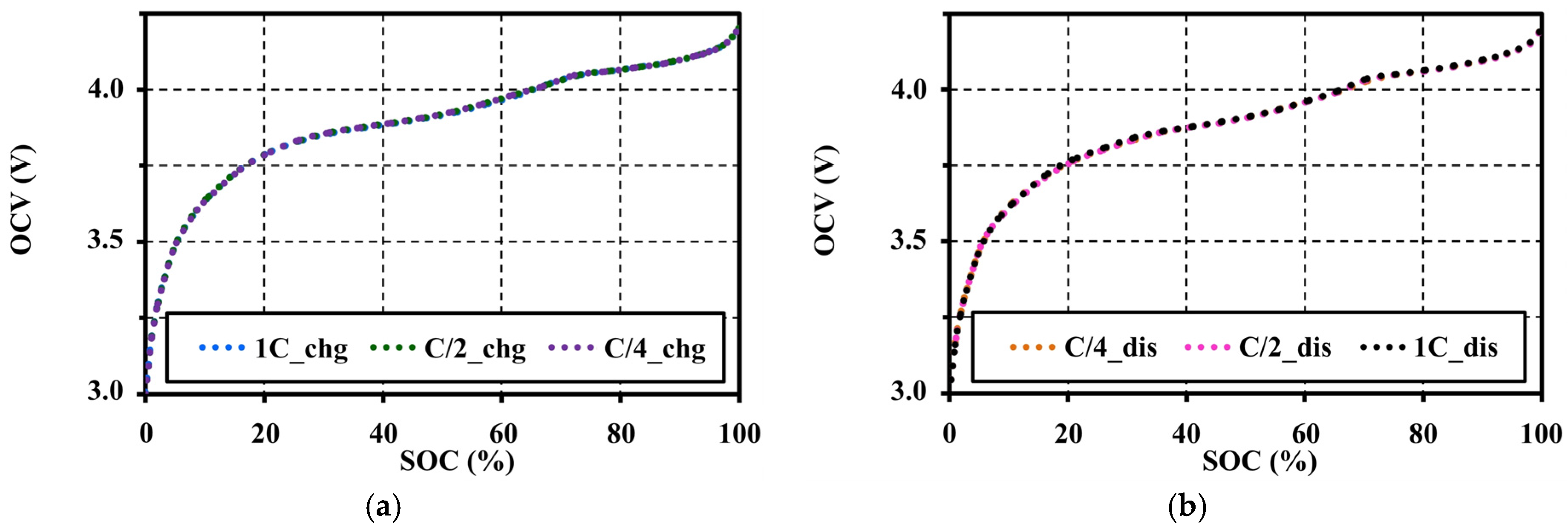
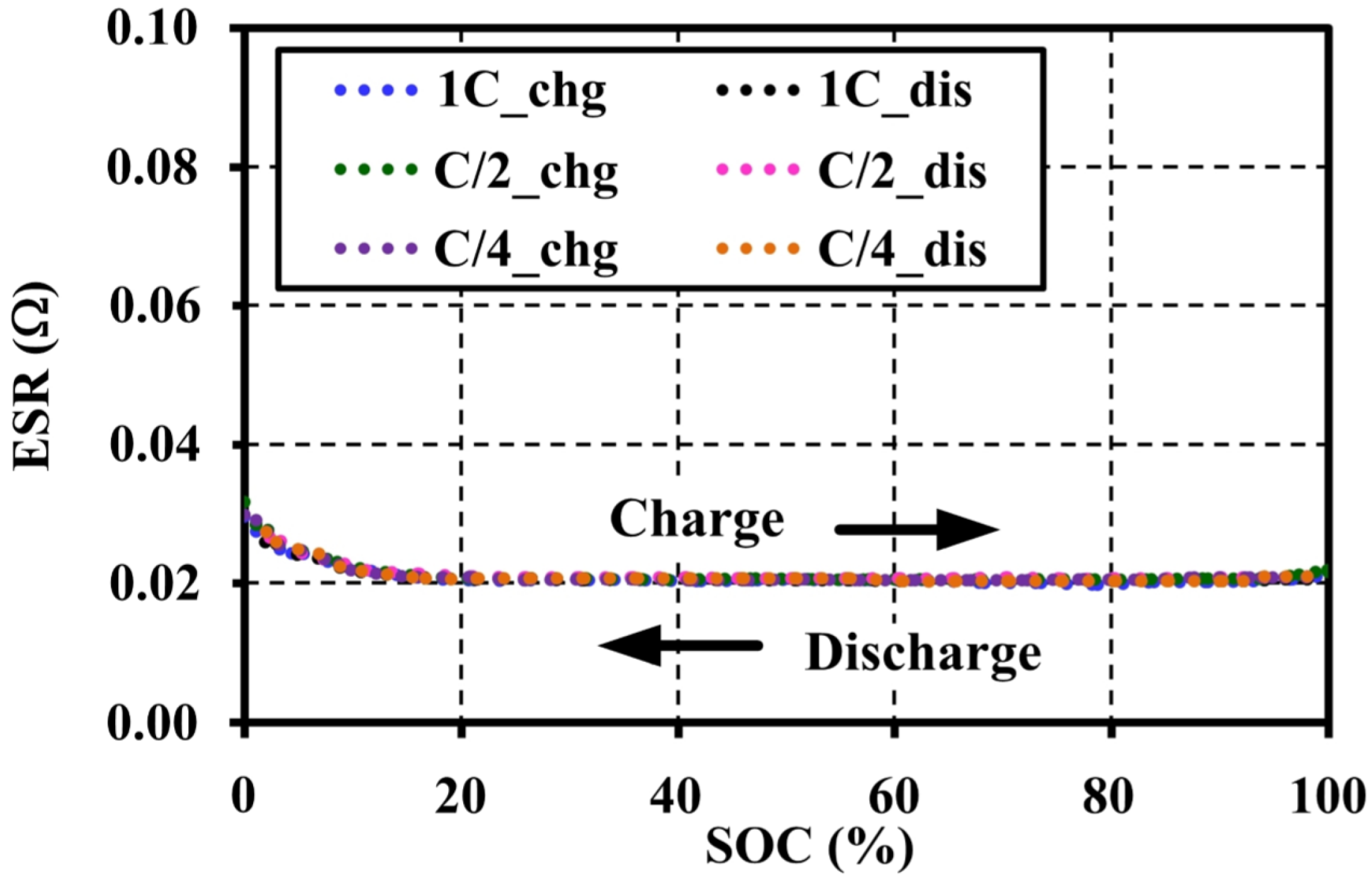
4.3. Effects of Current Amplitudes during Pulse Tests on the Open Circuit Voltage Characteristic
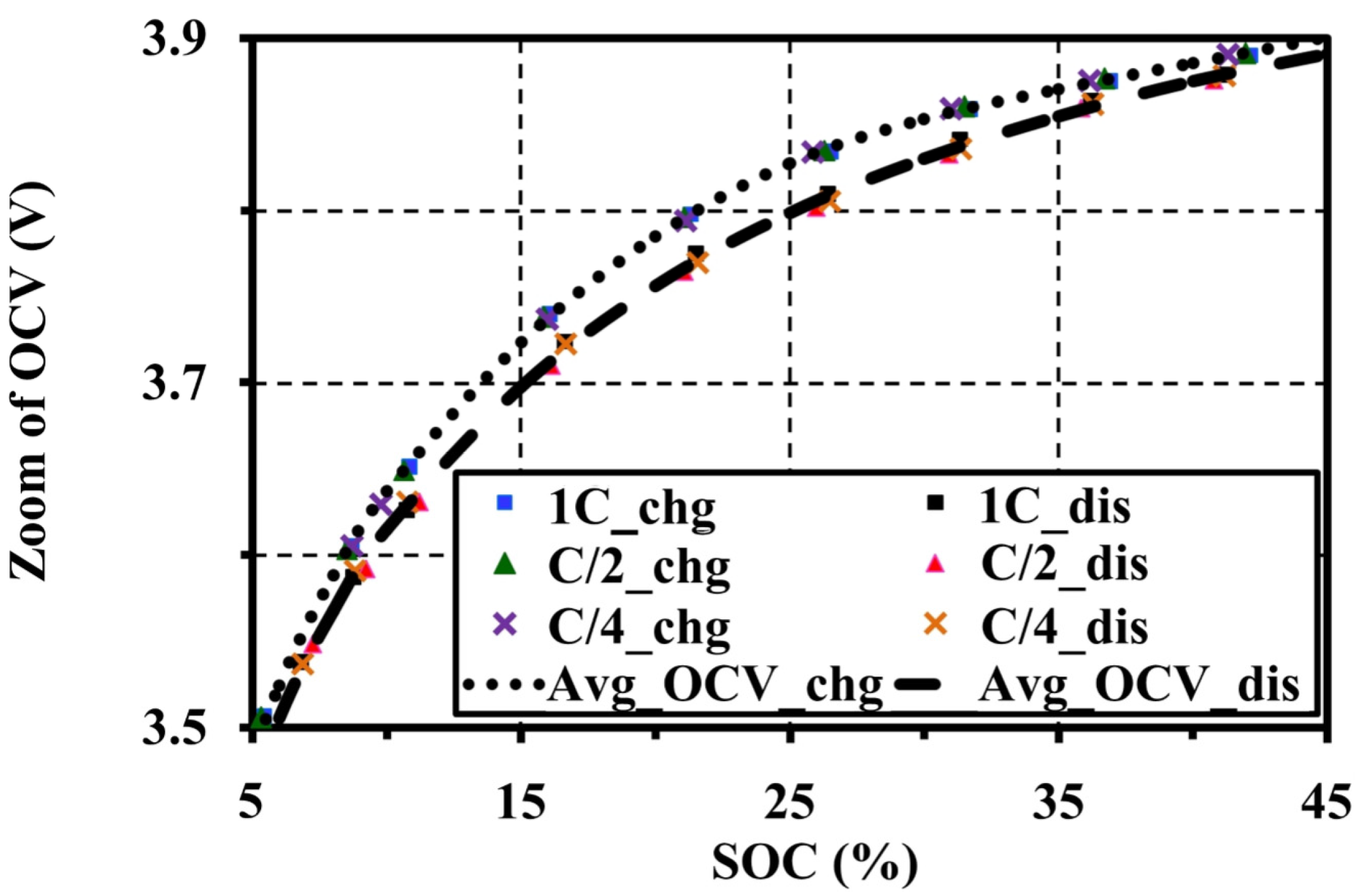
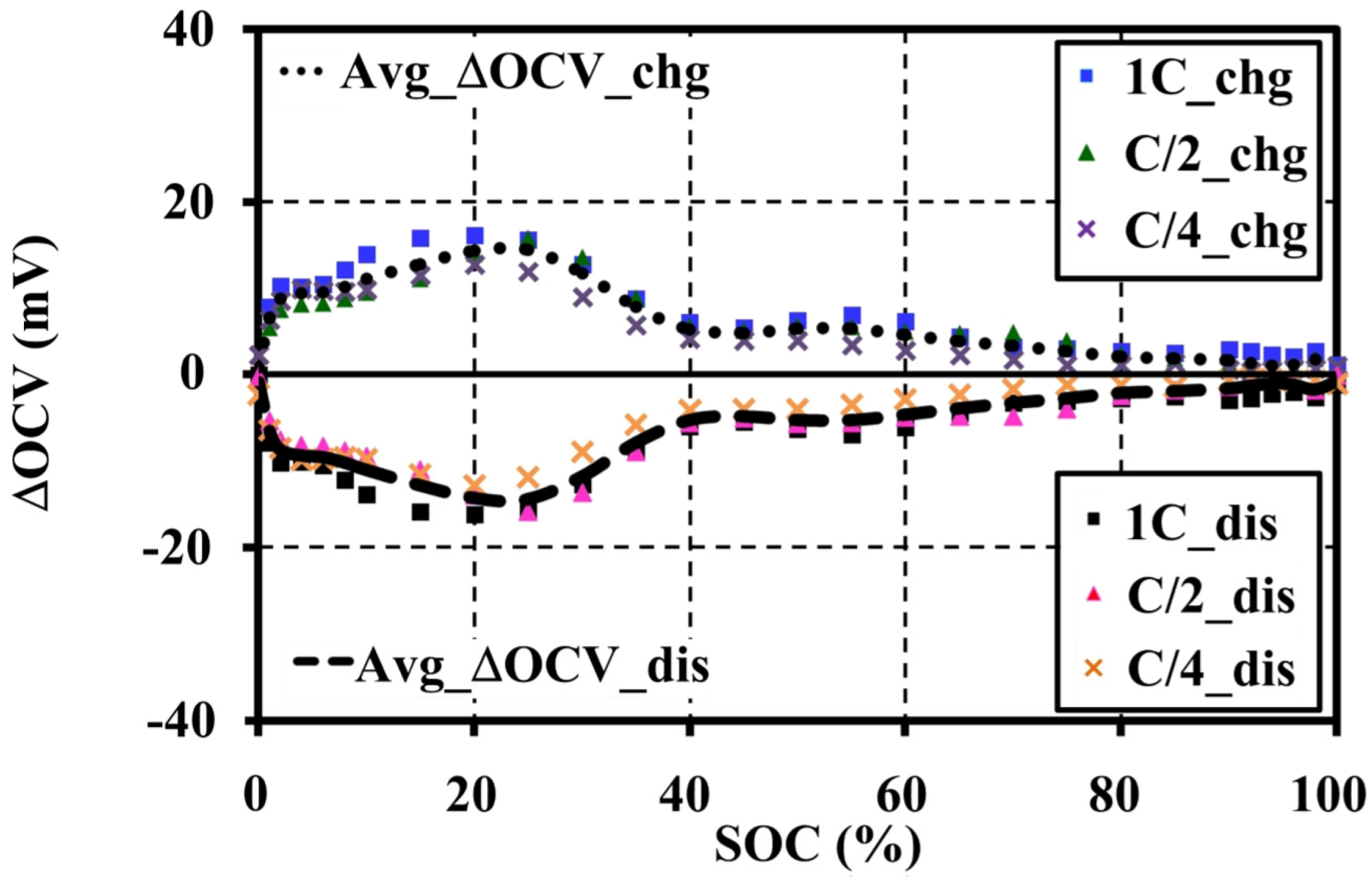
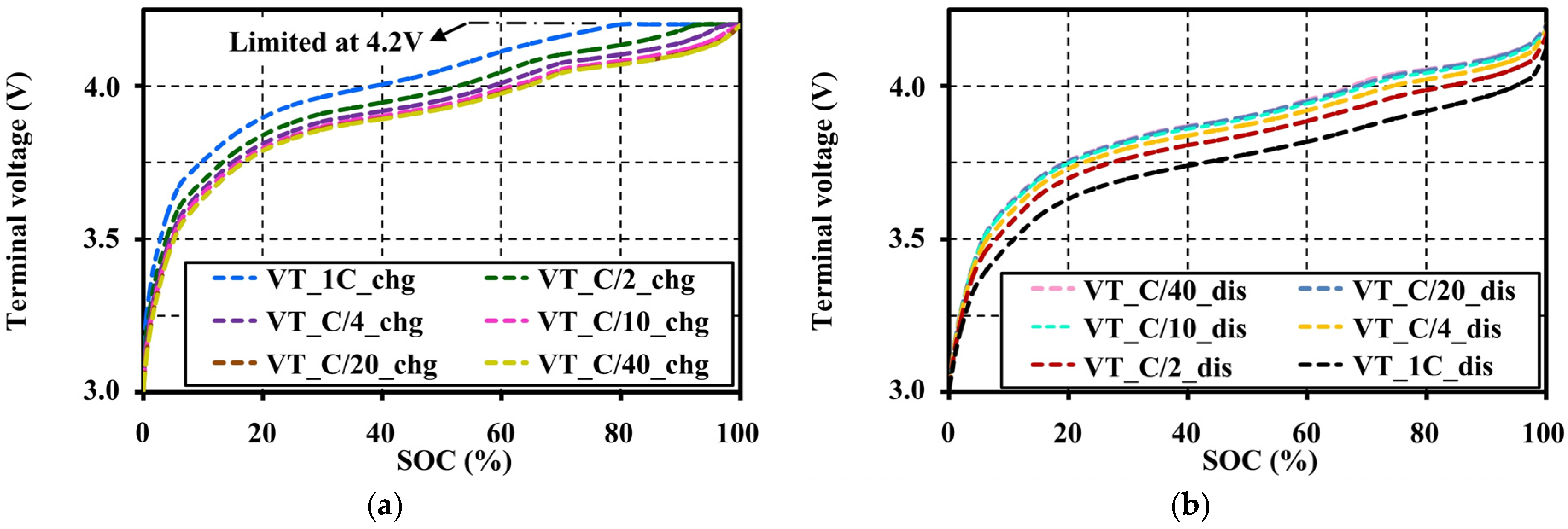
4.4. Effects of Current Amplitudes during Continuous Charge and Discharge Tests on the Open Circuit Voltage Approximation
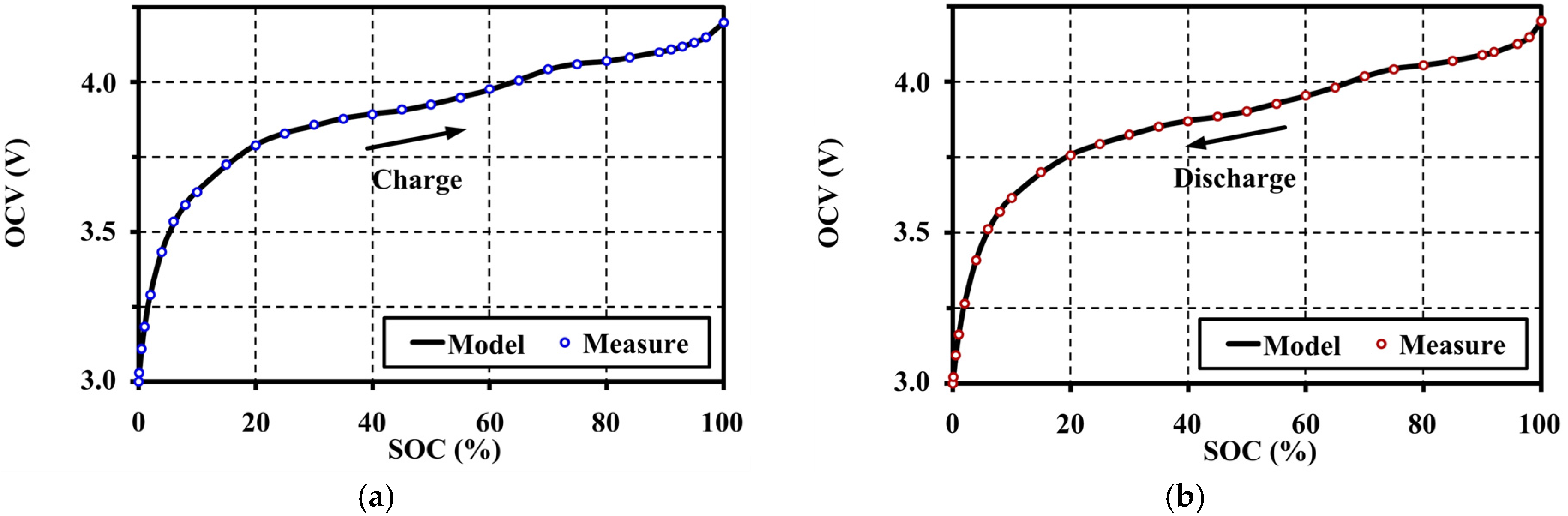
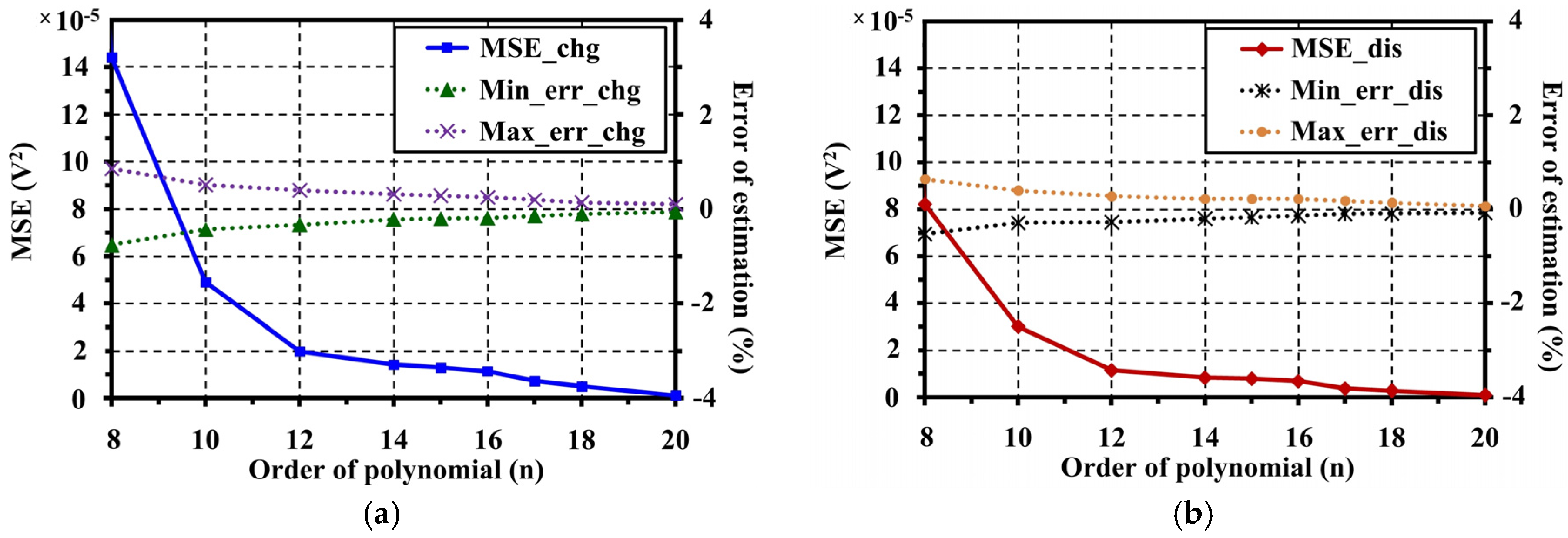
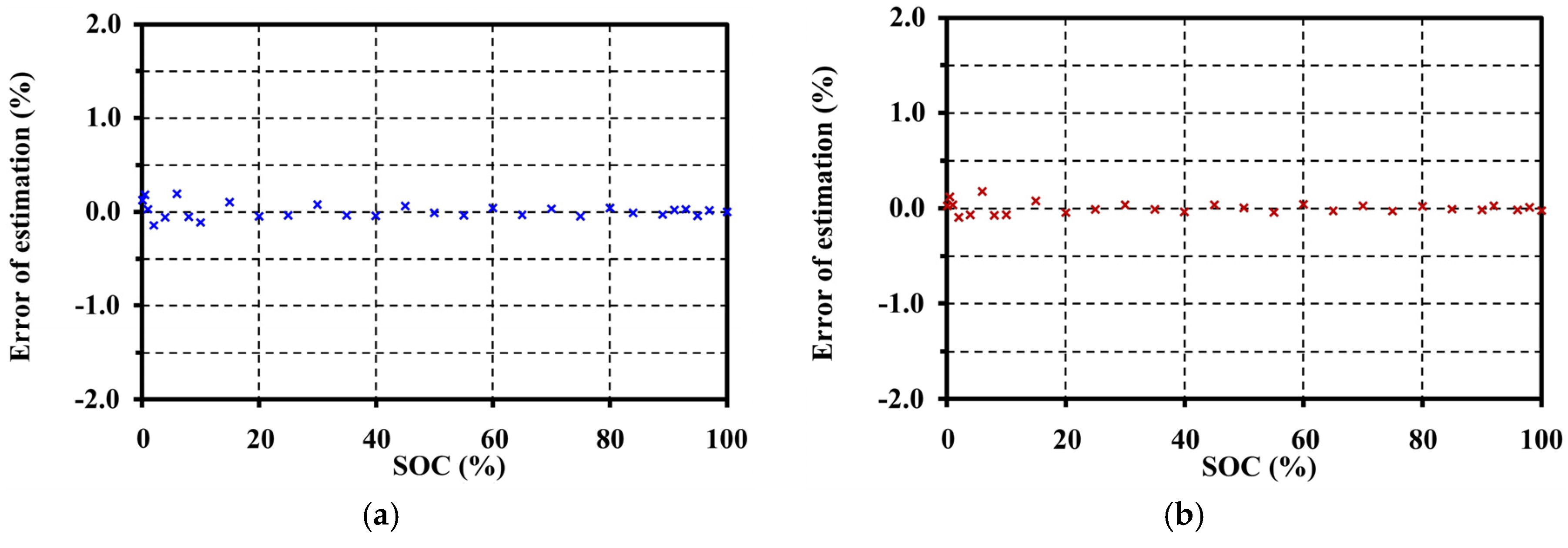
5. Open Circuit Voltage Modeling
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Pattipati, B.; Balasingam, B.; Avvari, G.V.; Pattipati, K.R.; Bar-Shalom, Y. Open circuit voltage characterization of lithium-ion batteries. J. Power Sources 2014, 269, 317–333. [Google Scholar] [CrossRef]
- Roscher, M.A.; Sauer, D.U. Dynamic electric behavior and open-circuit-voltage modeling of LiFePO4-based lithium ion secondary batteries. J. Power Sources 2011, 196, 331–336. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Lee, J.; Cho, B.H. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Roscher, M.A.; Assfalg, J.; Bohlen, O.S. Detection of utilizable capacity deterioration in battery systems. IEEE Trans. Veh. Technol. 2011, 60, 98–103. [Google Scholar] [CrossRef]
- Petzl, M.; Danzer, M.A. Advancements in OCV measurement and analysis for lithium-ion batteries. IEEE Trans. Energy Convers. 2013, 28, 675–681. [Google Scholar] [CrossRef]
- Codeca, F.; Savaresi, S.M.; Rizzoni, G. On Battery State of Charge Estimation: A New Mixed Algorithm. In Proceedings of the 17th IEEE International Conference on Control Applications, Part of 2008 IEEE Multi-conference on Systems and Control, San Antonio, TX, USA, 3–5 September 2008; pp. 102–107.
- Pattipati, B.; Sankavaram, C.; Pattipati, K.R. System identification and estimation framework for pivotal automotive BMS characteristics. IEEE Trans. Syst. Man Cybern.-Part C Appl. Rev. 2011, 41, 869–884. [Google Scholar] [CrossRef]
- Somakettarin, N.; Funaki, T. An Experimental Study on Modeling of Transient Response and Parameters Identification for Mn-Type Li-Ion Battery with Temperature Dependency. In Proceedings of the International Conference on Renewable Energy Research and Application (ICRERA), Milwaukee, WI, USA, 19–22 October 2014; pp. 804–809.
- Julien, C.M.; Mauger, A.; Zaghib, K.; Groult, H. Comparative issues of cathode materials for Li-ion batteries. Inorganics 2014, 2, 132–154. [Google Scholar] [CrossRef]
- Kim, D.K.; Muralidharan, P.; Lee, H.W.; Ruffo, R.; Yang, Y.; Chan, C.K.; Peng, H.; Huggins, R.A.; Cui, Y. Spinel LiMn2O4 nanorods as Lithium ion battery cathodes. Nano Lett. Am. Chem. Soc. 2008, 8, 3948–3952. [Google Scholar] [CrossRef] [PubMed]
- Patil, A.; Patil, V.; Shin, D.W.; Choi, J.W.; Paik, D.S.; Yoon, S.J. Review issue and challenges facing rechargeable thin film lithium batteries. Mater. Res. Bull. 2008, 43, 1913–1942. [Google Scholar] [CrossRef]
- Piao, T.; Parka, S.M.; Dohb, C.H.; Moon, S.I. Intercalation of Li-ion into graphite electrodes studied by AC impedance measurements. J. Electrochem. Soc. 1999, 146, 2794–2798. [Google Scholar] [CrossRef]
- Wang, J.; Purewal, J.; Liu, P.; Garner, J.H.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel-cobalt-manganese oxide + spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Sources 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Smith, A.J.; Burns, J.C.; Dahn, J.R. High-precision differential capacity analysis of LiMn2O4/graphite cells. Electrochem. Solid-State Lett. 2011, 14, A39–A41. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Aging of a commercial graphite/LiFePO4 cell. J. Electrochem. 2011, 158, A1123–A1135. [Google Scholar] [CrossRef]
- Weppner, W.; Huggins, R.A. Determination of the kinetic parameters of mixed-conducting electrodes and application to the system Li3Sb. J. Electrochem. Soc. 1977, 124, 1569–1578. [Google Scholar] [CrossRef]
- Bisquert, J. Nanostructured Energy Devices: Equilibrium Concepts and Kinetics, 1st ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2015; pp. 115–155. [Google Scholar]
- Roscher, M.A.; Bohlen, O.; Vetter, J. OCV hysteresis in Li-ion batteries including two-phase transition materials. Int. J. Electrochem. 2011, 2011. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H.; Sun, F. Robustness analysis of state-of-charge estimation methods for two types of Li-ion batteries. J. Power Sources 2012, 217, 209–219. [Google Scholar] [CrossRef]


| Description | Specification | Description | Charging | Discharging |
|---|---|---|---|---|
| Electrode/type | Spinel single cell | Operating voltage | 3.0 V | 4.2 V |
| Positive | Manganese (LiMn2O4) | Maximum current (C-rate) | 3.5 A (1C) | 20.0 A (5.7C) |
| Negative | Lithiated graphite (LiC6) | Operating temp. | 0–40 °C | −10–50 °C |
| Rated capacity | 3.5 Ah (Typical) | Cell dimension | 82 mm × 171 mm × 4.7 mm | |
| Voltage | 3.8 V (Nominal) | Weight | 100 g (Maximum) | |
| SOC Coefficient | Charge | Discharge | SOC Coefficient | Charge | Discharge |
|---|---|---|---|---|---|
| k0 | 3.0037 | 3.0016 | k9 | 1.0595 × 10−9 | 8.4261 × 10−10 |
| k1 | 2.3163 × 10−1 | 2.0082 × 10−1 | k10 | −2.2638 × 10−11 | −1.8003 × 10−11 |
| k2 | −6.5271 × 10−2 | −5.0440 × 10−2 | k11 | 3.6337 × 10−13 | 2.8847 × 10−13 |
| k3 | 1.4950 × 10−2 | 1.1287 × 10−2 | k12 | −4.3564 × 10−15 | −3.4474 × 10−15 |
| k4 | −2.3529 × 10−3 | −1.7962 × 10−3 | k13 | 3.8402 × 10−17 | 3.0257 × 10−17 |
| k5 | 2.5025 × 10−4 | 1.9382 × 10−4 | k14 | −2.4147 × 10−19 | −1.8926 × 10−19 |
| k6 | −1.8436 × 10−5 | −1.4444 × 10−5 | k15 | 1.0246 × 10−21 | 7.9827 × 10−22 |
| k7 | 9.6864 × 10−7 | 7.6498 × 10−7 | k16 | −2.6280 × 10−24 | −2.0344 × 10−24 |
| k8 | −3.7174 × 10−8 | −2.9500 × 10−8 | k17 | 3.0772 × 10−27 | 2.3659 × 10−27 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somakettarin, N.; Funaki, T. Study on Factors for Accurate Open Circuit Voltage Characterizations in Mn-Type Li-Ion Batteries. Batteries 2017, 3, 8. https://doi.org/10.3390/batteries3010008
Somakettarin N, Funaki T. Study on Factors for Accurate Open Circuit Voltage Characterizations in Mn-Type Li-Ion Batteries. Batteries. 2017; 3(1):8. https://doi.org/10.3390/batteries3010008
Chicago/Turabian StyleSomakettarin, Natthawuth, and Tsuyoshi Funaki. 2017. "Study on Factors for Accurate Open Circuit Voltage Characterizations in Mn-Type Li-Ion Batteries" Batteries 3, no. 1: 8. https://doi.org/10.3390/batteries3010008
APA StyleSomakettarin, N., & Funaki, T. (2017). Study on Factors for Accurate Open Circuit Voltage Characterizations in Mn-Type Li-Ion Batteries. Batteries, 3(1), 8. https://doi.org/10.3390/batteries3010008





