Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries
Abstract
:1. Introduction
2. Experimental Set-Up
3. Lithium-Ion Battery Characterization Methodology
3.1. Preconditioning Test
3.2. Relaxation Test
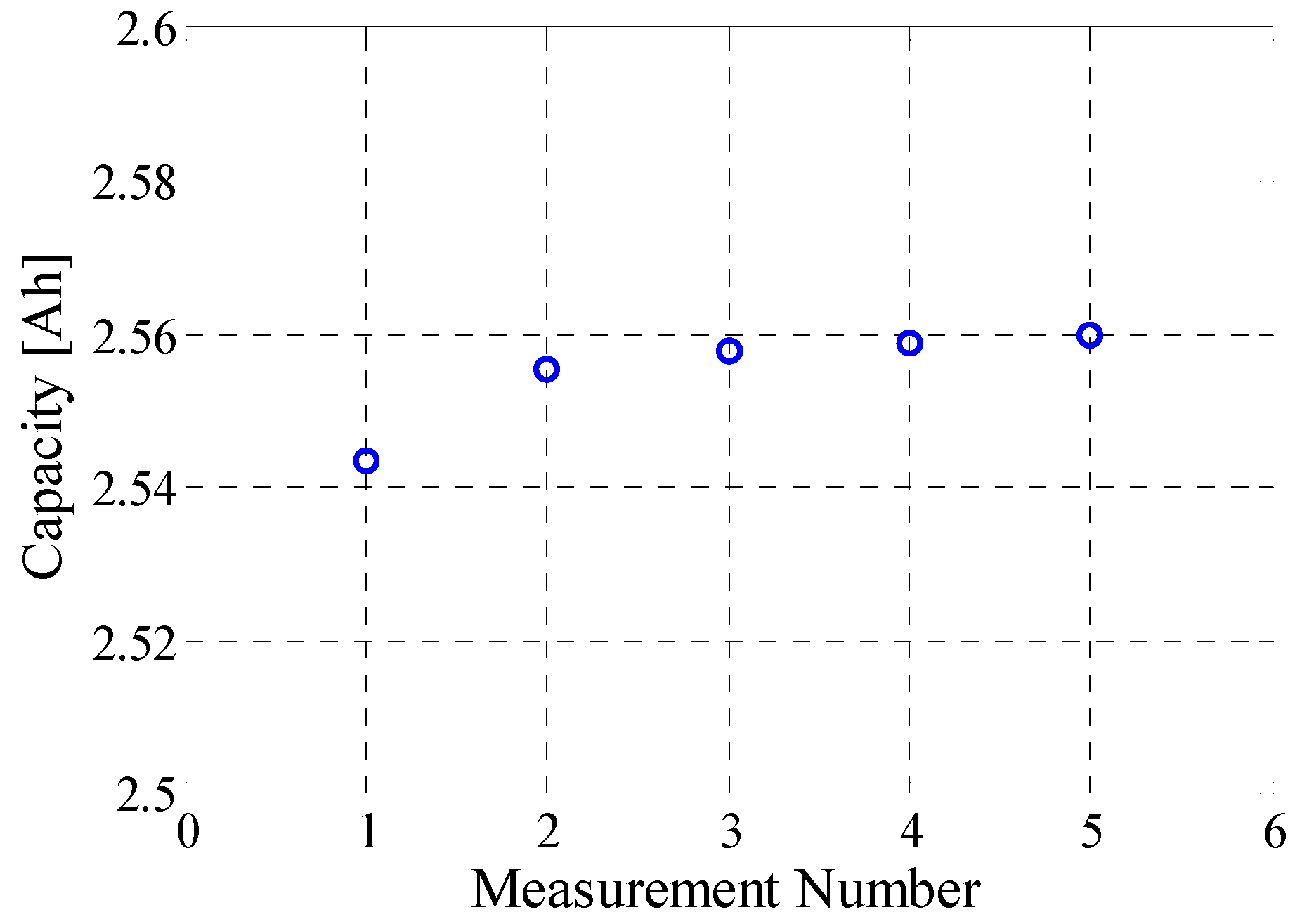
3.3. Capacity Test
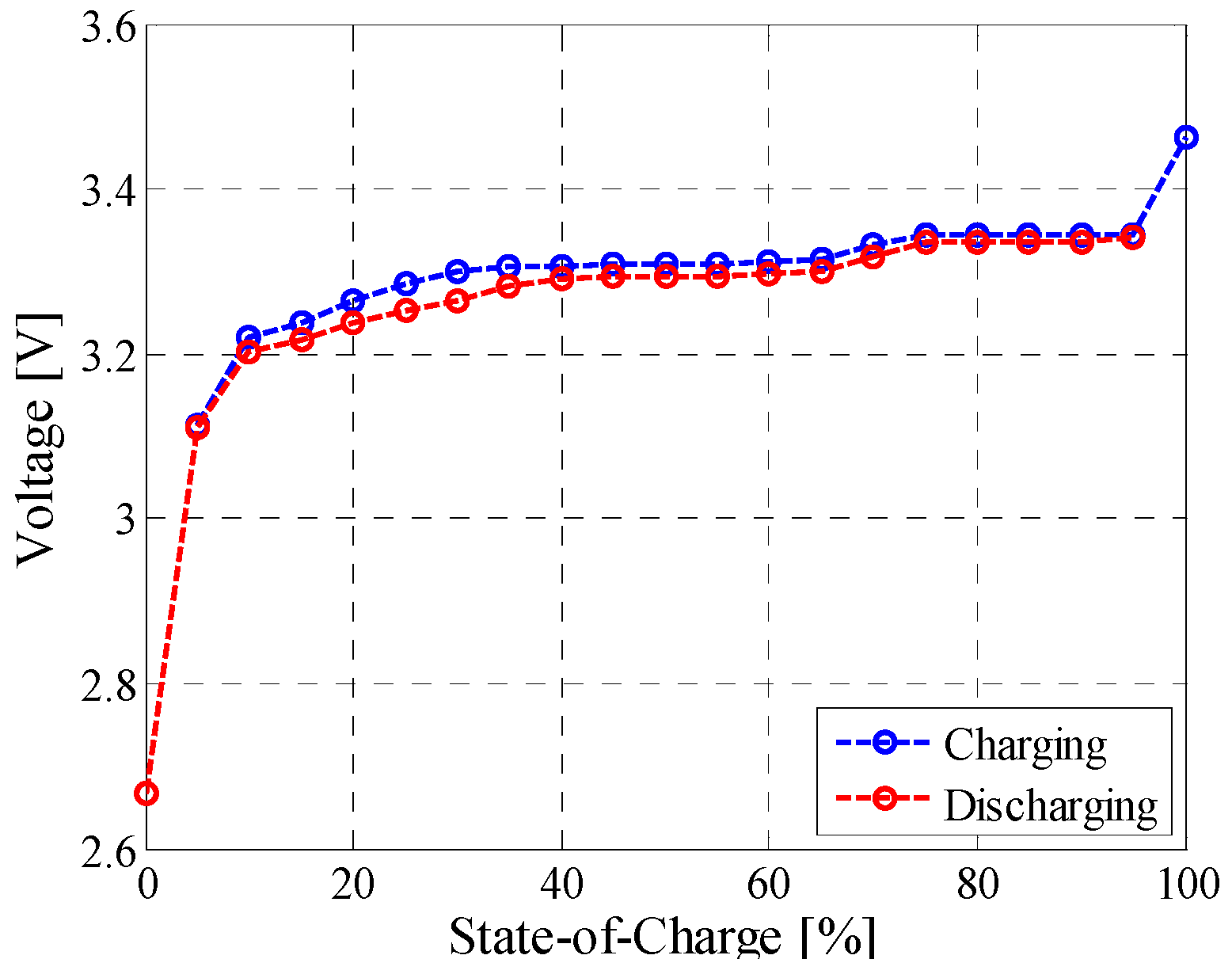
3.4. Open-Circuit Voltage versus State-of-Charge Test
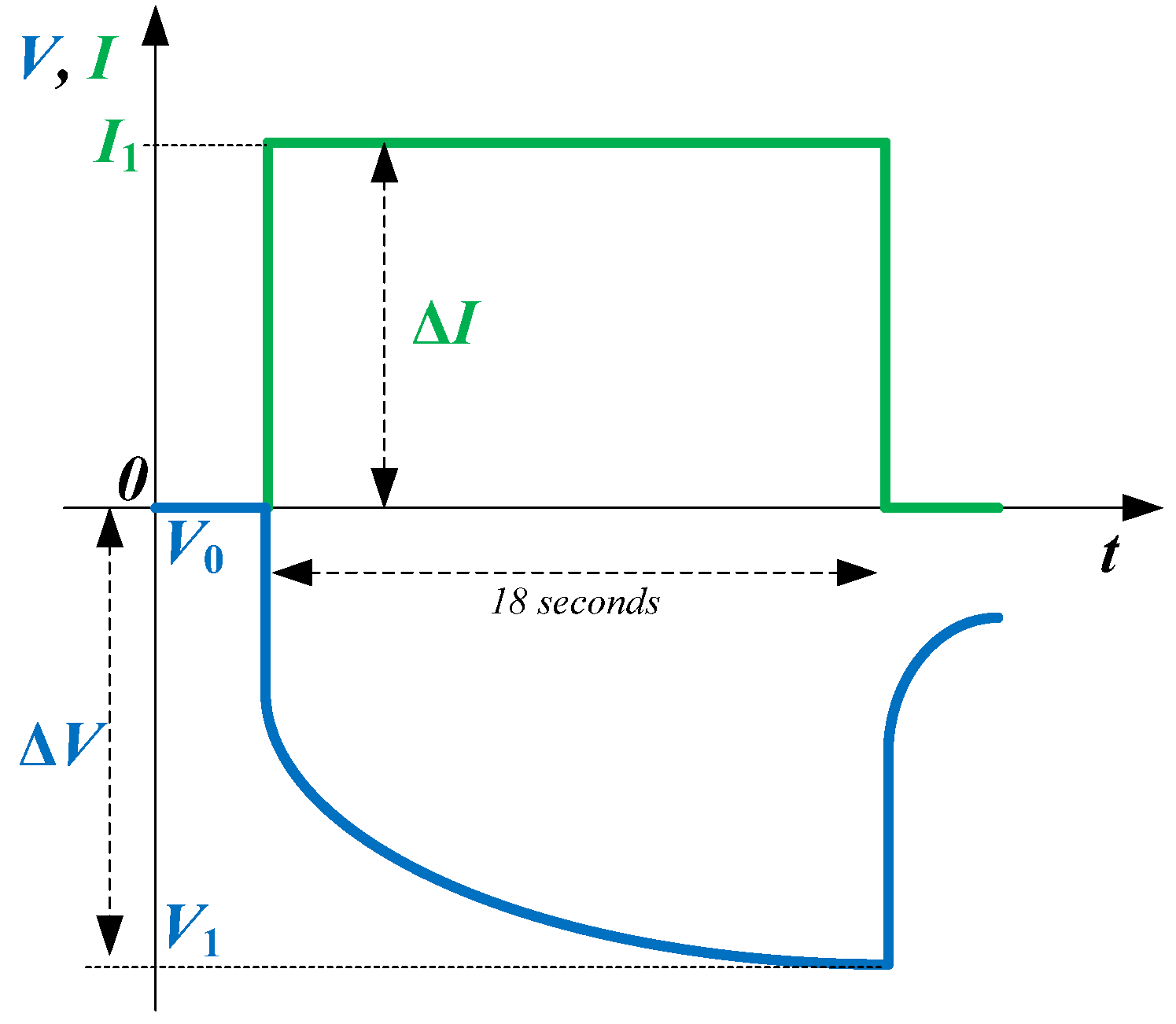
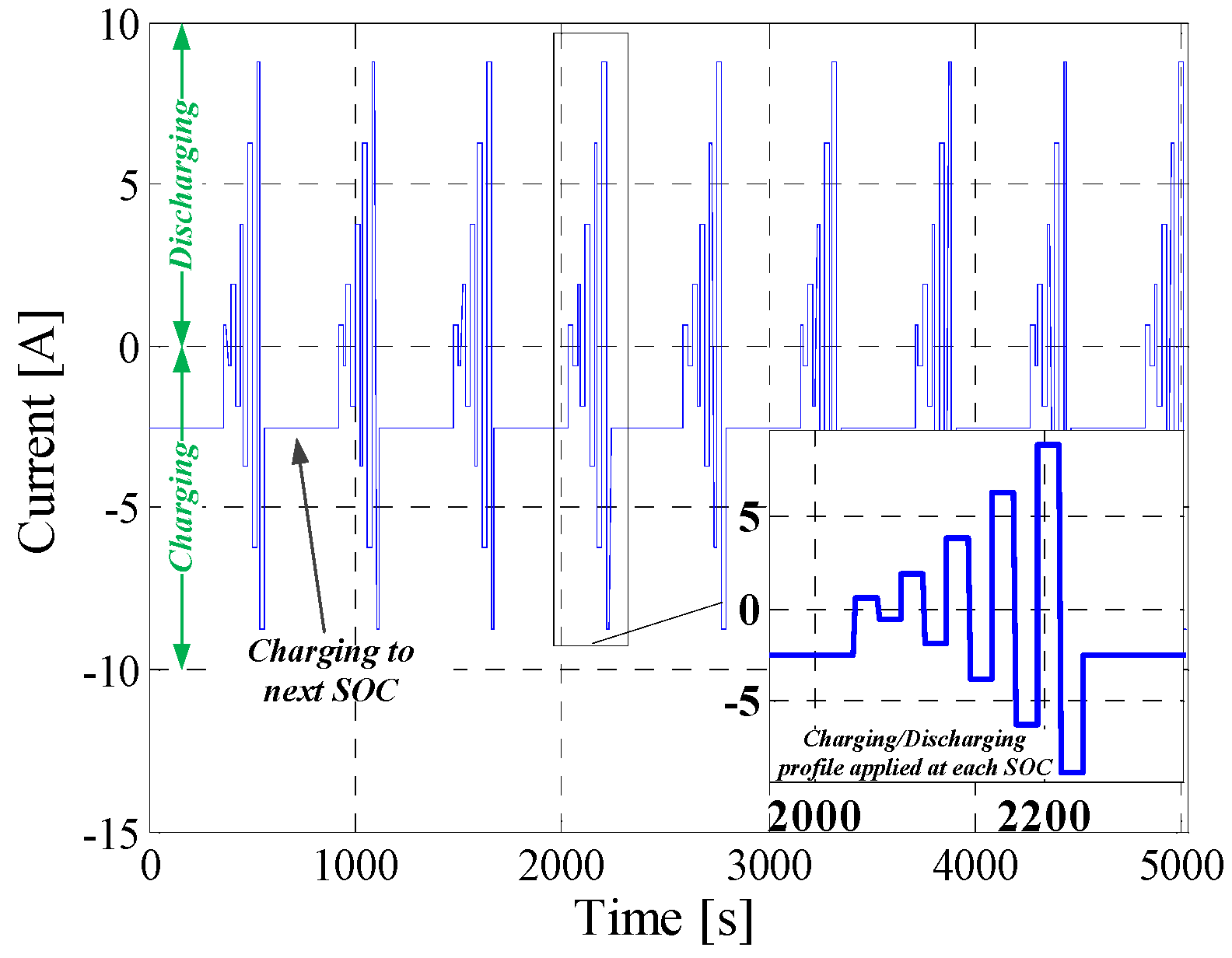
3.5. Hybrid Pulse Power Characterization Test
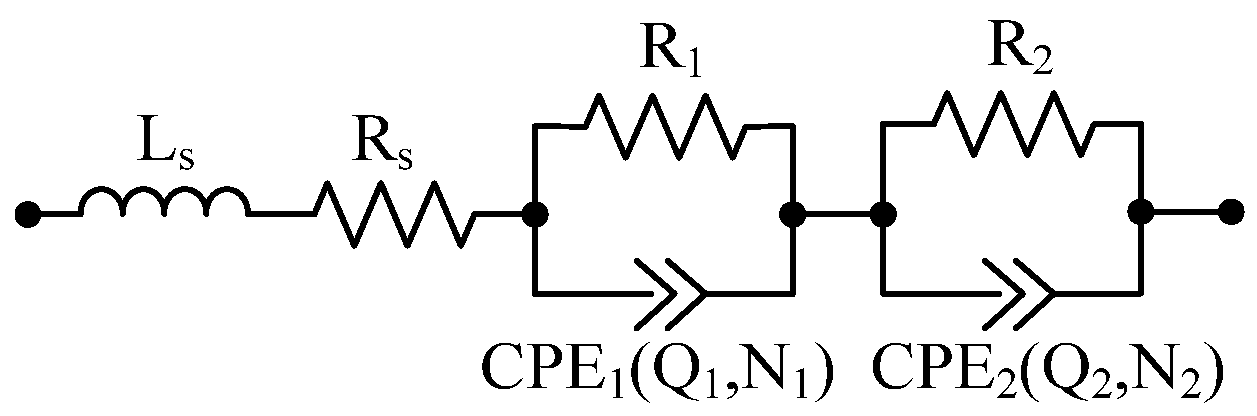
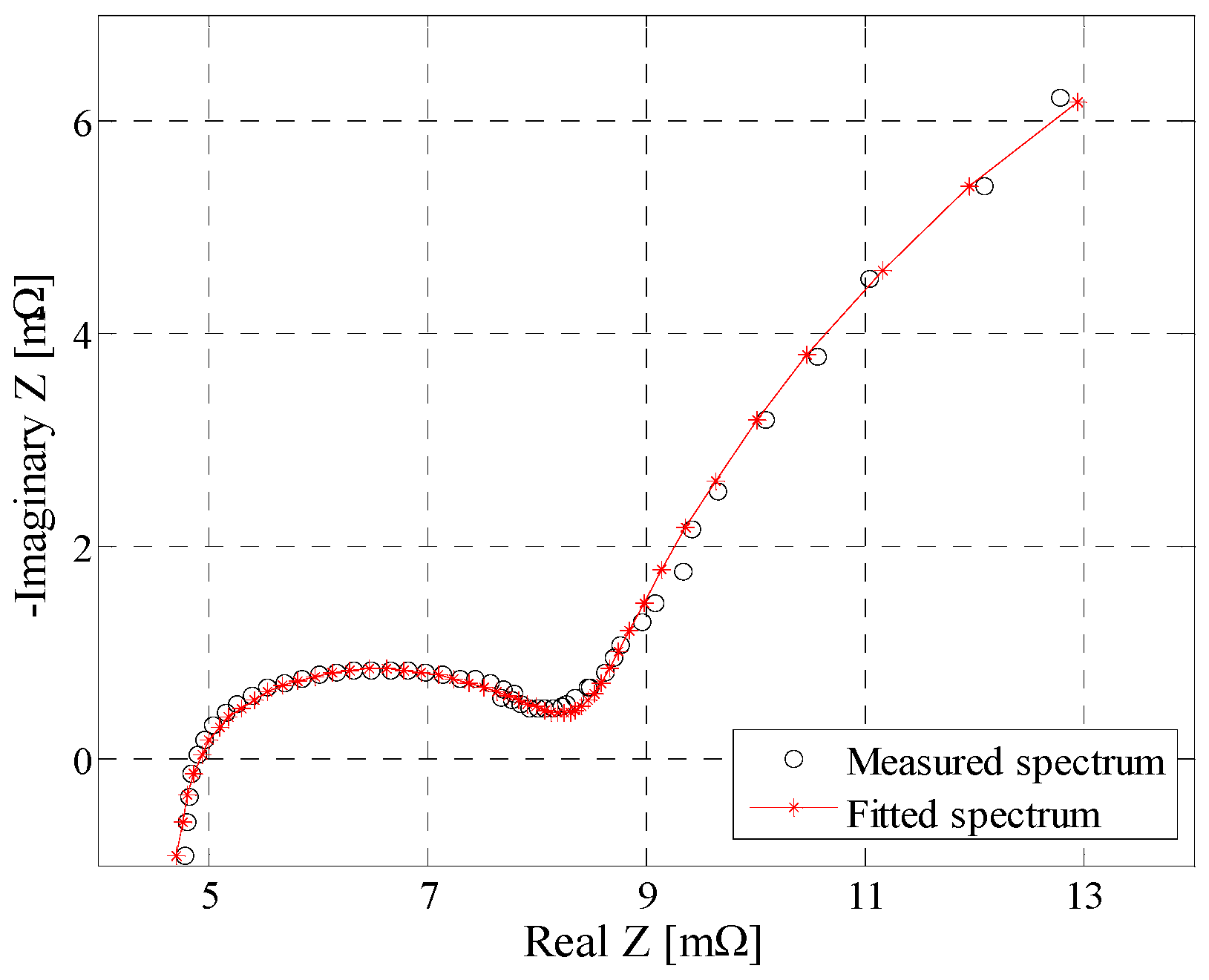
3.6. Electrochemical Impedance Spectroscopy Test
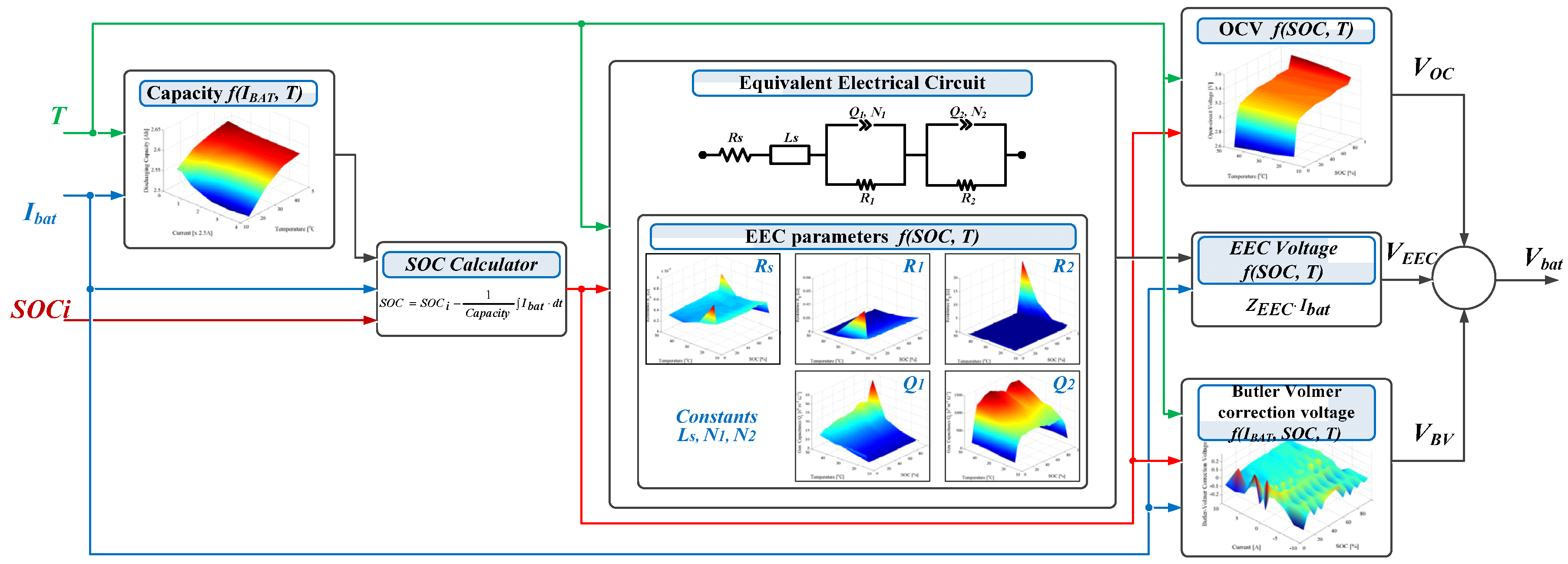
4. Lithium-Ion Battery Performance Model
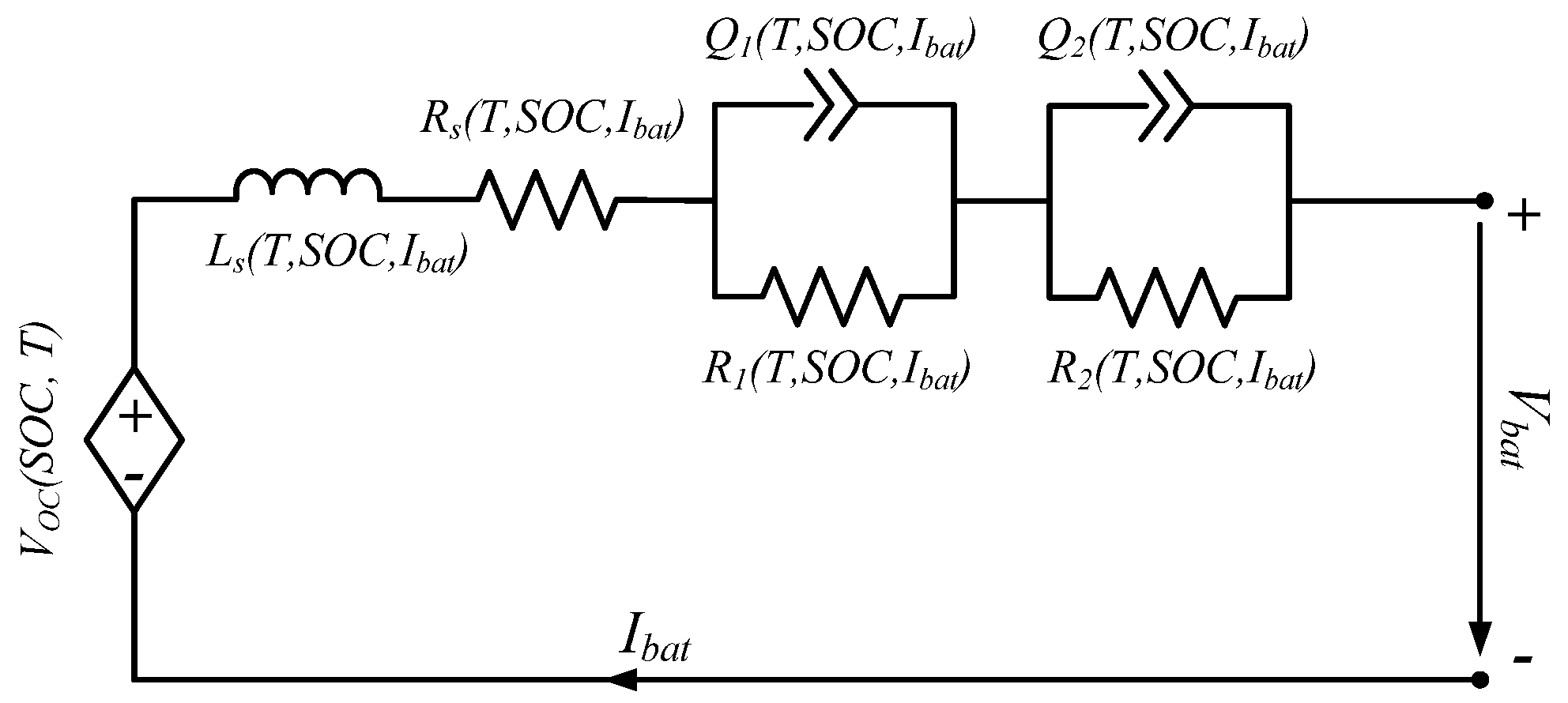
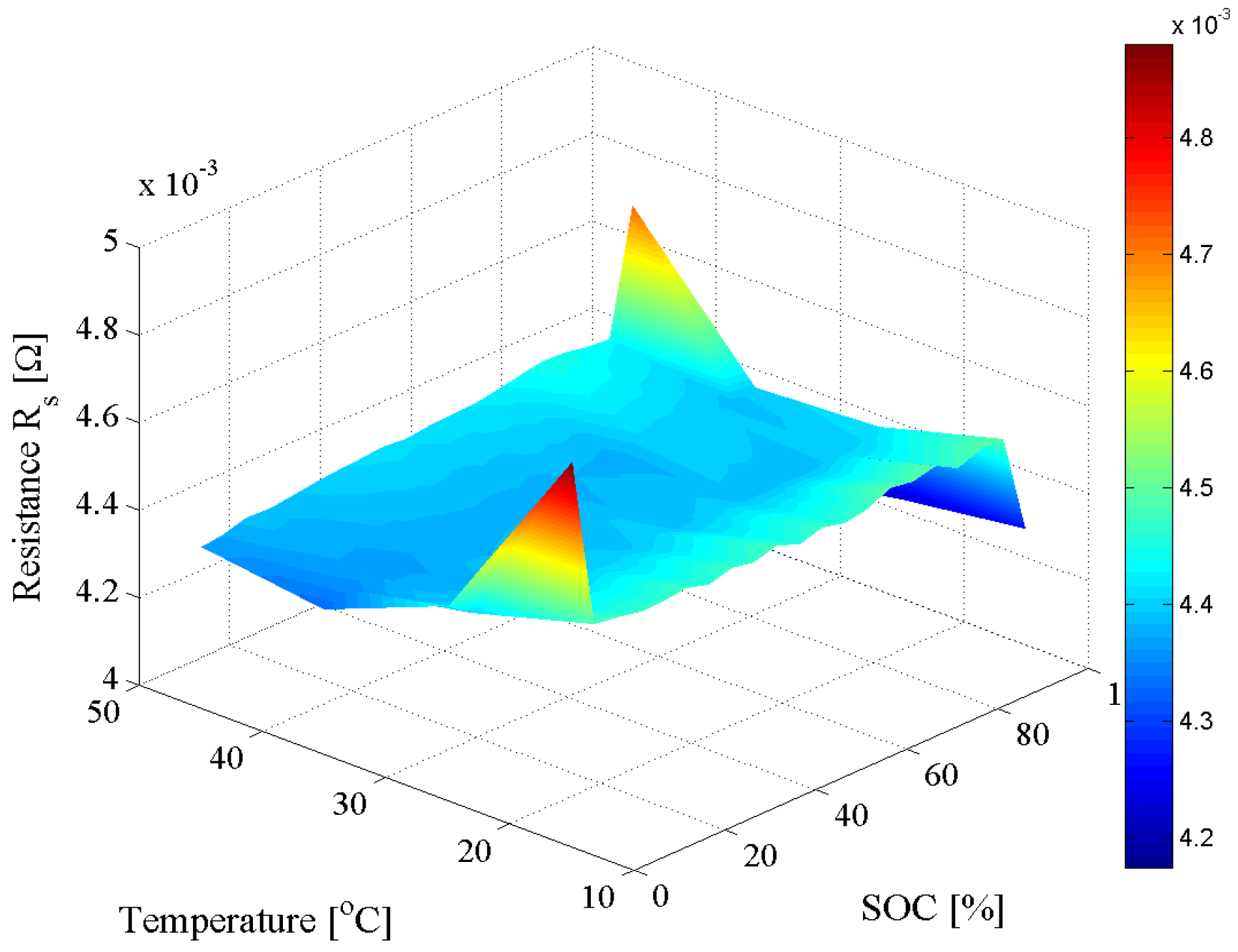
4.1. Equivalent Electrical Circuit Model
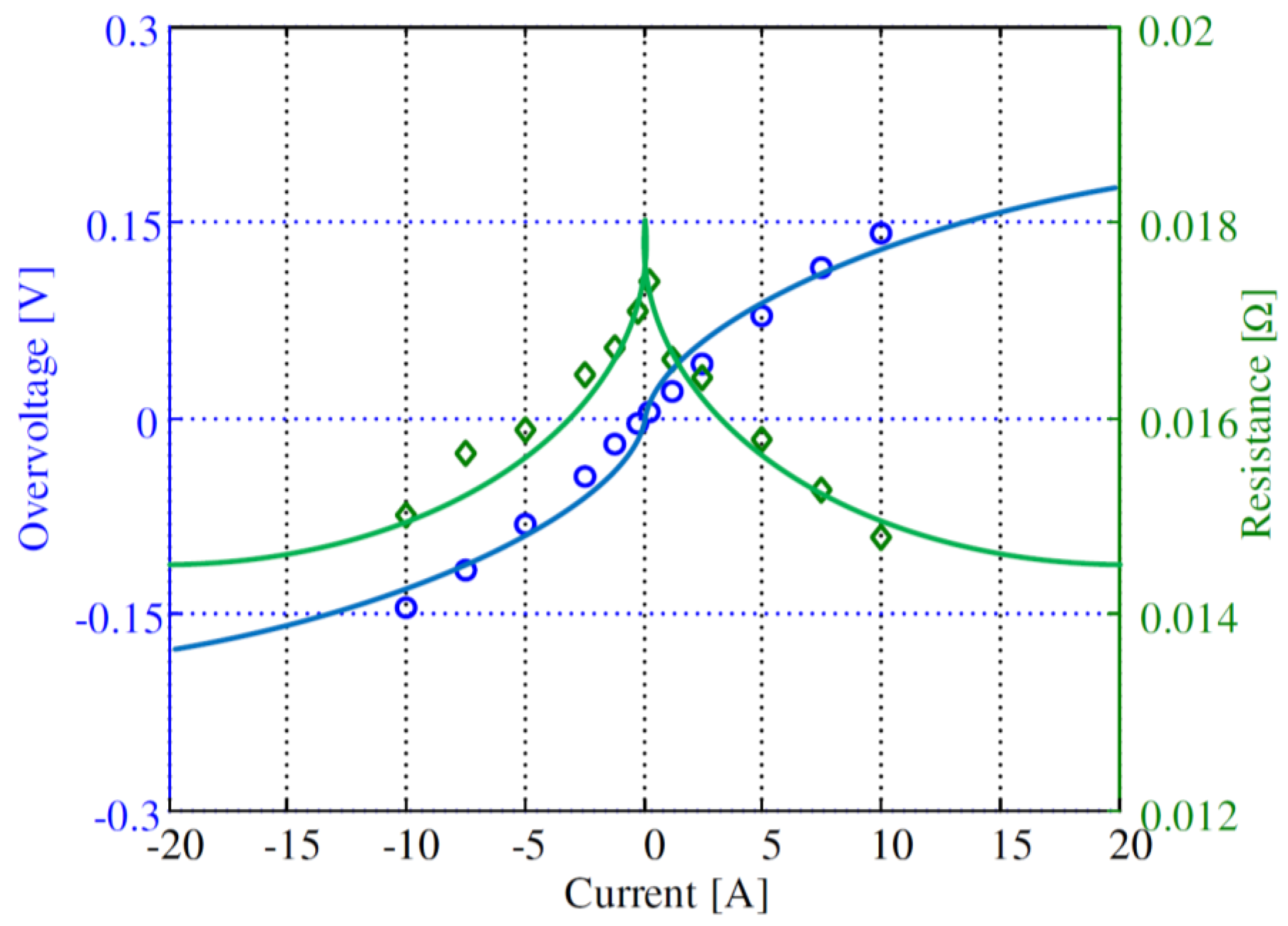
4.2. Dependence on Load Current
4.3. Model Implementation
5. Validation of the Performance Model
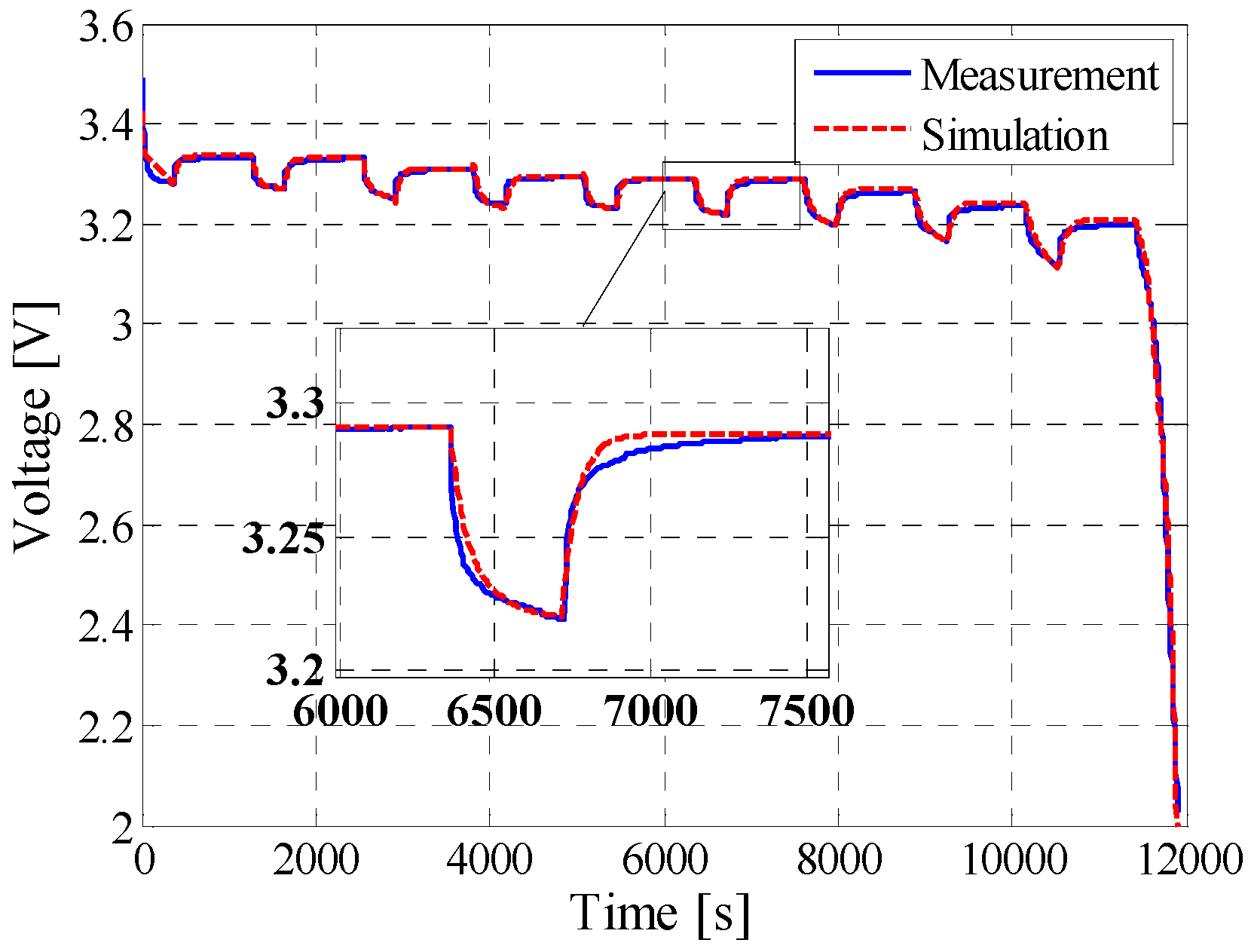
5.1. Pulse Discharge
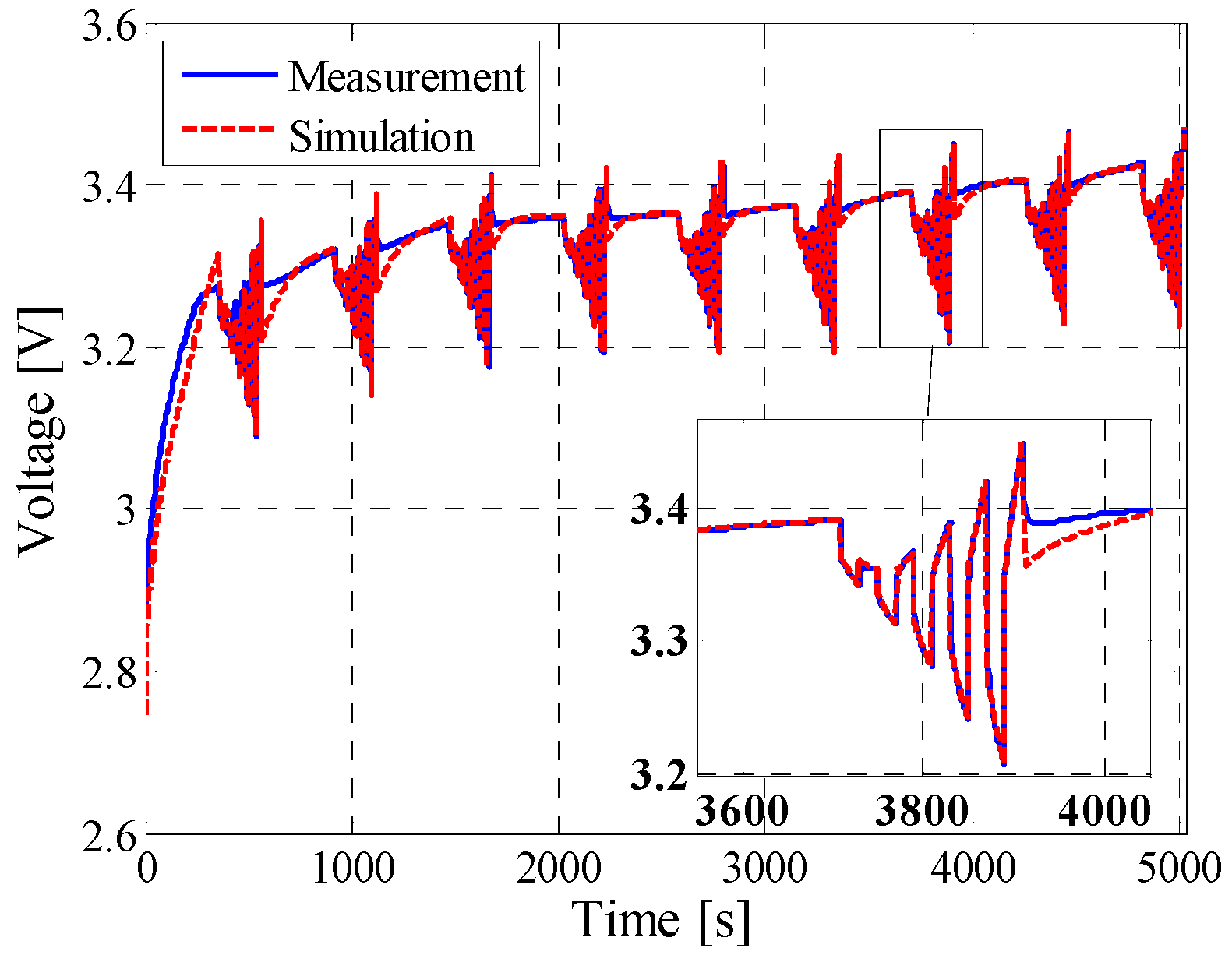
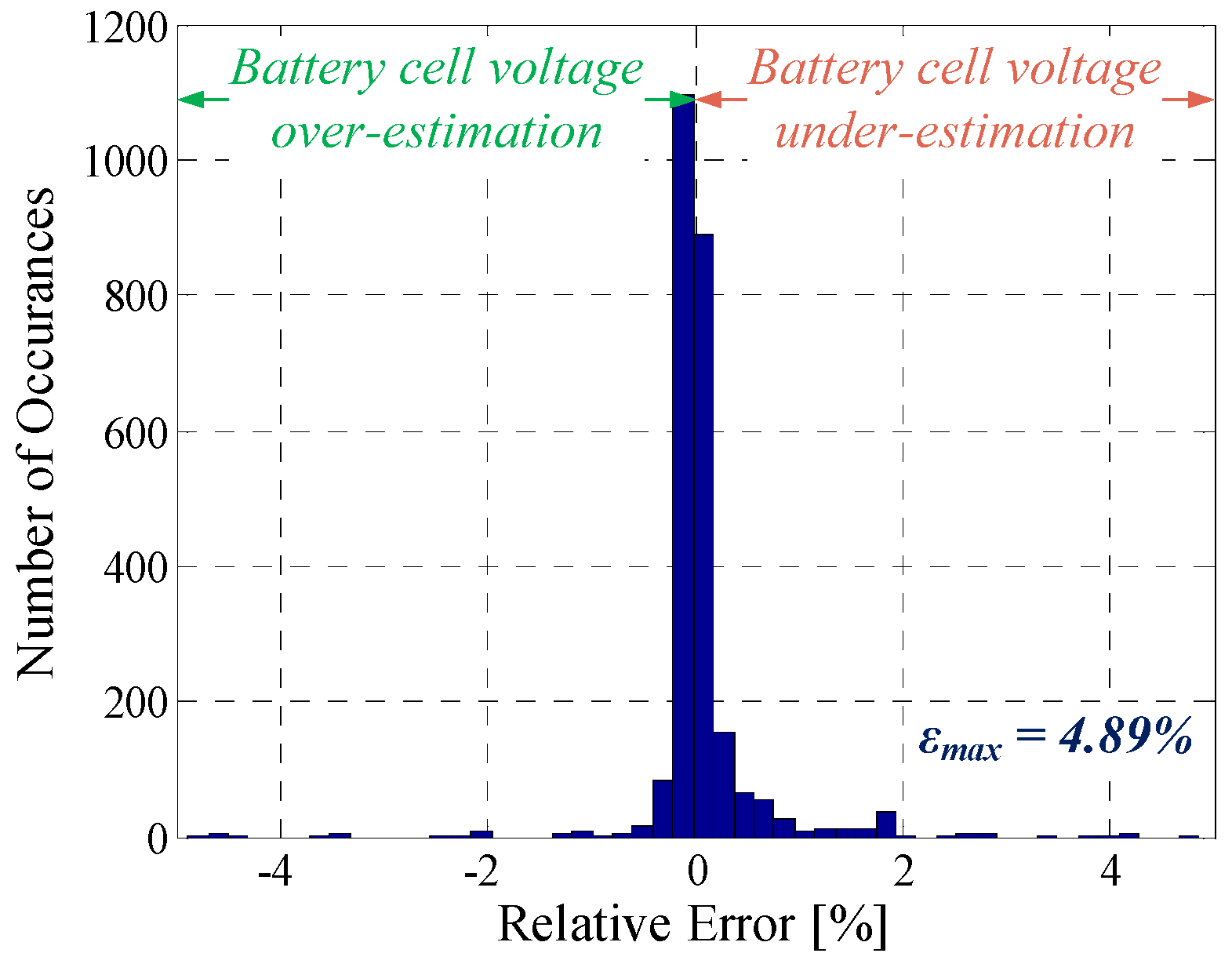
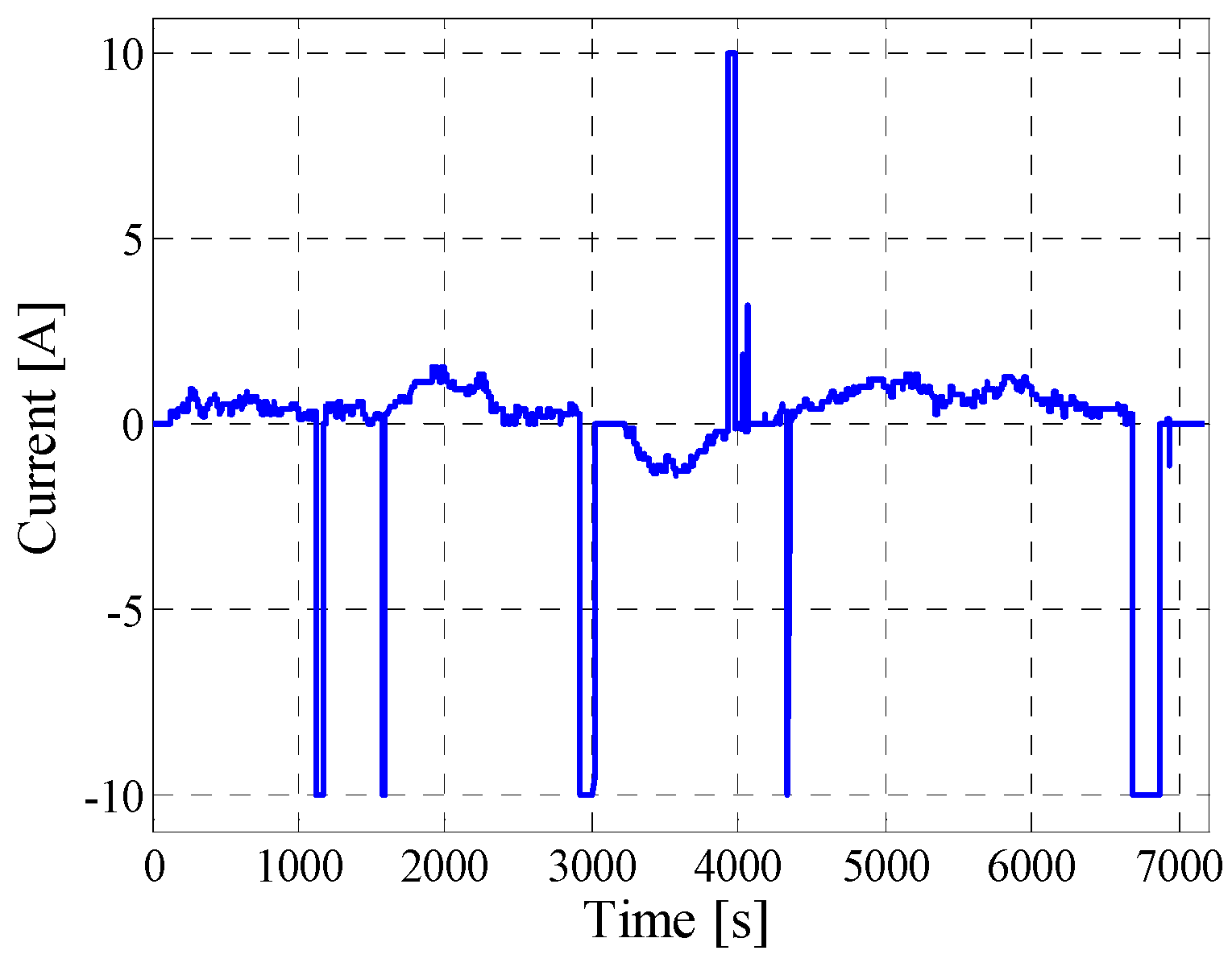
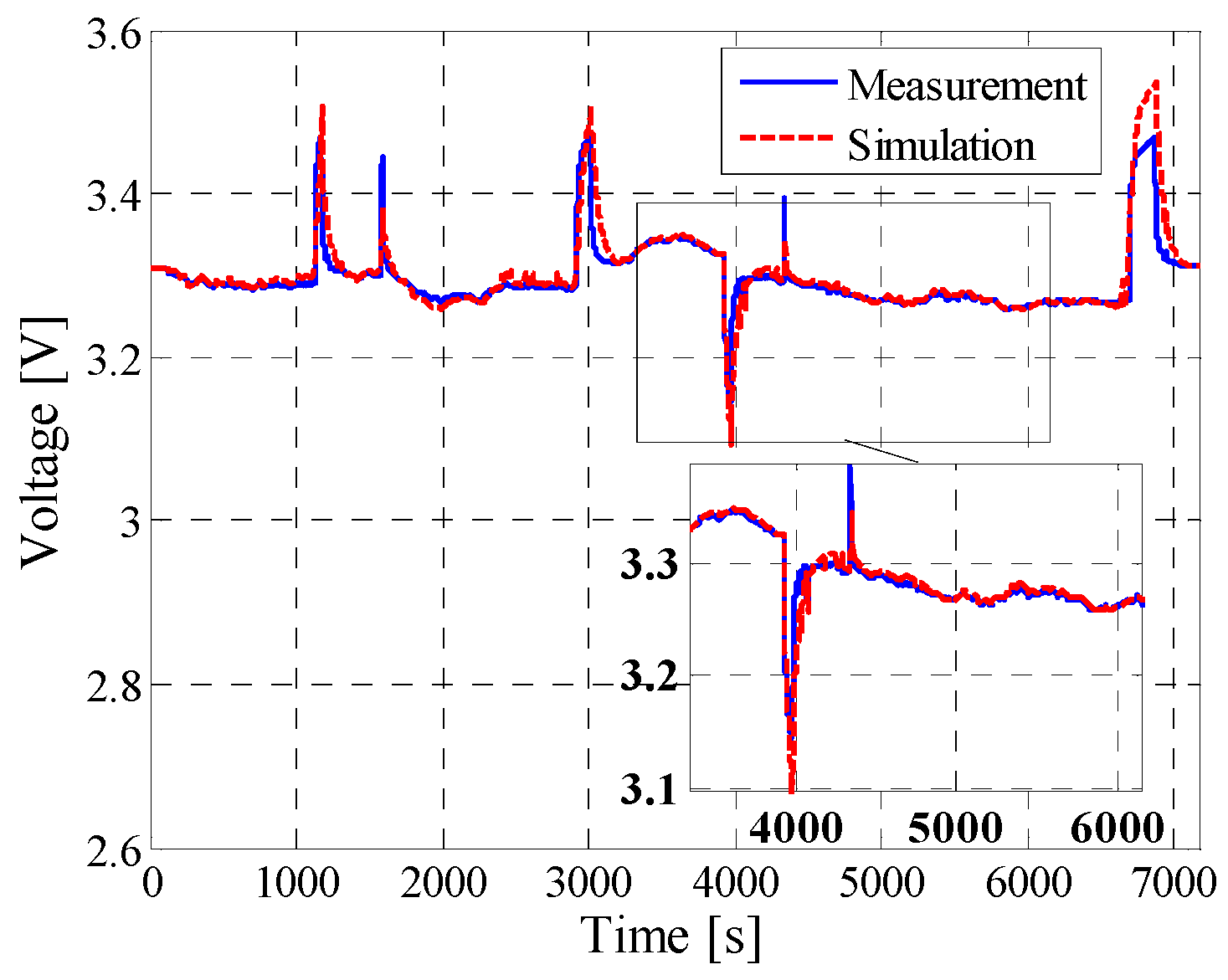
5.2. Dynamic Pulse Charging and Discharging
5.3. Field-Measured Profile
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Pistoia, G. (Ed.) Lithium-Ion Batteries: Advances and Applications; Elsevier: Amsterdam, The Netherlands, 2014.
- Scrosati, B.; Garche, J. Lithium batteries: Status, prospects and future. J. Power Sources 2010, 195, 2419–2430. [Google Scholar] [CrossRef]
- Alexander, D.; Gartner, J. Electric Vehicle Batteries—Lithium Ion Batteries for Hybrid, Plug-in-Hybrid, and Battery Electric Vehicles: Global Market Analysis and Forecasts; Navigant Research: Boulder, CO, USA, 2014. [Google Scholar]
- Catenacci, M.; Verdolini, E.; Bosetti, V.; Fiorese, G. Going electric: Expert survey on the future of battery technologies for electric vehicles. Energy Policy 2013, 61, 403–413. [Google Scholar] [CrossRef]
- Swierczynski, M.; Stroe, D.I.; Lærke, R.; Stan, A.I.; Kjær, P.C.; Teodorescu, R.; Kær, S.K. Field experience from Li-ion BESS delivering primary frequency regulation in the Danish energy market. ECS Trans. 2014, 61, 1–14. [Google Scholar] [CrossRef]
- Gaillac, L.; Castaneda, J.; Edris, A.-A.; Elizondo, D.; Wilkins, C.; Vartanian, C.; Mendelsohn, D. Tehachapi wind energy storage project: Description of operational uses, system components, and testing plans. In Proceedings of the 2012 IEEE PES Transmission and Distribution Conference and Exposition (T&D), Orlando, FL, USA, 7–10 May 2012; pp. 1–6.
- Rastler, D.M. Electric Energy Storage Technology Options: A White Paper Primer on Applications, Costs, and Benefits; Technical Report 1020676; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2010. [Google Scholar]
- Li, X.; Hui, D.; Xu, M.; Wang, L.; Guo, G.; Zhang, L. Integration and energy management of large-scale lithium-ion battery energy storage station. In Proceedings of the 2012 15th International Conference on Electrical Machines and Systems (ICEMS), Sapporo, Japan, 21–24 October 2012; pp. 1–6.
- Vartanian, C.; Bentley, N. A123 systems’ advanced battery energy storage for renewable integration. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition (PSCE), Phoenix, AZ, USA, 20–23 March 2011; pp. 1–6.
- Jeffe, S.; Adamson, K.-A. Advanced Batteries for Utility-Scale Energy Storage; Navigant Research: Boulder, CO, USA, 2014. [Google Scholar]
- Battery Storage for Renewables: Market Status and Technology Outlook; The International Renewable Energy Agency (IRENA): Masdar, United Arab Emirates, 2015.
- Klein, R.; Chaturvedi, N.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Electrochemical model based observer design for a lithium-ion battery. IEEE Trans. Control Syst. Technol. 2013, 21, 289–301. [Google Scholar] [CrossRef]
- Smith, K.; Rahn, C.; Wang, C.-Y. Model-based electrochemical estimation and constraint management for pulse operation of lithium ion batteries. IEEE Trans. Control Syst. Technol. 2010, 18, 654–663. [Google Scholar] [CrossRef]
- Shepherd, C. Design of primary and secondary cells—II. An equation describing battery discharge. J. Electrochem. Soc. 1965, 112, 657–664. [Google Scholar] [CrossRef]
- Gao, L.; Liu, S.; Dougal, R. Dynamic lithium-ion battery model for system simulation. IEEE Trans. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar]
- Chen, M.; Rincon-Mora, G. Accurate electrical battery model capable of predicting runtime and IV performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Swierczynski, M.; Stroe, D.; Stan, A.-I.; Teodorescu, R.; Sauer, D. Selection and performance-degradation modeling of LiMO2/Li4Ti5O12 and LiFePO4/C battery cells as suitable energy storage systems for grid integration with wind power plants: An example for the primary frequency regulation service. IEEE Trans. Sustain. Energy 2014, 5, 90–101. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Walz, H.; Soczka-Guth, T.; Sauer, D.U. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. II: Modelling. J. Power Sources 2011, 196, 5349–5356. [Google Scholar] [CrossRef]
- Rong, P.; Pedram, M. An analytical model for predicting the remaining battery capacity of lithium-ion batteries. IEEE Trans. Large Scale Integr. Syst. 2006, 14, 441–451. [Google Scholar] [CrossRef]
- Kim, T.; Qiao, W. A hybrid battery model capable of capturing dynamic circuit characteristics and nonlinear capacity effects. IEEE Trans. Energy Convers. 2011, 26, 1172–1180. [Google Scholar] [CrossRef]
- Stroe, D.-I. Lifetime Models for Lithium-Ion Batteries Used in Virtual Power Plants. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2014. [Google Scholar]
- Jackey, R.; Saginaw, M.; Sanghvi, P.; Gazzarri, J.; Huria, T. Battery Model Parameter Estimation Using a Layered Technique: An Example Using a Lithium Iron Phosphate Cell; Society of Automotive Engineers: Warrendale, PA, USA, 2013. [Google Scholar]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-domain parameter extraction method for Thévenin-equivalent circuit battery models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Zhang, H.; Chow, M.-Y. Comprehensive dynamic battery modeling for PHEV applications. In Proceedings of the 2010 IEEE Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–6.
- Rahimi-Eichi, H.; Balagopal, B.; Chow, M.-Y.; Yeo, T.-J. Sensitivity analysis of lithium-ion battery model to battery parameters. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON 2013), Vienna, Austria, 10–13 November 2013; pp. 6794–6799.
- Hsieh, Y.-C.; Lin, T.-D.; Chen, R.-J.; Lin, H.-Y. Electric circuit modelling for lithium-ion batteries by intermittent discharging. IET Power Electron. 2014, 7, 2672–2677. [Google Scholar] [CrossRef]
- Buller, S.; Thele, M.; Karden, E.; Doncker, R.W.D. Impedance-based non-linear dynamic battery modeling for automotive applications. J. Power Sources 2003, 113, 422–430. [Google Scholar] [CrossRef]
- Karden, E.; Buller, S.; Doncker, R.W.D. A frequency-domain approach to dynamical modeling of electrochemical power sources. Electrochim. Acta 2002, 47, 2347–2356. [Google Scholar] [CrossRef]
- Buller, S.; Thele, M.; de Doncker, R.; Karden, E. Impedance-based simulation models of supercapacitors and Li-ion batteries for power electronic applications. IEEE Trans. Ind. Appl. 2005, 41, 742–747. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D.U. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. (Eds.) Impedance Spectroscopy: Theory, Experiment, and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005.
- Stan, A.-I.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R.; Andreasen, S. Lithium ion battery chemistries from renewable energy storage to automotive and back-up power applications—An overview. In Proceedings of the 2014 International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 22–24 May 2014; pp. 713–720.
- Batteries for Electric Cars—Challenges, Opportunities, and the Outlook to 2020; The Boston Consulting Group: Boston, MA, USA, 2010.
- Electrical Propelled Road Vehicles—Test Specification for Lithium-Ion Traction Battery Packs and Systems—Part 1: High-Power Applications; ISO 12405-1:2011 Standard; The International Organization for Standardization (ISO): Geneva, Switzerland, 2011.
- Bohlen, O. Impedance Based Battery Monitoring. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2008. [Google Scholar]
- Stroe, D.-I.; Swierczynski, M.; Stan, A.-I.; Teodorescu, R.; Andreasen, S. Accelerated lifetime testing methodology for lifetime estimation of lithium-ion batteries used in augmented wind power plants. IEEE Trans. Ind. Appl. 2014, 50, 4006–4017. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.E. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Grolleau, S.; Delaille, A.; Gualous, H.; Gyan, P.; Revel, R.; Bernard, J.; Redondo-Iglesias, E.; Peter, J. Calendar aging of commercial graphite/LiFePO4 cell—Predicting capacity fade under time dependent storage conditions. J. Power Sources 2014, 255, 450–458. [Google Scholar] [CrossRef]
- Omar, N.; Verbrugge, B.; Mulder, G.; van den Bossche, P.; van Mierlo, J.; Daowd, M.; Dhaens, M.; Pauwels, S. Evaluation of performance characteristics of various lithium-ion batteries for use in BEV application. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference (VPPC), Lille, France, 1–3 September 2010; pp. 1–6.
- Omar, N.; van den Bossche, P.; Mulder, G.; Daowd, M.; Timmermans, J.M.; van Mierlo, J.; Pauwels, S. Assessment of performance of lithium iron phosphate oxide, nickel manganese cobalt oxide and nickel cobalt aluminum oxide based cells for using in plug-in battery electric vehicle applications. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 6–9 September 2011; pp. 1–7.
- Roscher, M.; Bohlen, O.; Vetter, J. OCV hysteresis in Li-ion batteries including two-phase transition materials. Int. J. Electrochem. 2011, 2011, 984320. [Google Scholar] [CrossRef]
- Roscher, M.; Bohlen, O.; Sauer, D. Reliable state estimation of multicell lithium-ion battery systems. IEEE Trans. Energy Convers. 2011, 26, 737–743. [Google Scholar] [CrossRef]
- Tang, X.; Mao, X.; Lin, J.; Koch, B. Li-ion battery parameter estimation for state of charge. In Proceedings of the American Control Conference (ACC), San Francisco, CA, USA, 29 June–1 July 2011; pp. 941–946.
- Waag, W.; Käbitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Stroe, D.; Swierczynski, M.; Stan, A.-I.; Teodorescu, R.; Andreasen, S. Experimental investigation on the internal resistance of lithium iron phosphate battery cells during calendar ageing. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON 2013), Vienna, Austria, 10–13 November 2013; pp. 6734–6739.
- Hafsaoui, J.; Scordia, J.; Sellier, F.; Aubret, P. Development of an electrochemical battery model and its parameters identification tool. Int. J. Automot. Eng. 2012, 3, 27–33. [Google Scholar]
- Bard, A.; Inzelt, G.; Scholz, F. (Eds.) Electrochemical Dictionary, 2nd ed.; Springer: Berlin, Germany, 2012.



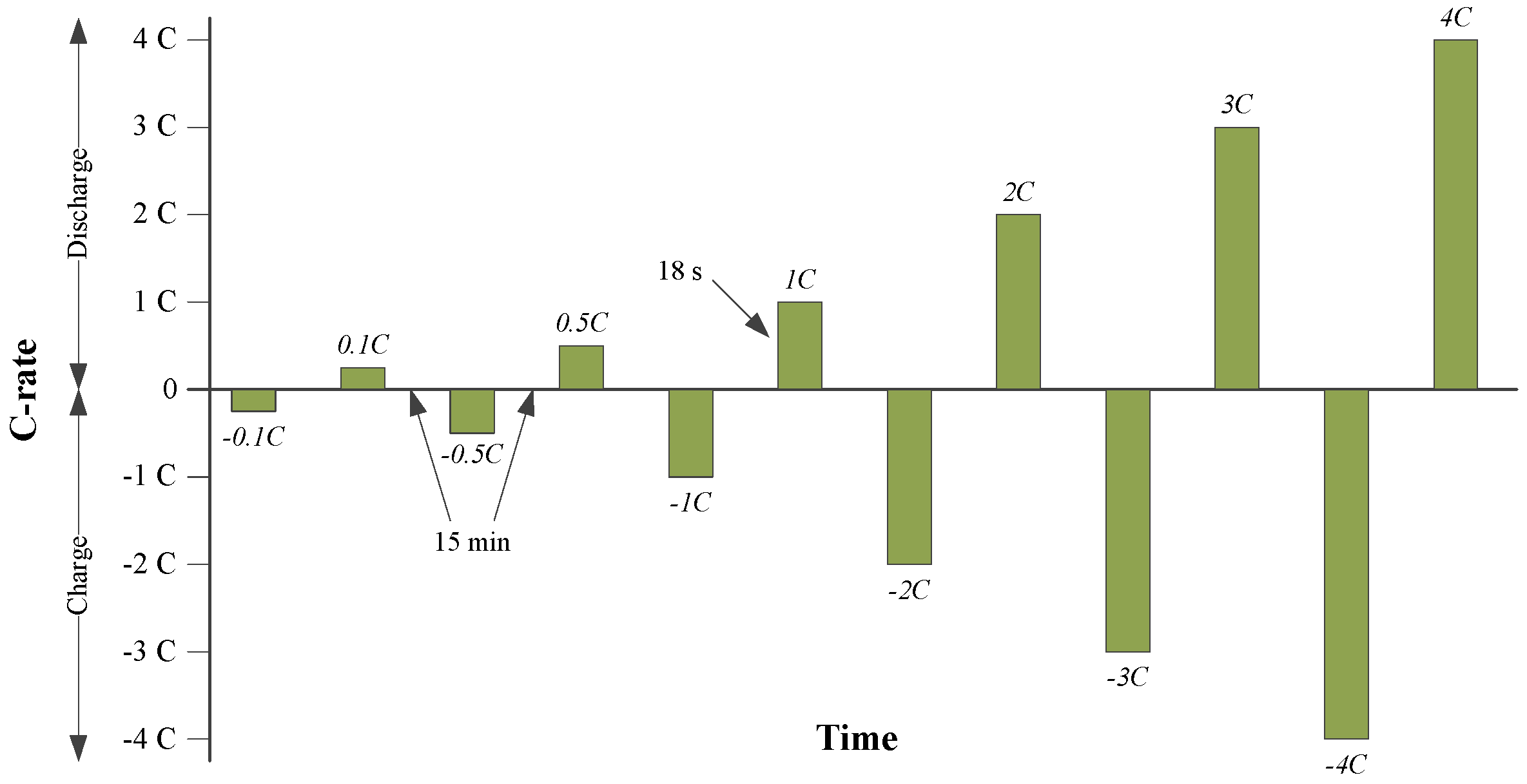
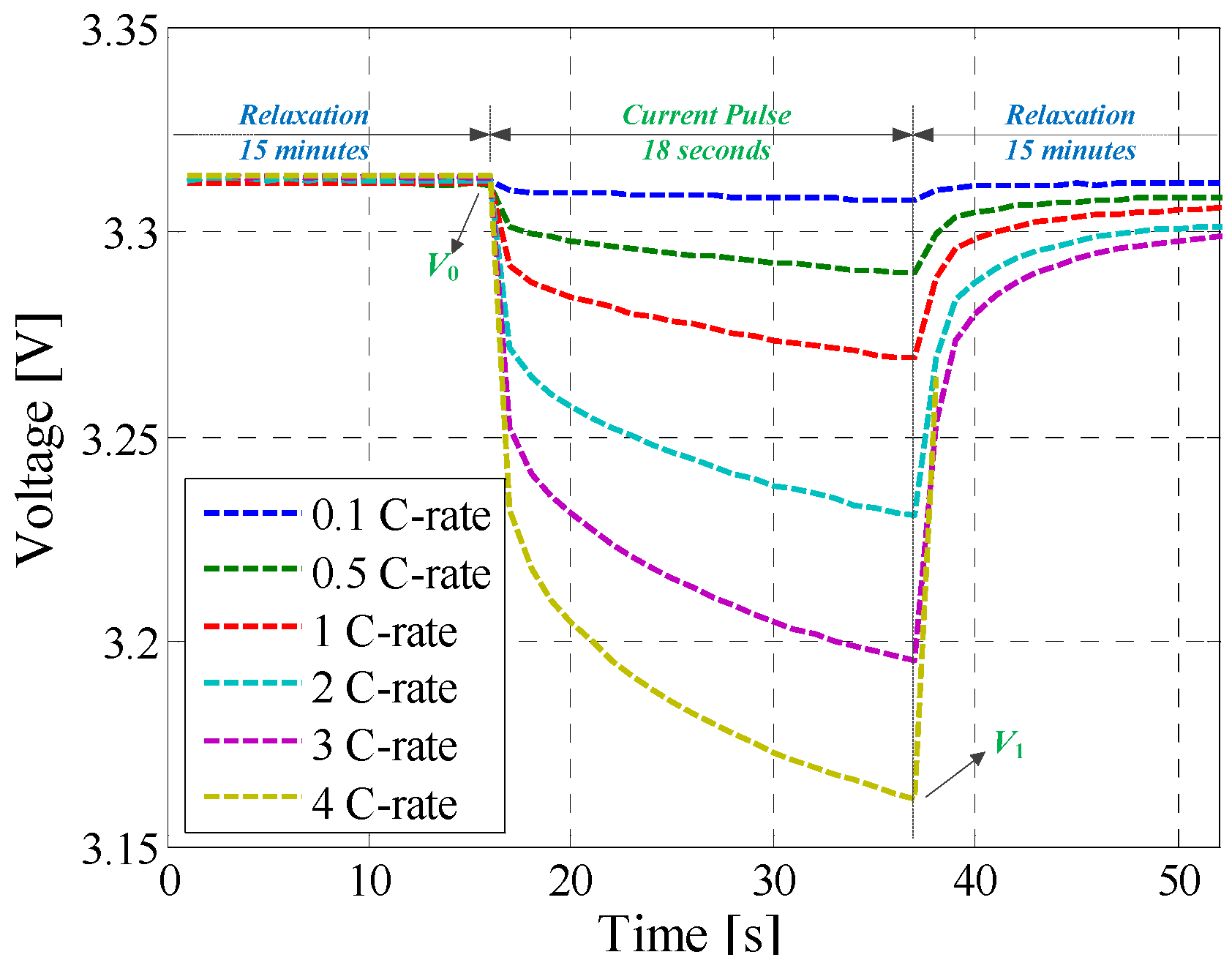

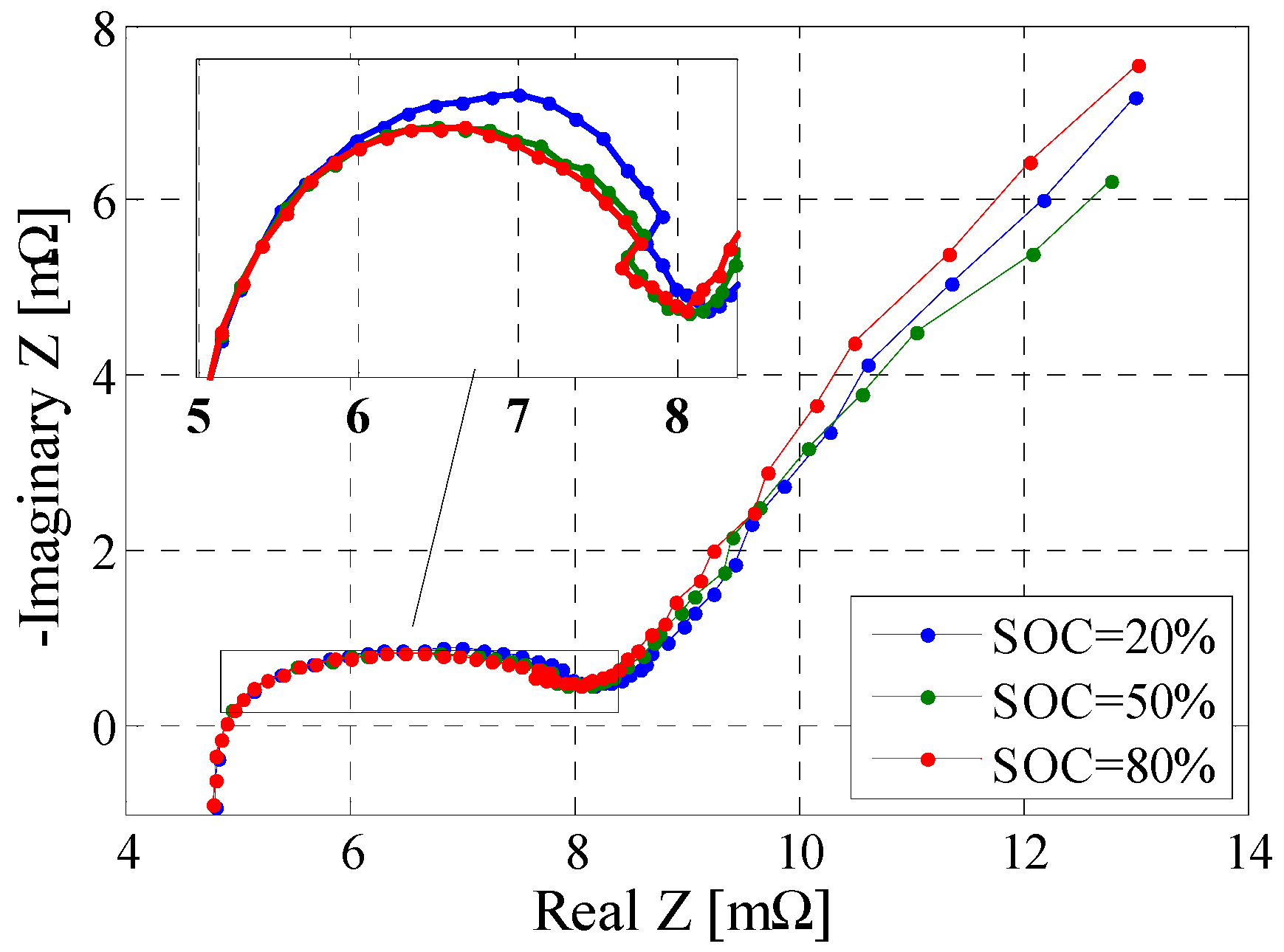
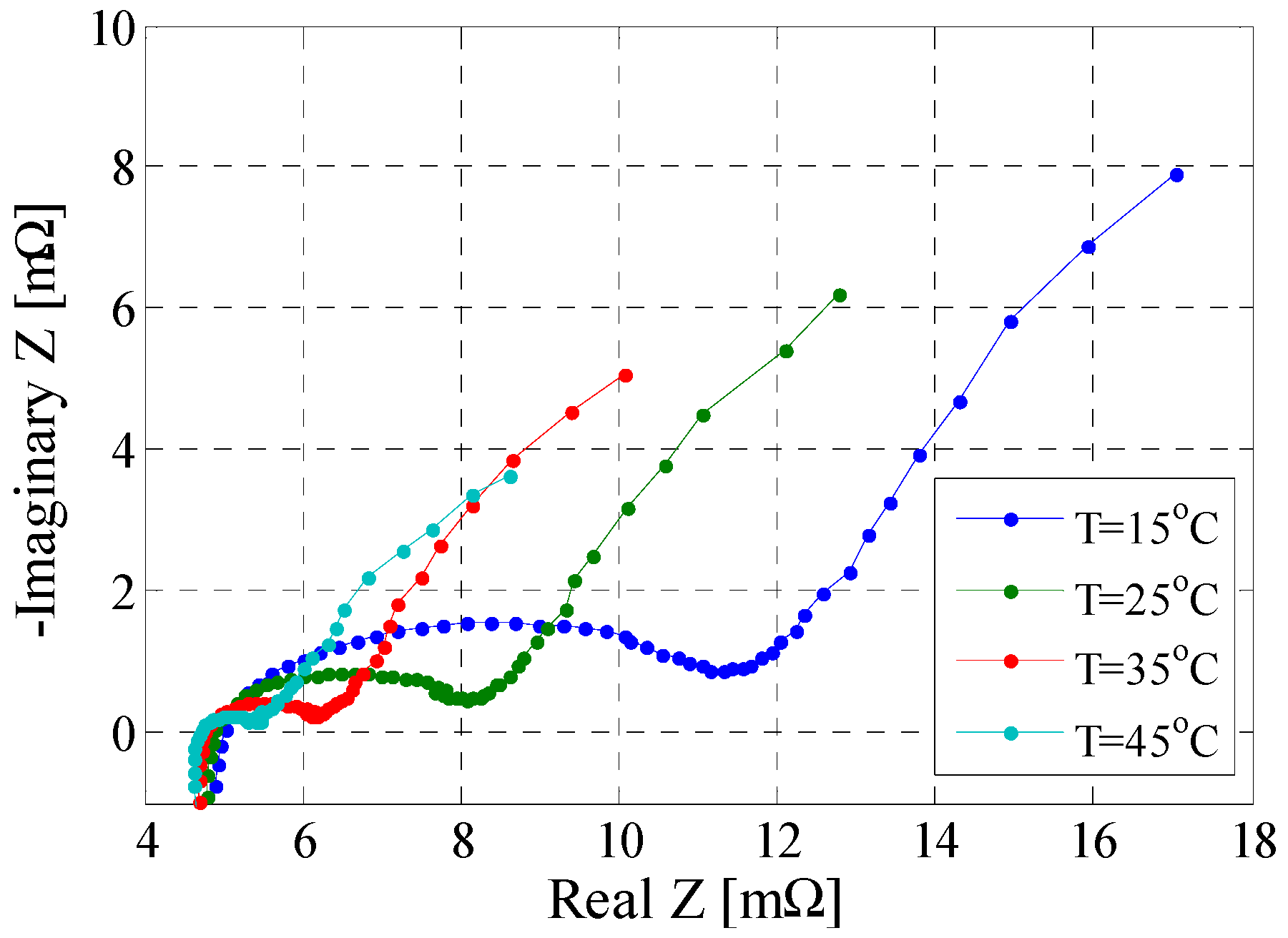
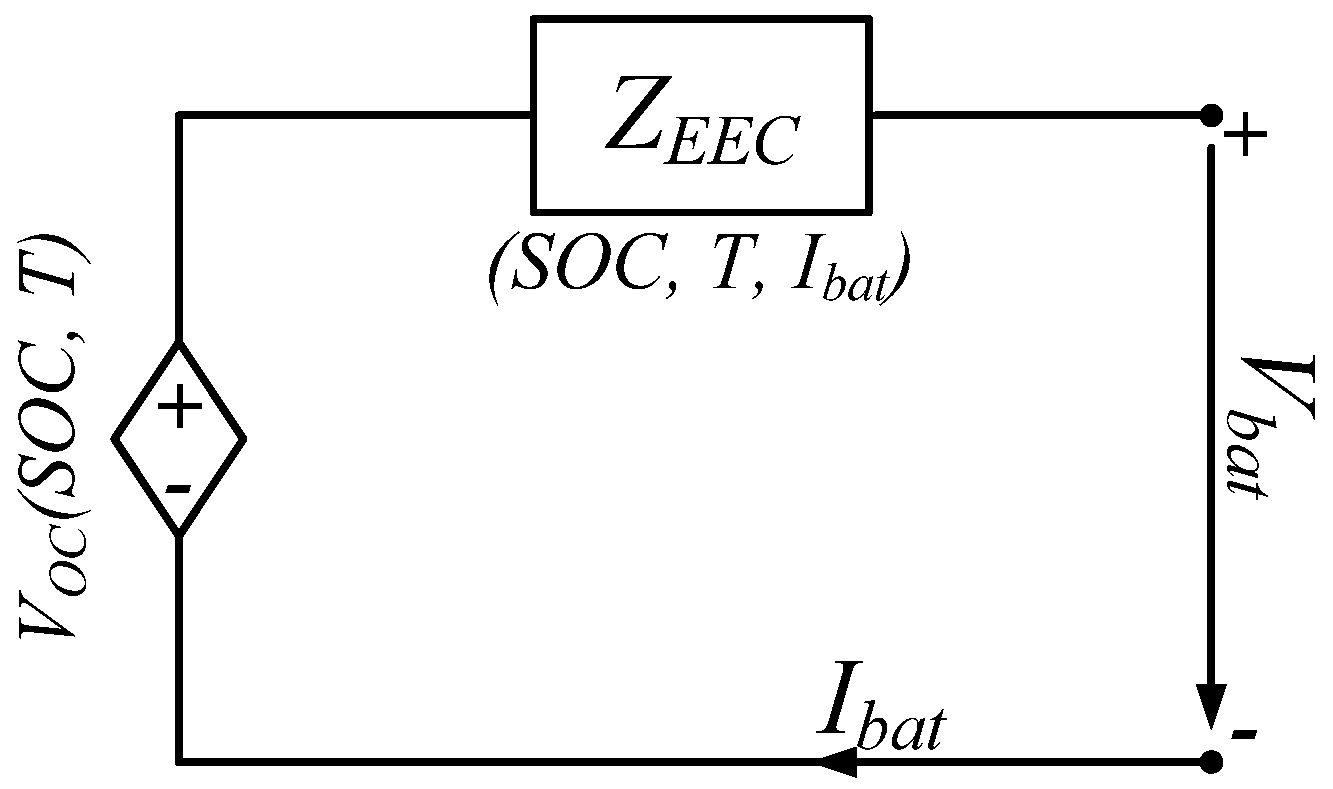


| Relaxation Time | SOC = 20% | SOC = 50% | SOC = 80% | |||
|---|---|---|---|---|---|---|
| Voltage (V) | OCV Error (%) | Voltage (V) | OCV Error (%) | Voltage (V) | OCV Error (%) | |
| 1 s | 3.157 | 2.80 | 3.230 | 2.03 | 3.270 | 2.00 |
| 15 min | 3.236 | 0.37 | 3.292 | 0.15 | 3.325 | 0.37 |
| 1 h | 3.241 | 0.23 | 3.295 | 0.07 | 3.335 | 0.07 |
| 2 h | 3.243 | 0.17 | 3.295 | 0.05 | 3.336 | 0.04 |
| 24 h | 3.248 | 0 | 3.297 | 0 | 3.337 | 0 |
| Profile | Mean Error, |ε| | Maximum Error, εmax | R2 |
|---|---|---|---|
| Pulse discharging | 6.8 mV | 3.66% | 0.9917 |
| Dynamic profile | 6.4 mV | 4.89% | 0.9255 |
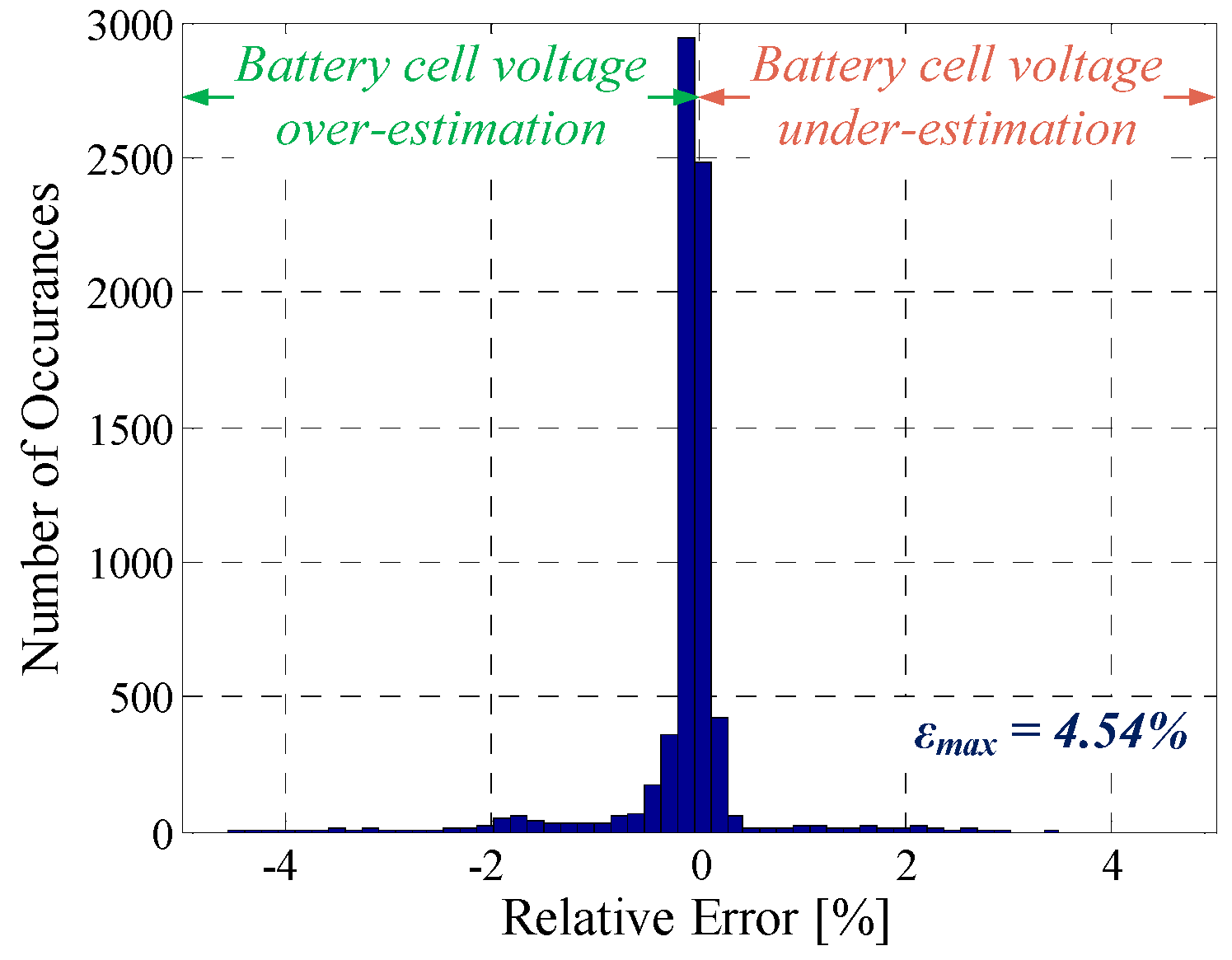
| PFR profile | 8.4 mV | 4.54% | 0.7724 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stroe, D.-I.; Swierczynski, M.; Stroe, A.-I.; Knudsen Kær, S. Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries 2016, 2, 37. https://doi.org/10.3390/batteries2040037
Stroe D-I, Swierczynski M, Stroe A-I, Knudsen Kær S. Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries. 2016; 2(4):37. https://doi.org/10.3390/batteries2040037
Chicago/Turabian StyleStroe, Daniel-Ioan, Maciej Swierczynski, Ana-Irina Stroe, and Søren Knudsen Kær. 2016. "Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries" Batteries 2, no. 4: 37. https://doi.org/10.3390/batteries2040037
APA StyleStroe, D.-I., Swierczynski, M., Stroe, A.-I., & Knudsen Kær, S. (2016). Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries, 2(4), 37. https://doi.org/10.3390/batteries2040037







