A Circuital Equivalent for Supercapacitors Accurate Simulation in Power Electronics Systems
Abstract
1. Introduction
1.1. The Need for SC Equivalent Circuits
1.2. Motivation and Literature Review
1.3. Contributions
2. Materials and Methods
2.1. Characterization Data of Commercial Supercapcitors in Wide Frequency Range
2.2. Selection of the Main Components for the Equivalent Circuit
2.3. Warburg Element
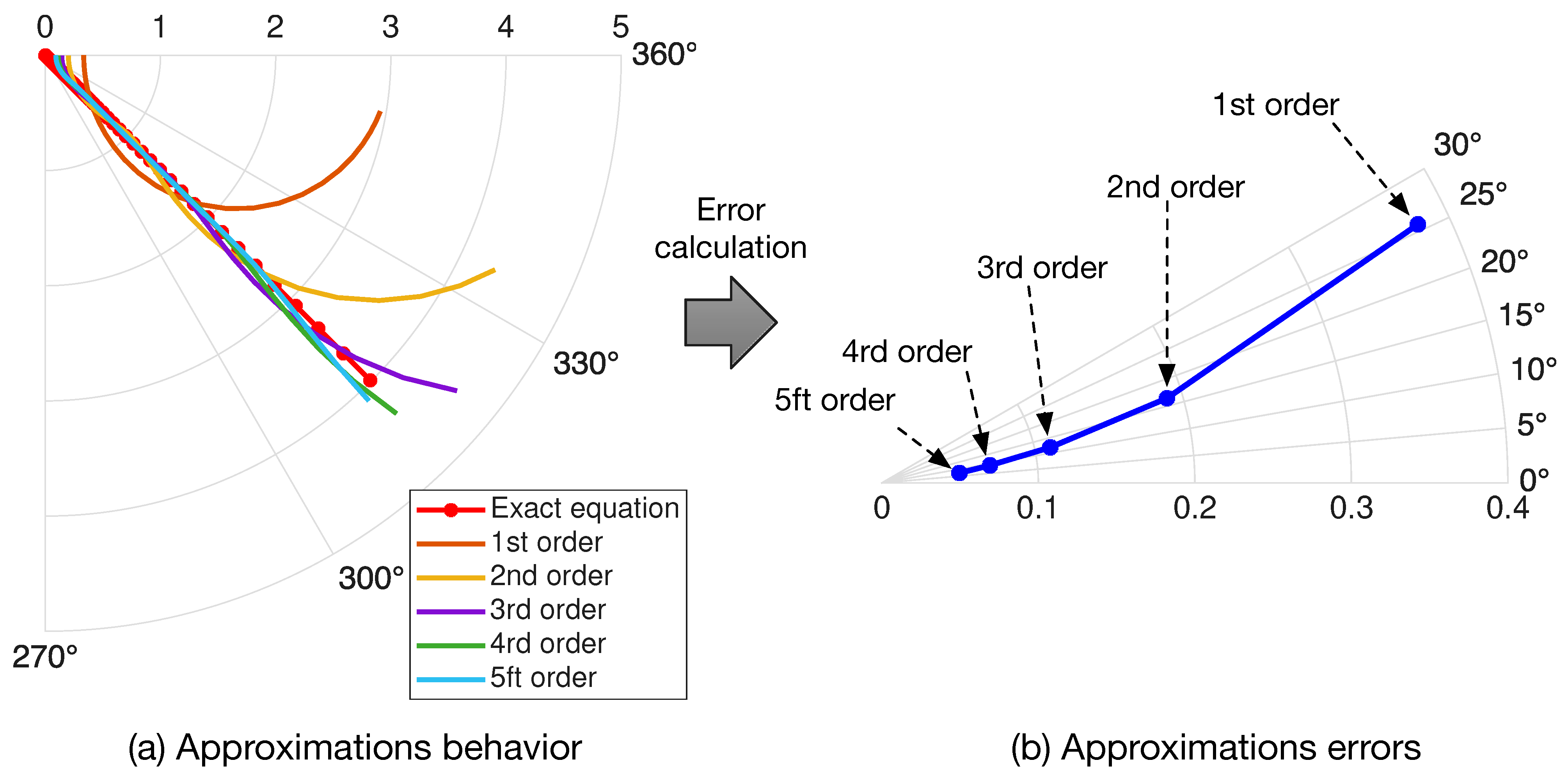
2.3.1. Circuital Approximation of the Warburg Element
2.3.2. Introduction of Warburg Elements into the Circuital Equivalent
3. Results and Discussion
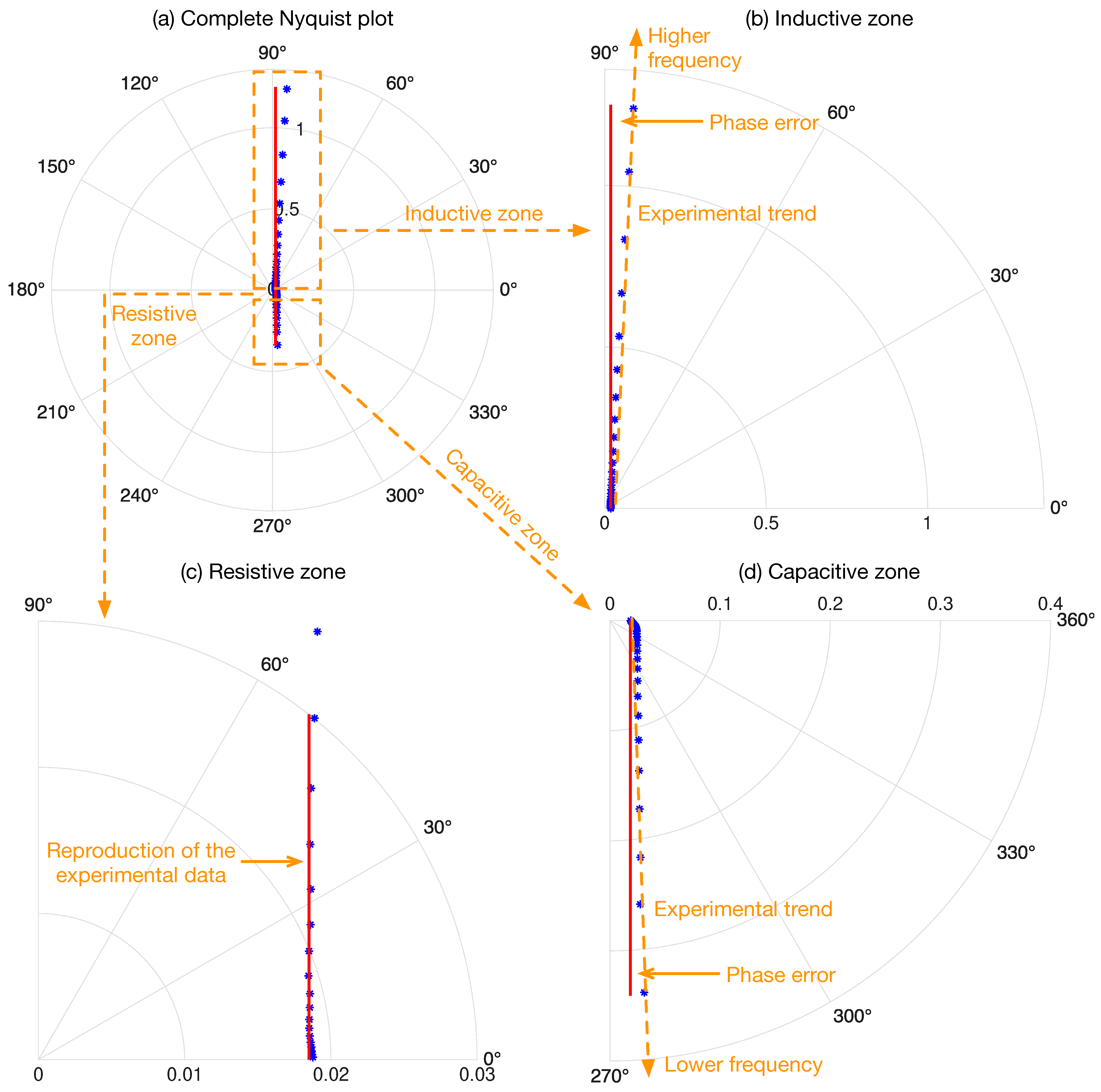
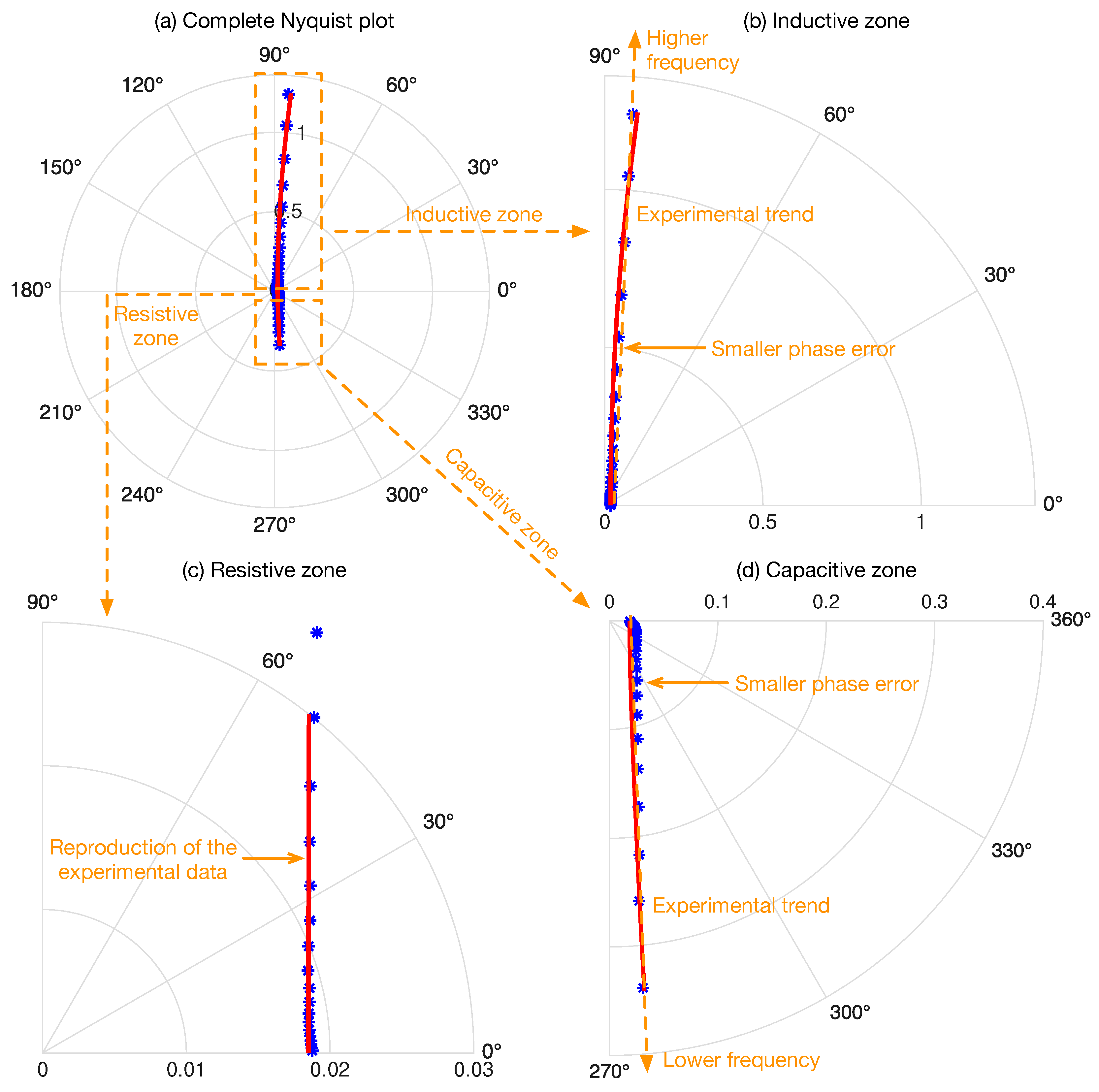
3.1. Frequency Response of the Complete Circuital Equivalent
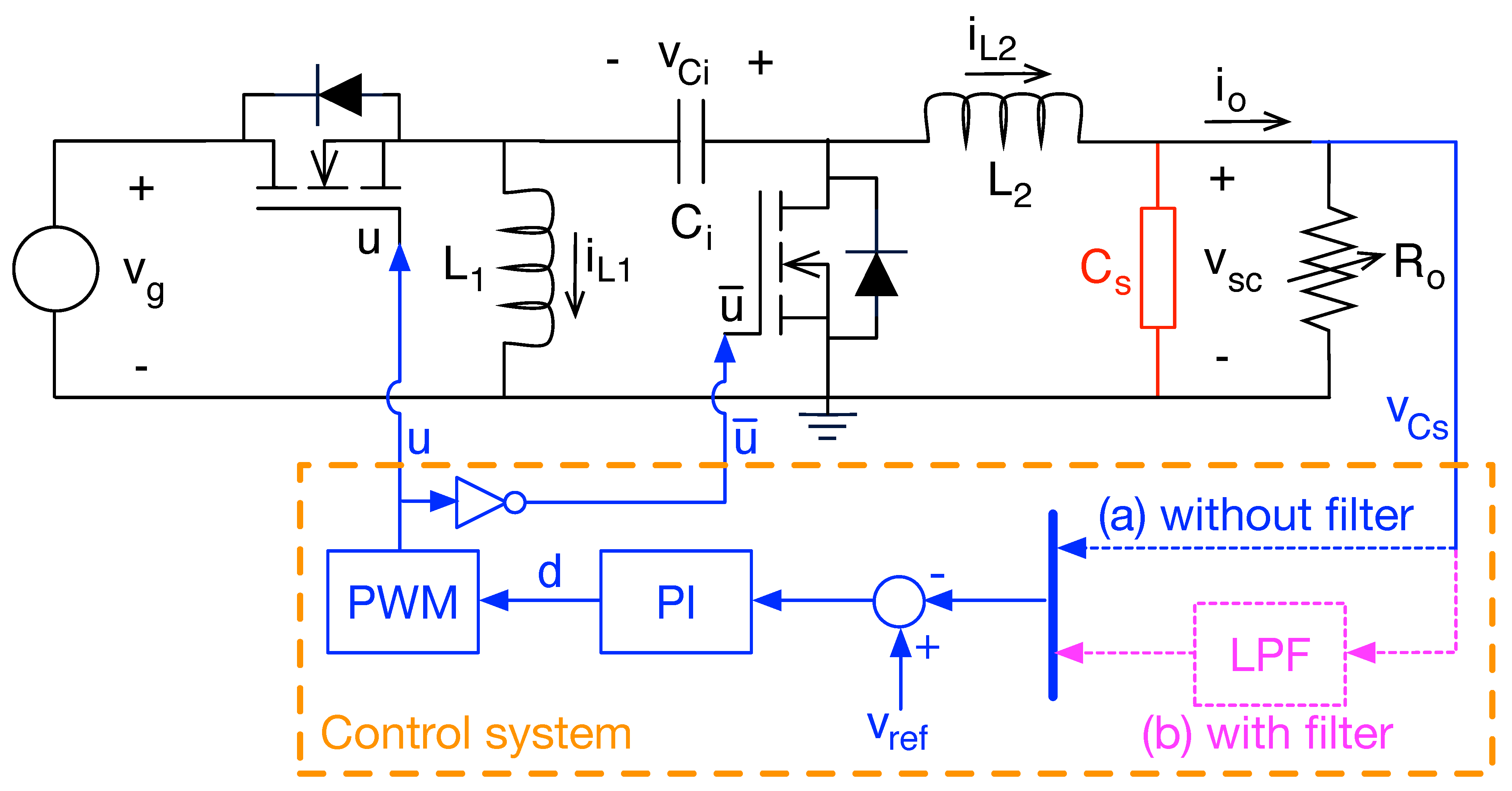
3.2. Power Electronics Examples
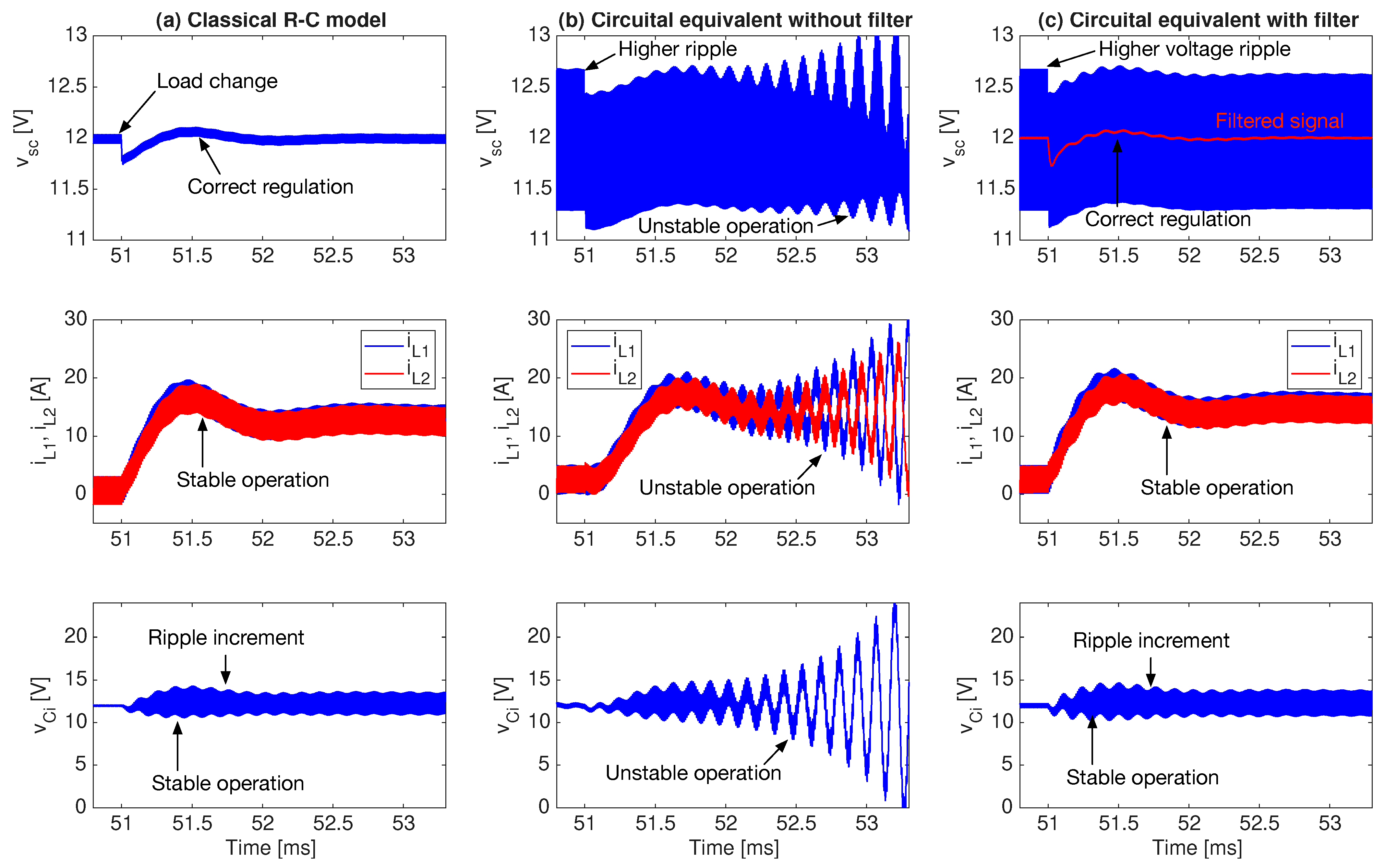
3.2.1. Control Problem
3.2.2. Ripple Specification Problem
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sustainable Energy for All-SEforALL. 24/7 Carbon-Free Energy Compact GuideBook; Technical Report; United Nations: New York, NY, USA, 2025. [Google Scholar]
- Tian, X.; An, C.; Chen, Z. The role of clean energy in achieving decarbonization of electricity generation, transportation, and heating sectors by 2050: A meta-analysis review. Renew. Sustain. Energy Rev. 2023, 182, 113404. [Google Scholar] [CrossRef]
- Alwaeli, M.F.; Galvani, S.; Talavat, V. Addressing power quality challenges in hybrid renewable energy systems through STATCOM devices and advanced gray wolf optimization technique. Results Eng. 2025, 25, 104405. [Google Scholar] [CrossRef]
- Jeyaraj, T.; Ponnusamy, A.; Selvaraj, D. Hybrid renewable energy systems stability analysis through future advancement technique: A review. Appl. Energy 2025, 383, 125355. [Google Scholar] [CrossRef]
- Muzammal Islam, M.; Yu, T.; Giannoccaro, G.; Mi, Y.; La Scala, M.; Rajabi Nasab, M.; Wang, J. Improving Reliability and Stability of the Power Systems: A Comprehensive Review on the Role of Energy Storage Systems to Enhance Flexibility. IEEE Access 2024, 12, 152738–152765. [Google Scholar] [CrossRef]
- Hernández-Mayoral, E.; Madrigal-Martínez, M.; Mina-Antonio, J.D.; Iracheta-Cortez, R.; Enríquez-Santiago, J.A.; Rodríguez-Rivera, O.; Martínez-Reyes, G.; Mendoza-Santos, E. A Comprehensive Review on Power-Quality Issues, Optimization Techniques, and Control Strategies of Microgrid Based on Renewable Energy Sources. Sustainability 2023, 15, 9847. [Google Scholar] [CrossRef]
- Georgious, R.; Refaat, R.; Garcia, J.; Daoud, A.A. Review on Energy Storage Systems in Microgrids. Electronics 2021, 10, 2134. [Google Scholar] [CrossRef]
- Choudhury, S. Review of energy storage system technologies integration to microgrid: Types, control strategies, issues, and future prospects. J. Energy Storage 2022, 48, 103966. [Google Scholar] [CrossRef]
- Elalfy, D.A.; Gouda, E.; Kotb, M.F.; Bureš, V.; Sedhom, B.E. Comprehensive review of energy storage systems technologies, objectives, challenges, and future trends. Energy Strategy Rev. 2024, 54, 101482. [Google Scholar] [CrossRef]
- Fotopoulou, M.; Pediaditis, P.; Skopetou, N.; Rakopoulos, D.; Christopoulos, S.; Kartalidis, A. A Review of the Energy Storage Systems of Non-Interconnected European Islands. Sustainability 2024, 16, 1572. [Google Scholar] [CrossRef]
- Rekioua, D. Energy Storage Systems for Photovoltaic and Wind Systems: A Review. Energies 2023, 16, 3893. [Google Scholar] [CrossRef]
- Mitali, J.; Dhinakaran, S.; Mohamad, A. Energy storage systems: A review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Almusawi, M.; Shukla, A.; S, H.; Kavitha, P.; Gambhire, G.; Pardeshi, P.R.; Pragathi, B. Comparative Analysis of Supercapacitors vs. Batteries. E3S Web Conf. 2024, 591, 01010. [Google Scholar] [CrossRef]
- Libich, J.; Sedlaříková, M.; Máca, J.; Čudek, P.; Kazda, T.; Fafilek, G.; Rodríguez, J.J.S. Supercapacitors vs. Lithium-ion Batteries: Properties and Applications. Chem. Ing. Tech. 2024, 96, 279–285. [Google Scholar] [CrossRef]
- Vukajlović, N.; Milićević, D.; Dumnić, B.; Popadić, B. Comparative analysis of the supercapacitor influence on lithium battery cycle life in electric vehicle energy storage. J. Energy Storage 2020, 31, 101603. [Google Scholar] [CrossRef]
- Aruna, P.; Vasan Prabhu, V.; Krishnakumar, V. Innovative optimization of hybrid energy storage systems for electric vehicles: Integrating FBPINN-SAO to enhance performance and efficiency. J. Energy Storage 2025, 108, 115021. [Google Scholar] [CrossRef]
- Blanch-Fortuna, A.; Zambrano-Prada, D.; López-Santos, O.; Aroudi, A.E.; Vázquez-Seisdedos, L.; Martinez-Salamero, L. Hierarchical Control of Power Distribution in the Hybrid Energy Storage System of an Ultrafast Charging Station for Electric Vehicles. Energies 2024, 17, 1393. [Google Scholar] [CrossRef]
- Hylla, P.; Trawiński, T.; Polnik, B.; Burlikowski, W.; Prostański, D. Overview of Hybrid Energy Storage Systems Combined with RES in Poland. Energies 2023, 16, 5792. [Google Scholar] [CrossRef]
- Hussain, S.; Ali, M.U.; Park, G.S.; Nengroo, S.H.; Khan, M.A.; Kim, H.J. A Real-Time Bi-Adaptive Controller-Based Energy Management System for Battery–Supercapacitor Hybrid Electric Vehicles. Energies 2019, 12, 4662. [Google Scholar] [CrossRef]
- Jauch Quartz. Jauch Battery Solutions-LI NCR18650-BF 2s1p; Datasheet 246480; Jauch Quartz GmbH: Villingen-Schwenningen, Germany, 2021. [Google Scholar]
- Jauch Quartz. Lithium-Ion Cell-LI INR21700JD-50E Energy Type; Datasheet 252240; Jauch Quartz GmbH: Villingen-Schwenningen, Germany, 2024. [Google Scholar]
- Varta. Easy Blade 24; Datasheet VKB: 56654 799 098; Varta Storage GmbH: Nördlingen, Germany, 2022. [Google Scholar]
- GlobTek. 1S5P Lithium-Ion Polymer Battery Pack with Built-in PCM, NTC(10K), Fuel Gauge, 5Cells, 3.7 Volts@9100mAh; Datasheet BL1880F6835661S5PX9M; GlobTek Inc.: Northvale, NJ, USA, 2023. [Google Scholar]
- Fedco Batteries. Lithium-Ion Rechargeable Battery Pack Model No DR202E; Datasheet DR202E; JFedco Batteries: Wisconsin, MN, USA, 2019. [Google Scholar]
- Jauch Quartz. Jauch Battery Solutions-LI18650JLS HB 1s2p; Datasheet 250480; Jauch Quartz GmbH: Villingen-Schwenningen, Germany, 2022. [Google Scholar]
- Jauch Quartz. Jauch Battery Solutions-LI NCR18650-BF 1s2p; Datasheet 246479; Jauch Quartz GmbH: Villingen-Schwenningen, Germany, 2018. [Google Scholar]
- Jauch Quartz. Jauch Battery Solutions-LI NCR18650-BF 2s2p; Datasheet 246478; Jauch Quartz GmbH: Villingen-Schwenningen, Germany, 2018. [Google Scholar]
- Data Power. Polymer Li-Ion Rechargeable Battery DTP605068-3P; Datasheet E-SPE-1106-01; Shenzhen Data Power Technology Ltd.: Shenzhen, China, 2015. [Google Scholar]
- Jauch Quartz. Jauch Battery Solutions-LI21700JSV-50; Datasheet 251511; Jauch Quartz GmbH: Villingen-Schwenningen, Germany, 2022. [Google Scholar]
- Jauch Quartz. Jauch Battery Solutions-LI INR 21700 50E; Datasheet 248574; Jauch Quartz GmbH: Villingen-Schwenningen, Germany, 2022. [Google Scholar]
- US Electronics. USE-18650-3500PCB; Datasheet E-SPE-1106-01; US Electronics Inc.: Saint Louis, MO, USA, 2021. [Google Scholar]
- Tecate Group. Type TLC Hybrid Capacitor (LIC); Datasheet TPLC-3R8/10MR8X14; Tecate Group: San Diego, CA, USA, 2025. [Google Scholar]
- Tecate Group. Type TLC Hybrid Capacitor (LIC); Datasheet TPLC-3R8/30MR10X16; Tecate Group: San Diego, CA, USA, 2025. [Google Scholar]
- Eaton. HS/HSL Supercapacitors Hybrid Cylindrical Cells; Datasheet 11043; Eaton Electronics Division: Cleveland, OH, USA, 2025. [Google Scholar]
- Knowles. DGH Low ESR Supercapacitor; Datasheet DGH505Q5R5; Knowles Precision Devices: Cazenovia, NY, USA, 2024. [Google Scholar]
- Kyocera. Series-Connected Super Capacitor Modules; Datasheet TDS-SC-0004; Kyocera Avx: Fountain Inn, SC, USA, 2024. [Google Scholar]
- Tecate Group. Type TLC Hybrid Capacitor (LIC); Datasheet TPLC-3R8/70MR10X25; Tecate Group: San Diego, CA, USA, 2025. [Google Scholar]
- Maxwell. Ultracapacitor Module BMOD0002 P005 B02; Datasheet 3001961-EN.5; Maxwell Technologies, Inc.: San Diego, CA, USA, 2020. [Google Scholar]
- Kyocera. Radial Leaded Aluminum Electrolityc Capacitors RET Series; Datasheet TDS-ALUM-0027; Kyocera Avx: Fountain Inn, SC, USA, 2024. [Google Scholar]
- Kyocera. SMD Aluminum Conductive Polymer Electrolytic Capacitor APA Series; Datasheet TDS-ALUM-0005; Kyocera Avx: Fountain Inn, SC, USA, 2024. [Google Scholar]
- Kyocera. Radial Leaded Aluminum Hybrid Electrolytic Capacitors RHA Series; Datasheet TDS-ALUM-0016; Kyocera Avx: Fountain Inn, SC, USA, 2024. [Google Scholar]
- Kyocera. SMD Aluminum Electrolytic Capacitors AEA Series; Datasheet TDS-ALUM-0001; Kyocera Avx: Fountain Inn, SC, USA, 2024. [Google Scholar]
- Fang, Z.; Shek, J.K.; Sun, W. A review of grid-connected hybrid energy storage systems: Sizing configurations, control strategies, and future directions. J. Energy Storage 2025, 118, 116226. [Google Scholar] [CrossRef]
- Urooj, A.; Nasir, A. Review of Hybrid Energy Storage Systems for Hybrid Electric Vehicles. World Electr. Veh. J. 2024, 15, 342. [Google Scholar] [CrossRef]
- Nkwanyana, T.B.; Siti, M.W.; Wang, Z.; Toudjeu, I.; Mbungu, N.T.; Mulumba, W. An assessment of hybrid-energy storage systems in the renewable environments. J. Energy Storage 2023, 72, 108307. [Google Scholar] [CrossRef]
- Atawi, I.E.; Al-Shetwi, A.Q.; Magableh, A.M.; Albalawi, O.H. Recent Advances in Hybrid Energy Storage System Integrated Renewable Power Generation: Configuration, Control, Applications, and Future Directions. Batteries 2022, 9, 29. [Google Scholar] [CrossRef]
- Alkafaji, A.S.; Al-Samawi, A.A.; Trabelsi, H. Hybrid Energy Storage Review for Renewable Energy System Technologies and Applications. In Proceedings of the 2021 18th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 22–25 March 2021; pp. 1059–1067. [Google Scholar] [CrossRef]
- Babu, T.S.; Vasudevan, K.R.; Ramachandaramurthy, V.K.; Sani, S.B.; Chemud, S.; Lajim, R.M. A Comprehensive Review of Hybrid Energy Storage Systems: Converter Topologies, Control Strategies and Future Prospects. IEEE Access 2020, 8, 148702–148721. [Google Scholar] [CrossRef]
- Devillers, N.; Jemei, S.; Péra, M.C.; Bienaimé, D.; Gustin, F. Review of characterization methods for supercapacitor modelling. J. Power Sources 2014, 246, 596–608. [Google Scholar] [CrossRef]
- Kopka, R.; Tarczyński, W. Measurement System for Determination of Supercapacitor Equivalent Parameters. Metrol. Meas. Syst. 2013, 20, 581–590. [Google Scholar] [CrossRef]
- Venable. 63XX Frequency Response Analyzer; Data Sheet 09052024; Venable Instruments: Austin, TX, USA, 2025. [Google Scholar]
- Kroics, K.; Gaspersons, K.; Zdanowski, M. Modular DC-DC Converter with Adaptable Fast Controller for Supercapacitor Energy Storage Integration into DC Microgrid. Electronics 2025, 14, 700. [Google Scholar] [CrossRef]
- Shen, C.; Wang, C. State-of-charge estimation for supercapacitors based on salp swarm algorithm-optimized high and low degree cubature Kalman filters considering temperature uncertainty. Electrochim. Acta 2024, 485, 144116. [Google Scholar] [CrossRef]
- Ma, N.; Yang, D.; Riaz, S.; Wang, L.; Wang, K. Aging Mechanism and Models of Supercapacitors: A Review. Technologies 2023, 11, 38. [Google Scholar] [CrossRef]
- Cabrane, Z.; Lee, S.H. Electrical and Mathematical Modeling of Supercapacitors: Comparison. Energies 2022, 15, 693. [Google Scholar] [CrossRef]
- Kroics, K.; Stana, G. Bidirectional Interleaved DC–DC Converter for Supercapacitor Energy Storage Integration with Reduced Capacitance. Electronics 2022, 12, 126. [Google Scholar] [CrossRef]
- Şahİn, M.E.; Blaabjerg, F.; Sangwongwanİch, A. Modelling of Supercapacitors Based on Simplified Equivalent Circuit. CPSS Trans. Power Electron. Appl. 2021, 6, 31–39. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Jakubowska-Ciszek, A.; Walczak, J. Analysis of the transient state in circuit with supercapacitor. Pozn. Univ. Technol. Acad. J. Electr. Eng. 2015, 81, 71–77. [Google Scholar]
- Li, W.; Huang, Q.; Bai, Y.; Wang, J.; Wang, L.; Liu, Y.; Zhao, Y.; Li, X.; Zhang, J. Model reduction of fractional impedance spectra for time–frequency analysis of batteries, fuel cells, and supercapacitors. Carbon Energy 2024, 6, e360. [Google Scholar] [CrossRef]
- Naseri, F.; Karimi, S.; Farjah, E.; Schaltz, E. Supercapacitor management system: A comprehensive review of modeling, estimation, balancing, and protection techniques. Renew. Sustain. Energy Rev. 2022, 155, 111913. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Breitkopf, C. Determination of Diffusion Coefficients Using Impedance Spectroscopy Data. J. Electrochem. Soc. 2018, 165, E826–E831. [Google Scholar] [CrossRef]
- Randles, J.E.B. Kinetics of rapid electrode reactions. Discuss. Faraday Soc. 1947, 1, 11. [Google Scholar] [CrossRef]
- Logerais, P.; Camara, M.; Riou, O.; Djellad, A.; Omeiri, A.; Delaleux, F.; Durastanti, J. Modeling of a supercapacitor with a multibranch circuit. Int. J. Hydrogen Energy 2015, 40, 13725–13736. [Google Scholar] [CrossRef]
- Nelms, R.; Cahela, D.; Tatarchuk, B. Modeling double-layer capacitor behavior using ladder circuits. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 430–438. [Google Scholar] [CrossRef]
- Ates, M.; Chebil, A. Supercapacitor and battery performances of multi-component nanocomposites: Real circuit and equivalent circuit model analysis. J. Energy Storage 2022, 53, 105093. [Google Scholar] [CrossRef]
- Sofia, J.; Wilson, K.J. Electrical circuit modeling of photo–supercapacitor using Zubieta–Bonert model. Optik 2022, 251, 168448. [Google Scholar] [CrossRef]
- Faranda, R. A new parameters identification procedure for simplified double layer capacitor two-branch model. Electr. Power Syst. Res. 2010, 80, 363–371. [Google Scholar] [CrossRef]
- Navarro, G.; Nájera, J.; Torres, J.; Blanco, M.; Santos, M.; Lafoz, M. Development and Experimental Validation of a Supercapacitor Frequency Domain Model for Industrial Energy Applications Considering Dynamic Behaviour at High Frequencies. Energies 2020, 13, 1156. [Google Scholar] [CrossRef]
- Buller, S.; Karden, E.; Kok, D.; De Doncker, R. Modeling the dynamic behavior of supercapacitors using impedance spectroscopy. IEEE Trans. Ind. Appl. 2002, 38, 1622–1626. [Google Scholar] [CrossRef]
- Ramu, S.K.; Vairavasundaram, I.; Aljafari, B.; Kareri, T. Design of PV, Battery, and Supercapacitor-Based Bidirectional DC-DC Converter Using Fuzzy Logic Controller for HESS in DC Microgrid. J. Electr. Comput. Eng. 2024, 2024, 1–16. [Google Scholar] [CrossRef]
- Montenegro-Oviedo, J.A.; Ramos-Paja, C.A.; Orozco-Gutierrez, M.L.; Franco-Mejía, E.; Serna-Garcés, S.I. Design and Experimental Validation of a Battery/Supercapacitor Hybrid Energy Storage System Based on an Adaptive LQG Controller. Appl. Syst. Innov. 2024, 8, 1. [Google Scholar] [CrossRef]
- Maxwell. BMOD0058 E016 B02-16V Small Cell Module; Datasheet 1015371.6; Maxwell Technologies: San Diego, CA, USA, 2014. [Google Scholar]
- IEC 62391-2; Fixed Electric Double-Layer Capacitors for Use in Electronic Equipment-Part 2: Sectional Specification-Electric Double Layer Capacitors for Power Application. International Electrotechnical Commission: Geneva, Switzerland, 2006.
- Lazanas, A.C.; Prodromidis, M.I. Electrochemical Impedance Spectroscopy A Tutorial. ACS Meas. Sci. Au 2023, 3, 162–193. [Google Scholar] [CrossRef]
- Gerard, O.; Numan, A.; Krishnan, S.; Khalid, M.; Subramaniam, R.; Kasi, R. A review on the recent advances in binder-free electrodes for electrochemical energy storage application. J. Energy Storage 2022, 50, 104283. [Google Scholar] [CrossRef]
- USB Implementers Forum Inc. Universal Serial Bus-Power Delivery Specification; Standard USB Power Delivery, Revision 3.2, Version 1.1; USB Implementers Forum Inc.: Beaverton, OR, USA, 2024. [Google Scholar]
- Nichicon. Aluminum-Polymer Capacitor RDS1C470MCNAFEGS; Datasheet RDS; Nichicon: Kyoto, Japan, 2022. [Google Scholar]
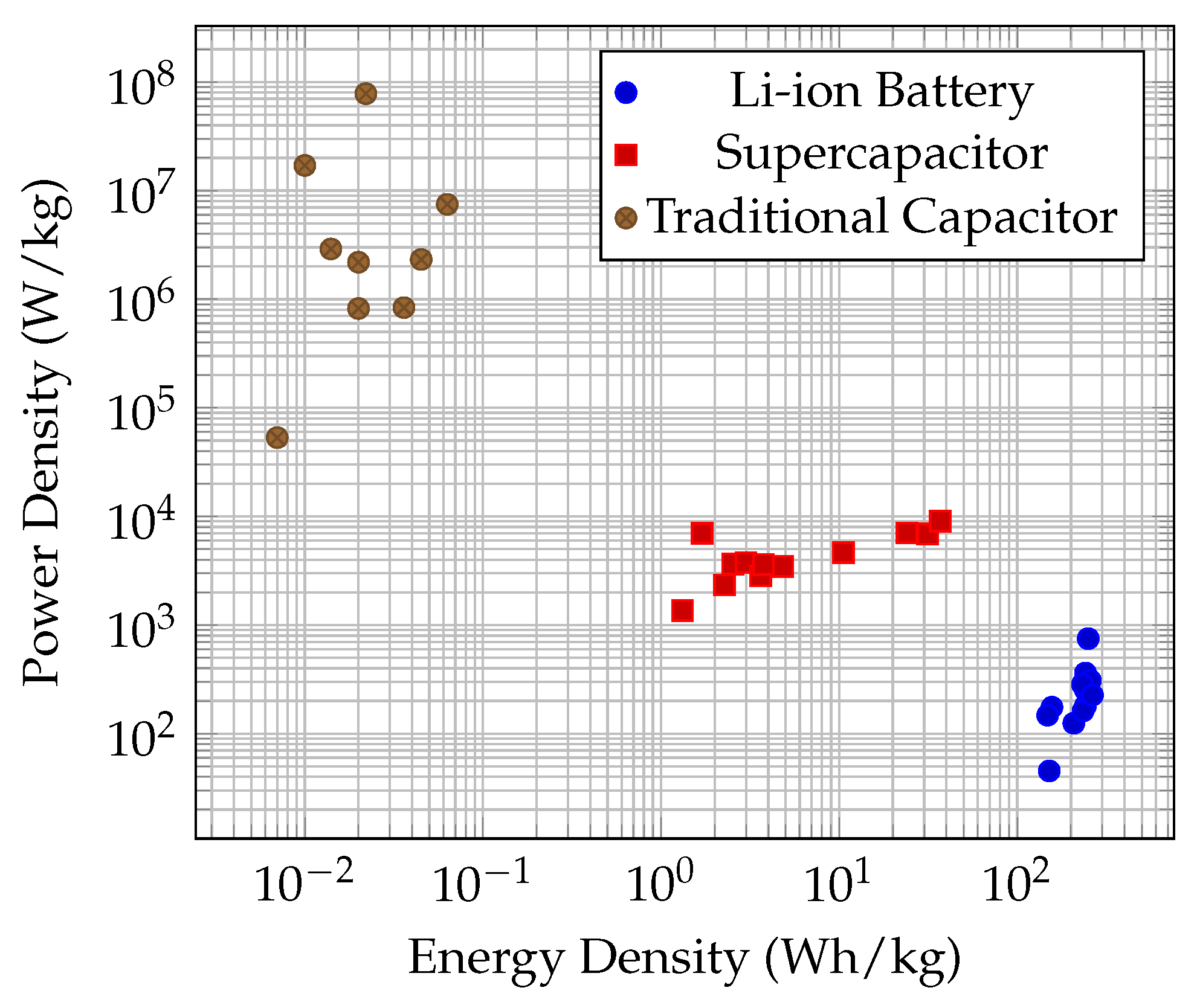









| Parameter | SCs | Li-Ion Battery | Capacitors |
|---|---|---|---|
| Power density (W/kg) | 1000–10,000 | 200–500 | 104–105 |
| Energy density (Wh/kg) | 1–10 | 100–265 | <0.1 |
| Life cycles | 105–106 | 500–2000 | > |
| Efficiency | 85– | – | > |
| Charge/discharge time | s to min | min to h | s to s |
| Type | Reference | ED (W-h/kg) | PD (W/kg) |
|---|---|---|---|
| Battery | LI18650JP2S1P [20] | 241.2 | 361.8 |
| LI INR21700JD-50E [21] | 250 | 750 | |
| 56654 799 098 [22] | 156.48 | 175.35 | |
| BL1880F6835661S5PX9M [23] | 151.22 | 45.37 | |
| DR202E [24] | 207.61 | 124.79 | |
| LI18650JLS HB 1S2P [25] | 241.2 | 180 | |
| LI18650JP1S2P [26] | 234 | 162 | |
| LI18650JP2S2P [27] | 241.2 | 252 | |
| DTP605068-3P [28] | 148 | 148 | |
| LI21700JSV-50 [29] | 257.14 | 308.57 | |
| LI INR21700 50E [30] | 232.11 | 284.21 | |
| USE-18650-3500PCB [31] | 264.29 | 226.53 | |
| Supercapacitor | TPLC-3R8/10MR8X14 [32] | 10.56 | 4642.11 |
| TPLC-3R8/30MR10X16 [33] | 24.01 | 7056 | |
| HS1020-3R8506-R [34] | 31.34 | 6890.63 | |
| DGH505Q5R5 [35] | 2.53 | 3650 | |
| DGH335Q8R1 [35] | 3.00 | 3750 | |
| DGH107Q2R7 [35] | 4.82 | 3471 | |
| DGH506Q2R7 [35] | 3.62 | 2840 | |
| SCMR22L105SRBB0 [36] | 2.27 | 2338 | |
| SCMT32H755SSBB0 [36] | 3.75 | 3600 | |
| TPLC-3R8/70MR10X25 [37] | 36.94 | 9047.62 | |
| BMOD0002 P005 B02 [38] | 1.70 | 7000 | |
| Traditional Capacitor | RET0820152M010B [39] | 19.84−3 | 821.02 × 103 |
| RET0820391M035# [39] | 63.19 × 10−3 | 7478.63 × 103 | |
| APA1012821M016# [40] | 19.97−3 | 2191.78 ×103 | |
| APA0809100M100# [40] | 21.70−3 | 78,125 ×103 | |
| RHA1011561M016# [41] | 13.55−3 | 2902.49 ×103 | |
| RHA1009150M080# [41] | 9.95−3 | 17,057.57 ×103 | |
| AEA1616682M006R [42] | 7.03−3 | 53.19 ×103 | |
| AEA1616222M025R [42] | 35.83−3 | 837.58 ×103 | |
| AEA1213221M063R [42] | 45.42−3 | 2322.68 ×103 |
| Name | Circuital Equivalent | Characteristics |
|---|---|---|
| Simple R-C [49,52,53,54,55,56,57,58,59] |  | Analysis and implementation simplicity. It does not include diffusion effects, voltage dependency, or leakage effects. |
| Randles [60,61,62,63] | 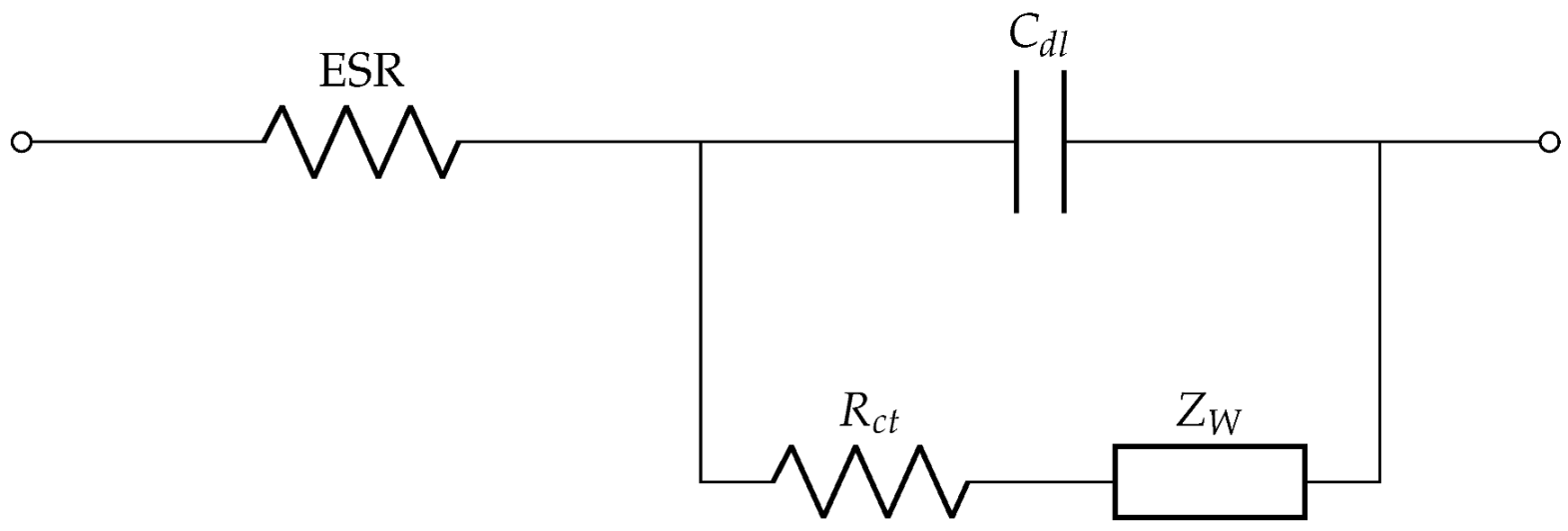 | It incorporates electrode–electrolyte interface effects and charge transfer processes. More accurate than the simple R-C model, especially for capturing dynamic and impedance phenomena. |
| Ladder R-C [64,65] |  | Used to represent the physical phenomenon of the progressive penetration of ions into the porous structure of the electrodes. Good accuracy at mid-high frequencies. Slower simulations and does not capture self-relaxation and leakage. |
| Zubieta [57,61,66,67,68] | 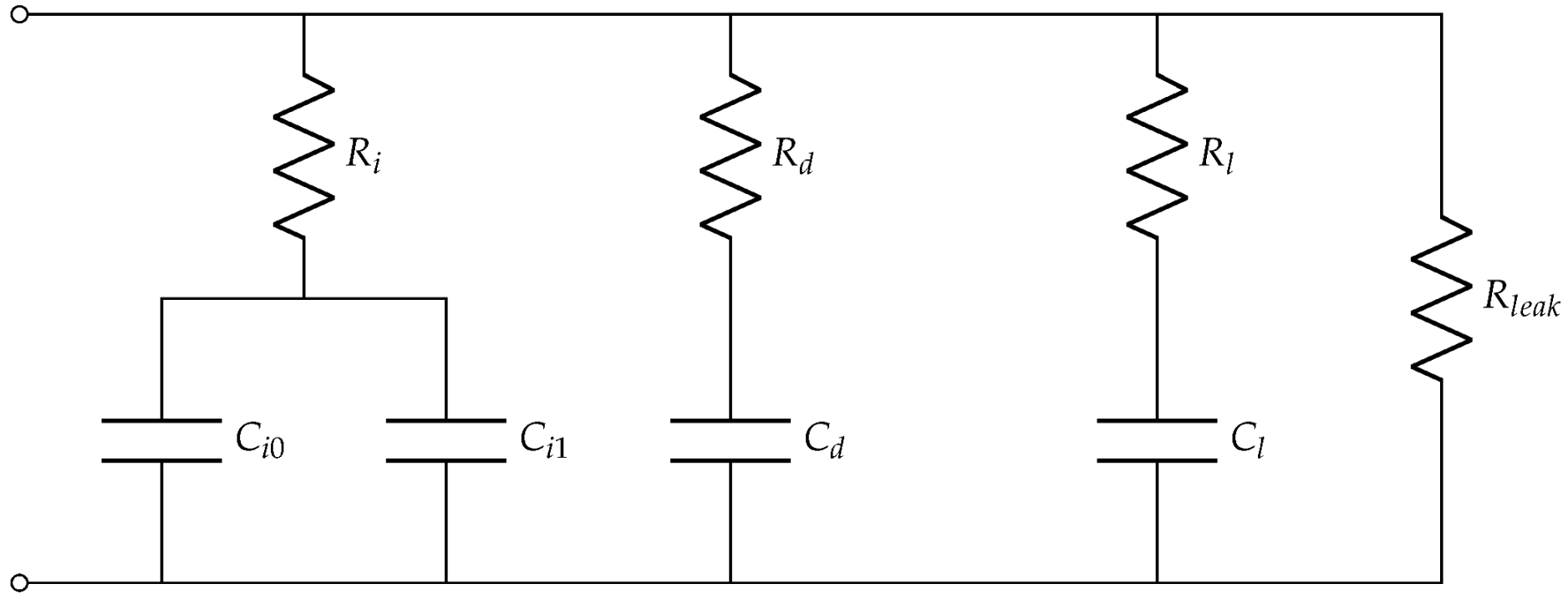 | Captures ionic diffusion effects. Complex parameterization on real systems. |
| TLM [54,61] |  | Ideal for physical modeling of electrolyte. Computationally intensive. Impractical for real-time simulations. |
| Order (n) | ||
|---|---|---|
| 1 | 3, 1 | 1, 3 |
| 2 | 5, 10, 1 | 1, 10, 5 |
| 3 | 7, 35, 21, 1 | 1, 21, 35, 7 |
| 4 | 9, 84, 126, 36, 1 | 1, 36, 126, 84, 9 |
| 5 | 11, 165, 452, 330, 55, 1 | 1, 55, 330, 462, 165, 11 |
| Order (n) | Resistors | Capacitors |
|---|---|---|
| 3 | , , , | , , |
| 4 | , , , , | , , , |
| 5 | , , , , , | , , , , |
| Zone | Frequency Range | Improvement over R-L-C Circuit |
|---|---|---|
| Capacitive | 0.01 Hz to 0.1 Hz | reduced by 27% reduced by 37.23% |
| Resistive | 0.1 Hz to 3 kHz | reduced by 4.5% reduced by 4.82% |
| Inductive | 3 kHz to 300 kHz | reduced by 16.1% reduced by 36.45% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rus-Casas, C.; Ramos-Paja, C.A.; Serna-Garcés, S.I.; Gilabert-Torres, C.; Aguilar-Peña, J.D. A Circuital Equivalent for Supercapacitors Accurate Simulation in Power Electronics Systems. Batteries 2025, 11, 307. https://doi.org/10.3390/batteries11080307
Rus-Casas C, Ramos-Paja CA, Serna-Garcés SI, Gilabert-Torres C, Aguilar-Peña JD. A Circuital Equivalent for Supercapacitors Accurate Simulation in Power Electronics Systems. Batteries. 2025; 11(8):307. https://doi.org/10.3390/batteries11080307
Chicago/Turabian StyleRus-Casas, Catalina, Carlos Andrés Ramos-Paja, Sergio Ignacio Serna-Garcés, Carlos Gilabert-Torres, and Juan Domingo Aguilar-Peña. 2025. "A Circuital Equivalent for Supercapacitors Accurate Simulation in Power Electronics Systems" Batteries 11, no. 8: 307. https://doi.org/10.3390/batteries11080307
APA StyleRus-Casas, C., Ramos-Paja, C. A., Serna-Garcés, S. I., Gilabert-Torres, C., & Aguilar-Peña, J. D. (2025). A Circuital Equivalent for Supercapacitors Accurate Simulation in Power Electronics Systems. Batteries, 11(8), 307. https://doi.org/10.3390/batteries11080307









