1. Introduction
Sodium-ion batteries (SIBs), as an emerging energy storage technology, have gained considerable attention due to their advantages, such as low cost, environmental friendliness, and abundance of raw materials. These characteristics make them highly suitable for various application scenarios including stationary energy storage, electric vehicles, low-speed electric vehicles, and renewable energy systems [
1]. With ongoing technological advancements and cost reductions, SIBs are expected to achieve even broader adoption in the near future [
2].
State of charge (SOC) is a critical indicator for battery energy management and operational control. Accurate SOC estimation not only helps prevent overcharging or over-discharging of the battery but also extends the battery’s lifespan and ensures the safe operation of the battery system [
3,
4,
5]. As a core function of the battery management system (BMS), SOC estimation is inherently challenging due to its sensitivity to factors such as aging, temperature, and operational dynamics. Nevertheless, precise SOC estimation is crucial as it prevents unexpected system failures and ensures safety for both the battery and its users [
6]. Furthermore, by monitoring the rate of SOC change during charge and discharge cycles, users can intuitively evaluate the battery’s health status and remaining useful life [
7,
8,
9,
10].
Current research on SOC estimation methods can be broadly categorized into three groups: traditional estimation methods, model-based methods, and learning-based methods [
11].
Traditional approaches mainly include the ampere-hour integration method and the open-circuit voltage (OCV) method. The ampere-hour integration method, also known as Coulomb counting, estimates SOC by integrating the charge/discharge current over time [
12]. The OCV method predicts SOC based on the known relationship between the battery’s OCV and its SOC [
13]. However, the ampere-hour integration method is an open-loop technique and is highly sensitive to initial SOC errors and current measurement noise. Meanwhile, the OCV method requires long rest periods to obtain accurate readings, which is impractical for real-time applications [
14].
Model-based estimation methods are primarily represented by the Kalman filter family. These algorithms have demonstrated significant advantages in battery SOC prediction due to their ability to fuse model dynamics with real-time measurements through recursive estimation [
15]. The extended Kalman filter (EKF), for example, estimates SOC by minimizing the covariance between measured and predicted values using a battery model. However, as battery systems are inherently nonlinear, the linearization process in the EKF often leads to estimation accuracy loss [
16]. The unscented Kalman filter (UKF) addresses this limitation by using the nonlinear transformation of sigma points, thereby improving estimation accuracy without requiring linearization. Essentially, these methods construct an equivalent circuit model (ECM) to translate battery dynamics into a mathematically tractable form, providing physically interpretable estimations—an important distinction from purely data-driven methods. For instance, Machin A et al. [
17] propose a UKF–based SOC estimation method with favorable performance in terms of computational efficiency and estimation accuracy. Takyi-Aninakwa P et al. [
18] introduce a Kalman-filter-based ECM tailored for electric vehicle applications, though lacking experimental validation. Zhang Y et al. [
19] introduce an adaptive singular value decomposition-based UKF that integrates all unknown variables while maintaining a vector-form covariance matrix for enhanced fusion estimation.
Learning-based methods, also referred to as data-driven methods, leverage machine learning algorithms for SOC estimation. These methods are known for their strong nonlinear fitting capabilities and high estimation accuracy, though they often require large amounts of high-quality offline training data. Their performance is significantly influenced by dataset quality and the training strategy. Typical implementations involve constructing nonlinear mappings between input features and SOC using neural networks, with approaches such as end-to-end estimation, hybrid frameworks, and feature enhancement techniques. For example, Prasanthi A et al. [
7] present a bidirectional long short-term memory-based hybrid prediction method, achieving high estimation accuracy but facing increasing computational demands with larger data volumes. Wang J et al. [
20] propose an LSTM–based method that reduces SOC estimation errors under aging conditions, although its feedback mechanism depends heavily on accurate voltage prediction and is sensitive to noise, requiring frequent parameter updates. Despite their strong nonlinearity handling, these methods often suffer from issues such as high data dependency, poor online adaptability, and limited interpretability. To address these challenges, some studies have integrated learning-based methods with Kalman filtering. Xu H et al. [
21] propose a hybrid method combining genetic algorithms, LSTM, and improved adaptive Kalman filtering, showing robust performance but requiring retraining over time. Zhang Z et al. [
22] introduce an EKF combined with particle swarm optimization and LSTM for accurate SOC estimation in power batteries, effectively mitigating estimation errors under noisy conditions. Xie Y et al. [
23] compare filter-based and deep learning-based SOC estimation methods, including recursive least squares (RLS), EKF, and gated RNNs, showing improved accuracy and reduced computational time, although there is a lack of neural network structure optimization. Chen J et al. [
24] introduce an enhanced method using a multi-layer LSTM and suboptimal fading EKF capable of fast convergence and strong tracking ability for dynamic data, demonstrating high estimation accuracy and robustness.
In recent years, data-driven methods have emerged as some of the most promising solutions for SOC estimation, aiming to overcome the limitations of traditional and model-based approaches. Neural networks, with their strong adaptability, self-learning capability, and powerful modeling performance, have been widely used to estimate the SOC of SIBs [
25]. These model-free approaches depend heavily on the quality and quantity of input data, as well as on proper training and hyperparameter selection. In such methods, the battery is treated as a “black box” rather than a physical model, reducing computational complexity and the number of required variables. They directly model complex nonlinear relationships, such as electrochemical reactions, aging effects, and self-discharge, using extracted features without prior knowledge of the system [
26]. These methods aim to estimate SOC by learning from nonlinear battery data, considering factors such as ohmic resistance, polarization effects, and self-discharge, thus achieving high accuracy. This is in contrast to model-based approaches, which require these factors to be explicitly incorporated into the observer design [
27].
In SOC estimation, single-method strategies face notable technical bottlenecks. Data-driven methods based on LSTM, for example, require high-quality, labeled datasets that cover a wide range of operating conditions, which are costly to acquire and offer limited generalization to unseen scenarios. Model-based methods such as the UKF depend on the accuracy of ECMs, where the complexity of parameter identification increases exponentially with model order—typically beyond third-order models—and where multi-state estimation under time-varying conditions imposes significant computational burdens on embedded systems. These challenges highlight the difficulty of achieving a balance between robustness, adaptability, and real-time performance using a single approach.
Motivated by these limitations, a hybrid LSTM-UKF method is proposed in this study. The method combines the long-term temporal modeling capabilities of LSTM with the accurate state estimation features of the UKF in nonlinear systems, aiming to leverage observational battery data for improved SOC estimation. By integrating LSTM and UKF with a forgetting-factor recursive least squares (FFRLS) algorithm for the online identification of RC model parameters, the proposed approach effectively overcomes the drawbacks of standalone methods and enhances estimation stability and accuracy. Experimental results show that the fused model reduces prediction error by 2% compared to single-method approaches. Furthermore, the effects of training and testing under different operating conditions on the accuracy of the LSTM-UKF framework are also investigated.
The remainder of this paper is structured as follows:
Section 2 introduces the battery model, LSTM network, and UKF algorithm;
Section 3 presents the algorithm design;
Section 4 discusses the performance of the proposed LSTM-UKF method under various operating conditions; and
Section 5 provides the conclusions.
3. Algorithm Design
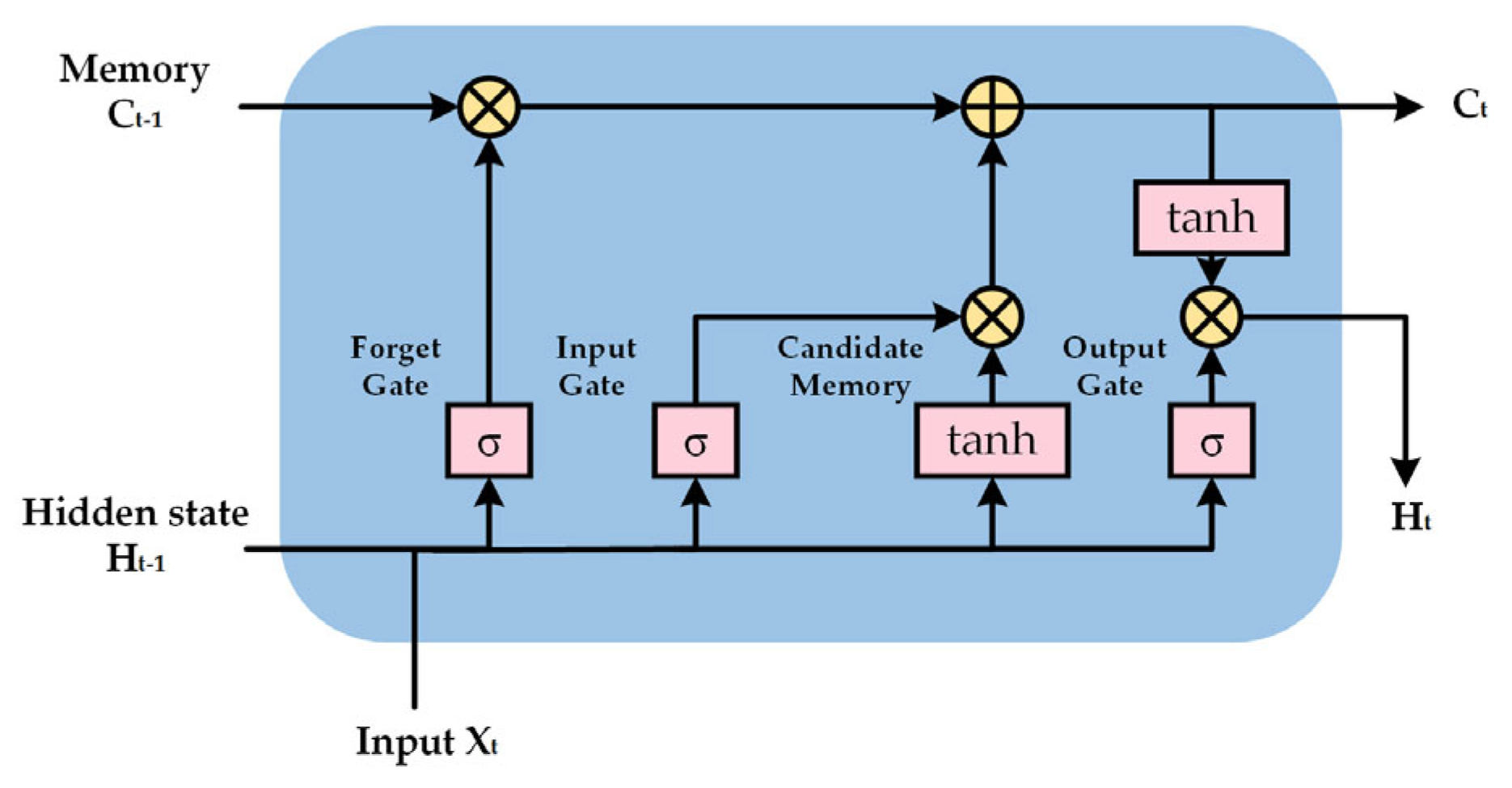
To enhance robustness and accuracy in nonlinear SOC estimation, a hybrid LSTM-UKF strategy was introduced. While UKF provides real-time error correction and physical interpretability, LSTM captures nonlinear time-dependent behaviors. Their outputs were dynamically fused using weights updated via FFRLS, forming an adaptive SOC estimation architecture.
3.1. Algorithm Procedure
By analyzing the current mainstream SOC estimation algorithms, a hybrid SOC estimation method is proposed that integrates LSTM and UKF. The aim of this fusion algorithm is to combine the theoretical advantages of physical modeling with the temporal learning capability of data-driven methods to achieve high-precision SOC prediction under dynamically complex operating conditions. The overall implementation process of the algorithm is illustrated in
Figure 3 and mainly consists of three parts: a parameter identification and UKF module, an LSTM module, and a fusion mechanism.
Firstly, the parameters of the second-order ECM were calculated using the FFRLS algorithm. Then, the identified parameters were employed to initialize the battery system state variables in the UKF module, including the state vector and covariance matrix. The state transition matrix was derived based on the constructed ECM of the battery. Subsequently, the state was predicted and updated using observation data; the Kalman gain was computed; and the current SOC of the battery was recursively estimated. This module effectively copes with noise interference and parameter uncertainties, demonstrating strong robustness.
The LSTM module extracts features from historical operational data, which are normalized and preprocessed before constructing the LSTM prediction model. This module deeply mines the nonlinear dynamic characteristics of the battery during different charge/discharge phases, thereby enhancing prediction accuracy.
During the fusion stage, to ensure the accuracy of the output results, the outputs of the UKF and LSTM were combined with different weighting ratios.
Although the LSTM-UKF fusion structure is generally applicable across battery chemistries, all components in this study were implemented specifically for SIBs. The equivalent circuit model parameters were identified using SIB–specific dynamic current-voltage data, and the OCV curve was fitted using experimental SIB OCV-SOC measurements. The FFRLS algorithm was also initialized using parameters tuned to the polarization behavior and time constants of SIBs. As such, no assumptions, model structures, or data from lithium-ion batteries were reused. This ensures that the modeling framework is intrinsically tailored to SIB characteristics.
3.2. Parameter Identification
In this study, a battery parameter identification model was established, aimed at achieving accurate SOC estimation. During the filtering process of parameter identification, an accurate battery model is essential. The internal SOC of the battery is closely related to external voltage, load current, temperature, and other relevant variables. The accuracy of the model directly affects the estimation precision of the Kalman filter and thus determines the reliability of the results. Among various models, the ECM is widely adopted due to its convenience for parameter identification and its minimal interference with battery characteristics.
In system analysis, system identification refers to the process of selecting a model equivalent to the measured system from a predefined model class by collecting the system’s input and output data. Simply put, system identification involves using optimization algorithms to iteratively adjust model parameters by minimizing the error between the model output and actual output until the optimal model is obtained. In the parameter identification domain, the least squares method serves as a fundamental estimation technique applicable to both static and dynamic systems, as well as linear and nonlinear systems. It is favored for its simplicity and ease of implementation. The core concept of least squares identification is to compute the optimal solution within a given model structure framework to minimize the sum of squared errors.
3.2.1. RLS
The RLS algorithm belongs to the category of adaptive filtering algorithms, primarily used for the online estimation of parameters in dynamic systems. This algorithm obtains the optimal weight vector by minimizing the sum of squared errors and possesses the capability of recursively updating the estimates without the need to store historical data. Widely applied in system parameter identification, the RLS algorithm is typically derived based on the discrete-time least squares criterion to achieve parameter estimation. Its core principle can be expressed as
, where
represents the observation data matrix and
denotes the parameter vector as shown in Equation (17):
The parameter identification of the RLS algorithm is expressed as Equation (18):
where
is the covariance matrix;
is the gain matrix;
is the error;
y is the output variable; and
I is the identity matrix.
3.2.2. FFRLS
The Forgetting Factor FFRLS algorithm is based on the RLS algorithm, incorporating a forgetting factor λ as a weight in the observation data matrix and system output vector. When new observation data arrive, the algorithm adjusts the weighting ratio of old and new data through exponential weighting, performing a weighted average to update the identified parameters. Thus, as the input variables change and observation data accumulate, the FFRLS algorithm can respond more quickly and obtain more optimal identification parameters.
When λ equals 1, the FFRLS algorithm degenerates to the traditional RLS algorithm. Since λ is a constant, if the parameter error is small during online identification, introducing λ may increase the parameter estimation error. However, when the parameter error is large, an appropriate choice of λ can optimize the algorithm by accelerating the convergence speed of the online identification process, thereby reducing the error. Therefore, selecting a suitable λ not only improves convergence speed but also effectively reduces the error.
To perform parameter identification of the established second-order RC ECM of the battery, the battery model needs to be transformed into a mathematical form applicable for least squares methods. Based on the ECM shown in
Figure 1, the following can be derived:
Let
and
. By discretizing Equation (19) and introducing parameters
,
,
,
, and
, the following expression can be obtained:
Equation (19) can thus be rewritten as follows:
The above equation can be directly applied to the RLS identification method with a forgetting factor, where is used as the parameter vector for direct identification. The battery model parameters can then be derived from the identification results of these parameters.
In the FFRLS algorithm, the choice of the forgetting factor λ is crucial. To achieve optimal identification performance, λ is usually determined experimentally. During experiments, different values of λ can be tested to observe their effects on the identification results. By comparing the identification errors and convergence speeds under various λ values, the most suitable λ for the current system can be selected. Once the optimal λ is determined, it can be applied in the FFRLS algorithm to precisely identify the battery model.
During the identification process, new observational data are continuously fed into the algorithm, and the weighting of data is adjusted according to the forgetting factor λ. As data accumulate, the algorithm gradually converges to the final identified parameters.
These identified parameters can be used to describe the internal characteristics and dynamic behavior of the battery, providing essential support for battery management and control. The FFRLS–based identification of the battery model allows for a more accurate prediction of the battery’s remaining capacity and lifespan, thereby improving battery utilization efficiency and safety.
4. Experimental Analysis
4.1. Platform Setup
In this study, voltage and current data of the battery under actual operating conditions were collected using a self-developed experimental platform. This setup aims to simulate the real working state of the battery and provide a solid foundation for validating the superiority of the proposed estimation method. During the fusion stage, to ensure the stability of the predictions, a weighted fusion of the outputs from UKF and LSTM with equal weights was initially applied. In the final one-eighth segment of the prediction horizon, due to increasing deviation of the LSTM module’s error, the fusion weights were adjusted to 0.8 for UKF and 0.2 for LSTM, making the prediction rely more on the stability and disturbance rejection capability of the UKF model. The self-developed experimental platform is shown in
Figure 4.
To prevent look-ahead bias and ensure reliable time-series learning, all datasets were partitioned strictly in chronological order. For each battery cell, the first 70% of time-series data was used for training, and the remaining 30% for testing. This approach simulates realistic online estimation scenarios and ensures that the LSTM model does not gain access to future information during training. No overlap or mixing occurred between the training and testing periods.
Furthermore, to evaluate the generalization ability of the model across different battery samples, cross-cell validation was conducted. Specifically, the model was trained on the entire dataset from Cell 1 and tested on Cell 2, and vice versa. This procedure helps assess whether the model captures transferable temporal representations rather than overfitting to the characteristics of a specific cell. Within each cell, data partitioning remained strictly chronological, ensuring full temporal separation between training and testing sets.
Battery testing was conducted using a Neware BTS-5V12A testing system (Neware BTS-5V12A, manufactured by Neware Technology Limited, Shenzhen, China), with a voltage and current accuracy of 0.05%. Two batches of sodium-ion batteries were selected: six 18650E-1300 cells and several NaCR26700-ME30 cells. The 18650E-1300 sodium-ion batteries have a nominal capacity of 1.3 Ah and a nominal voltage of 3.1 V, while the NaCR26700-ME30 sodium-ion batteries have a nominal capacity of 3 Ah and a nominal voltage of 3 V. All experiments were carried out in a temperature-controlled chamber (Sanwood SMG-150-CC) at a constant temperature of 25 °C, with a temperature deviation of less than or equal to ±1 °C.
4.2. Comparison Under Different Operating Conditions
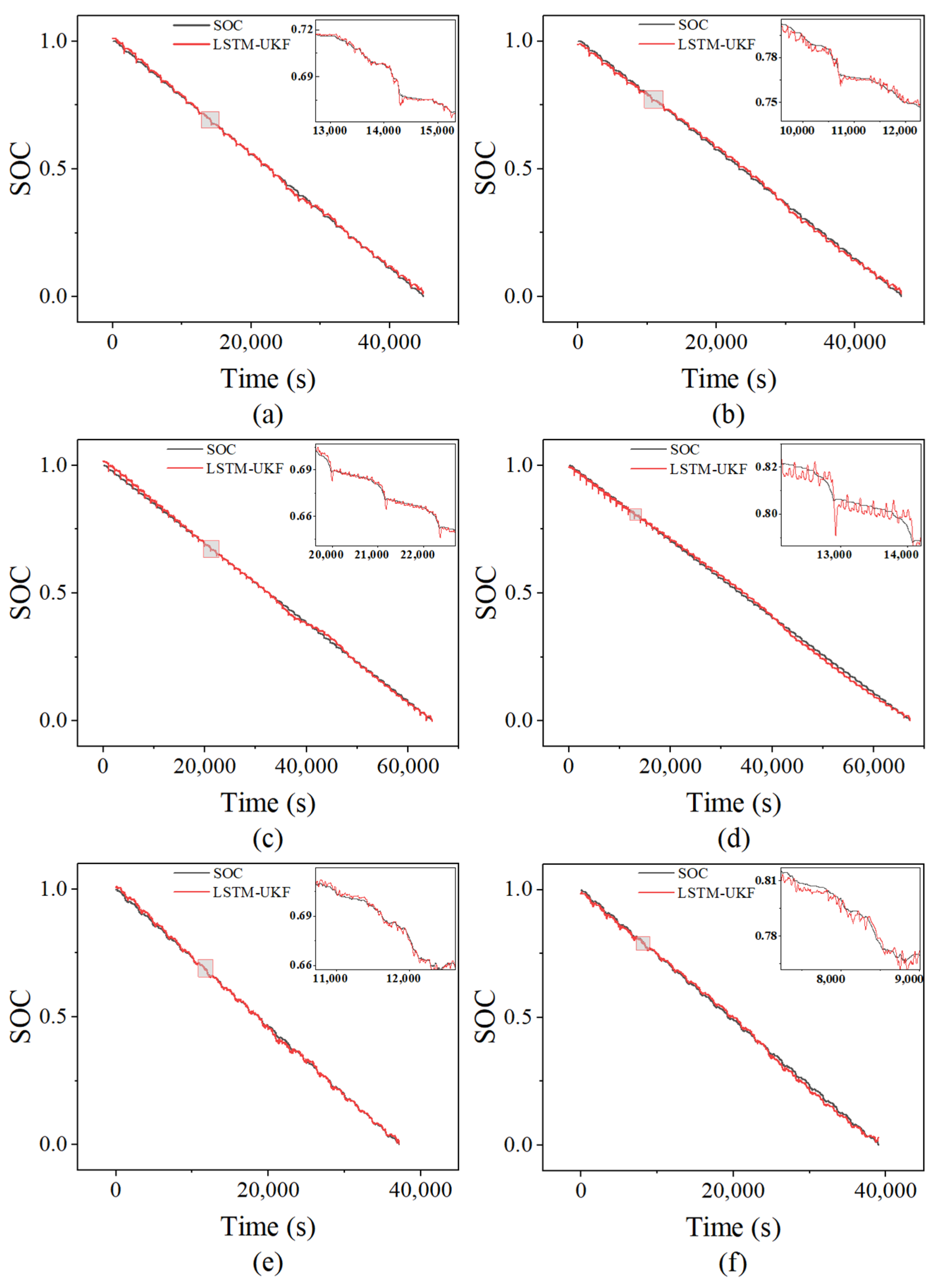
In practical operation, a single working condition cannot accurately reflect prediction accuracy. Therefore, datasets collected under different operating conditions but within the same ambient temperature were used as training data for the model, enabling the training data to better represent the performance of the proposed method.
As shown in
Figure 5, the LSTM-UKF fusion model demonstrates excellent SOC prediction performance under various operating conditions. Its core advantage lies in the ability to jointly model dynamic disturbances, nonlinear characteristics, and noisy environments. Notably, under scenarios with significant condition variations, the LSTM-UKF fusion model can quickly adapt its prediction strategy and maintain high prediction accuracy, whereas single models tend to exhibit prediction deviations and fail to capture the real-time variation of battery SOC accurately. These results validate the superior performance of the LSTM-UKF fusion model in handling complex operating conditions, offering a novel approach and methodology for the accurate SOC estimation of SIBs.
4.3. Comparison Under Different Methods
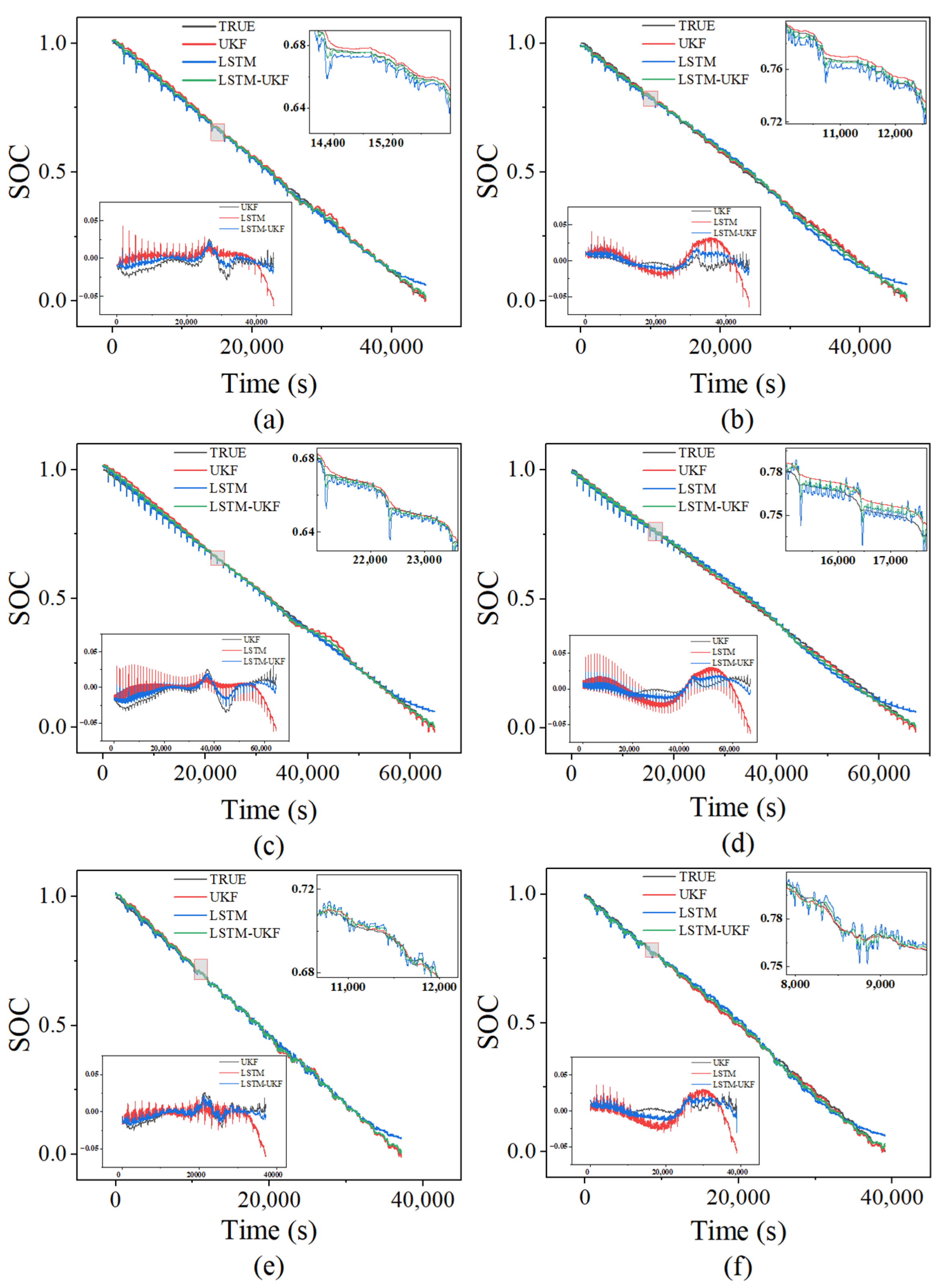
To evaluate the effectiveness of the proposed LSTM-UKF fusion model compared to conventional approaches, we conducted a comprehensive comparison using three baseline methods: standalone UKF, standalone LSTM, and the proposed LSTM-UKF fusion. All methods were tested under identical experimental conditions across CLTC, NEDC, and WLTC driving cycles.
The standalone UKF model relies entirely on the equivalent circuit model and is effective in handling sensor noise through recursive estimation. However, it struggles with nonlinearities, parameter drift, and aging effects, particularly under dynamic driving conditions. Conversely, the LSTM model, being data-driven, captures nonlinear temporal dependencies effectively but lacks real-time correction and physical constraints, which may lead to accumulated prediction errors over long horizons.
The proposed hybrid method integrates the temporal modeling capability of LSTM with the state correction ability of UKF. Fusion is guided by a confidence weighting mechanism dynamically adjusted using FFRLS, which allocates greater influence to the model with better short-term accuracy. This synergy results in improved estimation stability, especially under variable load conditions. To evaluate the effectiveness of these models, detailed experiments were conducted, and the results are illustrated in
Figure 6.
Table 1 and
Table 2 present the RMSE and nRMSE values for each method across the three driving conditions. While all methods perform within the 3% RMSE range, the hybrid method consistently shows lower nRMSE values. To further validate the significance of these improvements, Wilcoxon signed-rank tests were conducted between the fusion model and each baseline. The results (
p < 0.05) confirm that the performance enhancements are statistically significant.
As
Table 3 The Wilcoxon signed-rank test was applied to compare the proposed LSTM-UKF fusion model with standalone LSTM and UKF across six driving segments. The results show that the fusion model significantly outperforms the standalone LSTM in both MAE and RMSE metrics (
p = 0.03125). However, no statistically significant difference was observed compared to the UKF (
p = 0.84375), likely due to UKF’s strong baseline under certain conditions. These results validate the effectiveness of the hybrid model in reducing learning-related error accumulation, especially over LSTM.
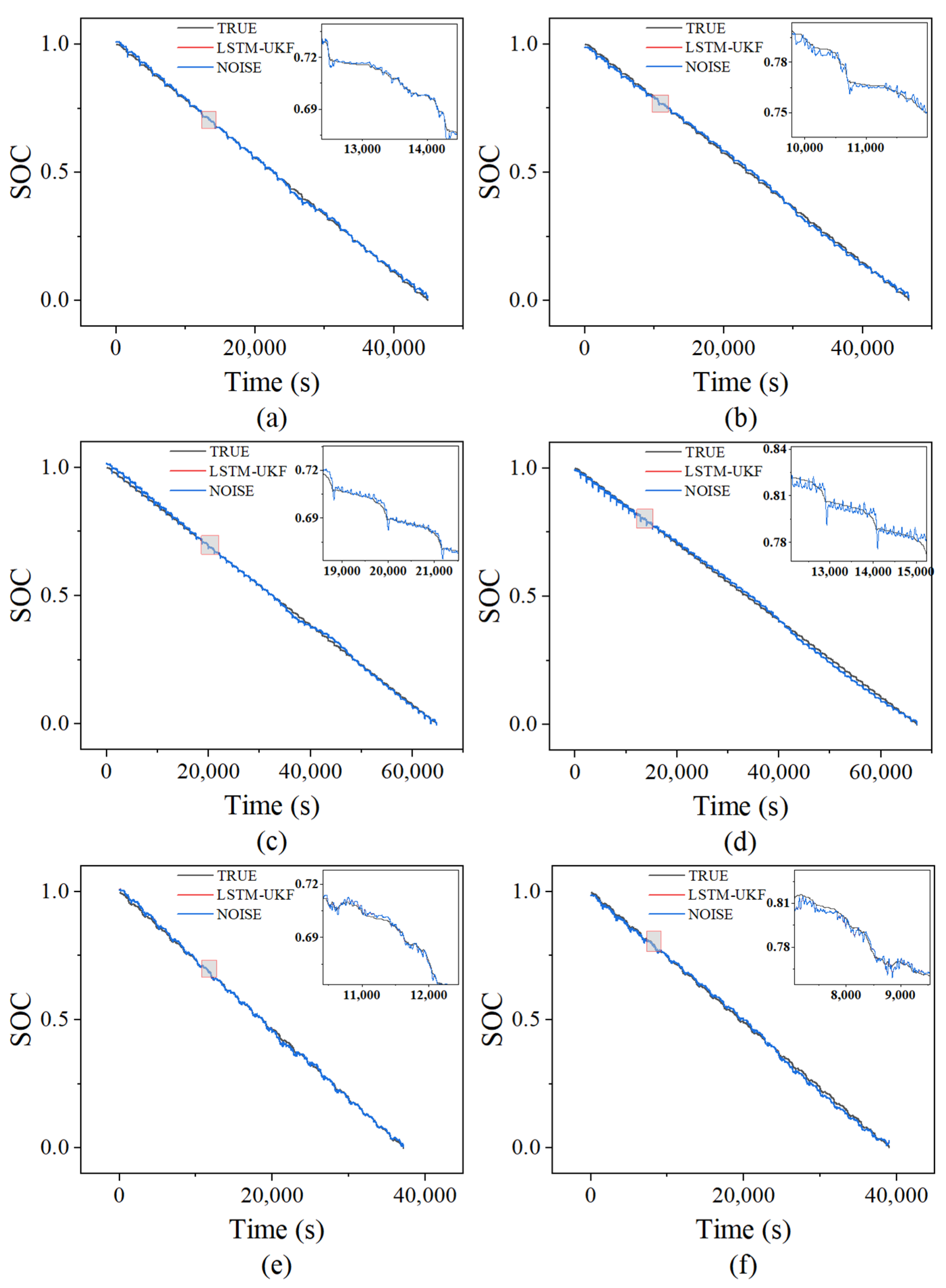
4.4. Comparison Under Noise Disturbance
To evaluate the robustness and stability of the proposed LSTM-UKF fusion algorithm under complex environments, Gaussian white noise was artificially introduced in the experiments to simulate common non-ideal factors, such as sensor inaccuracies, environmental disturbances, and model uncertainties. Specifically, voltage noise with a standard deviation of σ = 10 mV and current noise with σ = 50 mA were added to the measurement signals. Multiple interference levels with signal-to-noise ratios (SNRs) of 20 dB, 30 dB, and 40 dB were set to cover the disturbance range commonly encountered in industrial scenarios.
As shown in
Figure 7 and
Table 4, even under strong noise interference, the RMSE of the LSTM-UKF algorithm remained stably controlled within 1.04%, with only a slight increase compared to the noise-free condition, demonstrating significantly better performance than the standalone UKF or LSTM models. This result fully validates the engineering applicability and generalization capability of the algorithm in complex real-world environments.
Further analysis reveals that the robustness of the fusion algorithm mainly benefits from the complementary advantages of LSTM and UKF in prediction mechanisms: LSTM captures the system’s nonlinear dynamic characteristics by learning from historical data, possessing strong short-term memory capability; meanwhile, the UKF utilizes state-space modeling and Kalman gain to dynamically correct observation errors, effectively suppressing random disturbances caused by sensor noise. Especially when noise intensity increases, the filtering advantage of the UKF is fully leveraged to provide real-time correction of biases in LSTM outputs. Simultaneously, the memory units of LSTM help alleviate the UKF’s sensitivity to model mismatch to some extent. The synergistic interaction of these two modules within a unified framework achieves effective noise suppression and error propagation control.
In summary, the proposed LSTM-UKF fusion architecture not only provides high-precision SOC estimation under ideal conditions but also maintains stable and reliable performance in harsh environments, demonstrating strong anti-interference capability and practical deployment potential.